引 言
精确模拟高超声速流动问题需要高分辨率以及鲁棒性好的激波捕捉格式.在过去几十年,基于Riemann解法器的Godunov型数值方法在计算流体力学中取得了巨大的成功.在大多数情形下它们都有很好的鲁棒性.然而,在数值模拟多维强激波问题时,一些低耗散的数值格式,例如Roe[1]和HLLC[2],会遭遇激波不稳定现象,包括carbuncle、奇偶失联和双Mach杆等现象,这会严重影响数值格式在高超声速流动问题中的应用.探究和消除低耗散数值格式的激波不稳定现象吸引了众多研究人员的关注.
Quirk[3]首先开始对数值格式的激波不稳定现象进行系统研究,通过数值实验,他得到了一个经验性的结论:能够精确捕捉接触间断的数值格式都会遭受激波不稳定现象的困扰.Gressier和Moschetta[4]利用特殊的线性稳定性分析证实了这一结论.但是在文献[5-6]中,研究人员构造的数值格式既能准确分辨孤立静止的接触波还能抑制不稳定现象的出现,从而间接地反驳了Quirk的观点.Liou[7]认为质量通量中含有压力耗散项是诱发carbuncle现象的根源.但是存在一些反例来质疑Liou的论断,例如AUSM+格式[8].在研究Godunov型数值格式的耗散机制时,Xu和Li[9]指出,只有当激波面和网格线平行时才会发生激波不稳定现象,并且横向通量剪切黏性不足是诱发不稳定现象的根源.通过分析驻激波数值激波面的结构,他们认为激波不稳定现象是由激波层亚声速区的数值扰动所造成的.Dumbser等[10]设计了一种矩阵稳定性分析方法来研究Godunov型数值格式的激波稳定性.通过分析他们发现:二维定常激波的不稳定性与Mach数和数值激波结构密切相关,并且与文献[9]相反的是,他们认为激波不稳定现象源于数值激波层的超声速区而不是亚声速区.我们对于数值结果的观察以及文献[11]的结论都证明了不稳定性源于数值激波层的亚声速区.通过分析和数值实验,Shen等[5]发现剪切耗散不足是造成不稳定现象的唯一原因.Xie等[12]认为正激波波前和波后质量通量的不一致诱发了格式的不稳定性,并且增加格式的剪切黏性可以消除不稳定现象.Simon等[13]认为质量方程和界面法向动量方程中的反扩散项诱发了数值格式的不稳定性.通过分析和数值实验,我们发现在某些情形下单纯增加剪切黏性不能完全消除激波异常现象,横向通量缺乏足够的熵波黏性和剪切波黏性是导致激波失稳的根本原因.
消除数值格式激波不稳定现象的方法主要分成三类:将低耗散格式和耗散格式进行混合,构造多维迎风格式以及控制格式的耗散机制.Quirk[3]利用压力梯度函数来探测激波附近的网格界面,并且使用耗散格式HLLE来计算该界面的数值通量,进而消除Roe格式的不稳定现象.Wu等[14]将Roe格式和HLL格式的质量通量和切向动量通量进行加权来构造一种稳定的Roe-HLL混合格式.Ren[15]和Nishikawa等[16]通过构造旋转Roe Riemann解法器来实现格式的多维迎风性进而消除Roe格式的不稳定现象.Peery等[17]构造了一个各向同性函数来对Roe格式进行熵修正,其本质是通过增加线性波的波速来增加格式的耗散,从而消除Roe格式的carbuncle现象.Fleischmann等[18]通过减少非线性波中声波的速度来减少耗散矩阵的刚性,进而消除Roe格式的不稳定现象.Kim等[19]通过引入两个用Mach数定义的函数来平衡扰动的增长和衰减速度,进而得到一种激波稳定的Roe格式.通过比较不稳定的Roe格式和稳定的HLL格式,Chen等[11]发现亚声速区剪切波波速的差异,解释了两者不同的激波行为,并且在激波附近的亚声速区增加Roe格式的剪切黏性来抑制不稳定性.Rodionov[20]用人工黏性代替物理黏性来消除Roe格式的carbuncle现象,并且将该方法推广到了三维情形和高阶精度格式[21-22].
尽管研究人员进行了大量的研究,但是关于数值格式激波不稳定现象的根源仍然存在争议,因此一些改进方法都存在一定的局限性.本文以低耗散的Roe格式为例,利用小扰动分析来探究激波不稳定现象的根源,进而提出一种改进的Roe格式来消除原始Roe格式的不稳定现象.全文结构如下:第一节简单介绍一些预备知识;第二节对Roe格式进行小扰动分析,进而揭示不稳定现象产生的原因;第三节构造一种鲁棒的Roe格式;第四节展示数值测试的结果和分析;第五节是全文的结论.
1 预 备 知 识
1.1 控制方程组
考虑二维无黏可压缩Euler方程组:
(1)
式中
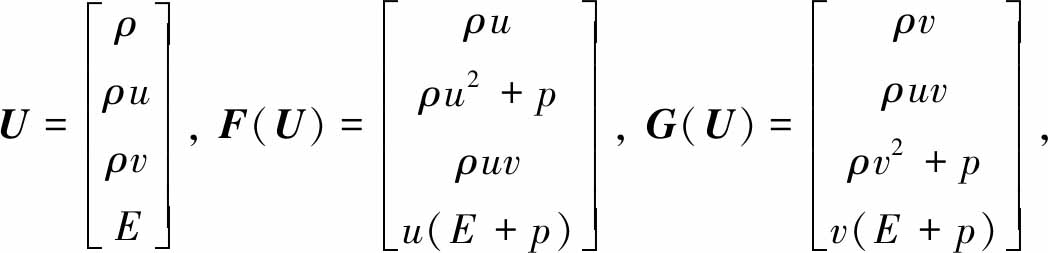
(2)
ρ为密度,u,v分别为x方向和y方向的流体速度,p为压力,E为总能.使用理想气体状态方程来使方程组(1)封闭:
p=(γ-1)[E-0.5ρ(u2+v2)],
(3)
式中,比热比γ=1.4.
使用结构化的四边形网格来离散计算区域并且利用有限体积方法进行空间离散,进而得到半离散方程:
(4)
式中,![]() 为守恒量U的网格平均值,|Ωi,j|为控制体Ωi,j的面积,nk和Δsk分别为第k条边的单位外法向量和长度,(F,G)k·nk为第k条边中点处的数值通量,利用Euler方程的旋转不变性可将其改写成
为守恒量U的网格平均值,|Ωi,j|为控制体Ωi,j的面积,nk和Δsk分别为第k条边的单位外法向量和长度,(F,G)k·nk为第k条边中点处的数值通量,利用Euler方程的旋转不变性可将其改写成
(5)
式中,Tk和![]() 为旋转矩阵.
为旋转矩阵.
1.2 Roe格式
网格界面(i+1/2,j)处,Roe格式[1]数值通量的表达式为
(6)
式中
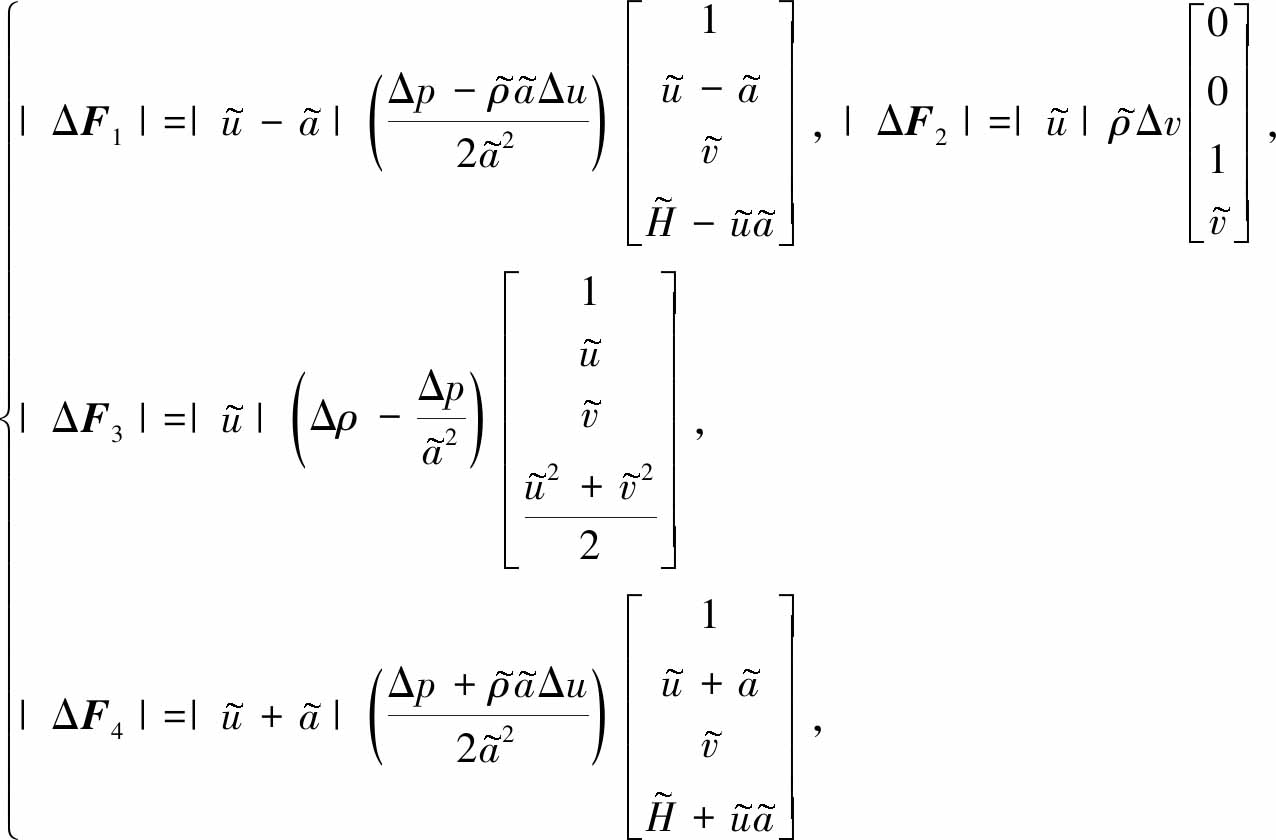
(7)
![]() 表示当地声速,H=(E+p)/ρ表示总焓,
表示当地声速,H=(E+p)/ρ表示总焓,![]() 表示物理量q的Roe平均值,Δ(·)=(·)R-(·)L.
表示物理量q的Roe平均值,Δ(·)=(·)R-(·)L.
2 Roe格式激波不稳定现象的机理分析
低耗散的Roe格式在计算中可以精确捕捉接触间断和剪切波,但是和其他低耗散格式(例如HLLC)一样,在计算多维强激波问题时,会出现激波不稳定现象.这一节我们将利用小扰动分析来探究Roe格式不稳定现象产生的根源.
2.1 小扰动分析
利用文献[4]中的小扰动分析方法来对Roe格式的不稳定性进行机理分析.与文献[4]不同的是,本文不仅研究了横向扰动的发展趋势,还对纵向扰动的发展趋势进行了详细的分析,从而确定造成激波失稳的扰动来源.初始时,流体介质以速度u0=Ma0a0沿着x正向(纵向)运动,沿y方向(横向)速度v0=0,其中Ma0为Mach数.
首先,在x方向(纵向)增加奇偶对称扰动,y方向无扰动.对于特定的网格(i,j)以及该方向上与其相邻的网格(i-1,j)和(i+1,j),扰动后的流场分布为
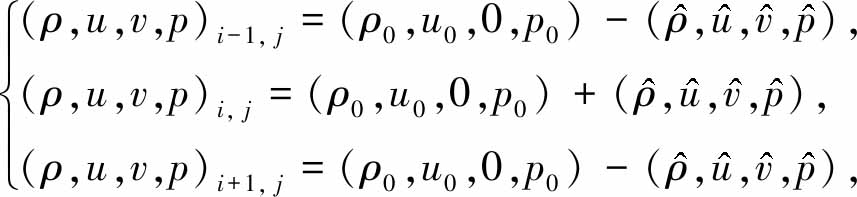
(8)
式中,![]() 为各个物理量的扰动量.使用Roe格式计算界面数值通量Fi-1/2,j和Fi+1/2,j,经过矩阵计算可以得到各个扰动量的发展方程.
为各个物理量的扰动量.使用Roe格式计算界面数值通量Fi-1/2,j和Fi+1/2,j,经过矩阵计算可以得到各个扰动量的发展方程.
亚声速(0<Ma0<1)情形下,扰动量发展方程为

(9)
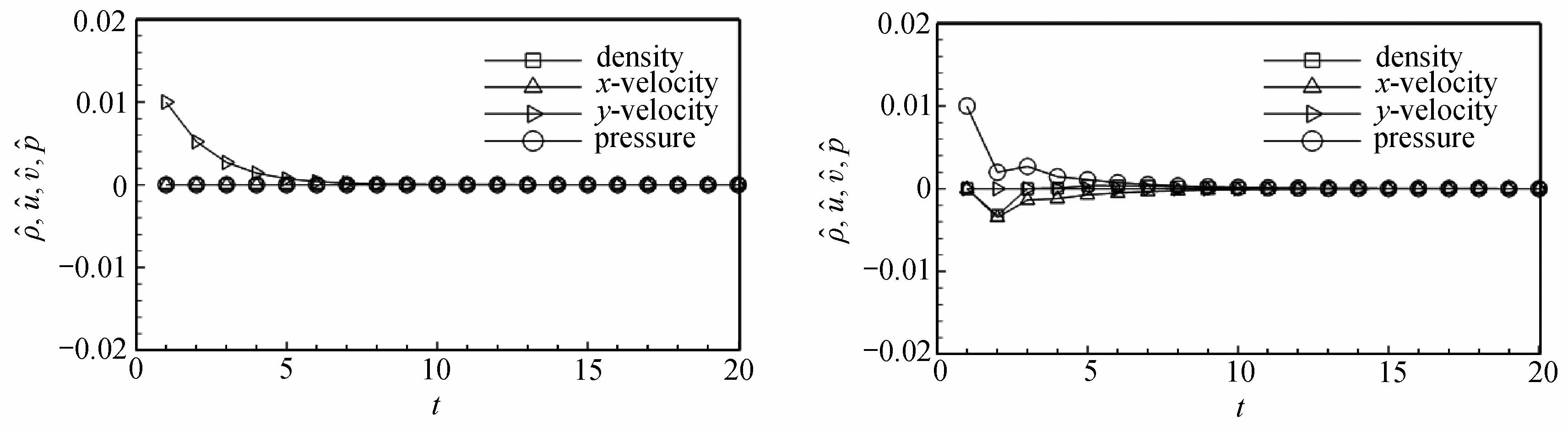
式中,σx=Δt/Δx为线性化的CFL数.为了清晰地看到各个扰动量的发展趋势,选取一组特定的初值ρ0=1.4,p0=1,Ma0=0.6,在4种不同的初始扰动下,迭代20步,各物理量的扰动发展趋势如图1所示.从图中可以清晰地看到,各个扰动量都会衰减到0.
![]()
图1 亚声速情形下纵向扰动的发展趋势
Fig.1 The evolution of longitudinal perturbations under subsonic condition
超声速(Ma0>1)情形下,扰动量发展方程为
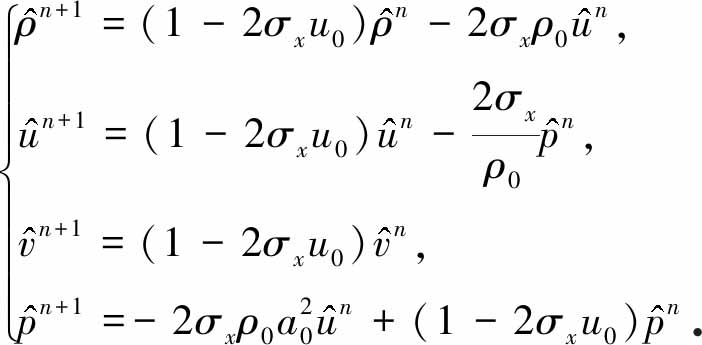
(10)
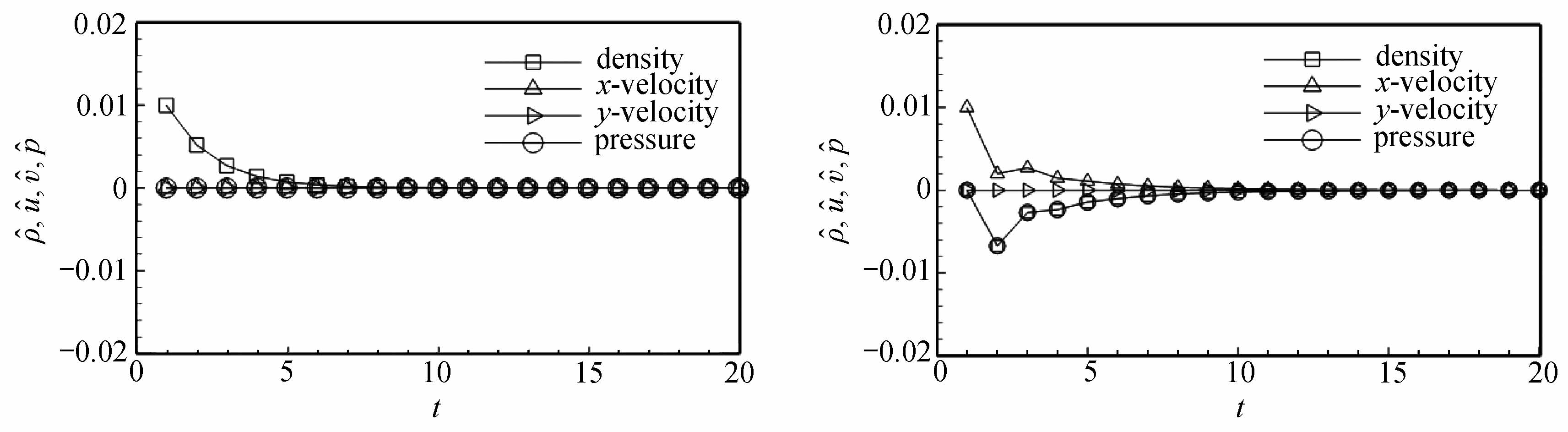
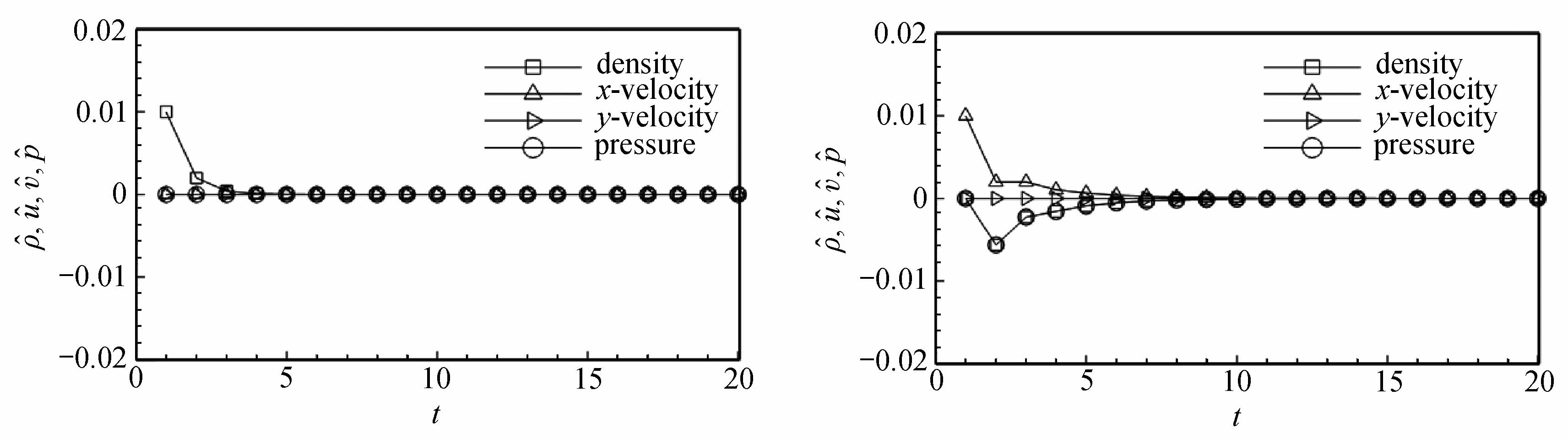
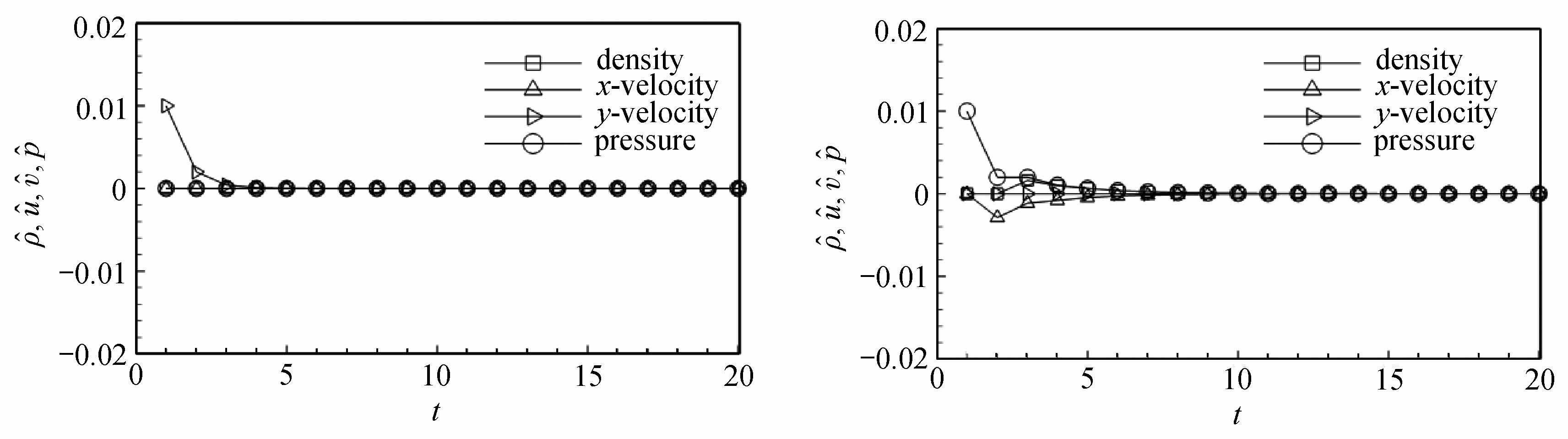
选取一组特定的初值ρ0=1.4,p0=1,Ma0=2.0,在4种不同的初始扰动下,经过时间迭代20步,各物理量的扰动发展趋势如图2所示.从图中可以清晰地看到,各个扰动量都会衰减到0.综上所述,在纵向存在扰动时,无论是亚声速还是超声速情形下,所有物理量的扰动都会衰减到0.因此,纵向扰动不会诱发激波不稳定现象.
![]()
![]()
![]()
图2 超声速情形下纵向扰动的发展趋势
Fig.2 The evolution of longitudinal perturbations under supersonic condition
接下来,在y方向(横向)增加奇偶对称扰动,x方向无扰动.对于特定的网格(i,j)以及该方向上与其相邻的网格(i,j-1)和(i,j+1),扰动后的流场分布为
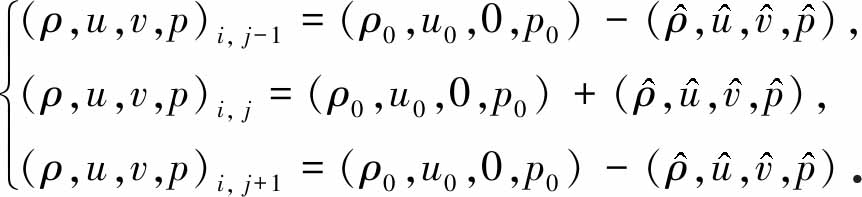
(11)
使用Roe格式计算界面数值通量Gi,j-1/2和Gi,j+1/2,进而得到各个扰动量的发展方程.由于横向速度v0=0,此时只有亚声速一种情形:
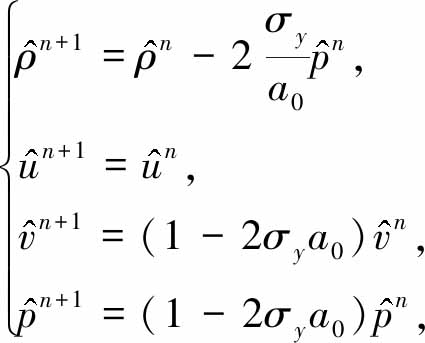
(12)
式中,σy=Δt/Δy.从式(12)可以看到,选取合适的时间步长,![]() 和
和![]() 都会衰减,但是密度扰动
都会衰减,但是密度扰动![]() 和剪切速度的扰动
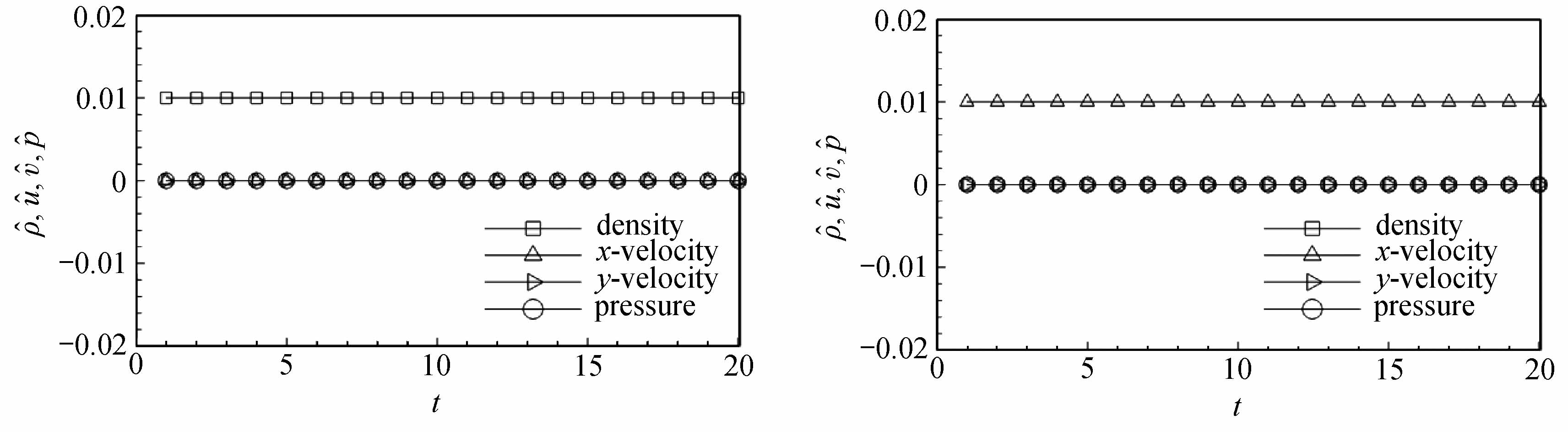
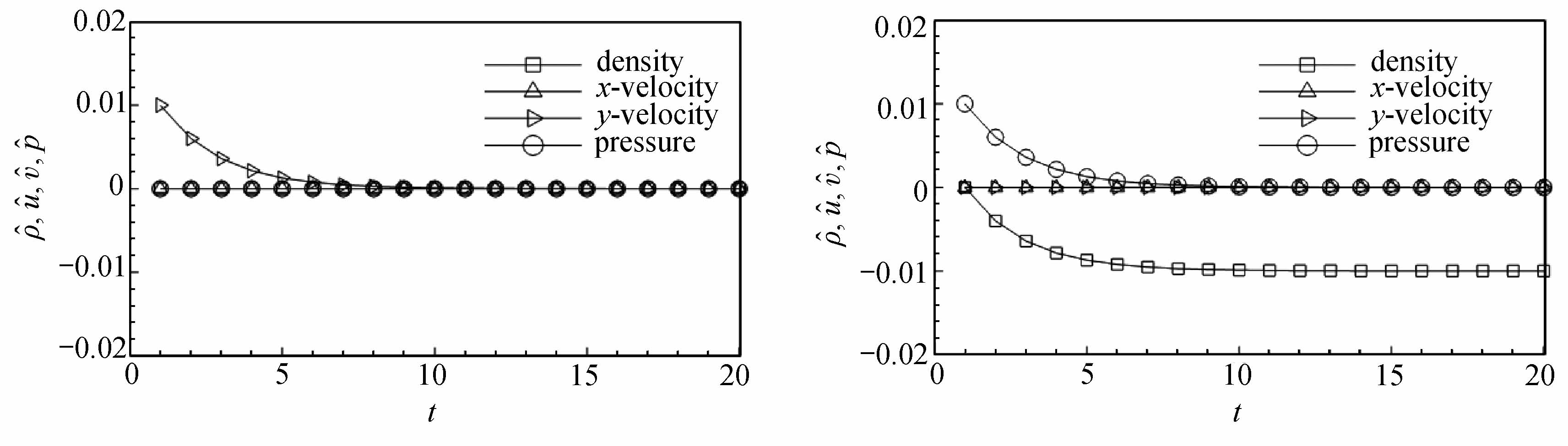
和剪切速度的扰动![]() 不会衰减.选取一组特定的初值ρ0=1.4,p0=1,在4种不同的初始扰动情形下,经过时间迭代20步,各个物理量的扰动发展趋势如图3所示.从图中可以清晰地看到,
不会衰减.选取一组特定的初值ρ0=1.4,p0=1,在4种不同的初始扰动情形下,经过时间迭代20步,各个物理量的扰动发展趋势如图3所示.从图中可以清晰地看到,![]() 和
和![]() 总是会衰减到0,但是密度自身的初始扰动或者压力的初始扰动会造成
总是会衰减到0,但是密度自身的初始扰动或者压力的初始扰动会造成![]() 不会衰减,而剪切速度自身的初始扰动
不会衰减,而剪切速度自身的初始扰动![]() 也不会衰减.
也不会衰减.
![]()
![]()
图3 横向扰动的发展趋势
Fig.3 The evolution of transverse perturbations
2.2 横向通量与激波不稳定现象的联系
小扰动分析的结果表明:当纵向存在扰动时,所有的扰动量都会衰减,而横向的密度扰动和剪切速度扰动不会衰减.我们推测:Roe格式横向通量中的密度和剪切速度的数值误差无法有效地衰减诱发了激波不稳定现象.接下来,计算文献[18]中的二维Sedov爆轰波问题来证明横向数值通量与激波不稳定现象之间的密切联系.
初始时,计算区域[0,2.4]×[0,2.4]中心高压区的压力pin=3.5×105,周围由pout=10-10的低压区所包围,整个区域ρ0=1,u0=v0=0.计算时采用480×480的直角网格,中心的高压区由4个象限相邻的4个网格所组成.4个边界均采用反射边界条件,CFL数取0.4.图4展示了时间t=0.1时的密度等值线.从中可以看到,当x方向和y方向的数值通量均采用不稳定的Roe格式计算时,在激波面和网格线平行的位置会出现4个对称的carbuncle,这是一种典型的激波不稳定现象.当x方向使用稳定的HLLE通量,y方向依然使用不稳定的Roe通量时,y方向的carbuncle消失了,但x方向的carbuncle依然存在,反之亦然.一个方向采用不稳定的Roe通量,会导致另外一个方向出现不稳定现象,这充分说明了横向数值通量与激波不稳定现象之间存在密切的关系.
(a) x-Roe+y-Roe (b) x-HLLE+y-Roe (c) x-Roe+y-HLLE
图4 二维Sedov爆轰波问题的密度等值线
Fig.4 Density contour lines of two-dimensional Sedov blast wave problem
3 一种激波稳定的Roe格式
研究人员[5,9,11-12]曾经指出,与线性波对应的数值黏性可以有效抑制激波不稳定性.对于二维Euler方程,这分别对应熵波黏性和剪切波黏性.借鉴文献[12]中纵向通量的熵波和剪切波黏性项表达式,可以得到横向通量的熵波和剪切波黏性项的表达式分别为
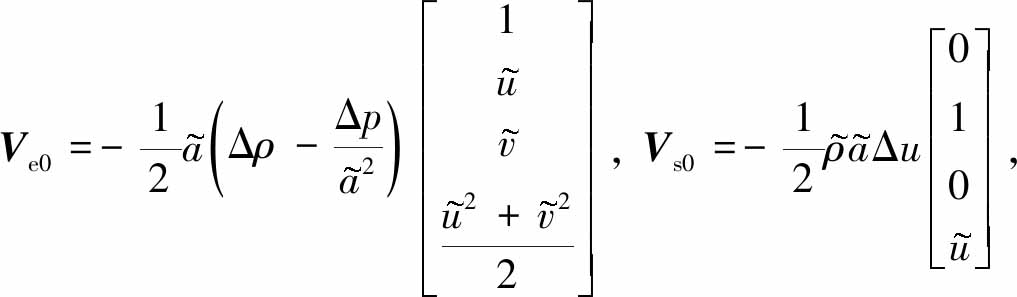
(13)
式中,Ve0代表横向通量的熵波黏性项,Vs0代表横向通量的剪切波黏性项.文献[11-12]通过添加剪切波黏性来分别消除Roe格式和HLLEM格式的不稳定性.由于剪切波黏性项的第一个分量为0,因此仅仅添加剪切黏性,横向的密度扰动依然不会衰减.后面我们将通过数值实验来证明仅仅增加剪切黏性并不能完全消除激波异常现象.如果在横向通量上既增加熵波黏性又增加剪切波黏性,此时横向扰动的发展方程为
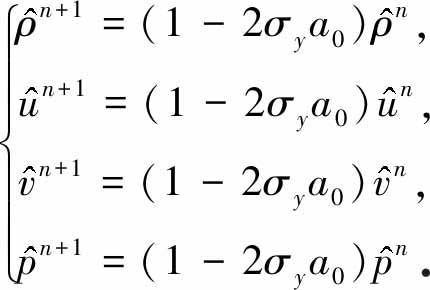
(14)
式(14)表明,在一定的时间步长限制下,所有扰动量都会衰减.
3.1 探测激波的开关函数
为了防止在不合适的位置增加黏性,进而影响接触间断和剪切层的分辨率,利用左右网格的压力比来探测激波的位置:
(15)
由于激波不稳定现象是由于横向数值通量的黏性不足所造成的,因此在计算x方向的数值通量Fi+1/2,j时,需要探测与之相邻的y方向的网格界面,反之亦然.即
(16)
随着激波强度的增加,不稳定现象的严重程度也会增加,从而需要更大的黏性来抑制不稳定现象.定义3种不同的开关函数来控制黏性的大小:
(17)
在接触间断和剪切层,由于压力是连续的,所以h=1,g1=g2=g3=0. 在激波附近,由于压力的间断,从而0<h<1,0<g1<g2<g3<1.并且随着激波强度的增加,h会更接近于0,从而g1,g2,g3会更接近于1.图5展示了g1,g2,g3随着h变化的示意图.后面通过数值实验来讨论不同的开关函数对于格式稳定性的影响.
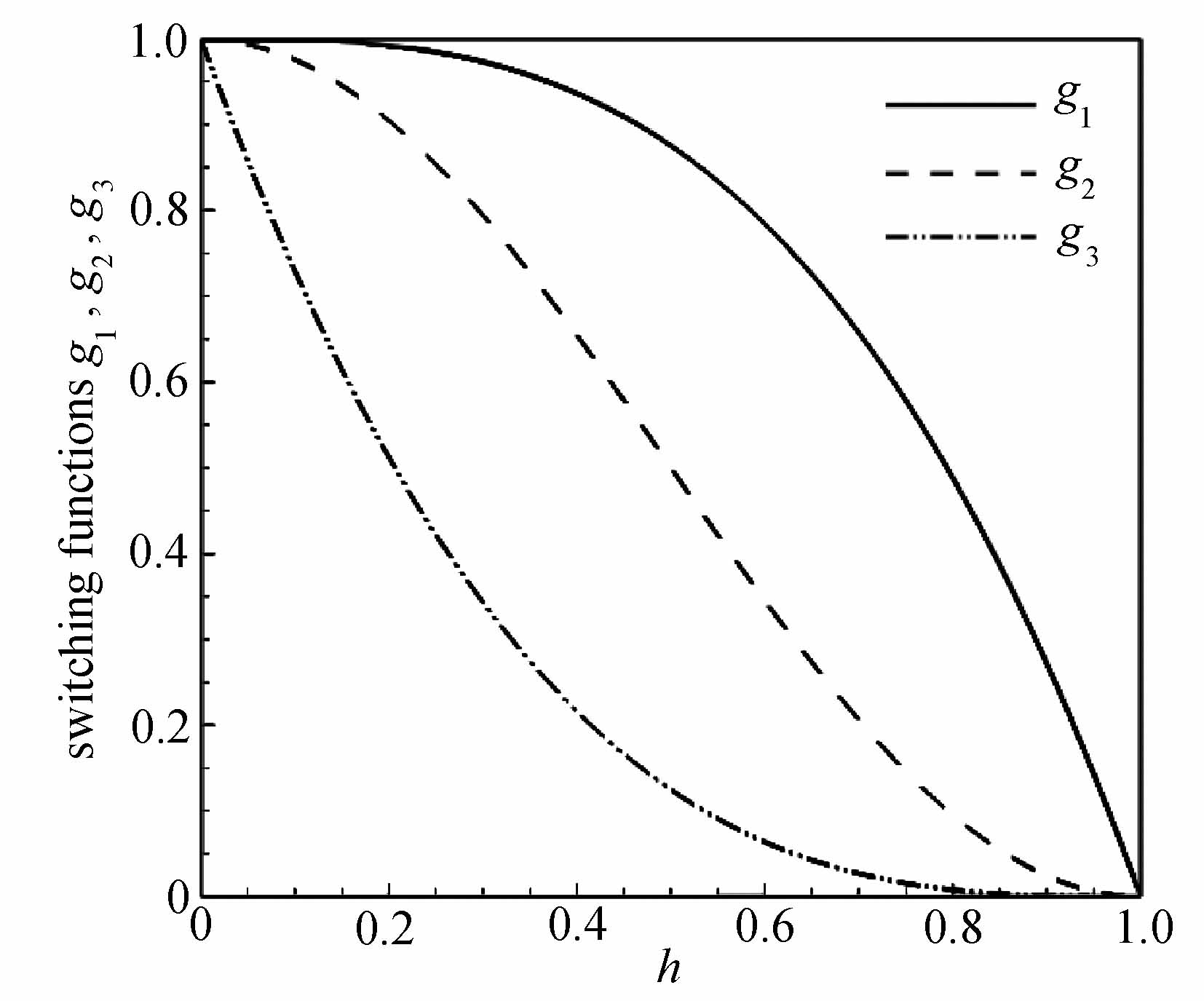
图5 3种开关函数的曲线图
Fig.5 Curves of 3 switching functions
3.2 R-Roe格式
Xu和Li[9]在分析Godunov型数值格式的耗散机制时,将数值激波面分为亚声速区和超声速区,并且主张激波不稳定现象源于亚声速区的扰动增长,这一结论得到了众多研究人员的支持[5,11,18].采用文献[11]的方法来定义亚声速区开关函数:
(18)
式中,Ma为Mach数.从式(18)可知:在超声速区,f=0;在亚声速区,0<f<1.
结合探测激波的开关函数式(17)和亚声速区开关函数式(18),横向通量熵波黏性项和剪切波黏性项最终的表达式为
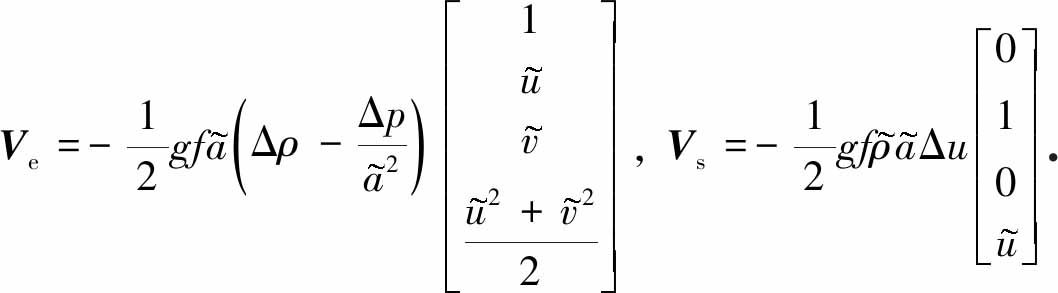
(19)
因此,一种鲁棒的Roe格式(命名为R-Roe,robust Roe)数值通量的表达式为
(20)
值得注意的是,Chen等[11]通过添加剪切波黏性来消除Roe格式的不稳定现象,本文的工作与其相比有两点不同:1) 通过小扰动分析和相关数值实验,我们证明了激波不稳定现象仅与横向通量有关,因此仅在横向通量上增加黏性来消除Roe格式的不稳定现象,而文献[11]在两个方向的数值通量上都增加了黏性;2) 根据小扰动分析的结论,本文通过增加熵波黏性和剪切波黏性来抑制Roe格式的不稳定性,而文献[11]仅仅添加了剪切波黏性.
我们发现,在某些情形下,仅仅添加剪切黏性,不稳定现象依然会出现.接下来,计算Mach数为7的二维稳态激波问题来证明这一点.计算区域[0,1]×[0,1]被划分成50×50的直角网格,初始时激波面位于x=0.5处,波前和波后状态分别为
(21)
左边界采用波前超声速边界条件,右边界采用波后亚声速边界条件,上下边界采用周期性边界条件.图6展示了时间t=1时的密度等值线.从图中可以看到,Roe格式出现了明显的不稳定现象,而文献[11]通过增加剪切黏性构造的Roe-SV格式在某种程度上减轻了不稳定现象的严重程度,但是不稳定现象依然存在.本文构造的R-Roe格式完全消除了不稳定现象,得到了清晰的激波面,甚至时间t=100时,依然不会出现不稳定现象.

(a) Roe (b) Roe-SV[11] (c) R-Roe
图6 二维稳态激波问题的密度等值线
Fig.6 Density contour lines of the 2D steady shock wave problem
4 数 值 结 果
计算一系列数值算例来展示本文构造的R-Roe格式的鲁棒性和精度.
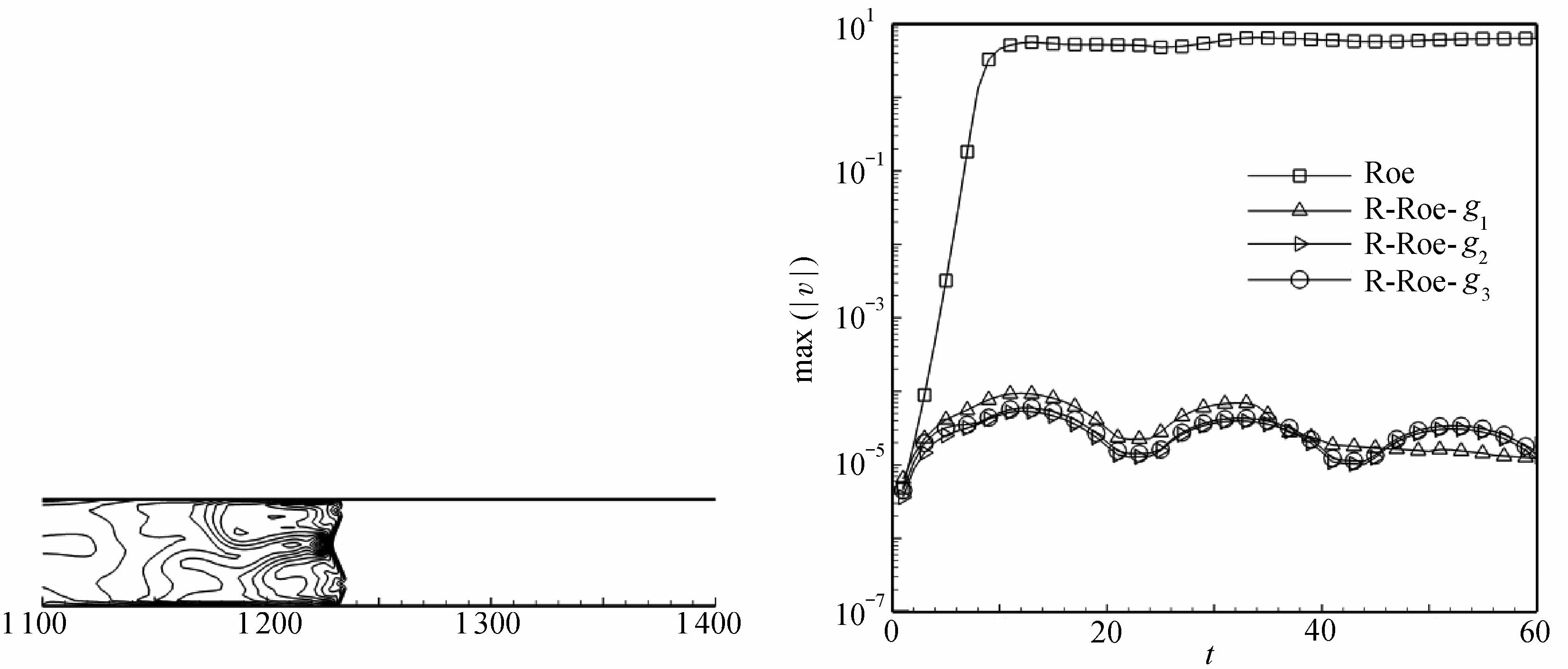
4.1 随机数值噪声问题
Mach数为20的平面激波沿着x正向运动,初始时激波位于x=5处,波前静止流体的密度为1.4,压力为1.0,波后状态可以根据激波与Mach数之间的关系式计算得到.计算区域[0,1 500]×[0,20]被划分成1 500×20的直角网格.在波前状态上增加取值从-0.5×10-5到0.5×10-5的随机数值噪声,扰动后的波前状态为
(ρ0,u0,v0,p0)i,j=(1.4,0,0,1)+(α1,α2,α3,α4)i,j·10-5,
(22)
式中,αk(k=1,2,3,4)表示取值从-0.5到0.5的随机数.

(a) Roe (b) R-Roe-g1

(c) R-Roe-g2 (d) R-Roe-g3
(e) Roe-SV-g3 (f) max(|v|)
图7 随机数值噪声问题的密度等值线以及y方向速度的最大振幅
Fig.7 Density contour lines of the random numerical noise problem and the maximum magnitude of the y-direction velocity
该算例中,整个计算区域内y方向速度的最大振幅max(|v|)可以用来衡量不稳定现象的严重程度.图7展示了时间t=60时,使用Roe格式和3种不同的激波开关函数所构造的R-Roe格式计算得到的密度等值线和y方向速度的最大振幅.作为比较,我们还给出了Roe-SV格式结合开关函数g3计算所得结果.从图中可以清晰地看到,Roe和Roe-SV格式均出现了严重的不稳定现象,激波面完全被破坏,并且y方向速度的最大振幅max(|v|)也由初始的10-5量级增长到100量级.3种R-Roe格式均能有效地抑制不稳定现象,且y方向速度的最大振幅一直维持在10-5量级附近.由于三者之间没有明显的差异,后面的算例均采用余弦函数g2作为激波开关函数.
4.2 二维Sedov爆轰波问题
使用Roe、R-Roe以及Roe-SV格式计算二维Sedov爆轰波问题,问题的详细描述见2.2小节.图8展示了时间t=0.1时的压力等值线.从图中可以清晰地看到,本文构造的R-Roe格式消除了原始Roe格式的carbuncle现象,得到了清晰的激波面.值得注意的是,文献[11]构造的Roe-SV格式计算该算例时依然会出现轻微的carbuncle现象.
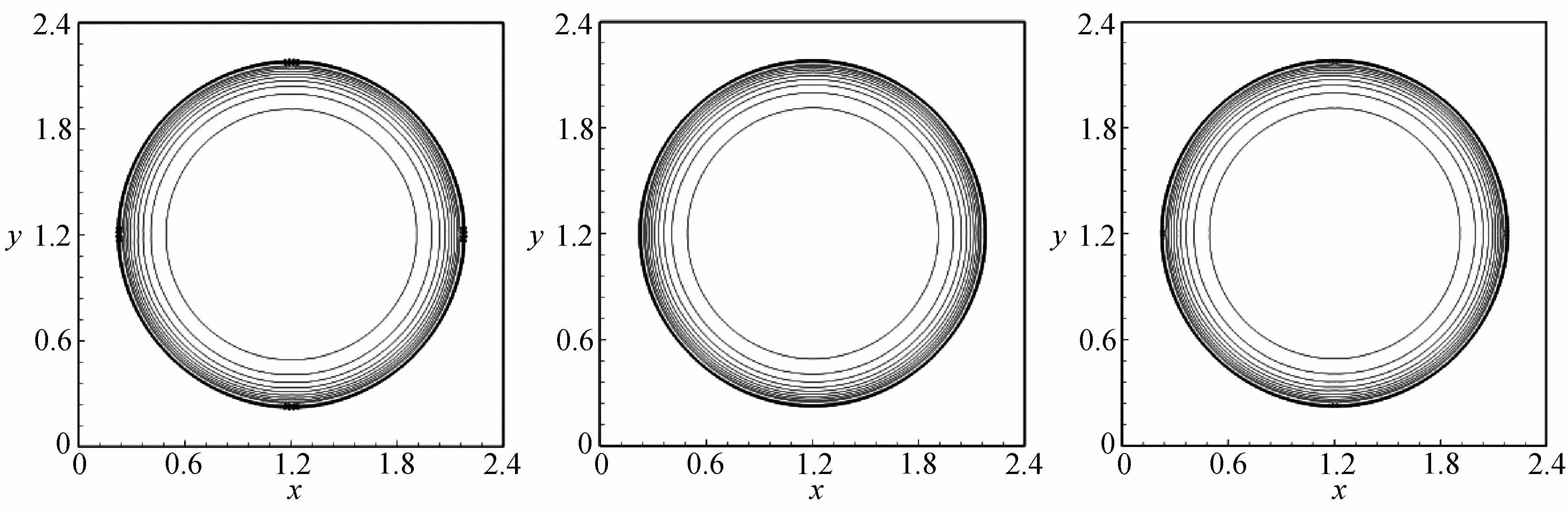
(a) Roe (b) R-Roe (c) Roe-SV
图8 二维Sedov爆轰波问题的压力等值线
Fig.8 Pressure contour lines of the 2D Sedov blast wave problem
4.3 双Mach反射问题
Mach数为10的斜激波与底部壁面成60°角,计算区域[0,4]×[0,1]被划分成480×120的直角网格.初始状态为

(23)

(a) Roe

(b) R-Roe (c) Roe-SV
图9 双Mach反射问题的密度等值线
Fig.9 Density contour lines of the double Mach reflection problem
详细的边界条件描述可参考文献[23].图9展示了时间t=0.2时的密度等值线.从图中可以清晰地看到,Roe格式的计算结果出现了明显弯曲的非物理Mach杆,Roe-SV格式的Mach杆有些轻微的弯曲,而本文构造的鲁棒的R-Roe格式消除了不稳定现象,得到了清晰的激波结构.
4.4 超声速绕柱流问题
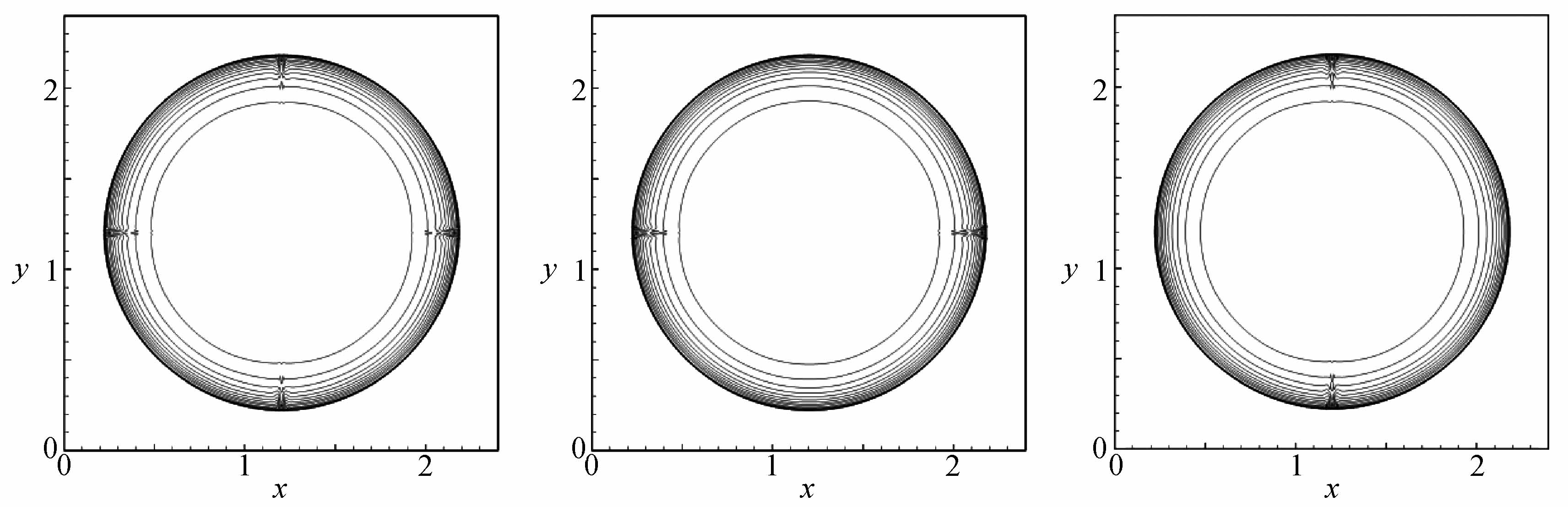
Mach数为20的自由来流流经一圆柱体,流场的初始分布为(ρ0,u0,v0,p0)=(1.4,20,0,1),详细的区域描述、网格划分和边界条件可以参考文献[24].本文使用40×80的结构化贴体四边形网格来计算.图10展示了时间t=4时的密度等值线.从图中可以清晰地看到,Roe格式的计算结果在中间停滞线出现了明显的carbuncle现象,Roe-SV格式虽然在很大程度上抑制了carbuncle现象,但没有完全消除,而R-Roe格式完全消除了不稳定现象,得到了清晰的稳态弓形激波.
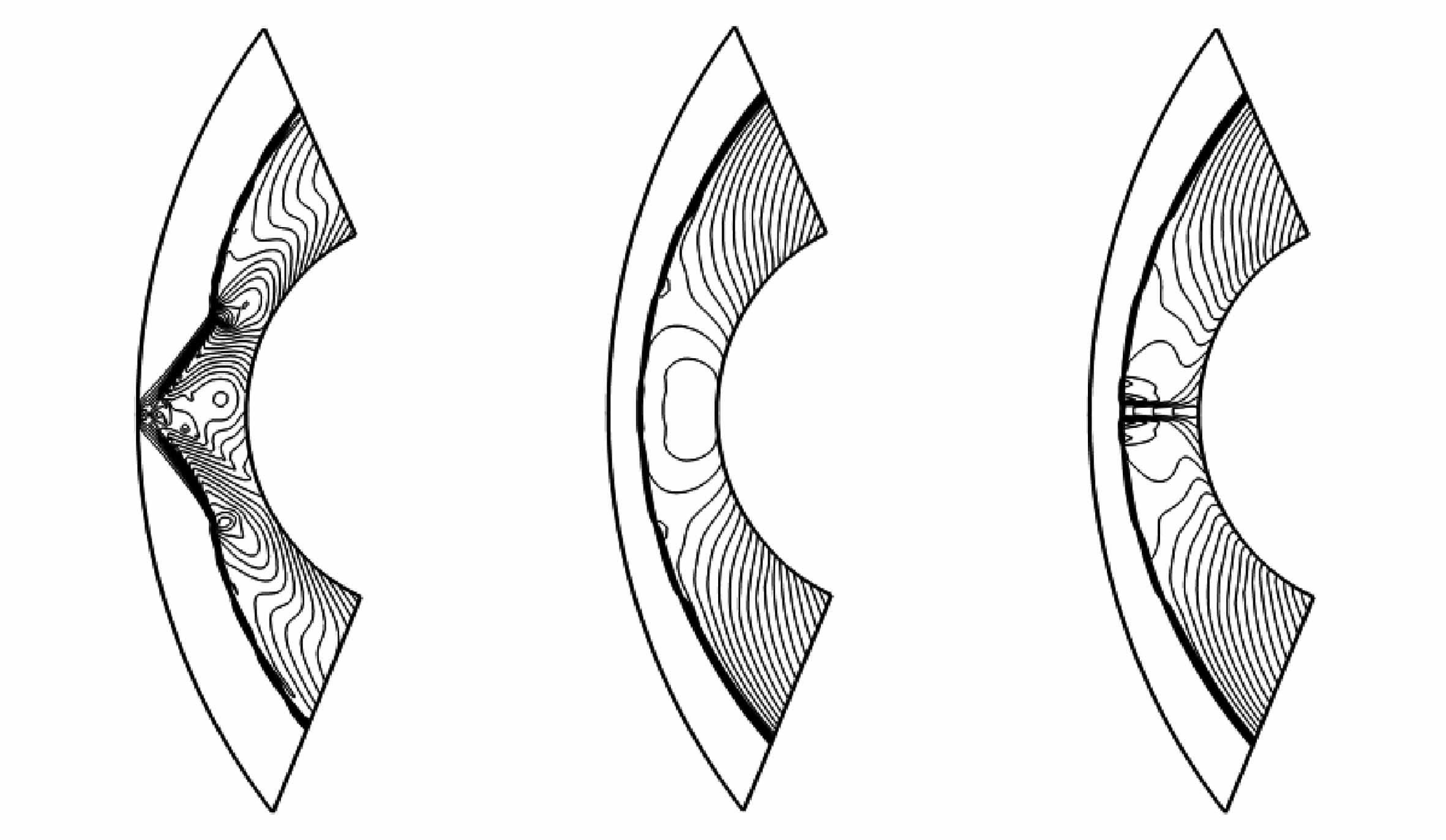
(a) Roe (b) R-Roe (c) Roe-SV
图10 超声速绕柱流问题的密度等值线
Fig.10 Density contour lines of the supersonic flow over a cylinder
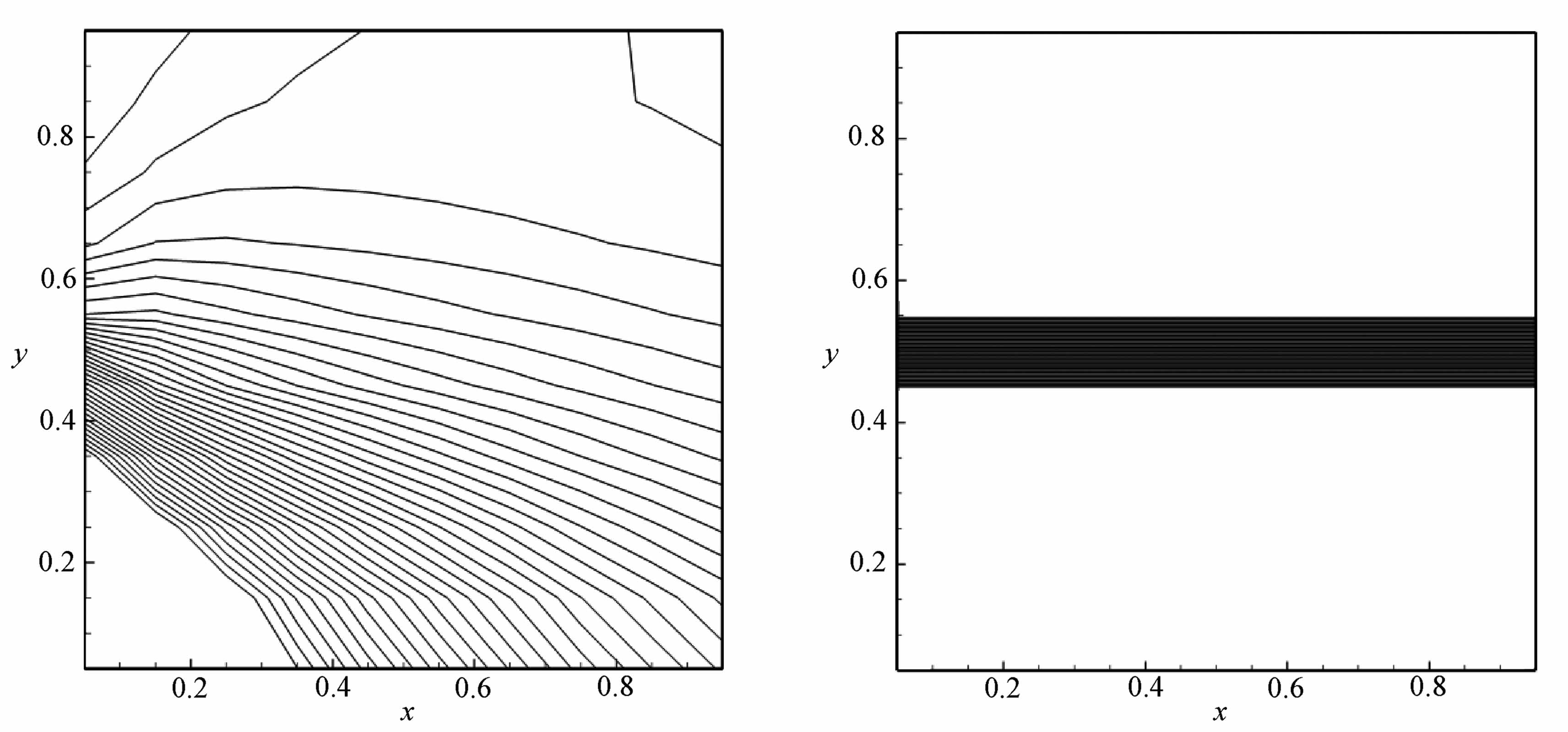
(a) HLLE (b) Roe
(c) R-Roe (d) 密度分布 (d) Density distribution
图11 二维无黏剪切流问题的密度等值线以及沿着y方向的密度分布
Fig.11 Density contour lines of the 2D inviscid shear flow problem and the density distribution along the y-direction
4.5 二维无黏剪切流问题
前面的算例证明了R-Roe格式具有很好的鲁棒性,可以有效地抑制激波不稳定现象的发生.接下来,计算二维无黏剪切流问题来检验R-Roe格式捕捉接触间断的能力.初始时,两种流体以不同的速度在区域[0,1]×[0,1]的上、下两部分流动,初始状态为
(24)
计算中采用10×10的直角网格.图11展示了时间迭代1 000步之后的密度等值线以及沿着y方向的密度分布.我们给出耗散的HLLE格式的计算结果来作为对比.从图中可以清晰地看到,HLLE格式在接触间断有很大的耗散,而R-Roe格式保留了原始Roe格式精确捕捉接触间断的优点.
5 结 论
小扰动分析和数值实验表明:Roe格式横向通量中的密度扰动和剪切速度扰动不会衰减,这会导致激波不稳定现象的出现.通过增加熵波黏性和剪切波黏性来构造一种激波稳定的Roe格式.为了防止不适当位置的黏性影响格式对于接触间断和剪切层的分辨率,本文定义了两个开关函数,使得黏性仅仅添加到激波层亚声速区的横向数值通量上.数值实验表明:本文构造的R-Roe格式不仅保留了原始Roe格式高分辨率的优点,而且具有更好的鲁棒性,可以有效抑制激波不稳定现象的出现.因此,它是一种精确并且鲁棒的激波捕捉方法,可以广泛应用于高超声速可压缩流的数值模拟中.将小扰动分析方法和格式的改进方法推广到其他低耗散Godunov型数值格式,构造三维和非结构网格上的R-Roe格式,结合高阶精度重构方法(例如WENO方法)来获得空间的高阶精度以及将R-Roe格式应用到其他的守恒律系统可以作为未来的研究工作.
[1] ROE P L.Approximate Riemann solvers,parameter vectors,and difference schemes[J].Journal of Computational Physics,1981,43(2):357-372.
[2] TORO E F,SPRUCE M,SPEARES W.Restoration of the contact surface in the HLL Riemann solver[J].Shock Waves,1994,4(1):25-34.
[3] QUIRK J J.A contribution to the great Riemann solver debate[J].International Journal for Numerical Methods in Fluids,1994,18(6):555-574.
[4] GRESSIER J,MOSCHETTA J M.Robustness versus accuracy in shock-wave computations[J].International Journal for Numerical Methods in Fluids,2000,33(3):313-332.
[5] SHEN Z J,YAN W,YUAN G W.A robust HLLC-type Riemann solver for strong shock[J].Journal of Computational Physics,2016,309:185-206.
[6] XIE W J,LI H,TIAN Z Y,et al.A low diffusion flux splitting method for inviscid compressible flows[J].Computers &Fluids,2015,112(2):83-93.
[7] LIOU M S.Mass flux scheme and connection to shock instability[J].Journal of Computational Physics,2000,160(2):623-648.
[8] LIOU M S.A sequel to AUSM:AUSM+[J].Journal of Computational Physics,1996,129(2):364-382.
[9] XU K,LI Z W.Dissipative mechanism in Godunov-type schemes[J].International Journal of Numerical Methods in Fluids,2001,37(1):1-22.
[10] DUMBSER M,MOSCHETTA J M,GRESSIER J.A matrix stability analysis of the carbuncle phenomenon[J].Journal of Computational Physics,2004,197(2):647-670.
[11] CHEN S S,YAN C,LIN B X,et al.Affordable shock-stable item for Godunov-type schemes against carbuncle phenomenon[J].Journal of Computational Physics,2018,373:662-672.
[12] XIE W J,LI W,LI H,et al.On numerical instabilities of Godunov-type schemes for strong shocks[J].Journal of Computational Physics,2017,350:607-637.
[13] SIMON S,MANDAL J C.A cure for numerical shock instability in HLLC Riemann solver using antidiffusion control[J].Computers &Fluids,2018,174:144-166.
[14] WU H,SHEN L J,SHEN Z J.A hybrid numerical method to cure numerical shock instability[J].Communications in Computational Physics,2010,8:1264-1271.
[15] REN Y X.A robust shock-capturing scheme based on rotated Riemann solvers[J].Computers &Fluids,2003,32(10):1379-403.
[16] NISHIKAWA H,KITAMURA K.Very simple,carbuncle-free,boundary-layer-resolving,rotated-hybrid Riemann solvers[J].Journal of Computational Physics,2008,227(4):2560-2581.
[17] PEERY K M,IMLAY S T.Blunt-body flow simulations[C]//24th Joint Propulsion Conference.Boston,MA,1988.
[18] FLEISCHMANN N,ADAMI S,HU X Y,et al.A low dissipation method to cure the grid-aligned shock instability[J].Journal of Computational Physics,2020,401:109004.
[19] KIM S,KIM C,RHO O H,et al.Cures for the shock instability:development of a shock-stable Roe scheme[J].Journal of Computational Physics,2003,185(2):342-374.
[20] RODIONOV A.Artificial viscosity in Godunov-type schemes to cure the carbuncle phenomenon[J].Journal of Computational Physics,2017,345:308-329.
[21] RODIONOV A.Artificial viscosity to cure the shock instability in high-order Godunov-type schemes[J].Computers &Fluids,2019,190:77-97.
[22] RODIONOV A.Artificial viscosity to cure the carbuncle phenomenon:the three-dimensional case[J].Journal of Computational Physics,2018,361:50-55.
[23] WOODWARD P,COLELLA P.The numerical simulation of two-dimensional fluid flow with strong shocks[J].Journal of Computational Physics,1984,54(1):115-173.
[24] HUANG K B,WU H,YU H,et al.Cures for numerical shock instability in HLLC solver[J].International Journal of Numerical Methods in Fluids,2011,65(9):1026-1038.