引 言
近几十年来,微流控技术由于安全性高、易于控制、高效率以及耗能少等一系列优点[1-2],获得了工业界与学术界的广泛关注,并得到了迅速发展.作为微流控技术的一个重要分支,液滴微流控技术主要研究液滴破裂[3-4]、变形[5-6]及融合[7]等行为,广泛用于化工[8]、医学工程[9]、细胞工程[10]与食品科学[11]等领域.T型微通道作为被控制的基础单元,因其结构简单、加工容易,被广泛用于研究两相传热传质问题.由于液滴在T型微通道中破裂时会分裂成两个小液滴,因而为制备微小液滴提供了新的途径[12].基于此,充分了解T型微通道内液滴破裂过程的动力学行为有重要意义.
王维萌等[13]通过实验研究了毛细数为0~0.1时T型微通道中液滴破裂的流型,通过改变两相流速得到隧道破裂、不连续阻塞破裂、永久阻塞破裂以及未破裂四种流型,并根据实验数据得到了破裂流型与隧道破裂流型临界分界线满足形如l0/w=αCa-β的拟合公式.Jullien等[14]通过实验研究了毛细数范围为4×10-4~2×10-1时T型微通道内液滴的破裂动力学行为,发现了不破裂、隧道破裂以及永久阻塞破裂三种液滴流型.Haringa等[15]通过实验研究了T型微通道内细长液滴的破裂情形,发现在毛细数较低、液滴初始长度大于三倍管径长度的破裂情形中,液滴破裂与未破裂情形的临界分界线可用![]() 拟合.Samie等[16]通过实验研究了子管道出口截面宽度不同时产生不同液滴大小的方法.
拟合.Samie等[16]通过实验研究了子管道出口截面宽度不同时产生不同液滴大小的方法.
以上学者运用实验方法对T型微通道内液滴破裂的动力学行为进行了研究.随着计算机科技和数值方法的迅速发展,采用数值方法研究复杂系统内流动问题被广大学者所认可.王澎等[17]运用计算流体力学(CFD)方法中的流体体积(volume of fluid,VOF)模型对T型微通道内液滴破裂过程进行了数值模拟,主要分析了破裂与不破裂两种流型,重点研究了黏度比对液滴破裂行为的影响.他们发现黏性比越大,液滴越容易破裂,并拟合得到了不同黏度比下临界毛细数与液滴初始长度L0的关系.Chen等[18]用CFD-VOF对T型微通道内液滴的破碎机理进行了三维仿真研究,模拟得到了隧道破裂、不连续阻塞破裂、连续阻塞破裂与不破裂四种流型,发现了液滴破裂与不破裂主要取决于与表面张力相关的毛细数以及液滴相对长度.该工作还采用了经典的Rayleigh-Plateau不稳定性分析[19]描述了液滴破裂机理,提出了用无量纲时间描述永久阻塞破碎过程中液滴大小随时间变化的方法,并得到了不同流型之间的临界分界线关系式.相比于CFD方法,格子Boltzmann方法(LBM)作为近几十年来迅速发展的一种介观数值算法,因其易于处理流体之间以及流体和固体壁面之间的相互作用、计算效率高等优点,被众多学者用来研究流动与传热问题.娄钦等[20]与陆威等[21]用LBM研究了方腔内双扩散问题;谢驰宇等[22]用LBM研究了固壁表面液滴受热蒸发问题.Liu等[23]基于多松弛(MRT)颜色多相流LBM模型[24-25],研究支路为非理想润湿表面时液滴在T型微通道内的破裂行为,发现当一个分支是理想润湿表面,另一个分支是非理想润湿表面时液滴分裂为两个不对称的子液滴,且较小的子液滴在非理想润湿表面的支路中.该文中还发现,黏度比越小,接触角滞后性作用越强.Fu等[26]基于相同的LBM多相流模型[24-25],从理论和数值上分析了两个不同出口压差下T型微通道内液滴非对称破裂的过程,尤其对阻塞破裂过程中液滴的动力学行为进行了分析,发现液滴大小不等时其不对称破裂分为填充阶段和破碎阶段,并根据数值结果提出了一个描述液滴非对称性破裂的通用参数.Chen等[27]基于相场LBM多相流模型研究了T型微通道内液滴破裂与不破裂的运动机理,分析了T型微通道内液滴的流场分布、液滴的形变参数变化和液滴运动相图,重点讨论了液滴隧道破裂时剪切作用和内部涡流对液滴破裂过程的影响,得到了不同毛细数、黏性比以及子管道与母管道的宽度比时的液滴流型相图,并得到了不同流型之间临界分界线的拟合公式.
以上研究工作揭示了Newton液滴在T型微通道中的运动机理,而非Newton液滴在T型微通道中的运动行为广泛存在于工业应用中,如药物输送过程中的药物通常是非Newton流体,其与通道中的管道分支构成了非Newton液滴在T型微通道内的多相流动问题.鉴于此,本文采用格子Boltzmann非Newton两相流模型研究了非Newton液滴在T型微通道中的运动过程,主要探究了T型微通道内非Newton液滴的幂律指数n对液滴破裂流型的形态变化以及流型相图的影响.
1 非Newton气液两相流格子Boltzmann模型
本文采用娄钦等[28]最近提出的非Newton两相流模型,研究非Newton液滴在T型微通道中的运动过程,该模型分别用分布函数fα和gα描述指标参数和速度/压力的演化过程,其形式如下:

(1)
其中α=0,1,2,…,b-1,b为离散速度方向的数量;δt代表时间步长;x和t分别表示粒子运动的位置和时间;eα为离散速度;τ为松弛时间,其与运动黏度ν相关;φ,u与ρ分别代表指标函数、流体速度与流体密度;κ代表决定表面张力大小的系数;![]() 其中p为流体压强;演化方程中ψ(φ)由状态方程决定.在本文中采用Carnahan-Starling状态方程,其对应的ψ(φ)可写为如下形式:
其中p为流体压强;演化方程中ψ(φ)由状态方程决定.在本文中采用Carnahan-Starling状态方程,其对应的ψ(φ)可写为如下形式:
(2)
其中a决定分子间相互吸引力强度,R为气体常数,T为流体温度.在方程(1)中函数Γα(u)表达式为
其中ωα代表权重系数.演化方程中![]() 和
和![]() 为分布函数对应的平衡态,形式如下:
为分布函数对应的平衡态,形式如下:
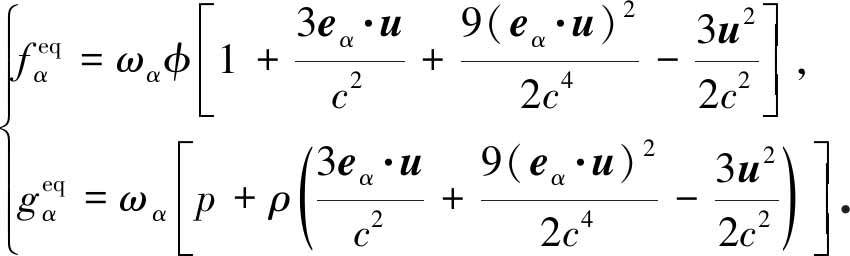
(3)
宏观量指标参数φ、压力p以及速度u的统计由如下方程给出:
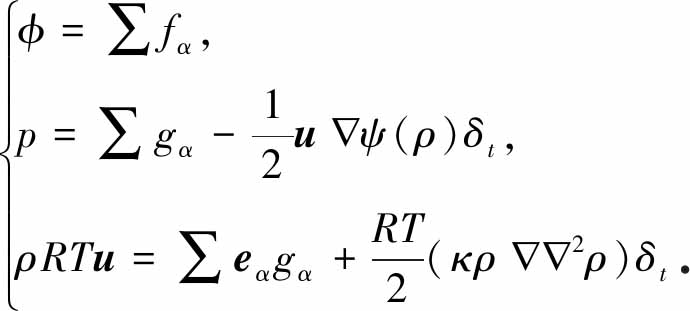
(4)
流体密度ρ(φ)和运动黏度ν(φ)可由指标参数φ计算得到:
(5)
(6)
其中ρg代表气相流体密度,ρl代表液相流体密度,φh为指标参数最大值,φl为指标参数最小值,它们可根据状态方程由Maxwell重构得到.演化方程中梯度和Laplace算子的离散方法均采用二阶中心各向同性方法(ICS) [29]:

(7)
该模型中用幂律流体模型来体现流体的非Newton特性,动力黏度η的表达式为
η=η0γn-1=η0(SαβSαβ)(n-1)/2,
(8)
其中γ为剪切速率,η0为稠度系![]() 为应变张量,当未考虑外力项时,Sαβ与分布函数之间有如下关系:
为应变张量,当未考虑外力项时,Sαβ与分布函数之间有如下关系:
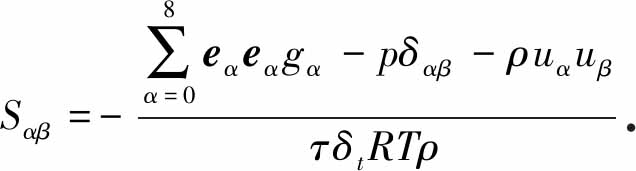
(9)
n为非Newton流体幂律指数,当n<1时,流体为剪切变稀流体,即其动力黏度η随着剪切速率γ的增大而减小;当n=1时,流体为Newton流体,其动力黏度η为一个定值η=η0=ρν;当n>1时,流体为剪切变稠流体,其动力黏度η随着剪切速率γ的增大而增大.通过Chapman-Enskog分析可以得到方程(1)对应的宏观动力学方程为
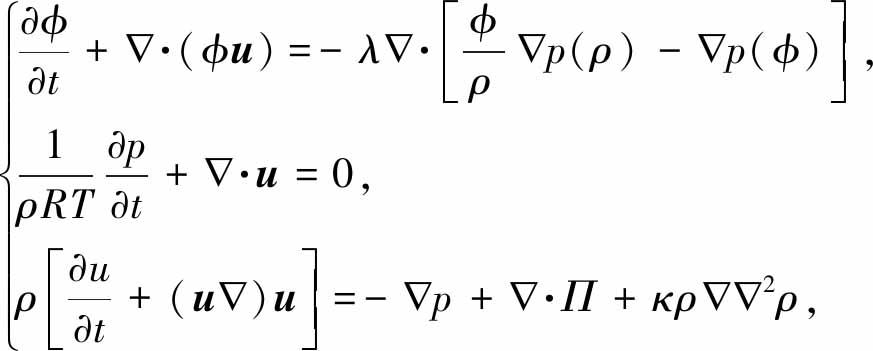
(10)
其中Π=ρν( u+u
u+u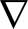 )是黏性应力张量.运动黏度系数和松弛时间τ之间的关系为
)是黏性应力张量.运动黏度系数和松弛时间τ之间的关系为![]() 是与格子速度(c=dx/dt)相关的常数.
是与格子速度(c=dx/dt)相关的常数.
本文使用D2Q9模型来进行数值模拟研究,权重系数ωα设置为:当α=0时,ω0=4/9;当α=1~4时,ωα=1/9;当α=5~8时,ωα=1/36.离散速度eα的表达式为
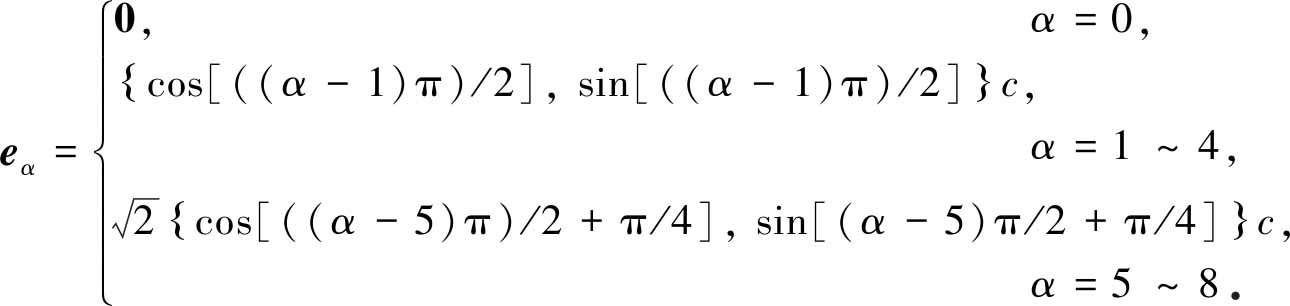
(11)
2 模 型 验 证
2.1 Laplace定律验证
本小节采用Laplace定律验证模型的正确性.初始时在网格数为128×128区域中心内放置半径r、密度为ρl=0.5的静止非Newton幂律流体圆形液滴,其余区域充满着密度为ρg=0.1的Newton气体,计算域四周的边界条件均为周期性边界条件.
根据Laplace定律可知,当系统达到稳定时,表面张力系数σ恒定,且液滴内外的压力差Pi-Po与液滴半径的倒数1/r呈线性关系:
(12)
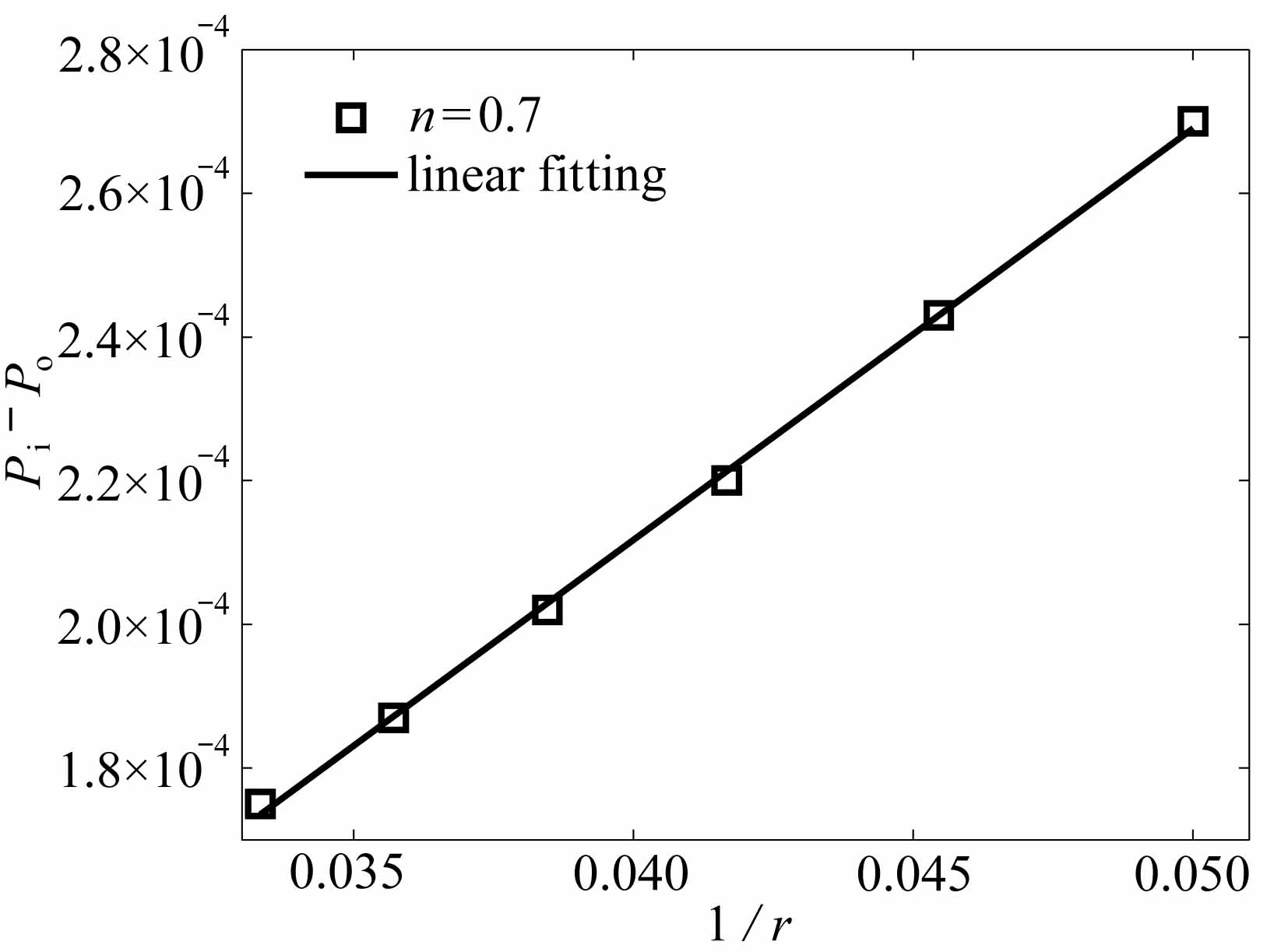
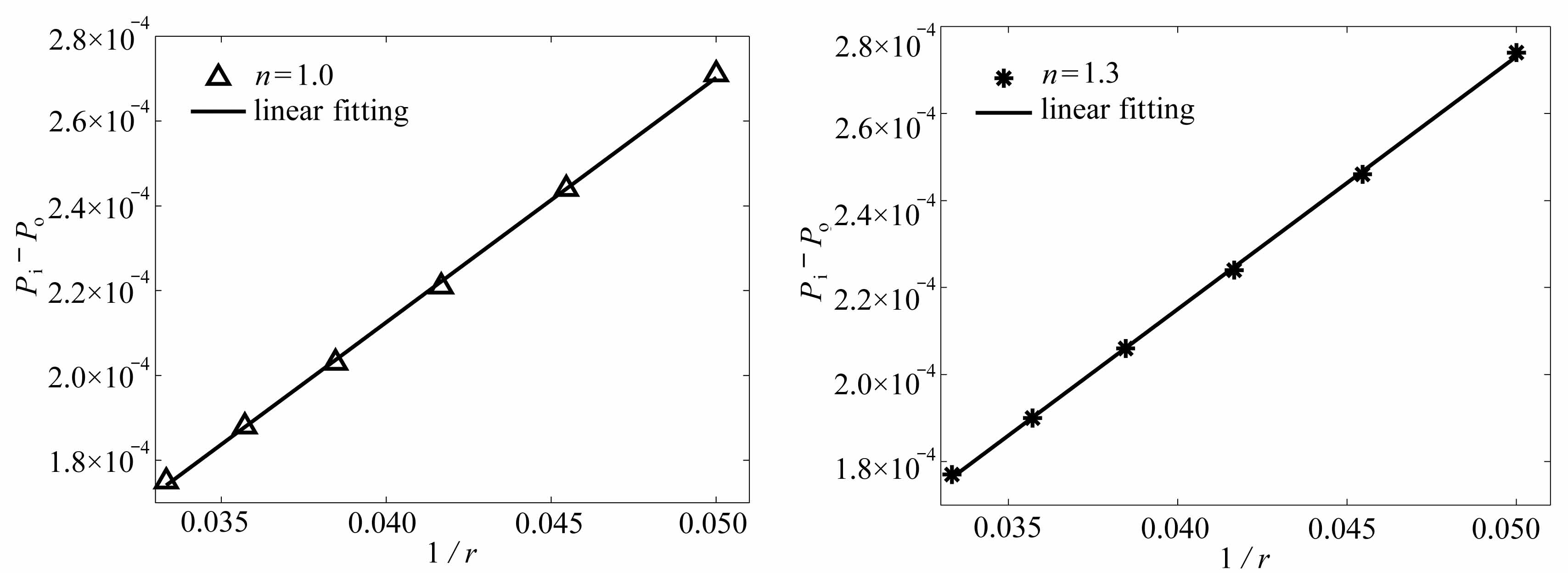
为了验证Laplace定律,在数值模拟中分别考虑了r=20,22,24,26,28和30六种情况.为了保证数值模拟结果具有一般性,研究了液滴为剪切变稀(n=0.7)、Newton(n=1.0)与剪切变稠(n=1.3)流体三种情形.图1(a)、1(b)与1(c)分别给出了在幂律指数n为0.7、1.0与1.3时得到的液滴内外压力差Pi-Po与半径倒数1/r的关系.由图1可知,模拟结果与Laplace定律一致.

(a) θeq=60° (b) θeq=90° (c) θeq=120°
图2 不同初始静态接触角θeq时得到的稳态接触角θ
Fig.2 Variant values of steady state contact angle θ obtained with different values of static contact angle θeq
(a) n=0.7
(b) n=1.0 (c) n=1.3
图1 液滴内外压力差Pi-Po和半径倒数1/r之间的关系
Fig.1 Relationship between pressure jump across the droplet interface Pi-Po and reciprocal of the droplet radius 1/r
2.2 润湿性固壁面静态接触角验证
润湿现象在自然界中普遍存在,例如水银滴在玻璃板上会呈现出球滴状,而水滴滴在玻璃板上将迅速铺展开.润湿性反映流体和固体之间相互作用力强度.在复杂微通道内,其是影响气-液-固或液-液-固三相动态行为的重要指标参数.在LBM中通过润湿性边界条件来描述壁面的润湿性.润湿性边界条件采用Davies等[30]提出的方法,其壁面的润湿强度采用表面亲和性αs来刻画,并把表面亲和性与指标参数φ联系起来,其关系式为
(13)
其中![]() 取值范围位于-1~1之间,αs=-1对应完全亲气表面,αs=1对应完全亲水表面.静态接触角θeq与αs关系式为
取值范围位于-1~1之间,αs=-1对应完全亲气表面,αs=1对应完全亲水表面.静态接触角θeq与αs关系式为
(14)
其中σ12为气-液表面张力,σs1与σs2分别代表固-液表面张力与固-气表面张力.
本小节对非Newton剪切变稀静态液滴的静态接触角进行验证.数值模拟中网格数为128×65,在计算区域下边界中心处放置半径r=20,密度ρl=0.5以及幂律指数n=0.7的非Newton半圆液滴,液滴周围充满了ρg=0.1的Newton气体,初始气液两相的运动黏度均为νg=νl=1/6.计算域的边界条件设置为:上下壁面是无滑移边界条件,左右是周期边界条件.
图2展示了当数值模拟达到稳定时,壁面静态接触角θeq分别为60°,90°与120°时,模拟所得到的稳态接触角θ,其数值分别为57.6°,87.3°与117.7°.模拟结果和理论值之间的相对误差分别为4.0%,3.0%与1.9%.图3展示了数值模拟得到的壁面稳态接触角θ与固壁面上的指标参数φwall的关系,结果与式(13)和(14)吻合较好.
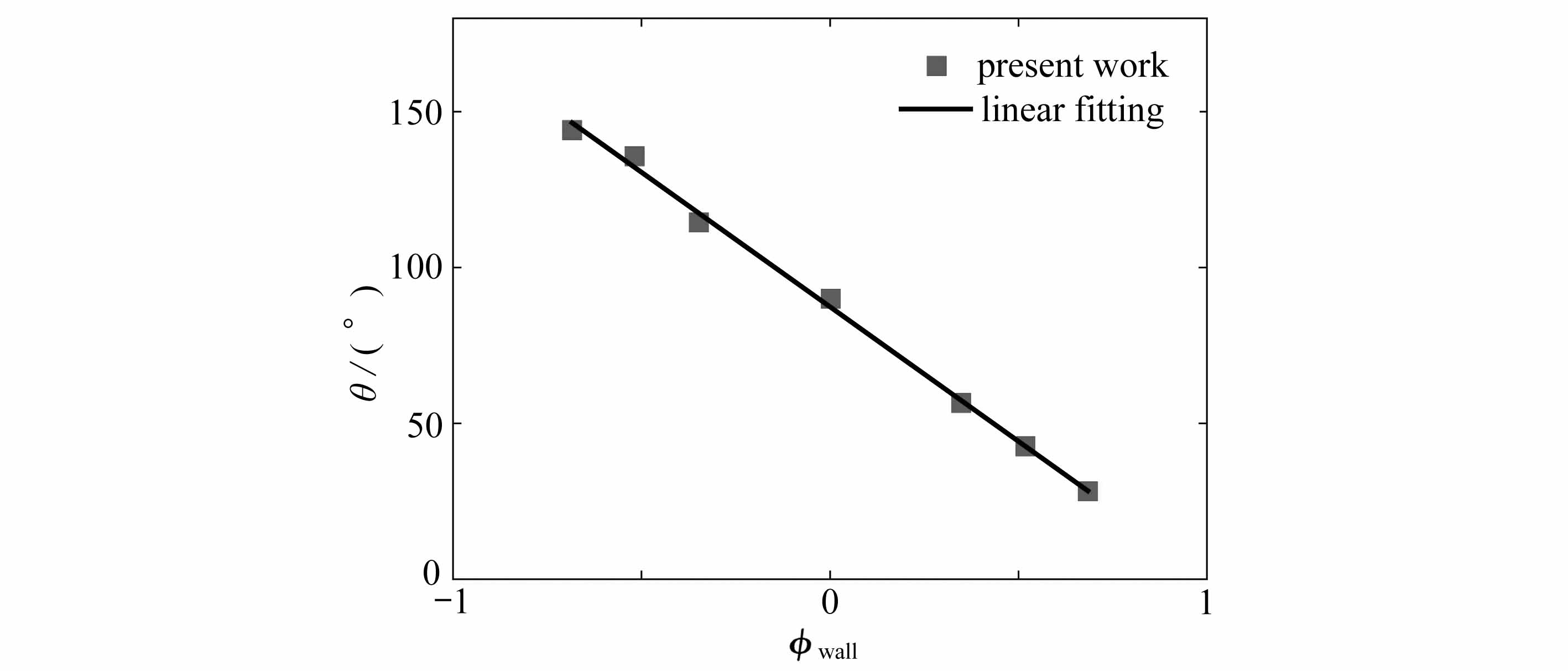
图3 稳态接触角θ与指标参数φwall的线性关系
Fig.3 The linear relationship between steady state contact angle θ and solid wall order parameter φwall
3 T型微通道内幂律流体液滴破裂的计算模拟与结果
本节将研究T型微通道内非Newton液滴破裂的形变机理.物理问题如图4所示,主管道的宽度为W0,长度为L0,子管道的宽度为W1,长度为L1,液滴的初始长度为l0,液滴初始放置时,液滴右端离子管道的距离为l1.主管道驱替相为Newton气体,密度ρg=0.1,运动黏度νg=1/6,非Newton液滴的密度为ρl=0.5.
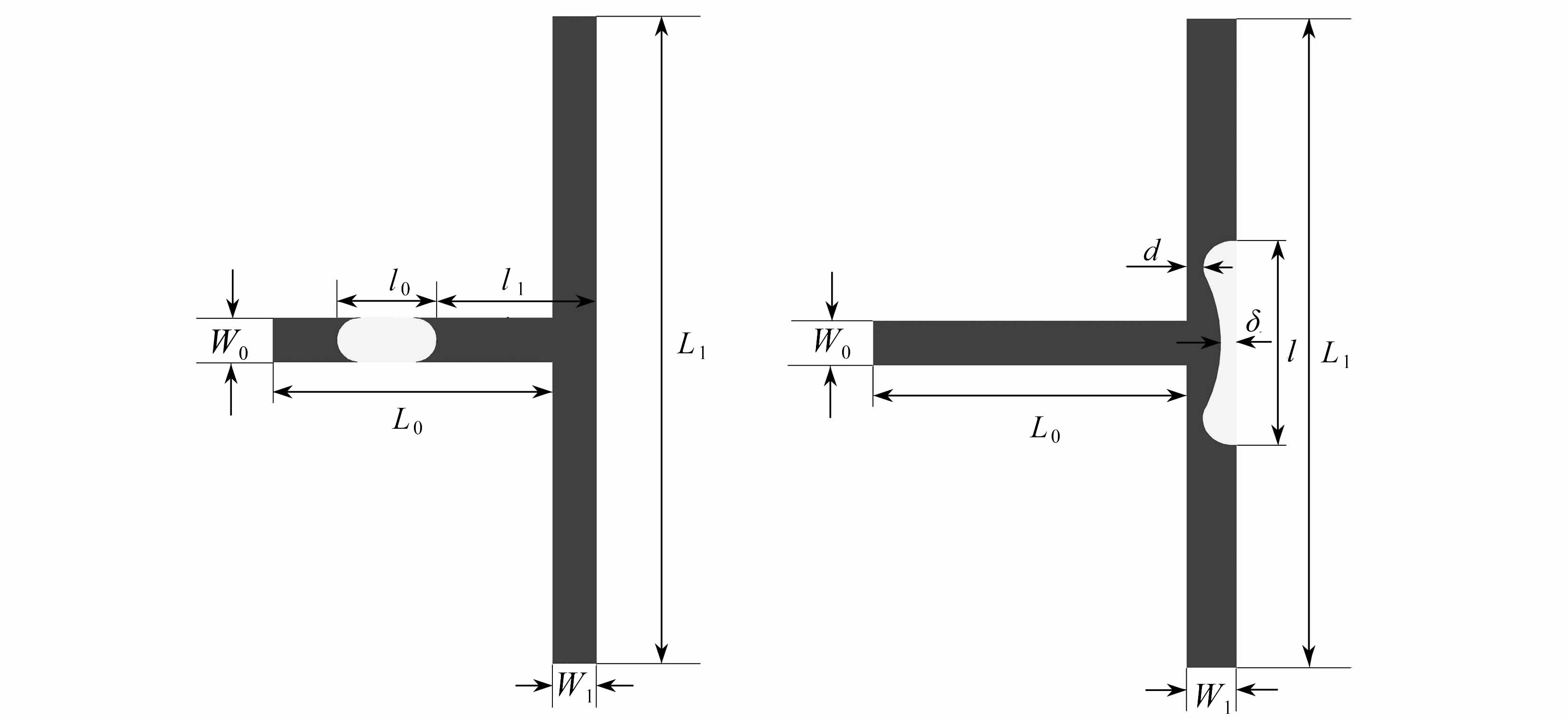
图4 T型微通道初始液滴模型 图5 液滴颈部厚度δ、液滴长度l以及液滴与壁面的隧道宽度
Fig.4 The model for the initial droplet in a T-junction d示意图 Fig.5 Schematic of droplet neck thickness δ,droplet length l and droplet-wall gap width d
此问题中,T型微通道进口、出口以及固壁面边界均采用half-way格式[31-34].不失一般性,以进口为例,未知分布函数(1,5,8三个方向)可由下式得到:
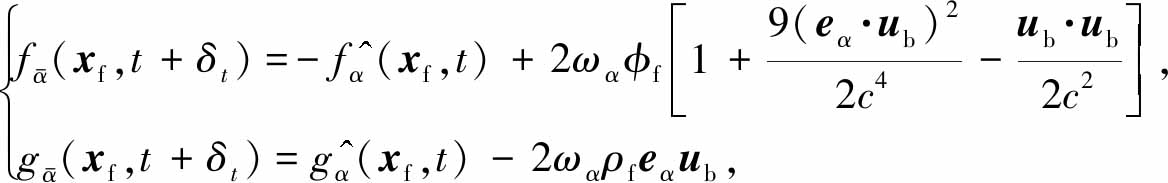
(15)
其中![]() 是最靠近边界点xb的流体点,φf=φ(xf,t),ρf=(xf,t),ub=u(xb)为主管道进出口速度,
是最靠近边界点xb的流体点,φf=φ(xf,t),ρf=(xf,t),ub=u(xb)为主管道进出口速度,![]() 和
和![]() 为碰撞后的分布函数,其表达式为
为碰撞后的分布函数,其表达式为
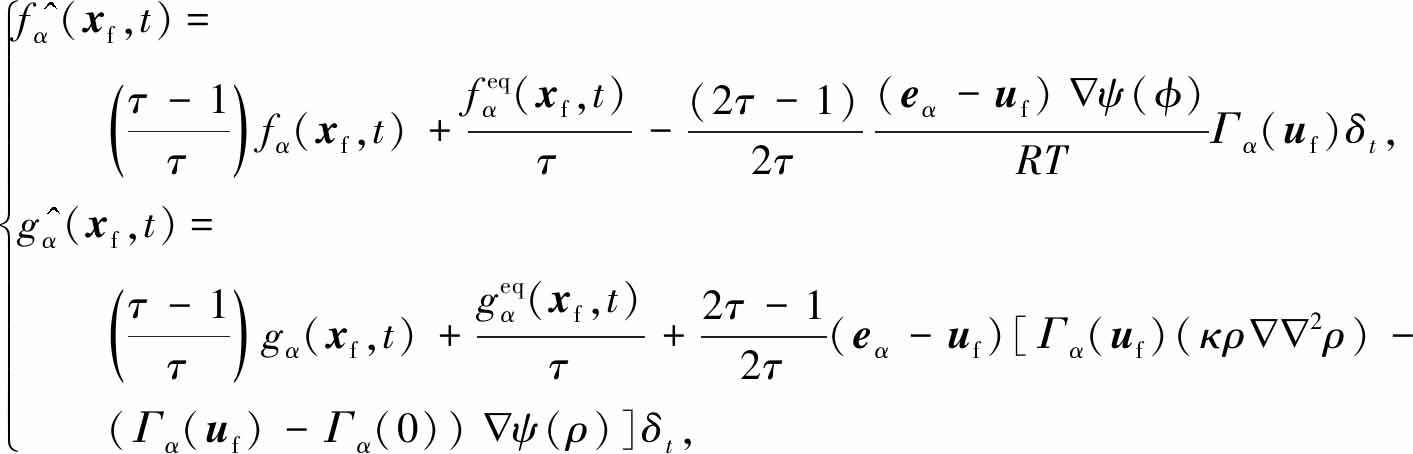
(16)
式中 uf=u(xf).
决定该问题运动特性的无量纲数主要为毛细数Ca,其定义式为Ca=uηg/σ,表征黏性力与表面张力的比值,式中σ为气液两相表面张力系数,u是主管道的驱替速度,ηg=ρgvg为驱替相动力黏度.为深入了解液滴在T型微通道内的破裂机理,下文将引用三个无量纲参数描述T型微通道内液滴的动力学行为及其液滴形状变化过程.分别为无量纲颈部厚度δ*、无量纲液滴前端运动距离l*与无量纲隧道宽度d*,其表达式分别为δ*=δ/W0,l*=(l-l0)/(2W0)与d*=d/W0.其中δ,l以及d分别为液滴颈部厚度、液滴的长度以及液滴与壁面的隧道宽度,其示意图如图5所示.
为保证计算结果的可靠性,首先对网格无关性进行了验证.在数值模拟中,Ca=0.056 4,νl=1/6,固壁面表面润湿性θ=180°,σ=0.005 6,W0=W1=30 um,L0=190 um,L1=440 um,l1=52 um,液滴初始长度为l0=2.0W0.分别选取了110×220,220×440以及440×880三种网格大小,图6给出了不同网格大小时液滴无量纲颈部厚度δ*随无量纲时间t的变化.由图6可知,当网格大小为220×440时,其与网格大小为110×220以及440×880得到的液滴无量纲颈部厚度δ*的最大误差不超过5%.因此从计算精度以及效率考虑,下文中均选取网格大小为220×440.

图6 不同网格大小时无量纲液滴颈部厚度δ*随无量纲时间的演化情况
Fig.6 Evolution of dimensionless characteristic parameters δ* with dimensionless time for different lattice domains
3.1 幂律流体液滴不同流型的形变特性
如同文献[14,27],本文中主要观察到了三种流型:不破裂流型、隧道破裂流型以及阻塞破裂流型,其示意图如图7所示.图7(a)为不破裂流型,此时黏性剪切力不能克服表面张力的束缚,因此液滴不破裂.图7(b)与图7(c)为隧道破裂流型与阻塞破裂流型,此时黏性剪切力能挣脱表面张力的束缚,从而使液滴分裂成两个小液滴,两者的区别是隧道流型中,液滴与壁面之间有通道出现.需要指出的是由于气液两相LBM是扩散界面模型,得到的气液界面通常有3~5个网格厚度,因此当液滴破裂时其界面位置距离分支通道壁面小于等于0.5个界面厚度时,即为阻塞破裂.
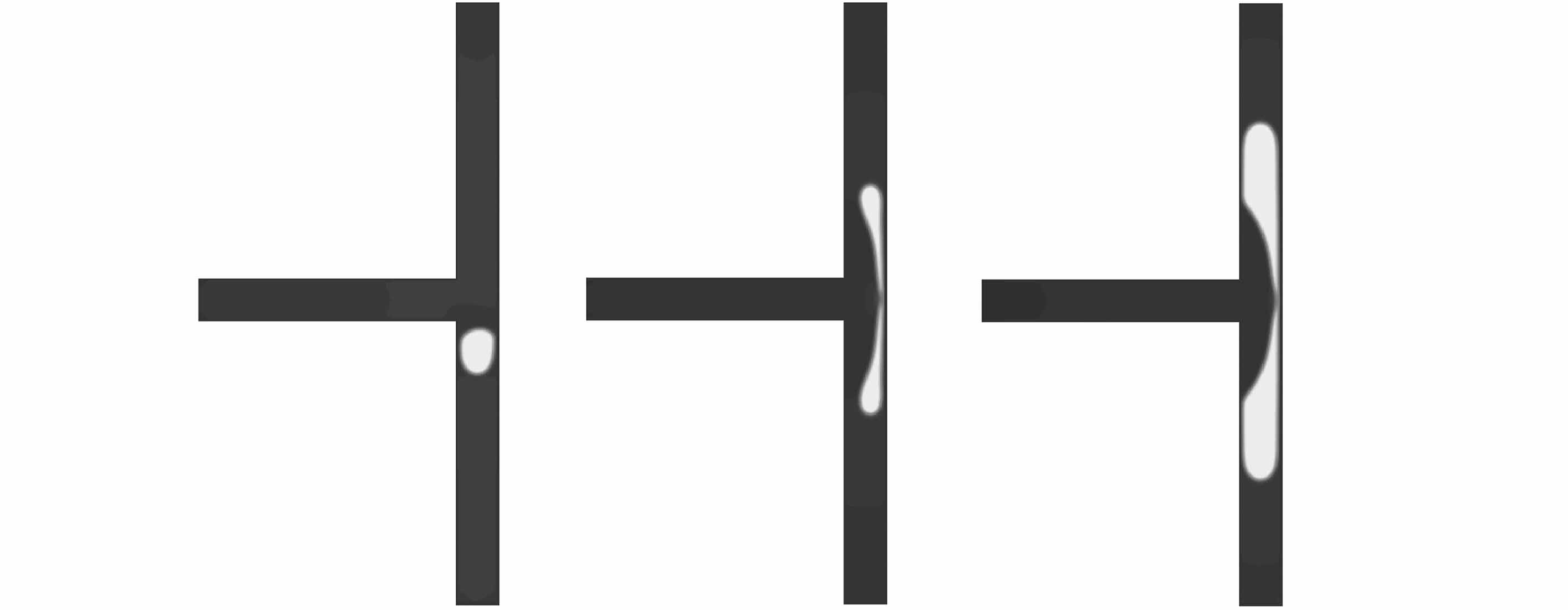
(a) 不破裂 (b) 隧道破裂 (c) 阻塞破裂
(a) Non-breakup (b) Breakup with a tunnel (c) Breakup with obstruction
图7 T型微通道内幂律流体液滴的三种流型
Fig.7 Three types of power-law fluid droplet behaviours in T-junctions
如图8所示,为幂律流体(n=1.4)液滴在T型微通道内完整破裂形变过程图,其中Ca=0.028 2,液滴初始长度l0=4.0W0=120,l1=52,W0=W1=30,L0=190,L1=440,液滴初始运动黏度为νl=1/6,初始黏度比M=5.0(被驱替液滴动力黏度ηl与驱替气相动力黏度ηg的比值),固壁表面为完全润湿性表面(θ=180°),σ=0.005 6.液滴的破裂过程可分为三个过程:entering阶段(图8(a)~8(d))、squeezing阶段(图8(e)~8(g))与post-breakup阶段(图8(h)).在entering阶段,液滴在进口Newton流体的驱动下从主支路通道的初始位置对称进入两个分支通道中,液滴前端为弹状,液滴尾部仍然在主支路通道中;在squeezing阶段,液滴尾部离开主支路进入到分支通道中,同时伴随着驱替Newton气体向右的挤压,液滴的颈部慢慢变薄,使得流动剪切力大于气液两相表面张力,液滴挣脱表面张力的束缚而发生破裂;在post-breakup阶段,液滴分裂成两个对称的子液滴.
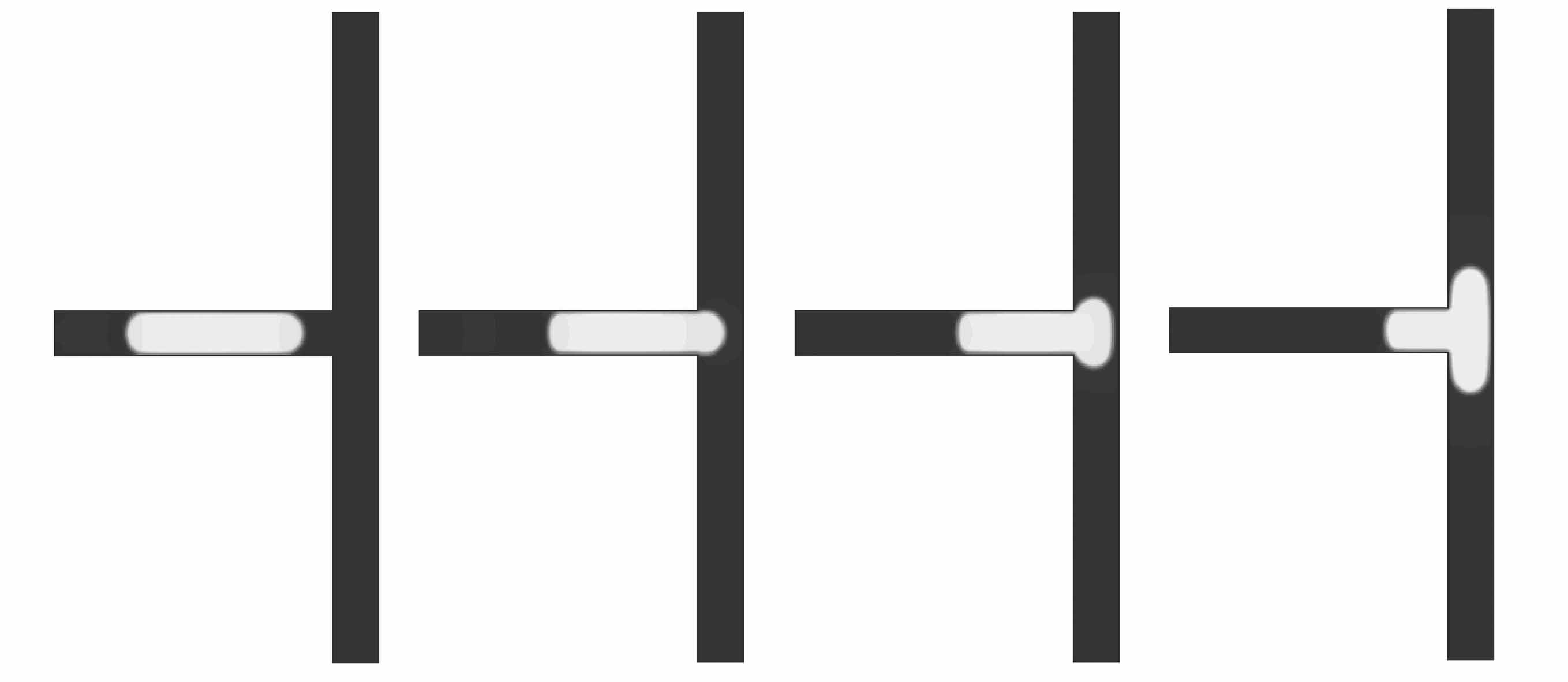
(a) T=0.5 ms (b) T=4.0 ms (c) T=6.0 ms (d) T=9.0 ms
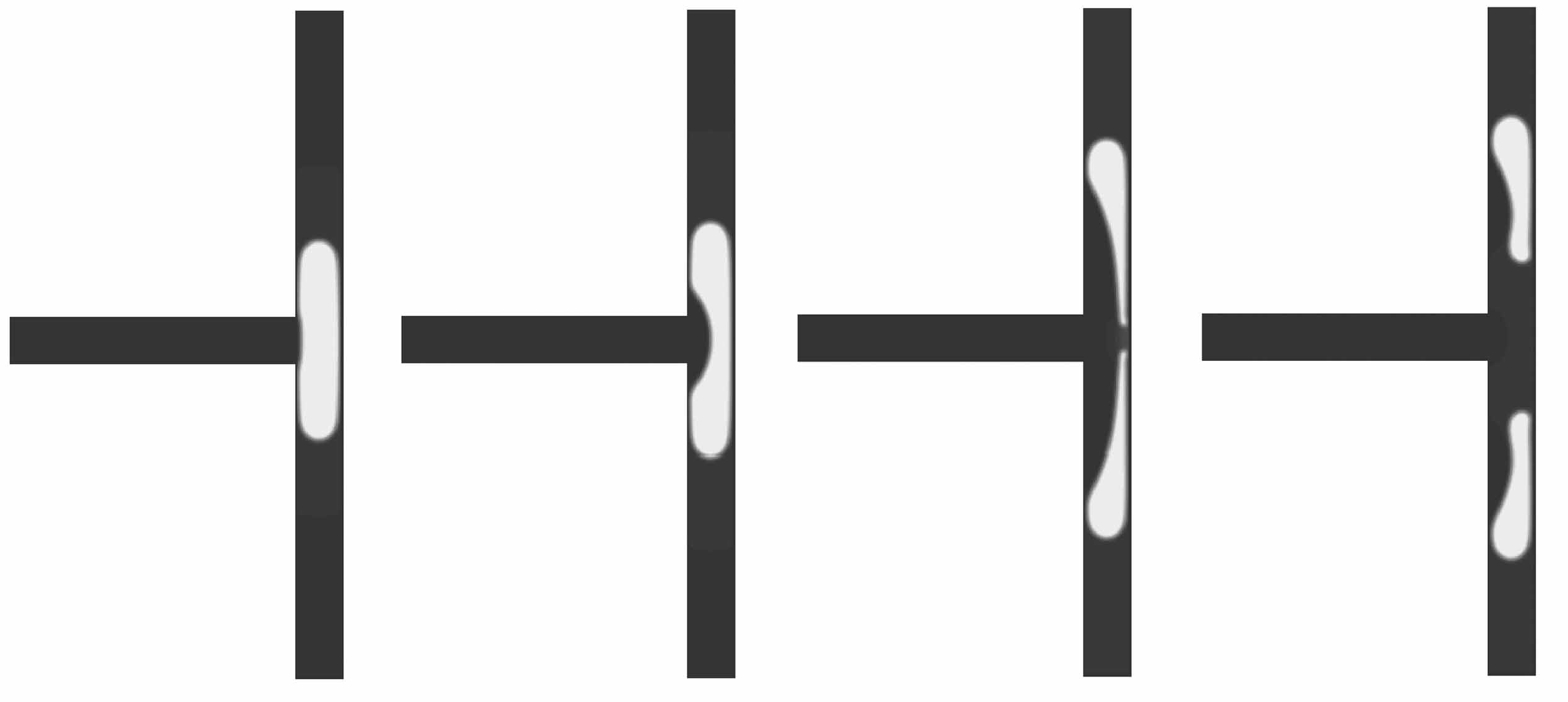
(e) T=13.0 ms (f) T=15.0 ms (g) T=24.5 ms (h) T=27.0 ms
图8 T型微通道内液滴破裂形态过程图(n=1.4)
Fig.8 Evolution of the droplet breakup form (n=1.4)
3.1.1 不同流型的液滴形变动力学行为
本小节将研究非Newton幂律流体液滴的幂律指数n对液滴破裂流型的影响.
① 阻塞破裂流型
首先研究n对阻塞破裂流型的影响,数值模拟中W0=W1=30,L0=190,L1=440,l1=52,Ca=0.056 4,液滴初始运动黏度为νl=1/6,初始黏度比M=5.0,固壁表面为完全润湿性表面(θ=180°),σ=0.005 6,液滴初始长度为l0=5.5W0=165.
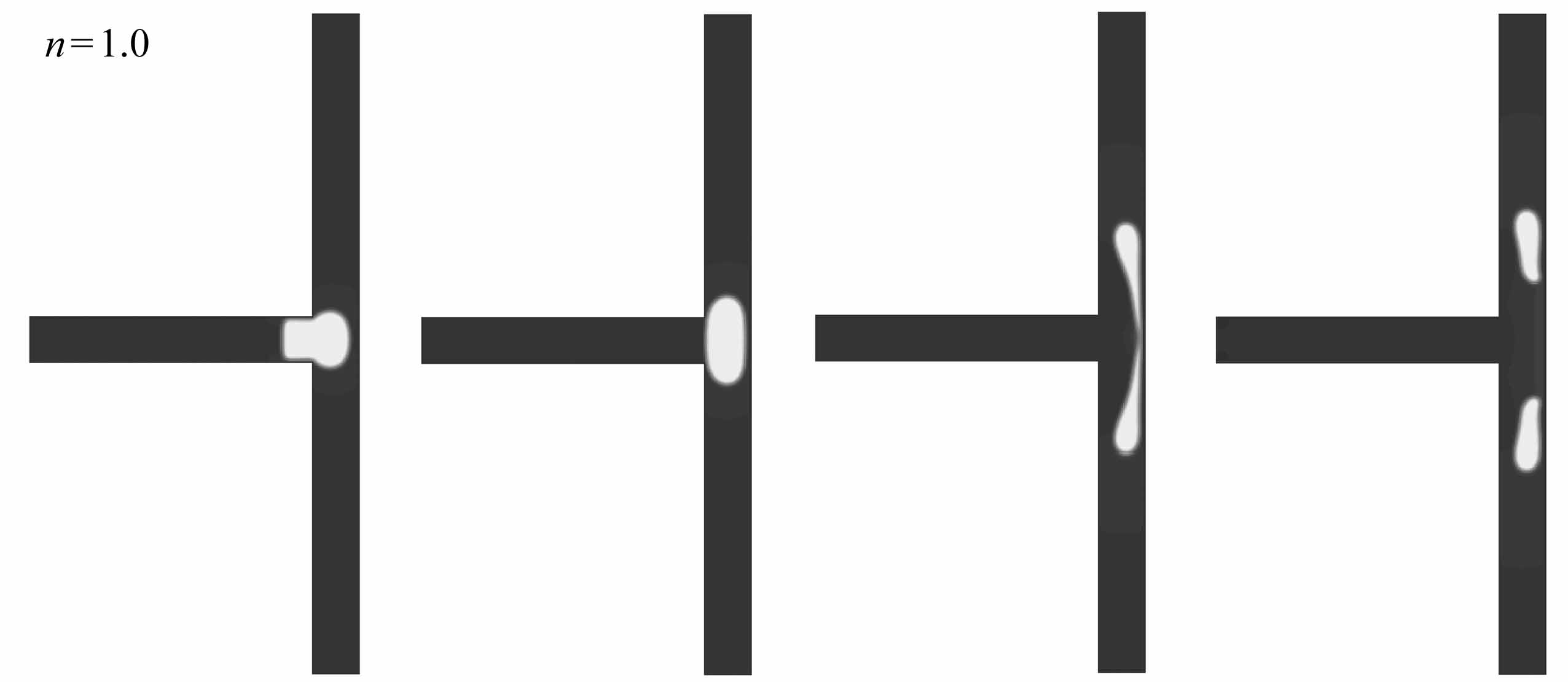
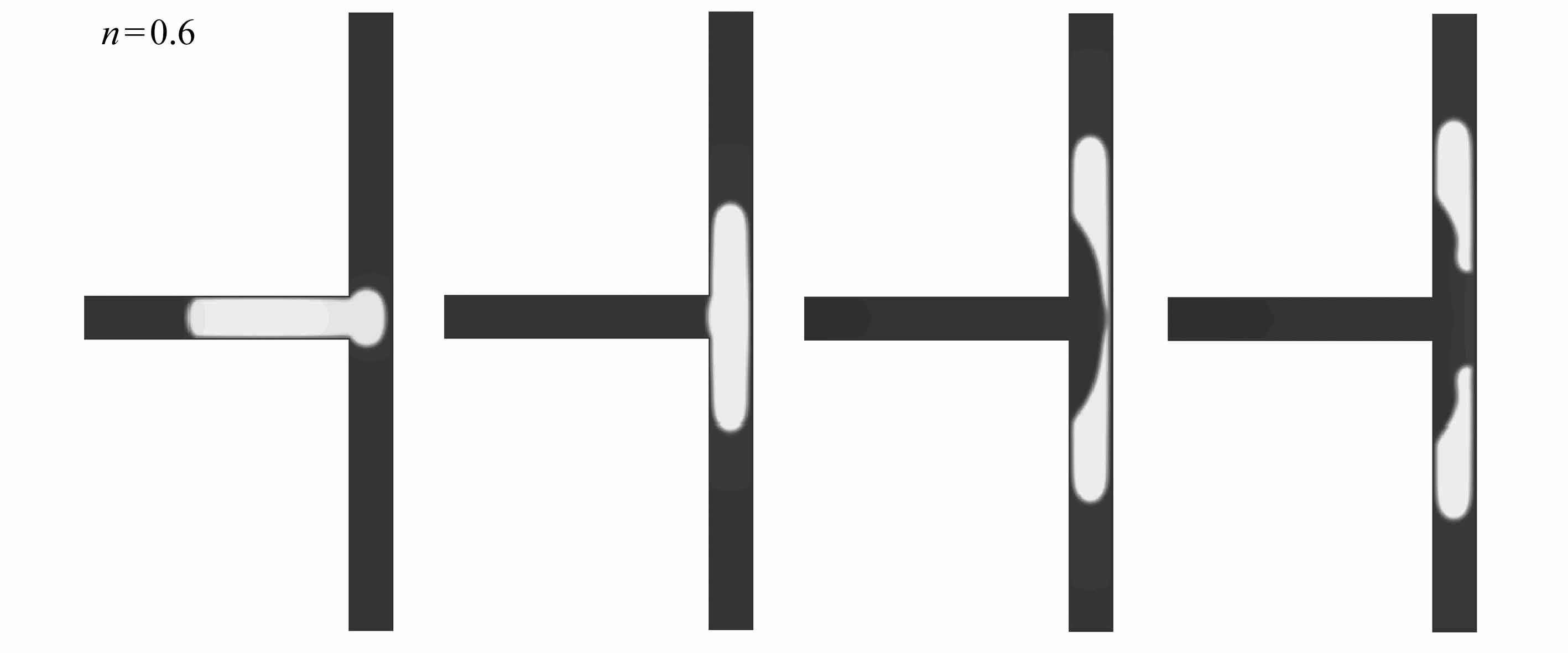
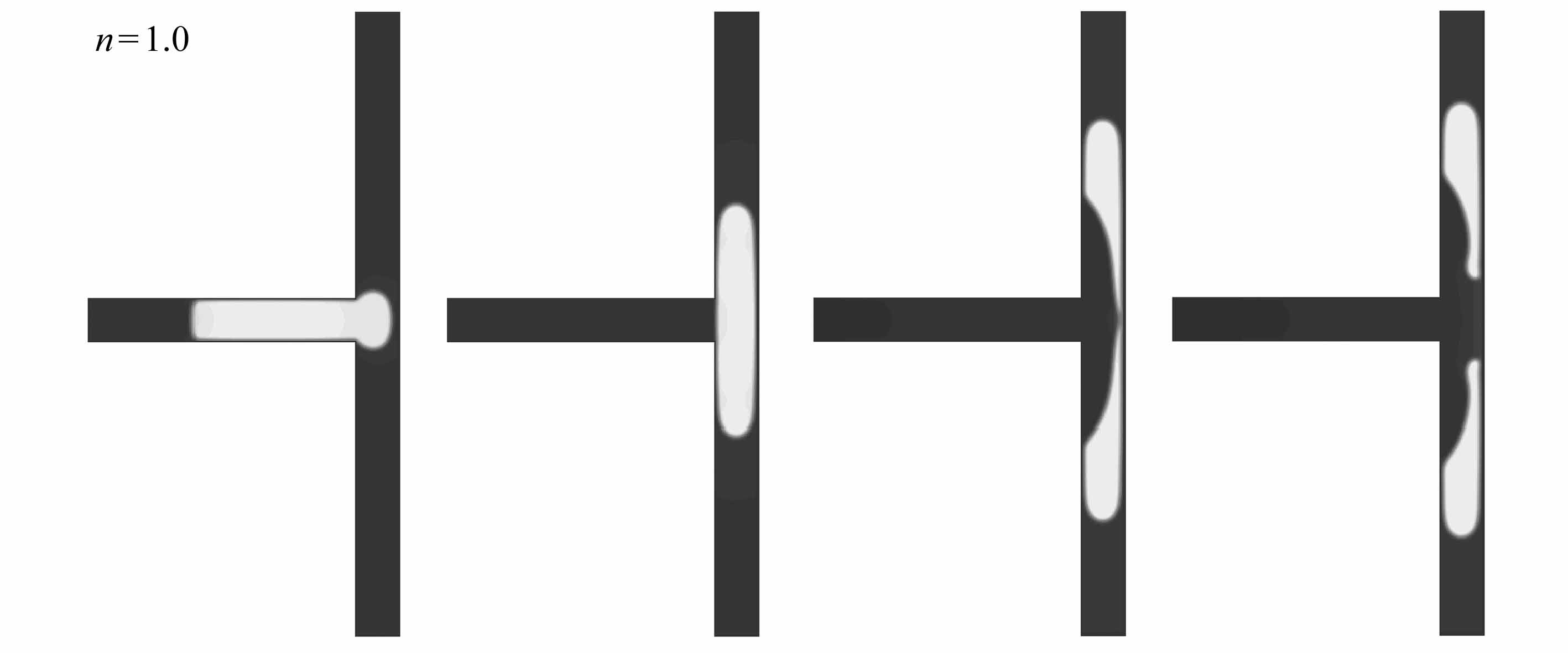
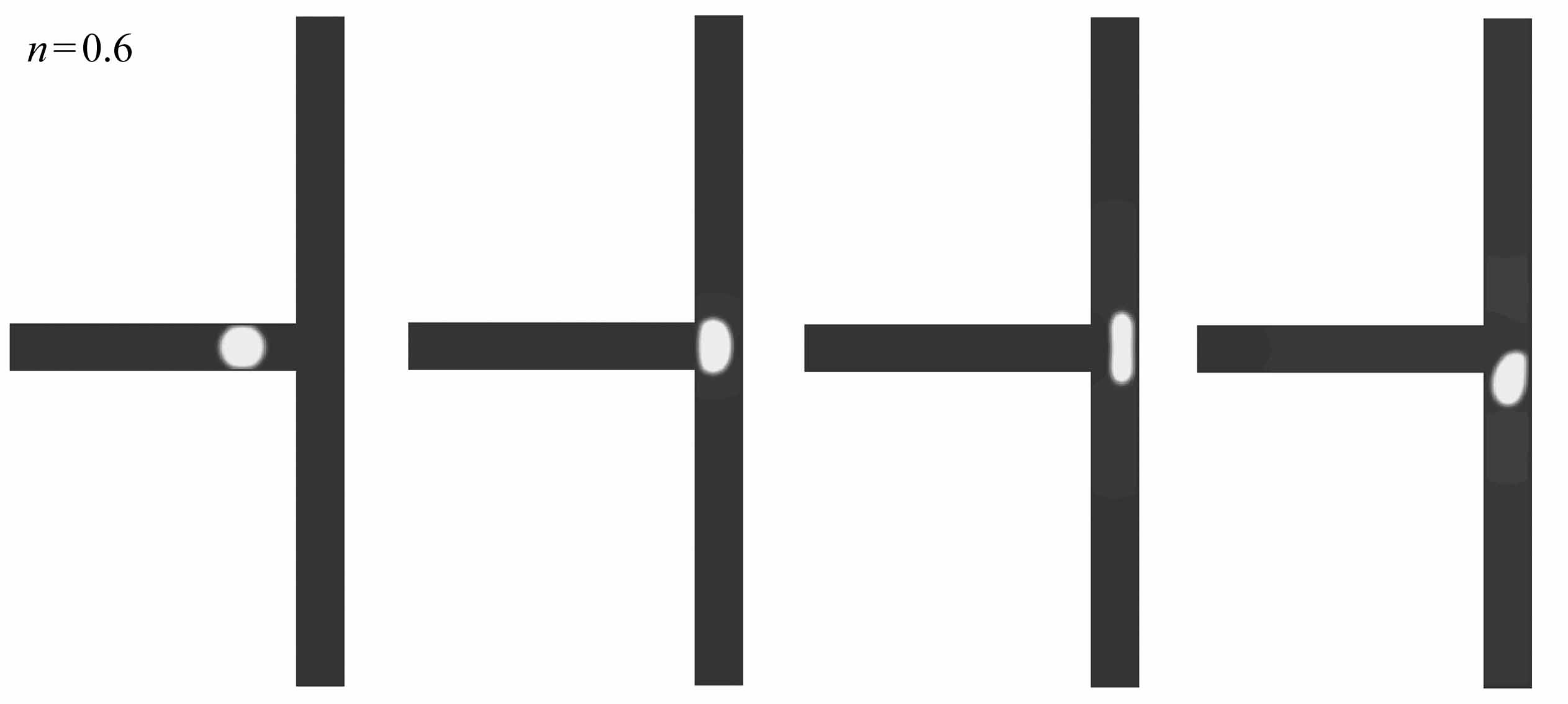
图9给出了液滴为剪切变稀(n=0.6,图9(a)~9(d))、Newton(n=1.0,图9(e)~9(h))与剪切变稠(n=1.4,图9(i)~9(l))流体时阻塞破裂流型图.从图9中可以看出,液滴的幂律指数n不同时,液滴的阻塞破裂行为的过程基本一致,其主要经历以下三个过程:entering阶段(图9(a)、9(e)、9(i))、squeezing阶段(图9(b)和9(c)、9(f)和9(g)、9(j)和9(k))与post-breakup阶段(图9(d)、9(h)、9(l)).以液滴为剪切变稀流体为例来分析其形变破裂过程.在entering阶段(图9(a)),液滴在Newton流体的驱动下从主支路通道对称进入两个分支通道中,液滴前端为弹状,且堵塞分支通道,液滴的尾部仍然在主支路通道中;在squeezing阶段(图9(b)、9(c)),液滴尾部平整地离开主支路进入到分支通道中,同时伴随着驱替Newton气体向右的挤压,液滴的颈部慢慢变薄,使得流动剪切力大于气液两相表面张力,液滴挣脱表面张力的束缚而发生破裂;在post-breakup阶段(图9(d)),分裂成两个对称的且阻塞分支通道的液滴.
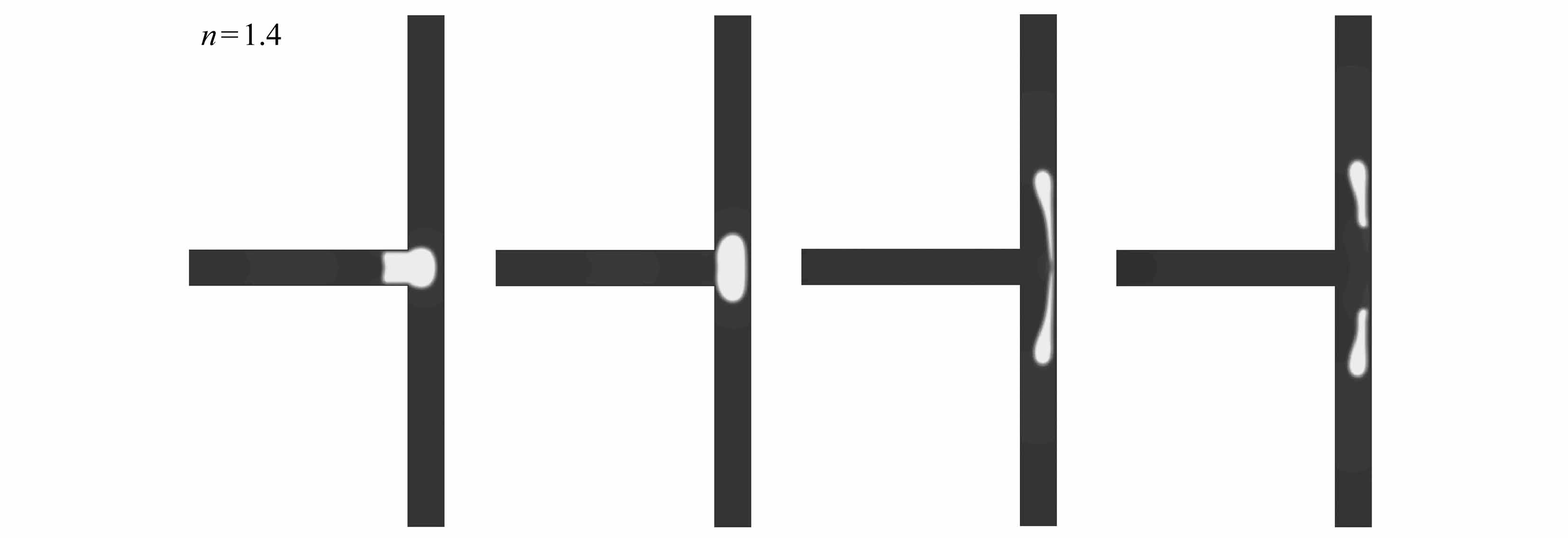
(i) T=2.5 ms (j) T=3.5 ms (k) T=9.5 ms (l) T=11.0 ms
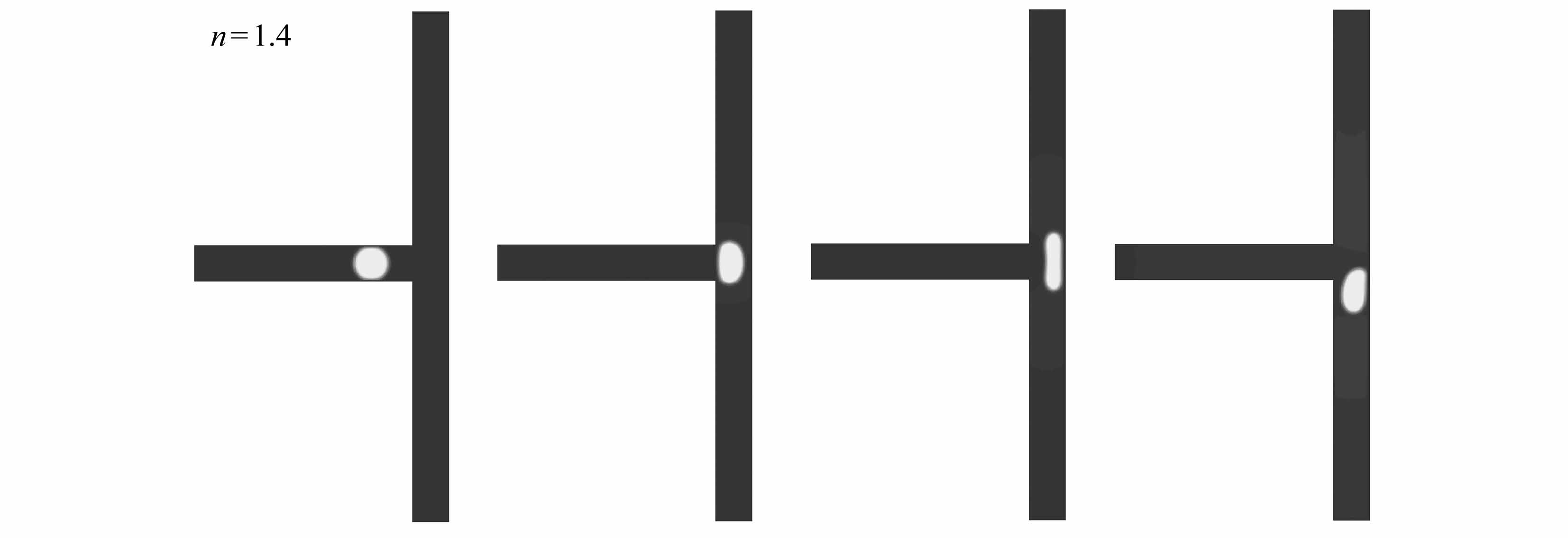
图11 液滴为剪切变稀、Newton以及剪切变稠流体时,T型微通道内隧道破裂的流型形态图
Fig.11 Evolution of the droplet breakup form with a tunnel for shear-thinning,Newtonian and shear-thickening fluids
(e) T=2.5 ms (f) T=3.5 ms (g) T=8.3 ms (h) T=9.5 ms
(a) T=2.5 ms (b) T=7.5 ms (c) T=11.6 ms (d) T=12.6 ms
(e) T=2.5 ms (f) T=7.4 ms (g) T=12.5 ms (h) T=13.6 ms

(i) T=2.5 ms (j) T=7.2 ms (k) T=13.6 ms (l) T=15.0 ms
图9 液滴为剪切变稀、Newton以及剪切变稠流体时,T型微通道内阻塞破裂时的形态演化图
Fig.9 Evolution of the droplet breakup form with obstruction for shear-thinning,Newtonian and shear-thickening fluids
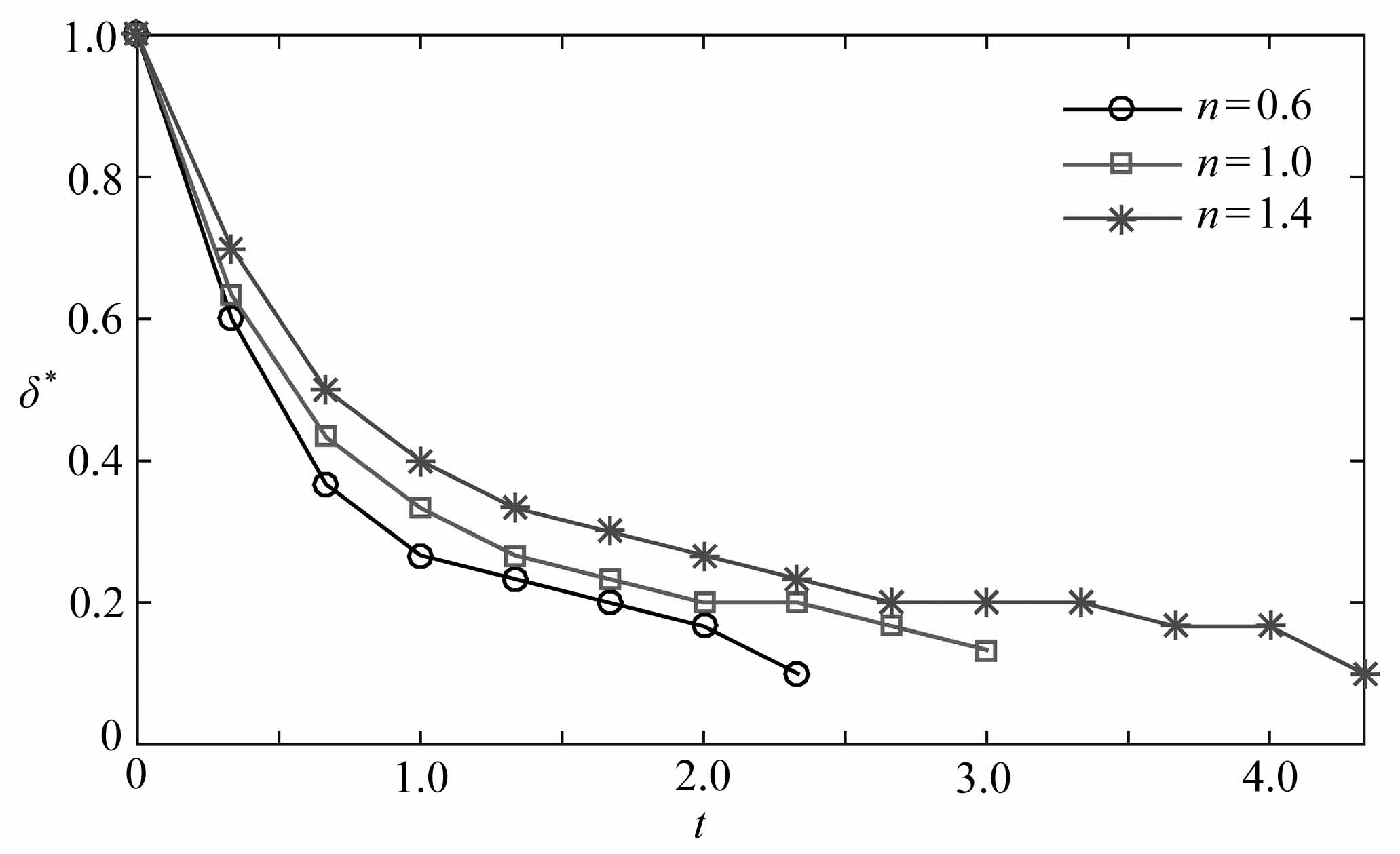
为深入分析液滴在T型微通道内阻塞破裂流型的流动机理,图10给出了无量纲液滴颈部厚度δ*与液滴前端运动距离l*随无量纲时间t的变化过程.无量纲时间t的表达式为t=u(T-Tc)/W1,其中Tc为液滴全部离开主管道进入到子管道的时刻,下文中定义为临界时刻.根据Tc的定义可知图9(b)、9(f)与9(j)分别为液滴的幂律指数n为0.6,1.0与1.4时所对应的临界时刻图.另外需要指出的是,在图10(a) 中液滴颈部厚度的最小值为0.1,这是因为当液滴颈部厚度减小到0.1时,液滴就会发生破裂,该结论与前人研究T型微通道内Newton液滴破裂机理时得到的结论一致[18,27].
(a) 液滴颈部厚度δ*
(a) Droplet neck thickness δ*
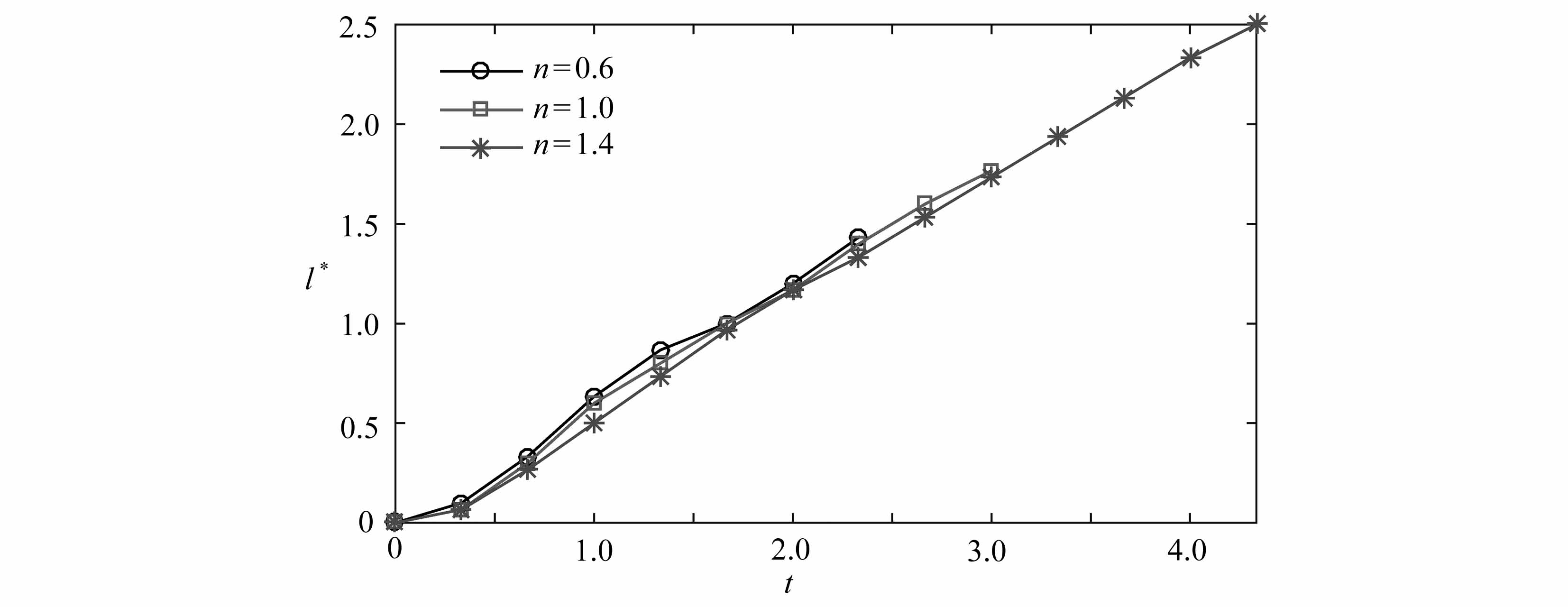
(b) 液滴前端运动距离l*
(b) Droplet motion distance tip l*
图10 阻塞破裂过程中幂律指数n不同时,得到的各参数在squeezing阶段随无量纲时间的变化情况
Fig.10 The droplet breakup with obstruction for different values of power-law exponent n,and obtained dimensionless time-varying parameters in the squeezing stage
从图10(a)可以发现,液滴颈部厚度随时间逐渐减小,且液滴的幂律指数n越大,液滴颈部厚度随时间减小得越慢.液滴的幂律指数n为0.6,1.0与1.4时,液滴颈部厚度降低到0.1的时间分别为2.45,3.0与4.1,表明随着液滴的幂律指数n的增加,液滴的破裂时间增加.这是因为剪切变稠液滴在被驱替过程中,运动黏度会变大,剪切变稀流体的运动黏度会变小,而Newton流体的运动黏度一直保持不变[35-37].液滴的动力黏度越大,被驱替过程中,受到的黏性阻力越大,因此随着液滴幂律指数n的增加液滴破裂时间变长,Liu等[23]在研究Newton液滴在T型微通道内破裂的问题时也得到了相似的结论.从图10(b)可以发现,对于不同的幂律指数n,液滴前端运动距离l*随时间线性增加,且n越大,液滴破裂时对应的前端运动距离l*越长.这是由于液滴在被驱替过程中同时受到连续相的挤压力、黏性力以及表面张力三个力的相互作用,幂律指数n越大对应液滴的运动黏度越大,则挤压力和黏性力会超过表面张力成为流体系统中起主导作用的力,导致其变得很细长.
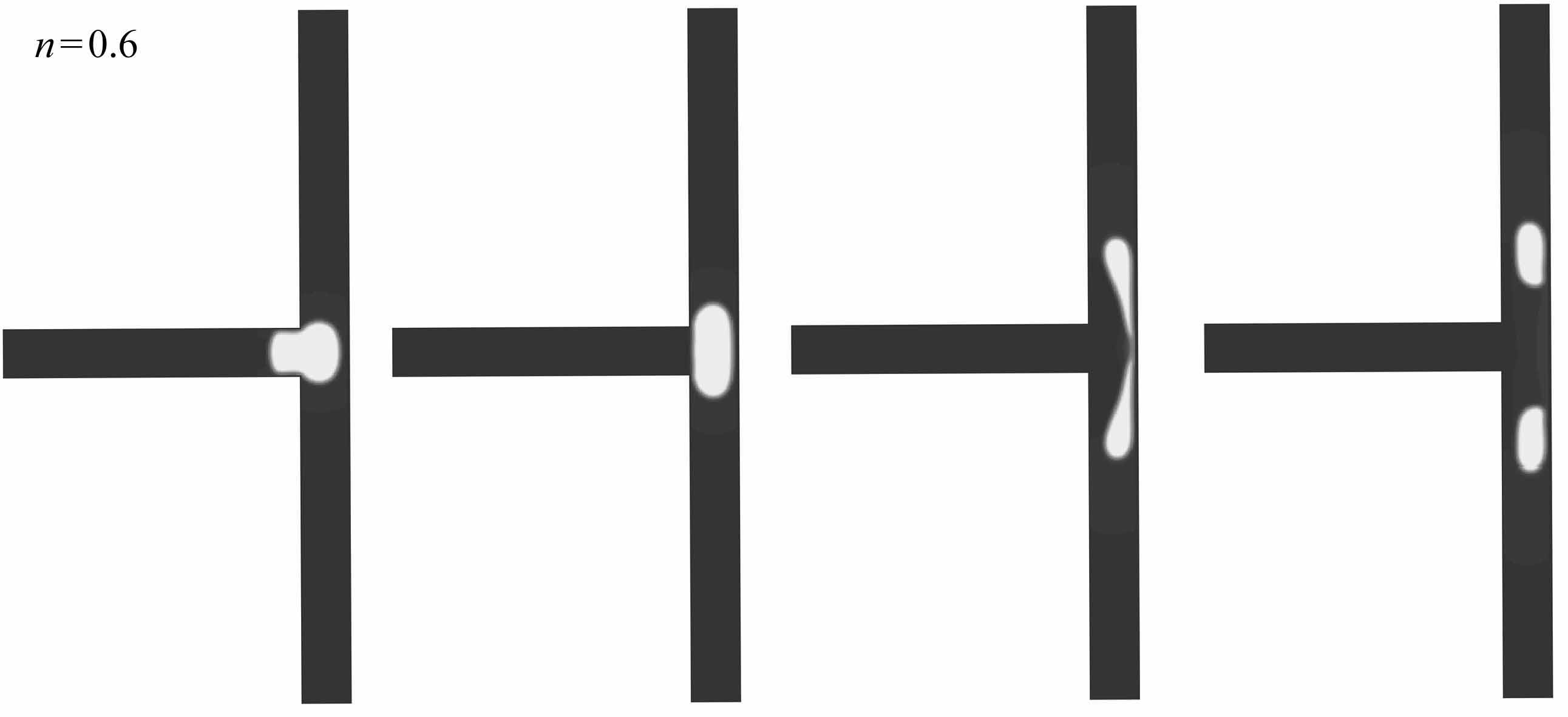
(a) T=2.5 ms (b) T=3.5 ms (c) T=7.4 ms (d) T=8.0 ms
② 隧道破裂流型
本小节将研究液滴幂律指数n对隧道破裂流型的影响,其中液滴初始长度为l0=1.75W0=52.5,l1=52,W0=W1=30,L0=190,L1=440,其他参数与上一小节相同.
图11给出液滴为剪切变稀(n=0.6,图11(a)~11(d))、Newton(n=1.0,图11(e)~11(h))与剪切变稠(n=1.4,图11(i)~11(l))流体时液滴在T型微通道内的形变过程图.从图中可以看出隧道破裂主要经历以下几个过程:entering阶段(图11(a)、11(e)、11(i))、squeezing阶段(图11(b)和11(c)、11(f)和11(g)、11(j)和11(k))与post-breakup阶段(图11(d)、11(h)、11(l)).对比隧道破裂和阻塞破裂可以发现(图9(c)和图11(c)、图9(g)和图11(g)以及图9(k)和图11(k)),这两者的主要区别是在隧道破裂流型中,液滴与壁面之间出现两条明显的隧道.
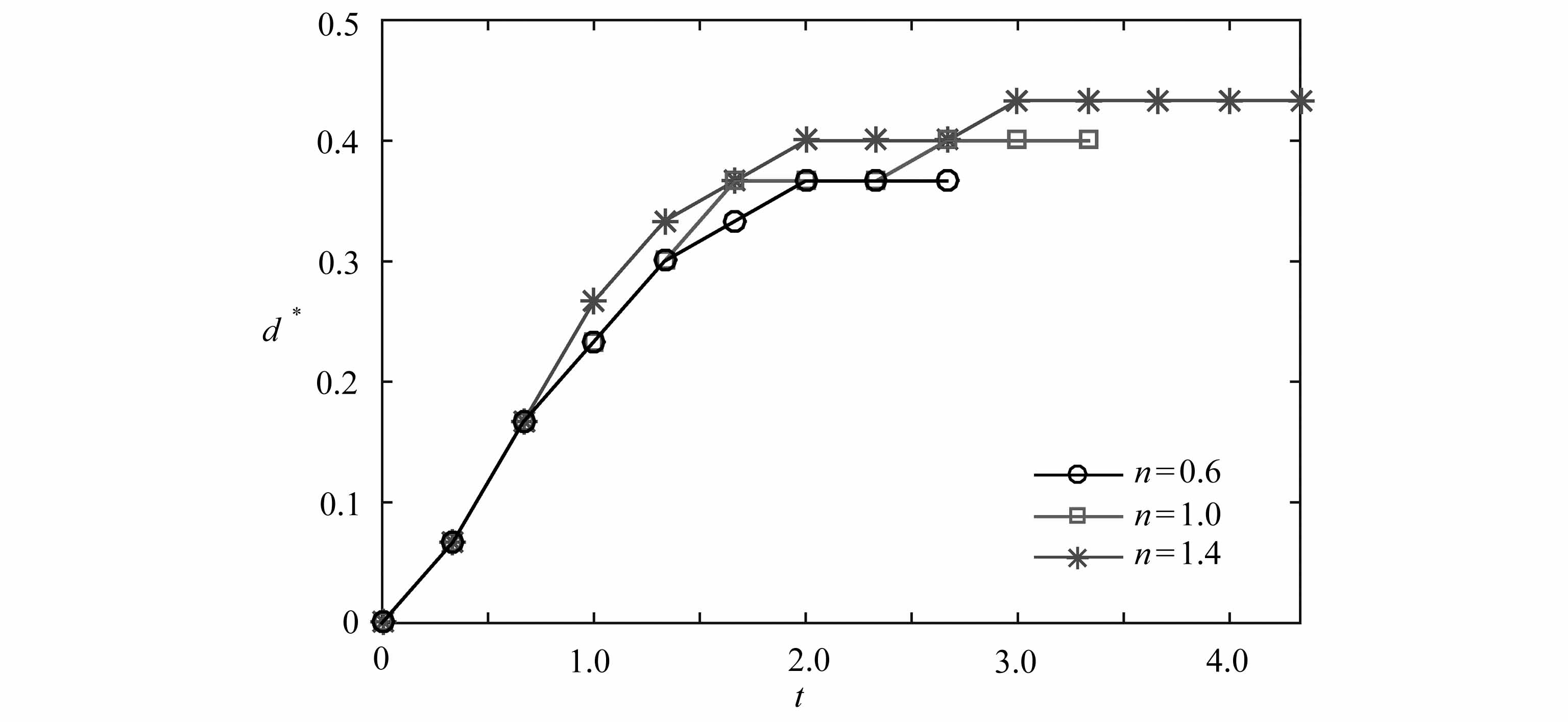
(c) 隧道宽度d*
(c) Droplet-wall gap width d*
图12 隧道破裂过程中幂律指数n不同时,得到的各参数在squeezing阶段随无量纲时间的变化情况
Fig.12 Droplet breakup with a tunnel for different values of power-law exponent n,and obtained dimensionless time-varying parameters in the squeezing stage
为分析液滴在T型微通道内隧道破裂流型的破裂机理,图12展示了无量纲液滴颈部厚度δ*、液滴前端运动距离l*与隧道宽度d*在squeezing阶段随无量纲时间t的变化过程.图11(b)、11(f)以及11(j)分别是n为0.6,1.0以及1.4时所对应的临界时刻图,从初始时刻达到临界时刻所需的时间T分别为3.5 ms,3.5 ms与3.5 ms.对比液滴为阻塞破裂流型(图9(b)、9(f)以及9(j))n为0.6,1.0以及1.4时,从初始时刻达到临界时刻所需的时间T分别为7.5 ms,7.4 ms以及7.2 ms.由此可知,液滴为阻塞破裂流型时从初始时刻到达临界时刻所需的时间比液滴为隧道破裂流型时从初始时刻到达临界时刻所需的时间要多.从图12(a)可知,在隧道破裂过程中液滴的颈部厚度随时间逐渐减小,且与阻塞破裂一样,n越大,液滴颈部厚度减小得越慢,因此液滴到达最小颈部厚度的时间随n的增加而增加.具体地说,当隧道破裂发生且n为0.6,1.0以及1.4时,达到临界颈部厚度所需的无量纲时间分别为2.67,3.45以及4.15,此时对应的液滴颈部厚度为0.15.
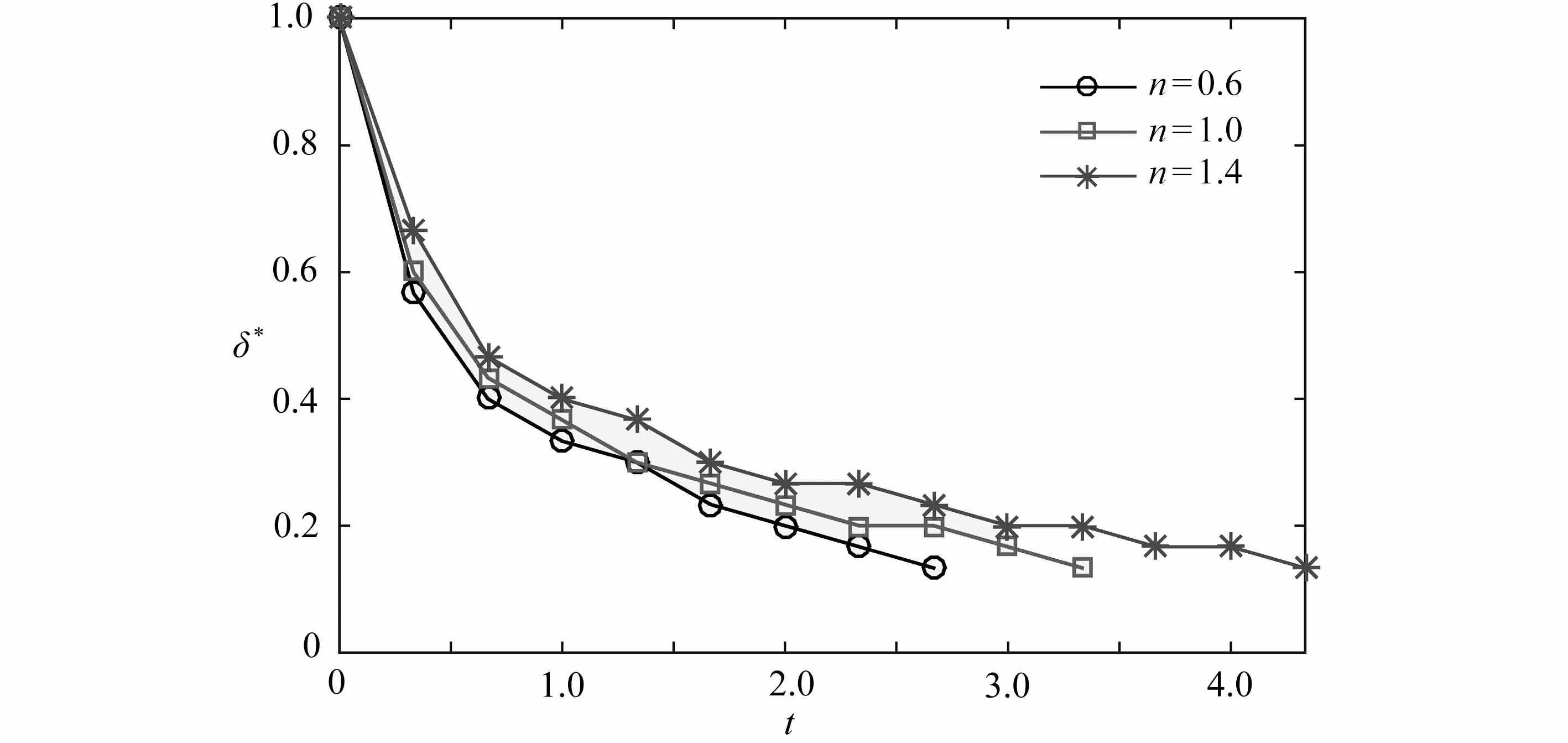
(a) 液滴颈部厚度δ*
(a) Droplet neck thickness δ*

(b) 液滴前端运动距离l*
(b) Droplet motion distance tip l*
观察图12(b)可以发现,隧道破裂过程中液滴前端运动距离l*与阻塞破裂也有较大不同.在隧道破裂过程中,液滴前端运动距离l*不再随时间线性增加,而是在演化初期先随时间快速增加,在中途出现一个转折点后,再随时间缓慢增加.该现象说明隧道的出现减慢了液滴的拉伸速率,这一结论与学者在研究Newton流体液滴破裂机理中得到的结论相似[18,27].从图12(b)还可以发现,在隧道破裂时,伴随着液滴幂律指数n的增加,液滴破裂时对应的前端运动距离l*也相应地越长.图12(c)给出了隧道宽度随无量纲时间的变化关系,从图中可以看出,不同幂律指数n时隧道宽度随时间近似呈对数增长,且由于幂律指数n的增加,液滴在被拉伸的过程中也变得越细长,因此幂律指数n越大得到的隧道间距也越大.
③ 不破裂流型
本小节将研究幂律指数n对液滴不破裂流型的影响,在数值模拟中液滴初始长度l0=30,l1=52,W0=W1=30,L0=190,L1=440.其他参数与上一小节一致.
图13给出了液滴为剪切变稀(n=0.6,图13(a)~13(d))、Newton(n=1.0,图13(e)~13(h))以及剪切变稠(n=1.4,图13(i)~13(l))流体时在T型微通道内的形变过程图.从图中可以看出,对于不同幂律指数n下的微液滴,在Newton气体的挤压下,将在分叉处向子管道的两侧延展,但流体的黏性剪切力不足以使微液滴挣脱表面张力的束缚而断裂,此时增加微小的扰动使上管道的速度减少而下管道的速度增加,最后在持续的微小扰动下(图13(c)、13(g)、13(k))液滴流向下侧(图13(d)、13(h)、13(l))[13,17,18,27].如果不加微小扰动使液滴往一侧流动(图13(c)、13(g)、13(k)),液滴会一直停留在分叉处,然后在Newton气体连续不断的冲刷下,液滴体积会越变越小,最后直至消失.
(c) n=1.4
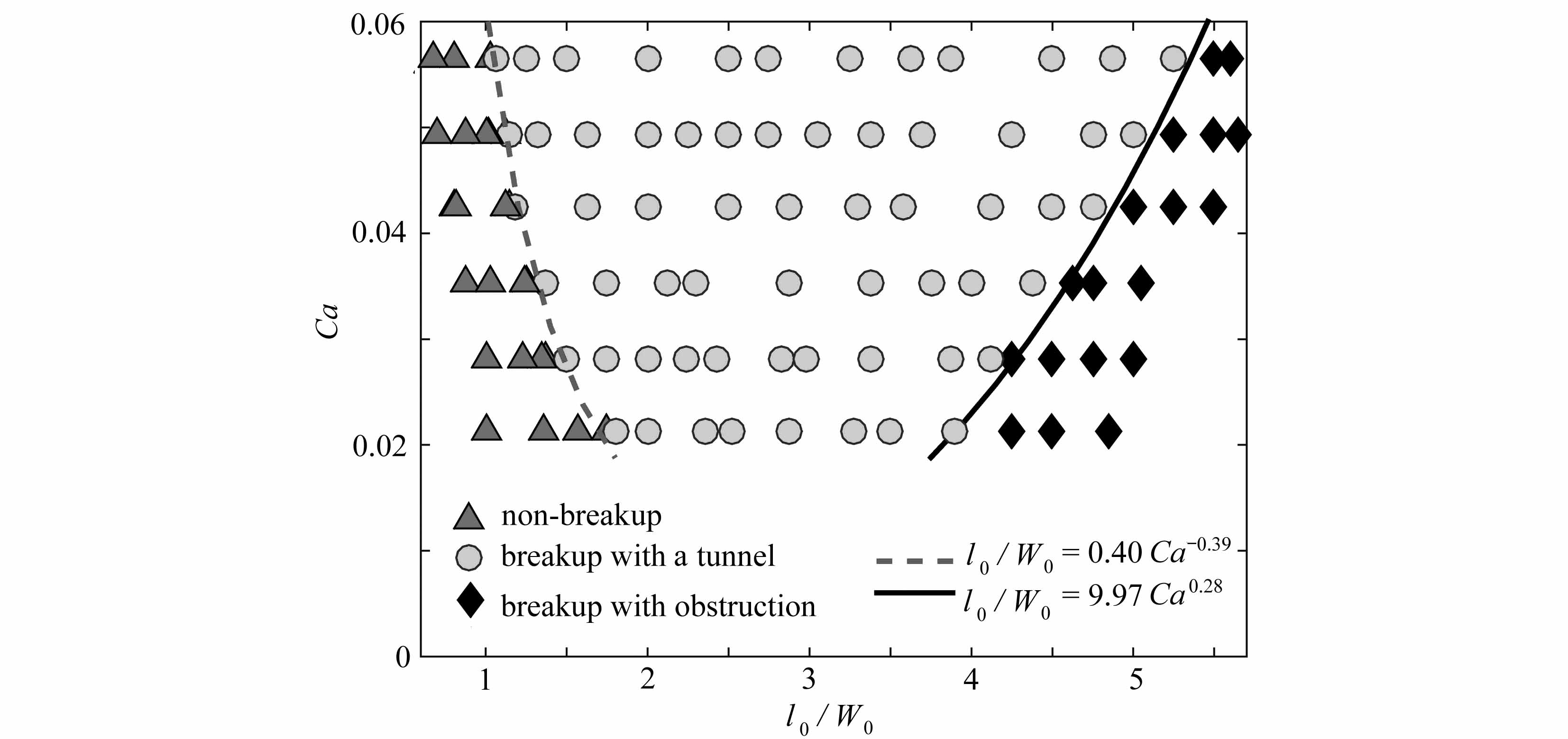
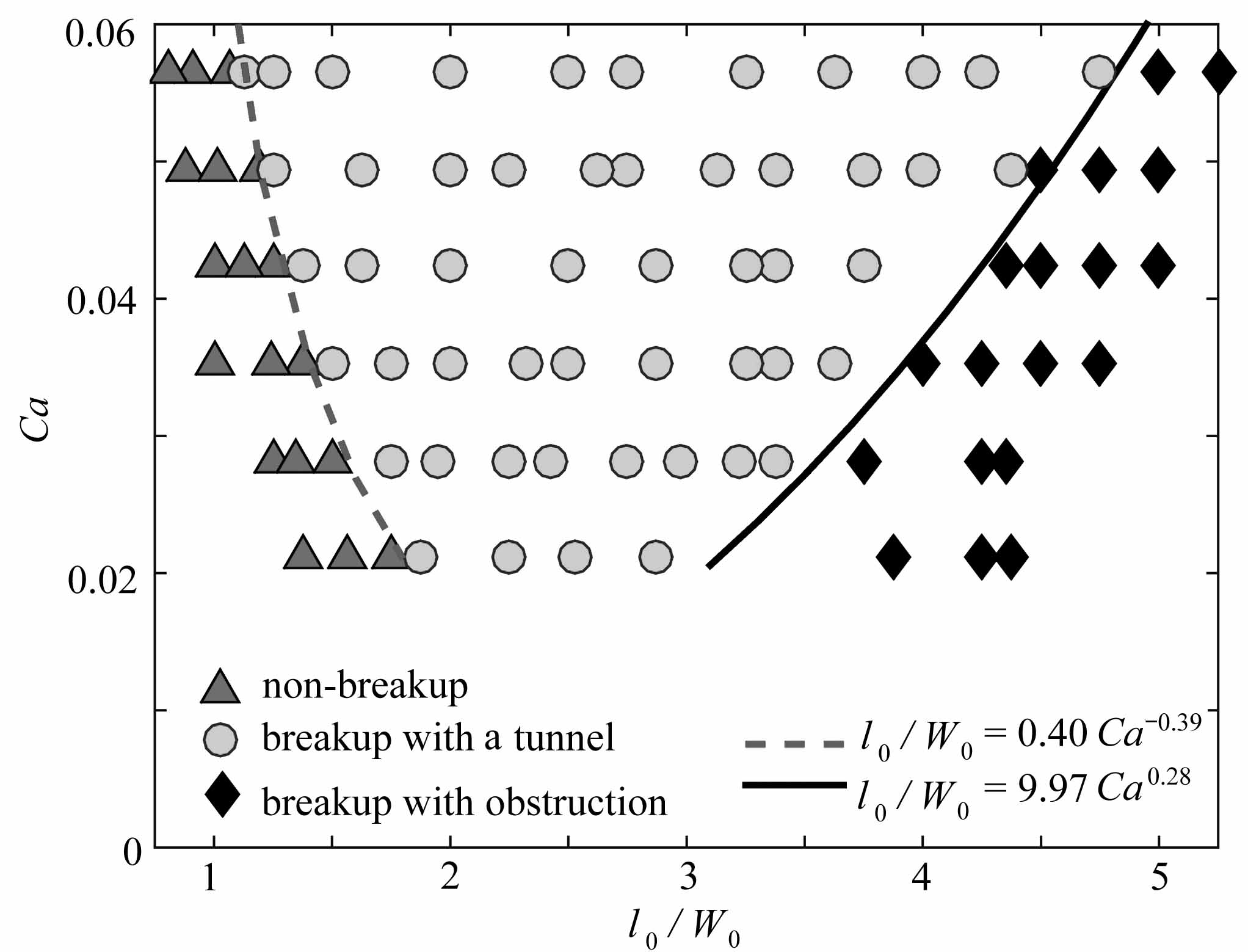
图15 液滴为剪切变稀、Newton与剪切变稠流体时得到的流型相图
Fig.15 Phase diagrams of droplet behaviours in the T-junctions for shear-thinning,Newtonian and shear-thickening fluids
(a) T=0.0 ms (b) T=2.4 ms (c) T=5.0 ms (d) T=6.8 ms

(e) T=0.0 ms (f) T=2.4 ms (g) T=5.0 ms (h) T=7.0 ms
(i) T=0.0 ms (j) T=2.4 ms (k) T=5.0 ms (l) T=7.5 ms
图13 液滴为剪切变稀、Newton与剪切变稠流体时,T型微通道内未破裂流型形态演化图
Fig.13 Evolution of the droplet non-breakup form for shear-thinning,Newtonian and shear-thickening fluids
为深入分析液滴在T型微通道内液滴未破裂流型的运动机理,图14定量分析了无量纲液滴颈部厚度δ*以及液滴前端运动距离l*随无量纲时间t的变化过程.从图中可以看出,在t=3.375时,无量纲颈部厚度δ*(图14(a))会有一个向上的波动,这是因为在t=3.0时上支路受到微小的扰动,导致液滴会向下运动的缘故,相应的上支路的液滴运动距离l*(图14(b))在t=3.0时逐渐减少,直至减为0,相应的下支路的液滴前端运动距离l*在t=3.0时逐渐增加,且n=1.4时,液滴前端运动距离l*最长.Chen等[27]研究Newton液滴也观察到了相似的现象.

(b) n=1.0
(a) n=0.6
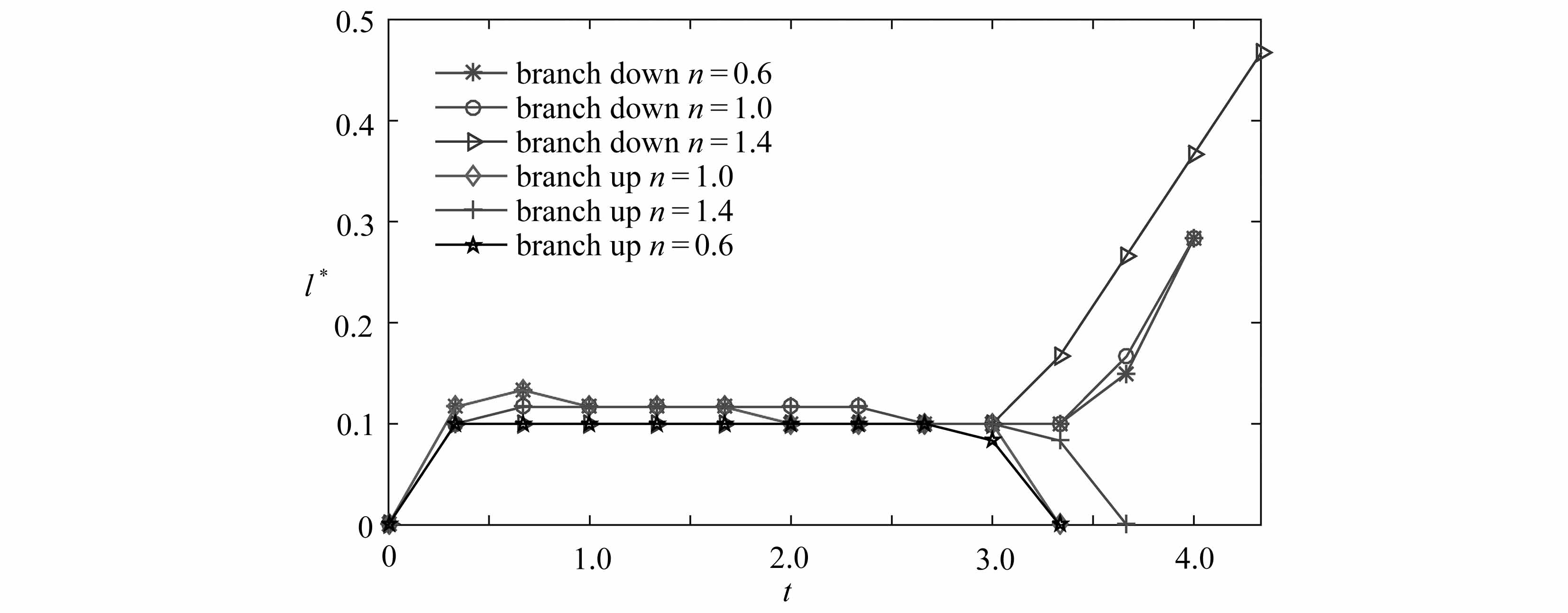
(b) 液滴前端运动距离l*
(b) Droplet motion distance tip l*
图14 液滴未破裂过程中幂律指数n不同时,得到的各参数在squeezing阶段随无量纲时间的变化情况
Fig.14 Droplet non-breakup for different values of power-law exponent n,andobtained dimensionless time-varying parameters in the squeezing stage
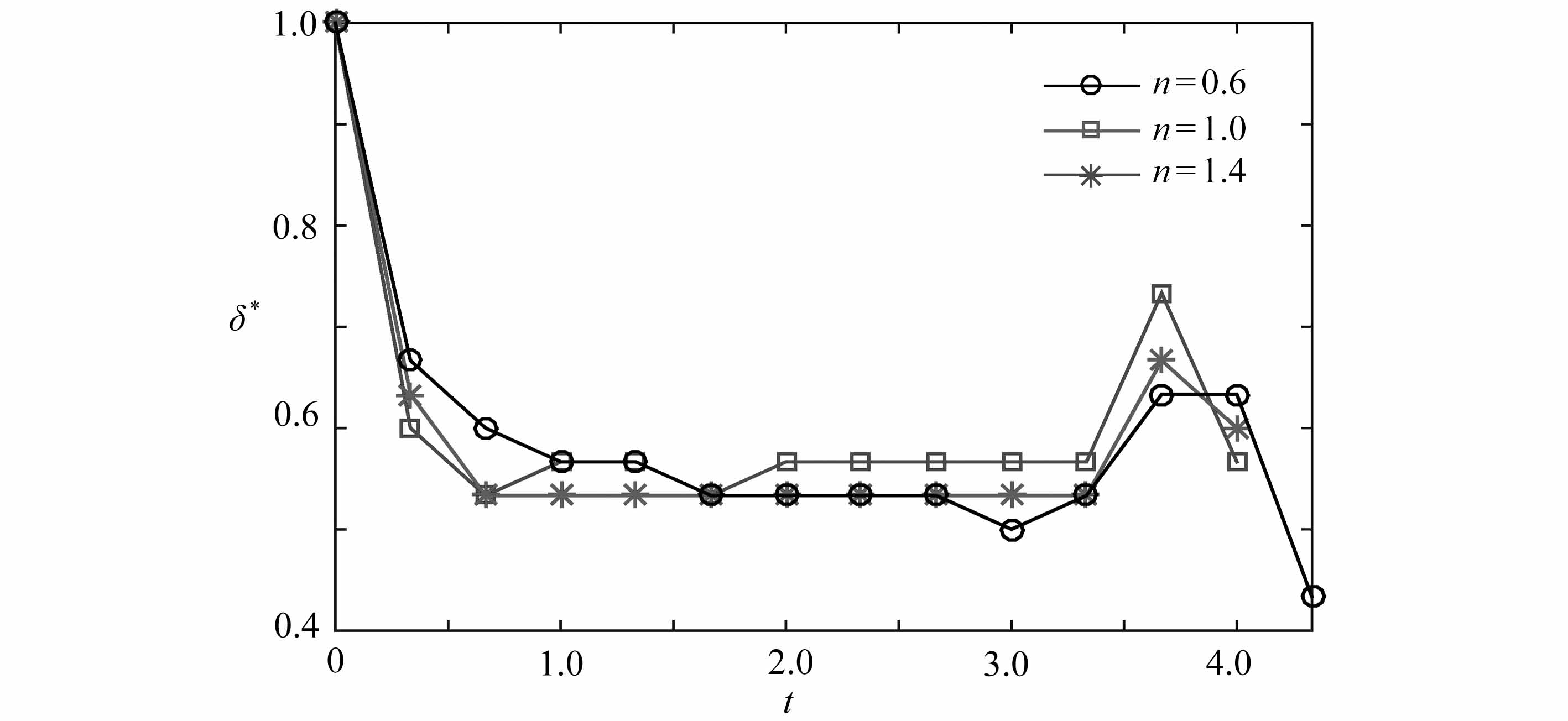
(a) 液滴颈部厚度δ*
(a) Droplet neck thickness δ*
3.2 T型微通道内幂律流体液滴的流型形态相图
从前文分析可以看出,在T型微通道中,液滴能否破裂取决于表面张力以及黏性力的相对大小.换句话说,对于一个特定的初始液滴长度l0以及给定的管道宽度W0,存在一个临界毛细数Cacr,当毛细数Ca大于临界毛细数Cacr时,T型微通道内液滴发生破裂,否则液滴不破裂.本小节中将系统地分析液滴为不同幂律指数n时三种流型之间的临界分界线,并根据数值结果,拟合得到临界毛细数Cacr与液滴初始长度l0的关系.在数值模拟中,νl=1.0/6,l1=52,η0=ηl=1.0/12,W0=W1=30,L0=190,L1=440,σ=0.005 6,固体表面是完全润湿性表面(θ=180°).
图15分别给出了非Newton液滴为剪切变稀(n=0.6)、Newton(n=1.0)与剪切变稠(n=1.4)流体时得到的相图以及三种流型过渡时对应的拟合曲线.从图中可以看出,对不同的n从不破裂到隧道破裂,以及从隧道破裂到阻塞破裂流型之间的分界线对应的毛细数Ca和l0/W0之间都满足形如l0/W0=aCab的关系,且随着非Newton液滴幂律指数n的增加,未破裂流型与隧道破裂流型的临界线将左移,而隧道破裂流型与阻塞破裂流型之间的临界分界线将右移.这是因为随着驱替的进行,液滴的黏性会发生变化.当液滴为剪切变稠流体时,其在驱替过程中动力黏度会大于初始动力黏度,当液滴为剪切变稀流体,其在驱替过程中动力黏度会小于初始动力黏度;而当液滴为Newton流体时,其动力黏度会保持不变.液滴的黏性越大,在同一Ca对应的剪切力作用下,其两相界面越容易变形,液滴会被拉伸得更长,越容易破裂.同时,液滴拉伸得越长也越不容易阻塞子管道,即难以达到阻塞破裂流型.因此幂律流体液滴的幂律指数n越大,液滴越容易破裂,但却不容易阻塞管道.
4 结 论
本文基于格子Boltzmann气液两相流非Newton模型,研究了二维T型微通道内幂律流体液滴的破裂机理.主要分析了幂律指数n对幂律流体液滴在T型微通道内的形变特性,并得到了不同流型相图的临界分界线.文中的主要结论如下:
1) 幂律流体液滴在T型微通道内有三种液滴流型,分别为阻塞破裂流型、隧道破裂流型与未破裂流型.
2) 随着幂律指数n的增加,液滴发生破裂时,其颈部厚度随时间减小得越慢,且液滴破裂所需时间越长.相对于阻塞破裂流型,隧道破裂流型在挤压阶段的液滴前端运动速度会明显减慢.
3) 液滴不破裂流型中,颈部厚度以及液滴前端运动距离随时间会出现波动.
4) 对不同的n,不破裂流型到隧道破裂流型,以及隧道破裂流型到阻塞破裂流型之间的临界分界线对应的毛细数Ca和l0/W0之间都满足形如l0/W0=aCab的幂函数关系,且随着n的增加,其对应的不破裂流型与隧道破裂流型的临界分界线将左移,隧道破裂与阻塞破裂流型分界线将右移.也即随着n的增加,液滴越容易破裂,但却越难以达到阻塞破裂.
[1] 陈金阳,李春荣,吉邢虎,等.微流控液滴操控技术及其生物分析应用[J].分析科学学报,2018,34(3):422-428.(CHEN Jinyang,LI Chunrong,JI Xinghu,et al.Droplet manipulation in microfluidics and bioanalytical applications[J].Journal of Analytical Science,2018,34(3):422-428.(in Chinese))
[2] PATABADIGE D E W,SADEGHI J,KALUBOWILAGE M,et al.Integrating optical fiber bridges in microfluidic devices to create multiple excitation/detection points for single cell analysis[J].Analytical Chemistry,2016,88(20):9920-9925.
[3] HUDGINS D,ABHARI R S.Rupture time of droplets impacted by a burst of picosecond laser pulses[J].Physical Review E,2019,99(3):1-6.
[4] HOANG D A,PORTELA L M,KLEIJN C R,et al.Dynamics of droplet breakup in a T-junction[J].Journal of Fluid Mechanics,2013,717(4):1-11.
[5] GLAWDEL T,ELBUKEN C,REN C L.Droplet formation in microfluidic T-junction generators operating in the transitional regime,Ⅱ:modeling[J].Physical Review E,2012,85(1/2):1-12.
[6] SUN X,ZHU C Y,FU T T,et al.Dynamics of droplet breakup and formation of satellite droplets in a microfluidic T-junction[J].Chemical Engineering Science,2018,188:158-169.
[7] MASHAGHI S,OIJEN A M V.Droplet microfluidics for kinetic studies of viral fusion[J].Biomicrofluidics,2016,10(2):1-8.
[8] PI Q M,MAHARJAN S,YAN X,et al.Microfluidic bioprinting:digitally tunable microfluidic bioprinting of multilayered cannular tissues[J].Advanced Materials,2018,30(43):1-10.
[9] 李樊,朱珉,付向宁.T微流控分析芯片在循环肿瘤细胞检测中的运用[J].医学与哲学,2014,35(3):72-74.(LI Fan,ZHU Min,FU Xiangning.The use of microfluidic device in the detection of the circulating Tumor cells [J].Medicine &Philosophy,2014,35(3):72-74.(in Chinese))
[10] HOU Y,XIE W Y,ACHAZI K,et al.Injectable degradable PVA microgels prepared by microfluidic technology for controlled osteogenic differentiation of mesenchymal stem cells[J].Acta Biomaterialia,2018,77:28-37.
[11] GUNES D Z.Microfluidics for food science and engineering[J].Current Opinion in Food Science,2018,21:57-65.
[12] ADAMSON D N,MUSTAFI D,ZHANG J X J,et al.Production of arrays of chemically distinct nanolitre plugs via repeated splitting in microfluidic devices[J].Lab on a Chip,2006,6(9):1178-1186.
[13] 王维萌,马一萍,王澎,等.T型微通道中微液滴被动破裂的可视化实验研究[J].工程热物理学报,2015,36(2):338-341.(WANG Weimeng,MA Yiping,WANG Peng,et al.The visualization study of breakup of drops in T-shaped micro-fluidic devices[J].Journal of Engineering Thermophysics,2015,36(2):338-341.(in Chinese))
[14] JULLIEN M C,CHING M J T M,COHEN C,et al.Droplet breakup in microfluidic T-junctions at small capillary numbers[J].Physics of Fluids,2009,21(7):1-6.
[15] HARINGA C,JONG C D,HOANG D A,et al.Breakup of elongated droplets in microfluidic T-junctions[J].Physical Review Fluids,2019,4(2):1-14.
[16] SAMIE M,SALARI A,SHAFII M B.Breakup of microdroplets in asymmetric T junctions[J].Physical Review E,2013,87(5):1-8.
[17] 王澎,陈斌.T型微流控芯片中微液滴破裂的数值模拟[J].化工学报,2012,63(4):999-1003.(WANG Peng,CHEN Bin.Numerical simulation of micro-droplet breakup in T-shaped micro-fluidic chip[J].Ciesc Journal,2012,63(4):999-1003.(in Chinese))
[18] CHEN B,LI G J,WANG W M,et al.3D numerical simulation of droplet passive breakup in a micro-channel T-junction using the volume-of-fluid method[J].Applied Thermal Engineering,2015,88:94-101.
[19] STONE H A.Dynamics of drop deformation and breakup in viscous flows[J].Annual Review of Fluid Mechanics,2003,26(1):65-102.
[20] 娄钦,罗祝清,王俊,等.基于Soret和Dufour效应的方腔内双扩散自然对流振荡特性研究[J].应用数学和力学,2018,39(2):147-159.(LOU Qin,LUO Zhuqing,WANG Jun,et al.Oscillating characteristics of double diffusive natural convection with soret and dufour effects in square cavities[J].Applied Mathematics and Mechanics,2018,39(2):147-159.(in Chinese))
[21] 陆威,王婷婷,徐洪涛,等.多孔介质复合方腔双扩散混合对流LBM模拟[J].应用数学和力学,2017,38(7):780-793.(LU Wei,WANG Tingting,XU Hongtao,et al.LBM simulation of double diffusive mixed convection in a porous medium composite cavity[J].Applied Mathematics and Mechanics,2017,38(7):780-793.(in Chinese))
[22] 谢驰宇,张建影,王沫然.液滴在固体平表面上均匀蒸发过程的格子Boltzmann模拟[J].应用数学和力学,2014,35(3):247-253.(XIE Chiyu,ZHANG Jiangying,WANG Moran,et al.Lattice Boltzmann simulation of droplet evaporation on flat solid surface[J].Applied Mathematics and Mechanics,2014,35(3):247-253.(in Chinese))
[23] LIU H H,JU Y P,WANG N N,et al.Lattice Boltzmann modeling of contact angle and its hysteresis in two-phase flow with large viscosity difference[J].Physical Review E,2015,92(3):1-12.
[24] HALLIDAY I,LAW R,CARE C M,et al.Improved simulation of drop dynamics in a shear flow at low Reynolds and capillary number[J].Physical Review E,2006,73(2):1-11.
[25] HALLIDAY I,HOLLIS A P,CARE C M.Lattice Boltzmann algorithm for continuum multicomponent flow[J].Physical Review E,2007,76(2):1-13.
[26] FU Y H,BAI L,JIN Y,et al.Theoretical analysis and simulation of obstructed breakup of micro-droplet in T-junction under an asymmetric pressure difference[J].Physics of Fluids,2017,29(3):1-12.
[27] CHEN Y P,DENG Z L.Hydrodynamics of a droplet passing through a microfluidic T-junction[J].Journal of Fluid Mechanics,2017,819:401-434.
[28] 娄钦,黄一帆,李凌.不可压幂律流体气-液两相流格子Boltzmann模型及其在多孔介质内驱替问题中的应用[J].物理学报,2019,68(21):191-203.(LOU Qin,HUANG Yifan,LI Ling.Lattice Boltzmann model of gas-liquid two-phase flow of incomprssible power-law fluid and its application in the displacement problem of porous media[J].Acta Physica Sinica,2019,68(21):191-203.(in Chinese))
[29] GUO Z L,ZHENG C G,SHI B C.Force imbalance in lattice Boltzmann equation for two-phase flows[J].Physical Review E,2011,83(2/3):1-8.
[30] DAVIES A R D,SUMMERS J L,Wilson M C T.On a dynamic wetting model for thefinite-density multiphase lattice Boltzmann method[J].International Journal of Computational Fluid Dynamics,2006,20(6):415-425.
[31] LADD A J C.Numerical simulations of particulate suspensions via a discretized Boltzmann equation,part Ⅰ:theoretical foundation[J].Journal of Fluid Mechanics,1993,271(3):285-310.
[32] LOU Q,LI T,YANG M.Numerical simulation of the bubble dynamics in a bifurcated micro-channel using the lattice Boltzmann method[J].Journal of Applied physics.2019,126(3):034301.
[33] LOU Q,GUO Z L,SHI B C.Evaluation of outflow boundary conditions for two-phase lattice Boltzmann equation[J].Physical review E,2013,87(6):1-16.
[34] 梁宏,柴振华,施保昌.分叉微通道内液滴动力学行为的格子Boltzmann方法模拟[J].物理学报,2016,65(20):139-148.(LIANG Hong,CHAI Zhenhua,SHI Baochang.Lattice Boltzmann simulation of droplet dynamics in a bifurcating micro-channel[J].Acta Physica Sinica,2016,65(20):139-148.(in Chinese))
[35] SHI Y,TANG G H.Simulation of Newtonian and non-Newtonian rheology behavior of viscous fingering in channels by the lattice Boltzmann method[J].Computers and Mathematics With Applications,2014,68(10):1279-1291.
[36] SHI Y,TANG G H.Non-Newtonian rheology property for two-phase flow on fingering phenomenon in porous media using the lattice Boltzmann method[J].Journal of Non-Newtonian Fluid Mechanics,2016,229:86-95.
[37] SONTTI S G,ATTA A.CFD analysis of microfluidic droplet formation in non-Newtonian liquid[J].Chemical Engineering Journal,2017,330:245-261.