在周期变化阶段，经过行波对流斑图和对流参数的过渡调整区后，对流进入斑图和对流参数的稳定周期变化区．对于给定的Rar=5时，行波对流的无量纲周期Tt随着Re变化的关系式为Tt=0.001 4Re2.363 5．摘要：采用二维流体力学基本方程组对Prandtl数Pr=0.72具有水平流动的对流斑图成长和动力学特性进行了数值模拟．结果说明，对于给定的相对Rayleigh数Rar=5(Rayleigh数Ra=8 540)和Reynolds数Re=22.5，行波对流斑图的成长分为三个阶段，即对流发展阶段、指数成长阶段、周期变化阶段(过渡调整区、稳定周期变化区)．行波对流的平均波数随着时间的发展或者对流斑图的成长而减小．随着相对Rayleigh数的增加，行波对流的指数成长阶段的时间变短，对流最大垂直流速的成长率变大．对于水平流动Re=5时，对流最大垂直流速的成长率γm与Rar的关系为在周期变化阶段，经过行波对流斑图和对流参数的过渡调整区后，对流进入斑图和对流参数的稳定周期变化区．对于给定的Rar=5时，行波对流的无量纲周期Tt随着Re变化的关系式为Tt=0.001 4Re2.363 5．
Rayleigh-Bénard对流作为研究非平衡对流的非线性特性及对流时空结构的模型被广泛采用[1-2]．这是因为对它的研究不仅具有重要的理论意义[3-6]，而且具有广泛的实际应用价值．在理论方面，文献[3]在研究具有缺陷的对流行波形成过程中观察到了扰动的指数成长率及非线性对流场的特性．文献[4]研究了有限腔体中弱的负分离比情况下的对流特性．文献[5-8]揭示了行波、局部行波及不同结构局部行波的动力学特性．文献[9-10]发现了随着反映加热特性的Rayleigh数的变化而出现的不同结构的行波解．在实际应用方面，天然液化气储罐安全性问题，地幔对流运动，水库、湖泊、海洋中温盐双扩散对流问题，冻土路基的处理等问题都会应用到Rayleigh-Bénard对流的原理[11]．人们已经发现，对Rayleigh-Bénard对流系统施加一个水平流动，可以改变Rayleigh-Bénard对流系统的非线性特性及对流时空结构，形成一个新的斑图形成系统．关于这方面的研究也已经获得许多进展．文献[12-15]就边界条件、进口条件及水平流动对斑图的影响进行了数值模拟研究．文献[16-19]就对流斑图的成长、局部行波对水平来流的依赖性及局部行波的结构进行了数值分析研究．文献[20-21]探讨了行波及局部行波的结构特性．文献[22-24]通过数值模拟讨论了周期变化的局部行波的时空结构．文献[25]给出了具有水平流动的充分发展的行波的扰动方程组，并对其进行了数值分析．文献[26-27]对倾斜腔体与侧向加热腔体的对流进行了研究．所有这些研究都为深入了解并进一步探讨具有水平流动的行波对流的非线性特性及对流时空结构提供了基础．由于Rayleigh-Bénard对流的复杂性和它在探索非平衡对流非线性特性及对流时空结构的重要地位，自从Rayleigh-Bénard对流问题被发现一百多年来，这个对流系统的研究一直被人们所重视．进一步探讨这个对流系统中的非线性动力学特性问题具有重要的现实意义．
本文采用二维流体力学基本方程组对Prandtl数Pr=0.72具有水平流动的对流斑图成长和动力学特性进行了数值模拟，发现行波对流斑图的成长分为三个阶段，即对流发展阶段、指数成长阶段、周期变化阶段(过渡调整区、稳定周期变化区)．行波对流的平均波数随着时间的发展或者对流斑图的成长而减小．在指数成长阶段，对于Reynolds数Re=5时，对流垂直最大流速的成长率γm与相对Rayleigh数Rar的关系为
在周期变化阶段，经过行波对流斑图和对流参数的过渡调整区后，对流进入斑图和对流参数的稳定周期变化区．
对于底部加热并施加水平流动的两平面腔体内的运动，当上下面之间的温度差ΔT超过某个临界值时对流发生．图1为施加水平流动的对流示意图．考虑密度变化为ρ=ρ0[1-α(T-T0)]，其中，ρ为密度，T为温度，α为体积膨胀系数，α=-(1/ρ0)(∂ρ(T,p)/∂T)，p为压强，下标0表示相应物理量的参考值．这时，对流运动的流体力学方程组为
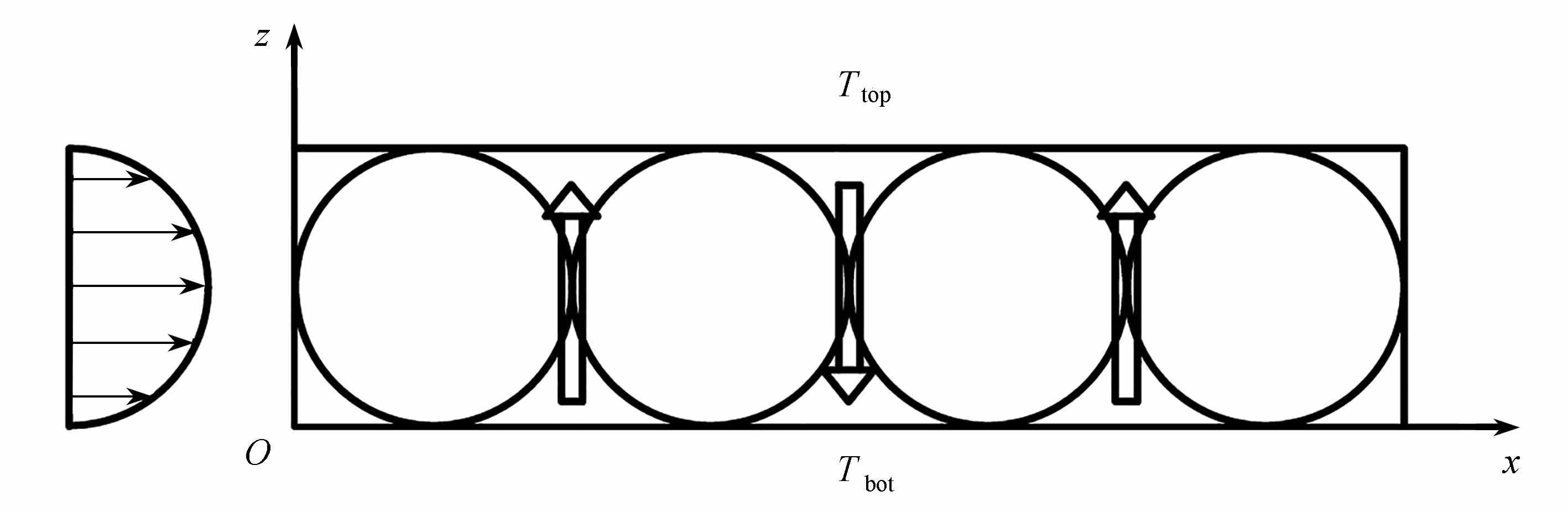
图1 施加水平流动的对流
Fig.1 Convection with horizontal flows
·U=0,
(1)
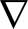)U=-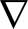
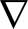2U-α(T-T0)g,
(2)
)T=κ2T,
(3)
式中，U(u,0,w)为速度矢量场，τ为时间，ν为运动黏性系数，κ为热扩散系数，κ=λ/(ρ0cp)，λ为热传导系数，cp为定压比热容，g=-gez，ez为z方向的单位矢量，g为重力加速度．
上下壁面的速度为
在z=0，d时，u=w=0,
式中，d为腔体高度．
上下壁面温度恒定，即
在z=0时，T=Tbot;
在z=d时，T=Ttop,
式中，Ttop为上壁面温度，Tbot为下壁面温度．
左端部进口条件为
在x=0时，
其中umax为水平流动最大值;
在x=0时，
在x=Lx时，右端部出口为自由出流,其中，Lx为腔体长度．
流速初始条件为 u=w=0，初始温度取平均值(一般取T=293.15 K)．
采用SIMPLE算法对式(1)～(3)的流体力学基本方程组进行数值求解．对流项和扩散项采用二阶迎风差分格式，时间项采用一阶差分．文献[17]对d/20和d/30两种网格的比较说明最大垂直流速很接近，因此，采用d/20的网格．无量纲时间步长采用Δt=Δτ/(d2/κ)=0.002 1．为了说明方便，腔体尺寸无量纲化为X=x/d,Z=z/d．通常温度差ΔT采用Ra=(αgd3/(κν))ΔT来表征，临界值取为Rac=1 708，相对Rayleigh数为Rar=Ra/Rac．水平流动由Reynolds数Re=umaxd/ν用来表征．物性参数用Prandtl数Pr=ν/κ来表征．本文模拟采用的Prandtl数Pr= 0.72，腔体长高比Γ=Lx/d=12．
对于本文的对流模型，对流系统由水平流动Reynolds数和相对Rayleigh数控制．图2给出了Prandtl数Pr=0.72的流体在相对Rayleigh数Rar=5时水平流动Reynolds数Re=22.5的情况下，对流垂直最大流速随着时间的发展．可以看出，行波对流的发展为以下三个阶段，即对流发展阶段、指数成长阶段、周期变化阶段．
对流发展阶段也是对流的初生、启动阶段，在这一阶段由于热作用较弱，对流已经初生，但对流垂直最大流速随着时间的发展缓慢，基本保持为常数．对流被水平流动抑制．这一阶段大概需要t=0.4的时间．经过这段时间的加热后，较大的温度差形成，在水平流动Reynolds数和相对Rayleigh数的相互作用下,对流垂直最大流速随着时间按指数规律发展．对流垂直最大流速的成长率保持为常数．对流进入指数成长阶段，这一阶段时间较短．然后，对流变成周期变化阶段，在这一阶段，对流首先经过周期变化的过渡调整，然后进入稳定的周期变化阶段．在水平流动Reynolds数和相对Rayleigh数的相互作用平衡下，对流垂直最大流速随着时间围绕着某个值周期变化．对流垂直最大流速饱和．
图3给出了相应于图2流体参数情况下，对流垂直最大流速在成长阶段时的行波对流结构．每个框子内为某一时刻的流线图，每两个框子之间的时间间隔Δt=0.21，时间发展方向向上．开始对流初生阶段，腔体中基本没有扰动，t=0.42后从下游发生，向上游发展．行波对流向下游传播，行波的波数和波长随着时间调整，对流振幅迅速增大．大致在6<X<12的范围内，水平流动和热对流的相互作用下的行波对流控制了局面，平均波数为k=8π/6=4.19．大致在0<X<6的上游范围内，水平流动支配了流动区域，热作用被抑制．此区域为水平流动．从而，在腔体内形成了局部行波对流．但随着时间的发展，水平流动控制的范围在缩小，行波对流控制的范围在扩大．位于4<X<6范围的水平流动和行波对流的交界面不断向左移动．这个调整过程明显．
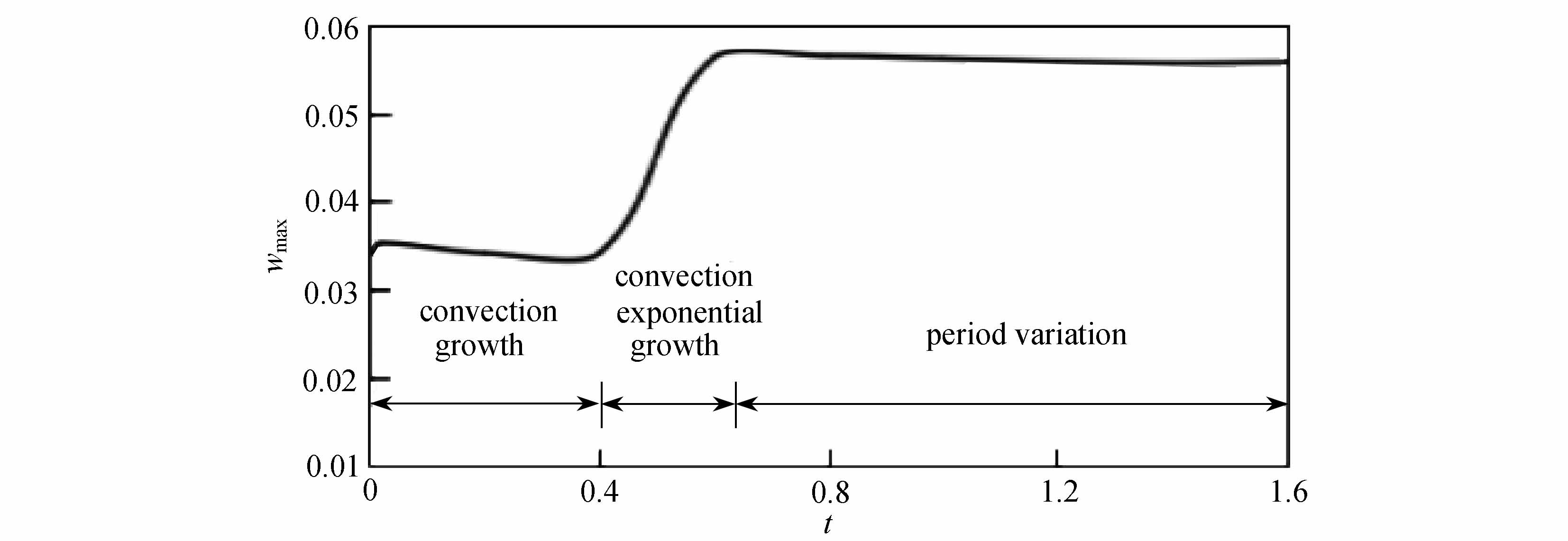
图2 Rar=5和Re=22.5时行波对流垂直最大流速的成长
Fig.2 The growth of the maximum vertical velocity in traveling wave convection for Rar=5 and Re=22.5
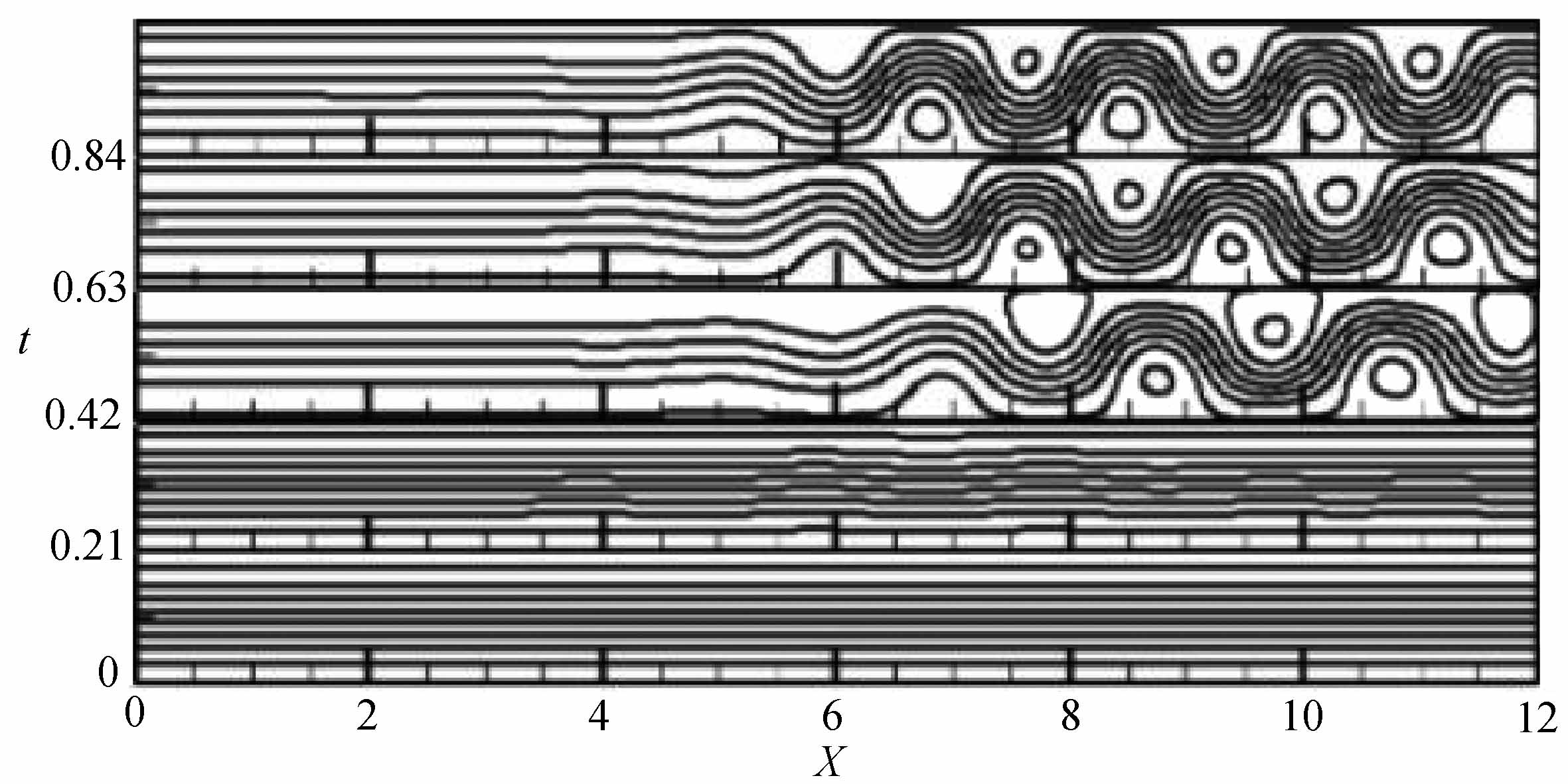
图3 行波对流成长阶段的时空结构
Fig.3 The spatiotemporal structure in growth stage of traveling wave convection
在对流分析中，一般用对流垂直最大流速来特征对流振幅．图4给出了水平流动Reynolds数Re=5时七个不同相对Rayleigh数情况下，行波对流的指数成长阶段对流垂直最大流速随着时间的变化．可以看出，不同的相对Rayleigh数对应于不同的对流垂直最大流速成长曲线．行波对流的初始发展阶段随着相对Rayleigh数的增加而变短．这是因为较大的相对Rayleigh数，意味着较大的温度差，相应的底部流体加热的较快，从而促使热扰动更迅速的成长．经过短暂的初始发展阶段后，行波对流的成长进入指数阶段．在这一阶段，行波对流的成长率保持为常数．随着相对Rayleigh数的增加，行波对流的指数成长的起始点时间越早，结束点时间也越早．行波对流的指数成长阶段的时间变短，对流垂直最大流速随着时间的变化率变大而变大，也就是说，对流垂直最大流速的成长率变大．最后，行波对流达到稳定，对流垂直最大流速保持周期变化的常数．相对Rayleigh数越大，行波对流稳定下来的对流垂直最大流速越大．这是因为相对Rayleigh数越大，意味着温度差越大，相应的热扰动越大，从而形成较大的对流垂直最大流速．
对于底部均匀加热的腔体，指数成长阶段的对流垂直最大流速wmax可表示为[3]
wmax∝exp(γmt),
(4)
式中，γm是指数成长阶段的对流垂直最大流速的成长率．指数成长阶段的对流垂直最大流速的成长率可被定义为
γm=d(ln wmax)/dt．
(5)
根据对流垂直最大流速的成长率的定义式，对图4中的参数进行分析计算，将对流垂直最大流速的成长率和相对Rayleigh数的关系点绘于图5．可以看出，指数成长阶段的对流垂直最大流速的成长率随着相对Rayleigh数的增加而增加，呈曲线变化关系．对其进行拟合分析，可得对流垂直最大流速的成长率与相对Rayleigh数的关系为
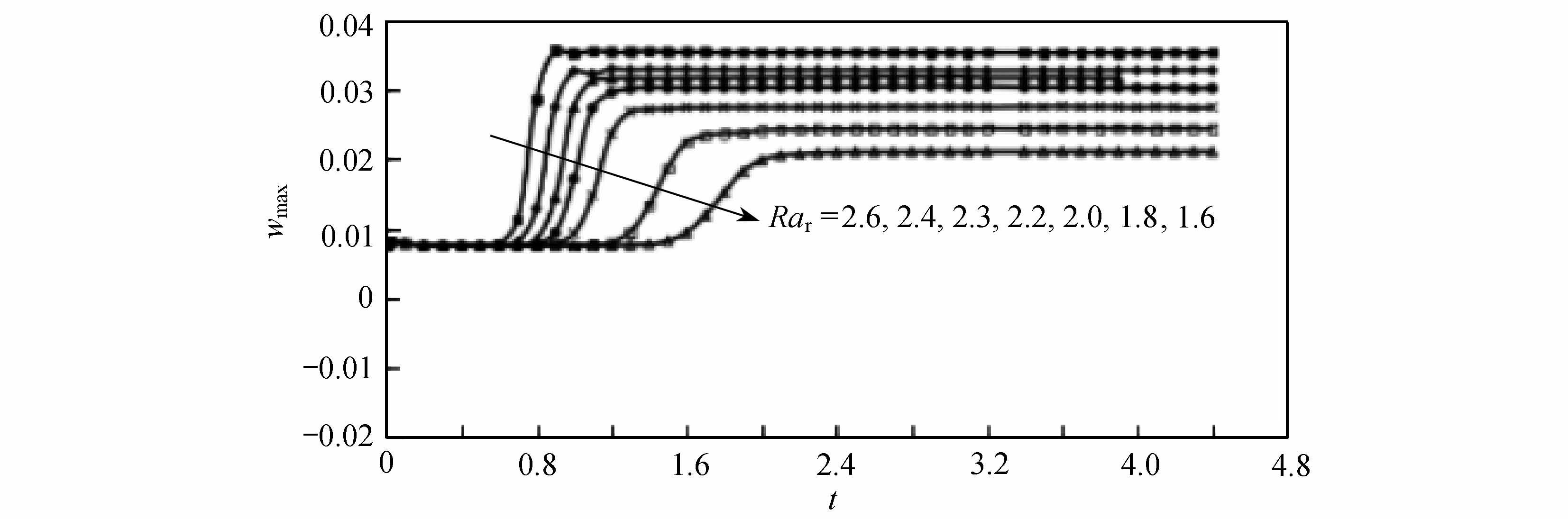
图4 Re=5时不同相对Rayleigh数下垂直最大流速的成长
Fig.4 The growth of the maximum vertical velocity for different reduced Rayleigh numbers for Re=5
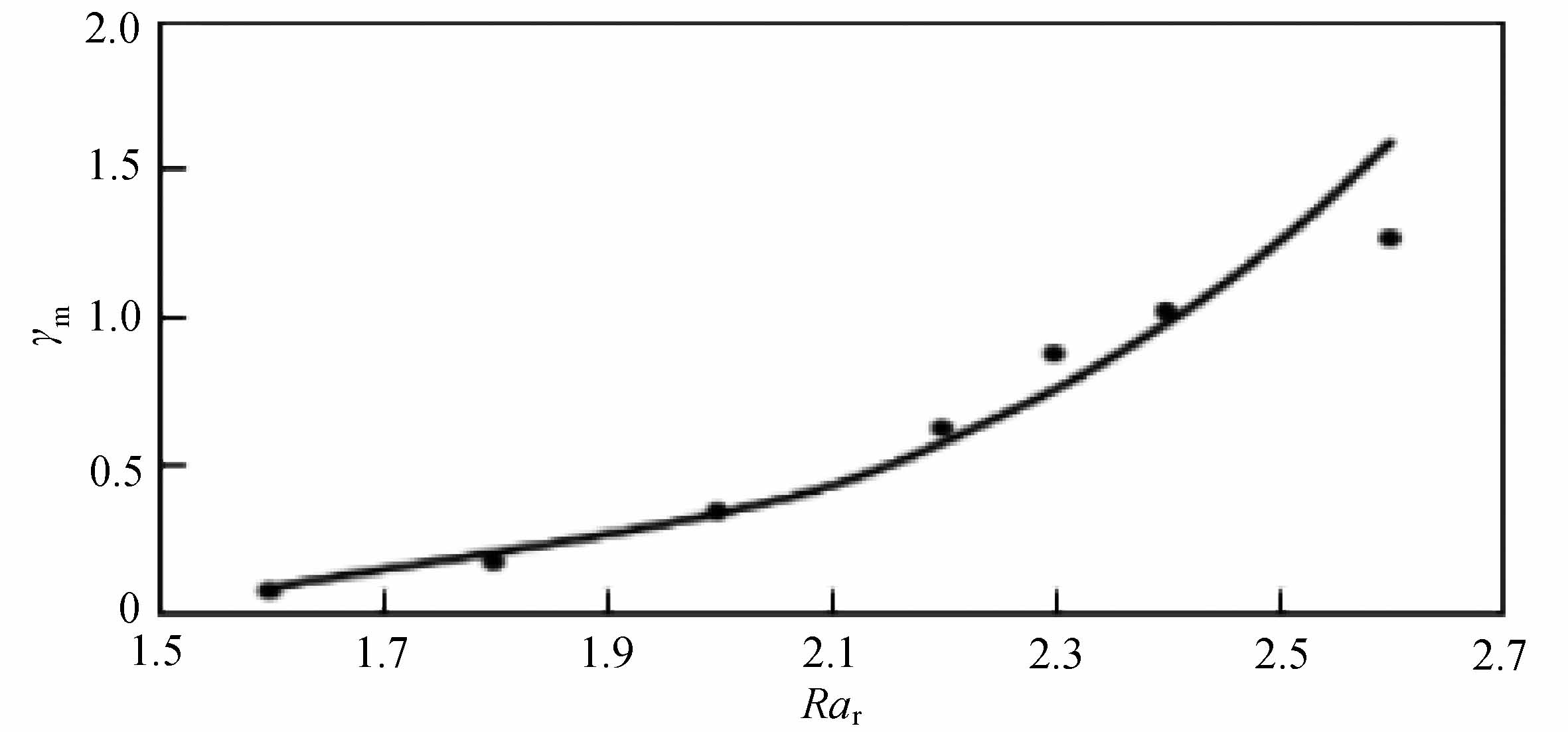
图5 Re=5时垂直最大流速的成长率γm
Fig.5 The growth rate γm of the maximum vertical velocity for Re=5
当对流垂直最大流速指数成长阶段结束后，行波对流进入周期性变化阶段．周期性变化阶段又分为过渡调整区和稳定周期变化区．图6给出了在Rar=5时水平流动Reynolds数Re=22.5的情况下，周期性变化阶段内对流垂直最大流速和下壁面Nusselt数随着时间的发展．可以看出，大约在t=5之前对流属于周期性变化阶段的过渡调整区．对流垂直最大流速和下壁面Nusselt数的大小及其变化周期都随着时间的发展不断调整．大约在t=5之后对流进入周期性变化阶段的稳定周期变化区．对流垂直最大流速的均值大约稳定在wmax=0.055 8的数值，然后随着时间在其上下周期振动．变化周期保持为一个定值．下壁面Nusselt数也进入稳定的周期变化，下壁面Nusselt数摆动幅度与均值也保持为一个定值．
在行波对流周期性变化阶段的过渡调整区，Rar=5时水平流动Reynolds数Re=22.5情况下的行波对流过渡调整区时空结构如图7所示．每个框子内为某一时刻的流线图，每两个框子之间的时间间隔Δt=0.21，时间发展方向向上．但随着时间的发展，行波对流向下游传播，向上游发展．水平流动控制的范围在缩小，行波对流控制的范围在扩大．位于4<X<6范围的水平流动和行波对流的交界面不断向左移动．这个调整过程很缓慢．行波对流滚动区平均波数大约为k=10π/8=3.927． 由图6(a)可以看出，行波对流的最大垂直流速随着时间在大周期变化的同时，也在小周期的调整；由图6(b)可以看出，下壁面Nusselt数随着时间在周期变化的同时，其数值在减小．
(a) 最大垂直流速
(a) The maximum vertical velocity
(b) 下壁面Nusselt数
(b) The Nusselt number on the bottom wall
图6 周期变化阶段的对流参数
Fig.6 Convection parameters in the period variation stage
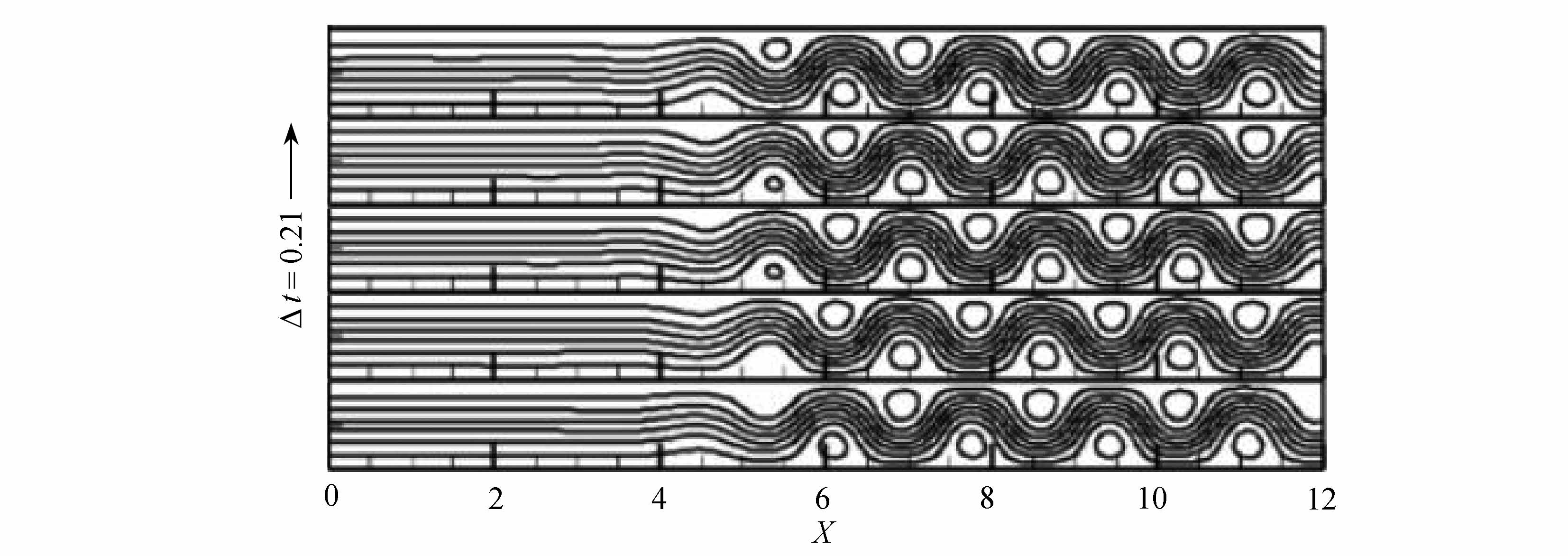
图7 行波对流过渡调整区的时空结构
Fig.7 The spatiotemporal structure in the transitional stage of traveling wave convection
经过行波对流的振幅，周期及行波对流滚动控制的范围不断调整后，行波对流系统进入稳定周期变化区．Rar=5时水平流动Reynolds数Re=22.5情况下的行波对流稳定周期变化区时空结构如图8所示．每个框子内为某一时刻的流线图，每两个框子之间的时间间隔Δt=0.21，时间发展方向向上．随着时间的发展，行波对流向下游传播，水平流动和行波对流的交界面不再向左移动，稳定在X=3.5附近．水平流动控制的范围和行波对流控制的范围基本不再变化．在3.5
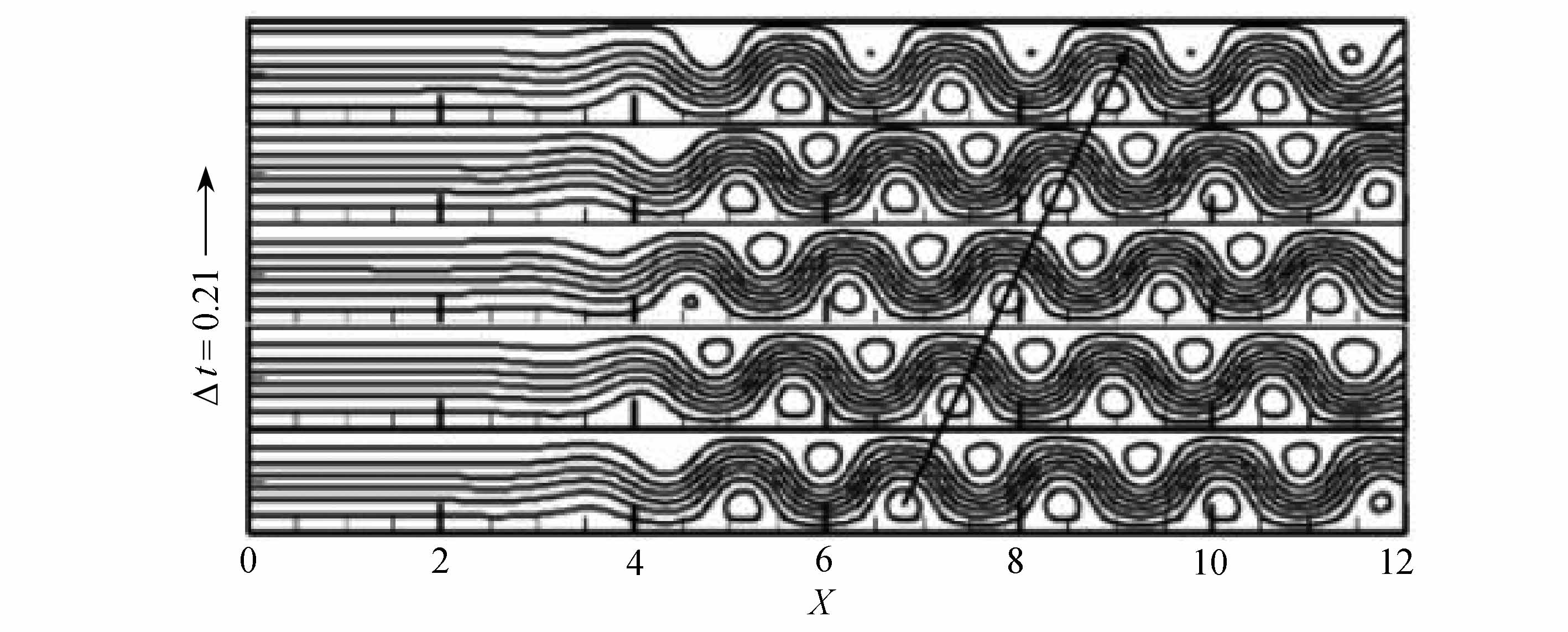
图8 行波对流稳定周期变化区的时空结构
Fig.8 The spatiotemporal structure in the stable period variation stage of traveling wave convection
下面探讨行波对流稳定周期变化区的行波对流周期随着水平流动Reynolds数的变化规律．本文对Rar=5时数个水平流动Reynolds数下的行波对流稳定周期变化区的行波对流周期进行了数值模拟，获得了相应的行波对流周期T． 为了比较的方便，对行波对流周期T用d2/κ无量纲化处理，得到行波对流的无量纲周期Tt=T/(d2/κ)=0.21T．按照上式对不同水平流动Reynolds数时获得的行波对流周期T进行无量纲化，结果见表1．可见，行波对流的无量纲周期Tt随着水平流动Reynolds数Re的增加而增加．对表1的数据进行拟合分析，结果如图9所示．行波对流的无量纲周期Tt随着水平流动Reynolds数Re变化的关系式为Tt=0.001 4Re2.363 5．另外，根据前面的分析可知，对于给定的相对Rayleigh数和水平流动Reynolds数，在不同的行波对流发展阶段行波对流区的对流波数是不同的．但随着行波对流的成长，对流波数是减小的，在到达行波对流的稳定周期变化区后，对流波数保持为常数．
表1 不同水平来流Reynolds数时的行波对流周期
Table 1 Convective periods for different Reynolds numbers of horizontal flow
Reynolds number Reconvective period Tt12.50.63150.8417.51.0522.52.1284.2
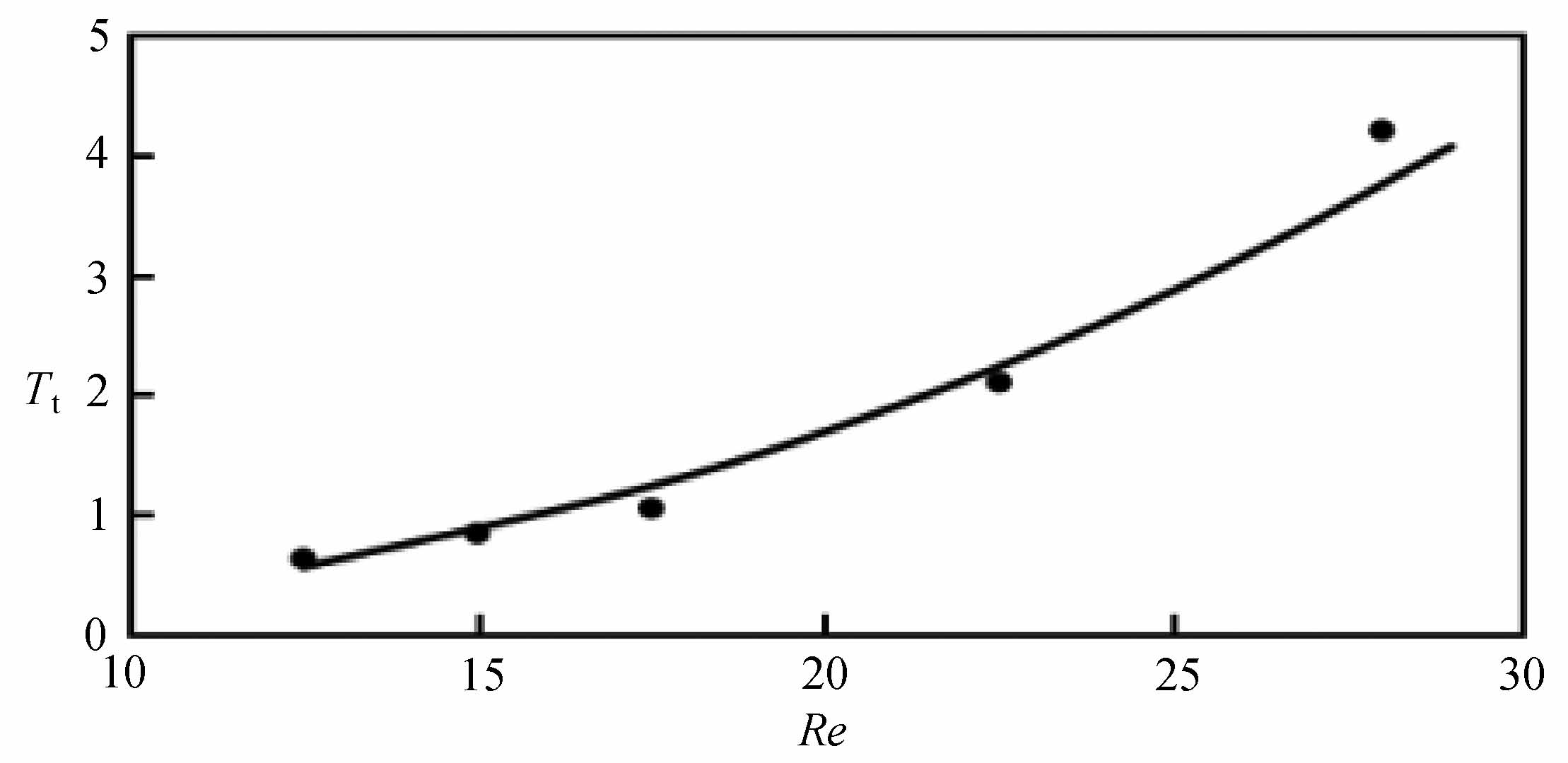
图9 对流周期随着Reynolds数的变化
Fig.9 Variation of the convective period with the Reynolds number
本文采用二维流体力学基本方程组对Prandtl数Pr=0.72的具有水平流动的对流斑图成长和动力学特性进行数值模拟．可以得出以下结论:
1) 对于给定的相对Rayleigh数Rar=5和Reynolds数Re=22.5，行波对流斑图的成长分为三个阶段，即对流发展阶段、指数成长阶段、周期变化阶段(过渡调整区、稳定周期变化区)．
2) 对于给定的相对Rayleigh数和水平流动Reynolds数，在不同的行波对流发展阶段，行波对流区的对流波数是不同的．但随着行波对流的成长，对流波数是减小的，在到达行波对流的稳定周期变化区后，对流波数保持为常数．
3) 在指数成长阶段，随着相对Rayleigh数的增加，行波对流的指数成长的起始点时间越早，结束点时间也越早．行波对流的指数成长阶段的时间变短，对流垂直最大流速随着时间的变化率变大．对于水平流动Reynolds数Re=5时，对流垂直最大流速的成长率γm与Rar的关系为
4) 在周期变化阶段，经过行波对流斑图和对流参数的过渡调整区后，对流进入斑图和对流参数的稳定周期变化区．在行波对流的稳定周期变化区，行波对流的最大垂直流速随着时间在周期变化．下壁面Nusselt数随着时间周期变化的同时，在每个周期内又振动多次．对于给定的Rar=5时，行波对流的无量纲周期Tt随着Re变化的关系式为Tt=0.0014Re2.363 5．
致谢 本文作者衷心感谢西北旱区生态水利国家重点实验室基金项目(2017ZZKT-2)对本文的资助．
[1] CROSS M C,HOHENBERG P C.Pattern formation outside of equilibrium[J].Reviews of Modern Physics,1993,65(3):851-1112.
[2] BODENSCHATZ E,PESCH W,AHLERS G.Recent developments in Rayleigh-Bénard convection[J].Annual Review of Fluid Mechanics,2000,32(1):709-778.
[3] NING L Z,HARADA Y,YAHATA H.Formation process of the traveling wave state with a defect in binary fluid convection[J].Progress of Theoretical Physics,1997,98(3):551-566.
[4] ZHAO B X,TIAN Z F.Numerical investigation of binary fluid convection with a weak negative separation ratio in finite containers[J].Physics of Fluids,2015,27(7):074102.
[5] MERCADER I,BATISTE O,ALONSO A,et al.Traveling convectons in binary fluid convection[J].Journal of Fluid Mechanics,2013,722:240-265.
[6] WATANABE T,IIMA M,NISHIURA Y.Spontaneous formation of travelling localized structures and their asymptotic behaviour in binary fluid convection[J].Journal of Fluid Mechanics,2012,712:219-243.
[7] MERCADER I,BATISTE O,ALONSO A,et al.Convectons,anticonvectons and multiconvectons in binary fluid convection[J].Journal of Fluid Mechanics,2011,667:586-606.
[8] 宁利中,王永起,袁喆,等.两种不同结构的混合流体局部行波对流斑图[J].科学通报,2016,61(8):872-880.(NING Lizhong,WANG Yongqi,YUAN Zhe,et al.Two types of patterns of localized traveling wave convection in binary fluid mixtures with different structures[J].Chinese Science Bulletin,2016,61(8):872-880.(in Chinese))
[9] 宁利中,余荔,袁喆,等.沿混合流体对流分叉曲线上部分支行波斑图的演化[J].中国科学:物理 力学 天文学,2009,39(5):746-751.(NING Lizhong,YU Li,YUAN Zhe,et al.Evolution of traveling wave patterns along upper branch of bifurcation diagram in binary fluid convection[J].Scientia Sinica:Physica,Mechanica &Astronomica,2009,39(5):746-751.(in Chinese))
[10] 宁利中,王娜,袁喆,等.分离比对混合流体Rayleigh-Bénard对流解的影响[J].物理学报,2014,63(10):104401.(NING Lizhong,WANG Na,YUAN Zhe,et al.Influence of separation ratio on Rayleigh-Bénard convection solutions in a binary fluid mixture[J].Acta Physica Sinica,2014,63(10):104401.(in Chinese))
[11] 余荔,宁利中,魏炳乾,等.Rayleigh-Benard 对流及其在工程中的应用[J].水资源与水工程学报,2008,19(3):52-54.(YU Li,NING Lizhong,WEI Binqian,et al.Rayleigh-Benard convection and application in engineering[J].Journal of Water Resources and Water Engineering,2008,19(3):52-54.(in Chinese))
[12] JUNG D,LUCKE M,BUCHEL P.Influence of through-flow on linear pattern formation properties in binary mixture convection[J].Physical Review E,1996,54(2):1510-1529.
[13] BUCHEL P,LUCKE M.Influence of through flow on binary fluid convection[J].Physical Review E,2000,61(4):3793-3810.
[14] ROTH D,BUCHEL P,LUCKE M,et al.Influence of boundaries on pattern selection in through-flow[J].Physica D:Nonlinear Phenomena,1996,97(1/3):253-263.
[15] JUNG D,LUCKE M,SZPRYNGER A.Influence of inlet and bulk noise on Rayleigh-Benard convection with lateral flow[J].Physical Review E,2001,63(5):056301.
[16] 宁利中,胡彪,宁碧波,等.Poiseuille-Rayleigh-Benard流动中对流斑图的分区和成长[J].物理学报,2016,65(21):214401.(NING Lizhong,HU Biao,NING Bibo,et al.Partition and growth of convection patterns in Poiseuille-Rayleigh-Bénard flow[J].Acta Physica Sinica,2016,65(21):214401.(in Chinese))
[17] 胡彪,宁利中,宁碧波,等.局部行波对水平来流的依赖性[J].水动力学研究与进展,2017,32(1):110-116.(HU Biao,NING Lizhong,NING Bibo,et al.The dependence of localized traveling wave on horizontal flow[J].Chinese Journal of Hydrodynamics,2017,32(1):110-116.(in Chinese))
[18] 宁利中,周洋,王思怡,等.Poiseuille-Rayleigh-Benard流动中的局部行波对流[J].水动力学研究与进展,2010,25(3):299-306.(NING Lizhong,ZHOU Yang,WANG Siyi,et al.Localized traveling wave convection in Poiseuille-Rayleigh-Benard flows[J].Chinese Journal of Hydrodynamics,2010,25(3):299-306.(in Chinese))
[19] 胡彪,宁利中,宁碧波,等.周期性加热Poiseuille-Rayleigh-Benard流动中局部行波的研究[J].水动力学研究与进展,2017,32(3):336-343.(HU Biao,NING Lizhong,NING Bibo,et al.Localized traveling waves in Poiseuille-Rayleigh-Benard flows under periodic heating[J].Chinese Journal of Hydrodynamics,2017,32(3):336-343.(in Chinese))
[20] 赵秉新,田振夫.底部加热平面Poiseuille流中的局部行波结构[J].水动力学研究与进展,2012,27(6):649-658.(ZHAO Bingxin,TIAN Zhenfu.Localized traveling wave convection in plan Poiseuille flow heated from below[J].Chinese Journal of Hydrodynamics,2012,27(6):649-658.(in Chinese))
[21] 赵秉新.水平流作用下的混合流体行波对流[J].水动力学研究与进展,2012,27(3):264-274.(ZHAO Bingxin.Traveling wave convection in binary fluid mixtures with lateral flow[J].Chinese Journal of Hydrodynamics,2012,27(3):264-274.(in Chinese))
[22] NING L Z,QI X,HARADA Y,et al.A periodically localized traveling wave state of binary fluid convection with horizontal flows[J].Journal of Hydrodynamics,2006,18(2):199-205.
[23] 李国栋,黄永念.水平流作用下行波对流的成长及周期性重复[J].物理学报,2004,53(11):3800-3805.(LI Goudong,HUANG Yongnian.Growth and periodic repeating of traveling-wave convection with through-flow[J].Acta Physica Sinica,2004,53(11):3800-3805.(in Chinese))
[24] NING L Z,HARADA Y,YAHATA H,et al.The spatio-temporal structure of binary fluid convection with horizontal flow[J].Journal of Hydrodynamics,2004,16(2):151-157.
[25] NING L Z,HARADA Y,YAHATA H,et al.Fully-developed traveling wave convection in binary fluid mixtures with lateral flow[J].Progress of Theoretical Physics,2001,106(3):503-512.
[26] 宁利中,吴昊,宁碧波,等.倾斜层中的对流斑图及其临界条件[J].应用数学和力学,2019,40(4):398-407.(NING Lizhong,WU Hao,NING Bibo,et al.Convection patterns and corresponding critical condition in an inclined layer[J].Applied Mathematics and Mechanics,2019,40(4):398-407.(in Chinese))
[27] 宁利中,张珂,宁碧波,等.侧向加热腔体中的多圈型对流斑图[J].应用数学和力学,2020,41(3):250-259.(NING Lizhong,ZHANG Ke,NING Bibo,et al.Multi-roll type convection pattern in cavity heated laterally[J].Applied Mathematics and Mechanics,2020,41(3):250-259.(in Chinese))
Abstract:The growth and dynamic characteristics of convection patterns with horizontal flow for Prandtl number Pr=0.72 were numerically simulated with 2D basic equations of fluid mechanics.The results show that,for given relative Rayleigh number Rar=5(Rayleigh number Ra=8 540) and Reynolds numberRe=22.5,the growth of the traveling wave convection pattern can be divided into 3 stages:the convection development stage,the exponential growth stage and the periodic variation stage (including the transition adaptation region and the stable periodic variation region).The average wave number in the traveling wave convection decreases with time or with the growth of the convection pattern.The exponential growth stage length in traveling wave convection becomes shorter and the growth rate of the maximum vertical velocity of convection increases with relative Rayleigh number Rar.For Reynolds number Re=5,the growth rate of the maximum vertical velocity of convection relates with the variation of relative Rayleigh number Rar in the form of γm=0.004 
In the periodic variation stage,after the transition adaptation region of the convection pattern and parameters in traveling wave convection,the convection enters the stable periodic variation region of the convection pattern and parameters.For given relative Rayleigh number Rar=5,dimensionless period Tt of traveling wave convection varying with Re can be expressed as Tt=0.001 4Re2.363 5.