引 言
泡状流动广泛存在于诸多工业过程,在这些过程中,由于杂质(或添加剂)的存在,气泡界面会受到不同程度的污染.气泡界面受污染后,其水动力学特性会发生改变,进而影响流动结构以及气-液交界面的传热和传质性能[1],从而对实际工业过程的效率产生显著影响.因此,研究受污染气泡的水动力学特性具有重要的现实意义.
国内外学者以表面活性剂作为污染源,对界面受污染气泡的水动力学特性进行了大量研究.Palaparthi等[2]、Cuenot等[3]、Jarek等[4]和Saboni等[5]使用停滞帽模型针对不同表面活性剂溶液,数值研究了受污染气泡界面浓度分布、停滞角大小、停滞帽尺寸、切向速度和涡量变化,并给出了气泡阻力系数表达式.Kishore等[6-8]使用球形停滞帽模型,对幂律流体中受表面活性剂污染气泡界面的动力学特性、气泡阻力及其周围流场随“帽角”的变化进行了详细研究.Pesci等[9]采用亚网格(SGS)模型数值研究了表面活性剂溶液中单气泡上浮速度和界面浓度分布,发现当气泡速度达到准稳态时,吸附解析不一定处于平衡状态.Fei和Pang[10]利用改进的停滞帽模型研究了不同表面活性剂浓度下气泡界面浓度、界面性质和尾流特征等.Hosokawa等[11-12]使用时空滤波测速仪(SFV)测试了不同表面活性剂浓度下受污染气泡/液滴的界面浓度分布,发现聚集在气泡界面分布不均的表面活性剂会产生表面张力梯度,进而产生与界面流向相反的Marangoni力,降低气泡表面的流动性.
目前关于受污染气泡水动力学特性的研究,主要集中于单气泡的研究.而在现实工业过程中,当气泡的体积分数较高时,气泡间的相互影响比较明显.鉴于此,本文采用改进的停滞帽模型模拟研究了两个受污染气泡之间的间距(即体积分数)对其界面参数和尾流的影响.由于每个气泡界面仅能与其邻近的流域进行质量交换,所以采用改进的停滞帽模型模拟两个气泡时,需要识别各自的吸附域,以实现多个气泡对临近污染物的同时吸附.
1 物 理 模 型
1.1 几何建模
考虑直径为db、间距为h的两共轴线球形气泡在静置不可压缩Newton流体中作上浮运动,忽略气泡间相互作用对气泡上浮运动的影响.为了简化研究,采用轴对称几何模型,将直径为db、间距为h的两球形气泡固定在直径为Dt、长为L的圆柱域轴线上,让速度为U的溶液对于气泡发生流动,流动方向与轴线平行,如图1所示.图1中,整个流域分为两个部分,一是紧贴气泡表面法向厚度为δD的吸附层,二是吸附层以外的主流区域;θ为“帽角”,表示气泡干净界面的角度范围;α为方位角,表示气泡表面上任意位置与气泡左顶点的夹角;a为速度进口到气泡1中心的距离,b为气泡2中心到出口的距离.为了防止壁面效应的影响,上壁面以与来流相同的速度与溶液一起运动.
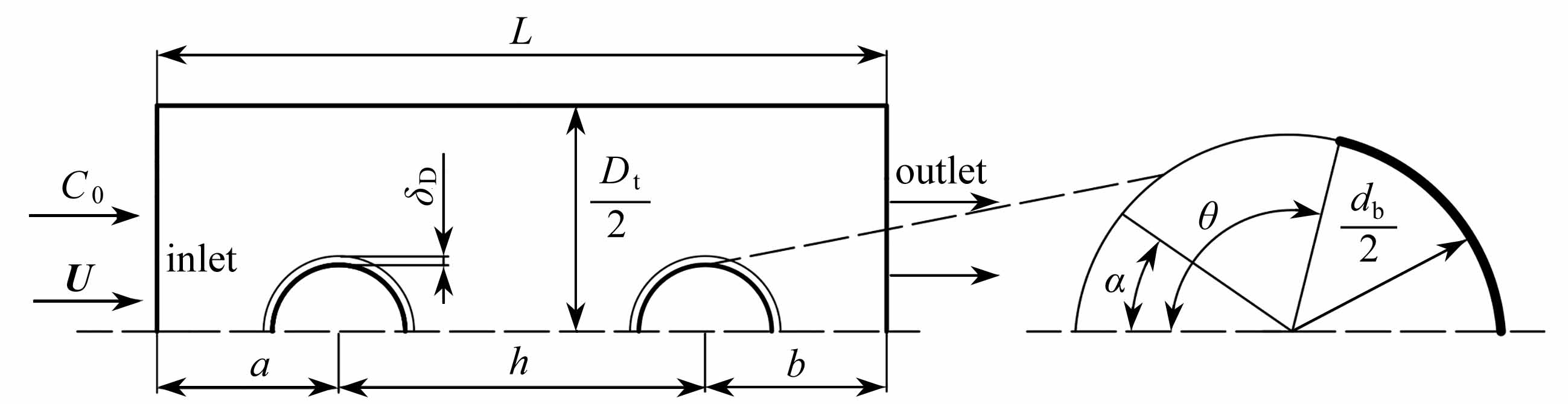
图1 计算区域
Fig.1 The computation domain
1.2 假设合理性说明
针对两球形气泡均以速度U稳态上浮、忽略气泡相互作用对上浮速度的影响以及呈轴对称流动这一假设给予说明.文中气泡Reynolds数Re=150,Eötvös数Eo为0.14,Morton数Mo为2.6×10-6,最小气泡间距为2.8倍气泡直径.由Clift等[13]给出的关于Re,Eo和Mo的气泡形状关系图可知,当前所研究气泡的形状为球形.对于受浮力作用单上浮气泡,当不考虑气泡界面性质变化(即忽略气泡界面受污染)、气泡Reynolds数Re<400时,气泡周围流场呈轴对称分布[14-16].文献[17]指出,当考虑污染物在气泡界面吸附时(即气泡界面受污染),轴对称模型成立的条件是流场和浓度场必须同时呈轴对称分布,此时气泡Reynolds数应满足Re≤200.
文献[18-21]研究表明,当气泡Reynolds数Re<200时,即使气泡尾流效应较强(如Eo=100),两气泡仍呈直线上升,其周围流动仍呈轴对称分布.文献[19]指出,在弱尾流效应(如Eo=1)下,气泡Reynolds数Re=100和气泡间距为2.5倍气泡直径时,两共轴线上浮气泡间仅存在微弱相互作用.文献[20]指出,当尾流效应非常弱时(如Eo=0.1),对于Reynolds数较小的球形气泡,气泡间距为1.5倍气泡直径时,两共轴线上浮气泡间互不影响.可见,对于目前研究的两共轴线上浮球形气泡,可近似采用轴对称模型进行计算.所涉及的Eo、Re和Mo定义式如下:
(1)
(2)
(3)
式中,ρ为密度,kg/m3;g为重力加速度,m/s2;μ为动力黏度,kg/(m·s);σ表示气泡表面张力,N/m;db为气泡直径,m.
1.3 控制方程
所需的控制方程除了流域内的连续性方程和动量方程外,还需求解气泡表面吸附层内与主流域中表面活性剂浓度的输运方程.流域中的连续性方程和动量方程为:
连续性方程
 ·u=0;
·u=0;
(4)
动量方程
![]()
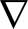
![]()
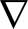 p+υ
p+υ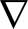 2u,
2u,
(5)
式中,u为速度,m/s;t为时间,s;p为压力,Pa;υ为运动黏度,m2/s.
气泡表面吸附层内表面活性剂的浓度可由下式求解:
(6)
式中,Γ为吸附层内表面活性剂的浓度,mol/m2;SΓ为吸附层表面活性剂浓度方程的源项;uτ为气泡表面切向速度,m/s;DS为气泡表面活性剂的扩散系数,m2/s; S为梯度沿气泡表面的切向分量,定义为
S为梯度沿气泡表面的切向分量,定义为
 S=
S= -n·(n·
-n·(n·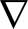 ),
),
(7)
其中,n为垂直于气泡界面的单位法向量.
Muradoglu与Tryggvason[22]基于Frumkin-Levich模型[23],将吸附层表面活性剂浓度方程的源项定义为
SΓ=k[CS(Γmax-Γ)-βΓ],
(8)
式中,k为吸附系数,m3/(mol·s);β为解吸系数,m3/(mol·s);Γmax为极限吸附下气泡表面允许达到的最大浓度,mol/m2;CS为紧邻气泡表面流域中表面活性剂的浓度,mol/m2.
整个流域(包括吸附层和主流域)中活性剂浓度的输运方程为
![]()

![]()
(9)
式中,C为主流域中表面活性剂的浓度,mol/m3;D为主流域中表面活性剂的扩散系数,m2/s;SC为主流域中表面活性剂浓度方程的源项,该源项与吸附层内表面活性剂浓度方程的源项关系为
(10)
其中,A为紧邻气泡表面网格单元的面积,m2 ;V为紧邻气泡表面网格单元的体积,m3.
对于非吸附层流域,式(9)可简化为
![]()
 ·(Cu)=D
·(Cu)=D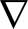 2C.
2C.
(11)
1.4 边界条件
计算所涉及的速度、气泡表面活性剂浓度,以及流域中表面活性剂浓度在进口、出口、对称轴处和气泡表面的边界条件表述如下:
进口
u=U,C=C0;
(12)
出口
∂u/∂n=0,∂C/∂n=0;
(13)
对称轴处
u·n=0,∂C/∂n=0,∂(u·τ)/∂n=0;
(14)
气泡表面
![]()
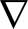 SΓ,∂Γ/∂n=0,
SΓ,∂Γ/∂n=0,
(15)
式中,τ为气泡表面的切应力,Pa;R是气体常数,J/(mol·K);T是绝对温度,K.
当不考虑气体黏性时,气泡表面的切应力与Marangoni应力相平衡,同时Marangoni应力又可表示为气泡界面表面张力梯度的切向分量.
τ=-τMa=-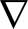 Sσ,
Sσ,
(16)
式中,τMa为Marangoni应力,Pa;σ通过Langmuir吸附状态方程[24-25]与气泡表面活性剂的浓度联系起来:
(17)
其中,σ0是干净气泡的表面张力,N/m.
2 数值方法和关键参数确定
2.1 网格划分
如图2所示,靠近气泡的区域使用四边形和三角形混合网格,远离气泡的区域使用四边形网格.由于靠近气泡表面区域的流场较为复杂,因此气泡表面附近区域的网格较为密集;随着远离气泡表面,网格逐渐变得稀疏,如图2(a)所示.气泡吸附层周向上采用均匀网格,径向上采用非均匀网格,共10层,如图2(b)所示.表1给出了不同Reynolds数下球形气泡周向网格的划分.对比发现,将气泡周向网格划分为256份满足计算要求.

(a) 整体视图 (b) 临近气泡界面局部放大图
(a) The overall view (b) The amplified view near the bubble surface
图2 圆球域示意图
Fig.2 The spherical domain
表1 不同Re下气泡周向网格划分
Table 1 Grid numbers along the bubble circumference under different Re values

Recircumferential divisionFukuta et al.[24]100144Palaparthi et al.[26] 0.91100Fukuta et al.[27]100168this paper150256
2.2 数值方法
本文使用的数值方法如下:压力-速度耦合采用SIMPLEC算法以加快收敛速度,单元中心的变量梯度采用基于网格单元的Gauss-Green公式离散,压力项采用二阶离散格式,对流项采用三阶QUICK格式离散,气泡表面活性剂的浓度采用三阶QUICK格式离散,流域中表面活性剂的浓度采用三阶QUICK格式离散,时间项采用二阶隐式离散格式.
2.3 工况设置
假设气泡受正戊醇污染,入口浓度为C0=1.5 mol/m3,其吸附-解吸动力学参数根据文献[28]选取.吸附系数k=5.08 m3/(mol·s),解吸系数β=21.7 m3/(mol·s),极限吸附下气泡表面允许最大浓度Γmax=5.9×10-6 mol/m2,扩散系数DS=D=1.1×10-9 m2/s.由于表面活性剂浓度较低,因此液相热物性数据选用常温下水的物性参数.气泡直径db=1 mm,U=0.15 m/s,Re=150.计算区域尺寸为Dt=10db,a=b=12.5db,L最小值为27.8db(对应的h=2.8db).在气泡间距h=2.8db~6db的工况下,研究了气泡间距对两气泡界面参数和局部流动的影响.
2.4 吸附层厚度确定
吸附层厚度的选取会对模拟结果产生重大的影响,文献[23]提出了估算吸附层边界厚度的计算方法(见式(18)).但该方法精确度不高,与实际值会产生偏差.因此,在依据式(18)对吸附层厚度估算的基础上,选用不同的吸附层厚度进行了计算对比,以获得最佳厚度值.
(18)
式中,Pe为Péclet数,表示对流与扩散之比.在估算值的基础上,并在间距h=2.87db的工况下,对两受污染气泡阻力系数给予检测,结果如表2所示.当δD/db减小至δD/db=1.2×10-2时,两气泡的阻力系数基本不变,同时权衡计算量的影响,选取δD/db=1.2×10-2.
表2 吸附层厚度对两受污染气泡阻力系数的影响
Table 2 Influence of the adsorption layer thickness on the drag coefficient of contaminated bubbles

δD/dbbubble 1bubble 21.35×10-20.670.541.2×10-20.620.551.1×10-20.620.55
基于确定的吸附层厚度,下面对气泡吸附层第一层网格的尺寸进行分析与讨论.图3给出了气泡间距h=2.87db时,吸附层第一层网格尺寸分别为Δ1=2.4×10-4 mm,Δ2=3.0×10-4 mm,Δ3=5.0×10-4 mm时两气泡界面浓度分布.如图3所示,两个气泡的界面浓度分布在网格尺寸为Δ1,Δ2时基本一致,因此当第一层网格尺寸为3.0×10-4 mm时已满足要求,不需要再减小网格尺寸.文献[6]指出,当Re<200时,使用简化停滞帽模型的计算时间步长要小于10-3 s,而文中计算时间步长设为0.000 5 s,满足计算要求.
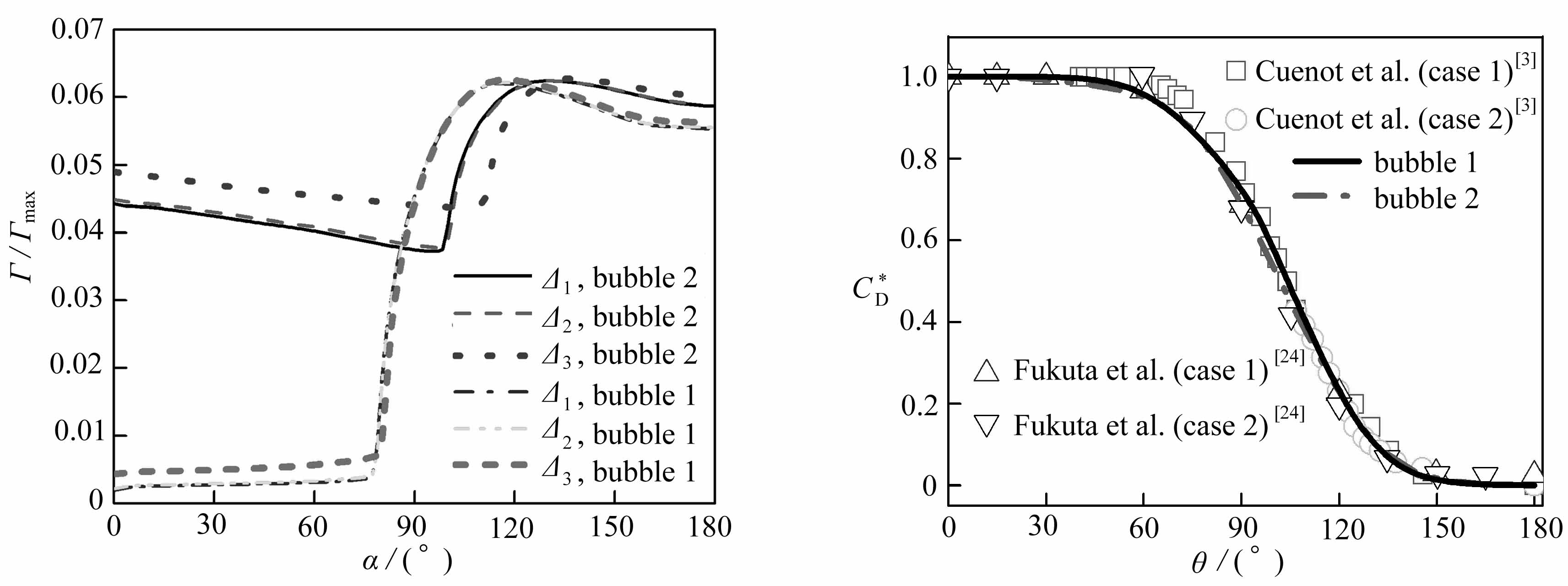
图3 网格尺寸对界面浓度的影响 图4 气泡阻力系数对比
Fig.3 Influences of grid sizes on the interface concentration Fig.4 Comparison of bubble drag coefficients
2.5 结果准确性验证
为了验证计算结果的可靠性,在气泡Reynolds数Re=100和气泡间距h=6db时,将不同“帽角”θ下受污染气泡阻力系数的计算结果与文献的结果进行了比较,如图4所示.从图4可知,几组结果吻合良好,说明计算结果是可信的.相对阻力系数计算式如下:
(19)
式中,CD,clean是界面干净气泡的阻力系数,CD,rigid是界面完全污染气泡的阻力系数,CD是不同界面污染程度气泡的阻力系数.
3 结果与讨论
3.1 界面浓度
单个受污染气泡界面参量的变化已经被进行了深入研究.结果表明,吸附于气泡表面的表面活性剂在对流作用影响下,流向气泡尾部,形成界面浓度梯度.而受界面浓度梯度产生的Marangoni应力的影响下,气泡尾部区域的表面活性剂又会向气泡前部扩散.于是气泡前部是相对干净的界面,气泡尾部则是相对污染严重的界面,中间是界面浓度逐渐升高的过渡区域[11-12,16 ].图5给出了h/db对气泡界面浓度的影响.图5(a)为h/db对气泡1界面浓度的影响.从图中可以看出,h/db对气泡1界面浓度的影响轻微,即各间距下,其界面浓度分布趋势相似.与单个受污染气泡的结果相似,即相同Re下,当流域中表面活性剂浓度为定值时,气泡受污染程度不变,“帽角”θ为定值.图5(b)为h/db对气泡2界面浓度的影响.从图中可以看出,h/db对气泡2界面浓度的影响非常明显.随着h/db的减小,“帽角”停滞点前相对干净界面上的界面浓度逐渐升高,而“帽角”则是先略微逐渐减小再逐渐增大至180°.
为了分析气泡2界面浓度分布的原因,额外计算了h/db=2.87时,气泡1有无吸附时对尾流和气泡2界面浓度分布的影响,计算结果见图6和图7.图6(a)为h/db=2.87时,气泡1无吸附而气泡2有吸附时的流场分布;图6(b)为h/db=2.87时,两气泡同时吸附时的流场分布.从图6中可以看出,气泡1有吸附时,其尾部会有涡形成.该尾涡对气泡2界面上污染物分布的影响不同于对流作用的影响,而是把流向气泡尾部的污染物重新带回到气泡上游界面,增加气泡2上游界面的浓度,导致气泡1有吸附时,气泡2上游界面浓度大大增加,而“帽角”前后部分的浓度差降低,如图7所示.文献[3,11-12,18]研究表明,当气泡界面未完全受污染时,随着气泡尾部受污染界面浓度与上游干净界面浓度差值的升高,气泡界面的流动性降低.因此,与气泡1不考虑吸附时相比,当气泡1考虑吸附时,气泡2前后部分界面浓度差的降低导致界面流动性增强,于是中间过渡区域的界面浓度更多地流向尾部界面,“帽角”随之增大.

图7 h/db=2.87时气泡1有无吸附对气泡2界面浓度分布的影响
Fig.7 Influences of the 1st bubble with or without adsorption on the interface concentration of the 2nd bubble for h/db=2.87
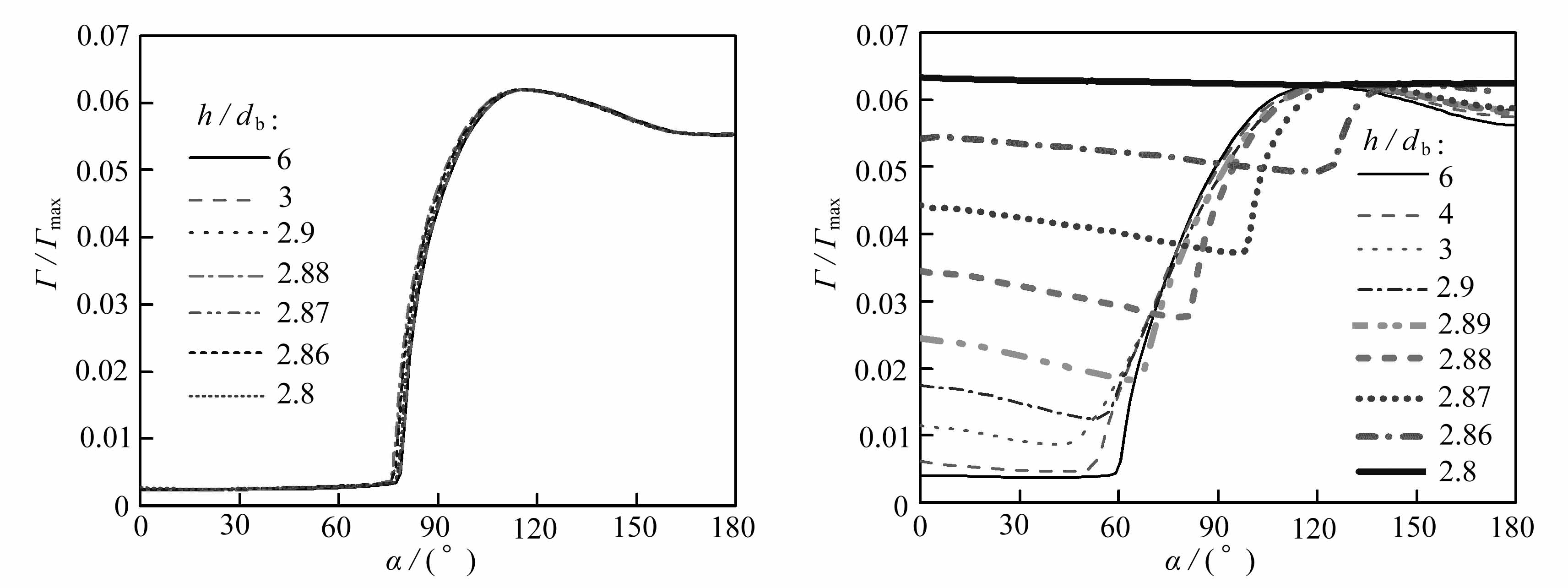
(a) 气泡间距对气泡1界面浓度的影响 (b) 气泡间距对气泡2界面浓度的影响
(a) Effects of h/db on Γ/Γmax of the 1st bubble interface (b) Effects of h/db on Γ/Γmax of the 2nd bubble interface
图5 气泡间距对气泡界面浓度的影响
Fig.5 Effects of h/db on Γ/Γmax of bubbles

(a) 气泡1无吸附 (b) 气泡1有吸附
(a) The 1st bubble without adsorption (b) The 1st bubble with adsorption
图6 h/db=2.87时气泡1有无吸附对尾流的影响
Fig.6 Influences of the 1st bubble with or without adsorption on the wake for h/db=2.87
对照图5(b)可以看出,当h/db在3~6范围内时,气泡1尾流对降低气泡2上游界面的对流作用较弱,仅导致气泡2相对干净界面上的界面浓度略微升高,气泡相对干净界面范围略微逐渐减小(即“帽角”减小);因逐渐降低的界面流动性,导致中间过渡区域浓度的变化率逐渐减小;尾部区域的界面浓度未受到较大的影响.当2.8<h/db<3时,随着h/db的减小,气泡1尾流对气泡2上游界面对流作用的影响增强,气泡2尾部受污染界面浓度与前部相对干净界面上浓度差值明显减小,气泡界面的流动性随之增强,导致中间过渡区域界面上的污染物更多地流向尾部,所以“帽角”不断增大.当h/db=2.8时,“帽角”增大到180°.因此,再减小h/db“帽角”不再变化.
3.2 界面速度
吸附于气泡表面的表面活性剂会降低气泡界面的流动性,因此气泡界面浓度分布的变化势必将会影响气泡的界面速度分布.图8给出了h/db对气泡1界面速度的影响.图8(a)为h/db对气泡1界面速度的影响.类似于气泡界面浓度分布,气泡1的界面速度分布趋势基本相同,即不受气泡间距h/db的影响.

(a) 气泡间距对气泡1界面速度的影响 (b) 气泡间距对气泡2界面速度的影响
(a) Effects of h/db on |uτ|/U of the 1st bubble interface (b) Effects of h/db on |uτ|/U of the 2nd bubble interface
图8 气泡间距对气泡界面速度的影响
Fig.8 Effects of h/db on |uτ|/U of bubbles
图8(b)为h/db对气泡2界面速度的影响.从图中可以看出,当h/db在3~6范围内时,气泡界面速度呈现出相似的分布趋势,随着h/db的减小,仅是速度峰值在减小.当2.8<h/db<3时,气泡界面速度呈现出另外一个相似的分布趋势,随着h/db的减小,非零界面速度范围增宽,速度峰值增大.当h/db=2.8时,气泡尾部几乎不存在零界面速度区.这可能是归因于气泡1的尾流对气泡2界面浓度分布的影响.
当h/db在3~6范围内时,随着h/db的减小,受气泡1尾流的影响,气泡2界面的流动性逐渐减弱.当h/db=2.8时(即“帽角”为180°),气泡2的界面速度分布与干净气泡的界面速度分布相似,仅是上游部分界面的界面速度因受到气泡1尾流的影响而较低.这可能是因不断减小的界面浓度差(如图5(b)所示,h/db<3)导致Marangoni切应力减小引起的.
3.3 界面切应力
受表面活性剂污染的气泡界面,其界面性质会发生不同程度的变化,从而会引起界面切向应力的阶跃现象.图9给出了h/db对气泡界面切向应力的影响.图9(a)为h/db对气泡1界面切应力的影响.可以看出,类似于气泡界面浓度和速度分布,气泡1界面切向应力分布也不受气泡间距h/db的影响.气泡界面切应力在相对干净和相对完全污染界面的过渡位置处出现一次阶跃现象,且阶跃幅度相同.这与单气泡受污染情况相似.

(a) 不同气泡间距下气泡的涡垂直中心分布 (b) 不同气泡间距下气泡的涡分离角分布
(a) Variations of q/db with different h/db values (b) Variations of φ with different h/db values

(a) 气泡间距对气泡1界面切应力的影响 (b) 气泡间距对气泡2界面切应力的影响
(a) Effects of h/db on |τ|/(0.5ρU2) of the 1st bubble interface (b) Effects of h/db on |τ|/(0.5ρU2) of the 2nd bubble interface
图9 气泡间距对气泡界面切向应力的影响
Fig.9 Effects of h/db on |τ|/(0.5ρU2) of bubbles
图9(b)给出了h/db对气泡2界面切应力的影响.根据式(15)可以看出,切应力分布与界面浓度在界面上的梯度和界面浓度差相关.气泡前部和尾部界面因较低的界面浓度梯度和界面浓度差,因此仅存在很小的切应力.而中间过渡区域界面上因较大的界面浓度梯度和界面浓度差,气泡界面切应力会出现一次阶跃现象.从图5(b)可以看出,当h/db在3~6范围内时,随着h/db的减小,中间过渡区域界面上的界面浓度梯度与界面浓度差值逐渐减小,而且气泡“帽角”逐渐减小;因而在图9(b)中表现为,气泡界面切应力阶跃幅度逐渐降低,阶跃位置逐渐向气泡上游轻微地移动.当2.8<h/db<3时,气泡2中间过渡区域界面上的界面浓度梯度先逐渐增大后减小,相应的气泡界面切应力的阶跃幅度也表现为先逐渐增大后减小的趋势(如图9(b)所示).但中间过渡区域界面上界面浓度差的逐渐减小,导致气泡2界面切应力的阶跃幅度都小于h/db=6时的阶跃幅度.当h/db=2.8时,“帽角”为180°,界面浓度分布均导致气泡2界面上的切应力都为零.
3.4 尾涡分析
如前所述,随着h/db的减小,气泡1的尾涡对气泡2界面参量分布的影响程度逐渐增强.因此有必要对不同h/db下两气泡的尾涡变化给予深入分析.图10给出了不同h/db下两气泡的流场分布.从图中可以看出,随着h/db的减小,气泡1的尾涡逐渐靠近气泡2上游界面,且强度逐渐增大.或许正是该尾涡的变化导致气泡2界面上的污染物分布不同,进一步导致气泡2其他的界面参量也不同.当h/db在3~6范围内时,随着h/db的减小,气泡1的尾涡面积逐渐增大,而气泡2的尾涡面积逐渐减小.当2.8≤h/db<3时,气泡1的尾涡直接作用于气泡2的上游界面,其尾涡面积未再发生明显的改变;然而气泡2的尾涡面积却逐渐减小直至消失.且当h/db=2.8时(即“帽角”为180°),气泡2的流场分布与干净气泡的流场分布相似,都没有尾涡的出现.

图10 不同气泡间距下两气泡的流场分布
Fig.10 Flow field distributions of 2 bubbles with different h/db values
为了定量分析尾涡的变化,文献[26]定义了描述尾涡变化的参数,即尾涡长度e、涡中心水平位置f、涡中心垂直位置q和分离角φ,如图11所示.
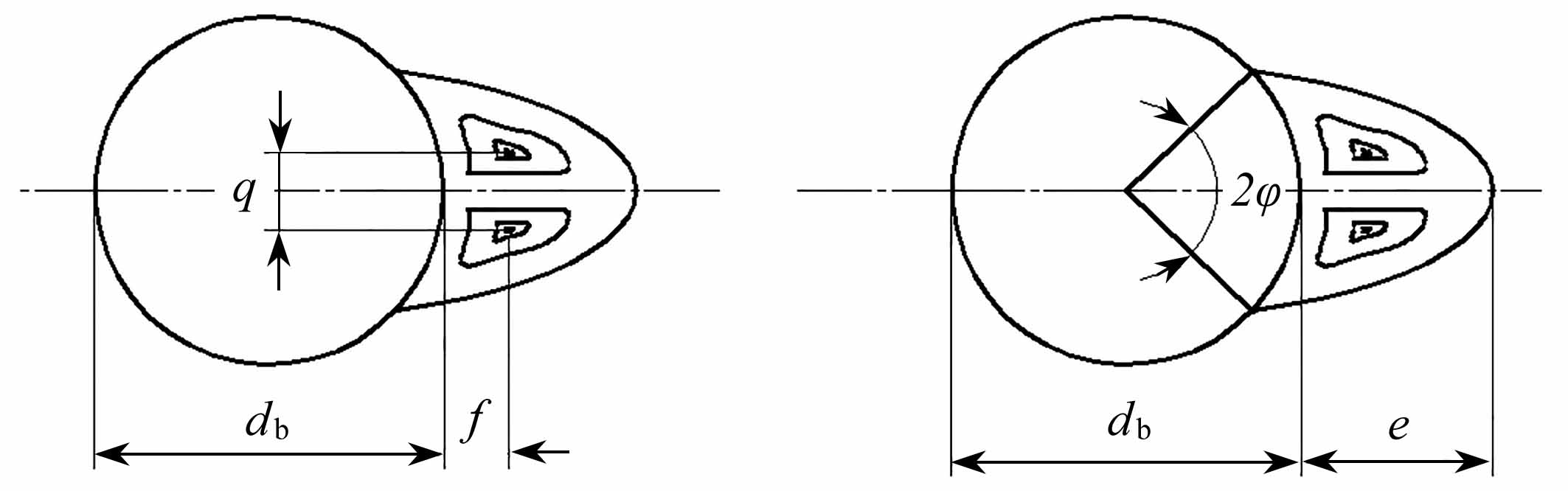
图11 气泡尾涡各参数的定义
Fig.11 Definition of parameters for the vortex
图12给出了不同h/db下两气泡尾涡参数的分布.如图所示,气泡1的涡中心垂直位置q/db和分离角φ的值基本上不受h/db的影响,而尾涡长度e/db和涡中心水平位置f/db的值却随着h/db的减小,呈现出先增加后减小的趋势.这是因为该气泡界面污染程度基本上不受h/db的影响,所以其涡中心垂直位置q/db和分离角φ分布未发生明显变化.而气泡尾涡长度e/db和涡水平垂直位置f/db的值先随着气泡2上游界面上界面浓度的升高而增加(3≤h/db≤6),又因气泡间距的减小而随之减小(h/db<3).
气泡2尾涡各参数随h/db的变化呈现出相似的分布趋势.该气泡的尾涡长度e/db、涡中心水平位置f/db、涡中心垂直位置q/db和分离角φ的值随上游界面上界面浓度的增加而减小直至为零.

(c) 不同气泡间距下气泡的涡中心水平位置分布 (d) 不同气泡间距下气泡的尾涡长度分布
(c) Variations of f/db with different h/db values (d) Variations of e/db with different h/db values
图12 不同气泡间距下气泡尾涡参数分布
Fig.12 Variations of vortex parameter distributions with different h/db values
4 结 论
采用改进的停滞帽模型对不同间距下两气泡的界面参数分布、尾涡和周围流场特征进行了数值研究,目前的分析对于今后开展多个受污染气泡水动力学特性的数值研究具有一定的借鉴作用.研究发现,当气泡间距小到一定程度时,气泡2出现界面完全均匀污染(“帽角”为180°)、界面切应力和流场分布与干净气泡类似的情况.在该情况下,停滞帽模型或许不再成立.具体结论如下:
1) h/db的减小不会对气泡1的界面参数产生明显的改变,而会显著影响气泡2的界面参数分布.
2) 气泡1尾涡向气泡2上游界面的逼近是气泡2界面参数改变的主要原因.该尾涡对气泡2界面上表面活性剂分布的影响不同于对流作用,而是把流向气泡尾部的表面活性剂重新拖回到气泡上游界面,从而影响气泡2的界面参数分布,并出现了低影响与高影响阶段.
3) 气泡1的尾涡长度e/db和涡水平位置f/db的值受气泡2上游界面上界面浓度和气泡间距的共同影响,而气泡2各尾涡参数值随其界面浓度差的减小而减小直至为零.
[1] TAKAGI S,MATSUMOTO Y.Surfactant effects on bubble motion and bubbly flows[J].Annual Review of Fluid Mechanics,2011,43(1):615-636.
[2] PALAPARTHI R,PAPAGEORGIOU D T,MALDARELLI C.Theory and experiments on the stagnant cap regime in the motion of spherical surfactant-laden bubbles[J].Journal of Fluid Mechanics,2006,559:1-44.
[3] CUENOT B,MAGNAUDET J,SPENNATO B.The effects of slightly soluble surfactants on the flow around a spherical bubble[J].Journal of Fluid Mechanics,1997,339:25-53.
[4] JAREK E,WARSZYNSKI P,KRZAN M.Influence of different electrolytes on bubble motion in ionic surfactants solutions[J].Colloids and Surfaces A:Physicochemical and Engineering Aspects,2016,505:171-178.
[5] SABONI A,ALEXANDROVA S,KARSHEVA M.Effects of interface contamination on mass transfer into a spherical bubble[J].Journal of Chemical Technology &Metallurgy,2015,50(5):589-596.
[6] KISHORE N,NALAJALA V S,CHHABRA R P.Effects of contamination and shear-thinning fluid viscosity on drag behavior of spherical bubbles[J].Industrial &Engineering Chemistry Research,2013,52(17):6049-6056.
[7] NALAJALA V S,KISHORE N.Drag of contaminated bubbles in power-law fluids[J].Colloids and Surfaces A:Physicochemical and Engineering Aspects,2014,443:240-248.
[8] NALAJALA V S,KISHORE N.Motion of partially contaminated bubbles in power-law liquids:effect of wall retardation[J].International Journal of Mineral Processing,2015,140:8-18.
[9] PESCI C,WEINER A,MARSCHALL H,et al.Computational analysis of single rising bubbles influenced by soluble surfactant[J].Journal of Fluid Mechanics,2018,856:709-763.
[10] FEI Y,PANG M J.A treatment for contaminated interfaces and its application to study the hydrodynamics of a spherical bubble contaminated by surfactants[J].Chemical Engineering Science,2019,200:87-102.
[11] HOSOKAWA S,MASUKURA Y,HAYASHI K,et al.Experimental evaluation of Marangoni stress and surfactant concentration at interface of contaminated single spherical drop using spatiotemporal filter velocimetry[J].International Journal of Multiphase Flow,2017,97:157-167.
[12] HOSOKAWA S,HAYASHI K,TOMIYAMA A.Evaluation of adsorption of surfactant at a moving interface of a single spherical drop[J].Experimental Thermal and Fluid Science,2018,96:397-405.
[13] CLIFT R,GRACE J R,WEBER M E.Bubbles,Drops,and Particles[M].New York:Academic Press,1978.
[14] SABONI A,ALEXANDROVA S,MORY M.Flow around a contaminated fluid sphere[J].International Journal of Multiphase Flow,2010,36(6):503-512.
[15] DANI A,COCKX A,GUIRAUD P.Direct numerical simulation of mass transfer from spherical bubbles:the effect of interface contamination at low Reynolds numbers[J].International Journal of Chemical Reactor Engineering,2006,4.DOI:10.2202/1542-6580.1304.
[16] 庞明军,牛瑞鹏,陆敏杰.壁面效应对剪切稀化流体内气泡上浮特性的影响[J].应用数学和力学,2020,41(2):143-155.(PANG Mingjun,NIU Ruipeng,LU Minjie.Wall effects on floating characteristics of bubbles in shear-thining fluids[J].Applied Mathematics and Mechanics,2020,41(2):143-155.(in Chinese))
[17] DUKHIN S S,LOTFI M,KOVALCHUK V I,et al.Dynamics of rear stagnant cap formation at the surface of rising bubbles in surfactant solutions at large Reynolds and Marangoni numbers and for slow sorption kinetics[J].Colloids and Surfaces A:Physicochemical and Engineering Aspects,2016,492:127-137.
[18] 李少白,徐双,范俊赓,等.非牛顿流体中在线双气泡相互作用的数值模拟[J].沈阳航空航天大学学报,2017,34(4):63-68.(LI Shaobai,XU Shuang,FAN Jungeng,et al.Numerical simulation of interaction between in-line two bubbles in non-Newtonian fluids[J].Journal of Shenyang Aerospace University,2017,34(4):63-68.(in Chinese))
[19] 孟辉,张兴伟,牛小东,等.格子Boltzmann方法分析气泡的运动及其相互作用[J].应用力学学报,2014,31(4):518-524.(MENG Hui,ZHANG Xingwei,NIU Xiaodong,et al.Lattice Boltzmann analysis of bubble motion and interaction[J].Chinese Journal of Applied Mechanics,2014,31(4):518-524.(in Chinese))
[20] 张磊.气泡间相互作用机理的数值模拟[D].硕士学位论文.重庆:重庆大学,2015.(ZHANG Lei.Numerical simulation of interaction mechanism between bubbles[D].Master Thesis.Chongqing:Chongqing University,2015.(in Chinese))
[21] 雷杰,王昱,马明,等.基于FTM方法的双气泡融合特性模拟[J].过程工程学报,2019,19(2):263-270.(LEI Jie,WANG Yu,MA Ming,et al.Numerical simulation of coalescence of double bubbles using FTM[J].The Chinese Journal of Process Engineering,2019,19(2):263-270.(in Chinese))
[22] MURADOGLU M,TRYGGVASON G.Simulations of soluble surfactants in 3D multiphase flow[J].Journal of Computational Physics,2014,274:737-757.
[23] LEVICH V G.Physicochemical Hydrodynamics[M].Englewood Cliffs:Prentice Hall,1962.
[24] FUKUTA M,TAKAGI S,MATSUMOTO Y.The effect of surface velocity on lift force for a spherical bubble in a linear shear flow[J].Theoretical &Applied Mechanics Japan,2005,54:227-234.
[25] TASOGLU S,DEMIRCI U,MURADOGLU M.The effect of soluble surfactant on the transient motion of a buoyancy-driven bubble[J].Physics of Fluids,2008,20(4):040805-040819.
[26] PALAPARTHI R,PAPAGEORGIOU D T,MALDARELLI C.Theory and experiments on the stagnant cap regime in the motion of spherical surfactant-laden bubbles[J].Journal of Fluid Mechanics,2006,559:1-44.
[27] FUKUTA M,TAKAGI S,MATSUMOTO Y.Numerical study on the shear-induced lift force acting on a spherical bubble in aqueous surfactant solutions[J].Physics of Fluids,2008,20(4):040704-040712.
[28] HAYASHI K,TOMIYAMA A.Effects of surfactant on terminal velocity of a Taylor bubble in a vertical pipe[J].International Journal of Multiphase Flow,2012,39:78-87.