引 言
湍流是工程中极为常见的一种流动现象,湍流问题是一个古老而尚未完全解决的问题.目前对于定常流,如槽道流、不可压及可压缩边界层中的湍流特性,人们已经有了一定的认识.而对于非定常流,相关的研究相对较少.
Stokes层又称振荡边界层,是一种典型的非定常流动,常见于固体与液体界面上,如波浪或潮汐作用下的水底,该流动与泥沙起动、海底沙纹床的形成及盐分输运等现象有着密切的联系,近年来,关于其特性的研究引起了国内外学者的广泛重视.多数理论分析中,Stokes层是由周期性压力或平板在其自身平面内的周期运动驱动流体产生的振荡.Stokes层的最大振荡速度记为U0,振荡频率记为Ω,δ为Stokes层的厚度.定义Reynolds数为Re=U0δ/(2ν),其中,ν是运动黏性系数.
早期的实验观测[1-4]发现,Stokes层中的流动随Reynolds数增大分为4种不同阶段:Ⅰ) 层流;Ⅱ) 扰动层流;Ⅲ) 间歇湍流;Ⅳ) 充分发展湍流.而流动从阶段Ⅱ转变为阶段Ⅲ被称为Stokes层的转捩,与此对应的Reynolds数通常称为转捩Reynolds数Recr1,虽然实验条件各有不同,但多数实验显示,当Recr1约为275时,Stokes层发生转捩;另一方面,流动从阶段Ⅲ转变为阶段Ⅳ为Stokes层向充分发展湍流的过渡阶段,对应的Reynolds数定义为Recr2,实验观测到的Recr2约为1 750.因此,将处于Recr1与Recr2之间的Reynolds数称为过渡Reynolds数.目前有关Stokes层的湍流研究大部分是针对充分发展的湍流,即上述的阶段Ⅳ中进行的,主要依靠大涡模拟(LES)(如Hsu等[5]、Scotti和Piomelli[6]、Lohmann等[7]、Salon等[8]、Zhang[9])和湍流模式(如Sheng[10]、Justesen[11]、Sajjadi等[12]、Thais等[13]、Foti等[14]、Sana等[15]、Shome[16])等方法.而相对于充分发展的湍流,处于过渡Reynolds数下Stokes层中间歇湍流特性的相关报告较少,需要进一步认识.
Vittori和Verzicco[17]的研究显示,壁面缺陷对促发湍流有着十分重要的作用.孔玮和罗纪生[18]计算了不同Reynolds数下二维壁面粗糙度引起的Stokes层的亚临界失稳问题,发现Re=300左右时,微米级壁面的表面粗糙度高度就可以导致Stokes层的亚临界失稳.本文首先以壁面的表面粗糙度为激励,通过扰动方程数值模拟过渡阶段某一Reynolds数下Stokes层的转捩过程,然后对相关物理量进行统计,研究过渡Reynolds数下的间歇湍流特性.
1 物理模型及控制方程
考虑半间距为h*的两平板间由于周期压力梯度形成的Stokes层,主流区的势流速度为
U0cos(Ωt*),
其中t*为时间.
本文采用时间模式数值模拟进行计算,各物理量用无量纲化形式进行规范,用最大振荡速度U0对速度u,v和w进行无量纲化,用Stokes层厚度δ及振荡周期1/Ω分别对坐标x,y和z及时间t*进行无量纲化,用![]() 对压力P*进行无量纲化,则无量纲的Stokes层基本流速度的解为
对压力P*进行无量纲化,则无量纲的Stokes层基本流速度的解为
(1)
其中h为无量纲半板间距,cc代表共轭部分,本文计算中取h=16.
壁面的粗糙度采取Fourier模态的形式:
ζ*=h*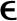 (eiα0x+beiβ0z)+cc,
(eiα0x+beiβ0z)+cc,
(2)
其中α0和β0分别为流向和展向的基本波数,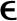 为用半槽道宽h*无量纲的粗糙度高度,b为三维粗糙度与二维粗糙度的幅值比,本文计算中取b=0.1.
为用半槽道宽h*无量纲的粗糙度高度,b为三维粗糙度与二维粗糙度的幅值比,本文计算中取b=0.1.
本文采取扰动方程求解,将瞬时物理量分解为基本流和扰动,即
(u,v,w,P)=(Ub,0,0,P0)+(u′,v′,w′,P′).
(3)
将式(3)代入无量纲的N-S方程(其中f=sin t为无量纲的流向外部体积力):
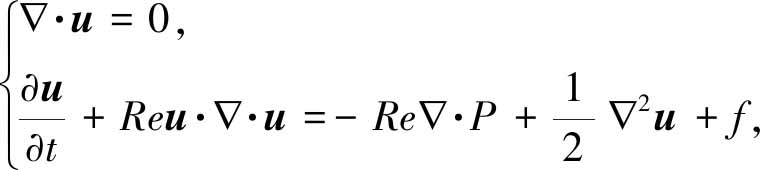
(4)
则可得到无量纲的扰动方程(式(3)中的上标在后文中省略)为
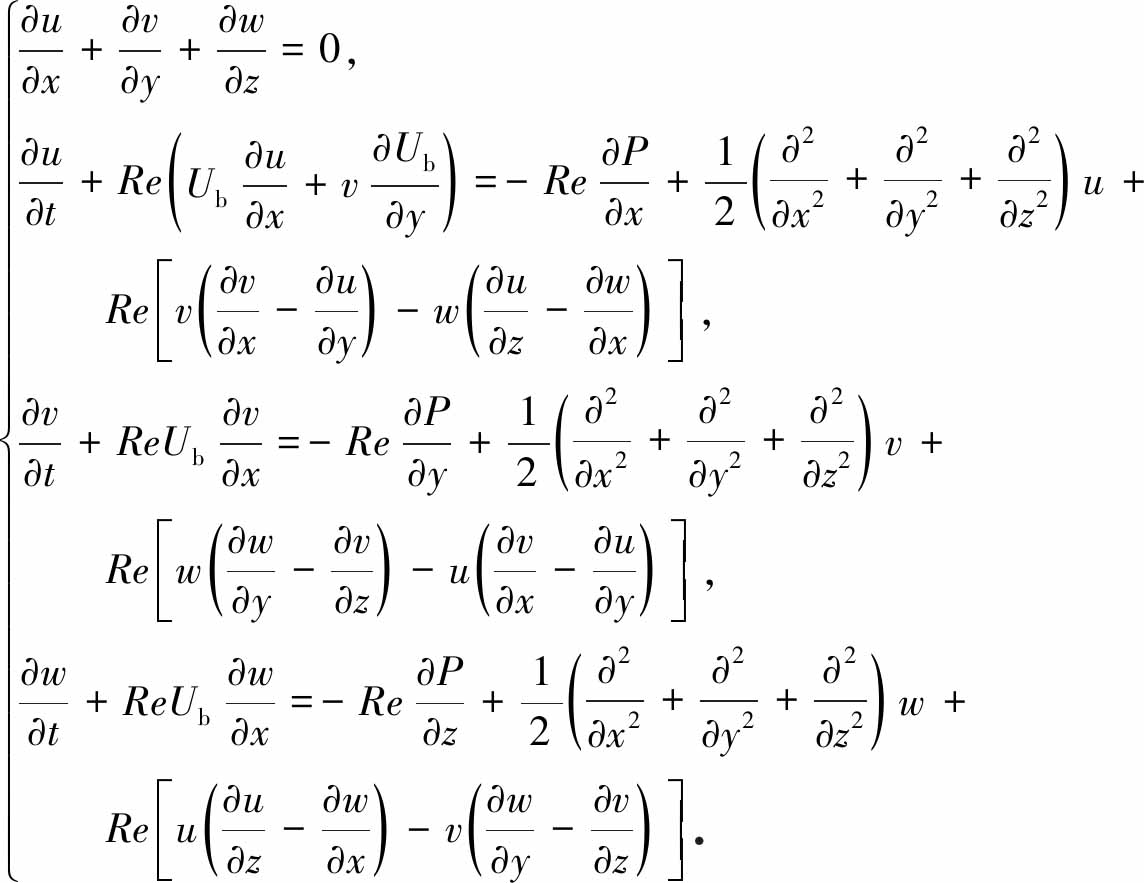
(5)
为了进行统一说明,将方程(5)写成算子的形式:
(6)
其中L(u)和N(u)分别为L0(u)的线性项和非线性项.
本文进行数值模拟时,流向x和展向z采用伪谱方法,将各物理量写成Fourier级数形式:
(7)
其中Nx和Nz分别为流向和展向的法向网格,y方向采用四阶精度差分格式,即
(8)
由于流体在边界处变化比较剧烈,因此在y方向采取变间距网格,即从边界向槽道中心逐渐变稀疏,其中y方向网格分布为
y=hcos(πj/Ny).
(9)
考虑壁面粗糙度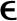 很小,计算中采用线性化处理,得到速度壁面边界条件为
很小,计算中采用线性化处理,得到速度壁面边界条件为
![]()
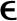 (eiα0x+beiβ0z)+cc.
(eiα0x+beiβ0z)+cc.
(10)
将式(10)代入到式(7)中,得到谱空间中边界条件的形式为
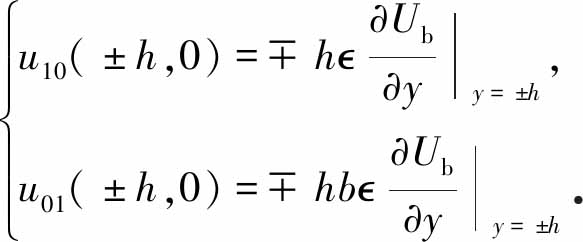
(11)
本文在时间t方向上采用二阶显隐格式进行离散,方程(6)变为
(12)
其中时间步长取Δt=π/2×10-4.本文计算的Reynolds数Re=495,壁面粗糙度参数参照文献[19]进行选取,即壁面粗糙度高度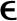 =10-5,流向和展向基本波数分别为 α0=0.35,β0=0.4.
=10-5,流向和展向基本波数分别为 α0=0.35,β0=0.4.
2 数值模拟结果与讨论
由于基本流的时间周期性,各物理量在统计时需要采用相位平均的方法,定义相位平均的物理量的统一形式为
(13)
其中n0为统计的第一个周期,Np为统计的最大周期数,本文Np=10.
设壁面平均速度梯度![]() 壁面摩擦力
壁面摩擦力![]() 壁面摩擦速度
壁面摩擦速度![]() 以壁面摩擦速度进行无量纲的平均速度及坐标为
以壁面摩擦速度进行无量纲的平均速度及坐标为
(14)
(15)
其中坐标y∈[0,16].
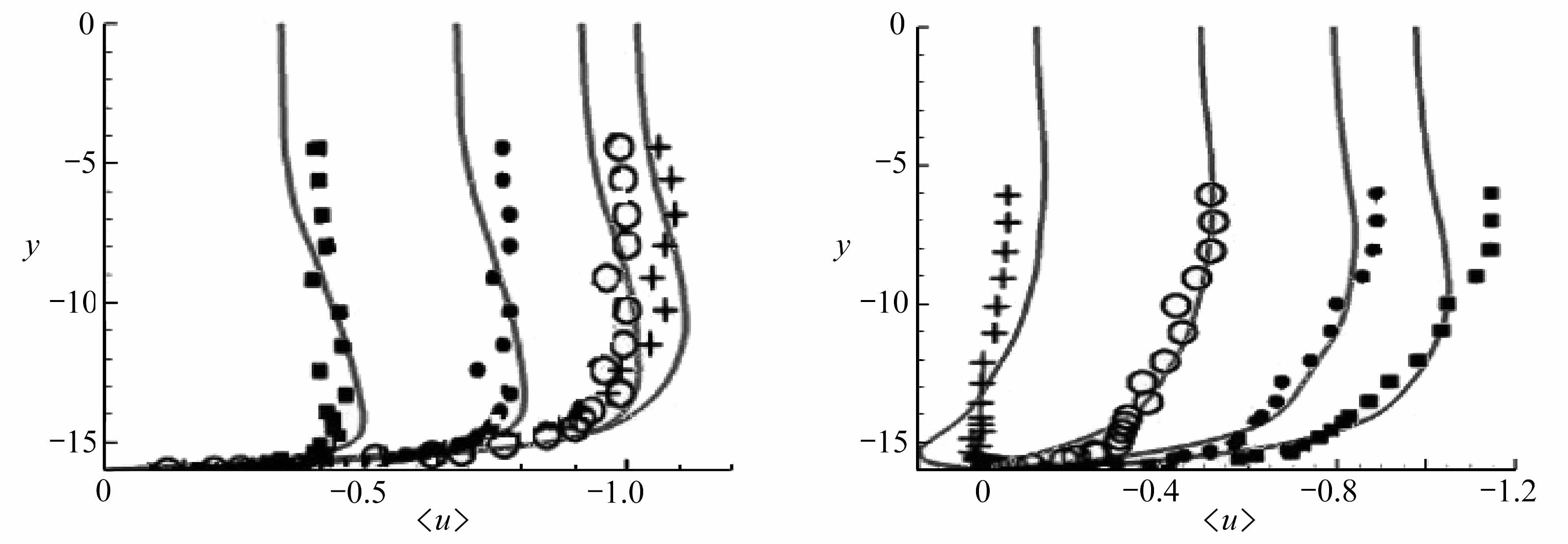
为了验证本文程序的正确性,将不同相位的统计平均速度与Akhavan等[4]的实验结果进行了比较,如图1所示,其中实线为本文的计算结果,特征点为Akhavan等[4]的实验结果.从图中可以看到,无论对于加速阶段还是减速阶段,本文的计算结果与实验吻合得都比较好,证明本文的数值计算结果是可信的.
2.1 转捩的速度演化特征
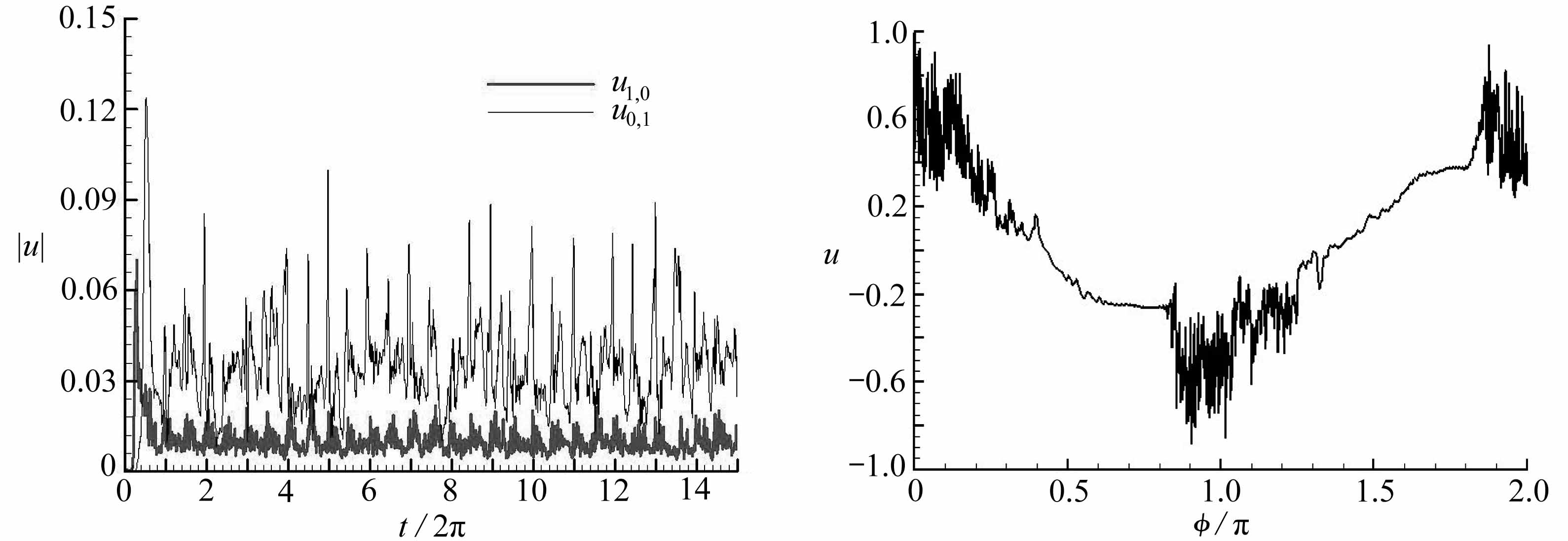
在本文的计算工况下流动发生了转捩,图2(a)给出的是基本扰动速度沿法向的最大值(用|u|表示)随时间的演化.从图中可以看出,扰动在转捩后呈现明显的高频脉动,并且扰动的峰值是在特定的时刻发生,表现出了湍流的间歇性.图2(b)为一个基本流周期内物理空间速度u的演化,可以看出,高频脉动出现于加速阶段末期,即基本流周期的相位角φ/π=n,且延续到减速阶段.具体地讲,从图中可以看出,从加速阶段后期,即相位角处于0.8<φ/π<1时,间歇湍流的扰动强度开始增加;在加速阶段转换为减速阶段时,即相位角φ/π=1左右,脉动强度达到最大;在减速阶段后期,即相位角1.3<φ/π<1.5时,扰动的强度逐渐减小.
(a) u10 (b) u01
图1 不同相位下平均速度〈u〉与实验的比较
Fig.1 Comparison of average velocity 〈u〉 with experimental results at different phases
(a) 基本扰动速度的演化 (b) 物理空间速度u的演化
(a) Fundamental disturbance velocity evolution (b) Evolution of velocity u in the physical space
图2 速度u随时间的演化
Fig.2 The evolution of velocity u with time
(a) t=38π+5π/8 (b) t=38π+6π/8
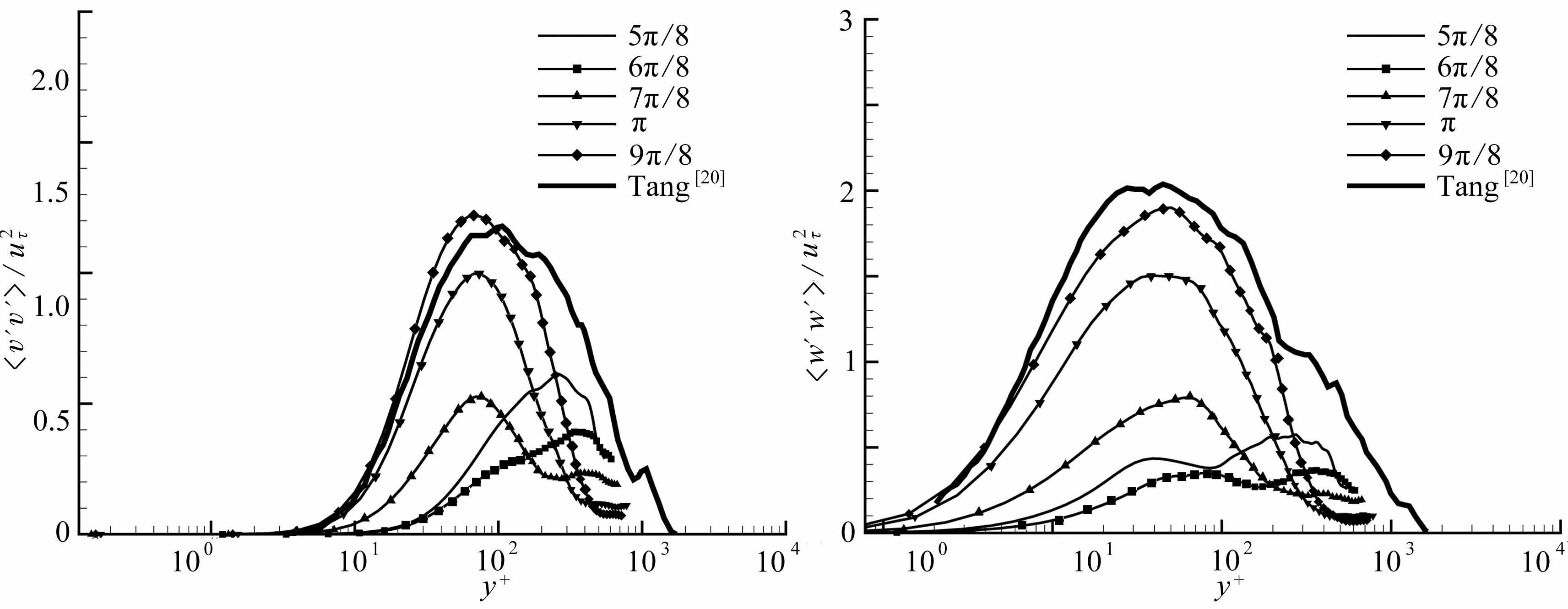
(b) y方向的正应力 (c) z方向的正应力
(b) Reynolds normal stresses in the y-direction (c) Reynolds normal stresses in the z-direction
图8 不同相位下Reynolds正应力与不可压缩边界层充分发展湍流结果的比较
Fig.8 Comparison of Reynolds normal stresses with the results of fully developed turbulencein the incompressible boundary layer at different phases
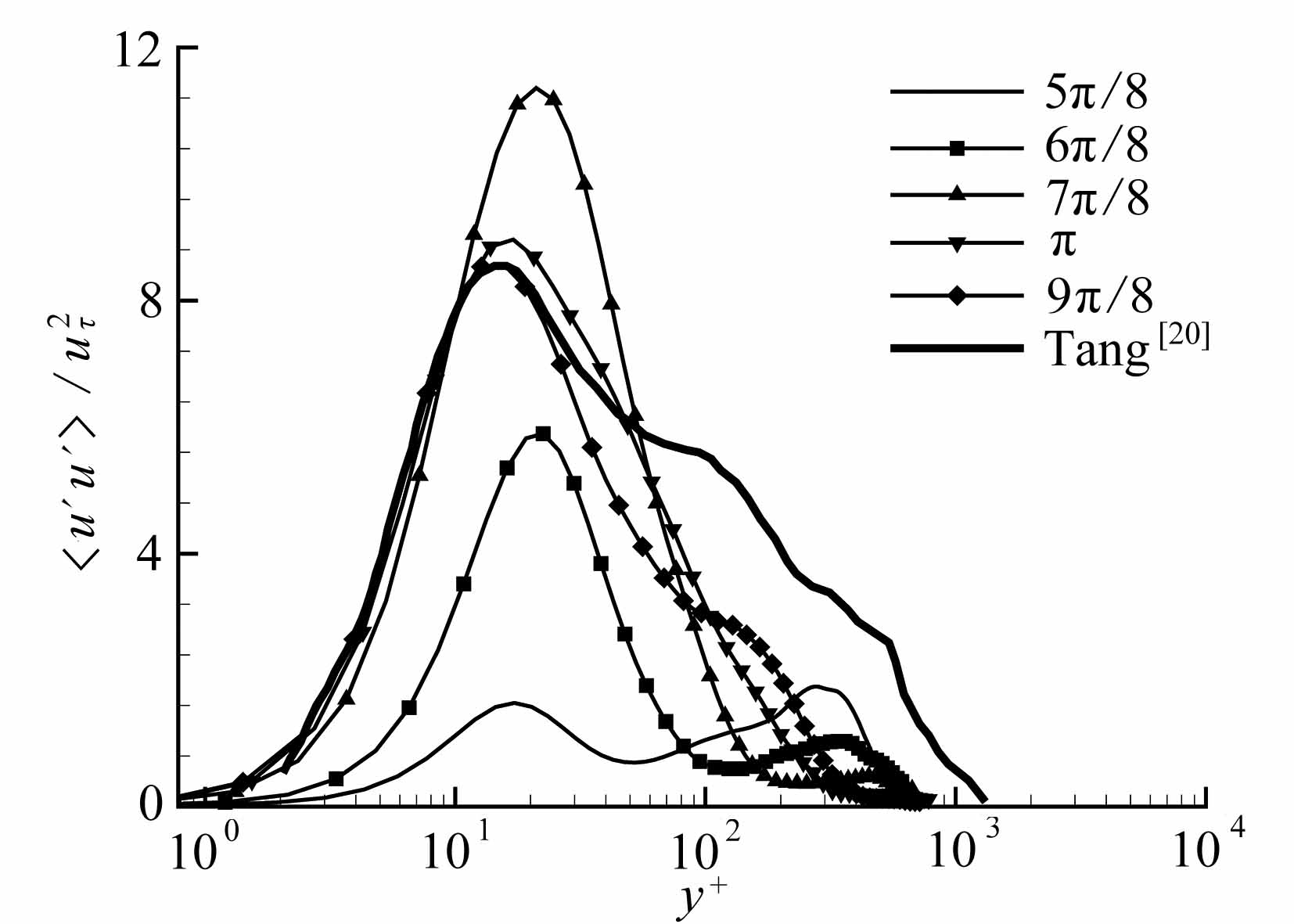
(a) x方向的正应力
(a) Reynolds normal stresses in the x-direction
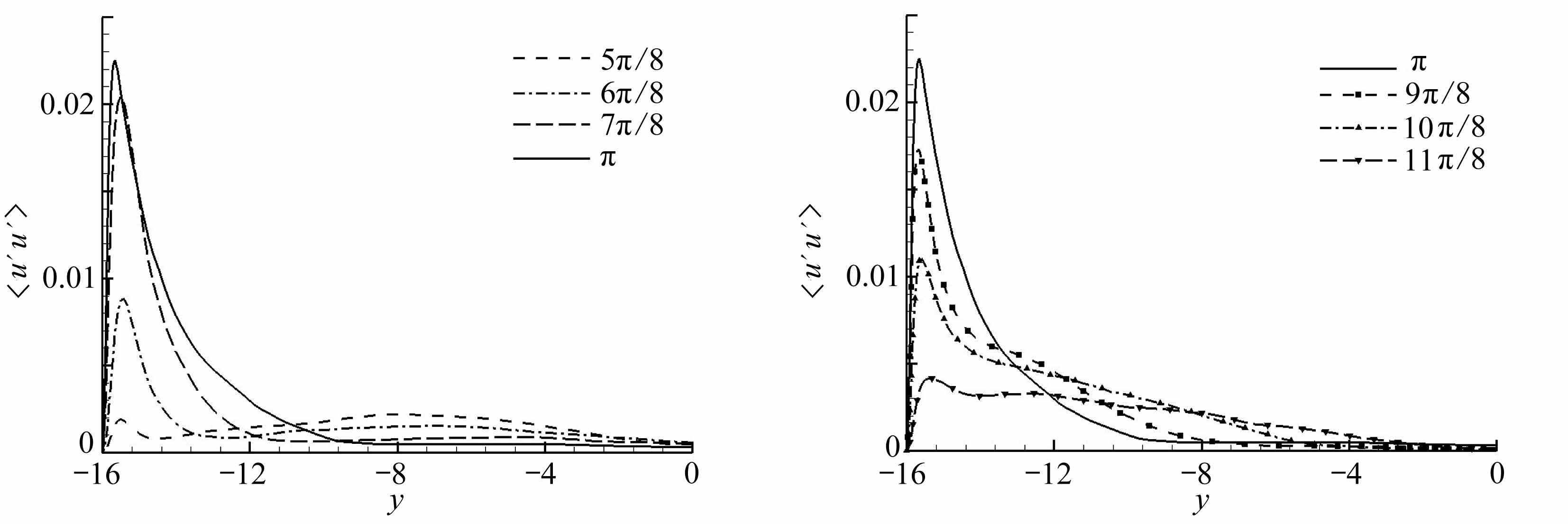
(a) 加速阶段 (b) 减速阶段
(a) The accelerating phase (b) The decelerating phase
图7 Reynolds正应力〈u′u′〉随时间的演化
Fig.7 The evolution of Reynolds normal stress 〈u′u′〉 with time
(a) φ/π=4/8 (b) φ/π=6/8
(a) φ/π=4/8 (b) φ/π=5/8
2.2 壁面速度梯度和平均脉动能量
壁面速度梯度是影响湍流形成的非常重要的因素,同时还影响着壁面律y+-u+,而湍流的许多特性都与壁面律有关,因此研究转捩中壁面速度梯度的变化对认识间歇湍流具有重要的意义.图3给出的是转捩后相位平均壁面速度梯度在一个基本流周期内的变化,其中实线为平均速度的壁面梯度![]() 虚线为基本流Ub的壁面梯度.从图3中可以看到,平均速度的壁面梯度
虚线为基本流Ub的壁面梯度.从图3中可以看到,平均速度的壁面梯度![]() 是以准周期形式进行演化,并且与基本流壁面梯度之间存在很大的差异:1) 零点相位不同.在一个周期内,相对于基本流壁面速度梯度,平均速度壁面梯度
是以准周期形式进行演化,并且与基本流壁面梯度之间存在很大的差异:1) 零点相位不同.在一个周期内,相对于基本流壁面速度梯度,平均速度壁面梯度![]() 的零点相位增大,从相位 φ/π=0.25变为0.4,从φ/π=1.25 变为1.4,这表明间歇湍流
的零点相位增大,从相位 φ/π=0.25变为0.4,从φ/π=1.25 变为1.4,这表明间歇湍流![]() 的零点时刻比层流要延迟. 2) 峰值不同.基本流壁面梯度在一个周期内的峰值只有1.5,而
的零点时刻比层流要延迟. 2) 峰值不同.基本流壁面梯度在一个周期内的峰值只有1.5,而![]() 的峰值达到了2.5.除此以外,还可以看到,在φ/π=0.8和1.8时,
的峰值达到了2.5.除此以外,还可以看到,在φ/π=0.8和1.8时,![]() 有一个拐点.
有一个拐点.
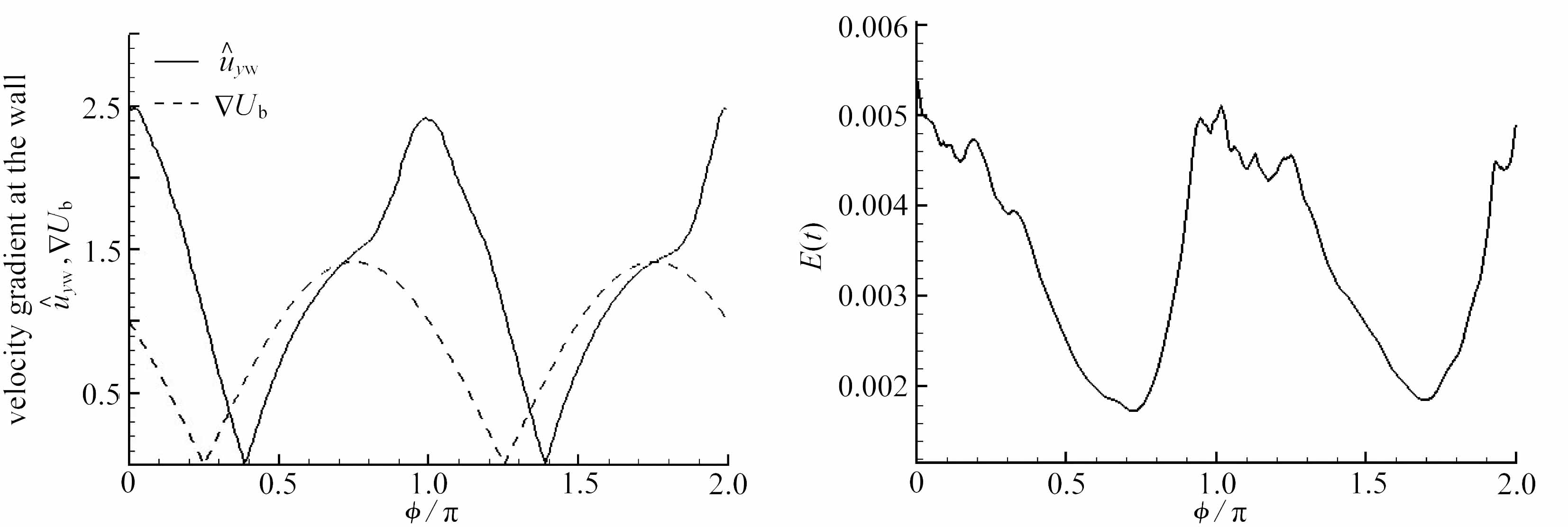
图3 壁面速度梯度在一个基本流周期内的变化 图4 平均脉动能量在一个周期内的变化
Fig.3 Variation of the average velocity gradient Fig.4 Variation of the average pulsating at the wall in one period of base flow energy in one period of base flow
另一方面,从图4可以看到,平均脉动能量在一个周期内的变化规律与壁面平均速度梯度基本类似,以准周期形式进行演化,即在加速阶段逐渐增大,在减速阶段的开始达到峰值,随后在减速阶段逐渐减小至0.
2.3 平均速度剖面的特征
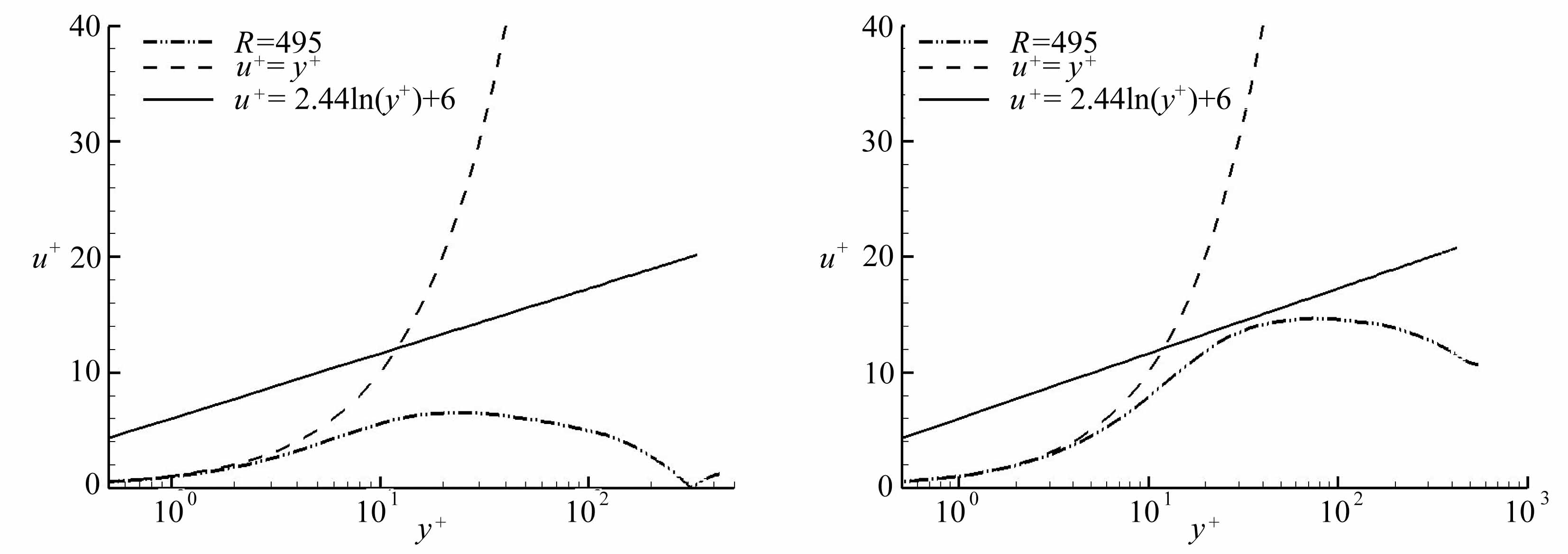
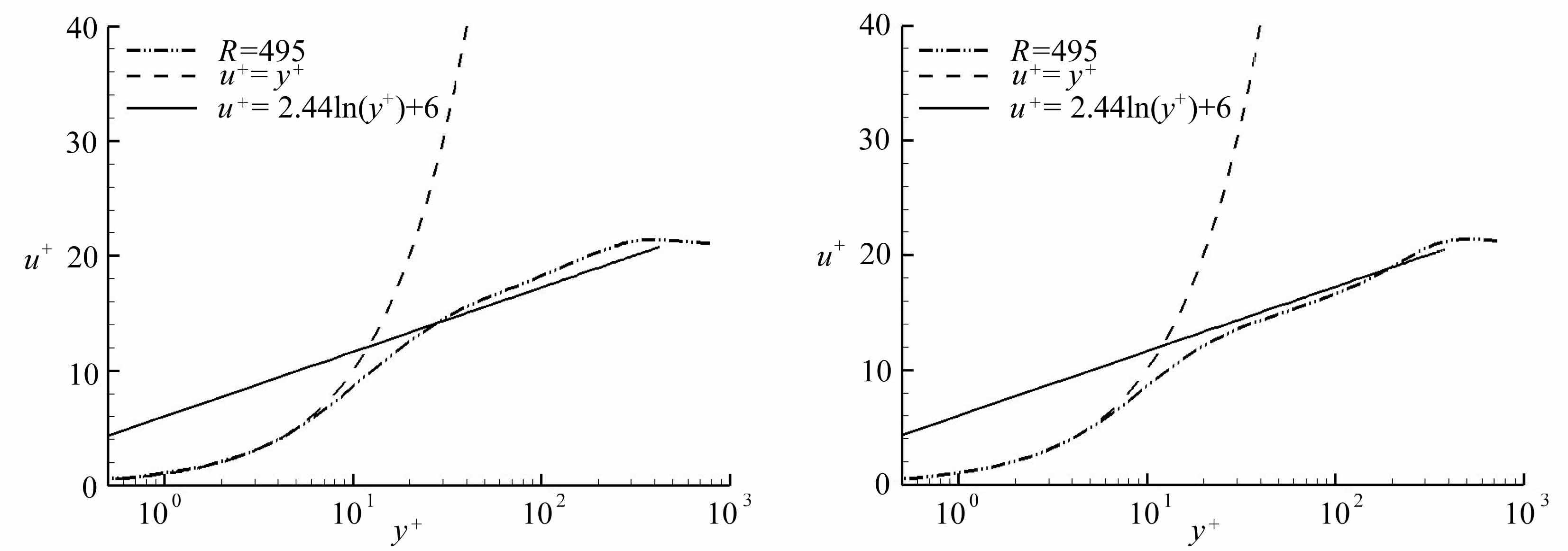
从定常流(槽道流、边界层等)的结果得知,充分发展的湍流速度分布满足对数律u+=kln(y+)+B.为了了解这一规律是否存在Stokes层间歇湍流中,图5给出了平均速度剖面与湍流对数律u+=(1/k)ln(y+)+B 的比较,其中B=6,k=0.41.从图中可以看到,对y+≤8,大部分相位下速度剖面都符合线性律u+=y+,只有在相位φ/π=11/8时不符合,原因是该相位对应了平均速度的转向点,壁面平均速度梯度在这时为零,因此用壁面律进行无量纲是不合适的.在对数律的范围内,加速阶段(φ/π=4/8~7/8 )的平均速度完全不符合对数律(注:由于周期性,φ/π=12/8 相当于前一周期的φ/π=4/8 ),φ/π=4/8 和5/8 时速度峰值低于对数律,而当 φ/π=6/8和7/8 时速度峰值超过对数律;随着流体进入减速阶段,平均流剖面逐渐靠近湍流的对数律分布,在 φ/π=1时,可以明显看到平均速度剖面已经比较符合对数律了;相位φ/π=9/8 时,平均速度与对数律符合得比较好;而当φ/π=10/8 时,二者的符合程度又开始变差;当φ/π=11/8时,由上文可知,平均速度发生转向,因此平均速度与壁面律的差别非常大.
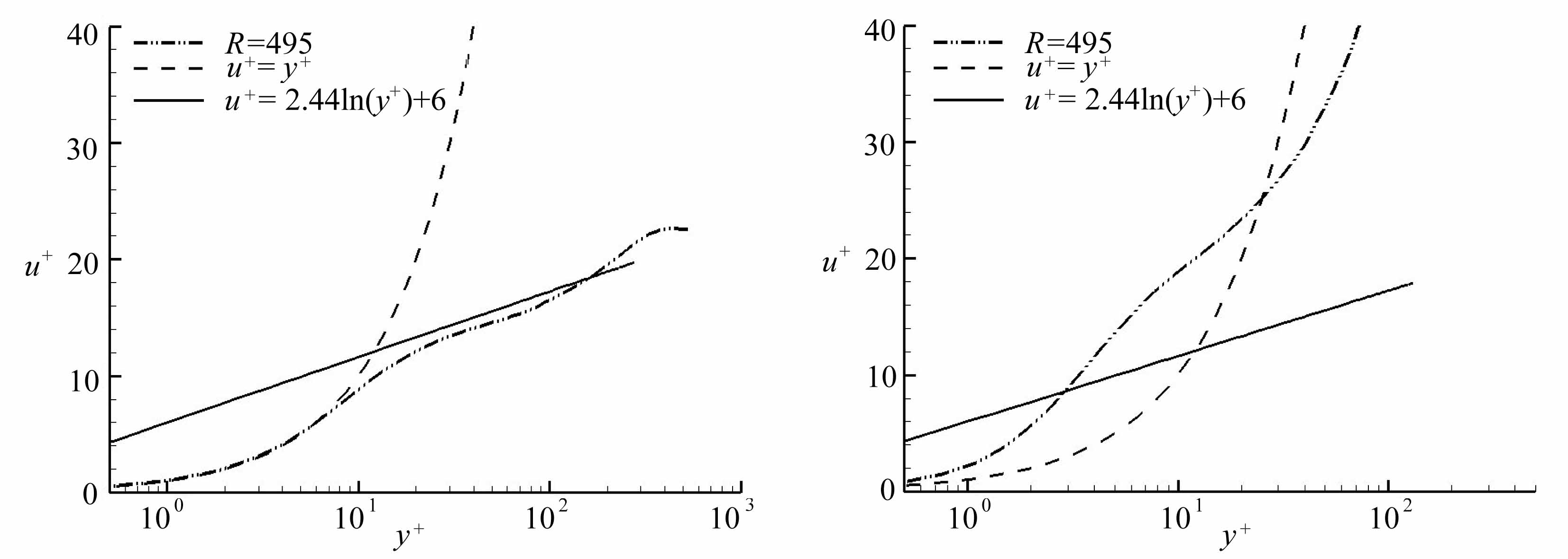
(g) φ/π=10/8 (h) φ/π=11/8
图5 不同相位下平均速度剖面
Fig.5 Average velocity profiles at different phases
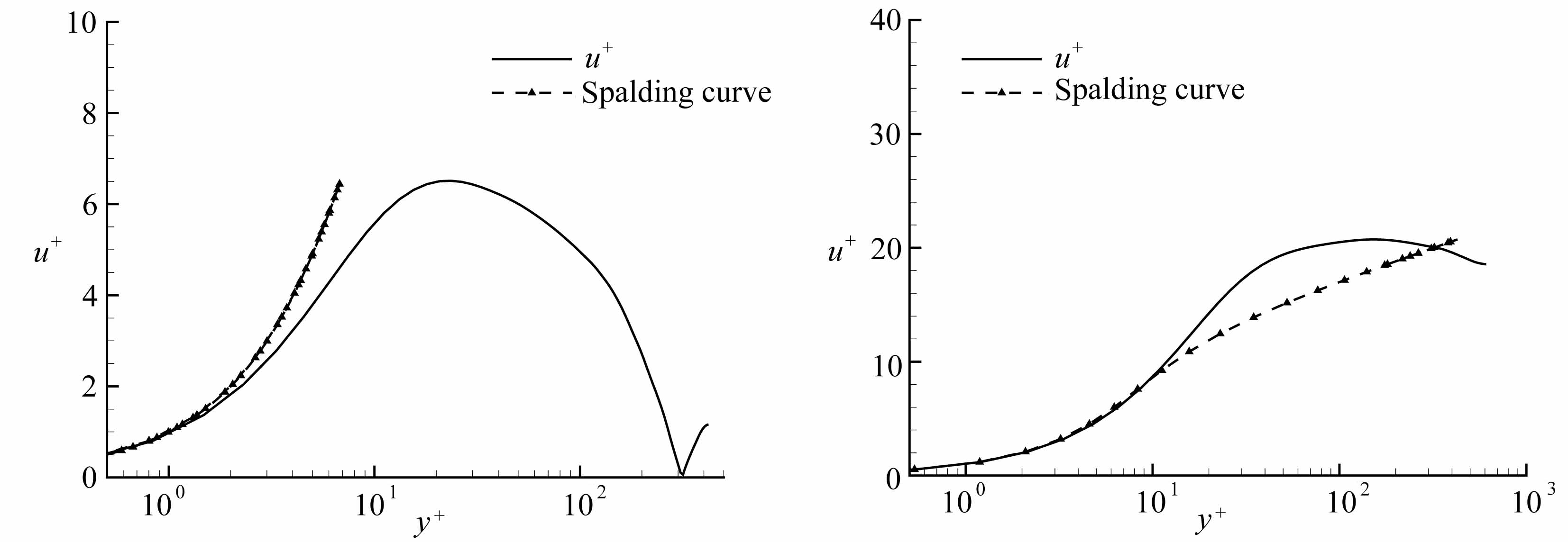
我们还可以将不同相位的平均速度与Spalding理论曲线进行比较,图6给出了4个相位下的比较结果,其中Spalding公式为
y+=u++e-kB[eku+-1-ku+-(ku+)2/2-(ku+)3/6],
(16)
式中k=4.1,B=6.可以看到,在加速阶段(φ/π=4/8,φ/π=6/8),平均速度只是在黏性底区与Spalding曲线相吻合,而随着流体进入减速阶段,二者符合的程度逐渐增加,从图6(c)、(d)中给出的减速阶段的两个相位来看,平均速度与Spalding公式符合得较好.
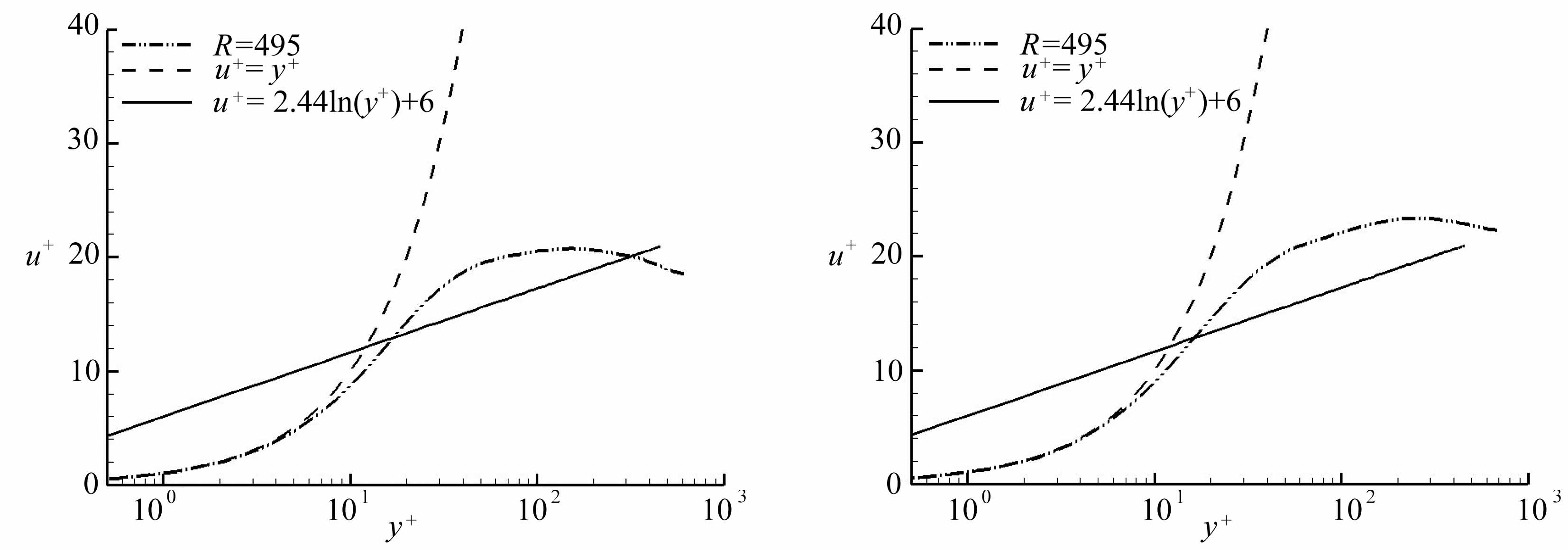
(c) φ/π=6/8 (d) φ/π=7/8
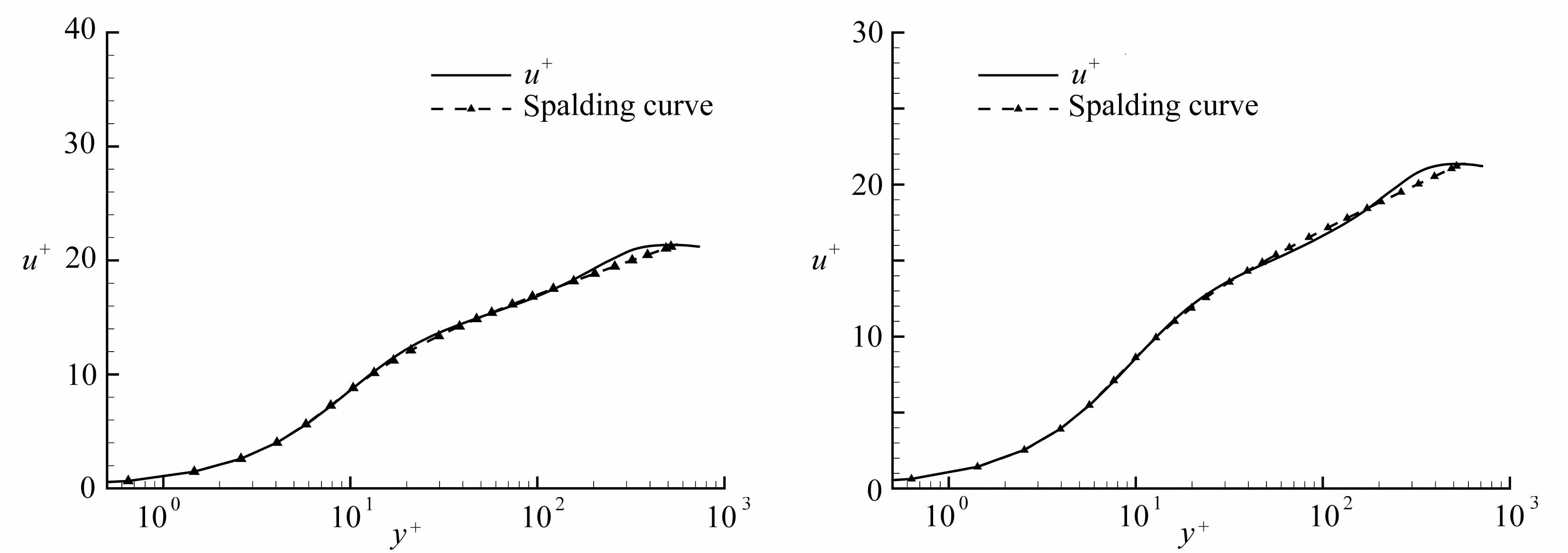
(c) φ/π=11/10 (d) φ/π=9/8
图6 不同相位平均速度剖面与Spalding曲线的比较
Fig.6 Comparison of average velocity profiles with Spalding curves at different phases in logarithmic coordinates
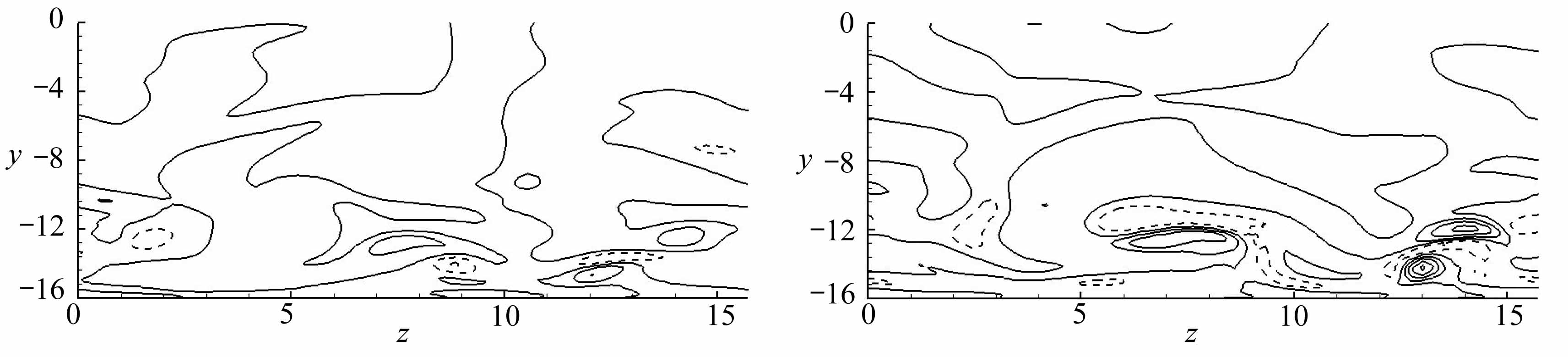
(c) t=38π+7π/8 (d) t=38π+π
2.4 Reynolds应力及流向涡
图7给出了Reynolds正应力〈u′u′〉在加速阶段和减速阶段的变化,其中显示的是半槽道的结果.从图中可以看到,加速阶段为脉动速度的产生阶段,〈u′u′〉从开始非常小逐渐增大,且峰值位置逐渐靠近壁面;当流动进入减速阶段,〈u′u′〉开始减小,峰值逐渐远离壁面.
图8给出了不同相位下Reynolds正应力与定常流结果的比较,图中显示的是以壁面摩擦速度uτ无量纲化后的结果,其中虚线为唐洪涛[20]通过直接数值模拟得到的不可压缩平板边界层充分发展湍流下的结果.从图8中可以看到,加速阶段时,无论是峰值位置还是大小,Reynolds应力都与充分发展湍流的结果相差很大;而当流动进入减速阶段后,二者的差距逐渐变小,尤其是峰值位置及大小,间歇湍流阶段下的Reynolds应力峰值大小及位置与不可压缩边界层充分发展湍流的情况相差不大,如流向Reynolds正应力〈u′u′〉,同样在y+=12左右取得最大值,并且峰值也为8.5.尽管如此,二者在湍流核心区( y+>100)还是存在较大的差异,这主要是由于间歇湍流的强非平衡性造成的.
实际上,Reynolds应力的变化与平均脉动能量的产生与耗散是密切相关的.从图4可以看到,当t/π∈(n+0.5,n+1),即加速阶段时,在Reynolds应力产生的阶段,湍动能同样处于增大阶段;当t/π∈(n,n+0.5),即减速阶段时,大部分时间内湍动能在进行消耗,同时也是Reynolds应力的衰减期.还可以明显看出,平均脉动能量达到最大值的时刻与Reynolds应力基本一致,出现在t/π=n附近.
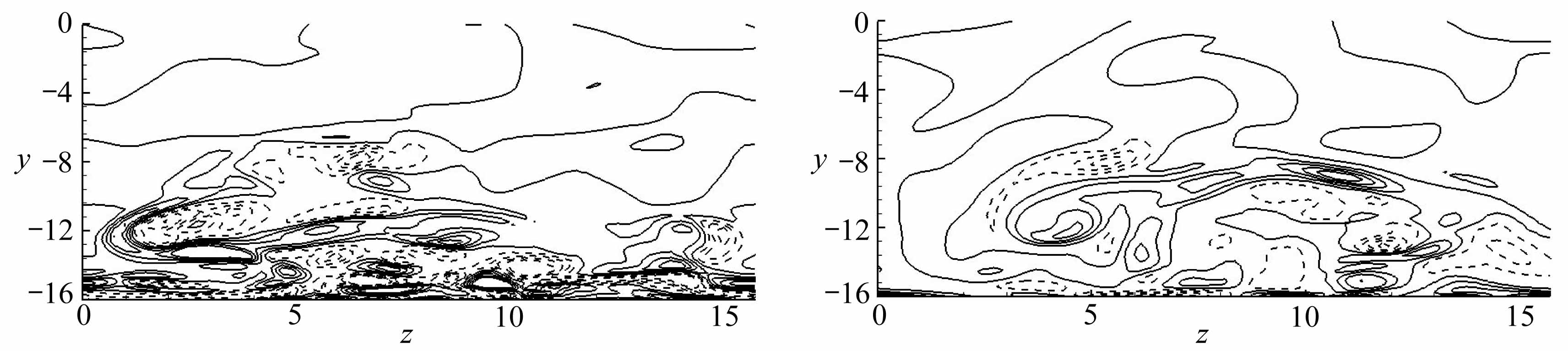
(g) t=38π+11π/8 (h) t=38π+12π/8
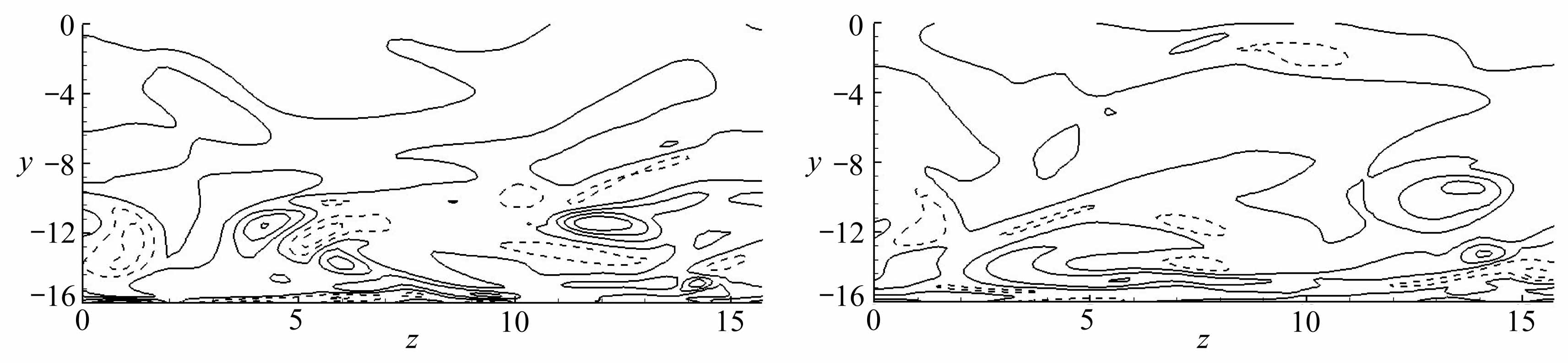
图9 不同时刻的流向涡量在y-z平面的分布
Fig.9 Distributions of streamwise vorticities in the y-z plane at different moments
为了更仔细观察流场的变化,图9给出了不同时刻的流向涡量在y-z平面的等值线图,其中分别给出的是加速阶段和减速阶段的4个不同时刻,纵坐标显示的是半槽道宽.从图中可以很明显看到,在加速阶段( φ/π=4/8~7/8),流场中基本上没有任何涡结构,到了减速阶段(φ/π=1~12/8),流场进入间歇湍流,从图9(e)中看到,近壁面开始卷起很多流向涡,并且随着减速的进行,流向涡逐渐破裂,到减速末期,流向涡又逐渐减小,流场重新变为层流.
(e) φ/π=1 (f) φ/π=9/8
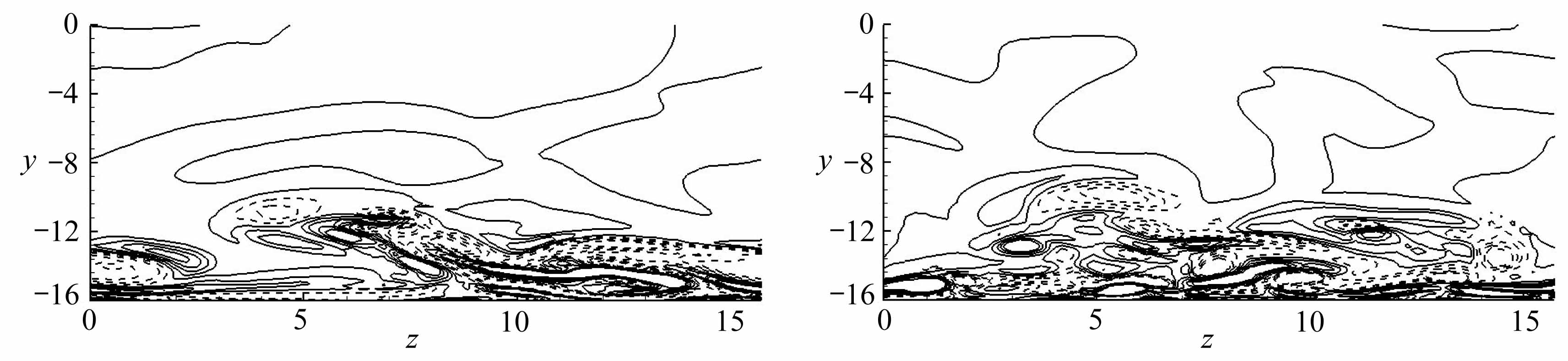
(e) t=38π+9π/8 (f) t=38π+10π/8
3 结 论
本文采用壁面的表面粗糙度为激励,针对过渡阶段Reynolds数Re=495下的间歇湍流特性进行了分析.所得结果如下:
1) 给出了平均速度的壁面梯度随时间的变化,结果表明,在一个周期内,相对层流的速度壁面梯度而言,间歇湍流的速度壁面梯度零点位置延迟,并且峰值增大很多;
2) 平均速度剖面在大部分相位下并不符合对数律,只有减速阶段的极少数相位处与对数律符合得较好;
3) 间歇湍流阶段Reynolds应力的分布与不可压缩平板边界层充分发展湍流的情况类似,但在湍流核心区存在较大的差异.
本文研究的Reynolds数距离充分发展湍流的临界Reynolds数Re=1 750较远,因此各统计特性均显示出Stokes层间歇湍流的强非平衡性,这也是过渡阶段湍流的特性.
[1] HINO M,SAWAMOTO M,TAKASU S.Experiments on transition to turbulence in an oscillatory pipe flow[J].Journal of Fluid Mechanics,1976,75(2):193-207.
[2] HINO M,KASGUWAYANAGI M,NAKAYAMA A,et al.Experiments on the turbulence statistics and the structure of a reciprocating oscillatory flow[J].Journal of Fluid Mechanics,1983,131(1):363-400.
[3] JENSEN B L,SUMER B M,FREDSOE J.Turbulent oscillatory boundary layers at high Reynolds numbers[J].Journal of Fluid Mechanics,1989,206(1):265-297.
[4] AKHAVAN R,KAMM R D,SHAPIRO A H.An investigation of transition to turbulence in bounded oscillatory Stokes flows,part 1:experiments[J].Journal of Fluid Mechanics,1989,225:395-422.
[5] HSU C T,LU X,KWAN M K.LES and RANS studies of oscillating flows over flat plate[J].Journal of Engineering Mechanics,2000,188:186-193.
[6] SCOTTI A,PIOMELLI U.Numerical simulation of pulsating turbulent channel flow[J].Physics of Fluids,2001,13(5):1367-1384.
[7] LOHMANN I P,FREDSΦE J,SUMER B M,et al.Large eddy simulation of the ventilated wave boundary layer[J].Journal of Geophysical Research,2006,111:21-39.
[8] SALON S,ARMENIO V,CRISE A.A numerical investigation of the Stokes boundary layer in the turbulent regime[J].Journal of Fluid Mechanics,2007,570:253-296.
[9] ZHANG Q.Large eddy simulation of oscillatory boundary layer at Reδ =3 500[J].Journal of Hydrodynamics,2010,22(5):160-165.
[10] SHENG Y P.Hydraulic applications of a second-order closure model of turbulent transport[C]//Applying Research to Hydraulic Practice,ASCE.2010.
[11] JUSTESEN P.A note on turbulence calculations in the wave boundary layer[J].Journal of Hydraulic Research,1991,29(5):699-711.
[12] SAJJADI S G,WAYWELL M N.Application of roughness-dependent boundary conditions to turbulent oscillatory flows[J].International Journal of Heat and Fluid Flow,1997,18(4):368-375.
[13] THAIS L,CHAPALAIN G,SMAOUI H.Reynolds number variation in oscillatory boundary layers,part Ⅰ:purely oscillatory motion[J].Coastal Engineering,1999,36(2):111-146.
[14] FOTI E,SCANDURA P A.A low Reynolds number k-ε model validated for oscillatory flows over smooth and rough wall[J].Coastal Engineering,2004,51(2):173-184.
[15] SANA A,GHUMMAN R A,TANAKA H.Modeling of a rough-wall oscillatory boundary layer using two-equation turbulence models[J].Journal of Hydraulic Engineering,2009,135(1):60-65.
[16] SHOME B.Numerical study of oscillating boundary layer flow over a flat plate using k-kL-ω turbulence model[J].International Journal of Heat and Fluid Flow,2013,42:131-138.
[17] VITTORI G,VERZICCO R.Direct simulation of transition in an oscillatory boundary layer[J].Journal of Fluid Mechanics,1998,371:207-232.
[18] 孔玮,罗纪生.壁面的表面粗糙度引起的Stokes层亚临界不稳定性[J].航空动力学报,2016,31(10):2500-2506.(KONG Wei,LUO Jisheng.Subcritical instability of a finite Stokes layer induced by wall surface roughness[J].Journal of Aerospace Power,2016,31(10):2500-2506.(in Chinese))
[19] KONG W,LUO J S.Influence of three-dimensional wall roughness on the transition of a finite Stokes layer[J].European Journal of Mechanics B:Fluids,2017,62:12-20.
[20] 唐洪涛.不可压缩平板边界层从层流突变为湍流的机理及湍流特性[D].博士学位论文.天津:天津大学,2007.(TANG Hongtao.The mechanism of breakdown in laminar-turbulent transition and the characteristics of turbulence in an incompressible boundary layer on a flat plate[D].PhD Thesis.Tianjin:Tianjin University,2007.(in Chinese))