引 言
并联机器人是由动平台(或称为末端)、静平台(或称为支架)以及连接着它们的若干运动分支(或称为腿)组成的机械系统,具有动力性能好、承载能力强、精度高及刚度大等优点,目前在工业、医疗和航空等领域上得到了广泛应用,如高精度机床、太空探索、医学和微动装置.为了实现高精度控制,需要一个准确的并联机器人动力学模型.但由于并联机器人结构之间耦合关系十分复杂,其动力学模型通常是一个多参数耦合及高度非线性的复杂系统,这使得并联机器人的动力学分析和建模十分困难.对机器人进行动态建模常用的几种方法包括Lagrange-d’Alembert法、Gibbs-Appell法、Newton-Euler法、Kane法、虚功原理和Hamilton原理等.姜峣等[1]基于Newton-Euler法,提出了一种对机构进行变形协调分析,并且增加补充方程的方法,得到了完整的机构动力学模型.Lagrange法建立Lagrange动力学方程主要通过能量守恒的原理,该方法是目前并联机器人动力学建模中应用较为广泛的一种方法.白志富等[2]通过Lagrange方法,获得了一种3自由度并联机器人的动力学模型,并且对驱动力进行了求解.文献[3]证明了Newton-Euler和Lagrange方法在获得动态模型的视角上是等价的,但Newton-Euler方法实现的角度比Lagrange方法更完整.Cheng等[4]利用Lagrange乘子法和d’Alembert原理相互结合的方法,推导得出了一种比较简洁的冗余驱动并联机器人的动力学方程.Geike等[5]结合符号法和虚功原理两种方法,建立了并联机构的完全机动性的动力学模型.Wu等[6]通过虚拟工作原理,进而得到了冗余驱动并联机械手的逆动力学模型,在得到动力学模型后,借助使用最小二乘法对驱动力进行了优化处理.Wang等[7]以 3自由度冗余驱动并联机构为研究对象,利用虚功原理获得了逆动力学模型,并应用最小二乘法对驱动力优化,但以上方法获得的动力学模型并不完整,只得到了驱动力的解.张国伟等[8]采用Kane法对并联机器人进行动力学建模.杨建新等[9]先对空间并联机构各种支链的动力学与运动学进行逆解分析,通过模块化计算方法分析并联机构逆解问题,然后结合Newton-Euler法与Lagrange法,建立了空间并联机构的运动学与动力学逆解模型,因此提高了计算效率.李永泉等[10-11]以球面2自由度过约束并联机器人为研究对象,该并联机器人的动力学模型为机电两种能量并存系统,通过旋量键合图的方法获得了球面2自由度过约束并联机器人的动力学模型.但机构中既有被动过约束也有主动过约束,这导致所建动力学模型未知数个数多于方程数.于是他们对机构进行变形协调分析和驱动力优化,由此增加补充方程,得到了该机器人完整的多能域动力学模型.
作为最为常见的动力学建模方法之一,Newton-Euler法的优点在于思路比较简单,直观易懂,但随着并联机器人自由度数目的增加,Newton-Euler法在使用过程中需要写出每个连杆的运动方程,因此要建立的方程个数就随之增加,使得计算过程的复杂程度增加.Kane方法的优势在于得到的动力学模型形式相对简洁,但是建模思路比较抽象难懂,相对于其他方法来说使用困难.Lagrange法建立的模型比较简洁,同时推导过程相对简单,但是对于并联机器人来说,由于并联杆件数目比较多,导致系统变量的数目增加,因此迭代步骤复杂,建模工作量大.Lagrange法和d’Alembert法相结合能够简洁地表达并联机构的闭环广义力,计算速度高于Lagrange法,但是步骤复杂,计算量大.上述传统的并联机器人动力学建模方法在工程实际中虽得到了广泛的应用,但随着机构复杂度的增加或者当约束为非完整约束时,建模过程会变得十分困难.在并联机器人的动力学建模方法研究中,目前还缺少一种系统、简洁的动力学解析建模方法和控制方法.因此,本文引入了一种新颖的Udwadia-Kalaba(U-K)[12]方法来快速有效地获得并联机器人的动力学模型并实现轨迹跟踪控制.赵韩等[13]在U-K方程的基础上找到了Hamel嵌入法有效性的分界线,并给出了特殊情况下的判定条件, 通过例子,得出在完整约束下利用Hamel嵌入法建立运动学方程可能得出错误结果,而在非完整约束下也可能得到正确结果.Zhao等[14]分别对U-K方程与Newton-Euler方程、Lagrange方程和Kane方程进行了比较,给出了3种不同类型的示例进行演示来说明如何构建模型以及如何处理约束.通过仿真演示了U-K方程的性能, 说明其极大地有助于解决复杂的约束运动.Zhao等[15]通过U链和鱼类机器人这两种情况,展示了如何使用U-K方程获得动力学模型,并提出了多体系统的建模方法,还证明了无论其质量矩阵是否是奇异的,U-K理论都适用于系统.U-K理论被创造性地应用于U链和鱼类机器人问题的动力学建模,并获得了明确的运动解析方程,但其未进一步将U-K用于控制.在解决运动轨迹跟踪方面,U-K方法也显示出其简洁性和有效性,其主要思想是将给定轨迹看成是虚拟约束,进而求解满足虚拟约束的约束力,如文献[16-17]分别实现对机械臂和AGV的轨迹跟踪控制.但文献[16]在建立机械臂动力学模型时未考虑U-K方法.
本文以平面2自由度冗余驱动并联机器人为研究对象,结合U-K方法和Lagrange方程建立了2自由度冗余驱动并联机器人的闭合运动方程.U-K方法在建立运动方程时不需要借助额外辅助变量,该方法最为显著的优点是建立的模型中约束力是解析解的表达式,并且建模的过程步骤清晰简洁,即首先利用Newton-Euler法或Lagrange法建立无约束系统模型,然后将物理约束转化为Pfaffian标准形式,最后利用U-K方法获得满足给定约束的约束力解析解并附加到无约束系统模型中.在文献[15,17]中,U-K方法主要用于开链机械系统建模.而闭链系统的结构更加复杂,冗余支链的引入使得系统约束也存在冗余,不能直接应用U-K方程.本文将U-K方法综合应用于复杂并联系统的建模和控制中.首先将并联系统拆分为3个子系统,通过巧妙地设计约束,将子系统之间的物理连接(例如基座固定连接、结构之间的连接等)抽象为一种运动约束,从而应用U-K方法建立动力学方程.获得模型后,进一步利用U-K方法进行轨迹跟踪控制,且只需要将轨迹约束施加到任意一个支链子系统,不需要分别对3个系统进行约束求解.本文为复杂并联系统的动力学建模和轨迹跟踪控制提供了一条简洁、有效的思路.文中通过数值仿真,验证了所建立的动力学模型和轨迹跟踪控制方法的有效性.
1 Udwadia-Kalaba方法
U-K方法是一种求解受约束系统约束力解析解的方法.假设一个无约束的机械系统有n个状态变量q=[q1,q2,q3,…,qn]T,根据Newton力学或者Lagrange力学可写出该系统的运动方程[16]:
(1)
其中初始条件为![]() 是时间,q∈Rn是广义的坐标,
是时间,q∈Rn是广义的坐标,![]() 是广义速度,
是广义速度,![]() 是广义加速度,M(q,t)=MT(q,t)∈Rn×n是惯性矩阵,
是广义加速度,M(q,t)=MT(q,t)∈Rn×n是惯性矩阵,![]() 包括由于重力、给定力(或压力)和科氏力/离心力引起的影响力.
包括由于重力、给定力(或压力)和科氏力/离心力引起的影响力.
若该系统存在m(m≤n)个一阶形式的约束:
(2)
其中A(q,t)为m×n阶矩阵,C(q,t)为m×1阶列向量.将一阶形式的约束对时间求一次导,可得到约束的二阶Pfaffian标准微分形式如下[12]:
(3)
其中A(q,t)为m×n阶矩阵,![]() 为m×1 阶列向量.若给定约束是零阶的,则需要将其对时间求二次导.当系统引入外界约束时,该机械系统就成为“受约束机械系统”,其运动学方程为
为m×1 阶列向量.若给定约束是零阶的,则需要将其对时间求二次导.当系统引入外界约束时,该机械系统就成为“受约束机械系统”,其运动学方程为
(4)
其中![]() 为由外加约束产生的额外约束力.假设式(2)中A(q,t)的秩大于等于1, 且惯性对称矩阵M(θ,t)可逆, 则根据U-K方法, 上述机械系统约束运动方程的解析形式如下[12]:
为由外加约束产生的额外约束力.假设式(2)中A(q,t)的秩大于等于1, 且惯性对称矩阵M(θ,t)可逆, 则根据U-K方法, 上述机械系统约束运动方程的解析形式如下[12]:
(5)
式中B(q,t)=A(q,t)M1/2(q,t),B+(q,t)为B(q,t)的Moore-Penrose广义逆矩阵.对比式(4)和(5),可得由于施加约束产生的额外约束力为
(6)
从上述约束力的求解过程可以看出,相比Lagrange方法,U-K方程不使用额外的辅助变量求解,约束力为解析解,且仅基于与“非约束系统”相同的系统状态变量q.
2 动力学建模
一个2自由度冗余驱动并联机器人如图1所示,其由3个子系统组成.每个子系统的一端通过旋转关节固定在支座上,3个支座上的旋转关节由3个电机提供驱动力矩.另一端则连接在一个末端执行器上.
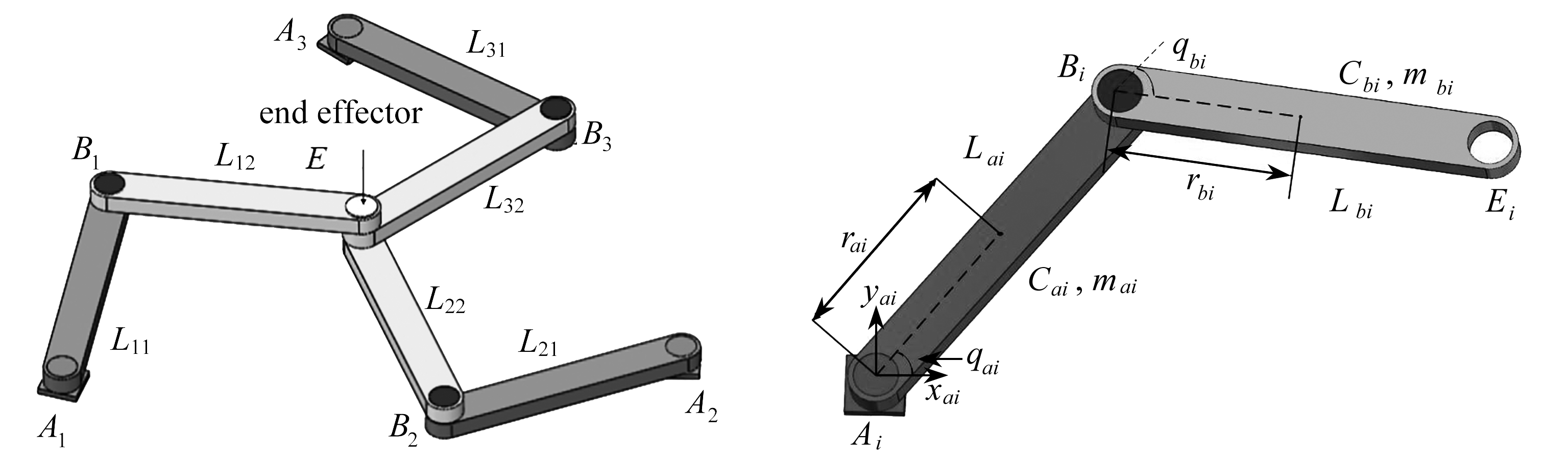
图1 平面2自由度冗余驱动并联机器人图2 子系统i
Fig. 1 The planar 2-DOF redundant drive parallel robotFig. 2 Subsystem i
由于直接写出2自由度冗余驱动并联机器人的动力学方程十分困难,本文根据U-K方程的级联特性,采用层级建模的方法得到2自由度冗余驱动并联机器人的动力学方程.首先将2自由度冗余驱动并联机器人分割成3个子系统(如图2所示).通过Lagrange力学,我们容易得到子系统的动力学方程.其次,我们将每个子系统看作“无约束系统”,同时引入支座约束和末端执行器约束,利U-K方程得到2自由度冗余驱动并联机器人的动力学方程.
先利用Lagrange方程得出一个子系统的动力学方程.Lagrange力学主要以两个基本方程为基础:其一是针对直线运动;其二是针对旋转运动.我们先定义Lagrange函数为
L=K-P,
(7)
其中L为Lagrange函数,K为系统的总动能,P为系统的总势能,K和P可以用任何方便的坐标来表示.于是系统的动力学方程式,即Lagrange方程如下:
(8)
其中Fi为xi方向的所有外力之和,Ti为产生qi方向旋转的所有外力矩之和,xi和qi为系统变量.为了得到运动方程,首先需要推导系统的能量方程,然后根据式(8)对Lagrange函数式(7)求导.
由于系统水平,所以重力势能始终不变,选取系统所在平面为0势能面,故P=0.系统总动能K为两个连杆的动能K1和K2之和.两个连杆均具有质量分布,将其质量等效看作在质点上,在计算动能时需要考虑转动惯量.第i个子系统的参数如表1所示.
表1 第i个子系统的参数(i=1,2,3)
Table 1 Parameters of the ith subsystem (i=1,2,3)

parameterphysical meaningxai,yaix- and y-axis coordinates of point Aixmai,ymaix- and y-axis coordinates of centroid 1 Caixmbi,ymbix- and y-axis coordinates of centroid 1 Cbiqaithe angle of connecting rod AiBi with respect to the horizontal lineqbithe angle of connecting rod BiEi with respect to the horizontal lineraithe center of mass Cai relative to active joint Airbithe center of mass Cbi relative to active joint BiLthe length of link AiBimai,mbimasses of links AiBi, BiEiIai,Ibithe moments of inertia of links AiBi, BiEi relative to the center of mass
根据第i个子系统的参数,写出两连杆质点速度如下:
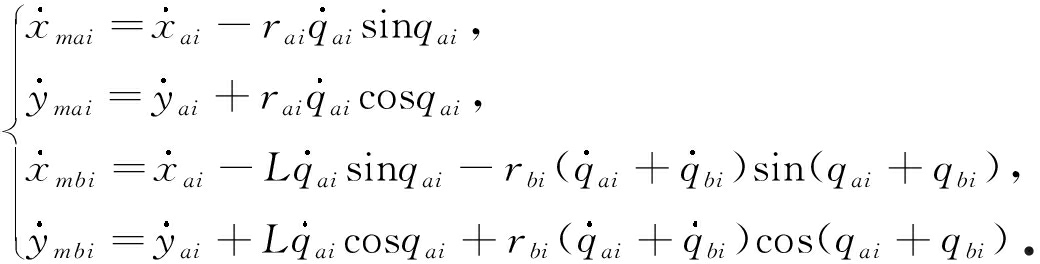
(9)
所以系统总动能为
K=K1+K2=
(10)
对Lagrange函数(10)求导可得
(11a)
(11b)
(12a)
(12b)
在式(11)和(12)中,选取qi=[qai,qbi,xai,yai]T 为系统第i(i=1,2,3)个机械臂子系统的状态变量.通过Lagrange方法,得出第i个机械臂子系统的运动方程的矩阵形式如下:
(13)
式中Mi和Ci分别是第i个子系统的质量矩阵和离心力/科氏力,τi是由组装在第i个主动关节中的制动器施加的外部扭矩.Mi和Ci如下所示:
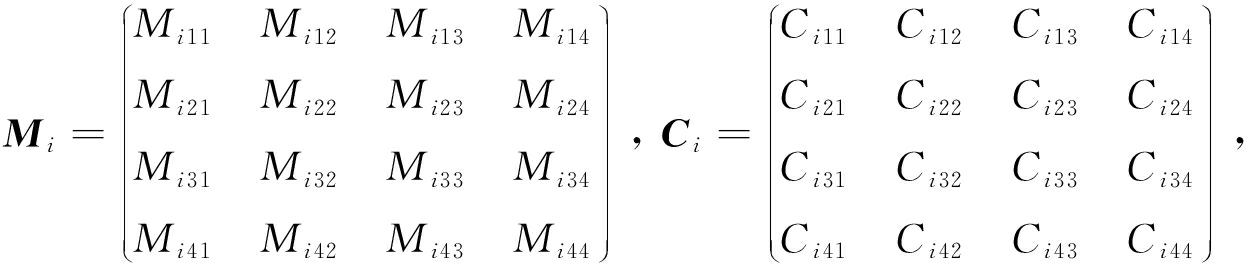
(14)
其中
Mi13=Mi31=-[(mairai+mbiL)sin qai+mbirbisin(qai+qbi)],
Mi14=Mi41=(mairai+mbiL)cos qai+mbirbicos(qai+qbi),
Mi23=Mi32=-mbirbisin(qai+qbi),
Mi24=Mi42=mbirbicos(qai+qbi),
Mi33=Mi44=mai+mbi,
Mi34=Mi43=0,
Ci13=Ci14=Ci22=Ci23=Ci24=Ci33=Ci34=Ci43=Ci44=0.
选取系统状态变量为q=[qa1,qb1,xa1,ya1,qa2,qb2,xa2,ya2,qa3,qb3,xa3,ya3]T,将这3个没有约束的子系统的运动方程联立成矩阵形式:
(15)
其中
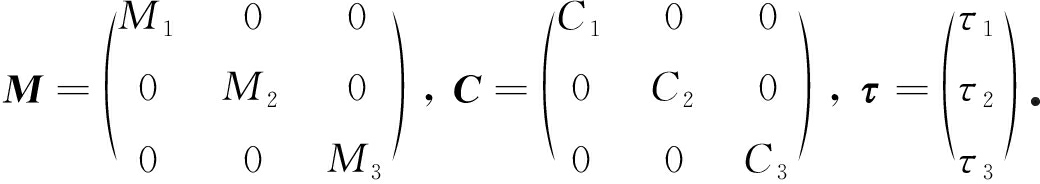
一方面,将3个子系统的一端利用约束各自固定在一个基座上,假设第i个子系统的末端主动关节为Ai,对应基座A′i的坐标为(x(A′i),y(A′i)).由于主动关节通过旋转关节与基座连接,因此第i个主动关节和基座之间的运动约束可表示为
x(Ai)=x(A′i), y(Ai)=y(A′i), i=1,2,3.
(16)
为了得到约束的二阶形式,将式(16)对时间t进行两次微分,得到二阶约束如下:
(17)

另一方面,把3个子系统的另一端Ei(i=1,2,3)通过旋转关节连接起来,将末端执行器固定在连接处E.设x(Ei)和y(Ei)表示末端执行器E在第i个子系统中的广义坐标.所以这3个子系统的运动学约束为
(18)
同样,为了得到约束的二阶形式,将式(18)对时间t进行两次微分,得到二阶约束如下:
(19)
其中
A2=(A21 A22 A23),
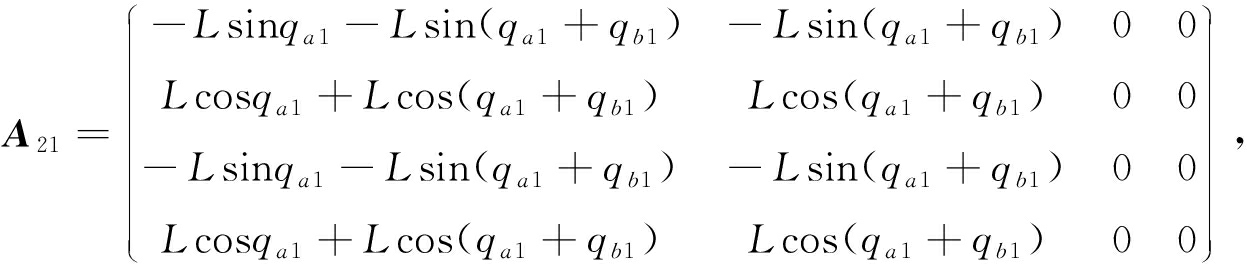
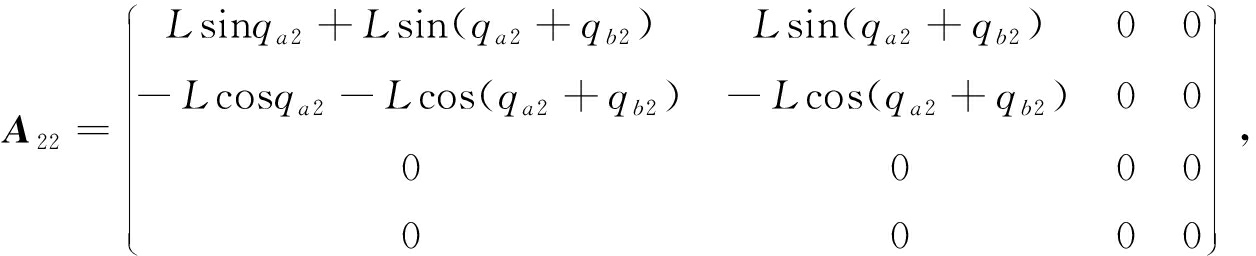
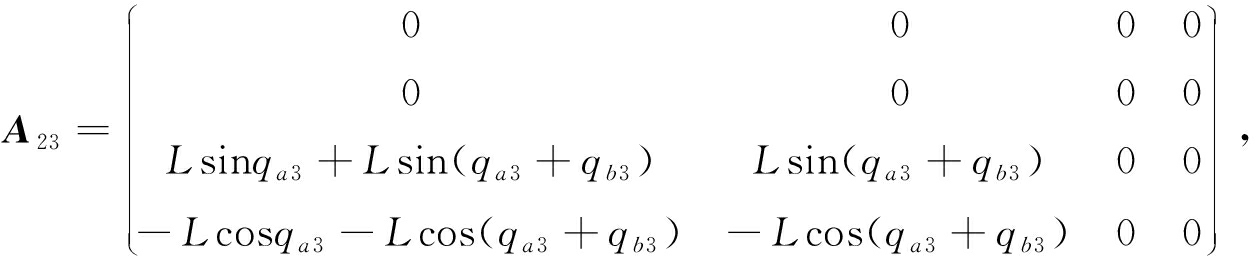
b2=
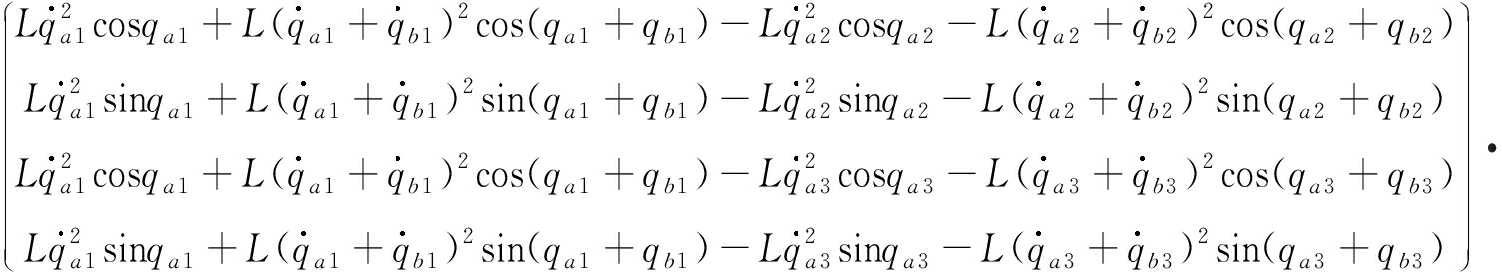
我们已经得到了支座约束和末端执行器约束的二阶形式,然后在式(15)上同时引入支座约束和末端执行器约束,通过U-K方程,可以得出2自由度冗余驱动并联机器人的动力学方程如下:
(20)
其中
B(q,t)=A(q,t)M-1/2(q,t),
A=(A1 A2), b=(b1 b2).
2自由度冗余驱动并联机器人的动力学建模过程总结如下:
步骤1 将2自由度冗余驱动并联机器人拆分为3个独立的无约束子系统.根据Lagrange方程,分别写出独立子系统的动力学方程,然后将3个方程联立成矩阵形式.
步骤2 同时引入末端执行器和基座的约束,将约束写成二阶Pfaffian标准微分形式.
步骤3 利用U-K方程,得到理想的2自由度冗余驱动并联机器人的约束力解析解.附加到第一步的方程中,得到完整的2自由度冗余驱动并联机器人的动力学模型.
3 轨迹跟踪控制
在得到了准确的2自由度冗余驱动并联机器人动力学模型后,为了让并联机器人完成期望功能,我们就必须对其进行轨迹控制,使其按期望轨迹运行.传统的轨迹跟踪控制大多是利用位置和速度传感器获得末端执行器的位置和速度,然后和给定的轨迹进行比较从而获得跟踪误差.最后采用不同控制方法(如PID控制、鲁棒控制、自适应控制等),将误差控制在合理范围内,从而实现轨迹跟踪.本文采用一种新的2自由度冗余驱动并联机器人轨迹跟踪控制思路.从U-K方法出发,将所需要跟踪的位置(或速度)轨迹抽象成虚拟的约束,然后将该约束转化为Pfaffian标准形式,再利用U-K方程获得机器人满足该轨迹约束所需要的驱动力矩,从而实现机器人的轨迹跟踪控制.
根据上述控制设计思想,进行轨迹跟踪控制时,先将2自由度冗余驱动并联机器人看作“无约束系统”.假设
(21)
将式(20)看作“无约束系统”,改写成无约束形式:
(22)
基于式(22)动力学方程,我们将期望的轨迹以二阶约束的形式引入.现在我们期望末端执行器E的x坐标和y坐标分别为时间t的函数fx(t)和fy(t),由于3个子系统已经在末端执行器处约束在一起,故只需在一个子系统的末端引入约束:
(23)
将式(23)对时间t求二次导,将二阶微分写成矩阵形式的约束:
(24)
若动力学模型式(22)要满足约束式(24),就需要给该“无约束系统”添加额外的约束力/力矩.假设额外的约束力/力矩为![]() 根据U-K方程可知
根据U-K方程可知
(25)
其中
B3(q,t)=A3(q,t)M-1/2(q,t),
至此,我们计算出跟踪期望轨迹所需要提供的额外力/力矩为![]()
4 数值仿真分析
4.1 动力学建模仿真
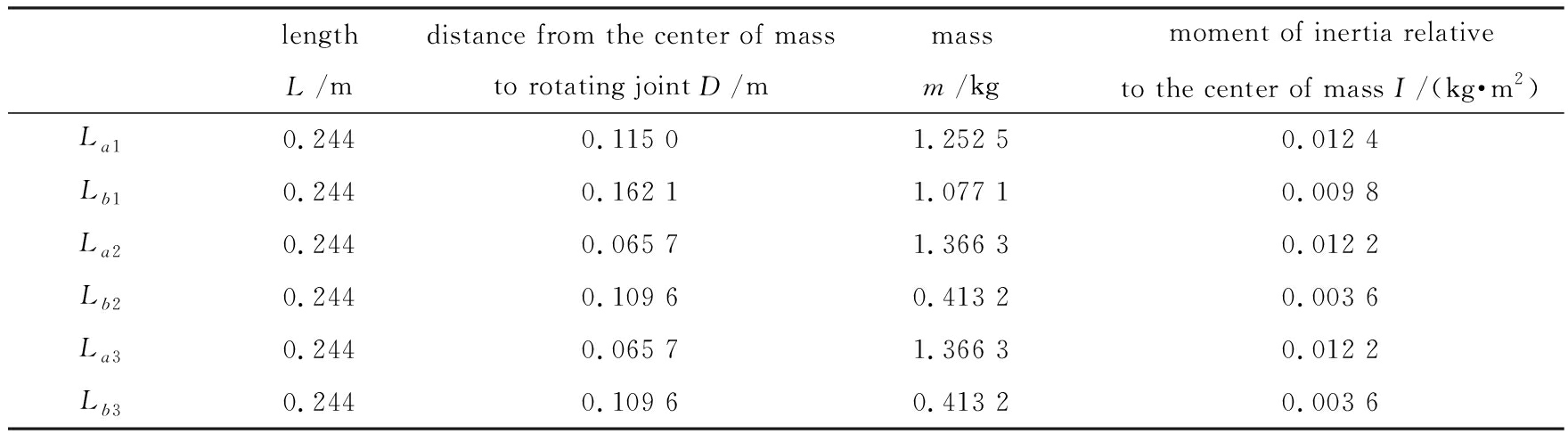
通过之前的动力学分析,并结合Lagrange方程和U-K方程,得到了理想的无关节摩擦的2自由度冗余驱动并联机器人的动力学方程.在本小节中,我们将通过数值模拟的方法来验证所提出的建模方法的有效性.当然,单个子系统的一些动力学参数,如连杆长度、连杆质量、质心位置、连杆相对质心的惯性矩等都是已知的[4].本文中3个子系统的动力学参数如表2所示.
表2 连杆动力学的参数
Table 2 Link dynamics parameters
lengthL/mdistance from the center of mass to rotating joint D/mmassm/kgmoment of inertia relativeto the center of mass I/(kg·m2)La10.2440.115 01.252 50.012 4Lb10.2440.162 11.077 10.009 8La20.2440.065 71.366 30.012 2Lb20.2440.109 60.413 20.003 6La30.2440.065 71.366 30.012 2Lb30.2440.109 60.413 20.003 6
在进行数值模拟之前,还需要知道每个子系统各个连杆之间的初始角度值和三个基座的位置坐标, 在这里我们假设初始的速度/角速度和加速度/角加速度在初始时刻都为0, 并选取任意一组满足约束的初始值进行仿真.选择初始状态q0=[1.301 5,-2.175 2,0,0.25,2.910 5,-1.459 3,0.43,0,2.981,1.877 6,0.426 9,0.500 5]T.另外,我们给该系统一个输入力矩,以验证3个子系统的末端轨迹是否重合以及与基座连接处是否固定,故令式(15)中的外加力矩τ=[0.1cos(πt),0,0,0,0,0,0,0,0,0,0,0]T,图3、4为数值仿真结果.
图3为3个子系统末端位置在xOy平面上的轨迹.我们将原系统拆分为3个子系统后,3个系统末端可以各自独立运动.但在引入末端约束后,由图3可知,3个子系统在外加力矩τ的作用下,末端运动轨迹重合.
我们在建立系统动力学模型时,基座与子系统也是通过引入约束来进行固定的,而不是一开始就将其固定在3个基座上.仿真结果(图4)展示了3个子系统基座连接处的坐标随时间的变化趋势.3个子系统与基座的连接处通过引入约束后,在外加力矩τ的作用下,坐标相对于时间的变化为常数,可知其固定在基座处不动.
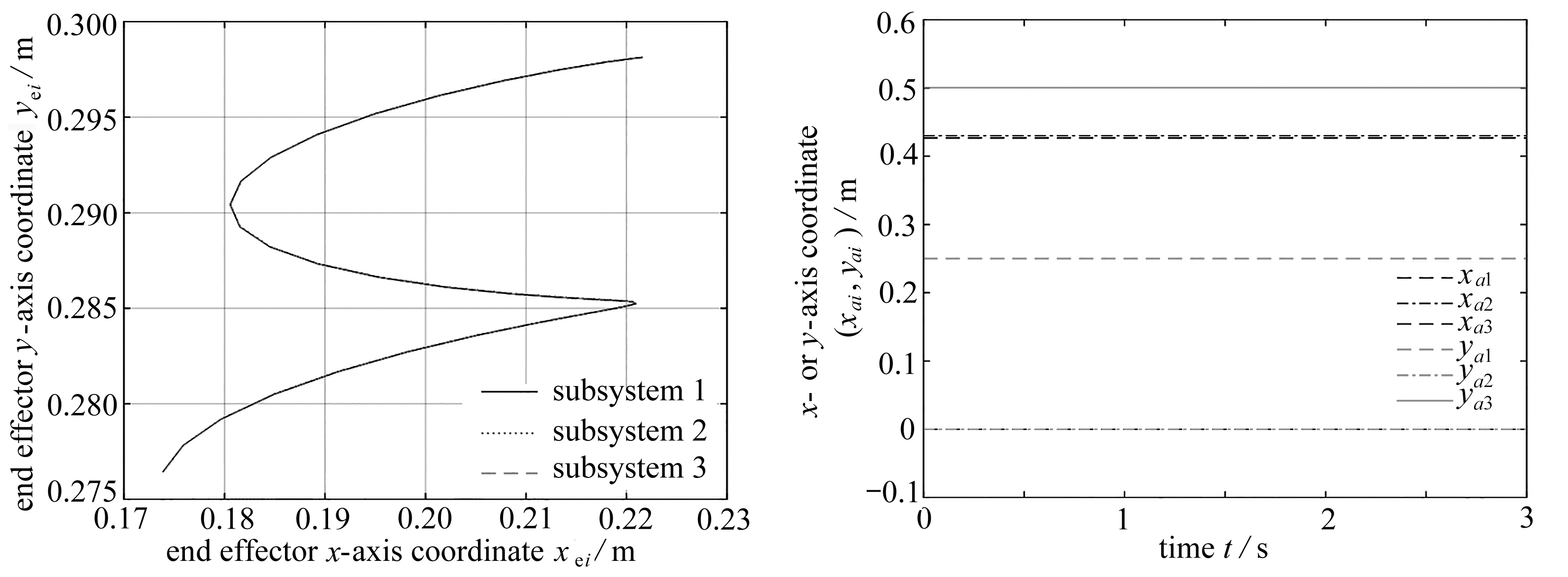
图3 3个子系统末端轨迹图(验证)图4 状态变量随时间变化趋势(验证)
Fig. 3 End traces of 3 subsystems(verification)Fig. 4 Trends of state variables over time(verification)
由仿真结果可知,运用本文提出的建模方法,子系统的基座连接处固定且末端执行器轨迹重合,故表明该方法准确、有效.
4.2 轨迹跟踪控制仿真
我们期望末端执行器E的x坐标和y坐标分别为时间t的函数fx(t)和fy(t),在进行轨迹跟踪控制数值仿真时,设fx(t)=ee1+0.01cos t, fy(t)=ye1,其中理想x坐标变化曲线为余弦函数,理想y坐标变化曲线为常数,合成理想的末端运动轨迹为水平往复运动的直线.根据式(23)和(24) 可得
(26)
将式(26)对时间t求二次导,将二阶微分写成矩阵形式的约束:
(27)
其中
式(26)中的(xe1,ye1)是选取的初始基准点的位置坐标,根据初始位置而定,为常数.
在进行期望的轨迹跟踪时,对于式(20)中的外加力矩τ,首先将其看作0,利用U-K方程求出![]() 此时
此时![]() 就是满足期望约束要提供的外加力矩τ.4.2小节的仿真初始状态和子系统动力学参数和4.1小节相同.根据式(22)和(27),数值仿真结果如图5所示.
就是满足期望约束要提供的外加力矩τ.4.2小节的仿真初始状态和子系统动力学参数和4.1小节相同.根据式(22)和(27),数值仿真结果如图5所示.
图5表示3个子系统末端执行器的x轴坐标和y轴坐标随时间的变化趋势.根据式(26),预期的轨迹为末端执行器x轴为余弦函数,y轴为静止.由仿真结果图5可知,各子系统x坐标和y坐标与理想轨迹重合,满足期望约束.
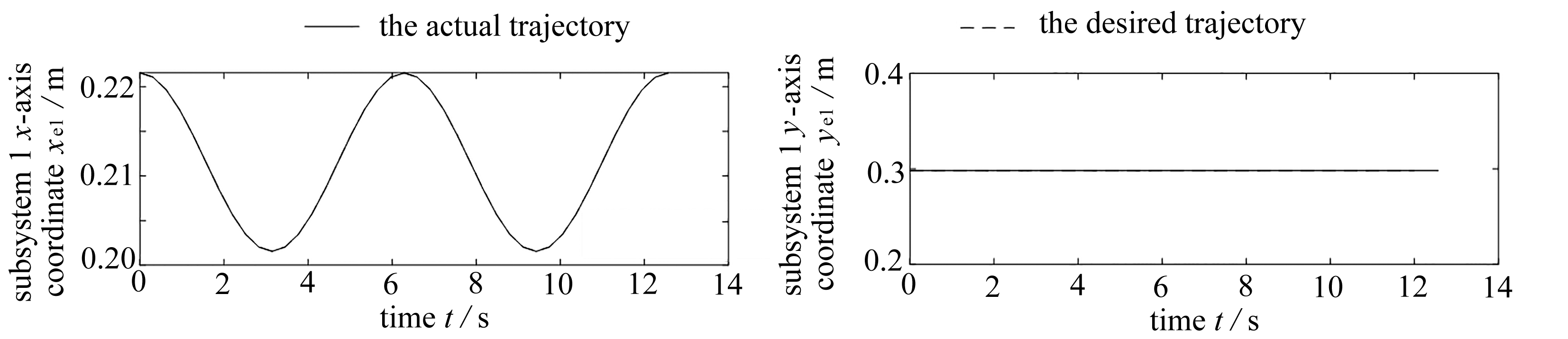
(a) 子系统1末端x轴坐标和y轴坐标随时间变化趋势
(a) The x- and y-axis coordinates of the end of subsystem 1 over time
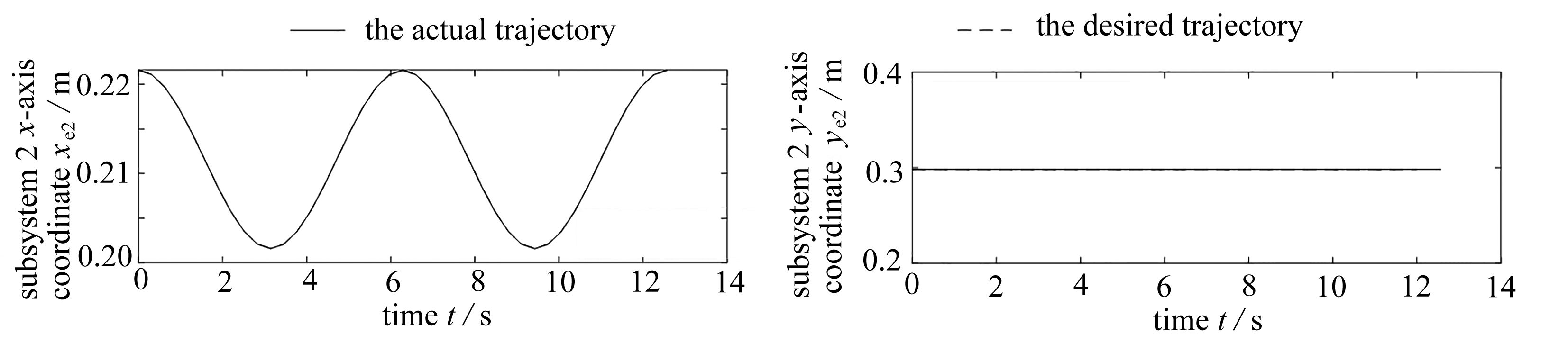
(b) 子系统2末端x轴坐标和y轴坐标随时间变化趋势
(b) The x- and y-axis coordinates of the end of subsystem 2 over time
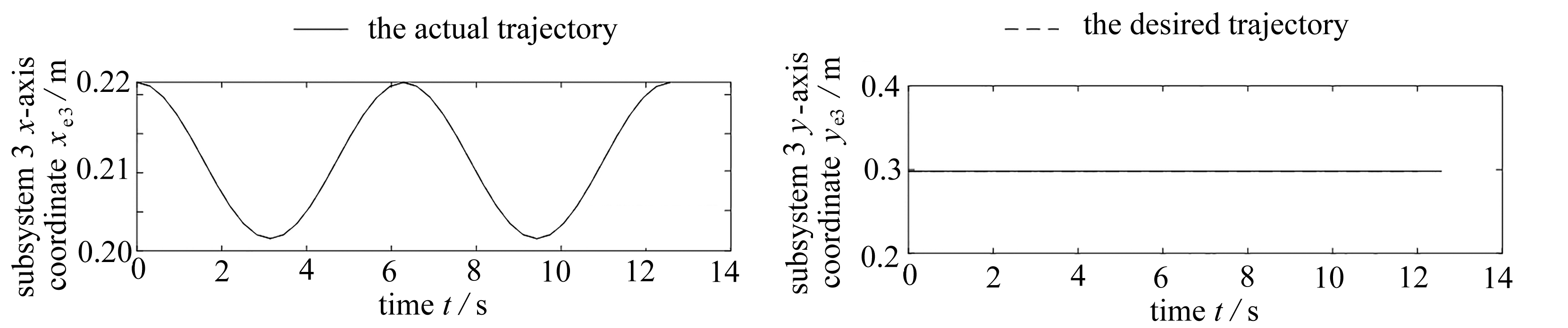
(c) 子系统3末端x轴坐标和y轴坐标随时间变化趋势
(c) The x- and y- axis coordinates of the end of subsystem 3 over time
图5 子系统末端坐标随时间变化
Fig. 5 The end coordinates of the subsystem over time
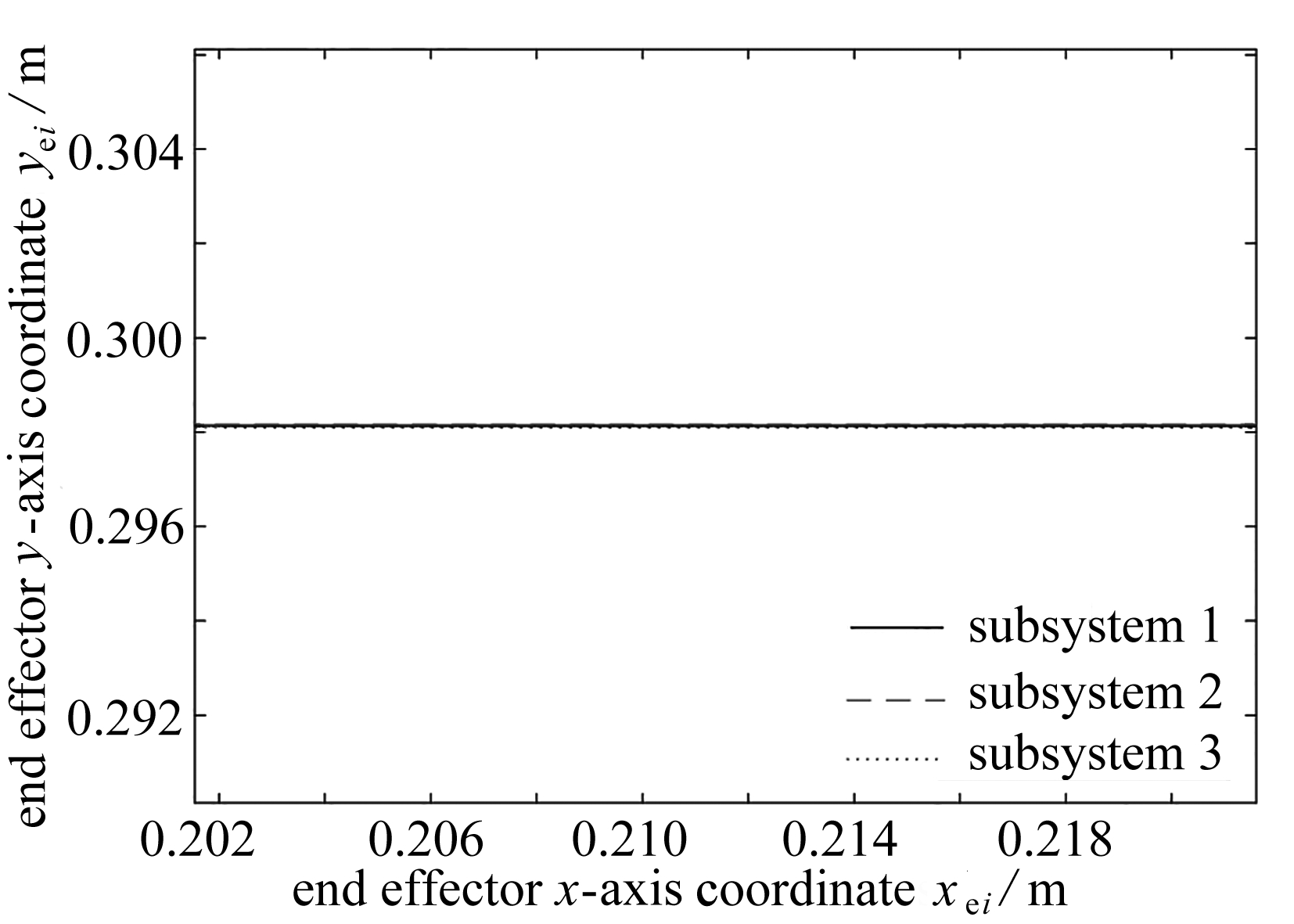
图6 3个子系统末端轨迹图
Fig. 6 End traces of 3 subsystems
图6为3个子系统末端位置在xOy平面上的轨迹.我们将原系统拆分为3个子系统后,3个系统末端可以各自独立运动.但在引入末端约束和期望轨迹约束后,由图6可知,3个子系统在外加力矩τ的作用下,末端执行器跟踪期望的水平直线,并且3个子系统轨迹重合.
运用本文提出的建模方法和轨迹跟踪控制方法, 3个子系统与基座连接处的广义坐标始终为常数, 视为固定不动.3个子系统的末端执行器运动轨迹重合, 且能良好地跟踪期望的轨迹.
5 结 论
并联机器人结构之间的耦合关系复杂,其动力学模型通常是一个多参数耦合及高度非线性的复杂系统,这使得常用的机器人建模方法在对并联机器人进行动力学分析和建模时十分困难.故在本文中,我们提出了一种基于U-K方程的新型建模方法.该方法利用U-K方程的级联性质建立并联机器人的运动方程.该方法最为显著的优点是分析形式的并联机器人的运动方程是在没有辅助变量的情况下获得的(例如Lagrange乘数或伪广义速度),建立的模型是解析形式,并且能够得到系统约束力的解析表达形式.该方法将并联机器人分成几个支链子系统,采用运动学约束来描述各子系统和末端执行器、子系统与基座之间的物理连接.通过级联特性,提出的方法在系统建模时具有普遍性、系统性和简单性.在得到准确的动力学模型后,将其视为无约束系统,同样利用U-K方程的级联性质,将期望轨迹以标准的二阶微分形式引入,求解额外约束力.最后通过数值仿真,证明了本文提出的建模方法和轨迹跟踪控制方法的有效性和准确性.
参考文献(References):
[1] 姜峣, 李铁民, 王立平. 过约束并联机构动力学建模方法[J]. 机械工程学报, 2013, 49(17): 123-129.(JIANG Yao, LI Tiemin, WANG Liping. Research on the dynamic model of an over-constrained parallel mechanism[J]. Chinese Journal of Mechanical Engineering, 2013, 49(17): 123-129.(in Chinese))
[2] 白志富, 韩先国, 陈五一. 基于Lagrange方程三自由度并联机构动力学研究[J]. 北京航空航天大学学报, 2004, 30(1): 51-54.(BAI Zhifu, HAN Xianguo, CHEN Wuyi. Study of a 3-DOF parallel manipulator dynamics based on Lagrange’s equation[J]. Journal of Beijing University of Aeronautics and Astronautics, 2004, 30(1): 51-54.(in Chinese))
[3] YIU Y K, CHENG H, XIONG Z H, et al. On the dynamics of parallel manipulators[C]//IEEE International Conference on Robotics & Automation. Seoul, 2001.
[4] CHENG H, YIU Y K, LI Z X. Dynamics and control of redundantly actuated parallel manipulators[J]. IEEE/ASME Transactions on Mechatronics, 2003, 8(4): 483-491.
[5] GEIKE T, MCPHEE J. Inverse dynamic analysis of parallel manipulators with full mobility[J]. Mechanism and Machine Theory, 2003, 38(6): 549-562.
[6] WU J, WANG J S, WANG L P. Dynamics and control of a planar 3-DOF parallel manipulator with actuation redundancy[J]. Mechanism and Machine Theory, 2009, 44(4): 835-849.
[7] WANG L P, WU J, WANG J S. Dynamic formulation of a planar 3-DOF parallel manipulator with actuation redundancy[J]. Robotics and Computer-Integrated Manufacturing, 2010, 26(1): 67-73.
[8] 张国伟, 宋伟刚. 并联机器人动力学问题的Kane方法[J]. 系统仿真学报, 2004, 16(7): 1386-1391.(ZHANG Guowei, SONG Weigang. A Kane formulation for the inverse dynamic of stewart platform manipulator[J]. Journal of System Simulation, 2004, 16(7): 1386-1391.(in Chinese))
[9] 杨建新, 汪劲松, 郁鼎文. 空间并联机构运动学与动力学逆解的模块化计算方法[J]. 机械工程学报, 2005, 41(5): 104-107.(YANG Jianxin, WANG Jingsong, YU Dingwen. Modular calculation method for kinematics and dynamics inverse solution of spatial parallel mechanism[J]. Journal of Mechanical Engineering, 2005, 41(5): 104-107.(in Chinese))
[10] 李永泉, 宋肇经, 郭菲. 多能域过约束并联机器人系统动力学建模方法[J]. 机械工程学报, 2016, 52(21): 17-20.(LI Yongquan, SONG Zhaojing, GUO Fei. Dynamic modeling method for overconstrained multi-energy domain parallel manipulator[J]. Chinese Journal of Mechanical Engineering, 2016, 52(21): 17-20.(in Chinese))
[11] 李永泉, 单张兵, 王立捷. 4-DOF混联机器人多能域动力学全解模型及试验[J]. 机械工程学报, 2017, 53(23): 92-100.(LI Yongquan, SHAN Zhangbing, WANG Lijie. Multi-energy domain dynamic full solution model and experiment for the 4-DOF hybrid robot[J]. Chinese Journal of Mechanical Engineering, 2017, 53(23): 92-100.(in Chinese))
[12] UDWADIA F E, KALABA R E. Analytical Dynamics: a New Approach[M]. New York: Cambridge University Press, 1996.
[13] 赵韩, 赵晓敏, 姜建满. 基于Udwadia-Kalaba理论的Hamel嵌入法研究[J]. 应用数学和力学, 2017, 38(6): 696-707.(ZHAO Han, ZHAO Xiaoming, JIANG Jianman. Study on Hamel’s embedding method via the Udwadia-Kalaba theory[J]. Applied Mathematics and Mechanics, 2017, 38(6): 696-707.(in Chinese))
[14] ZHAO X M, CHEN Y H, ZHAO H. Udwadia-Kalaba equation for constrained mechanical systems: formulation and applications[J]. Chinese Journal of Mechanical Engineering, 2018, 31(6): 11-24.
[15] ZHAO H, ZHEN S C, CHEN Y H. Dynamic modeling and simulation of multi-body systems using the Udwadia-Kalaba theory[J]. Chinese Journal of Mechanical Engineering, 2013, 26(5): 839-850.
[16] 张新荣, CHEN Y H, 平昭琪. 基于Udwadia和Kalaba方程的机械臂轨迹跟踪控制[J]. 长安大学学报(自然科学版), 2014, 34(1): 115-119.(ZHANG Xinrong, CHEN Y H, PING Zhaoqi. Mechanic manipulator tracking control based on Udwadia and Kalaba equation[J]. Journal of Chang’an University (Natural Science Edition), 2014, 34(1): 115-119.(in Chinese))
[17] SUN H, ZHAO H, ZHEN S C, et al. Application of the Udwadia-Kalaba approach to tracking control of mobile robots[J]. Nonlinear Dynamics, 2015, 83(1/2): 1-12.DOI: 10.1007/s11071-015-2335-3.