引 言
压电振动能量收集装置利用压电材料的正压电效应将环境中振动能量转化为电能,在微电子设备的自供能设计领域有广泛的应用前景.传统的振动能量收集技术主要基于线性振动理论,它们仅在系统的固有频率附近有较大的功率输出.为了克服线性振动能量收集装置的共振频带较窄这一缺陷,研究者们开始引入非线性因素来拓宽其工作应用频带[1-2].
作为一种特殊的非线性因素,双稳态以及多稳态被引入到能量收集装置的设计.轴向受压屈曲以及磁力耦合是实现多稳态的两种典型方法[3-9].Li等[9]研究了轴向受压的压电梁模型,当轴向载荷超过临界载荷时,压电梁呈现屈曲双稳态,有效地提高了大幅低频激励下的能量收集效果.Zhou等[10-11]建立了压电磁耦合振动能量收集系统,发现通过调整外磁铁的角度,可以使压电梁呈现多稳态,结果表明这种设计可有效地拓宽能量收集装置的工作频带.
常规的多稳态能量收集系统研究多是具有对称势能函数的理想情形,然而在装配过程中,磁铁的磁力强度以及装配位置会存在一定的允许偏差,这些将改变系统的平衡位置以及势能函数的对称特性[12].Chen等[13]使用Lyapunov稳定性分析了一类双稳态压电振子的平衡点特性,发现考虑非对称势能会影响平衡位置以及稳定性,从而引起系统的分岔.Wang等[14]考虑了重力因素,建立了非对称三稳态能量收集系统的分布参数模型,发现非对称势能函数提高了能量收集系统的有效工作效率.
多稳态压电能量收集系统中,同宿分岔是实现大幅阱间运动乃至混沌的原因,它本质上是在鞍点处稳定流形和不稳定流形在扰动因素的作用下发生横截相交,呈现相轨迹跨越势能垒的跳跃现象.借助于同宿分岔,能量收集装置产生大幅响应并高效地将应变能转化为电能.Melnikov方法是一种用于预测非线性压电振子同宿分岔的定性研究方法,被广泛应用于分析磁力耦合以及轴向受压梁双稳态能量收集系统[15-20].然而,目前关于三稳态能量收集的工作多基于实验或数值模拟,无法深入揭示非对称三稳态能量收集系统的混沌、跳跃等复杂的动力学行为发生机理.本文针对传统的磁力耦合三稳态能量收集系统,考虑由外磁场的非对称性引起的几何非线性,建立了集中参数模型.通过Melnikov理论获得系统在谐波激励下发生同宿分岔的必要条件,利用数值方法验证相关的解析结果,揭示了三稳态势能函数对能量收集效率的影响规律,为实现优化能量输出效率提供了理论参考.
1 模 型 分 析
图1(a)为本文所提出的三稳态能量收集系统,在长度为L的悬臂梁自由端附着一个磁铁A,压电片粘贴在悬臂梁的根部.悬臂梁在基础激励Acos(Ωt)作用下产生横向振动,结构振动产生的应变能通过压电薄膜(PVDF)转化为电能.永磁体A和基座上的永磁体B、C、D相互作用,势能函数存在三个最小值点,即系统呈现三稳态特点.如图1(b)所示,永磁体的位置调整将会导致势能函数形状的改变,从关于y轴的对称情形转变为非对称情形.为了研究三稳态能量收集系统的动态响应,下面直接给出能量收集系统的集中参数模型:
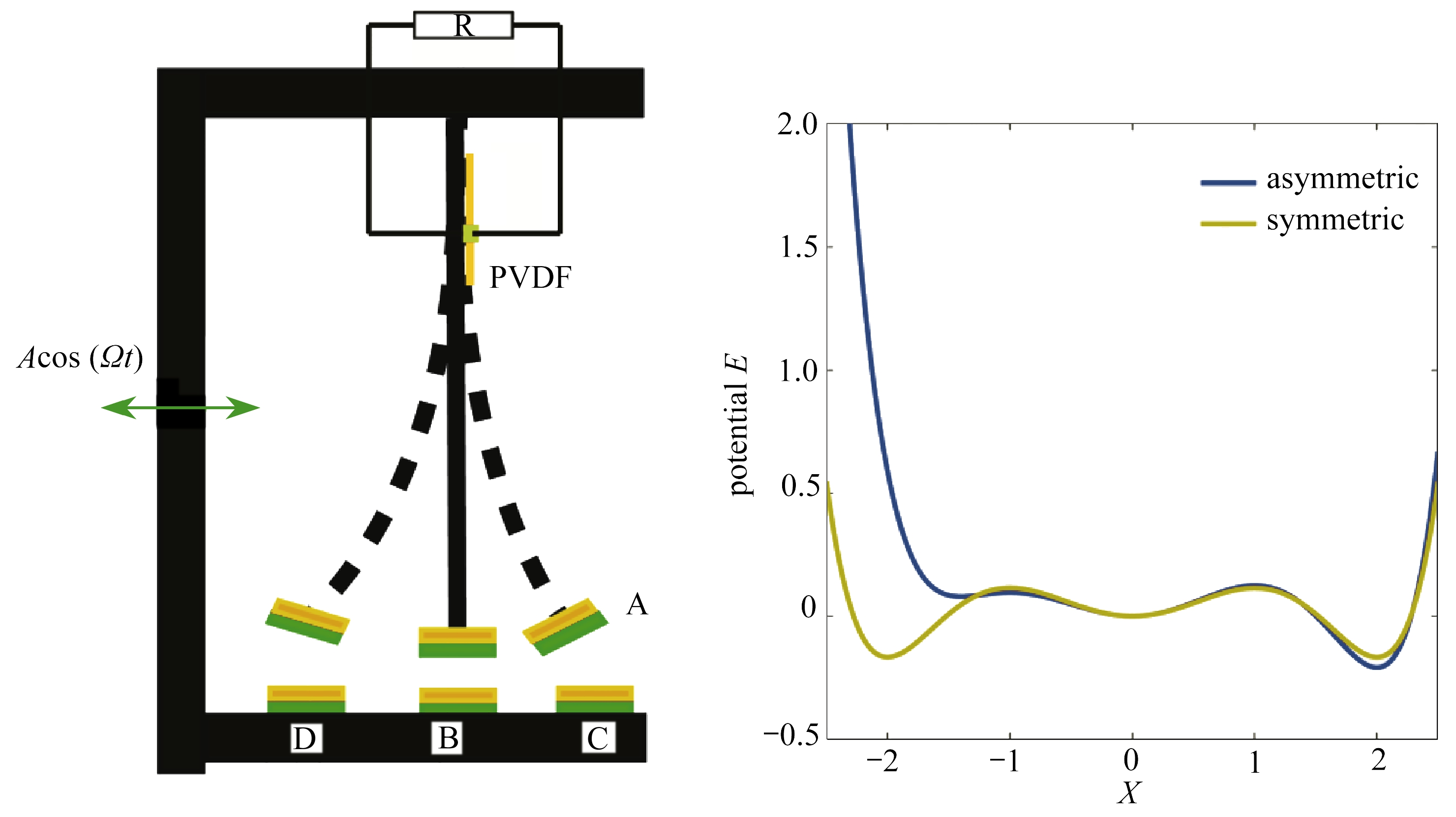
(a) 模型示意图 (b) 势能函数图
(a) Schematic diagram of the model (b) The potential function diagram
图1 三稳态能量收集系统的模型以及势能函数图
Fig. 1 The schematic diagram and potential function diagram of the tristable energy harvester

(a) α3=-1.4 (b) α3=-1.6
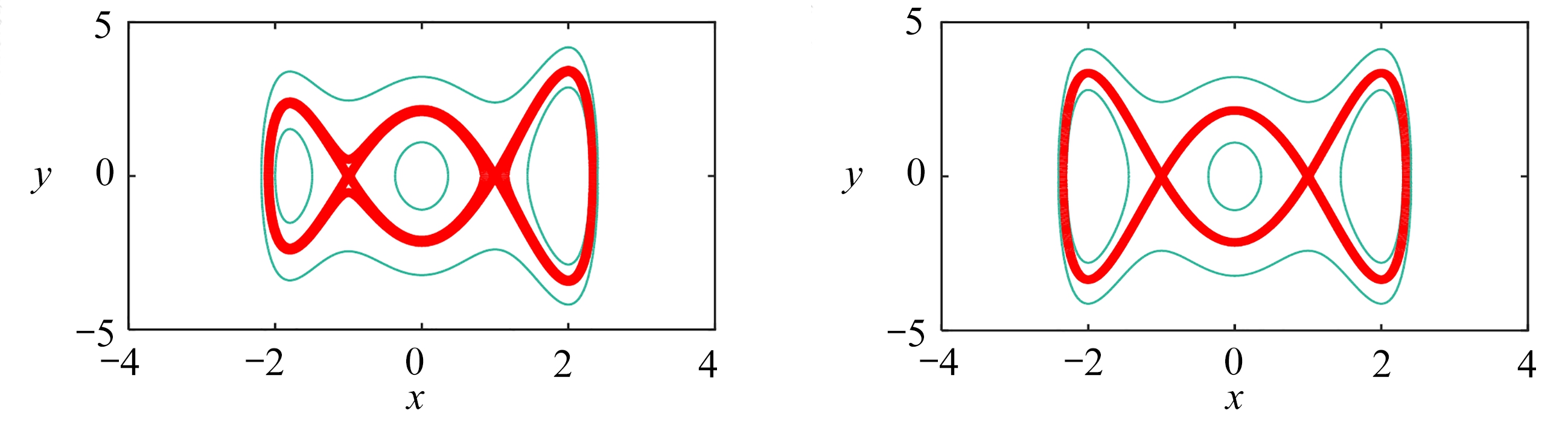
(c) α3=-1.8 (d) α3=-2
图2 α1=-1,α2=2时的未扰Hamilton系统相平面图
Fig. 2 Phase portraits of the undisturbed Hamiltonian system for α1=-1,α2=2
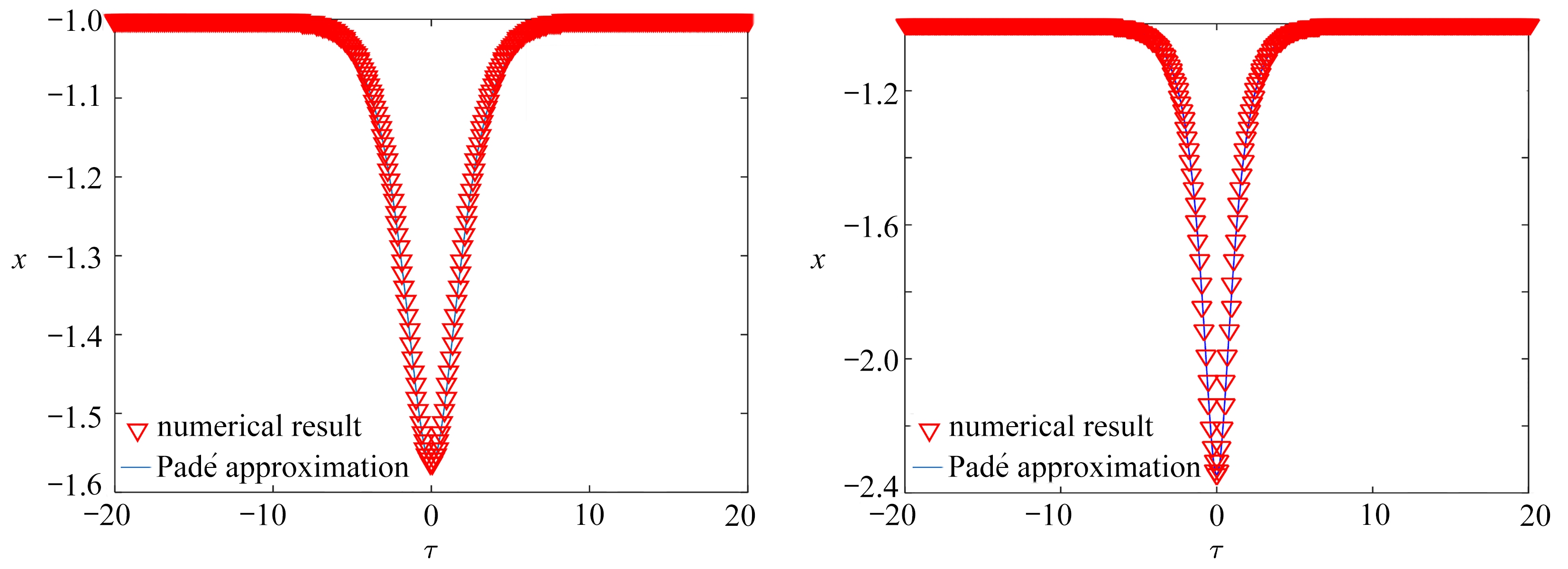
(a) α3=-1.4时的同宿解 (b) α3=-2时的同宿解
(a) Homoclinic solutions for α3=-1.4 (b) Homoclinic solutions for α3=-2
图3 同宿轨道数值结果和解析结果的比较
Fig. 3 The comparison between approximation results and numerical results of the homoclinic orbit
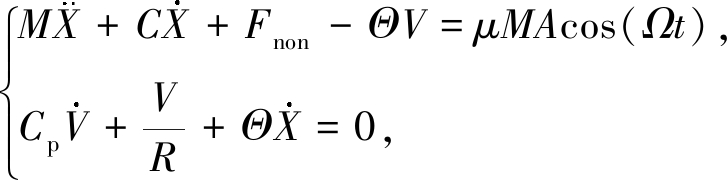
(1)
式中M为等效质量;C为等效阻尼;Fnon为非线性恢复力;Θ为等效的机电耦合系数;Acos(Ωt)为基础加速度激励,其中A表示加速度幅值,Ω表示加速度角频率;μ为集中参数模型的加速度修正因子;Cp为压电材料的等效电容;X为压电梁的横向位移;V为通过纯电阻R上的电压.
非线性恢复力Fnon可表示成多项式形式:
Fnon=K1X+K2X2+K3X3+K4X4+K5X5,
(2)
其中Ki(i=1,2,…,5)分别为三稳态能量收集系统的线性刚度以及非线性刚度系数.考虑到系统的平衡点位置,恢复力Fnon可以进一步因式分解成
Fnon=K5(X-x1)(X-x2)(X-x3)(X-x4)(X-x5),
(3)
其中xi(i=1,2,…,5)为三稳态能量收集系统的平衡点位置.
引入无量纲常数Q,令X=x1x,V=Qv和![]() 并考虑中间平衡位置为对称中心,即x3=0.方程(1)重新写成如下无量纲形式:
并考虑中间平衡位置为对称中心,即x3=0.方程(1)重新写成如下无量纲形式:
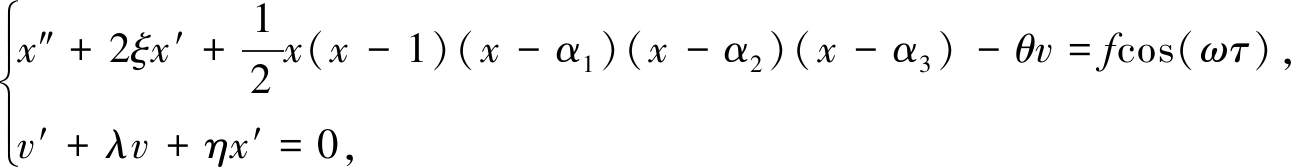
(4)
其中(·)′表示关于无量纲时间变量τ的导数,方程(4)中的其他无量纲参数可表示为
令x′=y,方程(4)重新写成状态方程形式:
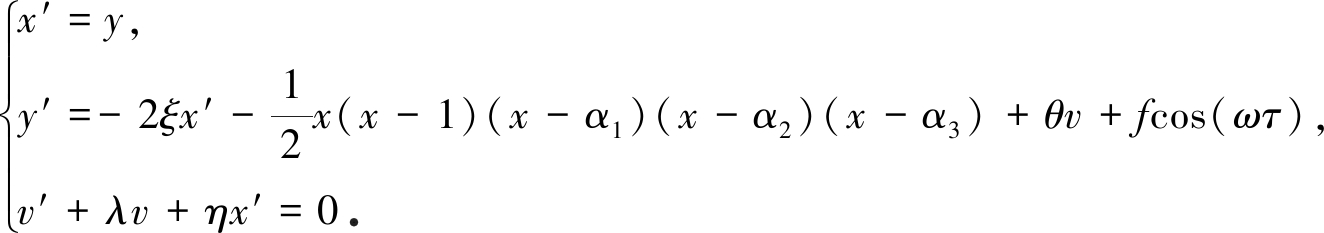
(5)
2 Melnikov方法分析
下面将采用Melnikov 方法来讨论系统的同宿分岔.如果将阻尼、机电耦合以及外激励都看成对系统(4)对应的Hamilton系统的扰动项,未扰的Hamilton系统可以写成
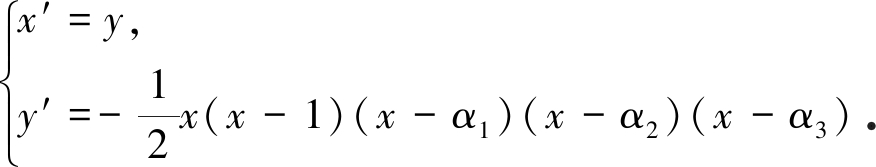
(6)
图2为根据未扰Hamilton系统(6)得到的相平面图,图中的深色实线即为同宿轨道,当α3分别取-1.4,-1.6和-1.8时,相平面图以及势能函数关于中轴都成非对称分布.未扰Hamilton系统在鞍点(1,0)和(-1,0)处有两条独立的同宿轨道.随着α3的减小,连接鞍点(-1,0)处的同宿轨道的负方向位移呈现明显的单调递增趋势.当α3取-2时,相平面上除了两条独立的同宿轨道还存在连接两个鞍点(1,0)和(-1,0)的异宿轨道,连接鞍点(-1,0)处的同宿轨道的负向位移达到最大值.值得注意的是,α3=-2时相平面以及势能函数都呈现对称分布.
方程式(7)为采用Padé 逼近方法[21]得到的同宿轨道解析表达式:

(7)
其中![]() 表示未扰Hamilton系统(6)的固有频率.
表示未扰Hamilton系统(6)的固有频率.
表1给出了α3分别取-1.4,-1.6,-1.8和-2时Padé逼近表达式(7)的系数.图3比较了非对称情形(α3=-1.4)和对称情形(α3=-2)同宿轨道解的解析结果和数值结果,可以看出两者一致性较好.因此逼近函数表达式(7)可用于解析计算Melnikov函数,获得发生同宿分岔的激励阈值.
表1 Padé逼近表达式的系数
Table 1 Coefficients of the Padé approximation

γ0γ1γ2γ3γ4β1β2β3β4α3=-1.40.71-11.57-19.13-11.57-18.978.388.971α3=-1.60.71-3.79-3.26-3.79-11.861.311.861α3=-1.80.71-1.08-1.16-1.076-1-0.581.7-0.581α3=-20.710.11-1.150.11-1-1.62.44-1.61
将方程(5)重新写成带有扰动项的Hamilton系统:
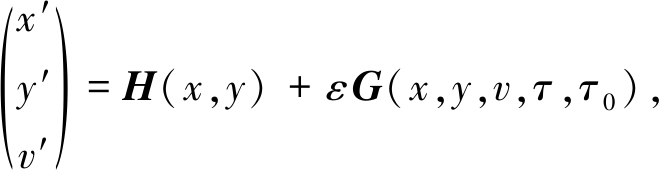
(8)
其中H(x,y)和G(x,y,v,τ,τ0)分别表示保守系统和扰动系统的向量函数,具体为
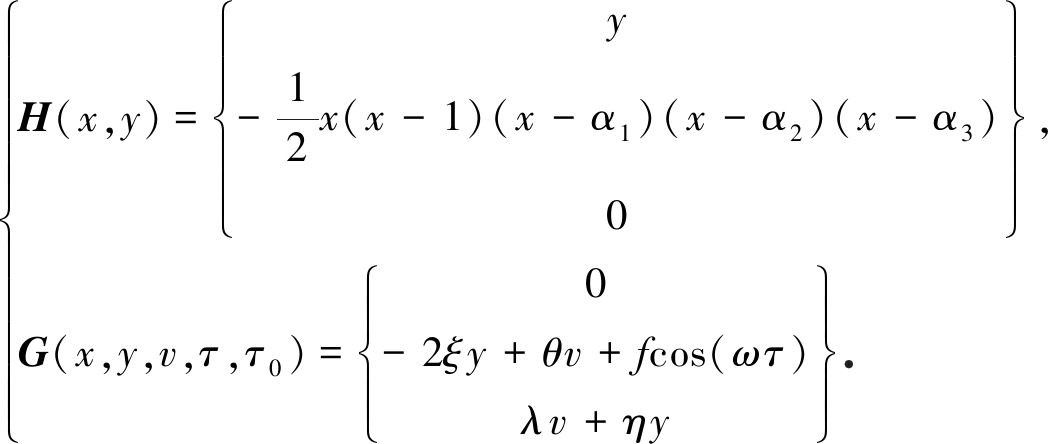
(9)
根据Smale-Birkhoff定理以及Melnikov理论,定义可以用来测量稳定流形和不稳定流形之间距离的函数,即Melnikov函数:
M(τ0)=![]() H(x,y)∧G(x,y,v,τ,τ0)dτ=
H(x,y)∧G(x,y,v,τ,τ0)dτ=
(10)
其中“∧”表示二维外积算子.
基于M(τ0)的定义可知,当M(τ0)存在零根时,系统的稳定流形和不稳定流形将横截相交,响应将会发生同宿分岔呈现Smale马蹄意义下的混沌.发生同宿分岔的必要条件就是当且仅当下面不等式(11)成立:
(11)
值得注意的是,不等式(11)仅仅是发生同宿分岔的必要条件,满足该条件并不一定会产生阱间跳跃或混沌响应,但是该方法依然能够为预测系统的同宿分岔提供解析形式的参考.
由不等式(11)可知三稳态能量收集系统发生同宿分岔时,激励幅值满足:

图4为根据参数ξ=0.05,θ=0.05,η=10,λ=5得到的同宿分岔阈值曲线,图中“★”为将Padé逼近近似表达式代入到Melnikov函数中所获得的解析结果.曲线上方即为特定激励频率下发生同宿分岔的激励幅值范围,从中可以看出非对称时的三稳态能量收集系统的同宿分岔阈值相比对称系统较低.

图4 同宿分岔阈值曲线图
Fig. 4 The homoclinic bifurcation threshold curves
3 数 值 模 拟
现在通过Runge-Kutta方法对三稳态能量收集系统(4)中的同宿分岔现象进行数值验证.图5为α3分别取-1.4,-1.6,-1.8和-2,其他无量纲参数为θ=0.05,ξ=0.05,η=10,λ=5,Ω=0.5时,输出电压v关于激励幅值f的分岔图和最大Lyapunov指数谱,图5(a)中的虚线为Melnikov方法得到的同宿分岔阈值.从图5(a)中可以看到,当f在0~0.75之间变化时,系统将会交替出现倍周期分岔以及混沌窗口,引起混沌的激励幅值有下限而没有上限.图5(b)中给出了相应的对称系统和非对称系统的Lyapunov 指数谱结果,它们与分岔图相互一致对应.当激励幅值小于Melnikov方法预测的阈值时,没有发现阱间跳跃现象.通过对比分岔图中的数值结果可知调整不同平衡点位置可使系统呈现不同的动力学响应,非对称系统发生同宿分岔的激励阈值要低于对称系统,这与图4中同宿分岔阈值曲线的规律一致.
图6、7为激励幅值f取不同数值时三稳态能量收集系统在非对称势能情形(α3=-1.4)和对称势能情形(α3=-2)的相平面图、Poincaré截面图以及电压时间历程图对比.图6(a)、(c)中,当f分别取0.05时,由于该激励强度在对称和非对称情形均无法满足同宿分岔必要条件(11),系统呈现小幅的阱内运动,输出电压幅值较低.如图6(b)、(d)所示,当f增加至0.09时,激励幅值大于非对称情形(α3=-1.4)的同宿分岔阈值,系统出现了阱间跳跃的混沌响应;然而由于输入的激励幅值小于对称情形(α3=-2)的同宿分岔阈值,不足以激发阱间振动,相轨迹曲线限制在单个的势能阱中.通过对比图6(b2)和图6(d2)中的电压输出时间历程,可见非对称系统中阱间混沌响应的有效电压高于对称势能系统的小幅阱内周期响应.因此,非对称势能函数能降低发生同宿分岔的阈值,使系统在较低的激励幅值下出现阱间跳跃,从而改善低强度激励时的能量输出效果.
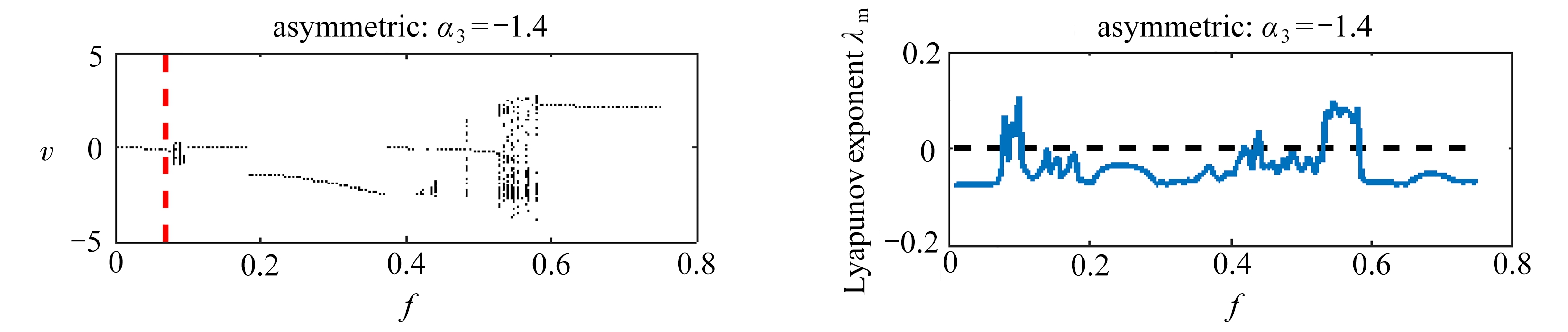
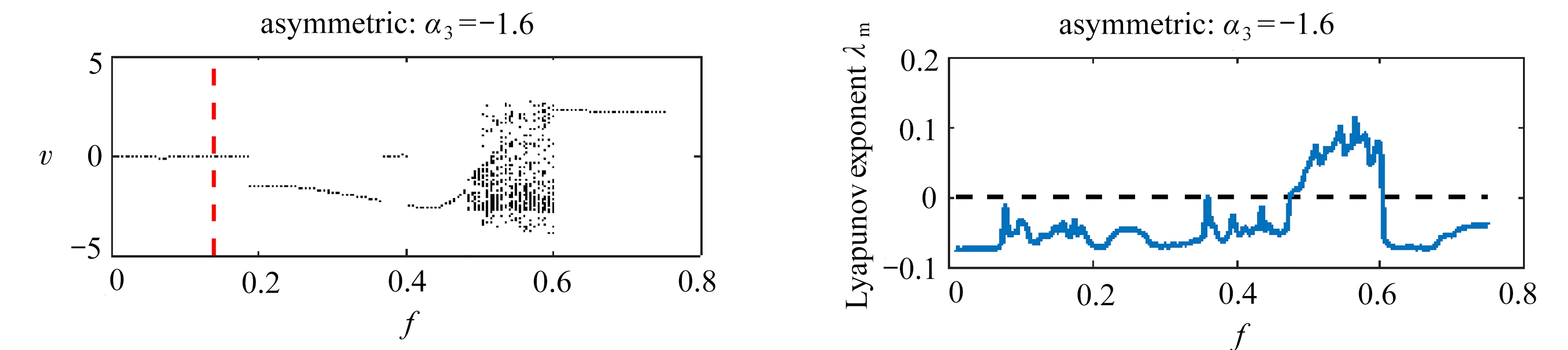
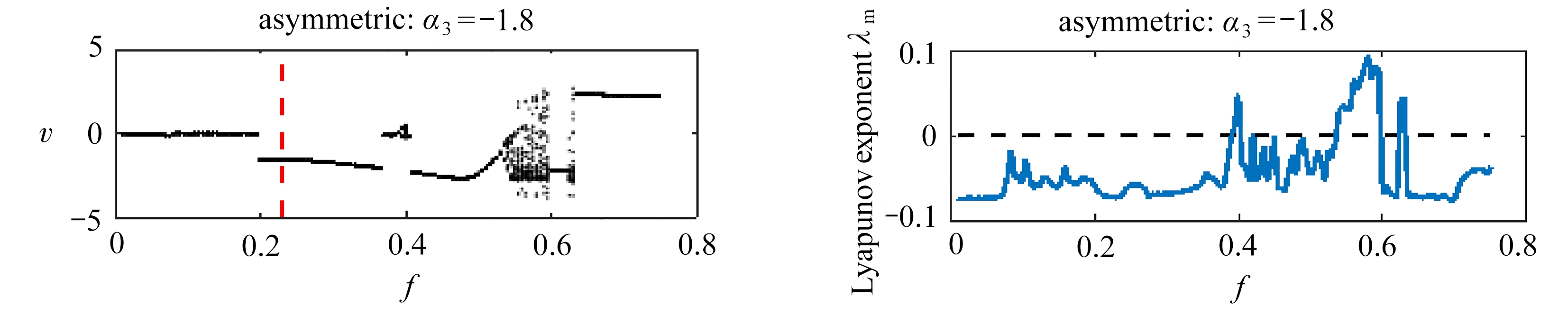
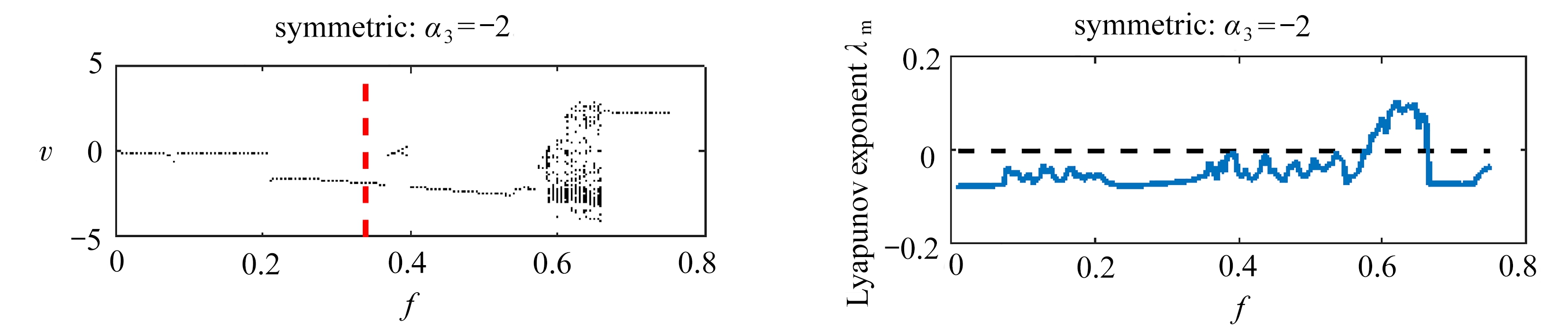
(a) 分岔图 (b) 最大Lyapunov指数
(a) Bifurcation diagrams vs. f (b) Maximum Lyapunov exponents vs. f
图5 同宿分岔阈值的数值验证
Fig. 5 Numerical verification of homoclinic bifurcation thresholds
图7(a)、(c)中,当激励幅值f进一步增加到0.2时,α3=-1.4时的非对称系统呈现大幅的周期阱间运动.从相轨迹图中可看出由于非对称势能阱的影响,位移和速度在正向的最大值高于负向.然而此激励强度仍小于对称势能系统的Melnikov阈值,输入能量不足以激发阱间振动,相轨迹曲线限制在单个较深的势能阱.如图7(b)、(d)所示,随着基础激励幅值增加到f=0.61,对称系统和非对称系统都能获得足够的能量越过势能垒,呈现出大幅的阱间振动.然而, 势能函数的差异导致了截然不同的两种动力学响应, 非对称情形时的相轨迹呈现大幅的周期-1运动,输出电压波形较为规整且有效幅值较高,而对称情形时的相轨迹为跨越多个势能阱的无规律混沌状态,Poincaré截面上出现了由无规则的点构成的吸引子.因此,非对称势能函数可用于调控能量收集系统的动力学行为,提高输出能量的品质.
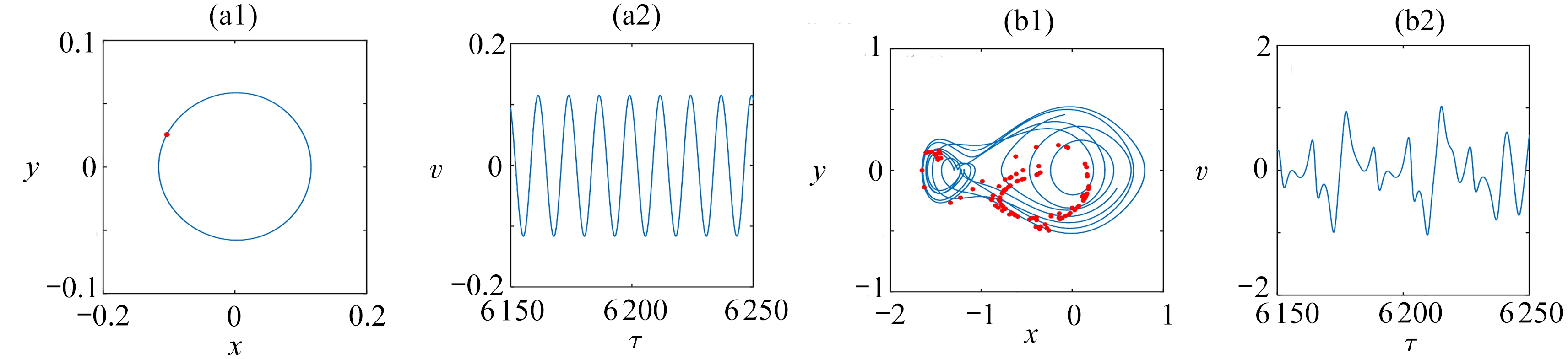
(a) f=0.05,非对称情形(α3=-1.4) (b) f=0.09,非对称情形(α3=-1.4)
(a) The asymmetric case for α3=-1.4, f=0.05 (b) The asymmetric case for α3=-1.4, f=0.09

(c) f=0.05,对称情形(α3=-2) (d) f=0.09,对称情形(α3=-2)
(c) The symmetric case for α3=-2, f=0.05 (d) The symmetric case for α3=-2, f=0.09
图6 f=0.05和f=0.09时的时间历程图以及带有Poincaré截面的相平面图
Fig. 6 The time histories and phase portraits with Poincaré sections for f=0.05 and f=0.09
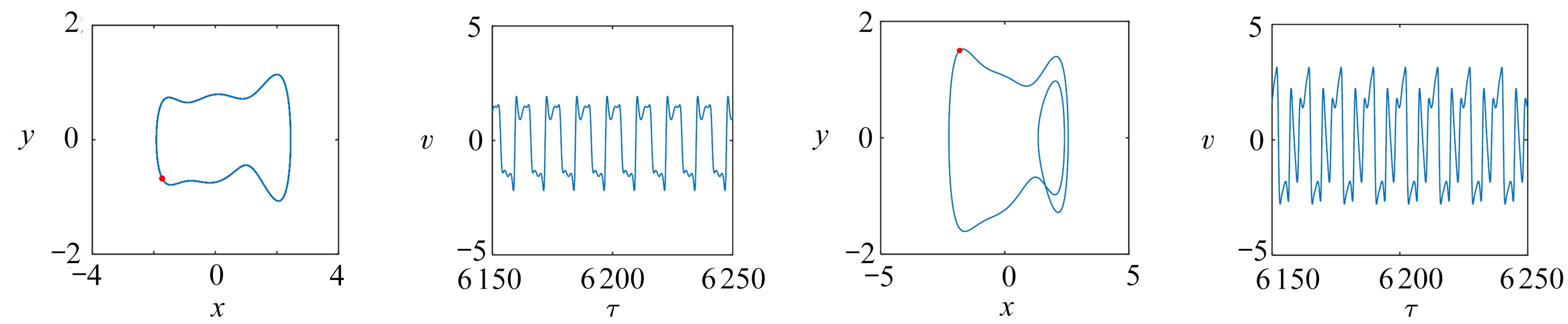
(a) f=0.2,非对称情形(α3=-1.4) (b) f=0.61,非对称情形(α3=-1.4)
(a) The asymmetric case for α3=-1.4, f=0.2 (b) The asymmetric case for α3=-1.4, f=0.61
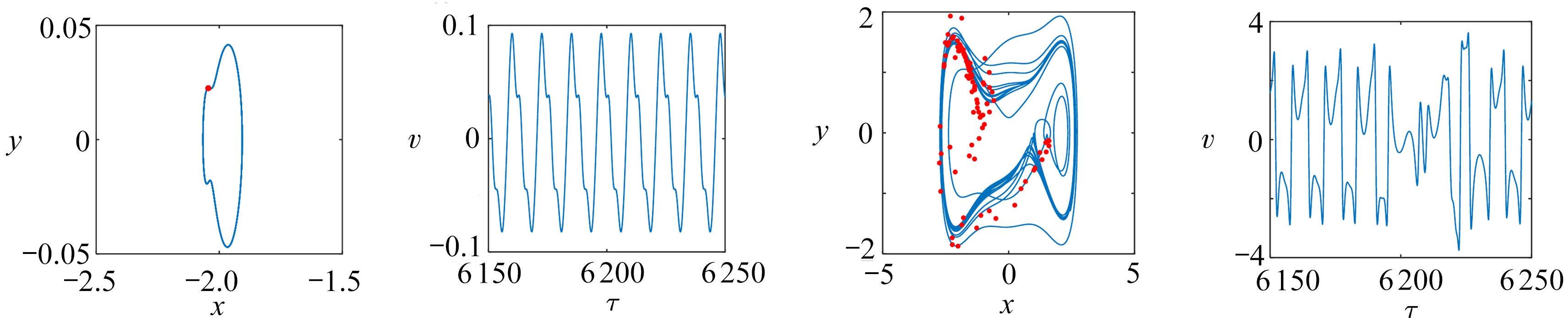
(c) f=0.2,对称情形(α3=-2) (d) f=0.61,对称情形(α3=-2)
(c) The symmetric case for α3=-2, f=0.2(d) The symmetric case for α3=-2, f=0.61
图7 f=0.2和f=0.61时的时间历程图以及带有Poincaré截面的相平面图
Fig. 7 The time histories and phase portraits with Poincaré sections for f=0.2 and f=0.61
为了直观展示系统从对称势能阱状态转变为非对称势能阱状态的动力学行为演化过程,图8(a)给出了f=0.5时输出电压v关于α3的分岔图.当参数α3从-2增大至-1的过程中,混沌和周期响应交替出现并最终呈现周期-1响应.如图8(b)所示,当α3处于区间[-2, -1.6]时,混沌响应占主要成分且有效输出电压整体较低;当α3从-1.6增大至-1时,输出电压单调递减.为进一步揭示系统的动力学行为演化过程,图8(c)、(d)分别给出了α3=-1.75和α3= -1.3时的吸引盆,深色区域为初始条件平面,浅色区域表示吸引子.从中能看出当相同的激励条件下,α3=-1.75时系统在任意初始条件下都呈现混沌响应,而α3=-1.3时系统将呈现周期-1响应.因此,适当增加系统的非对称性,一方面有利于抑制混沌响应的产生,实现混沌响应至周期响应的调控;另一方面根据优化后非对称调节参数α3,可进一步使系统输出电压达到最大,提高能量收集效率.
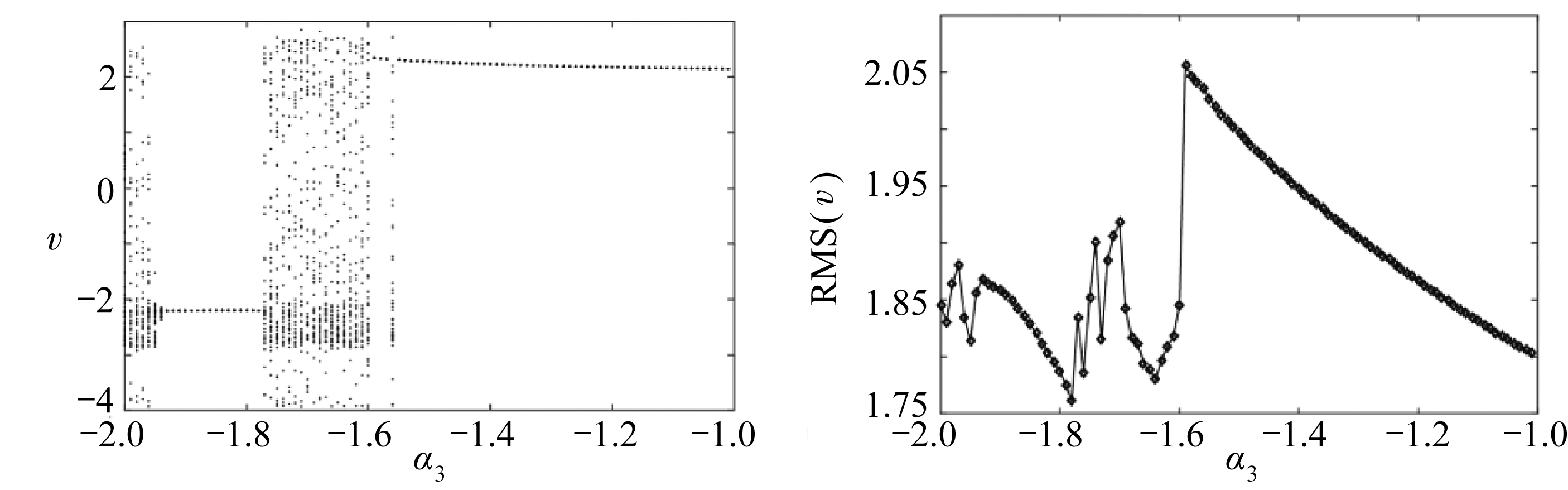
(a) 随参数α3变化的分岔图 (b) 随参数α3变化的有效电压
(a) The diagram of bifurcation vs. α3 (b) The effective voltage vs. α3

(c) α3=-1.75时的吸引盆 (d) α3=-1.3时的吸引盆
(c) The basin for α3=-1.75 (d) The basin for α3=-1.3
图8 参数α3变化对动力学响应的影响规律
Fig. 8 The dynamic responses influenced by parameter α3
4 结 论
本文基于Melnikov理论预测了一类三稳态能量收集系统在谐波激励下发生同宿分岔的阈值.首先考虑悬臂梁在磁力耦合作用下的多稳态特性,建立能够描述势能函数全局特性的三稳态集中参数能量收集系统模型.其次基于Padé逼近获得非对称势能函数和对称势能函数情形的同宿轨道近似表达式,结合Melnikov函数得到发生同宿分岔的必要条件.最后通过数值模拟验证理论分析,得到以下结论:
1) 关于三稳态能量收集系统同宿分岔的理论分析与分岔图、最大Lyapunov指数等数值结果相一致,当激励强度超过同宿分岔阈值后,系统出现输出能量较高的大幅阱间振动响应.
2) 非对称势能函数能降低发生同宿分岔的阈值,提高低强度激励下的能量输出.在较低的激励强度作用下,带有非对称势能函数的三稳态能量收集系统能产生阱间的混沌以及周期响应,而对称系统的响应限制在单个的势能阱.
3) 非对称势能函数在一定程度上有助于调控三稳态能量收集系统的响应特性, 当激励强度较大时, 非对称势能函数也可将混沌运动调整为高能的大幅周期运动, 提高收集到的能量品质.
致谢 本文作者衷心感谢中北大学自然科学研究基金(XJJ201810)对本文的资助.
[1] PRIYA S, INMAN D J. Energy Harvesting Technologies[M]. New York: Springer, 2009.
[2] 董彦辰, 张业伟, 陈立群. 惯容器非线性减振与能量采集一体化模型动力学分析[J]. 应用数学和力学, 2019, 40(9): 968-979.(DONG Yanchen, ZHANG Yewei, CHEN Liqun. Dynamic analysis of the nonlinear vibration absorber-energy harvester integration model with inerter[J]. Applied Mathematics and Mechanics, 2019, 40(9): 968-979.(in Chinese))
[3] HARNE R L, WANG K W. A review of the recent research on vibration energy harvesting via bistable systems[J]. Smart Materials and Structures, 2013, 22(2): 023001.
[4] 张小静, 刘丽兰, 任博林, 等. 势阱深度对双稳态电磁发电系统发电性能的影响研究[J]. 应用数学和力学, 2017, 38(6): 622-632.(ZHANG Xiaojing, LIU Lilan, REN Bolin, et al. Influence of potential well depth on power generation performance of bistable electromagnetic energy harvesting systems[J]. Applied Mathematics and Mechanics, 2017, 38(6): 622-632.(in Chinese))
[5] 吴子英, 牛峰琦, 刘蕊, 等. 有色噪声激励下双稳态电磁式振动能量捕获器动力学特性研究[J]. 应用数学和力学, 2017, 38(5): 570-580.(WU Ziying, NIU Fengqi, LIU Rui, et al. Dynamic characteristics of bistable electromagnetic vibration energy harvesters under colored noise excitation[J]. Applied Mathematics and Mechanics, 2017, 38(5): 570-580.(in Chinese))
[6] 刘蕊, 吴子英, 叶文腾. 附加非线性振子的双稳态电磁式振动能量捕获器动力学特性研究[J]. 应用数学和力学, 2017, 38(4): 432-446.(LIU Rui, WU Ziying, YE Wenteng. Dynamics research of bistable electromagnetic energy harvesters with auxiliary nonlinear oscillators[J]. Applied Mathematics and Mechanics,2017, 38(4): 432-446.(in Chinese))
[7] MASANA R, DAQAQ M F. Energy harvesting in the super-harmonic frequency region of a twin-well oscillator[J]. Journal of Applied Physics, 2012, 111(4): 044501.
[8] LI H T, QIN W Y, LAN C B, et al. Dynamics and coherence resonance of tri-stable energy harvesting system[J]. Smart Materials and Structures, 2016, 25(1): 015001.
[9] LI H T, QIN W Y, ZU J, et al. Modeling and experimental validation of a buckled compressive-mode piezoelectric energy harvester[J]. Nonlinear Dynamics, 2018, 92(4): 1761-1780.
[10] ZHOU S X, CAO J Y, ERTURK A, et al. Enhanced broadband piezoelectric energy harvesting using rotatable magnets[J]. Applied Physics Letters, 2013, 102(17): 173901.
[11] 周生喜, 曹军义, ERTURK A, 等. 压电磁耦合振动能量俘获系统的非线性模型研究[J]. 西安交通大学学报, 2014, 48(1): 106-111.(ZHOU Shengxi, CAO Junyi, ERTURK A, et al. Nonlinear model for piezoelectric energy harvester with magnetic coupling[J]. Journal of Xi’an Jiaotong University, 2014, 48(1): 106-111.(in Chinese)
[12] ZHOU S X, ZUO L. Nonlinear dynamic analysis of asymmetric tristable energy harvesters for enhanced energy harvesting[J]. Communications in Nonlinear Science and Numerical Simulation, 2018, 61: 271-284.
[13] CHEN L Q, LI K. Equilibriums and their stabilities of the snap-through mechanism[J]. Archive of Applied Mechanics, 2016, 86(3): 403-410.
[14] WANG G, ZHAO Z, LIAO W H, et al. Characteristics of a tri-stable piezoelectric vibration energy harvester by considering geometric nonlinearity and gravitation effects[J]. Mechanical Systems and Signal Processing, 2020, 138: 106571.
[15] 李海涛, 秦卫阳. 双稳态压电能量获取系统的分岔混沌阈值[J]. 应用数学和力学, 2014, 35(6): 652-662.(LI Haitao, QIN Weiyang. Bifurcation and chaos thresholds of bistable piezoelectric vibration energy harvesting systems[J]. Applied Mathematics and Mechanics, 2014, 35(6): 652-662.(in Chinese))
[16] SUN S, CAO S Q. Analysis of chaos behaviors of a bistable piezoelectric cantilever power generation system by the second-order Melnikov function[J]. Acta Mechanica Sinica, 2017, 33(1): 200-207.
[17] KITIO KWUIMY C A, NATARAJ C, LITAK G. Melnikov’s criteria, parametric control of chaos, and stationary chaos occurrence in systems with asymmetric potential subjected to multiscale type excitation[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2011, 21(4): 043113.
[18] OUMBÉ TÉKAM G T, KITIO KWUIMY C A, WOAFO P. Analysis of tristable energy harvesting system having fractional order viscoelastic material[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2015, 25(1): 013112.
[19] TIAN R, ZHOU Y, ZHANG B, et al. Chaotic threshold for a class of impulsive differential system[J]. Nonlinear Dynamics, 2016, 83(4): 2229-2240.
[20] LI H T, ZU J, YANG Y F, et al. Investigation of snap-through and homoclinic bifurcation of a magnet-induced buckled energy harvester by the Melnikov method[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2016, 26(12): 123109.
[21] FENG J, ZHANG Q, WANG W. Chaos of several typical asymmetric systems[J]. Chaos, Solitons and Fractals, 2012, 45(7): 950-958.