引 言
20世纪60年代,随着陀螺动力学与航天器动力学研究的深入,学者们开始关注多体系统动力学研究.时至今日,多体系统动力学模型与数值仿真仍是重要的研究内容.同一多体系统建立动力学模型可以选取不同的坐标,例如:相对坐标、绝对坐标、Lie群坐标和自然坐标等,其中自然坐标又称完全Descartes坐标.自然坐标法于20世纪80年代由de Jalón等[1]提出并发展,由每个物体上的若干基点和单位基矢量的Descartes分量构成,具有坐标选择灵活、坐标数量适中、约束Jacobi矩阵为线性、动力学方程不包含哥氏惯性力与离心力等特点[2].方向矢量法归属于自然坐标法,由von Schwerin[3]、Kraus等[4]、Uhlar等[5]先后提出并发展,兼具自然坐标的特点.除此之外,方向矢量法与绝对坐标有很好的兼容性,且较易程式化,便于实现编程.鉴于这些优点,方向矢量法已开始受到动力学领域的关注.
由方向矢量法建立的方程为微分-代数方程,其数值解法也是多体系统动力学研究的热点和难点,多数方法以常微分方程数值求解方法为基础.Runge-Kutta方法是求解常微分方程的经典方法,但是在微分-代数方程求解中存在约束违约等问题.多步块格式是具有Runge-Kutta稳定性的一类新的一般线性方法,基于Butcher[6]提出的一般线性方法进行构造,使用了更多的过去信息.Chollom等[7]提出了一种检测整个块格式性能的方法,确定了所构造格式的收敛性、稳定性和阶数.Olabode[8]采用配点法,在预测校正器模式下用分块线性多步法对特殊常微分方程初值问题进行求解.Mehrkanoon等[9]提出了求解变步长一阶常微分方程的四点隐式多步块方法,以Adams简单形式给出,并采用Gauss-Seidel方法实现.在一阶常微分求解的基础上,Mehrkanoon[10]用变步长直接求解三阶常微分方程,并研究了该方法的局部截断误差.Awoyemi等[11]基于幂级数近似解的配点法和插值法生成连续的线性多步块方法,为了适应一般的n阶常微分方程,对已有的块格式进行了改进.Majid等[12]实现了求解二阶常微分方程的一步法,无需将方程简化为一阶方程组.Olabode等[13]研究了自启动的块格式方法,不需要开发单独的预测器来实现.Mohamed等[14]采用了多步块方法求解第二类线性与非线性积分微分方程,将三阶多步块方法与Newton-Cotes方法相结合求解.
目前多步块格式更多是基于常微分方程求解,针对微分-代数方程的研究相对较少.本文针对方向矢量法描述的多体系统动力学微分-代数方程,构造多步块格式进行数值计算,在最大能量误差、位移约束、速度约束、加速度约束以及方向矢量误差方面进行分析比较,并基于Chebyshev多项式零点、Legendre多项式零点构造不等距节点多步块格式,通过平面双连杆机械臂进行仿真实验.
1 方向矢量法建立多刚体系统动力学方程
设系统是由ni个物体和nj个铰相互连接构成的多刚体系统,如图1所示,在Bi(i=1,2,…,n)的质心Ci处建立连体基坐标系![]() (三个轴为刚体的惯性主轴) ,原点Ci相对惯性基
(三个轴为刚体的惯性主轴) ,原点Ci相对惯性基![]() 的位矢
的位矢![]() 则物体Bi(i=1,2,…,n)的动能为
则物体Bi(i=1,2,…,n)的动能为
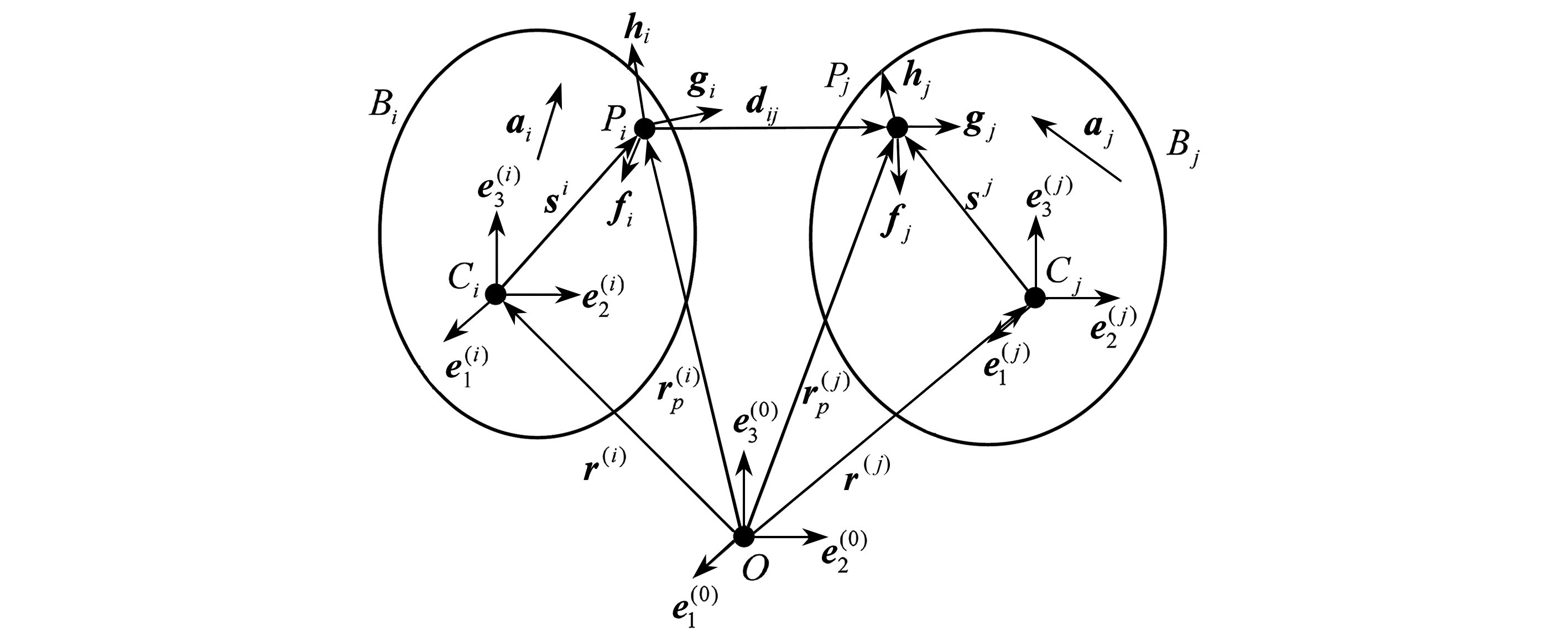
图1 任意两多刚体系统及铰的示意图
Fig. 1 Schematic diagram of any 2-multibody systems and hinges
(1)
其中![]() 为Bi上任意点P的绝对速度,
为Bi上任意点P的绝对速度,![]() 而
而![]() 物体Bi(i=1,2,…,n)的势能矩阵记为Vi=V(q(i)).
物体Bi(i=1,2,…,n)的势能矩阵记为Vi=V(q(i)).
约束分两部分:方向矢量性质约束和物体间铰的约束.方向矢量性质约束为
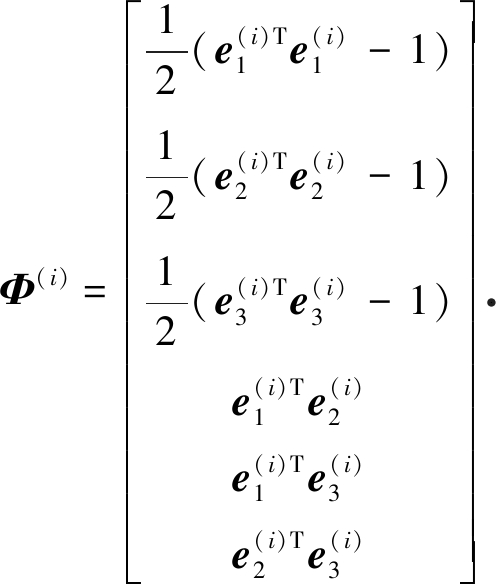
(2)
物体间铰的约束为:
① ai,aj为图1中Bi,Bj上任意矢量,当ai,aj垂直时,![]()
② dij为两点间的相对位矢,当矢量ai,dij垂直时,![]()
③ Pi,Pj为Bi,Bj的铰点,当Pi,Pj重合时,![]()
④ 当Pi,Pj间保持距离不变时,![]()
⑤ Pifigihi,Pjfjgjhj分别为固结于Pi,Pj点的坐标系,当hi,hj为平行矢量时,
⑥ 当hi,dij平行时,![]()
类似球铰、万向铰、转动铰、筒铰、滑移铰等都可由以上六种铰间约束表述.
由Lagrange-d’Alembert原理得
(3)
矩阵表示为
(4)
其中
F(q)=[F(q(1))T,F(q(2))T,…,F(q(ni))T]T,
λ为Lagrange乘子,Φ(q)为约束函数.
得到系统动力学指标3的微分-代数方程为

(5)
对约束进行二次时间求导,得到指标1的微分-代数方程为

(6)
对方程(6)进行降阶处理得
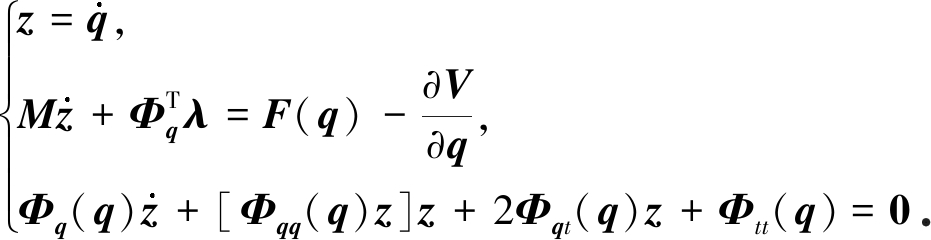
(7)
2 多步块法求解多体系统动力学方程
多步块格式属于一般线性方法范畴,是多值多级方法.在[ti,ti+1]计算步中,将时间离散为r个节点,采用上一步得到的r个已知信息Yi=[y1,y2,…,yr]T作为输入矢量,由yk在ti处的Taylor展式可得线性方程组
(8)
其中
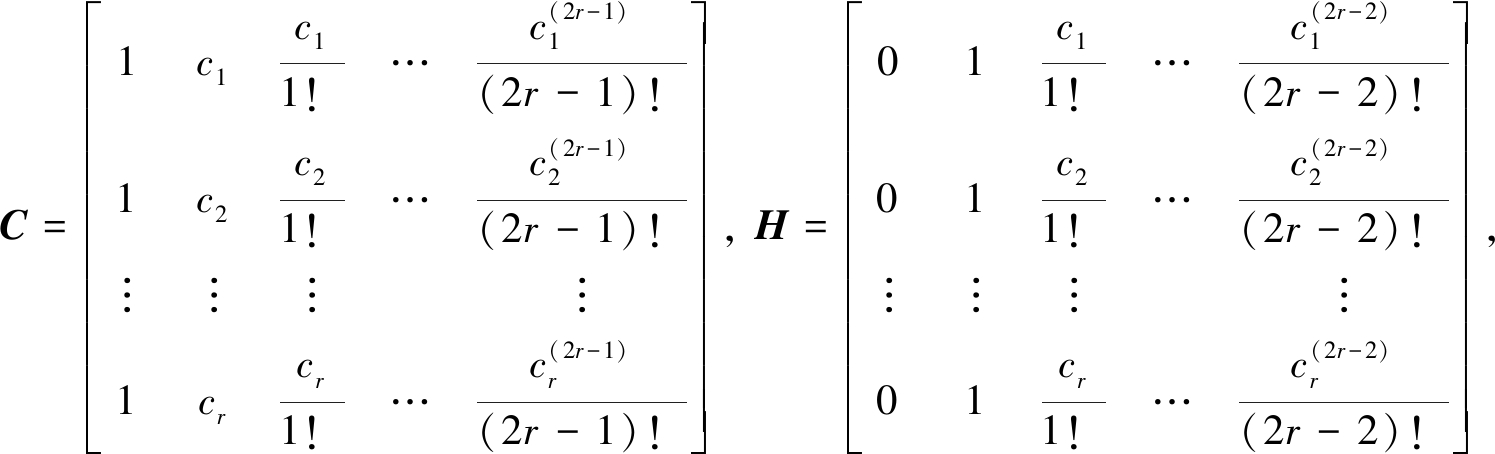
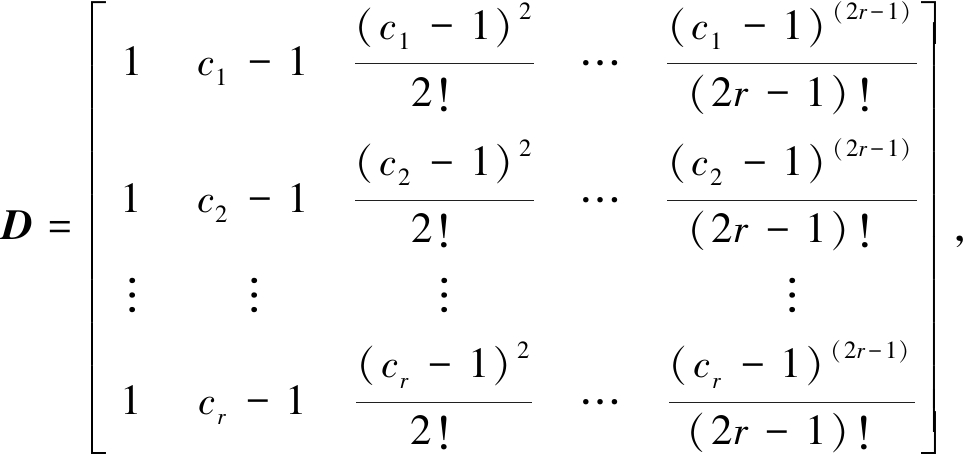
c1,c2,…,cr为节点.求解式(8)可以确定多步块格式中的A和U,从而可以得到时间步内r个时刻的输出值.
设时间单元为[ti,ti+1],h=ti+1-ti,选取等距节点或不等距节点ck(k=1,2,…,r),使得ti<c1<c2<…<cr=ti+1,Yi作为初始值,使
(9)
其中Im为m×m阶单位矩阵,⊗为Kronecker积,![]() 由Newton迭代求解式(7)得到,
由Newton迭代求解式(7)得到,![]() 由式(9)计算得到.
由式(9)计算得到.
选取r=3的等距节点,c=(1/3,2/3,1),由yk在ti处的Taylor展式可以确定式(9)中的A和U:

同样选取r=3,根据构造过程,选取Chebyshev多项式的零点![]() 为节点,得到
为节点,得到

以Legendre多项式的零点![]() 为节点,得到
为节点,得到
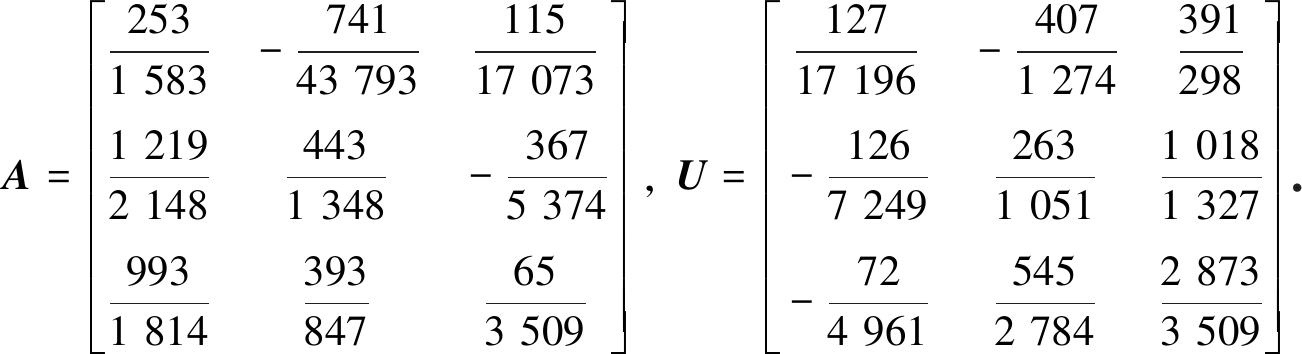
选取不同的节点,根据构造方法将得到的A与U代入式(9),确定多步块格式,可求得下一时间段[ti+1,ti+2]的初始值Yi+1.以此类推,可以求得各时刻的Y值.
3 数 值 算 例
以图2所示平面双连杆机械臂为例,各杆宽度均为a=0.1 m的均质杆,各杆长度L1=0.5 m,L2=1 m,质量m1=10 kg,m2=20 kg.初始时两杆水平,初速度为零.为了方便计算,在各物体质心建立沿惯性主轴的连体基坐标.
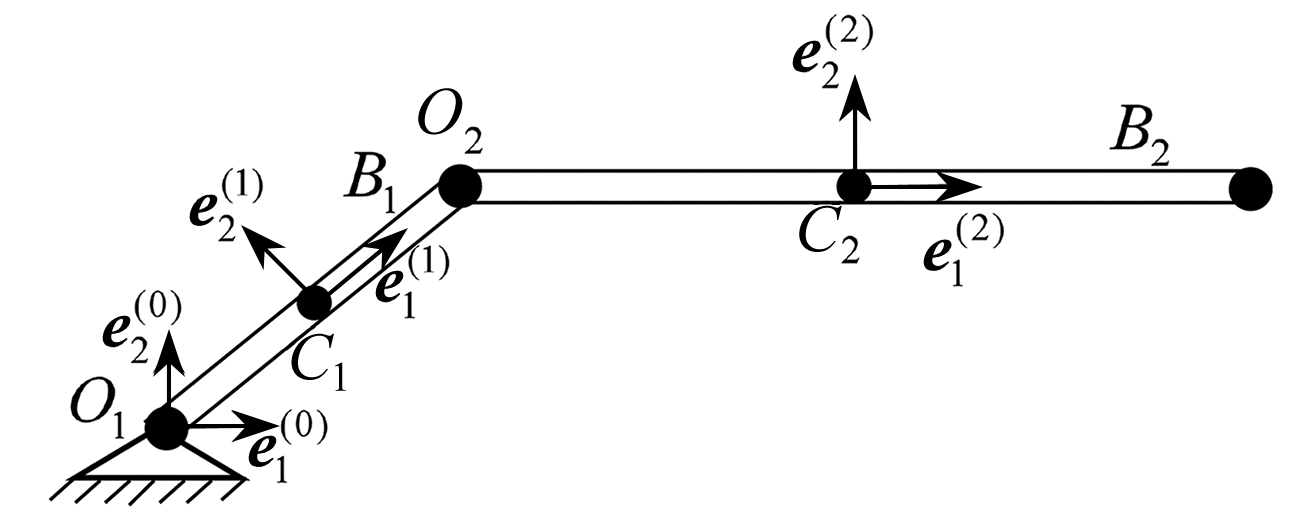
图2 平面双连杆机械臂
Fig. 2 A planar 2-link manipulator
对任意杆i(i=1,2),有广义坐标![]() 广义质量矩阵为
广义质量矩阵为
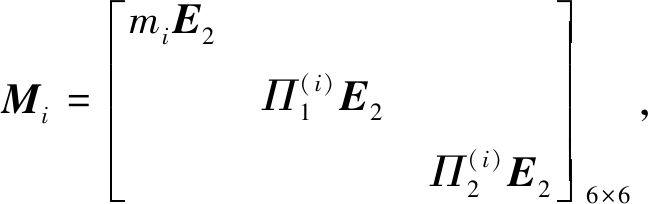
(10)
其中mi为杆i的质量,
系统势能为
(11)
方向矢量的约束条件为
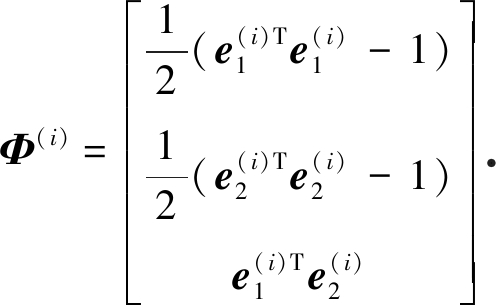
(12)
在转动铰O1,O2处的约束条件为
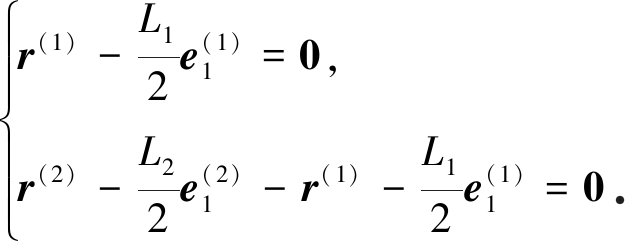
(13)
根据式(6)建立双连杆的动力学微分-代数方程,初始值![]() 当仿真时间为10 s,步长为0.001 s时,使用多步块方法计算微分-代数方程得到两杆末端运动轨迹图(见图3中实线部分)及
当仿真时间为10 s,步长为0.001 s时,使用多步块方法计算微分-代数方程得到两杆末端运动轨迹图(见图3中实线部分)及![]() 的时间历程图.总能量、动能、势能以及由式(12)、(13)所得的位移约束、速度约束、加速度约束的时间历程图见图4、5.为了进行比较,采用独立坐标θ1,θ2(其中θ1,θ2分别为杆L1,L2与水平坐标的夹角)得到的微分方程如下:
的时间历程图.总能量、动能、势能以及由式(12)、(13)所得的位移约束、速度约束、加速度约束的时间历程图见图4、5.为了进行比较,采用独立坐标θ1,θ2(其中θ1,θ2分别为杆L1,L2与水平坐标的夹角)得到的微分方程如下:
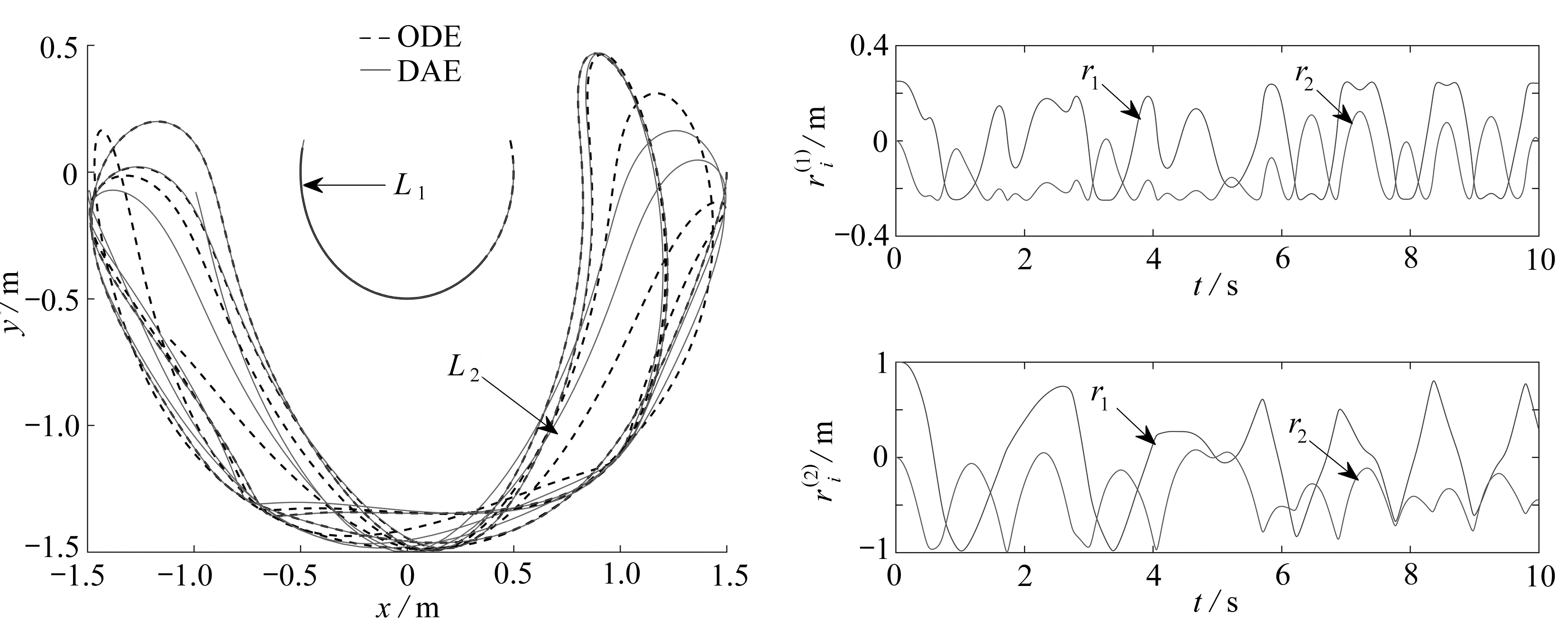
图3 运动轨迹图及各位矢分量仿真曲线
Fig. 3 Motion curves and simulation curves of vector components
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.

图4 系统各能量随时间变化历程
Fig. 4 The energy time histories of the system
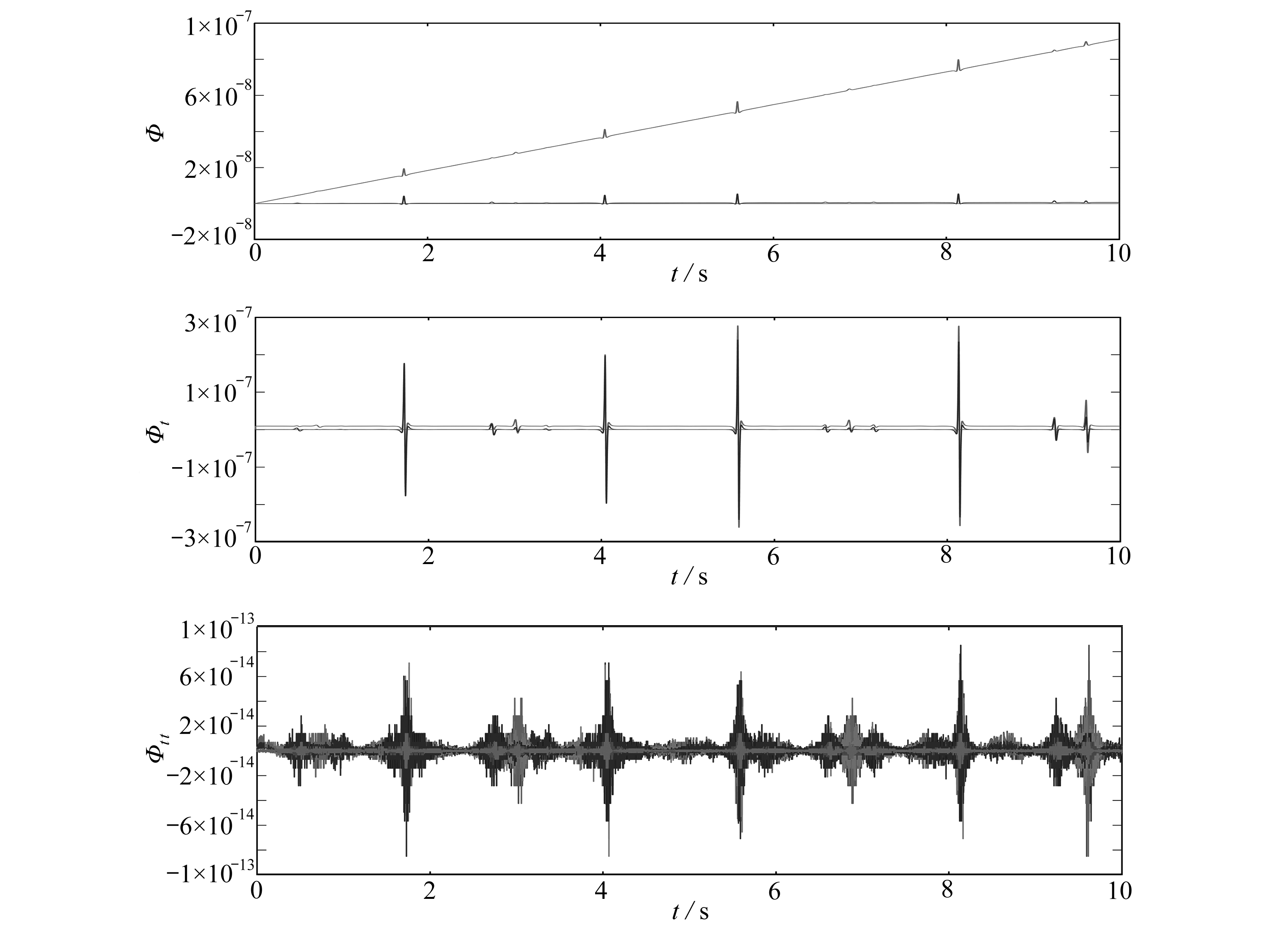
图5 位移约束、速度约束、加速度约束时间历程
Fig. 5 Time histories of the displacement constraint, the velocity constraint and the acceleration constraint

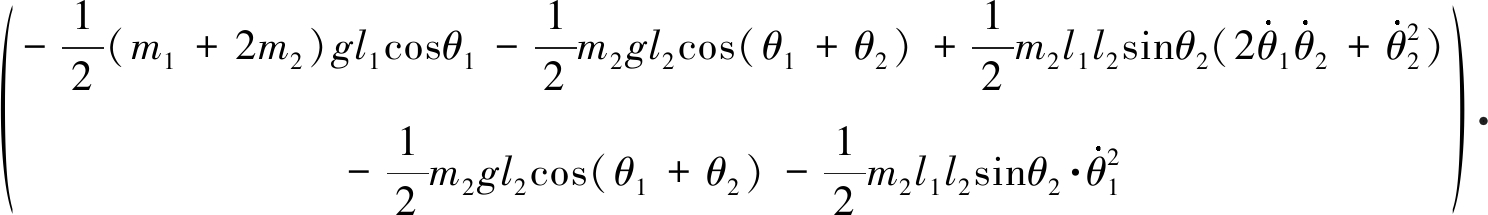
(14)
使用多步块方法计算微分方程(14),两杆末端运动轨迹图见图3虚线部分.
1) 当仿真时间为10 s,h=ti+1-ti时,选取不同的h值,由等距节点所构造的多步块方法求解微分-代数方程(7),对结果进行对照分析.由表1可知:步长越小,多步块格式求解同一微分-代数方程,所消耗时间虽然呈递增趋势,但是最大能量误差在减小,且位移约束、速度约束、加速度约束保持稳定.在仿真时间较短的情况下,选择多步块格式求解有利于减少误差,达到更好的仿真效果.
表1 多步块格式方法在不同步长下的结果比较
Table 1 Results of the multistep block method with different step sizes

step size h/sruntime t/s|H|maxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φtt0.0119.265 60.319 61.570 5E-43.000 0E-39.636 7E-130.007 526.078 10.093 95.086 6E-58.947 1E-46.927 8E-130.00540.171 90.017 59.952 4E-61.725 1E-43.259 6E-130.002 575.015 69.236 4E-41.380 0E-61.062 0E-58.881 8E-140.001177.578 15.099 6E-59.117 9E-52.771 2E-78.526 5E-14
2) 取相同步长h=0.01 s,对等距节点和不等距节点(由Chebyshev多项式零点和Legendre多项式零点所得)所构造的多步块格式求解微分-代数方程(7)的结果进行比较分析.由表2可知:当步长固定时,以Chebyshev多项式零点和Legendre多项式零点为节点所构造的多步块格式所得的最大能量误差小于等距节点所构造的多步块格式所得的最大能量误差.
表2 等距节点与不等距节点所构造的多步块格式的结果比较
Table 2 Comparison of the results from the multistep block method with uniform and non-uniform nodes

runtime t/s|H|maxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φttuniform nodes19.265 60.319 61.570 5E-43.000 0E-39.636 7E-13Chebyshev nodes22.390 60.059 05.817 1E-47.728 4E-41.122 7E-12Legendre nodes20.921 90.003 56.445 2E-53.052 0E-41.072 9E-12
3) 取相同步长h=0.01 s,从程序运行时间、最大能量误差、位移约束、速度约束以及加速度约束方面对多步块格式和Runge-Kutta方法求解同一微分-代数方程式(7)所得结果进行分析.由表3可知: 在较短时间间隔下,当仿真时间相同时,Runge-Kutta方法虽然在运行时间上占据优势,但最大能量误差大于多步块格式所得的最大能量误差;同样是求解指标-1的方程,在位移约束、速度约束的保持方面,多步块格式要好于Runge-Kutta方法,而对于多体系统来说,保持位移约束和速度约束是至关重要的.
表3 多步块格式方法与Runge-Kutta方法在相同步长下的结果比较
Table 3 Comparison between the multistep block method and the Runge-Kutta method with the same step

methodruntime t/s|H|maxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φttmultistep block19.265 60.319 61.570 5E-43.000 0E-39.636 7E-13Runge-Kutta1.734 49.87 350.031 50.008 13.98E-13
4) 当r=3,在相同步长h=ti+1-ti时,用Δ=|eTe-I|来计算方向矢量约束误差.由等距节点、Chebyshev多项式零点和Legendre多项式零点所得多步块格式的方向矢量约束误差如图6~9所示.与Runge-Kutta方法进行比较,可以看出,三种不同节点构造的多步块格式在保持方向矢量误差方面要精于Runge-Kutta方法.采取等距节点方法得到的多步块格式,虽然能够保持方向矢量约束误差达到比较好的状态,但是稳定性较差,而由Chebyshev多项式零点和Legendre多项式零点得到的多步块格式对方向矢量约束误差都能够达到很好的稳定效果,Legendre多项式选取节点比Chebyshev多项式选取节点达到的精度更高.
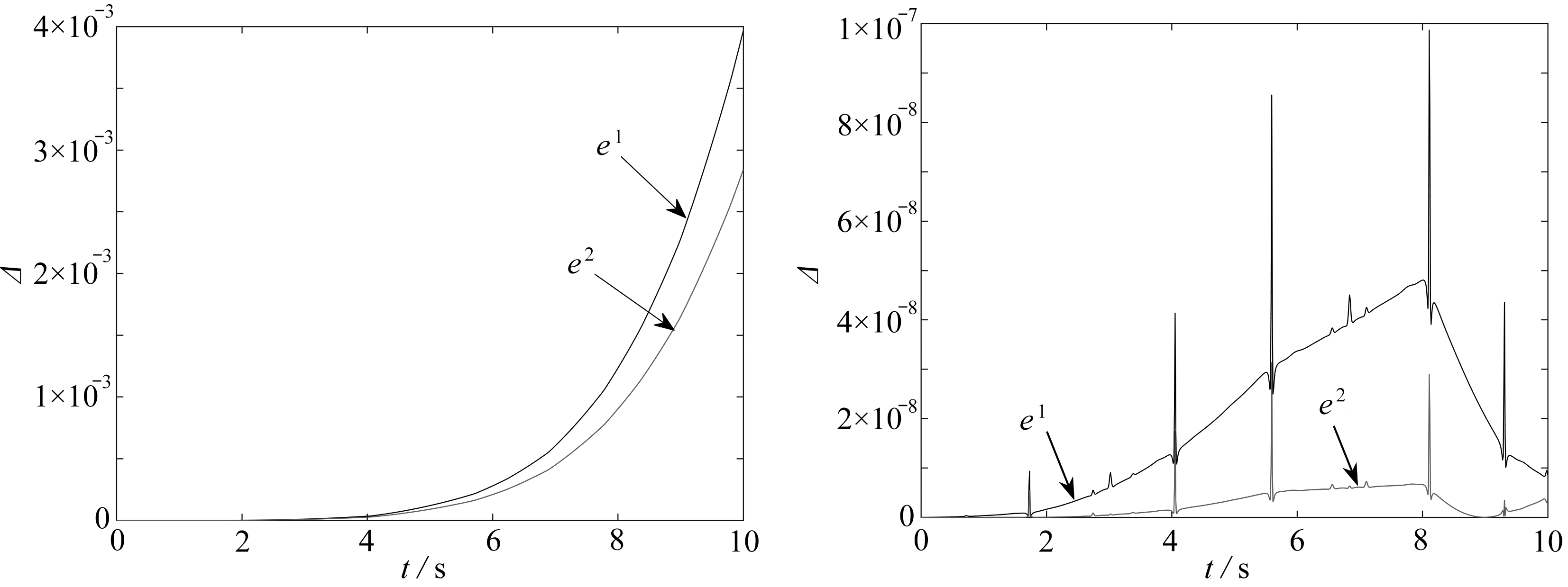
图6 方向矢量约束误差(Runge⁃Kutta 方法) 图7 方向矢量约束误差(等距节点)
Fig. 6 Direction vector constraint errors (Runge-Kutta method) Fig. 7 Direction vector constraint errors (uniform nodes)
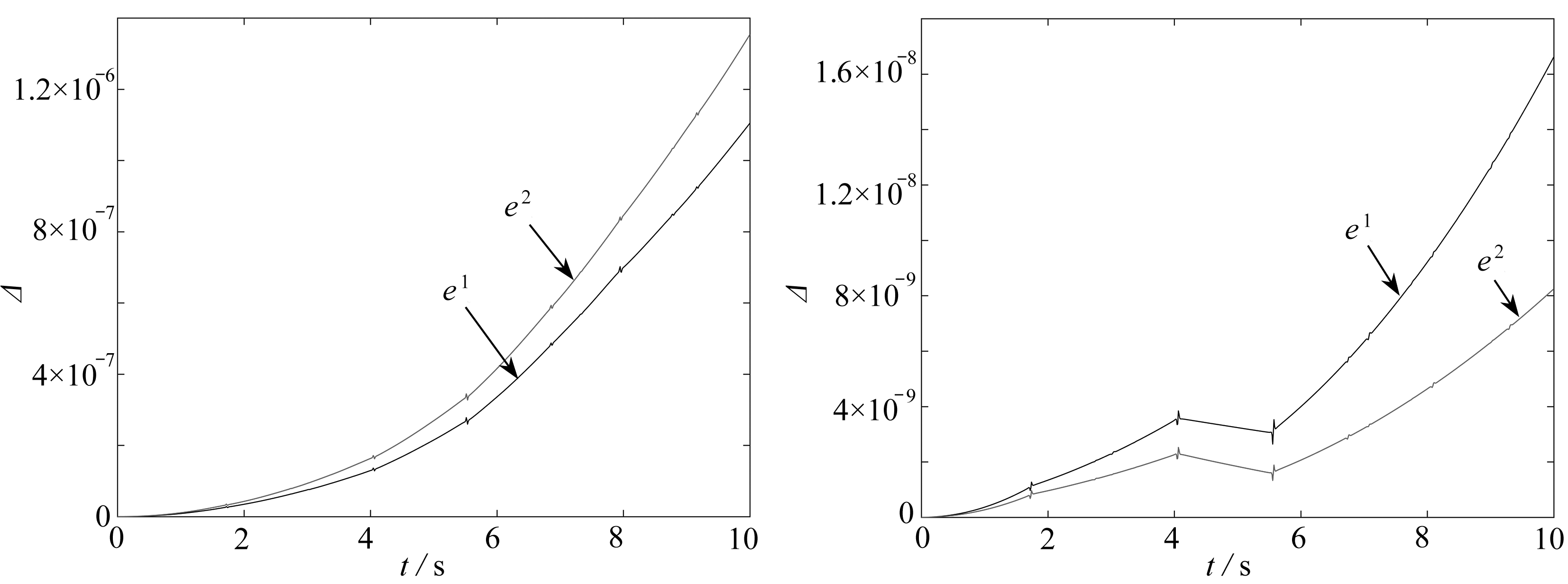
图8 方向矢量约束误差(Chebyshev多项式零点) 图9 方向矢量约束误差(Legendre多项式零点)
Fig. 8 Direction vector constraint errors (Chebyshev polynomial zero) Fig. 9 Direction vector constraint errors (Legendre polynomial zero)
5) 在相同步长h=0.01s下,仿真时间加长,由表4可知: 多步块格式在最大能量误差上呈递增趋势,加速度约束却依然保持稳定状态,相较于经典Runge-Kutta方法在仿真时间高于50 s时出现奇异状态,多步块格式更适合长时间的多体系统动力学仿真.
表4 多步块格式在不同仿真时间段下的结果比较
Table 4 Comparison between the multistep block method with different simulation times

simulation time ts/sruntime t/s|H|maxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φtt1019.265 60.319 61.570 5E-43.000 0E-39.636 7E-1325445.765 60.850 10.002 00.003 01.112 0E-1250989.218 83.802 80.011 10.004 01.112 0E-12751.556 8E+37.476 20.024 30.004 41.315 4E-121001.921 3E+314.075 10.043 80.004 41.319 9E-12
6) 仿真时间加大到100 s,h=ti+1-ti,选取不同的h值.在图4、图5和表1的基础上,由图10、图11、表5更可以体现多步块格式在长时间仿真下,在最大能量误差、位移约束、速度约束和加速度约束的控制上的优势.
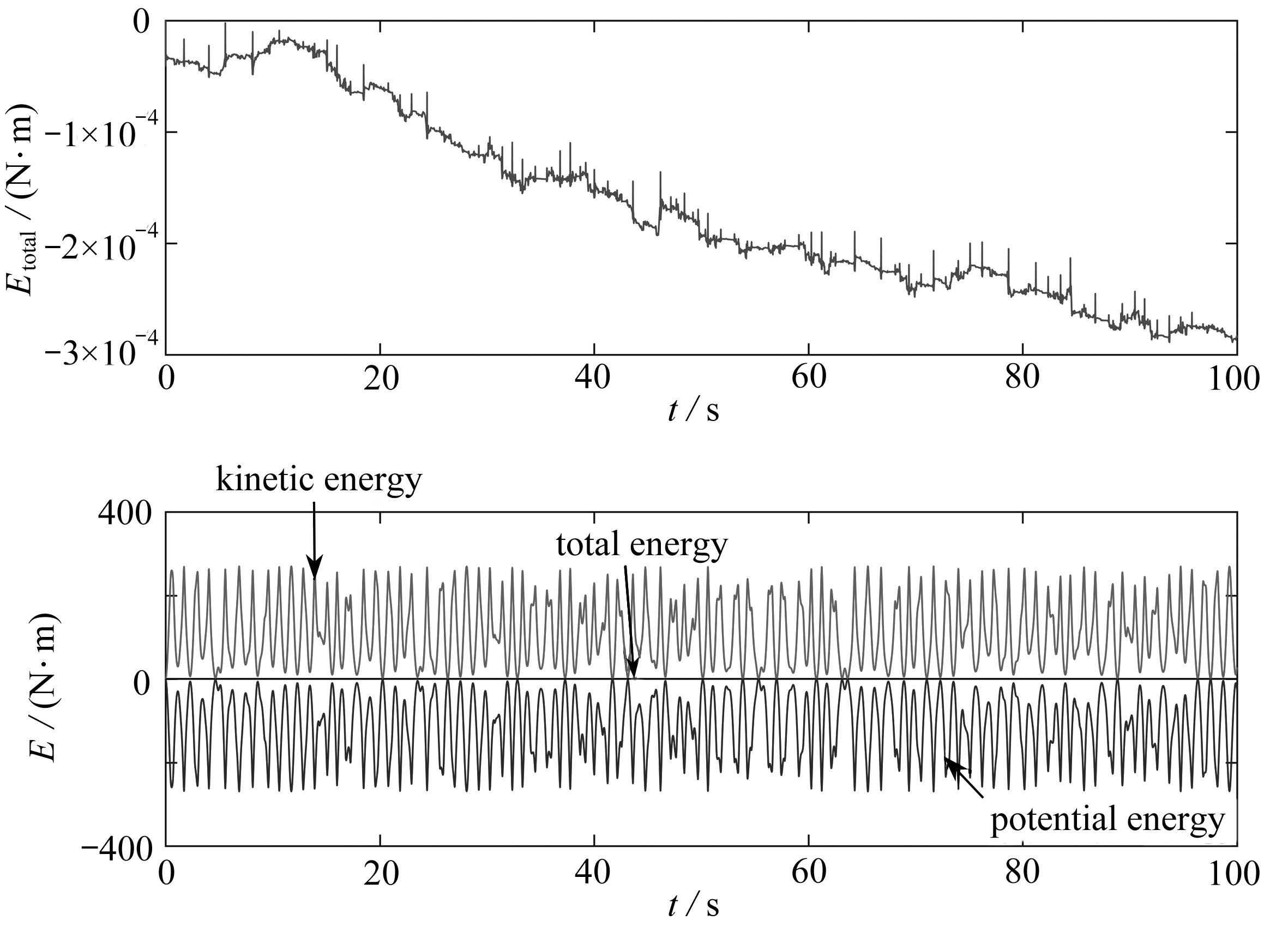
图10 系统各能量随时间变化历程
Fig. 10 The energy time histories of the system
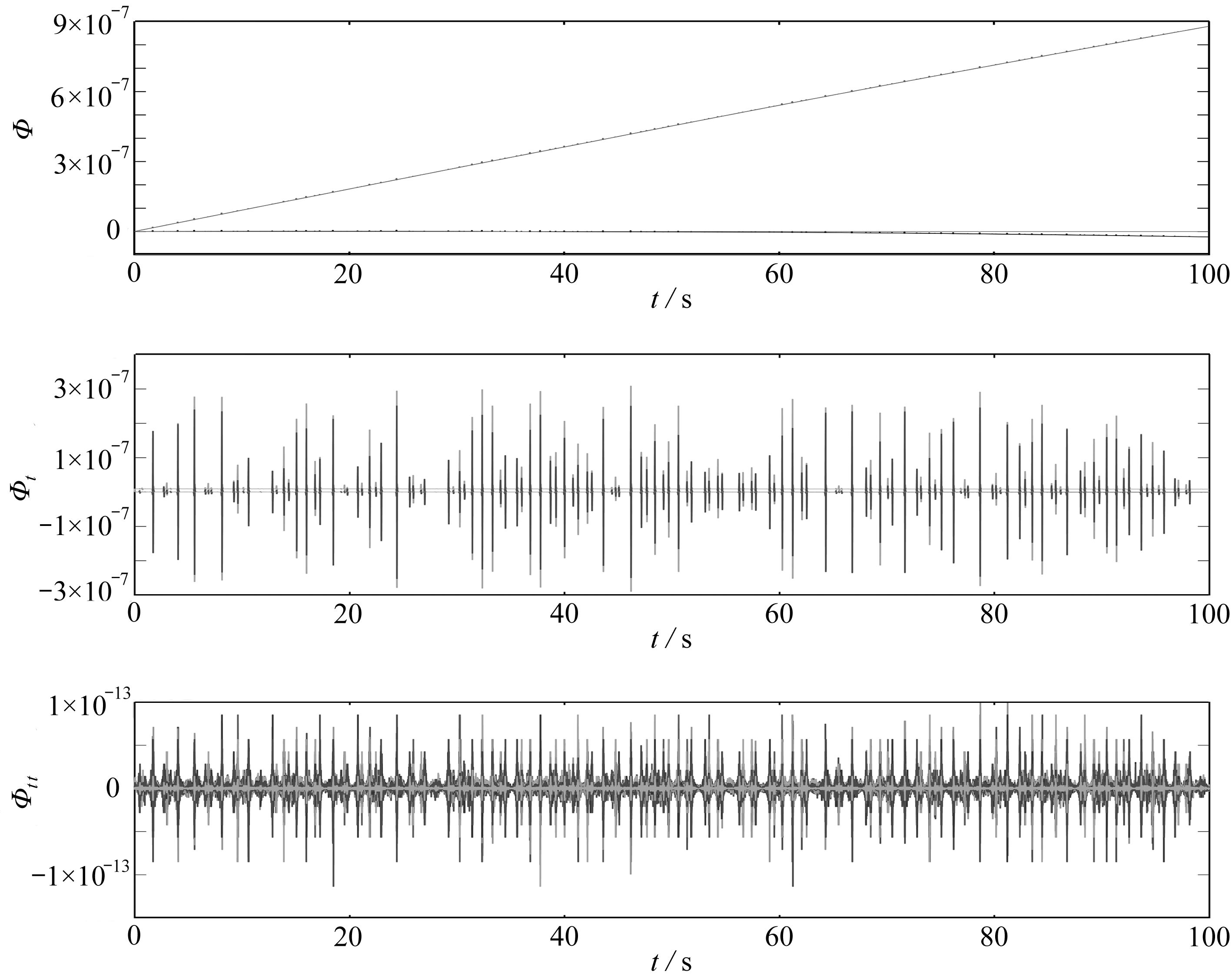
图11 位移约束、速度约束、加速度约束时间历程
Fig. 11 Time histories of the displacement constraint, the velocity constraint and the acceleration constraint
表5 多步块格式方法在不同步长下的结果比较
Table 5 Results of the multistep block method with different step sizes
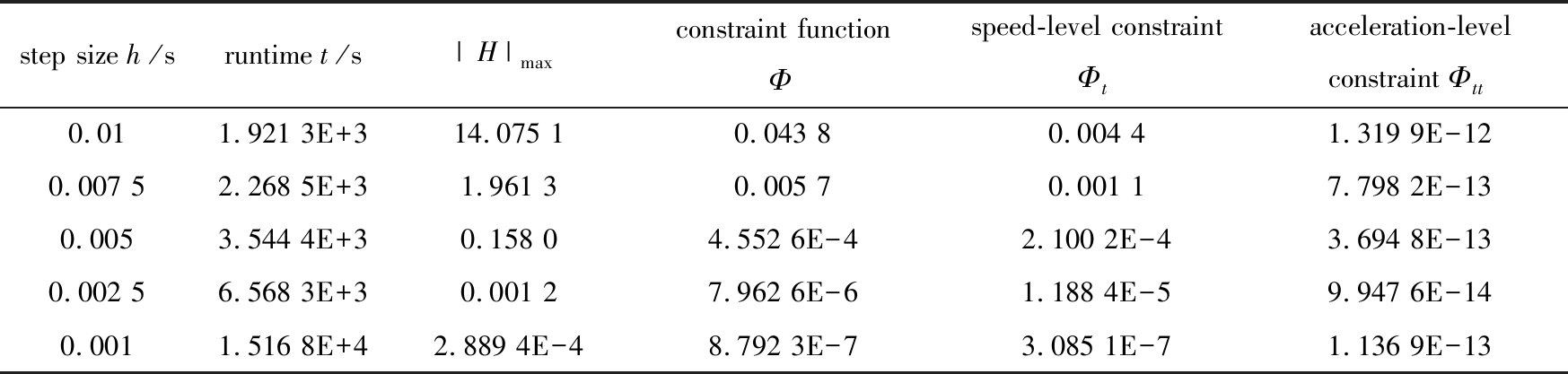
step size h/sruntime t/s|H|maxconstraint function Φspeed-level constraint Φtacceleration-level constraint Φtt0.011.921 3E+314.075 10.043 80.004 41.319 9E-120.007 52.268 5E+31.961 30.005 70.001 17.798 2E-130.0053.544 4E+30.158 04.552 6E-42.100 2E-43.694 8E-130.002 56.568 3E+30.001 27.962 6E-61.188 4E-59.947 6E-140.0011.516 8E+42.889 4E-48.792 3E-73.085 1E-71.136 9E-13
7) 取仿真时间为10 s,h=ti+1-ti,对不同的h值,比较含两个独立广义坐标的微分方程和方向矢量法描述的微分-代数方程使用等距节点多步块方法求解时的能量误差.由表6可以看出,随着步长减小,多步块方法求解广义坐标描述的微分方程能量H1的最大误差积累明显,而方向矢量法描述的微分-代数方程H2的最大误差控制较好,但计算时间较长.
表6 广义坐标方程在不同步长下的结果比较
Table 6 Comparison between the equation in generalized coordinates with different step sizes
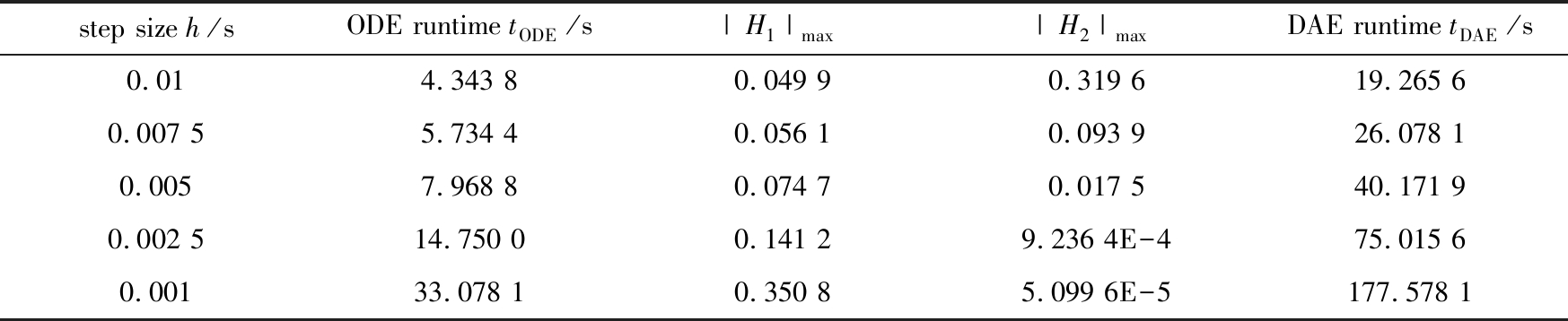
step size h/sODE runtime tODE/s|H1|max|H2|maxDAE runtime tDAE/s0.014.343 80.049 90.319 619.265 60.007 55.734 40.056 10.093 926.078 10.0057.968 80.074 70.017 540.171 90.002 514.750 00.141 29.236 4E-475.015 60.00133.078 10.350 85.099 6E-5177.578 1
4 结 论
相较于其他坐标建模方法,方向矢量法具有选择灵活、形式简单较易理解、比较程式化、易于编程实现等优点.通过数值实验综合比较可得: 等距节点多步块格式法以及根据构造方法得到的由Chebyshev零点和Legendre零点决定的不等距节点多步块格式在时间、步长固定的情况下所得结果优于Runge-Kutta方法的结果,并且由Chebyshev多项式零点和Legendre多项式零点所构造的多步块格式效果更好.在步长固定的情况下,多步块格式更适合长时间仿真.使用Runge-Kutta法求解,虽然该方法是计算微分-代数方程的经典算法,但是在短时间仿真、选取步长较大的情况下,会导致精度降低,总能量随时间增大;在长时间仿真时,可以选择多步块方法对方向矢量法描述的微分-代数方程进行仿真计算.
[1] DE JAL N J G, BAYO E. Kinematic and Dynamic Simulation of Multibody Systems the Real-Time Challenge[M]. Berlin: Springer, 1994.
N J G, BAYO E. Kinematic and Dynamic Simulation of Multibody Systems the Real-Time Challenge[M]. Berlin: Springer, 1994.
[2] DE JAL N J G. Twenty-five years of natural coordinates[J]. Multibody System Dynamics, 2007, 18(1): 15-33.
N J G. Twenty-five years of natural coordinates[J]. Multibody System Dynamics, 2007, 18(1): 15-33.
[3] VON SCHWERIN R. Multibody System Simulation, Numerical Methods, Algorithms and Software[M]. Berlin: Springer, 1999.
[4] KRAUS C, BOCK H G, MUTSCHLER H. Parameter estimation for biomechanical models based on a special form of natural coordinates[J]. Multibody System Dynamics, 2005, 13(1): 101-111.
[5] UHLAR S, BETSCH P. Arotationless formulation of multibody dynamics: modeling of screw joints and incorporation of control constraints[J]. Multibody System Dynamics, 2009, 22(1): 69-95.
[6] BUTCHER J C. On the convergence of numerical solutions to ordinary differential equations[J]. Mathematics of Computation, 1966, 20(93): 1-10.
[7] CHOLLOM J P, NDAM J N, KUMLENG G M. On some properties of the block linear multi-step methods[J]. Science World Journal, 2007, 2(3): 11-17.
[8] OLABODE B T. An accurate scheme by block method for third order ordinary differential equations[J]. Pacific Journal of Science and Technology, 2009, 10(1): 136-142.
[9] MEHRKANOON S, MAJID Z A, SULEIMAN M. A variable step implicit block multistep method for solving first-orderODEs[J]. Journal of Computational and Applied Mathematics, 2010, 233(9): 2387-2394.
[10] MEHRKANOON S. A direct variable step block multistep method for solving general third-order ODEs[J]. Numerical Algorithms, 2011, 57(1): 53-66.
[11] AWOYEMI D O, ADEBILE E A, ADESANYA A O, et al. Modified block method for the direct solution of second order ordinary differential equations[J]. International Journal of Applied Mathematics and Computation, 2011, 3(3): 181-188.
[12] MAJID A Z, MOKHTAR N Z, SULEIMAN M. Direct two-point block one-step method for solving general second-order ordinary differential equations[J]. Mathematical Problems in Engineering, 2012: 184253.
[13] OLABODE B T. Block multistep method for the direct solution of third order of ordinary differential equations[J]. FUTA Journal of Research in Sciences, 2013, 9(2): 194-200.
[14] MOHAMED N A, MAJID Z A. Multistep block method for solvingvolterra integro-differential equations[J]. Malaysian Journal of Mathematical Sciences, 2016, 10: 33-48.
[15] 李博文, 丁洁玉, 李亚男. 多体系统动力学微分-代数方程L-稳定方法[J]. 应用数学和力学, 2019, 40(7): 768-779.(LI Bowen, DING Jieyu, LI Yanan. An L-stable method for differential-algebraic equations of multibody system dynamics[J]. Applied Mathematics and Mechanics, 2019, 40(7): 768-779.(in Chinese))