引 言
随着分布式发电、储能、用户微网、充电桩等新的能源生产方式和消费模式的不断涌现,能源行业正在逐步向绿色、低碳、高效和能源互联共享的方向发展.“建设全业务泛在电力物联网”成为其中的关键.泛在电力物联网能够围绕电力系统各环节,充分应用移动互联、人工智能等现代信息技术、先进通信技术,实现电力系统各环节万物互联、人机交互,具有状态泛在感知、信息高效处理、应用便捷灵活的特征.其最主要的特点是实现电力网络的全面状态感知和控制.目前,用户需求端能源获取方式以及功能手段在不断地发生着变化.其中,分布式电源具有规模小、分布不均以及出力不稳定等特点,在泛在电力物联网的技术支撑下,是否可以实现分布式电源的有效控制管理和优化调度,是目前值得研究的问题[1].
传统的集中调度模式难以适应泛在电力物联网开放、可扩展等核心特征[2-3].P2P优化调度是一种在参与者之间分配任务和工作负载的分布式应用模式,其重要特点是“去中心化”.简单地说,P2P不存在调度中心节点,它将各节点直接连接起来,通过互联网交互.P2P调度模式与泛在电力物联网的理念不谋而合,泛在电力物联网为分布式电源的P2P优化调度提供了技术支撑.
目前,已有专家学者对分布式电源的优化调度运行方面进行了相关的研究.文献[4]提出了对多能源互联的分布式控制方法,在保证负荷功率在各分布式电源间精确分配的基础上,使各分布式电源的输出电压相角和幅值保持一致,从而减小甚至消除分布式电源间的计算电流;文献[5-6]提出了一种“一致项+修正项”的调度算法,一致项确保增量成本收敛到最优值,修正项根据物理设备的实际运行情况计算反馈量进行实时修正,保证供需平衡.上述一致性的创新方法使得主节点的设定不再必要.文献[7]针对分布式发电系统的经济特性进行了分析,提出了基于合作博弈的分布式电源优化运行策略,在传统分布式调度的基础上考虑了环境因素,更好地实现了电力系统的优化运行调度.文献[8]针对大量分布式电源接入的现状,提出了一种采用基于市场控制的微网分布式能量优化方法.文献[9]考虑微电网即插即用状态不确定性,提出了可以处理变量维数变化的分布式交互优化求解方法,通过迭代与信息交互,收敛到全局最优解.
综上所述,针对分布式电源的优化调度已有了相应的研究,基于泛在电力物联网的特征,通信技术对其正常运行起到了至关重要的作用.因此,本文根据泛在电力物联网中分布式电源的网络拓扑结构和通信技术特点,利用P2P技术,建立了分布式电源的去中心化调度结构,并介绍了用于求解该模型的分布式次梯度算法,同时考虑了泛在电力物联网中通信中断、误码对优化结果的影响,具有一定的工程实用性.
1 基于泛在电力物联网的P2P优化调度架构
1.1 P2P调度架构
由于分布式电源发电功率小、数量较大且地理位置分布较为分散,难以对它们建立统一的控制中心.对于所有分布式电源进行集中式调度,会导致成本过高,经济效益降低.而P2P架构是一种在对等的节点之间分配任务和工作负载的分布式应用架构,各节点间没有上下级之分,具有去中心化的特点.将P2P理念拓展到泛在电力物联网中,可以实现对分布式电源的优化调度,建立如图1所示的分布式电源优化调度架构.
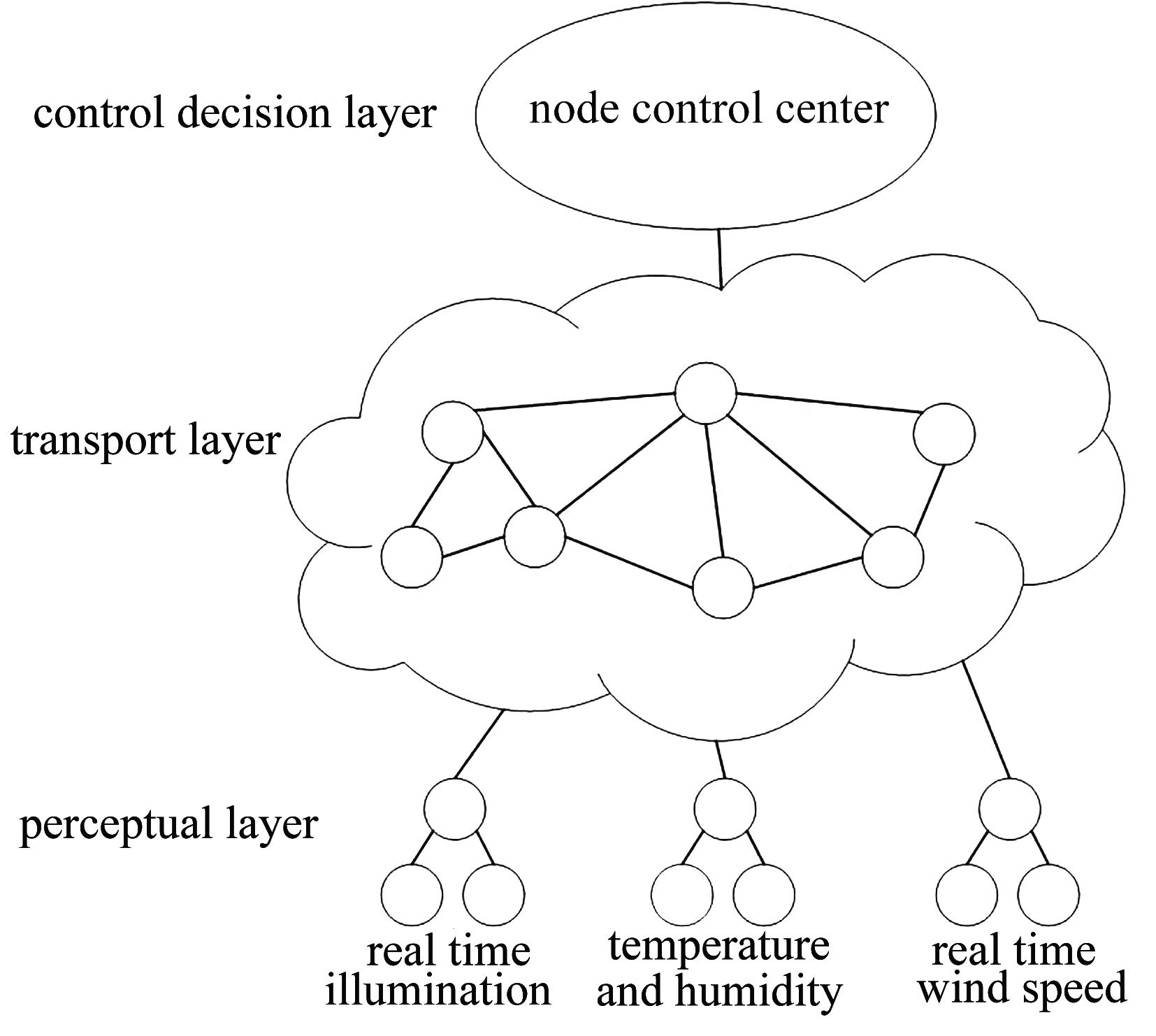
图1 分布式电源P2P调度架构
Fig. 1 The P2P scheduling architecture
根据P2P的特点,此优化调度架构主要包括三个层次:第一层是感知层,它是由众多传感器所组成,密集部署在分布式电源周围,实现对物理状态的泛在感知.在泛在电力物联网的背景下,泛在感知是指以微型系统与传感器等电子器件为泛在信息技术的硬件基础,借助嵌入各种应用环境的系统来实现对分布式电源状态及所处微环境下信息的捕获、分析和传递,从而使人们能够及时了解电力设备的运行状态,以实现对电力设备的合理化和精细化控制.第二层是传输层,通过现有的互联网、无线通信网或者一些专用的通信网络以及传统的物理传输网络,实现传感网探测数据和控制信息的传输和分发、信息的海量存储与管理、云计算、数据模型表示和智能化处理等.第三层是控制决策层,该层主要包括各节点内部的控制决策单元,以实现对各发电节点单元的有效控制.此架构具有以下几个特点: 1) 配合了能源逐渐分布化的演变方向,能更加合理充分地利用能源; 2) 具有去中心化特点,无需中心节点或中间层控制; 3) 各连接节点间依靠通信技术进行信息交互,具有信息高速流动的特点; 4) 具有良好的扩展性,节点能很方便地实现即插即用的功能,加大了电网的开放性.
1.2 泛在电力物联网通信特性分析
在泛在电力物联网的背景下,各能源节点之间可以进行信息交互,依照IEC 61850标准,分布式可再生能源入网作为特殊汇聚节点,入网位置比较灵活,根据需要选择的通信方式也会不同.泛在电力物联网的通信方式,分为有线通信方式和无线通信方式,各类通信方式的性能和优缺点如表1所示.有线通信方式包括光纤通信、PLC、EPON、GPON等,无线通信方式包括GPRS、3G/4G、WiMAX等一些方式[10-11].各能源节点发电系统内部通信业务量小、距离短,优选现场总线和PLC等传统的、经济性较好的通信方式;入网点信息量较大,对传输的实时性和可靠性要求高,优选光纤通信和3G/4G移动通信方式.
表1 各种通信方式特点
Table 1 Characteristics of various communication modes

communication modetransmission distancetransmission speedadvantagelimitationoptical fiber communication550 m~100 km<10 Mb/slong transmission distance, fast speed,anti-interferencehigh construction costPLC1~3 km2~3 Mb/slong transmission distancedependence on the existing power lines and poor anti-interference abilityEPON20 km1.25 Gb/sfast transmission speed, flexible networkinghigh initial investment and hindered spreadGPON20 km1.86 Gb/shigh bandwidth, high efficiency and wide coveragehigh threshold for technology access and lack of investmentGPRS1~10 km170 kb/slong transmission distance and low costlow transmission rate and poor security4G mobile communication-20 Mb/shigh speed, good communication qualitycomplex structure and high cost
由于各分布式电源地理位置特征等因素及其入网选择的通信方式不同,都可能存在一定的差异,信息传输的时效性、可靠性、安全性也会有所差异.故应该将通信中断、通信误码等通信情况纳入考虑之中.
2 基于泛在电力物联网的P2P优化调度模型
分布式电源具有规模小、分布不均以及出力不稳定等特点,在泛在电力物联网的技术支撑下,能否实现对其有效控制管理和优化调度是本文研究的关键问题.本文建立优化模型的目标是在总调度任务一定的情况下,在确保各分布式电源出力处于其自身出力上下界的条件下,达到总发电成本最低.
2.1 目标函数
本文以分布式电源的发电成本最小为优化目标,建立以下目标函数[12-13]:
(1)
其中,αi,βi,γi为分布式电源的发电成本系数,PDGi为第i个分布式电源的出力控制变量.
2.2 约束条件
1) 分布式电源调度任务等式平衡约束:
(2)
其中,Pinstruct表示分布式电源需完成的总调度任务.
2) 各分布式电源出力容量约束:
0≤PDGi≤PDGmax,i,
(3)
其中,PDGmax,i为节点i内部机组的容量上限值.
3) 风电出力实时功率约束[14]:
0≤PDGi≤Preal-wind,i,
(4)

(5)
其中,vci,vri,vcoi和wri分别代表风电机组i的切入风速、额定风速、切出风速和额定输出功率,Ai,Bi,Ci为风电机组i的出力系数,vi是泛在感知状态下风电机组i的实时风速,Preal-wind,i是泛在感知状态下的实时可用风电发电功率.
4) 光伏出力实时功率约束[15]:
0≤PDGi≤Preal-PV,i,
(6)
Preal-PV,i=riSiηi,
(7)
其中,ri是泛在感知状态下该光伏机组区域光照强度,Si代表光伏机组光照面积,ηi为光伏机组的光电转化效率.
3 P2P优化调度求解算法
本文采用分布式次梯度算法求解建立的P2P优化调度模型,其主要思路是:每个分布式电源的控制单元通过其自身的目标函数信息(即目标函数的次梯度)对决策变量进行估计,并与网络中的其他分布式电源交换信息,利用局部信息交换实现协调控制,最终给出全局目标最优时的决策变量.而双随机矩阵是分布式次梯度算法的重要元素,因此,本节将着重介绍双随机矩阵与分布式次梯度算法.
3.1 基于泛在电力物联网的双随机矩阵
为了易于描述,本文将分布式电源抽象为点(以下简称节点).如果两个节点之间存在通信连接,则代表它们的点相连,形成一条边.这样整个网络就形成了由点和连接这些点的边构成的图.进一步地,为了表示各节点之间互相影响的程度,可以定义每条边的权值,也即连接强度.一般仅考虑非负权值,权值越大,即表示两个节点互相影响越大.在此基础上,再对节点赋予序号,即可定义网络的通信连接矩阵:
MN×N=(mij)N×N,
(8)
其中,mij为由节点i指向节点j的边上的权值,N为网络中节点的数目.当第i个集群与第j个集群直接存在通信链路时,其权重mij=mji>0,否则mij=mji=0,权重值取决于链路传输效果,同时必须满足![]() 则称MN×N为双随机矩阵.
则称MN×N为双随机矩阵.
3.2 基于泛在电力物联网的P2P优化求解算法
在分布式次梯度算法中,首先定义Lagrange函数:
(9)
其中,λ,ζ,μi代表Lagrange乘子,DG1~DGk表示风电机组,DG(k+1)~DGN表示光伏机组.
按照分布式次梯度算法,各分布式电源之间进行交互迭代以寻求优化收敛:
(10)
(11)
(12)
(13)
其中,λi,ζi,μij代表第i个节点内部的Lagrange乘子.在迭代时,每一个分布式电源计算其Lagrange函数的次梯度方向,并接收相邻代理的信息以及迭代变量k,然后更新自己的决策变量,以使得该问题达到全局最优解.
4 算 例 分 析
4.1 算例场景
为了验证本文所提方法的有效性,本文采用了33节点配电网中7个分布式电源,进行优化调度仿真.其中,1~4号为风电机组,5~7号为光伏机组,各分布式电源的运行参数如表2所示.将每个分布式电源等效成一个节点,它们的通信连接情况如图2所示.
表2 分布式电源运行参数表
Table 2 Parameters of different distributed generations

parameterDG1DG2DG3DG4DG5DG6DG7α0.010.0150.0200.010.0150.018β118611.511.3129γ0000000maximum output PDGmax,i/MW2002002 000200280280280minimum output PDGmin,i/MW0000000initial value PDGinitial,i/MW60606060606060
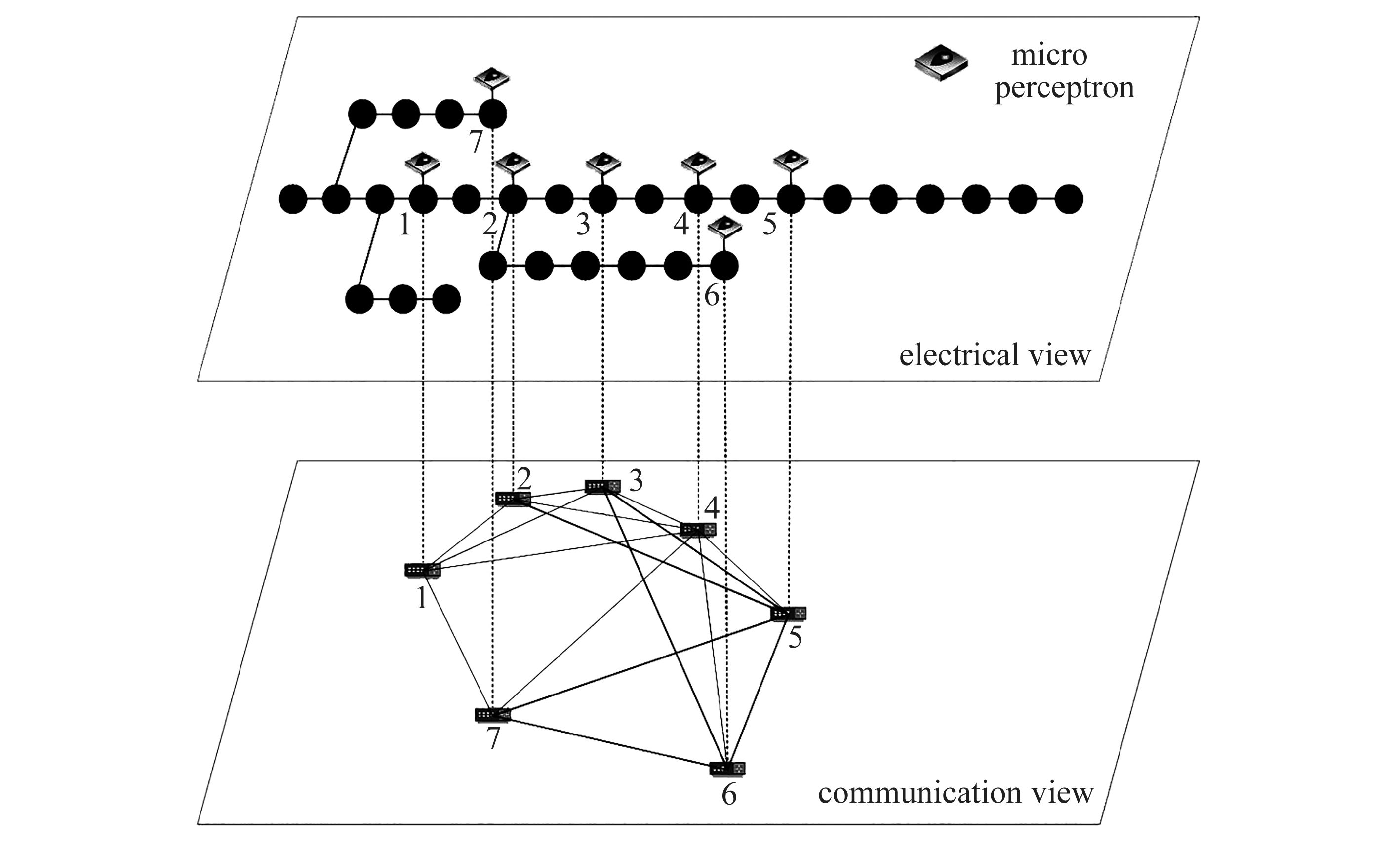
图2 泛在电力互联网通信网络拓扑
Fig. 2 The communication network topology of ubiquitous power internet of things
根据泛在电力物联网通信结构,其通信连接矩阵为
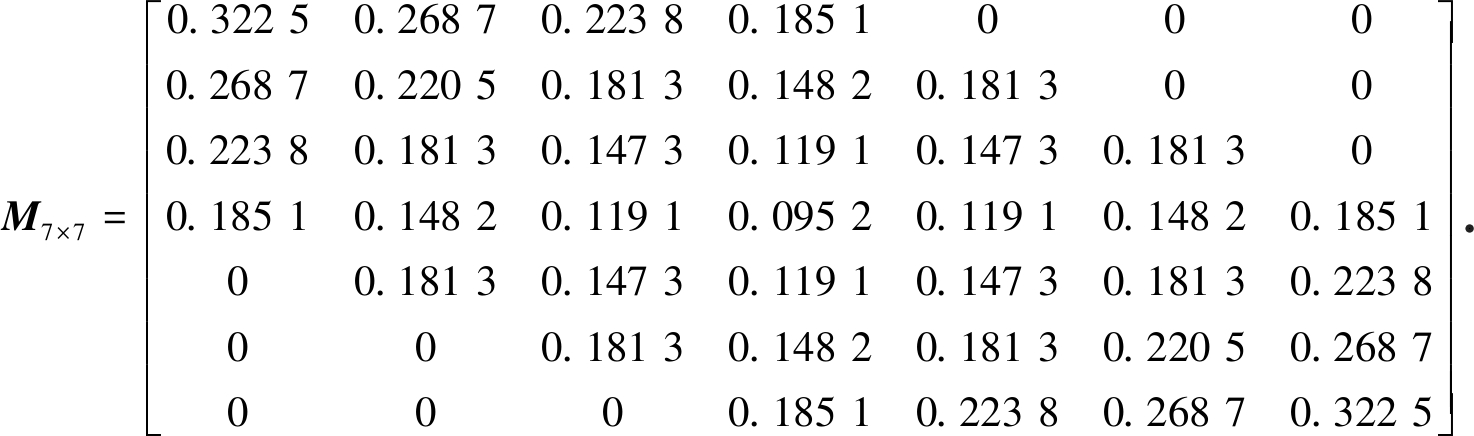
4.2 P2P优化调度与集中式调度对比分析
本文通过与集中式算法对比的方式来验证所提的分布式算法的有效性.采用本文所提的优化算法对所建立的P2P优化调度模型进行求解,选取适当的迭代精度.分布式电源出力值与总经济成本的优化结果如图3所示.

图3 P2P优化调度下分布式电源出力值
Fig. 3 Outputs of different distributed generations under the P2P optimal scheduling
由图3可知,该算法迭代收敛后,七个发电节点单元的出力值如表3所示.
表3 P2P优化调度下各分布式电源出力值(单位: MW)
Table 3 Outputs of different distributed generations under the P2P optimal scheduling(unit: MW)
PDG1PDG2PDG3PDG4PDG5PDG6PDG744.975 384.582 6102.596 456.531 539.909 521.218 566.773 5
从图3可知,本文所建立的P2P优化调度模型中,不同的发电单元节点之间通过其之间的通信链接交换其状态信息,通过不断的优化迭代,该算法可以逐渐收敛到全局最优解,即总出力∑PDGi=416.587 3 MW.与所设定实际要求的总出力420 MW相差3.412 7 MW,误差为0.813%,总发电成本为F=4 164.1$.
集中式算法下,基于 MATLAB优化工具箱建立子程序,通过调用fmincon函数的序列二次规划(SQP)算法进行求解.该算法结果如表4所示.
表4 集中式算法下各分布式电源出力值(单位: MW)
Table 4 Outputs of different distributed generations under the centralized scheduling(unit: MW)
PDG1PDG2PDG3PDG4PDG5PDG6PDG724.999 9116.667137.552.708 59.990.0078.125 0
在此情况下,总发电成本为F=4 128.4$.通过对比P2P优化调度与集中式调度的结果,可以发现: 1) 两者的调度结果有所差异,这是因为在P2P优化调度中,各分布式电源只能获得局部的信息,并结合自身的目标函数信息对决策变量进行迭代更新,且在此过程中还会受到双随机矩阵参数的影响.但调度结果误差仅为0.813%,准确性较高. 2) 在P2P优化调度中,每个分布式电源都有着相同的目标,即发电成本最低,从经济性角度分析,与集中式调度结果相比,误差仅为0.872%,经济性较高.因此,P2P优化调度可以同时满足准确性与经济性要求,保证该结果收敛到优化解.
4.3 信息中断及时恢复下算例分析
在泛在电力物联网中,通信环节在分布式优化过程中起到了至关重要的作用,但由于各分布式电源直接地理位置特征等因素及其入网选择的通信方式都可能存在一定的差异性,信息传输的时效性、可靠性、安全性也有所差异.故本文将通信中断情况纳入考虑之中.
本小节设置了通信中断下的算例来分析通信中断的产生对P2P优化调度结果的影响.假设整个通信网络的通信中断率较低,为了反映通信中断对优化结果的影响,若在整个数值模拟过程中出现通信中断情况,则该算法将重新进行,仿真结果如图4所示.
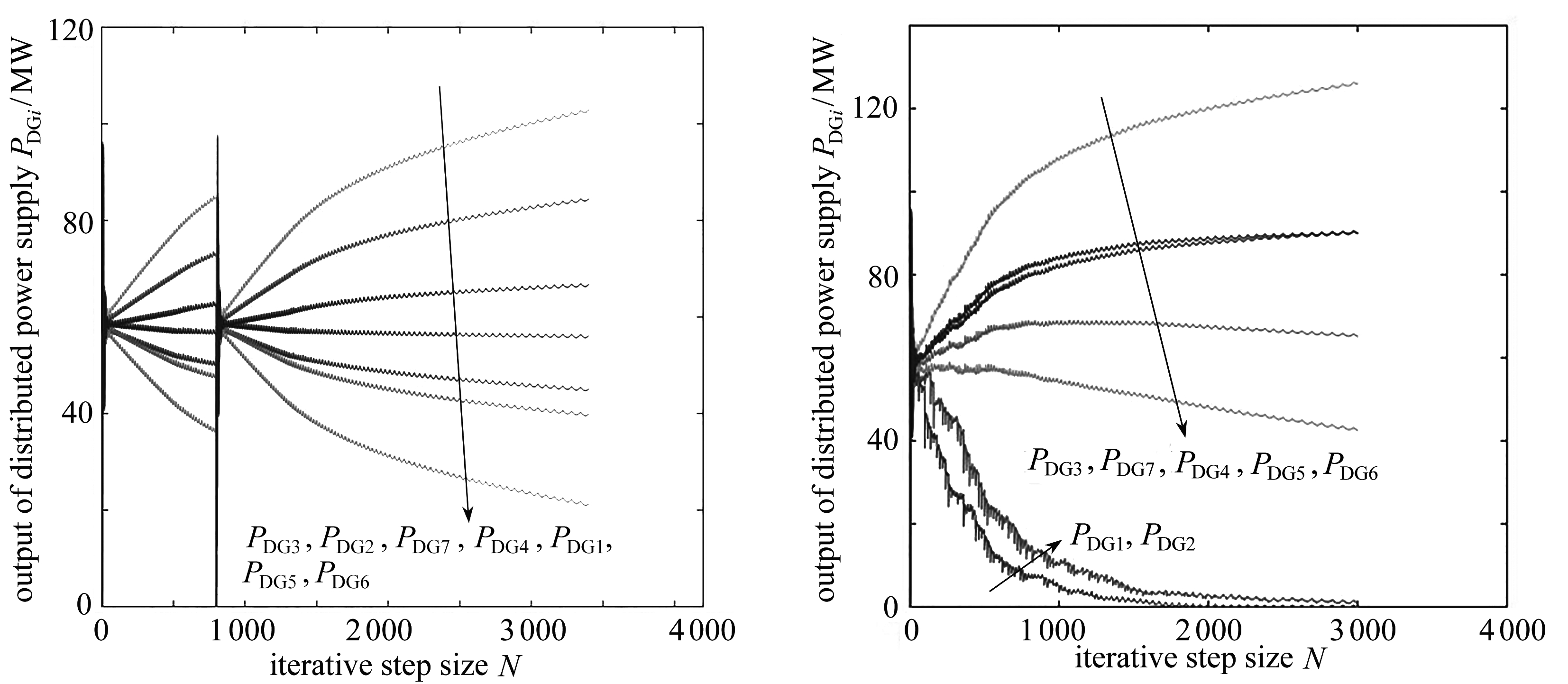
图4 信息中断情况下各分布式电源出力值图5 通信误码情况下各分布式电源出力值
Fig. 4 Outputs of different distributed generations under communication interrupts Fig. 5 Outputs of different distributed generations under communication errors
在考虑了通信中断情况后整个优化调度结果的收敛过程中,算法收敛的迭代次数有了较大增加,并且由于出现了通信中断后即时恢复的情况,各个发电单元出力出现了重置的情况.但随着算法迭代的不断进行,该算法最后仍然可以收敛到最优解,各分布式电源的出力值如表5所示.
表5 通信中断下各分布式电源出力值(单位: MW)
Table 5 Outputs of different distributed generations under communication interrupts(unit: MW)
PDG1PDG2PDG3PDG4PDG5PDG6PDG744.975 384.582 6102.596 456.531 539.909 521.218 566.773 5
此时,该结果与未发生通信中断情况下的优化结果一致.
在此情况下,最后的总成本仍为F=4 164.1$,考虑通信中断情况下的出力总成本也可达最优.由上述分析可知,通信中断的出现会导致整个优化过程迭代次数的增加,降低整个算法的求解效率,但依然可以保证收敛到最优解,说明该P2P优化调度算法在一定程度上可以避免通信中断的影响.
4.4 通信误码下算例分析
本小节设置了通信误码下的算例来分析通信误码对P2P优化调度的结果的影响.假设节点1与2之间的通信存在一定的误码率,为了反映通信误码对优化结果的影响,若在整个数值模拟过程中出现通信误码情况,则两节点之间传输的数据将产生一定的偏差,仿真结果如图5所示.
在考虑了通信误码情况后的整个优化调度结果的收敛过程中,由于节点1与2之间存在误码,随着算法的迭代进行,两节点的出力逐渐趋向于0.这意味着由于存在通信误码,1、2节点将不参与调度,整个调度任务将由其他几个节点完成,各发电节点单元的出力值如表6所示.
表6 通信误码下各分布式电源出力值(单位: MW)
Table 6 Outputs of different distributed generations under communication errors(unit: MW)
PDG1PDG2PDG3PDG4PDG5PDG6PDG702.390 4122.903 789.967 165.702 943.964 188.963 5
此时,各节点总出力∑PDGi=413.891 7 MW.最后的总成本为F=4 362.8$.这意味着在通信误码情况下,该调度结果准确性和经济性都有所下降.
5 结论与展望
本文在泛在电力物联网环境下,将P2P的理念用于建立分布式电源的去中心化调度架构,使分布式电源之间基于通信进行信息交互完成优化调度,结果表明:
1) 所提出的P2P优化调度算法具有较好的收敛速度和收敛性,同时可以较好地满足调度的准确性和经济性,为整个泛在电力物联网下的分布式电源能量管理提供了参考;
2) 该算法可以一定程度上避免优化过程中通信中断的影响,通信中断会在一定程度上降低算法的收敛速度,但并不会影响整个算法的收敛性.
泛在电力物联网是传统电力网络的延伸与拓展,分布式电源是其重要的组成部分.尽管本文论证了通信因素对P2P优化调度结果的影响,针对如何避免通信因素影响的问题,相关研究还未涉及,后续的研究中会进一步分析通信因素对P2P优化调度的影响机理.
致谢 本文作者衷心感谢南方电网科学研究院有限责任公司“基于广义能流优化监控的大用户参与多时间尺度售电市场策略及系统设计研究”项目对本文的资助.
[1] 张忠会, 胡国宝, 李瑞欣. 考虑电动汽车接入的分布式电源出力优化[J]. 电力系统保护与控制, 2018, 46(6): 120-127.(ZHANG Zhonghui, HU Guobao, LI Ruixin. Optimization of distributed generation output in electric vehicles integrating into distribution network[J]. Power System Protection and Control, 2018, 46(6): 120-127.(in Chinese))
[2] 孙宏斌, 郭庆来, 潘昭光. 能源互联网: 理念、架构与前沿展望[J]. 电力系统自动化, 2015, 39(19): 1-8.(SUN Hongbin, GUO Qinglai, PAN Zhaoguang. Energy internet: concept, architecture and frontier outlook[J]. Automation of Electric Power systems, 2015, 39(19): 1-8.(in Chinese))
[3] 姚建国, 高志远, 杨胜春. 能源互联网的认识和展望[J]. 电力系统自动化, 2015, 39(23): 9-14.(YAO Jianguo, GAO Zhiyuan, YANG Shengchun. Understanding and prospects of energy internet[J]. Automation of Electric Power Systems, 2015, 39(23): 9-14.(in Chinese))
[4] SUN Q, HAN R, ZHANG H, et al. A multiagent-based consensus algorithm for distributed coordinated control of distributed generators in the energy internet[J]. IEEE Transactions on Smart Grid, 2015, 6(6).
[5] HUG G, KAR S, WU C. Consensus + innovations approach for distributed multiagent coordination in a microgrid[J]. IEEE Transactions on Smart Grid, 2015, 6(4): 1893-1903.
[6] 吕朋蓬, 赵晋泉, 李端超, 等. 基于信息物理系统的孤岛微网实时调度的一致性协同算法[J]. 中国电机工程学报, 2016, 36(6): 1471-1480.(LÜ Pengpeng, ZHAO Jinquan, LI Duanchao, et al. A Consensus-based collaborative algorithm for real time dispatch of island microgrid in cyber physical system[J]. Proceedings of the CSEE, 2016, 36(6): 1471-1480.(in Chinese))
[7] 宋少群, 黄文英, 陈峰, 等. 基于合作博弈的分布式能源优化运行策略研究[J]. 电器与能效管理技术, 2018, 557(20): 21-27.(SONG Shaoqun, HUANG Wenying, CHEN Feng, et al. Design of distributed energy optimization operation strategy based on cooperative game[J]. Electrical & Energy Management Technology, 2018, 557(20): 21-27.(in Chinese))
[8] 季珉杰, 张沛超, 姚垚, 等. 采用基于市场控制的微网分布式能量优化方法[J]. 电力系统自动化, 2017, 41(15): 34-41.(JI Minjie, ZHANG Peichao, YAO Yao, et al. Distributed energy optimization method for microgrid using market-based control[J]. Automation of Electric Power Systems, 2017, 41(15): 34-41.(in Chinese))
[9] YU J, NI M, JIAO Y, et al. Plug-in and plug-out dispatch optimization in microgrid clusters based on flexible communication[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(4): 663-670.
[10] 杨志淳, 乐健, 刘开培, 等. 基于多智能体的含虚拟发电厂配电网的电压稳定性协调控制[J]. 电网技术, 2013, 37(7): 1922-1928.(YANG Zhichun, LE Jian, LIU Kaipei, et al. Coordinative voltage stability control based on multi-agent theory for distribution network with VPP[J]. Power System Technology, 2013, 37(7): 1922-1928.(in Chinese))
[11] 李克文, 高立克, 吴丽芳, 等. 配电网自动化通信方式分析与选择[J]. 广西电力, 2011, 34(5): 44-47.(LI Kewen, GAO Like, WU Lifang, et al. Analysis and choice of distribution automation communication mode[J]. Guangxi Electric Power, 2011, 34(5): 44-47.(in Chinese))
[12] 米阳, 刘红业, 宋根新, 等. 面向能源互联网的多能源局域网两层功率优化分配[J]. 电力自动化设备, 2018, 38(7): 1-10.(MI Yang, LIU Hongye, SONG Genxin, et al. Two-layer power optimization allocation of multi-energy local networks oriented to energy internet[J]. Electric Power Automation Equipment, 2018, 38(7): 1-10.(in Chinese))
[13] BINETTI G, DAVOUDI A, LEWIS F L, et al. Distributed consensus-based economic dispatch with transmission losses[J]. IEEE Transactions on Power Systems, 2014, 29(4): 1711-1720.
[14] 黄海煜, 于文娟. 考虑风电出力概率分布的电力系统可靠性评估[J]. 电网技术, 2013, 37(9): 2585-2591.(HUANG Haiyu, YU Wenjuan. Power grid reliability assessment considering probability distribution of wind farm power output[J]. Power System Technology, 2013, 37(9): 2585-2591.(in Chinese))
[15] 王健, 谢桦, 孙健. 基于机会约束规划的主动配电网能量优化调度研究[J]. 电力系统保护与控制, 2014, 42(13): 45-52.(WANG Jian, XIE Hua, SUN Jian. Research on energy optimization scheduling of active distribution network based on chance constrained programming[J]. Power System Protection and Control, 2014, 42(13): 45-52.(in Chinese))