引 言
建立数学模型来研究经济金融现象,揭示经济运行的内在规律已经引起了诸多学者的广泛关注．近几十年来,许多有关金融模型动力学的研究成果不断涌现．例如,Gao和Ma[1] 研究了一类金融模型的混沌和Hopf分支行为;Zhang等[2]讨论了一个金融混沌模型的随机Hopf分支现象；马军海和陈予恕[3-4] 详细分析了一类非线性金融模型的分支拓扑结构和全局复杂特性；Zhang等[5] 建立了时滞金融超混沌系统的稳定性条件；林勇新等[6]和Cai等[7]对复杂金融系统的混沌行为展开了详细的探讨；Ma和Bangura[8]揭示了经济金融系统的复杂特性．更多的关于金融模型的研究,可参见文献[9-16]．
我们知道,混沌现象经常出现在经济金融系统中．混沌行为的发生在一定程度上会造成经济秩序混乱,严重影响人们的日常生产生活．因此,控制金融模型的混沌现象引起了经济学家和数学家的高度重视．如何控制混沌现象的发生成为目前研究的一个焦点问题．过去的几十年,很多学者对此展开了研究．这里我们需要指出的是,前人大量的工作主要集中于对整数阶混沌模型的控制,对分数阶混沌模型的控制问题则研究得较少．
分数阶微积分是整数阶微积分的推广．由于长时间以来没有找到明确的物理意义和现实背景，分数阶微积分的发展一直比较缓慢．直到近几十年,经过诸多学者的不懈努力,分数阶微积分在自然科学和工程技术中得到广泛应用，特别是在电磁波、黏弹性系统、经济、生物、医学、保密通信等发挥了巨大的作用[9-11]．用分数阶微积分建立的数学模型比整数阶微积分模型更能准确地描述实际系统的动态响应，提高对动态系统的设计、表征和控制能力，更能准确地描述具有记忆特性和历史依赖性的物理变化．基于这种考虑， 我们认为很有必要建立分数阶金融模型来刻画我们生活的经济金融现象．
2001年,马军海和陈予恕[3-4]研究了如下金融模型:
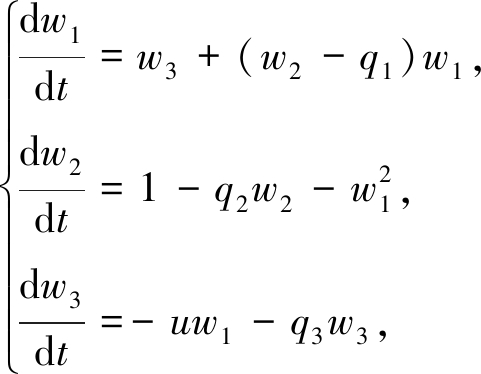
(1)
其中q1≥0代表储蓄量,q2≥0代表投资成本,q3≥0表示商品需求弹性,w1表示利率,w2表示投资需求,w3表示价格指数．诸多学者对模型(1)展开研究,取得了丰硕的成果[13-16]．
现实情况中,利率、投资需求及价格指数随着时间的变化不断发生改变,为了能更加精细地刻画利率、投资需求及价格指数不断变化的过程和揭示其中的变化规律．如在房地产市场中,按揭贷款利率、住房投资需求及住房的价格是相互影响的．为了较准确地描述它们之间的大范围的瞬时记忆特性和空间作用、刻画在三个量之间的整个物理过程,构建分数阶模型是一个重要的工具，根据以上讨论,我们建立如下分数阶金融模型:
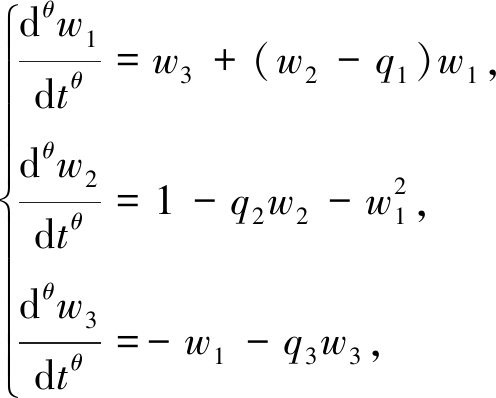
(2)
其中0<θ<1表示分数阶的阶数．研究发现:当θ=0.65,q1=0.6,q2=0.2,q3=1时,系统(2)出现混沌现象，见图1．
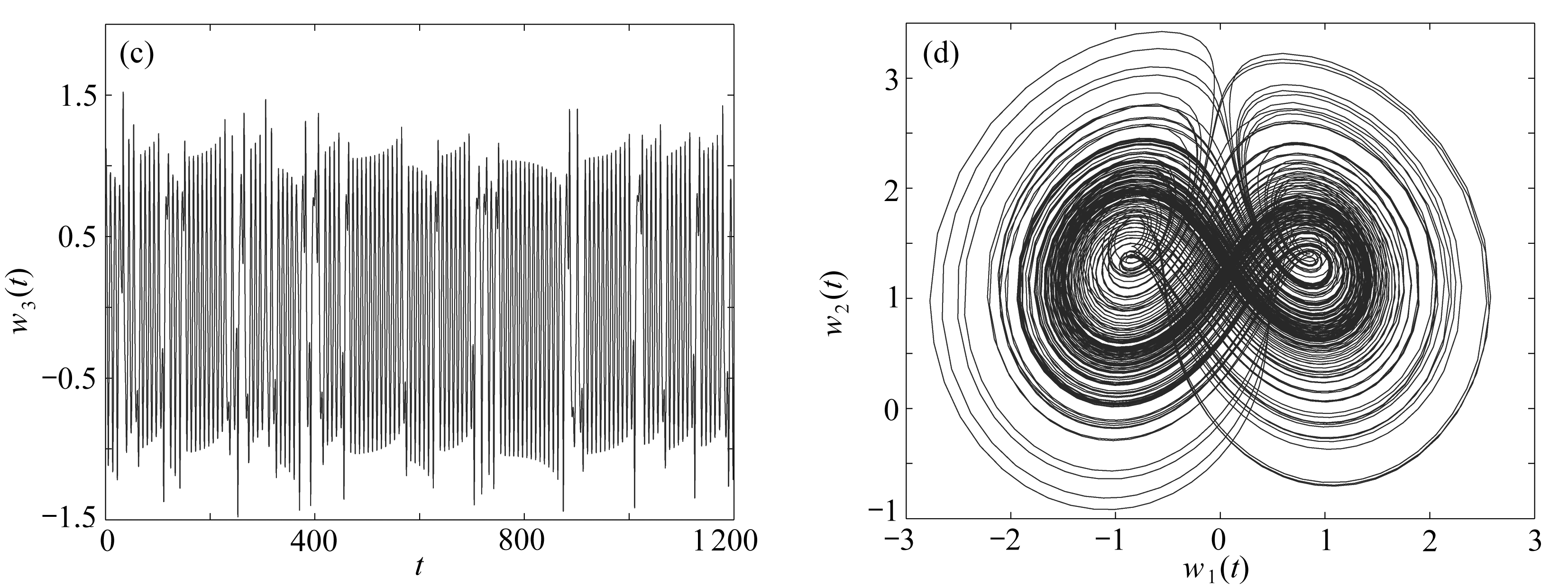
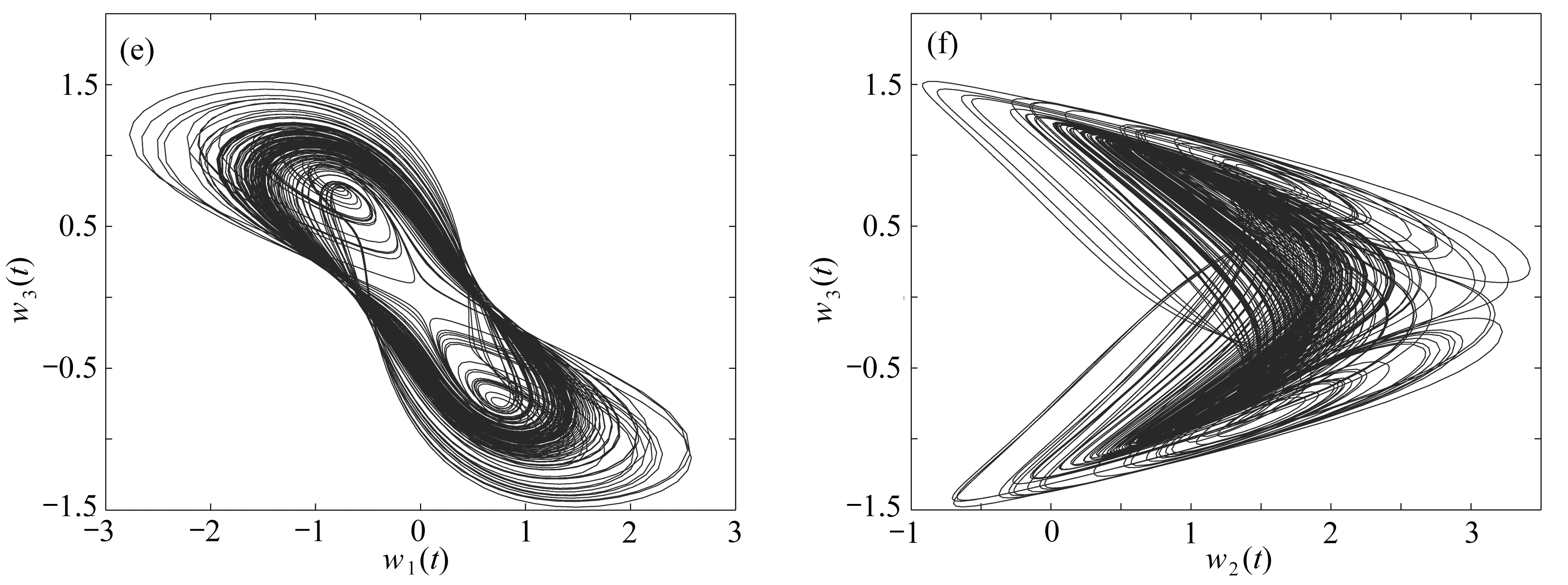
图1 系统(2)的相图和轨线图
Fig. 1 The phase diagrams and trajectory diagrams of system (2)
本文的主要目标是设计时滞反馈控制器控制混沌行为．
1 时滞反馈控制器的设计
如果条件
q2+q1q2q3>q3
(3)
成立,则系统(2)有唯一的平衡点:
(4)
如果条件
q2+q1q2q3<q3
(5)
成立,则系统(2)有三个平衡点:
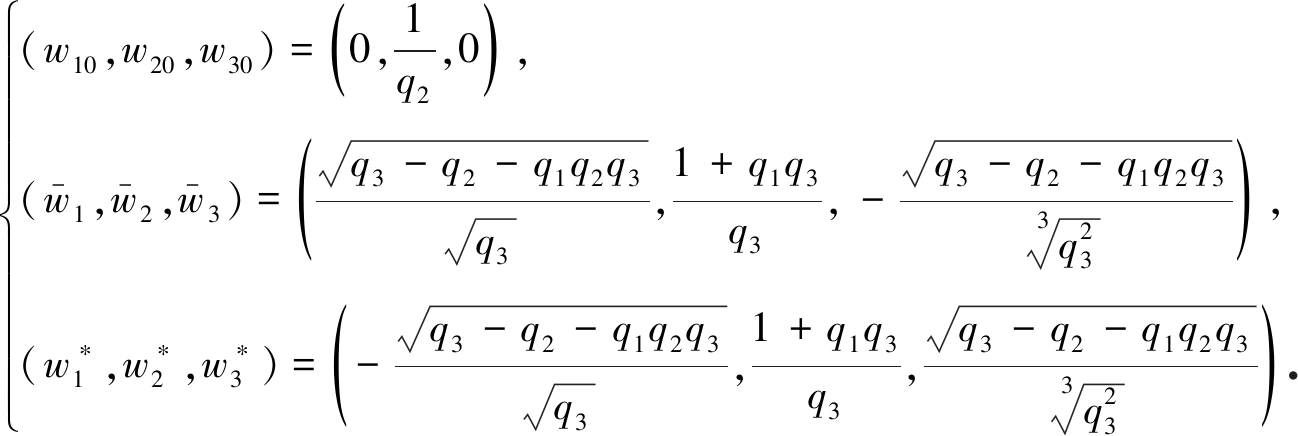
(6)
限于篇幅,本文仅考虑平衡点
对其他平衡点,我们类似考虑．
增加一个反馈控制器v(t)=κ[w1(t-τ)-w1(t)](κ是增益系数)到系统(2)的第一个方程,则受控的系统变为
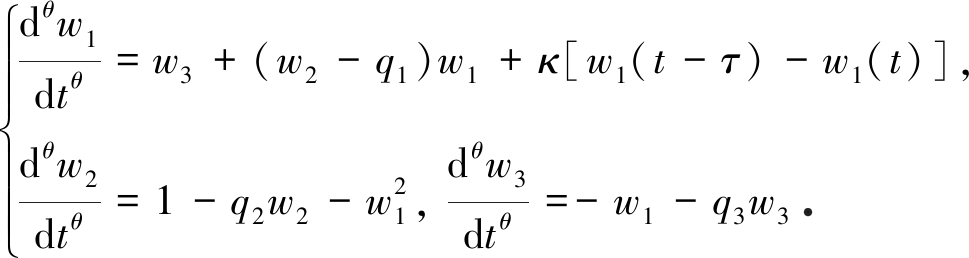
(7)
系统(7)在平衡点
处的线性化方程为
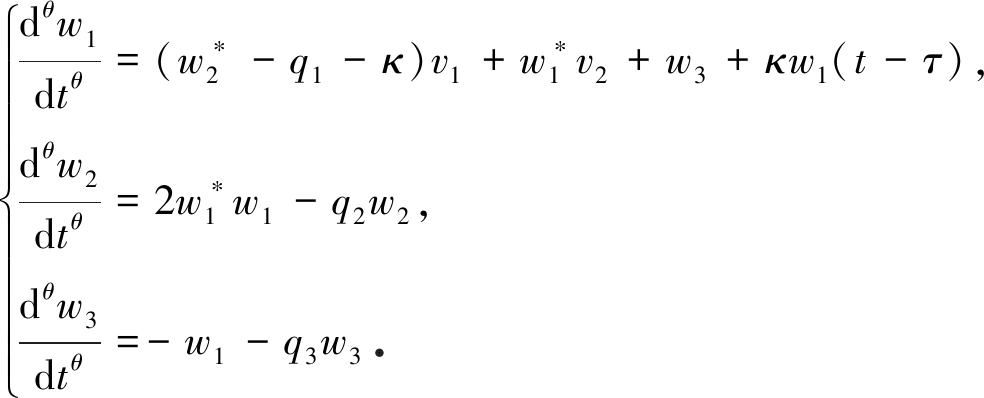
(8)
式(8)的特征方程为
(9)
于是
A1(s)+A2(s)e-sτ=0,
(10)
其中
A2(s)=-κ(s2θ+(q2+q3)sθ+q2q3)．
假设s=iχ=χ(cos(π/2)+isin(π/2))为方程(10)的根,则
(11)
其中
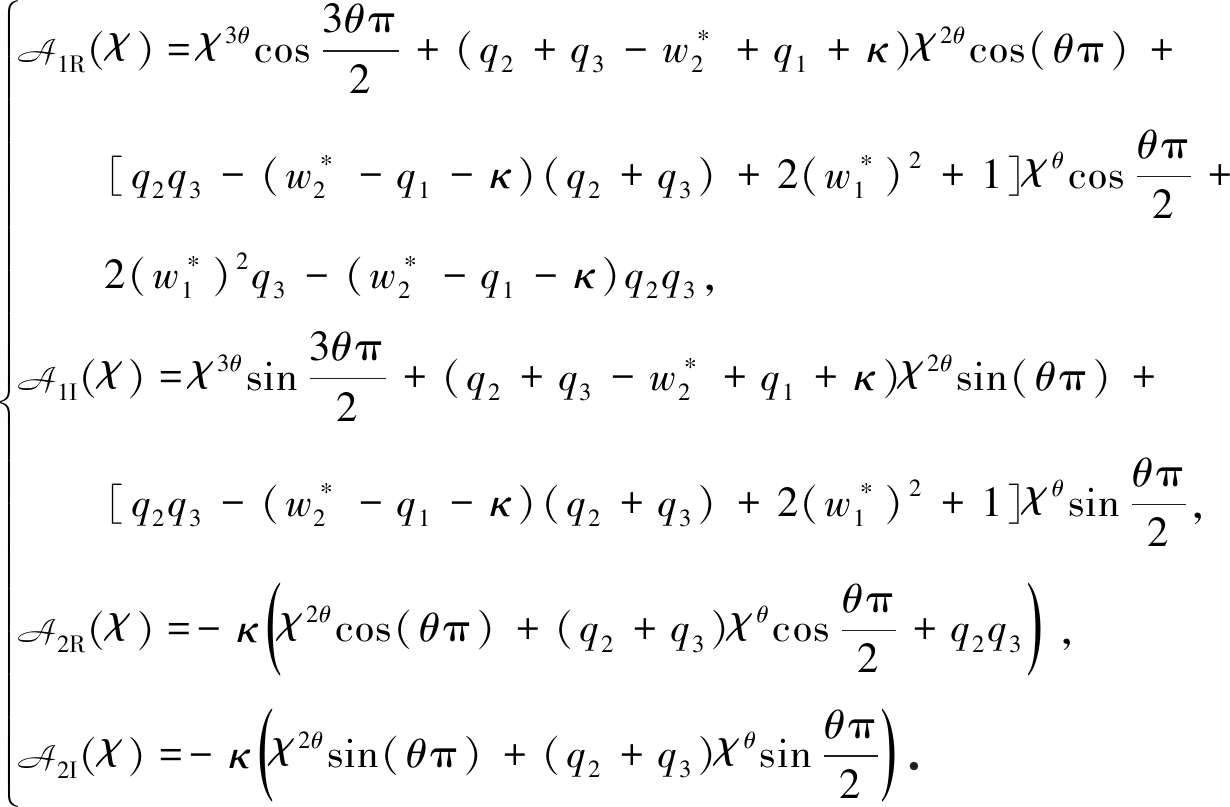
(12)
由式(11)得
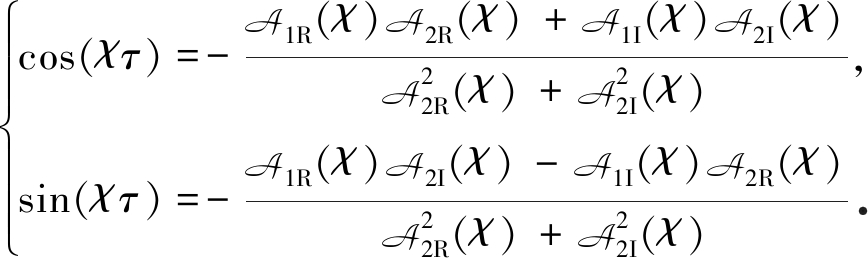
(13)
令
(14)
则
(15)
根据式(13)有
[A1R(χ)A2R(χ)+A1I(χ)A2I(χ)]2+[A1R(χ)A2I(χ)-A1I(χ)A2R(χ)]2=
(16)
注意到
[A1R(χ)A2R(χ)+A1I(χ)A2I(χ)]2=
(β1χ5θ+β2χ4θ+β3χ3θ+β4χ2θ+β5χθ+β6)2,
[A1R(χ)A2I(χ)-A1I(χ)A2R(χ)]2=(β7χ5θ+β8χ4θ+β9χ3θ+β10χ2θ+β11χθ)2,
其中
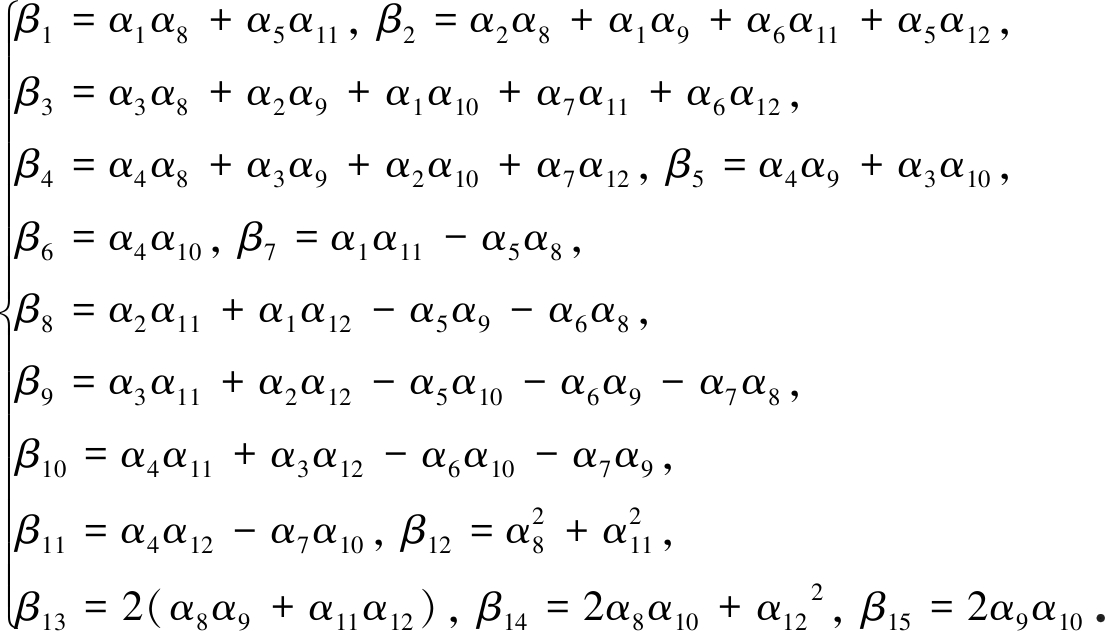
(17)
于是
γ1χ10θ+γ2χ9θ+γ3χ8θ+γ4χ7θ+γ5χ6θ+γ6χ5θ+
γ7χ4θ+γ8χ3θ+γ9χ2θ+γ10χθ+γ11=0,
(18)
其中
(19)
若γ11<0,则不难得到方程(18)至少有一个根．不失一般性,假设方程(18)有10个根,记为χi(i=1,2,…,10)，则由式(13)得
(20)
其中l=0,1,2,…,i=1,2,…,10．令
(21)
假设
(B1) I1J1+I2J2>0,
其中
引理1 若s(τ)=ζ(τ)+iυ(τ)是式(10)的根且满足ζ(τ0)=0,υ(τ0)=υ0,则
证明 由式(10)得
于是
其中
κ[2θs2θ-1+(q2+q3)θsθ-1]e-sτ,
G2(s)=A2(s)se-sτ．
因此
由假设(B1)得
证毕．
令
假设
(B2) δ1>0,δ1δ2>2δ3,δ3>0．
引理2 若τ=0且假设(B2)成立,则系统(2)是局部渐近稳定的．
证明 由τ=0,则式(10)可写成
λ3+δ1δ2+δ2λ+δ3=0．
根据假设(B2)得知方程(10)的所有根λi 满足|arg(λi)|>(θπ)/2(i=1,2,3)．因此,引理2的结论成立．证毕．
根据以上分析,我们得到如下结论．
定理1 如果条件(5)和假设(B1)和(B2)成立,则当τ∈[0,τ0)时,系统(2)的平衡点
是局部渐近稳定的．当τ=τ0时,系统(2)在平衡点附近出现Hopf分支．
2 计算机模拟
考虑下列金融系统:
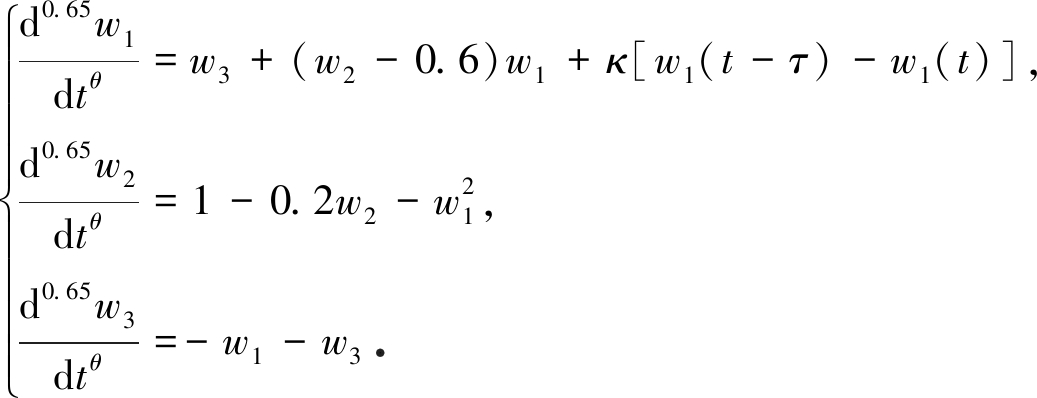
(22)
容易得到系统(22)有平衡点(-0.824 6,1.600 0,0.824 6)．定理1中的条件(5)和假设(B1)和(B2)满足．取κ=0.35，得到τ0≈0.745 5．当τ<τ0≈0.745 5时,平衡点(-0.824 6,1.600 0,0.824 6)是渐近稳定的；当τ>τ0≈0.745 5时,平衡点(-0.824 6,1.600 0,0.824 6)是不稳定的(见图2)；当τ=τ0≈0.745 5时,系统(22)在平衡点(-0.824 6,1.600 0,0.824 6)附近出现Hopf分支(见图3)．
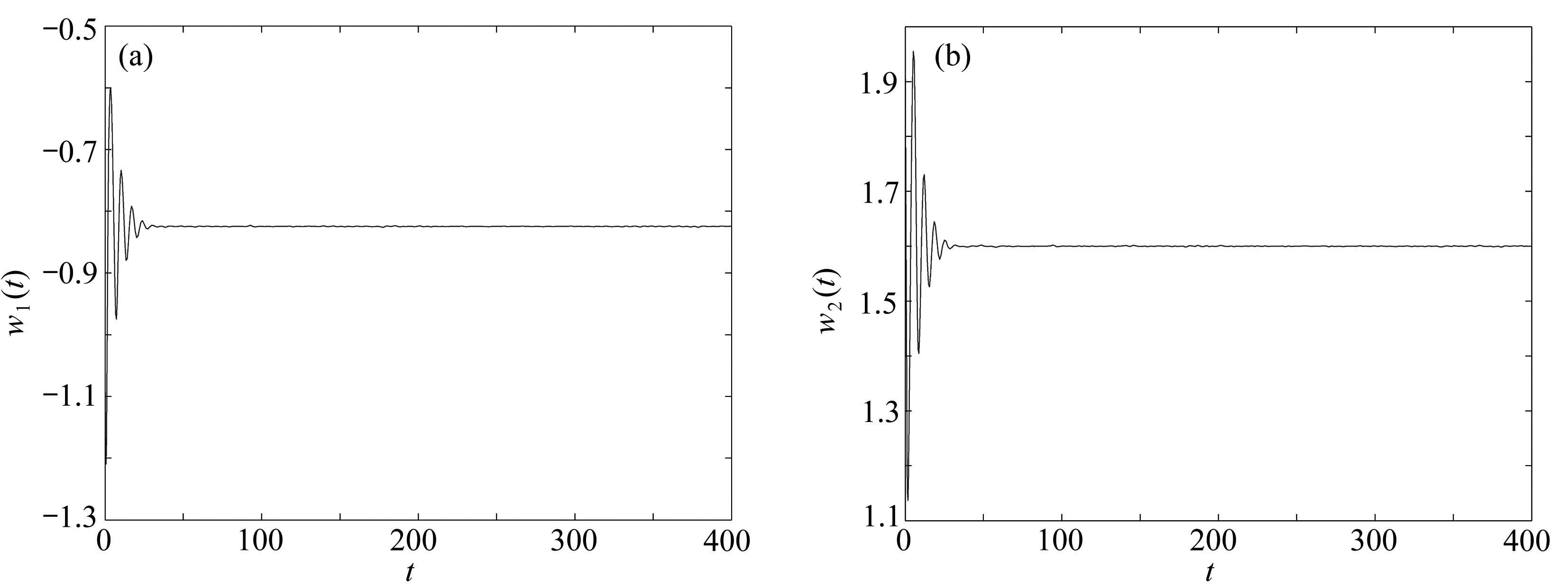
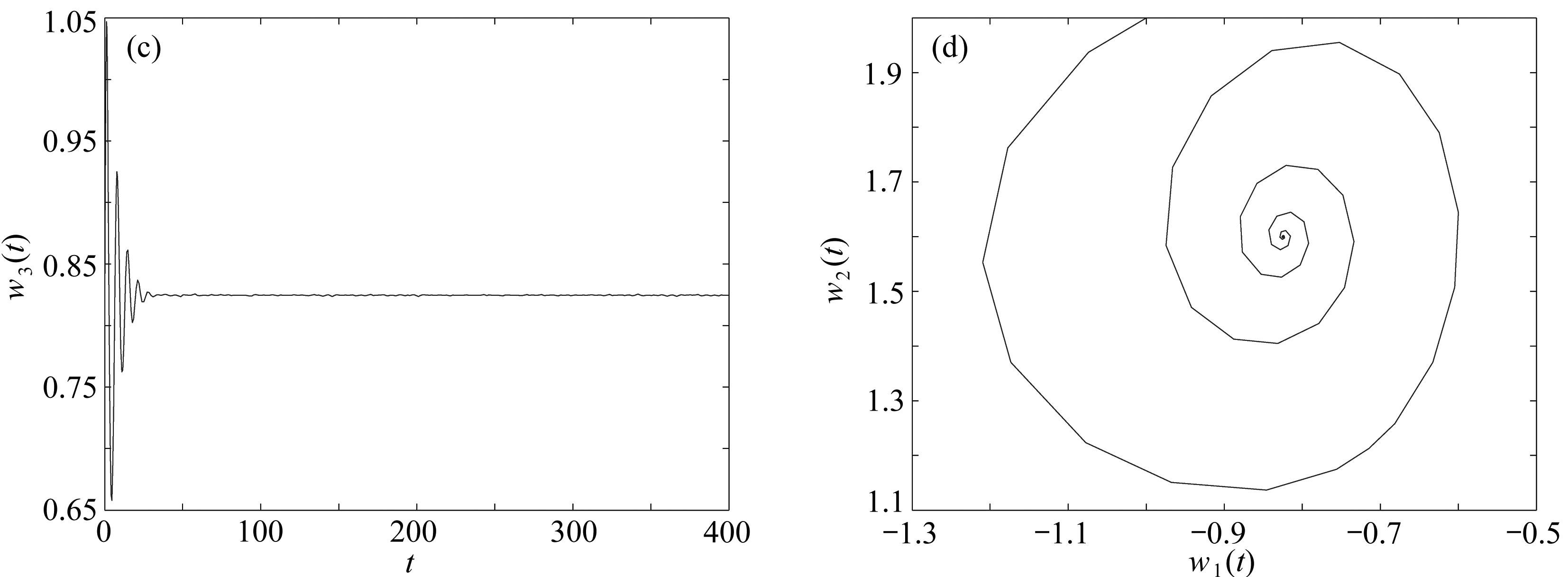
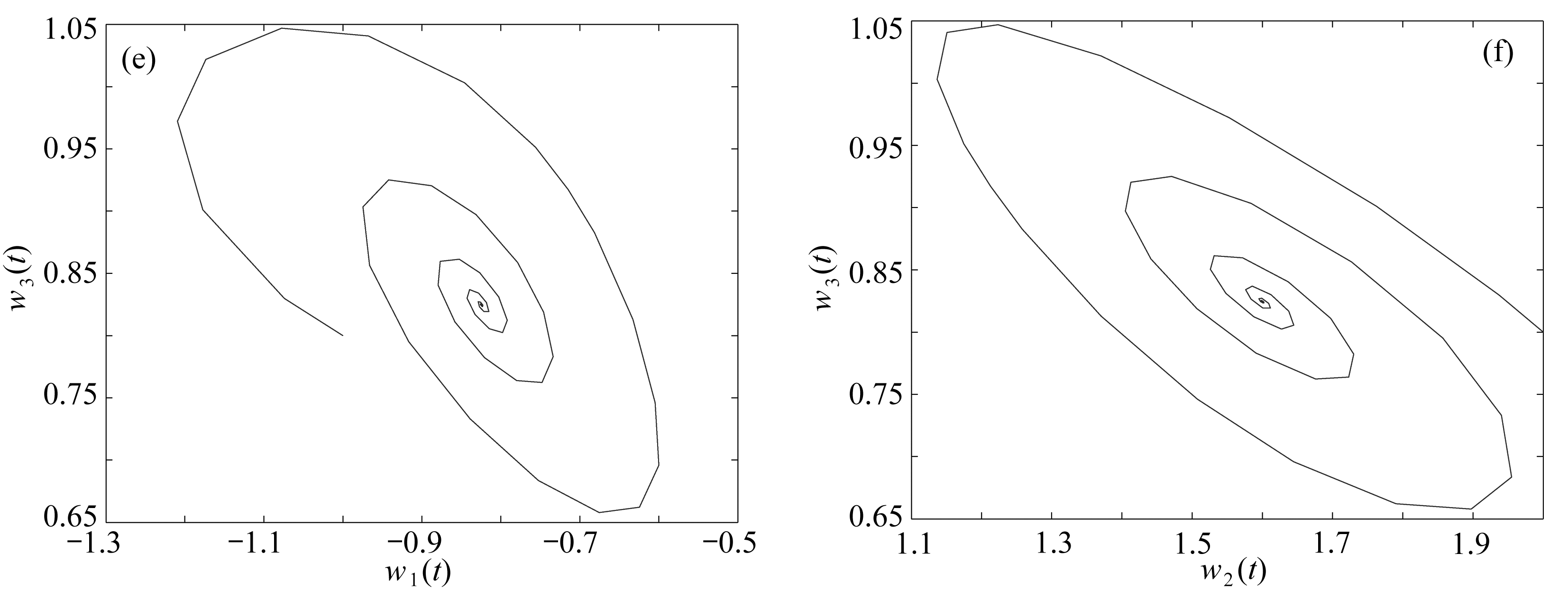
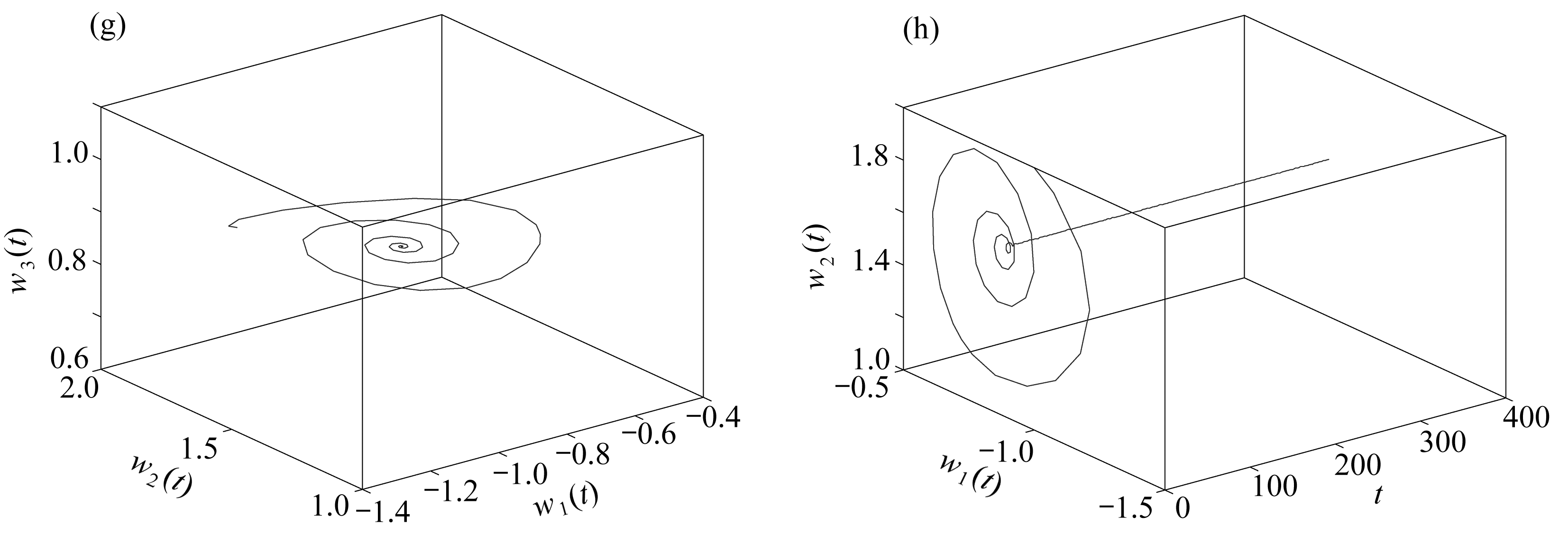
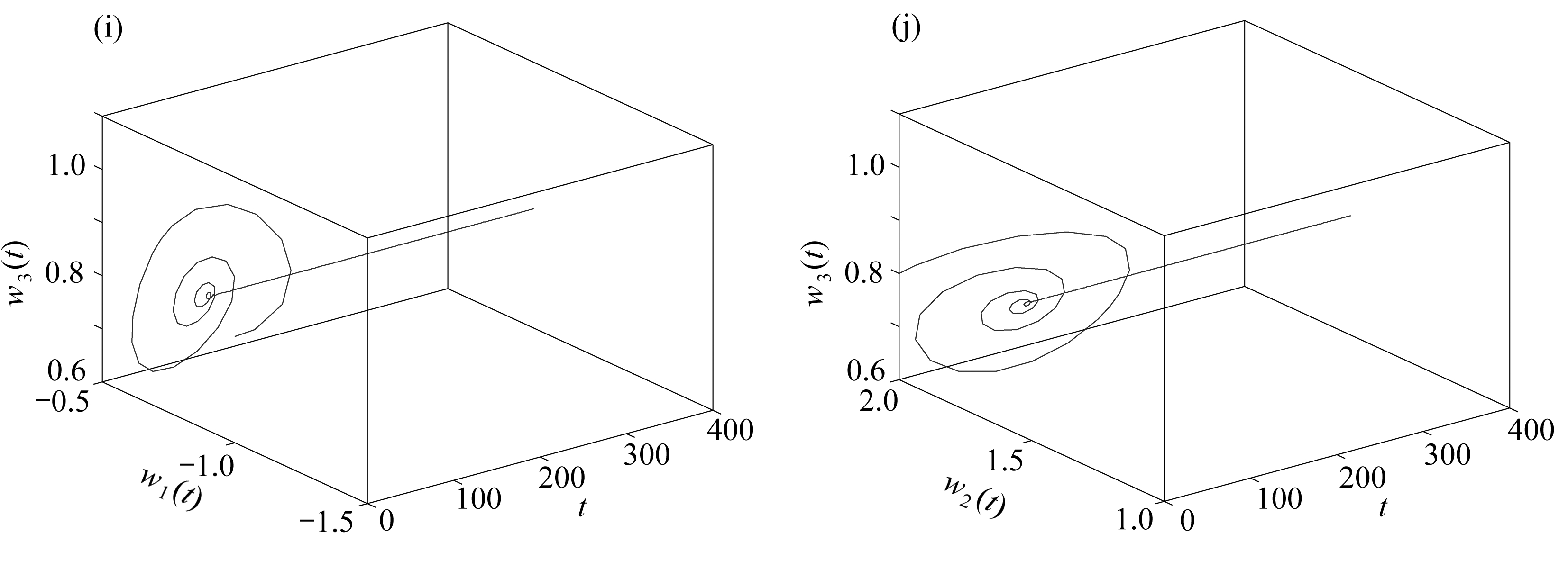
图2 系统(22)的相图和轨线图(τ=0.693 3<τ0≈0.745 5)
Fig. 2 The phase diagrams and trajectory diagrams of system (22) (τ=0.693 3<τ0≈0.745 5)
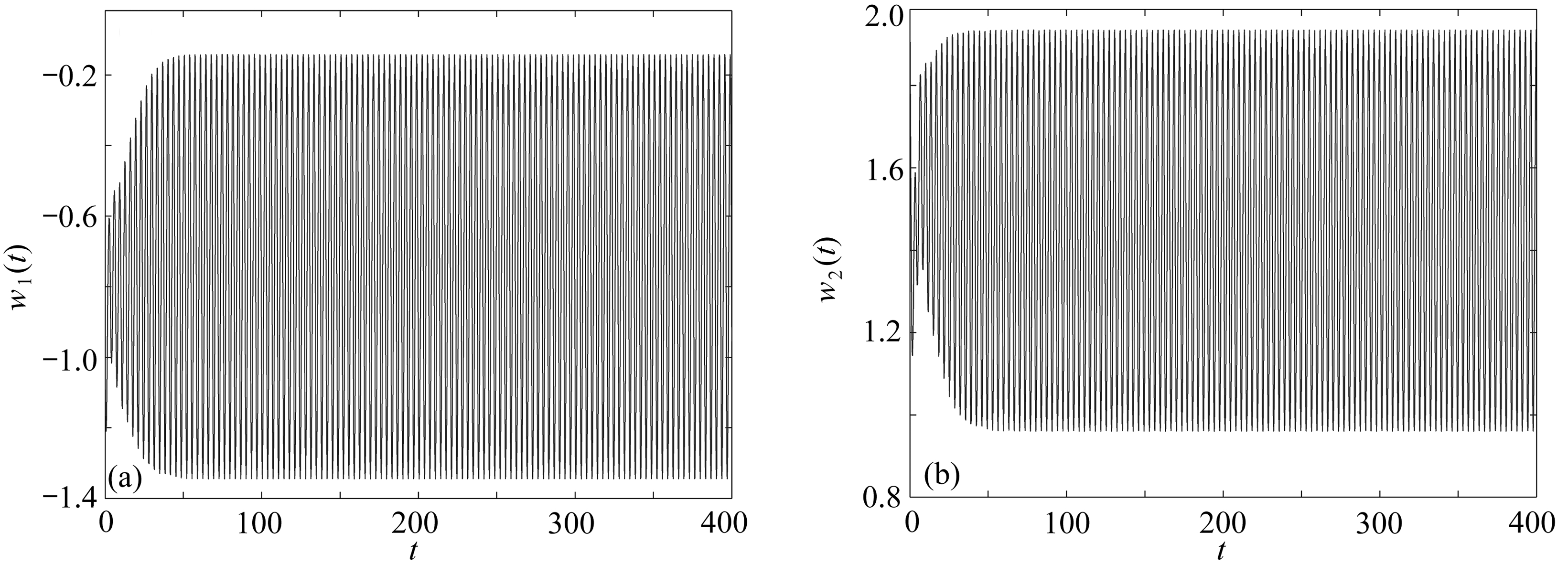
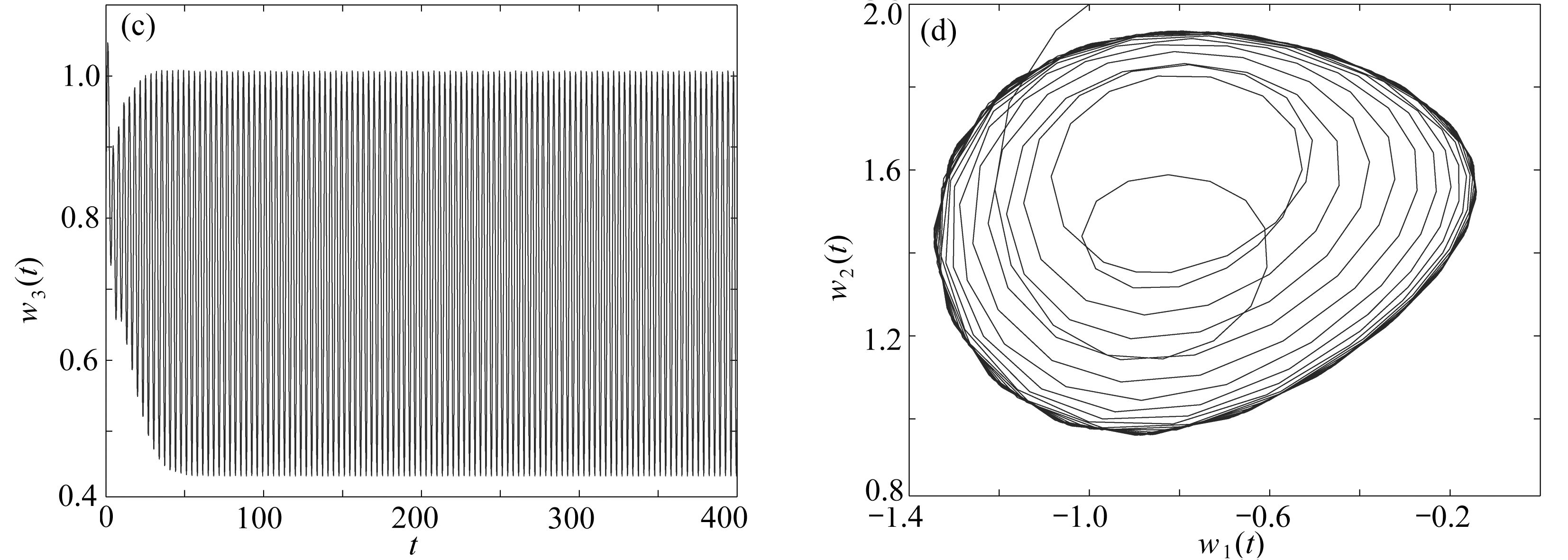
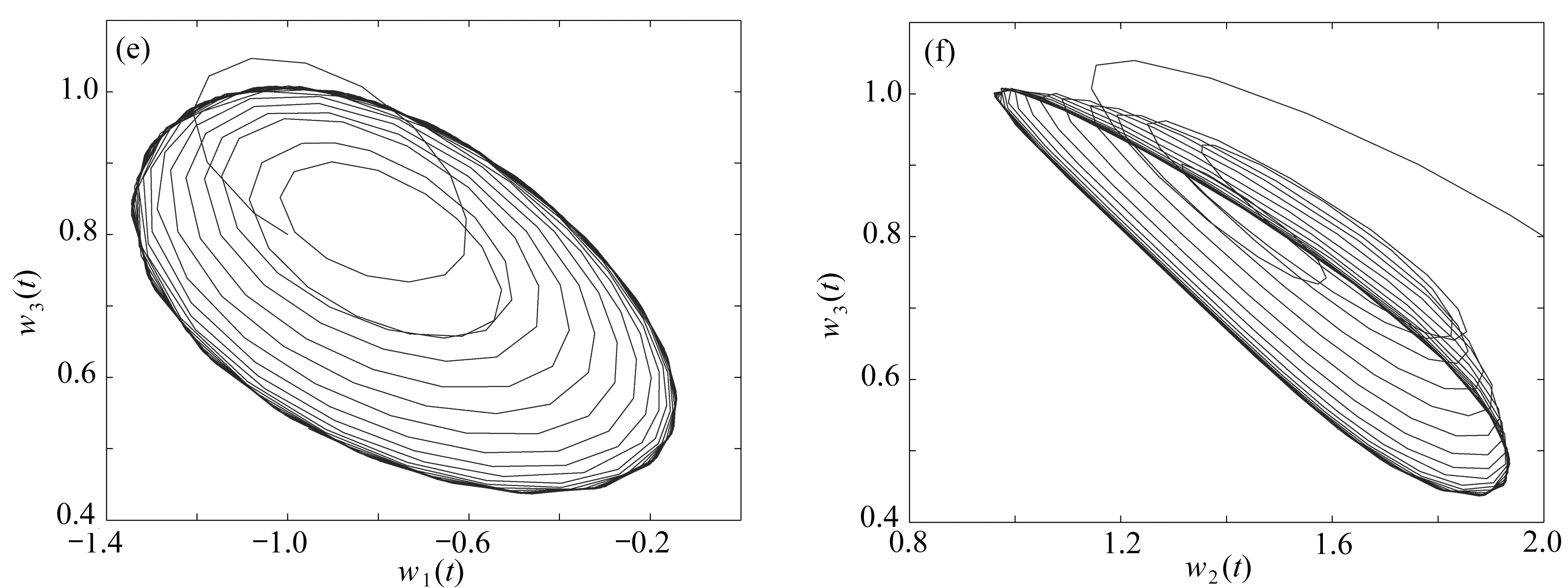
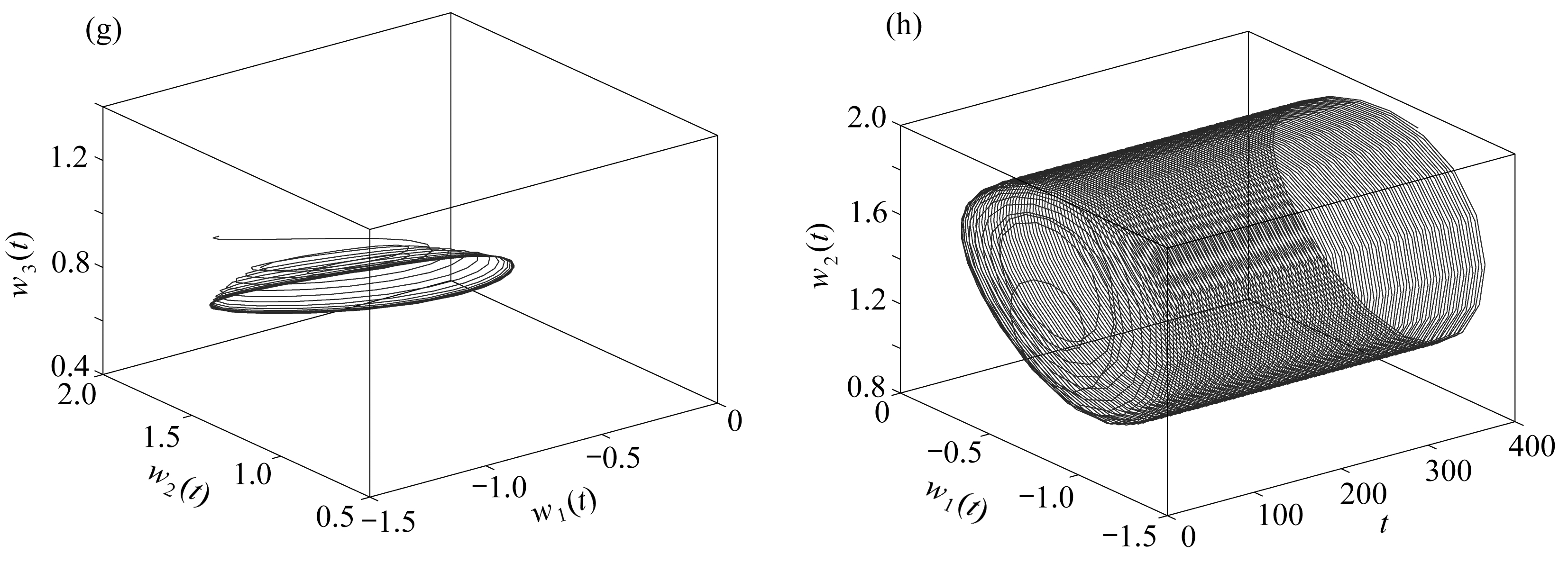
图3 系统(22)的相图和轨线图(τ=0.82>τ0≈0.745 5)
Fig. 3 The phase diagrams and trajectory diagrams of system (22) (τ=0.82>τ0≈0.745 5)
3 结 论
本文在前人工作的基础上构建了一个新的分数阶金融模型．通过设计恰当的时滞反馈控制器，有效地控制了该混沌金融模型的混沌行为,同时得到了受控金融模型的稳定性和Hopf分支存在的充分条件．运用MATLAB软件进行数值模拟，证实了理论分析的有效性．研究结果为维持金融稳定提供了一定的参考价值．
[1] GAO Q, MA J H. Chaos and Hopf bifurcation of a finance system[J]. Nonlinear Dynamics, 2009, 58(1/2): 209-216.
[2] ZHANG J G, NAN J, CHU Y D, et al. Stochastic Hopf bifurcation of a novel finance chaotic system[J]. Journal of Nonlinear Science and Applications, 2016,9(5): 2727-2739.
[3] 马军海, 陈予恕. 一类非线性金融系统分岔混沌拓扑结构与全局复杂性研究
[J]. 应用数学和力学, 2001, 22(11): 1119-1128.(MA Junhai, CHEN Yushu. Study for bifurcation topological structure and the global complicated character of a kind of non-linear finance system [J]. Applied Mathematics and Mechanics, 2001, 22(11): 1119-1128.(in Chinese))
[4] 马军海, 陈予恕. 一类非线性金融系统分岔混沌拓扑结构与全局复杂性研究
[J]. 应用数学和力学, 2001, 22(12): 1236-1242.(MA Junhai, CHEN Yushu. Study for bifurcation topological structure and the global complicated character of a kind of non-linear finance system [J]. Applied Mathematics and Mechanics, 2001, 22(12): 1236-1242.(in Chinese))
[5] ZHANG L L, CAI G L, FANG X L. Stability for a novel time-delay financial hyperchaotic system by adaptive periodically intermittent linear control[J]. Journal of Applied Analysis and Computation, 2017, 7(1): 79-91.
[6] 林勇新, 陈予恕, 曹庆杰. 一类金融系统行为的非线性混沌分析[J]. 应用数学和力学, 2010, 31(10): 1239-1248.(LIN Yongxin, CHEN Yushu, CAO Qingjie. Nonlinear and chaotic analysis of a financial complex system[J]. Applied Mathematics and Mechanics, 2010, 31(10): 1239-1248.(in Chinese))
[7] CAI G L, YAO L, HU P, et al. Adaptive full state hybrid function projective synchronization of financial hyperchaotic systems with uncertain parameters[J]. Discrete and Continuous Dynamical Systems(Series B), 2013, 18(8): 2019-2028.
[8] MA J H, BANGURA H I. Complexity analysis research of financial and economic system under the condition of three parameters’ change circumstances[J]. Nonlinear Dynamics, 2012, 70(4): 2313-2326.
[9] ABD-ELOUAHAB M S, HAMRI N E, WANG J W. Chaos control of a fractional-order financial system[J]. Mathematical Problems in Engineering, 2010, 2010: 270646. DOI:10.1155/2010/270646.
[10] HAJIPOUR A, TAVAKOLI H. Analysis and circuit simulation of a novel nonlinear fractional incommensurate order financial system[J]. Optik, 2016, 127(22): 10643-10652.
[11] HUANG C D, CAI L M, CAO J D. Linear control for synchronization of fractional-order time-delayed chaotic financial system[J]. Chaos, Solitons & Fractals, 2018, 113: 326-332.
[12] CHEN W C. Dynamics and control of a financial system with time-delayed feedbacks[J]. Chaos, Solitons & Fractals, 2008, 37: 1198-1207.
[13] ZHANG X B, ZHUA H L. Hopf bifurcation and chaos of a delayed finance system[J]. Complexity, 2019, 2019: 6715036.
[14] ZHANG R Y. Bifurcation analysis for a kind of nonlinear finance system with delayed feedback and its application to control of chaos[J]. Journal of Applied Mathematics, 2012, 2012: 316390.
[15] CHEN X L, LIU H H, XU C L. The new result on delayed finance system[J]. Nonlinear Dynamics, 2014, 78(3): 1989-1998.
[16] MIRCEA G, NEAMTU M, BUNDAU O, et al. Uncertain and stochastic financial models with multiple delays[J]. International Journal of Bifurcation and Chaos, 2012, 22(6): 19.
[17] 杜伟霞, 张思进, 殷珊. 一类对称碰撞系统的间歇混沌控制方法[J]. 应用数学和力学, 2018, 39(10): 1149-1158.(DU Weixia, ZHANG Sijin, YIN Shan. An intermittent chaos control method for a class of symmetric impact systems[J]. Applied Mathematics and Mechanics, 2018, 39(10): 1149-1158.(in Chinese))
[18] 张艳龙, 王丽, 石建飞. Duffing系统在双参数平面上的分岔演化过程[J]. 应用数学和力学, 2018, 39(3): 324-333.(ZHANG Yanlong, WANG Li, SHI Jianfei. Bifurcation evolution of Duffing systems on 2-parameter planes[J]. Applied Mathematics and Mechanics, 2018, 39(3): 324-333.(in Chinese))