引 言
在过去的几十年中,人工神经网络[1]由于在图像处理、模式识别、最优化问题等领域有着广泛的应用价值,受到了很多学者的关注.Cohen和Grossberg提出的C-G神经网络[2]被认为是最典型的神经网络,其他很多神经网络模型都是它的特殊情况.
混沌同步是指系统的轨道将收敛于另一系统轨道的同一值,它们之间保持步调一致,且这种步调一致是稳定的.研究表明,混沌同步在物理、力学、化学、生物、医学、信息科学、保密通讯、电子学等领域中具有极大的应用价值和巨大的市场潜力,引起了国内外学者的广泛关注[3-6].尽管有很多研究关注同步问题,但是大部分研究局限于无限时间内的渐进同步和指数同步[7-8].然而,人们希望系统能够在有限的、更短的时间内达到同步,进而可以节约时间和成本,还可以提高系统的抗干扰能力和鲁棒性[9-10].
适当地选择神经网络的参数和时延,神经网络可以展现出混沌特性.因此,神经网络尤其是C-G神经网络的同步得到了广泛关注和研究.文献[11]通过自适应控制实现了混合时滞的C-G神经网络的完全同步.文献[12]不需要求解线性矩阵不等式就可以实现不同C-G神经网络的自适应同步.近年来,由于了解到有限时间同步的优势,研究人员开始致力于混沌神经网络的有限时间同步问题.文献[13]提出了时滞反馈策略在有限时间内实现了C-G神经网络的同步.文献[14]研究了时变时滞耦合网络的有限时间同步.文献[15]实现了具有时滞的忆阻神经网络的有限时间同步.然而,大部分混沌神经网络有限时间同步的研究局限于完全同步、自适应同步.有限时间函数投影同步中驱动响应系统同步于尺度函数,是有限时间同步的一种扩展[16].尺度函数的复杂性和不可预测性,在保密通信领域可以很好地增强信息的安全性,因此具有极大的研究价值[17].但现有有限时间函数投影同步的研究并不多,也少见于保密通信的应用中,因此本文的研究可以在一定程度上填补该方向的空缺.此外,保密通信中所传递的信号往往会受到信道噪声和时延的影响,同步也会不可避免地受到影响,因此,为了更贴近真实环境,在同步中考虑扰动和时延具有很大意义[18-19].前面所提到的研究中,神经网络的参数都是已知确定的,但在实际情况中,系统参数往往无法预知,而未知参数会影响同步过程甚至使同步失败[20].
基于以上讨论,本文研究具有时延和随机扰动的未知C-G神经网络的有限时间函数投影同步在保密通信中的应用.与现有研究相比,本文的主要贡献在于: 1) 考虑保密通信的现实应用,构建系统模型,实现了驱动响应神经网络在有限时间内的函数投影同步; 2) 基于有限时间稳定性定理和Lyapunov稳定性理论设计控制策略和参数更新率,实现了同步的同时实现参数辨识; 3) 利用仿真实验,验证了所提方法在保密通信中应用的可行性.
1 网络模型与预备条件
考虑具有时延的C-G神经网络作为驱动系统,节点的状态方程描述如下:
dx(t)=-D(x(t))[A(x(t))-Bf(x(t))-Cg(x(t-τ))+J]dt,
(1)
式中,x(t)=[x1(t),x2(t),…,xn(t)]T∈Rn是n个神经元构成的状态向量;D(x(t))=diag[d1(x1(t)),d2(x2(t)),…,dn(xn(t))]为放大函数;A(x(t))=[a1(x1(t)),a2(x2(t)),…,an(xn(t))],适当选择该函数可使得式(1)的解有界;B=(bij)n×n,C=(cij)n×n为连接权重矩阵;J=[J1,J2,…,Jn]T表示外部常值输入向量;f和g为神经元激活函数且
f(x(t))=[f1(x1(t)), f2(x2(t)),…, fn(xn(t))]T∈Rn,
g(x(t-τ))=[g1(x1(t-τ)),g2(x2(t-τ)),…,gn(xn(t-τ))]T∈Rn,
其中,τ>0表示传输时延.
对于驱动系统 (1), 具有随机扰动和时延的未知响应系统可表示如下:
H(t,y(t)-m(t)x(t),y(t-τ)-m(t-τ)x(t-τ))dW,
(2)
式中,![]() 和
和![]() 是连接权重矩阵的估计,且
是连接权重矩阵的估计,且![]() 是n维Brown运动;H(t,u,v)=[h1(t,u,v),h2(t,u,v),…,hn(t,u,v)]T为噪声强度矩阵,m(t)为尺度函数;U=[u1,u2,…,un]为控制器向量.
是n维Brown运动;H(t,u,v)=[h1(t,u,v),h2(t,u,v),…,hn(t,u,v)]T为噪声强度矩阵,m(t)为尺度函数;U=[u1,u2,…,un]为控制器向量.
为了研究问题方便,给出相关的假设和引理.
假设1 存在常数![]() 使得
使得![]() 对于x,y,m∈R成立(i=1,2,…,n).
对于x,y,m∈R成立(i=1,2,…,n).
假设2 对于任意i=1,2,…,n,存在正数ri>0,使得![]() 对于x,y,m∈R且y≠mx成立.
对于x,y,m∈R且y≠mx成立.
假设3 对于任意i=1,2,…,n,存在常数![]() 和
和![]() 使得
使得![]() 对于x,y,m∈R且y≠mx成立.
对于x,y,m∈R且y≠mx成立.
假设4 对于噪声强度函数矩阵H(t,x,y),存在两个正定矩阵P1,P2,使得trace[HT(t,x,y)H(t,x,y)]≤xTP1x+yTP2y对于(t,x,y)∈R+×Rn×Rn成立,且H(t,0,0)≡0.
为了得到主要结果,下面给出关于随机微分方程的必要概念和引理.考虑下面的n维随机微分时滞方程:dx(t)=f(x(t),x(t-τ),t)dt+σ(x(t),x(t-τ),t)dW(t).选择初始值![]() 在t≥0上存在唯一解x(t,ξ).此外, f(x,y,t)和σ(x,y,t)在(x,y)是局部有界的并在t上一致有界.对于V∈C2,1(Rn×R+;R+),定义LV为
在t≥0上存在唯一解x(t,ξ).此外, f(x,y,t)和σ(x,y,t)在(x,y)是局部有界的并在t上一致有界.对于V∈C2,1(Rn×R+;R+),定义LV为
LV=∂V/∂t+∂V/∂x·f+(1/2)trace[σT(∂2V/∂xi∂xj)σ],
其中
∂V/∂x=(∂V/∂x1,∂V/∂x2,…,∂V/∂xn).
引理1[12] 对于向量x,y∈Rn和正定矩阵G∈Rn×n,矩阵不等式2xTy≤xTGx+yTG-1y成立.
引理2 如果m1,m2,…,mn是正数且r>1,则
引理3[21] 假设连续正定函数V(t)满足以下微分不等式:
其中c>0,0<η<1是两个常数.则对于任意给定t0,V(t)满足以下不等式:
V1-η(t)≤V1-η(t0)-c(1-η)(t-t0), t0≤t≤t1,
且
2 控制器设计与同步分析
定义1 设计合适控制器,如果存在常数T>0,使得
(3)
其中‖·‖表示向量范数,则称神经网络(1)和神经网络(2)实现有限时间函数投影同步.
注1 如果尺度函数选择为非零的常数:θi,1或-1,则该同步问题就转化为投影同步、完全同步和反同步问题.
基于定义1,可得到同步误差e(t)=y(t)-m(t)x(t),则误差系统为
m(t)D(x(t))Cg(x(t-τ))-[D(y(t))-m(t)D(x(t))]J-
(4)
设计混合控制器和其中的参数更新率如下:
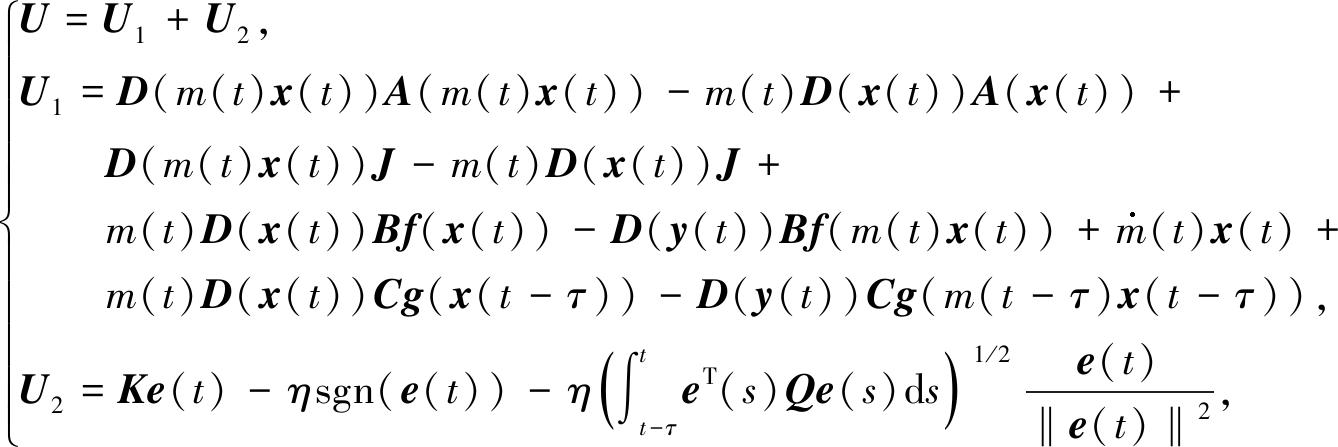
(5)
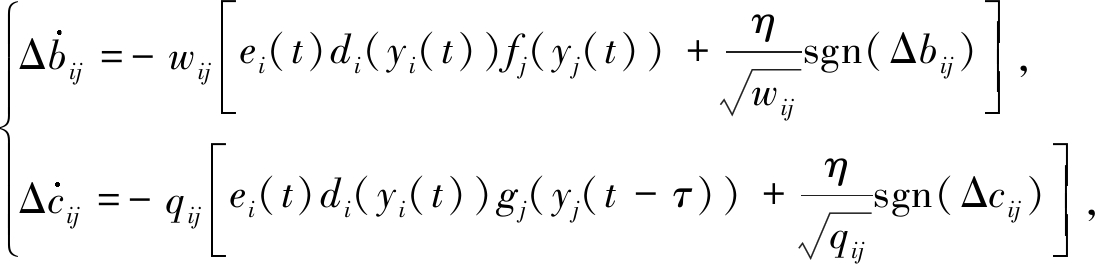
(6)
其中K=diag(k1,k2,…,kn)>0是待定的对角常数矩阵,η>0是一个可调常数.因此,在控制器(5)的作用下,误差系统为
D(y(t))Bf(e(t))+D(y(t))Cg(e(t-τ))+D(y(t))ΔBf(y(t))+
D(y(t))ΔCg(y(t-τ))-D(e(t))J-Ke(t)-ηsgn(e(t))-
(7)
其中
f(e(t))=f(y(t))-f(m(t)x(t)),
g(e(t-τ))=g(y(t-τ))-g(m(t-τ)y(t-τ)),
D(e(t))=D(y(t))-D(m(t)x(t)).
定理1 若假设1~4成立,则正定矩阵Q,K满足
(8)
(9)
则在控制策略(5)和(6)的作用下,驱动神经网络(1)和响应神经网络(2)可以实现有限时间函数投影同步,且
(10)
其中
此外,对于i, j=1,2,…,n,有
意味着未知参数可在有限时间内被辨识.
证明 构造Lyapunov-Krasovskii函数如下:
(11)
其中Q是一正定矩阵.
基于It 准则, 可以得到dV(e,t)=LV(e,t)+eT(t)H(t,e(t),e(t-τ))dW,其中
准则, 可以得到dV(e,t)=LV(e,t)+eT(t)H(t,e(t),e(t-τ))dW,其中
D(y(t))Bf(e(t))+D(y(t))Cg(e(t-τ))-
(D(y(t))-D(m(t)x(t)))J-Ke(t)-ηsgn(e(t))-
根据假设1,可得
其中
根据假设2~4,可得
其中
根据引理2,得到
eT(t-τ)Qe(t-τ)-eT(t)Ke(t)-ηeT(t)sgn(e(t))-
根据定理1,得到
根据引理2,得到
根据引理3可知, 在混合控制器(5)和自适应律(6)的作用下,驱动神经网络(1)和响应神经网络(2)能够在有限时间内实现函数投影同步,并且同步过渡时间满足式(10).
注2 从定理1中的证明中可以得出,ki和η越大同步越快,η影响同步的时间,ki决定是否能够实现同步.然而,控制输入U与η成比例, η越大U越大.因此,需要合理选择η使得收敛时间T较短,而控制输入U不是很大.
如果D(x(t))≡diag(1,…,1),t≥0,模型(1)就转变为下面的细胞神经网络:
dx(t)=(-A(x(t))+Bf(x(t))+Cg(x(t-τ))-J)dt.
(12)
相应地,响应神经网络可表示为
H(t,y(t)-m(t)x(t),y(t-τ)-m(t-τ)x(t-τ))dW.
(13)
在这种情况下,假设1可以被满足.从定理1中可以得到如下推论.
推论1 若假设2~4成立,正定矩阵Q,K满足
(14)
(15)
那么设计如下的控制策略:
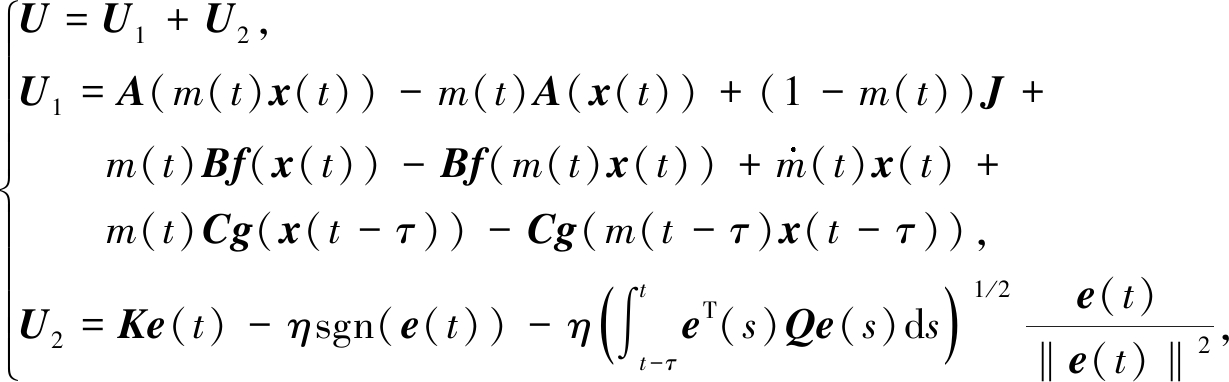
(16)
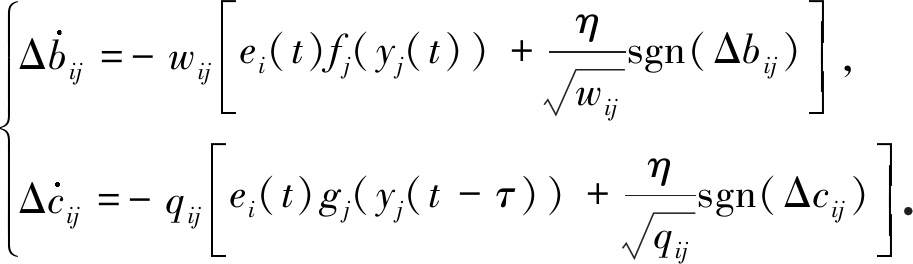
(17)
则驱动神经网络(12)和响应神经网络(13) 可以实现有限时间函数投影同步,且
其中
推论2 若假设1~4成立,且![]() 使用控制器(5), 驱动响应网络可在有限时间内实现函数投影同步,且
使用控制器(5), 驱动响应网络可在有限时间内实现函数投影同步,且
其中
3 数 值 仿 真
为了验证理论分析,考虑驱动神经网络(1)和响应神经网络(2)具有如下参数:
设置初值x(0)=[1,-1]T,噪声强度函数矩阵为
H(t,e(t),e(t-τ))=h0diag(e1(t)-e1(t-τ),e2(t)-e2(t-τ)).
同时,假设W=[W1,W2]T是一个二维的Brown运动,则H(t,e(t),e(t-τ))满足局部Lipschitz条件和线性增长条件,![]()
![]() 所有假设均成立.根据定理1,选择η=0.1,k1=k2=20.
所有假设均成立.根据定理1,选择η=0.1,k1=k2=20.
选择未知参数和反馈增益的初始值为bij(0)=cij(0)=0.1, λi=10,i, j=1,2.设置wij=qij=5,m(t)=1.5sin(0.5πt).图1显示在控制器作用下,驱动-响应神经网络的误差系统快速收敛为零,表示驱动-响应神经网络实现了有限时间函数投影同步.图2显示未知参数在有限时间内自适应地辨识至真实值.该仿真实验验证了所提控制策略的有效性和可行性.
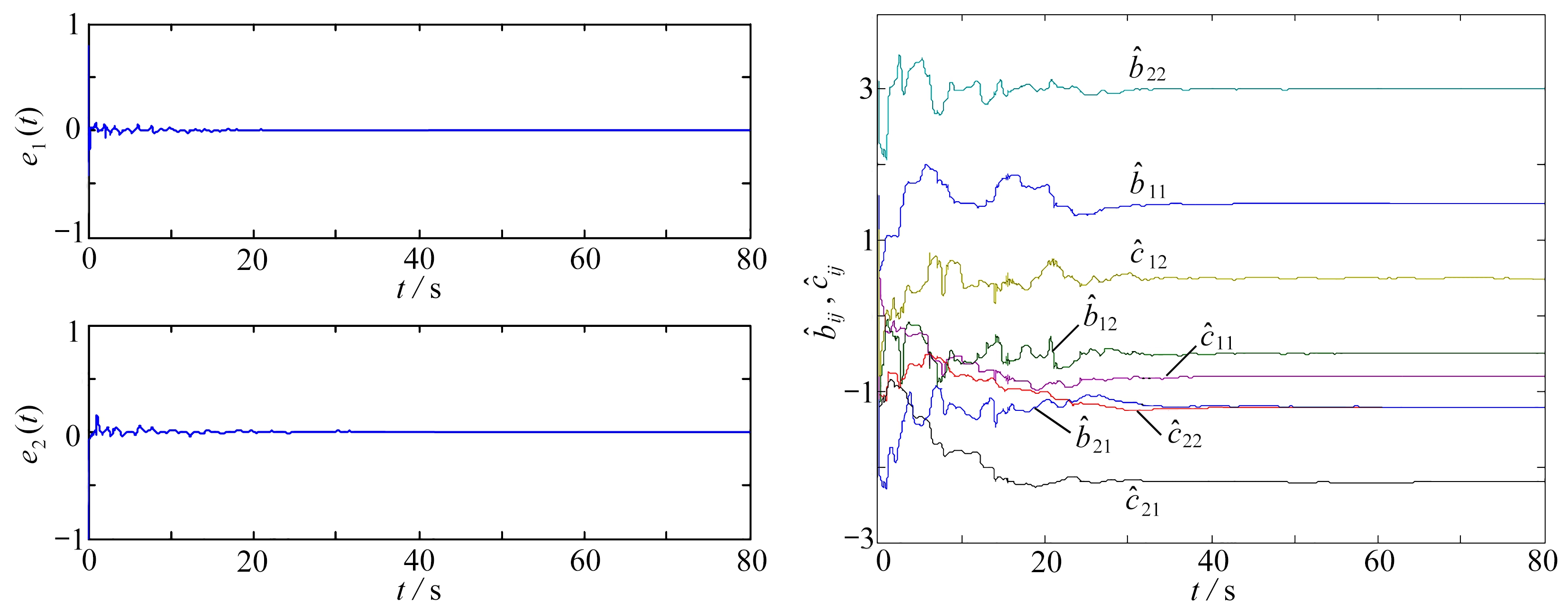
图1 同步误差 图2 未知参数![]()
Fig. 1 Time evolutions of synchronization errors Fig. 2 Dynamical behaviors of unknown ![]()
4 保密通信应用
混沌保密通信中,混沌系统作为发送端(驱动系统)载入要传送的有效信号生成混沌传输信号,传送至接收端(响应系统).当驱动响应系统同步时,有效信号才能在接收端被提取. 使用混沌系统传输信号的主要原因是混沌系统具有难预测性,不易被破解.
现有的混沌保密通信中大多使用完全同步来恢复有效信号.然而,函数投影同步可以极大地增强不可预测性,每次可以设计不同的投影函数m(t),使得攻击方无法预测两个网络之间的同步关系,从而大大增强信息的安全性.为了更快更及时地传送信息,希望发射端和接收端能够在有限的、很短的时间内达到同步,因此有限时间同步的应用更加有价值.此外,鉴于被传送的信息不可避免地会受到信道噪声、时延等随机因素的影响,因此,所设计的保密通讯策略应考虑时延因素,且具有较好的抗扰性.
下面将本文所提具有时延和随机扰动的未知C-G神经网络的有限时间函数投影同步方法应用于保密通信中.图3为保密通信系统框图.
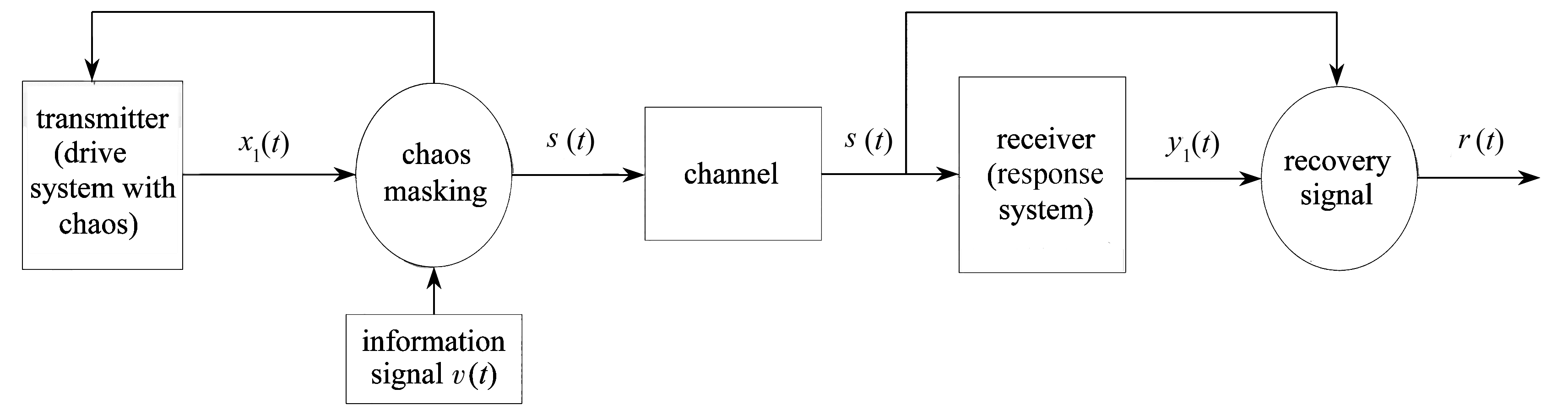
图3 保密通信系统
Fig. 3 The secure communication system based on the finite-time function projective synchronization
图3中,v(t)为待传输的有效信号.系统传输信号为s(t)=x1(t)+εv(t).发送端(驱动系统)可描述为
dx(t)=-D(x(t))[A(x(t))-Bf(x(t))-Cg(x(t-τ))+V(t)]dt,
其中V(t)=(εv(t),0)T是信息矩阵.设置ε=0.1使得有效信号的能量远小于混沌载波信号.相应地,接收端(响应系统)设置为
H(t,e(t),e(t-τ))dW,
其中
H(t)=(-y1(t)/m(t)+s(t),-y2(t)/m(t)+x2(t))T,
控制器和未知参数更新率设置如式(5)、(6).有限时间函数投影同步实现时,状态y1(t)趋近于m(t)x1(t),其中m(t)是提前定义的或者任意非零的尺度函数.被传递的有效信号可以通过转换r(t)=ε-1(s(t)-y1(t)/m(t))恢复得到.
本节中,设置的参数和函数与第3节数值仿真中相同.选择非零尺度函数为m(t)=1.5× sin(0.5πt)+π,任意选择有效信号为v(t)=sin(t).图4显示了仿真结果.图4(a)中,同步误差e1,e2迅速收敛为零.图4(b)、(c)显示了有效信号v(t)和恢复信号r(t)的演化过程.图4(d)显示了有效信号和恢复信号之间的误差,从仿真结果中可以看出,有效信号在很短的有限时间内被恢复.
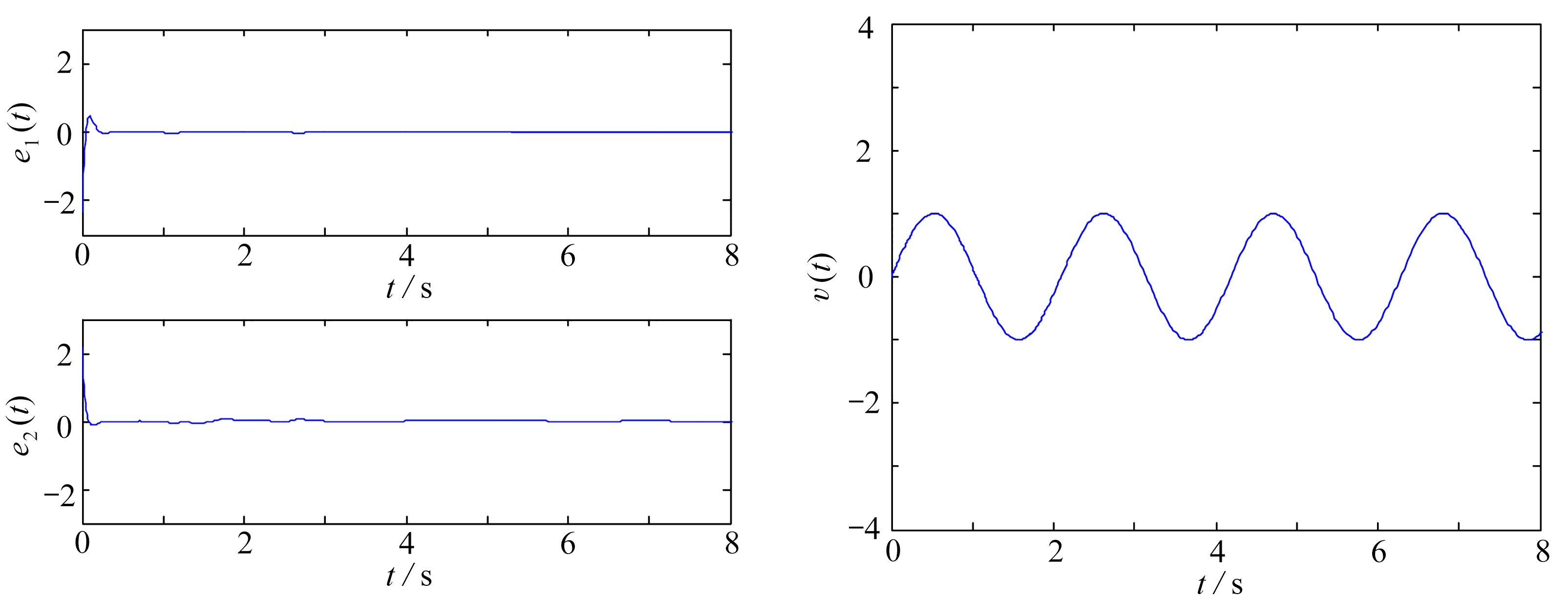
(a) 同步误差 (b) 有效信号
(a) Synchronization errors (b) The information signal
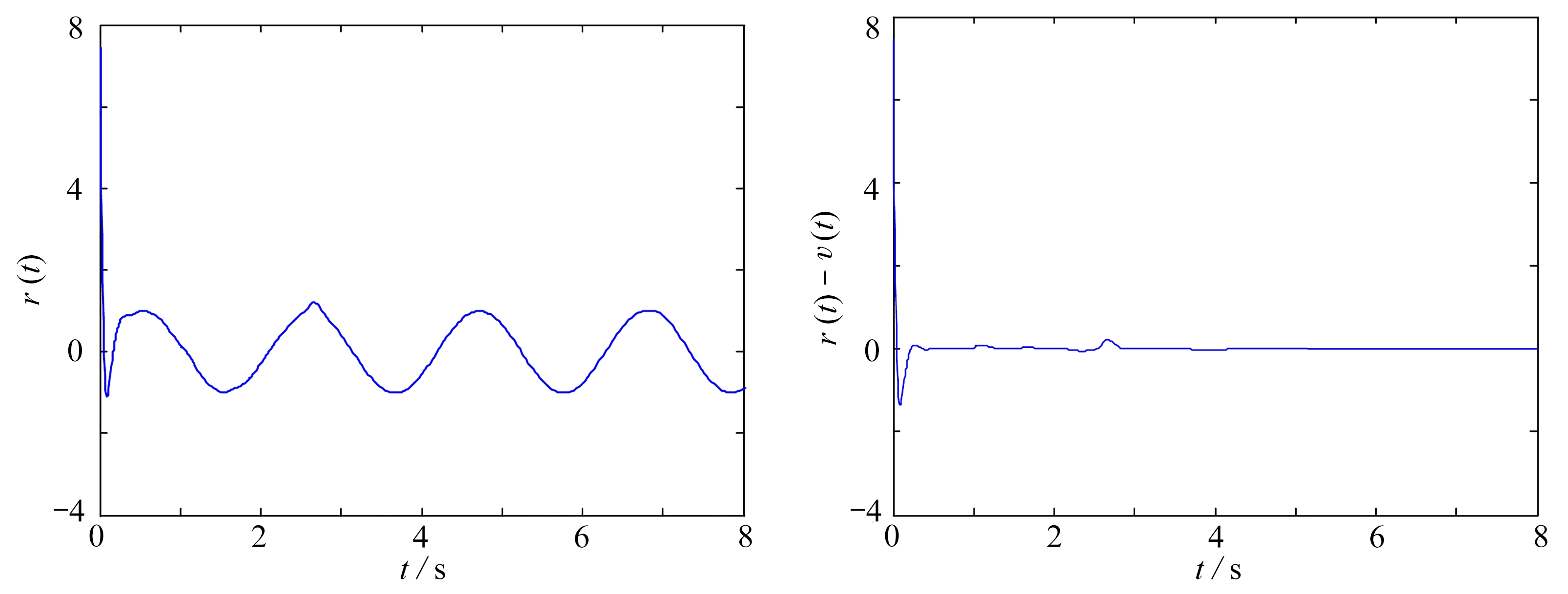
(c) 被恢复的信号 (d) 有效信号与被恢复信号间的误差
(c) The recovered signal (d) The error between the information signal and the recovered signal
图4 保密通信仿真
Fig. 4 Simulation results of recovering the information signal
5 结 论
本文研究了具有时延和随机扰动的未知C-G神经网络的有限时间函数投影同步在保密通信中的应用问题.与现有研究相比,本文所建立的神经网络模型含有时延、随机扰动和未知参数,更加符合保密通信的实际应用环境;提出的混合控制策略,使得驱动响应神经网络在有限时间内实现函数投影同步,同步速度快、鲁棒性强,应用于保密通信中,增强了信息的安全性,有效信号可以快速传输并恢复,仿真验证了所提同步策略的可行性.
[1] ZHANG H, WANG Z, LIU D. A comprehensive review of stability analysis of continuous-time recurrent neural networks[J]. IEEE Transactions on Neural Networks and Learning Systems, 2014, 25: 1229-1262.
[2] COHEN M, GROSSBERG S. Absolute stability of global pattern formation and parallel memory storage by competitive neural networks[J]. IEEE Transactions on Systems, Man and Cybernetics, 1987, 42: 288-308.
[3] WU Z G, SHI P, SU H Y, et al. Stochastic synchronization of Markovian jump neural networks with time-varying delay using sampled data[J]. IEEE Transactions on Cybernetics, 2013, 43: 1796-1806.
[4] WANG Y W, WANG H O, XIAO J W, et al. Synchronization of complex dynamical networks under recoverable attacks[J]. Automatica, 2010, 46(1): 197-203.
[5] WANG Z, ZHANG H. Synchronization stability in complex interconnected neural networks with nonsymmetric coupling[J]. Neurocomputing, 2013, 108: 84-92.
[6] 韩敏, 张雅美, 张檬. 具有双重时滞的时变耦合复杂网络的牵制外同步研究[J]. 物理学报, 2015, 64(7): 070506.(HAN Min, ZHANG Yamei, ZHANG Meng. Outer synchronization analysis of two time-varying networks with double delays based on pinning control[J]. Acta Physica Sinica, 2015, 64(7): 070506.(in Chinese))
[7] 艾合麦提·麦麦提阿吉, 李洪利. 含分布时滞递归神经网络的一般衰减同步[J]. 应用数学和力学, 2019, 40(11): 1204-1213.(MUHAMMADHAJI Ahmadjan, LI Hongli. General decay synchronization for recurrent neural networks with distributed time delays[J]. Applied Mathematics and Mechanics, 2019, 40(11): 1204-1213.(in Chinese))
[8] 张玮玮, 陈定元, 吴然超, 等. 一类基于忆阻器分数阶时滞神经网络的修正投影同步[J]. 应用数学和力学, 2018, 39(2): 239-248.(ZHANG Weiwei, CHEN Dingyuan, WU Ranchao, et al. Modified projective synchronization of memristor-based fractional-order delayed neural networks[J]. Applied Mathematics and Mechanics, 2018, 39(2): 239-248.(in Chinese))
[9] JING T Y, ZHANG D Y, MEI J, et al. Finite-time synchronization of delayed complex dynamic networks via aperiodically intermittent control[J]. Journal of the Franklin Institute, 2019, 356: 5464-5484.
[10] LU J Y, GUO Y P, JI Y D, et al. Finite-time synchronization for different dimensional fractional-order complex dynamical networks[J]. Chaos, Solitons & Fractals, 2020, 130: 109433.
[11] ZHU Q X, CAO J D. Adaptive synchronization of chaotic Cohen-Crossberg neural networks with mixed time delays[J]. Nonlinear Dynamics, 2010, 61: 517-534.
[12] GAN Q T. Adaptive synchronization of Cohen-Grossberg neural networks with unknown parameters and mixed time-varying delays[J]. Communications in Nonlinear Science and Numerical Simulation, 2012, 17(7): 3040-3049.
[13] HU C, YU J, JIANG H J. Finite-time synchronization of delayed neural networks with Cohen-Grossberg type based on delayed feedback control[J]. Neurocomputing, 2014, 143: 90-96.
[14] LI D, CAO J D. Finite-time synchronization of coupled networks with one single time-varying delay coupling[J]. Neurocomputing, 2015, 166: 265-270.
[15] SHI Y C, CAO J D. Finite-time synchronization of memristive Cohen-Grossberg neural networks with time delays[J]. Neurocomputing, 2020, 377: 159-167.
[16] ZHANG R, YANG Y Q, XU Z Y, et al. Function projective synchronization in drive-response dynamical network[J]. Physics Letters A, 2010, 374(30): 3025-3028.
[17] HAN M, ZHANG Y M. Complex function projective synchronization in drive-response complex-variable dynamical networks with coupling time delays[J]. Journal of the Franklin Institute, 2016, 353(8): 1742-1758.
[18] SUN Y Z, ZHAO D H. Effects of noise on the outer synchronization of two unidirectionally coupled complex dynamical networks[J]. Chaos: an Interdisciplinary Journal of Nonlinear Science, 2012, 22: 023131.
[19] LAI Y M, PORTER M A. Noise-induced synchronization, desynchronization, and clustering in globally coupled nonidentical oscillators[J]. Physical Review E, 2013, 88(1): 012905.
[20] SHI Y C, ZHU P Y. Adaptive synchronization of different Cohen-Grossberg chaotic neural networks with unknown parameters and time-varying delays[J]. Nonlinear Dynamics, 2013, 73(3): 1721-1728.
[21] ZHOU L L, WANG C H, HE H Z, et al. Time-controllable combinatorial inner synchronization and outer synchronization of anti-star networks and its application in secure communication[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22(1/3): 623-640.