引 言
混凝土是由骨料、硬化水泥砂浆、孔隙和裂纹等组成的非均质复合材料,而细观力学方法充分考虑了混凝土材料及其力学性质的非均匀性.在细观尺度下,利用数值方法模拟混凝土试件的裂缝扩展过程及破坏形态,能够直观地反映出试件的损伤断裂破坏机理[1].Roelfstra等[2]首次提出细观混凝土的概念,把混凝土看作由骨料、砂浆以及界面层组成的三相复合材料,为混凝土细观力学分析奠定基础.此后,为了找到混凝土细观损伤和破坏机理与宏观力学性能间的关联,国内外学者开展了大量的研究工作,提出了多种细观力学计算模型,如格构模型(lattice model)[3]、随机粒子模型(random particle model)[4]、随机骨料模型(random aggregate model)[5-6],其中随机骨料模型考虑了骨料在基质中分布的随机性以及各组分力学性质的随机本质,得到了广泛应用.起初的研究将骨料假定为圆形或球体,后来为了尽可能地模拟混凝土细观层次的实际形态,骨料的形状从圆形/球体向凸多边形/凸多面体发展演化.高政国和刘光廷[7-8]先后研究了二维混凝土多边形和凸多面体的投放骨料算法并形成相应的随机骨料模型.三维骨料模型能较真实地描述细观层次上混凝土的实际变形与损伤破坏情况[9],但对于大尺寸、大体积混凝土试件的数值模拟,求解计算量急剧增加.二维的混凝土细观结构,在一定工况下可近似地模拟三维混凝土材料的性质,克服了计算瓶颈问题,能够大量重复试验,通过结果统计消除随机性波动.但为了使其能够应用于更多的实际问题,针对骨料投放和入侵判定的算法仍有待改进和优化.
混凝土内部常常含有大量的孔隙或微裂纹,这些缺陷可能是材料原始存在的,也可能是受力后诱发产生的.孔隙和微裂纹的形成与扩展对材料的刚度、强度等力学性质都会有很大影响,导致含裂纹材料的力学性质非常复杂[10].混凝土中缺陷(包括孔隙及微裂纹等)的存在对其力学性能和失效破坏模式有明显影响.赵吉坤[11]将微裂纹、孔隙作为混凝土细观力学模型的第四相材料,采用材料弱化的方法来研究孔隙和微裂纹对混凝土宏观力学性质及细观破坏的影响.杜成斌等[12]以圆形孔隙和币形孔隙来表征缺陷,对不同孔隙率下混凝土的细观损伤破坏过程进行了数值模拟.王娟和卿龙邦等[13]采用三维随机缺陷界面弹簧元模型模拟混凝土单轴抗压强度的数值方法.Kumar和Bhattacharjee[14]研究了孔隙及微裂纹等细观缺陷对含孔基质材料强度及裂纹演化路径的影响.杜修力和金浏[15]采用细观单元等效化方法,针对初始孔隙和微裂纹对混凝土试件宏观静态力学性能的影响进行了数值研究.鉴于此,本文从细观角度出发,对传统建模方法进行了继承和改进,提出一种更高效的入侵判定算法,通过对不同形状的混凝土随机骨料/孔隙进行了细观建模,将缺陷直观地反映在混凝土随机骨料模型中,生成了含孔隙混凝土二维细观模型,通过实例对入侵判定算法的计算效率进行了验证,进而对单轴压缩下混凝土的裂纹扩展、破坏模式以及宏观应力-应变曲线进行了数值研究.
1 级 配 理 论
Fuller理想级配曲线是骨料在混凝土中以抛物线表示的空间级配曲线,其表达式为
(1)
式中,P为骨料通过筛孔直径D的质量百分数,Dmax为最大骨料粒径.
模拟混凝土二维模型时需将骨料的三维空间级配曲线转化为二维平面级配曲线,即将空间骨料模型转化为平面骨料模型.为保证混凝土骨料在二维级配和三维级配下的等效性,Walraven等[16]在球形骨料与等概率空间分布假定的基础上,建立了混凝土试件空间内骨料级配含量与其内截面内骨料面积之间的关系,即Walraven公式,该公式将三维Fuller级配曲线转化为混凝土试件内二维截面具有D<D0的内截面出现的概率:
(2)
式中,Pk为骨料占混凝土总体积的百分比,D0为级配骨料粒径,Pc为不同骨料级配在试件二维截面上出现的概率.
2 算 法 描 述
生成的混凝土细观模型需尽可能地与真实混凝土相一致,故要求细观结构的生成算法能满足如下几个条件[17]:
① 骨料的位置、形状和大小均随机且分布均匀;
② 精确满足已定的骨料级配与骨料体积分数;
③ 细观模型的骨料体积分数最大值和真实混凝土中骨料体积分数最大值相等.
为使随机投放的骨料含量达到较大并同时减少入侵判定次数,提高投放效率,采用从大级配到小级配的投放顺序.骨料级配包括两方面内容:1)骨料粒径范围;2)各粒径区间数量的相对多少,即粒径分布.不同级配对应不同的混凝土标准试件模型尺寸,本文模拟采用二级配混凝土,试件尺寸为150 mm×150 mm,粒径范围为5~30 mm.建模过程中级配模拟是利用指定骨料面积率(骨料填充面积占混凝土试件模拟区域面积比例)满足各粒径骨料占比的级配要求.
含孔隙混凝土模型的具体生成步骤与算法如下:
① 输入模型的特征参数.确定骨料投放区域,即输入混凝土的样本尺寸.模型整体控制需借助特征参数,骨料大小由粒径参数表征,圆形骨料由直径控制;椭圆形和多边形骨料则按相等面积圆换算为等效直径.Mora等[18]提出使用骨料长边与短边的长度比值β(长宽比)描述骨料的形状差异,文中椭圆形骨料/孔隙直接采用长径比控制形状,多边形骨料的不规则度则通过限制骨料最短边和最长边控制.
② 随机骨料的生成.判断新生成骨料是否与已生成骨料相交直至满足设定的骨料面积率.
③ 随机孔隙的生成.判断新生成孔隙是否与已生成骨料、孔隙相交直至满足设定的孔隙面积率.
④ 储存骨料与孔隙信息,将生成的混凝土模型图形输出.
算法流程如图1所示.

图1 含孔隙混凝土模型生成算法流程图
Fig.1 The flowchart to model random aggregates and voids
3 骨料投放准则与入侵判定
3.1 随机圆形骨料
为确保圆形骨料在投放过程中不超过投放区域,需满足以下边界条件:
(3)
式中,x0,y0,r为圆心横纵坐标与圆半径;x,y为圆边界上任意点的横纵坐标;xmin,xmax,ymin,ymax分别为骨料投放区域的横纵坐标最小、最大值.
圆形骨料避免入侵需满足条件:
(4)
式中,κ为骨料的颗粒影响系数,本文取κ=1.1.
混凝土骨料随机位置的确定需满足各骨料不相互接触,且有一定的最小距离,为此,假定每一个骨料颗粒都有一个影响范围,在该范围内其他骨料不能入侵,如图2所示.图3为随机圆形骨料的空间分布生成、投放结果,面积率为50.06%.
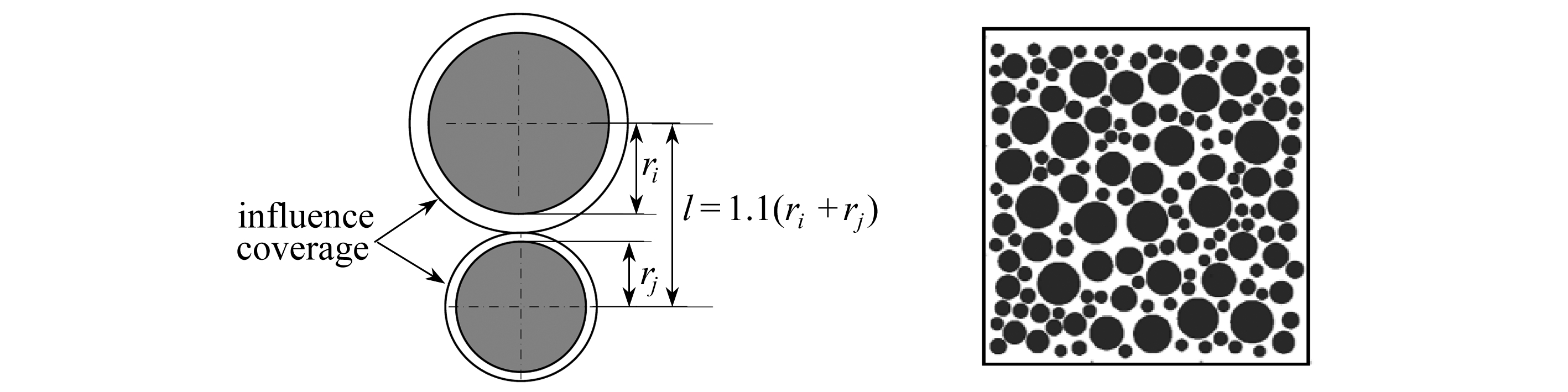
图2 圆形骨料间的最小距离
图3 圆形骨料模型
Fig.2 The minimum distance between
Fig.3 The meso-structure of concrete round aggregates with round aggregates
3.2 随机椭圆形骨料
椭圆骨料生成过程中由圆心坐标、长半轴a、长径比Re(椭圆长短半轴比值)、偏转角α多个参数控制椭圆位置与形状,图4给出随机椭圆示意图.对于椭圆形骨料,为保证其不超出投放区域,需满足下式条件:
(5)
式中,a,b为椭圆的长短半轴长;α为椭圆的偏转角,即椭圆长轴与x轴的夹角,逆时针为正;φ为椭圆边界上任意点与x轴夹角,且φ∈(0,2π).

(a)a=5, Re=0.8, α=64.9° (b)a=6, Re=0.5, α=135.1° (c)a=8, Re=0.2, α=29.7°
图4 随机椭圆示意图
Fig.4 The diagram of random ellipses
为提高椭圆骨料投放成功率和计算效率,本文采取分步入侵判定算法.第一步初判,即判断椭圆圆心距分别与两长、短半轴和的关系,存在以下三种情况:
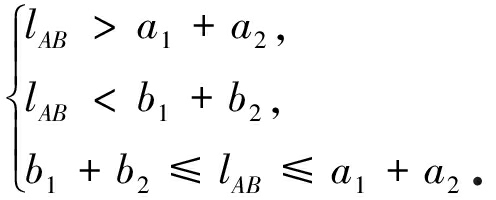
(6)
lAB>a1+a2表示两椭圆必然相容,骨料生成投放成功;lAB<b1+b2表示两椭圆发生入侵,需重新生成投放;b1+b2≤lAB≤a1+a2则需进行第二步细判:在新生成椭圆边界上取多个点离散为多边形,检查其每个顶点与未通过初判椭圆骨料的关系,若所有点均不在已生成椭圆内部和边界上,则不发生入侵可投放骨料,否则需重新生成椭圆.椭圆边界上的取点数目需同时保证算法的计算效率和入侵判定的准确性,经程序算法验证后取30个点沿周围均匀分布,故各点按φ=φ+π/15循环取得,椭圆入侵判定示意图如图5所示.
式(5)给出了极坐标下椭圆边界上的参数方程,椭圆线上任意点与其他椭圆S的位置关系可通过计算![]() 来确定:
来确定:
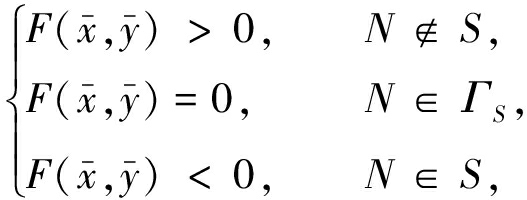
(7)
其中,S是椭圆,ΓS为椭圆边界,F(x,y)为椭圆的一般方程.则![]() 表示顶点N在椭圆外部;
表示顶点N在椭圆外部;![]() 表示N在椭圆边界上;
表示N在椭圆边界上;![]() 表示N在椭圆内部,仅当所有顶点均位于另一椭圆的外部才可认为两椭圆相容.椭圆线上任意点的坐标可通过式(4)的参数方程确定,图6为随机椭圆形骨料的空间分布生成、投放结果,面积分数为50.02%.
表示N在椭圆内部,仅当所有顶点均位于另一椭圆的外部才可认为两椭圆相容.椭圆线上任意点的坐标可通过式(4)的参数方程确定,图6为随机椭圆形骨料的空间分布生成、投放结果,面积分数为50.02%.

图5 随机椭圆入侵判定示意图
图6 椭圆形骨料模型
Fig.5 Intersection and overlap
Fig.6 The meso-structure of concrete checking for ellipses with elliptical aggregates
3.3 随机多边形骨料
本文采取圆内接多边形方法生成多边形骨料,以圆心角为参数在圆周上随机生成N个点(N∈(4,12)),顺次连接各点形成内接于圆的多边形,如图7所示.由于随机生成的圆心角并不稳定易导致骨料质量不佳,如图8所示,尤其尖角的生成使骨料呈针状,针状骨料颗粒的存在不仅对混凝土试件的抗压强度、弹性模量等力学性能有较大影响,同时尖角和短边的存在也极大地降低了有限元的计算效率,故可通过式(8)的控制条件对骨料形状做进一步优化,避免骨料生成中尖角和极短边的出现,提高骨料质量,如图9所示.图中
(8)
式中,Lmin,Lmax分别为多边形骨料的最短、最长边,ψmin和ψmax为形状控制参数,文中取ψmin=1/3,ψmax=1.8,通过控制多边形的最长、最短边来改善骨料形状,圆心位置、多边形顶点个数与位置为骨料生成过程中主要控制参数.图10为随机多边形骨料的空间分布生成、投放结果,面积分数为50.05%.
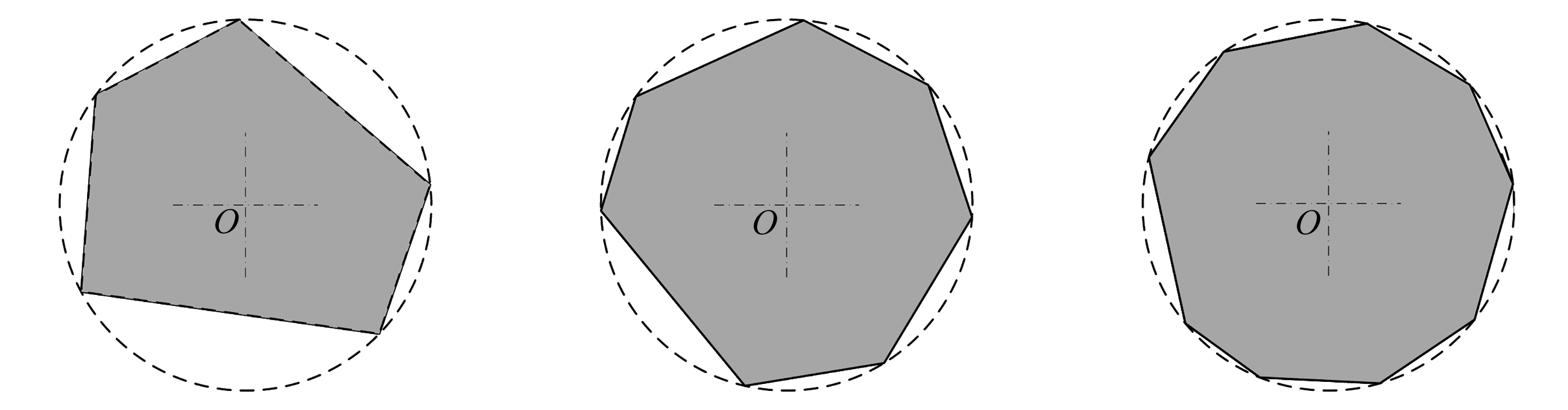
(a)N=5 (b)N=7 (c)N=9
图7 随机多边形示意图
Fig.7 The generated typical polygons
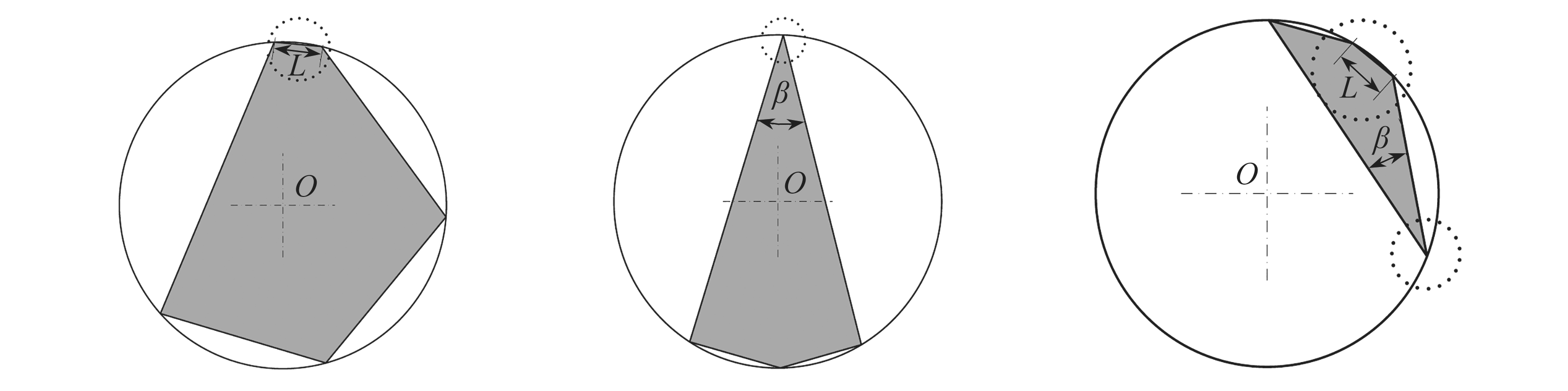
(a)短边 (b)尖角 (c)尖角和短边
(a)The short edge (b)The sharp angle (c)The short edge and the sharp angle
图8 多边形骨料质量不佳情形
Fig.8 Poor situation of polygonal aggregates

图9 多边形骨料生成示意图
图10 多边形随机骨料模型
Fig.9 The diagram of random polygonal
Fig.10 The meso-structure of polygonal-aggregate aggregates concrete
4 孔隙生成与投放
本文采用孔隙尺寸为2~4 mm,形状为圆形和椭圆,其生成方法同随机骨料类似,判定分为孔隙与骨料的判定及孔隙间的入侵判定.基于骨料投放已满足面积率要求,生成孔隙时应首先进行孔隙与骨料的判定,当孔隙与所有骨料都相容后再进行孔隙间的入侵判定.孔隙与骨料的入侵判定思想是: 采取分步入侵判定算法,先执行初判算法排除圆心距大于(r+a)/(r+r′)区域的骨料颗粒,再通过判定孔隙边界上顶点![]() 与表示骨料形状的一般方程H(x,y)进行入侵细判:
与表示骨料形状的一般方程H(x,y)进行入侵细判:
H(x,y)=Ax2+By2+Cx+Dy+E≤0,
(9)
其中,A,B,C,D,E是由随机圆/椭圆的圆心坐标和形状参数共同决定的常数.
圆边界上随机点的坐标可表示为
(10)
椭圆边界上随机点的坐标可表示为
(11)
在已成功投放了椭圆骨料的投放域中生成并投放圆形孔隙,采取分步入侵判定算法,判定示意图如图11所示,分别比较圆心距lAB与r+a和r+b的关系执行初判算法,lAB>r+a表示孔隙与该骨料相容,可进行孔隙与其他骨料的判定;lAB<r+b表示发生侵入,需重新生成并投放随机孔隙;而r+b≤lAB≤r+a则需执行细判:依次判定圆边界上均匀分布的30个点N(xi,yi)与椭圆一般方程H(x,y)的关系,仅当H(xi,yi)均大于0时孔隙与骨料相容,否则重新生成圆孔隙,直至孔隙面积率达到设计要求,最终生成圆形孔隙椭圆形骨料的混凝土随机模型.图12给出了骨料面积率为45%(Pagg=45%)且孔隙面积率为2%(Ppor=2%)时,不同椭圆长径比下的三种模型实例.
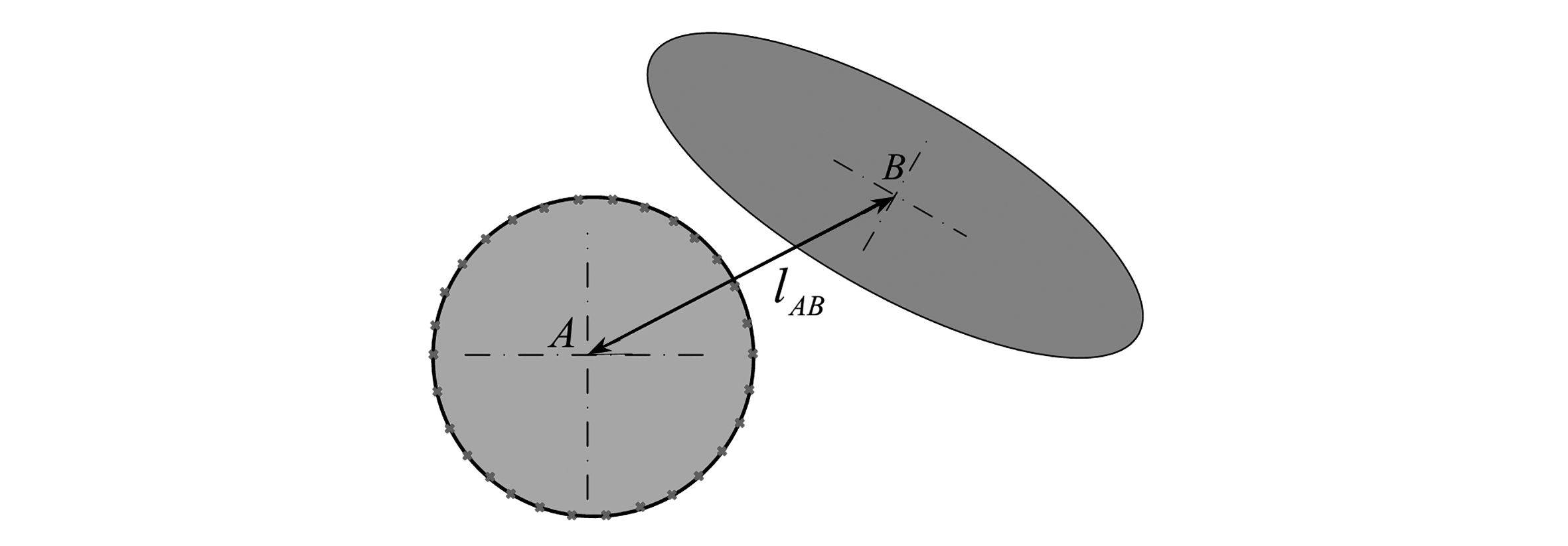
图11 圆与椭圆入侵判定示意图
Fig.11 Intersection and overlap checking between circles and ellipses

(a)Re=0.8 (b)Re=0.5 (c)Re=0.2
图12 骨料不同长径比下混凝土细观结构(Pagg=45%, Ppor=2%)
Fig.12 Meso-structures of concrete with different aspect ratios(Pagg=45%, Ppor=2%)
在已成功投放了多边形骨料的投放域中生成并投放圆形/椭圆形孔隙,图13(a)为多边形骨料与圆形孔隙判定示意图,用多边形的外接圆与孔隙的圆心距lAB与r+r′的关系直接判定入侵;图13(b)为多边形骨料与椭圆形孔隙的判定示意图,依据圆心距lAB与r′+a,r′+b的关系执行初判算法,缩减判定范围至r′+b≤lAB≤r′+a后执行细判算法.图14给出了多边形骨料中分别含圆形孔隙与椭圆形孔隙的模型实例.
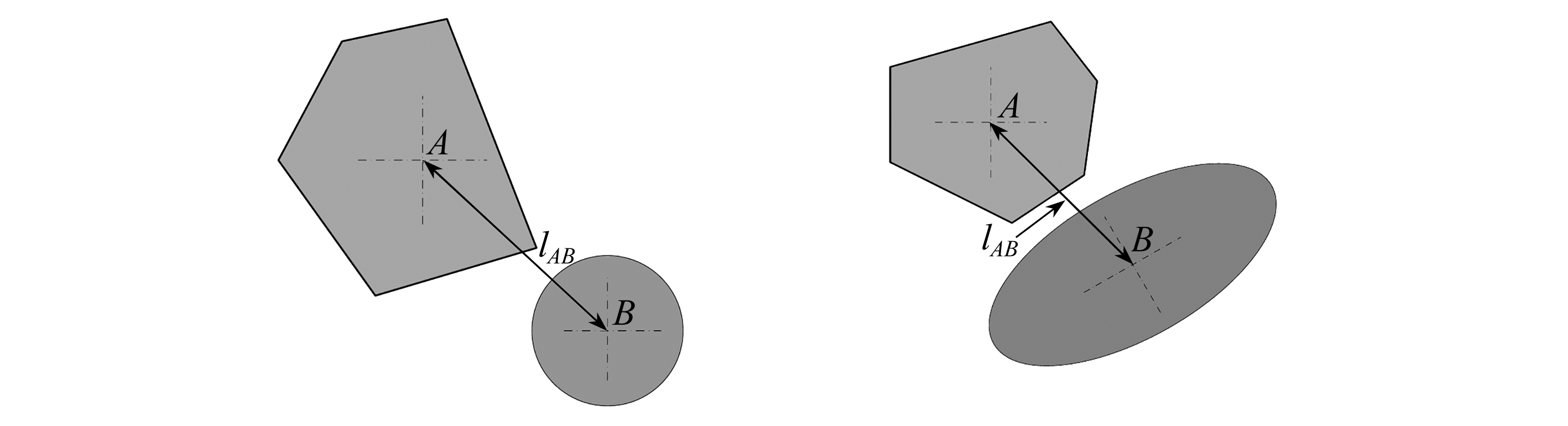
(a)圆形孔隙 (b)椭圆形孔隙
(a)Circular pores (b)Elliptical pores
图13 不同形状孔隙与多边形骨料入侵判定示意
Fig.13 Intersection and overlap checking between polygonal aggregates and different shapes of voids

(a)圆形孔隙 (b)椭圆形孔隙
(a)Circular pores (b)Elliptical pores
图14 多边形骨料混凝土随机细观结构(Pagg=40%, Ppor=2%)
Fig.14 Meso-structures of concretes with polygonal aggregates and different shapes of voids(Pagg=40%, Ppor=2%)
5 建模效率分析
投放试验中,控制模型特征参数不变,建立150 mm×150 mm的模型,骨料粒径在[5,20]mm,每种模型建模20次统计取得平均计算时间,以消除随机性的影响.表1和表2分别给出生成单一骨料混凝土和含孔隙混凝土的计算时间(计算机配置为双核CPU/2.5 GB主频、4.0 GB内存),单一骨料在面积率50%以下时,圆形/椭圆形计算时间不足1 s,而多边形最长时间约2 min;比较发现:同种骨料同等面积率下,椭圆孔隙的计算时间明显高于圆形孔隙,这是由于椭圆孔隙采用判定离散点与骨料边界的分步入侵算法,而圆形孔隙直接利用半径判别,可见分步算法的计算效率优势明显,随着骨料面积率的增加,计算时间增加.
表1 生成单一骨料混凝土计算时间(单位: s)
Table 1 Computing time to generate meso-structures of concretes with different shapes of aggregates(unit: s)
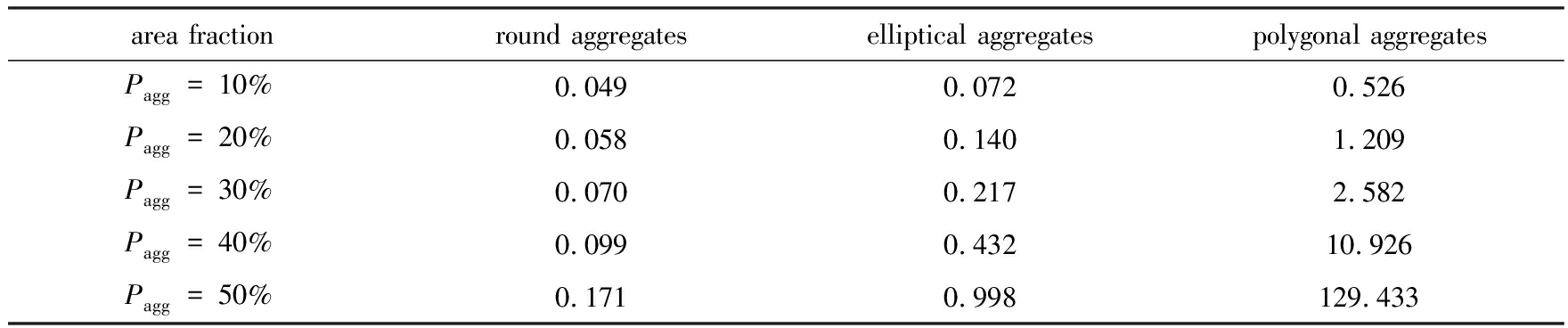
area fractionround aggregateselliptical aggregatespolygonal aggregatesPagg=10%0.0490.0720.526Pagg=20%0.0580.1401.209Pagg=30%0.0700.2172.582Pagg=40%0.0990.43210.926Pagg=50%0.1710.998129.433
表2 生成含孔隙骨料混凝土计算时间(单位: s)
Table 2 Computing time to generate meso-structures of concretes with different shapes of aggregates and voids(unit: s)
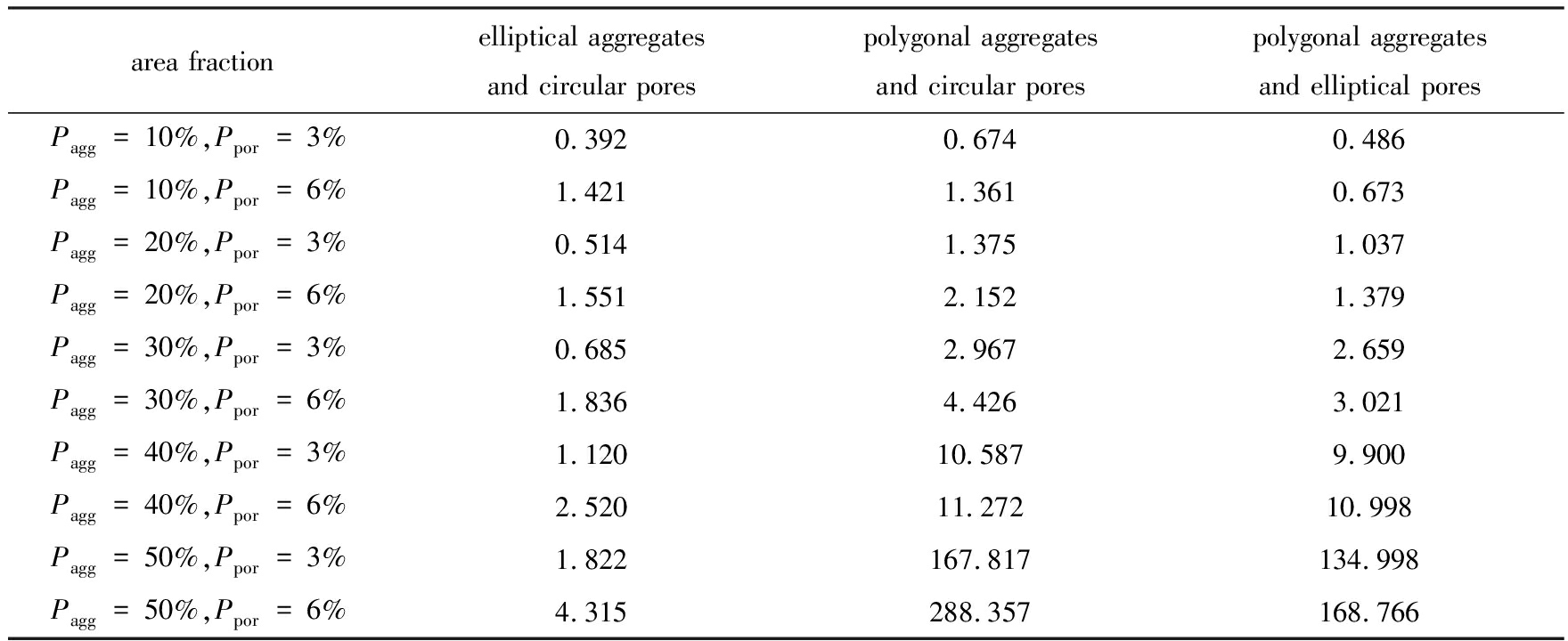
area fractionelliptical aggregates and circular porespolygonal aggregates and circular porespolygonal aggregates and elliptical poresPagg=10%,Ppor=3%0.3920.6740.486Pagg=10%,Ppor=6%1.4211.3610.673Pagg=20%,Ppor=3%0.5141.3751.037Pagg=20%,Ppor=6%1.5512.1521.379Pagg=30%,Ppor=3%0.6852.9672.659Pagg=30%,Ppor=6%1.8364.4263.021Pagg=40%,Ppor=3%1.12010.5879.900Pagg=40%,Ppor=6%2.52011.27210.998Pagg=50%,Ppor=3%1.822167.817134.998Pagg=50%,Ppor=6%4.315288.357168.766
6 算 例
在相同的模型参数控制下,生成了三个150 mm×150 mm的骨料面积率为35%且孔隙面积率为6%的混凝土样本,将生成的三个全级配混凝土样本嵌入有限元软件ABAQUS进行单轴压缩静态力学特性和破坏形态的模拟,有限元网格剖分时网格尺寸选用1 mm,经验证满足收敛性要求.因模型内部的骨料与孔隙为完全随机分布,故三个样本虽细观组分相同但结构内部形态不同,对比分析计算结果可消除样本的随机性影响,验证模型有效性.采用ABAQUS中损伤塑性模型(CDP)[19]模拟砂浆的力学性能,用弹性模型模拟粗细骨料的力学性能,细观各组分按照文献[20]取用材料参数,如表3所示,运用ABAQUS/Standard隐式计算模块进行计算,采用准静态光滑位移加载,获得应力-应变曲线下降段.其中,应力-应变关系式如下:
(12)
其中,d为损伤刚度因子,且![]() 为初始弹性刚度;ε为总应变;εpl为塑性应变.混凝土的刚度退化可由拉伸损伤因子和压缩损伤因子来描述,故混凝土在单轴拉伸和压缩时的应力-应变关系如下式所示:
为初始弹性刚度;ε为总应变;εpl为塑性应变.混凝土的刚度退化可由拉伸损伤因子和压缩损伤因子来描述,故混凝土在单轴拉伸和压缩时的应力-应变关系如下式所示:
(13a)
(13b)
图15为三个含孔隙混凝土细观模型样本的损伤演化图,图16为将孔隙视为骨料后的单一骨料模型的损伤演化图,试件上部施加位移载荷,随着荷载的增加,混凝土上下表面多条细裂纹汇聚成宏观裂纹,考虑孔隙时裂纹由孔隙处萌生扩展并贯穿孔隙,无孔隙时裂纹沿着粗骨料边界萌生并扩展至砂浆单元.由于孔隙、界面均为混凝土细观层面上的薄弱部分,因此成为裂纹优先扩展和损伤破坏的区域.
图17给出三组随机样本分别在考虑孔隙与无孔隙下的单轴压缩应力-应变关系曲线,通过计算得到,无孔隙时三个随机样本的单轴压缩强度分别为29.74,29.97,30.54 MPa,考虑孔隙时混凝土试件的强度分别为22.55,23.17,23.25 MPa,与无孔隙时强度的比值分别为75.8%,77.31%和76.13%.显然,孔隙的存在会降低混凝土的有效强度,同时也会影响混凝土裂纹扩展直至断裂的方式和方向.对比数值计算结果发现,同组样本不同的随机分布基本不会影响混凝土的峰值应力,但残余强度有一定的差别,且考虑孔隙时比无孔隙时抗压强度对应的临界应变值略小.由上述结果可知对混凝土力学特性以及混凝土损伤与断裂的研究不应忽略孔隙的影响.

(a)样本一 (b)样本二 (c)样本三
(a)Specimen 1 (b)Specimen 2 (c)Specimen 3
图15 含孔隙模型损伤演化图
Fig.15 Failure patterns of polygonal aggregates and circular pores

(a)样本一 (b)样本二 (c)样本三
(a)Specimen 1 (b)Specimen 2 (c)Specimen 3
图16 纯骨料模型破坏模式
Fig.16 Failure patterns of polygonal aggregates
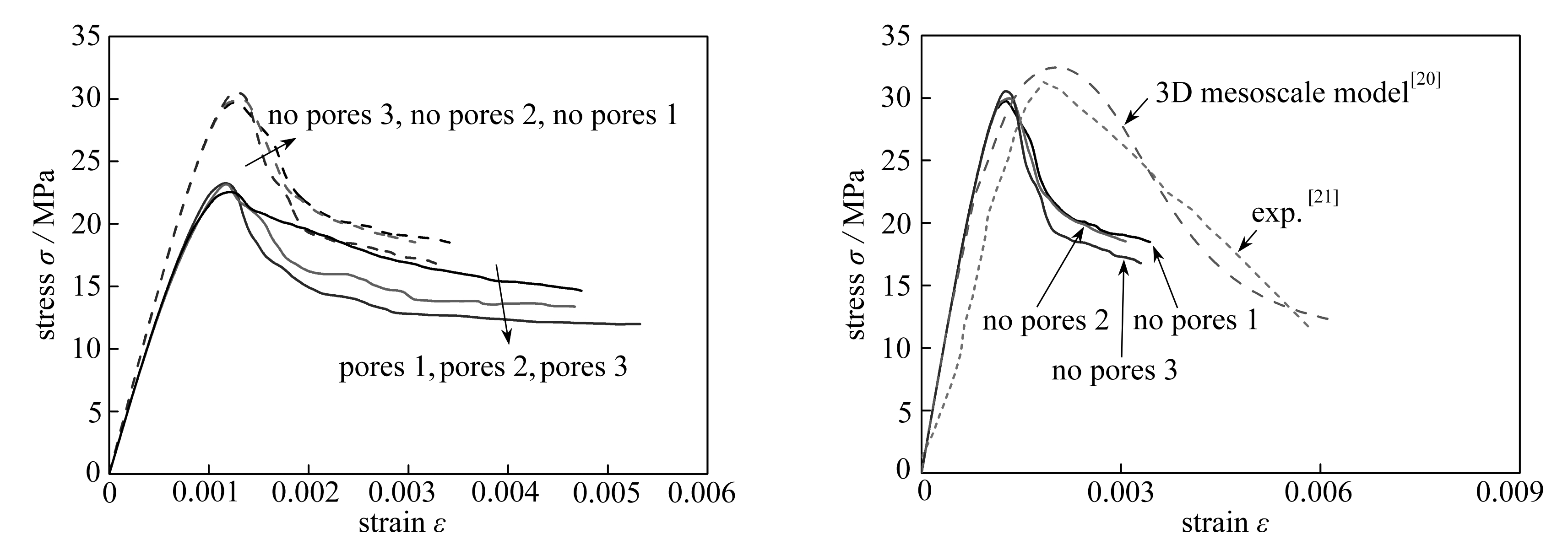
图17 单轴压缩应力-应变曲线
图18 计算与实验对比
Fig.17 The concrete uniaxial compression stress-strain curve
Fig.18 Comparison of calculation and experiment
注 为了解释图中的颜色,读者可以参考本文的电子网页版本.
图18给出混凝土样本分别与文献[20-21]三维模拟计算和实验的结果对比,可见本文的模拟结果与三维数值模拟和单轴压缩实验曲线趋势相同,且峰值应力接近,误差在10%以内,吻合较好.本文针对混凝土单轴压缩问题,采用平面应变假设将三维实际问题简化到二维平面上,与三维试样内部的应力状态不同,故曲线的峰值应变略小于三维数值模拟与试验的对应数值.
表3 细观组分材料参数
Table 3 Mechanical properties of phases in concrete

materialYoung’s modulus E/GPaPoisson’s ratio υcompressive strength fc/MPatensile strength ft/MPamortar matrix250.2353.5ITZ180.2203.0aggregate430.23--
7 结 论
基于混凝土材料细观结构特性,本文对传统的混凝土细观建模方法进行继承和改进,提出了一种适用于不同形状骨料/孔隙的分步入侵判定算法.生成的含缺陷二维混凝土细观模型有以下特点:
1)通过判别骨料/孔隙边界上离散点与一般函数的函数关系式来提高计算效率,为解决大尺寸、大体积混凝土试件三维模型的计算瓶颈问题提供优化思路,使其能够模拟更多的实际应用问题.
2)针对圆形、椭圆形和多边形骨料以及圆形、椭圆形孔隙,给出详细的建模方法,为研究不同骨料/孔隙形状对混凝土宏观力学性能的影响提供了模型基础.
3)生成混凝土模型实例表明,本文提出的分步入侵判定算法计算效率高、程序耗时少,良好的建模效率证明了算法较强的适用性,且算例生成的有限元模型可较好地模拟混凝土试件在单轴压缩下的静态力学性能,其损伤分布云图表明了试件的开裂围绕孔隙发生,裂缝贯通孔隙扩展破坏,孔隙对混凝土破坏路径有很大影响.
[1] 马怀发, 陈厚群, 黎保琨.混凝土试件细观结构的数值模拟[J].水利学报, 2004, 35(10): 27-35.(MA Huaifa, CHEN Houqun, LI Baokun.Meso-structure numerical simulation of concrete specimens[J].Journal of Hydraulic Engineering, 2004, 35(10): 27-35.(in Chinese))
[2] ROELFSTRA P E, SADOUKI H, WITTMANN F H.Le beton numerique[J].Material and Structure, 1985, 18: 327-335.
[3] SCHLANGEN E, VAN MIER J G M.Simple lattice model for numerical simulation of fracture of concrete materials and structures[J].Materials and Structure, 1992, 25(9): 534-542.
[4] BAZANT Z P, TABBARA M R, KAZEMI M T, et al.Random particle model for fracture of aggregate or fiber composites[J].ASCE Journal of Engineering Mechanics, 1990, 116(8): 1686-1705.
[5] 唐欣薇, 张楚汉.基于改进随机骨料模型的混凝土细观断裂模拟[J].清华大学学报(自然科学版), 2008, 48(3): 348-351.(TANG Xinwei, ZHANG Chuhan.Simulation of meso-fracture for concrete based on the developed random aggregate model[J].Journal of Tsinghua University(Science and Technology), 2008, 48(3): 348-351.(in Chinese))
[6] 朱万成, 唐春安, 赵文, 等.混凝土试样在静态载荷作用下断裂过程的数值模拟研究[J].工程力学, 2002, 19(6): 148-153.(ZHU Wancheng, TANG Chun’an, ZHAO Wen, et al.Numerical simulation on the fracture process of concrete specimen under static loading[J].Engineering Mechanics, 2002, 19(6): 148-153.(in Chinese))
[7] 高政国, 刘光廷.二维混凝土随机骨料模型研究[J].清华大学学报(自然科学版), 2003, 43(5): 710-714.(GAO Zhengguo, LIU Guangting.Two-dimensional random aggregate structure for concrete[J].Journal of Tsinghua University(Science and Technology), 2003, 43(5): 710-714.(in Chinese))
[8] 刘光廷, 高政国.三维凸形混凝土骨料随机投放算法[J].清华大学学报(自然科学版), 2003, 43(8): 1120-1123.(LIU Guangting, GAO Zhengguo.Random 3-D aggregate structure for concrete[J].Journal of Tsinghua University(Science and Technology), 2003, 43(8): 1120-1123.(in Chinese))
[9] ZHANG J, WANG Z Y, YANG H W, et al.3D meso-scale modeling of reinforcement concrete with high volume fraction of randomly distributed aggregates[J].Construction and Building Materials, 2018, 164: 350-361.
[10] 李天一, 章青, 夏晓舟, 等.考虑混凝土材料非均质特性的近场动力学模型[J].应用数学和力学, 2018, 39(8): 913-924.(LI Tianyi, ZHANG Qing, XIA Xiaozhou, et al.A peridynamic model for heterogeneous concrete materials[J].Applied Mathematics and Mechanics, 2018, 39(8): 913-924.(in Chinese))
[11] 赵吉坤.混凝土四相复合模型的三维细观破坏模拟[J].土木建筑与环境工程, 2009, 31(4): 37-43.(ZHAO Jikun.3D meso-scale failure simulation of four-phase composite concrete[J].Journal of Civil, Architectural and Environmental Engineering, 2009, 31(4): 37-43.(in Chinese))
[12] 杜成斌, 尚岩.三级配混凝土静、动载下力学细观破坏机制研究[J].工程力学, 2006, 23(3): 141-146.(DU Chengbin, SHANG Yan.Study on micro-mechanical failure mechanism of the three-gradation concrete under static and dynamic loadings[J].Engineering Mechanics, 2006, 23(3): 141-146.(in Chinese))
[13] 王娟, 李庆斌, 卿龙邦, 等.混凝土单轴抗压强度三维细观数值仿真[J].工程力学, 2014, 31(3): 39-44.(WANG Juan, LI Qingbin, QING Longbang, et al.3D simulation of concrete strength under uniaxial compressive load[J].Engineering Mechanics, 2014, 31(3): 39-44.(in Chinese))
[14] KUMAR R, BHATTACHARJEE B.Porosity, pore size distribution and in situ strength of concrete[J].Cement and Concrete Research, 2003, 33(1): 155-164.
[15] 杜修力, 金浏.考虑孔隙及微裂纹影响的混凝土宏观力学特性研究[J].工程力学, 2012, 29(8): 101-107.(DU Xiuli, JIN Liu.Research of the influence of pores and micro-cracks on the marcro-mechanical properties of concrete[J].Engineering Mechanics, 2012, 29(8): 101-107.(in Chinese))
[16] WALRAVEN J C, REINHARDT H W.Theory and experiments on the mechanical behavior of cracks in plain and reinforced concrete subjected to shear loading[J].Heron, 1991, 26(1A): 26-35.
[17] 伍君勇.混凝土细观结构的自动生成[D].硕士学位论文.大连: 大连理工大学, 2006.(WU Junyong.Automatic generation of meso-structure of concrete[D].Master Thesis.Dalian: Dalian University of Technology, 2006.(in Chinese))
[18] MORA C F, KWAN A K H.Sphericity, shape factor, and convexity measurement of coarse aggregate for concrete using digital image processing[J].Cement and Concrete Research, 2000, 30(3): 351-358.(in Chinese))
[19] 方秦, 还毅, 张亚栋, 等.ABAQUS混凝土损伤塑性模型静力性能分析[J].解放军理工大学学报(自然科学版), 2007, 8(3): 254-260.(FANG Qin, HUAN Yi, ZHANG Yadong, et al.Investigation into static properties of damaged plasticity model of concrete in ABAQUS[J].Journal of PLA University of Science and Technology(Nature Science Edition), 2007, 8(3): 254-260.(in Chinese))
[20] 张煜航, 陈青青, 张杰, 等.混凝土三维细观模型的建模方法与力学特性分析[J].爆炸与冲击, 2019, 39(5): 054205.(ZHANG Yuhang, CHEN Qingqing, ZHANG Jie, et al.3D mesoscale modeling method and dynamic mechanical properties investigation of concrete[J].Explosion and Shock Waves, 2019, 39(5): 054205.(in Chinese))
[21] 尚世明.普通混凝土多轴动态性能试验研究[D].博士学位论文.大连: 大连理工大学, 2013.(SHANG Shiming.Experimental study on the multi-axial dynamic behavior of plain concrete[D].PhD Thesis.Dalian: Dalian University of Technology, 2013.(in Chinese))