引 言
20世纪90年代,Wu等[1-6]提出了最优低维动力系统(以下简称“最优动力系统”)理论,其主要思想是对谱展开的基函数进行最优化,使低维动力系统最优地逼近原偏微分方程.近来,王金城等[7]完善了最优动力系统理论,使之可以对任意速度边界条件的流动问题进行建模和分析.对于更为复杂的流动,如双方柱绕流问题,某些重要的动力学特性蕴含在脉动流场中,因此需要采用Navier-Stokes方程的脉动速度方程来对该问题的脉动流场进行模拟,并构建与Navier-Stokes方程的脉动速度方程相对应的脉动最优动力系统.本文对Navier-Stokes方程的脉动速度方程进行最优低维建模,并用该新模型对复杂的并排双方柱绕流问题进行了流场分析和动力学分析.
本文的主要内容如下: 第1节推导了Navier-Stokes方程的脉动速度方程的建模过程,得到脉动速度方程的最优动力系统模型.第2节数值计算了并排双方柱绕流问题,结合近似全局最优化方法,获得了全局最优脉动速度基函数和脉动速度方程的最优动力系统模型,并分析了脉动流场.第3节借此分析了并排双方柱绕流的脉动最优动力系统的动力学特性.第4节给出了本文的结论.
1 Navier-Stokes方程的脉动速度方程的动力系统建模
1.1 脉动速度方程的动力系统建模理论
对于不可压缩流体力学问题,动量守恒方程(无量纲Navier-Stokes方程)、质量守恒方程、初始条件和边界条件为
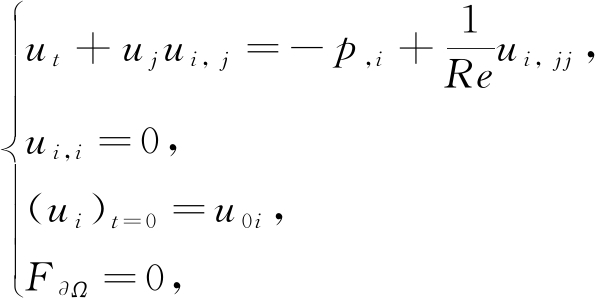
(1)
其中,p为压力,Re为Reynolds数,F∂Ω表示各种边界条件,具体形式见后文.
本文中用指标记号[8]表示所有公式,指标i和j代表物理空间坐标(i, j=1,2,3) .
首先,在速度场中扣除时间平均流![]() 得到脉动速度场
得到脉动速度场![]() 有
有
(2)
定义脉动速度基函数φki所在的函数空间BN满足条件:
(3)
其中,φki二阶可微,HN为N维Hilbert空间[7].
将脉动速度![]() 表示为在函数空间BN中的低维近似形式如下:
表示为在函数空间BN中的低维近似形式如下:
(4)
其中,uRi为余项,k=1,2,…,N,N为截断维数,在后文中省略.
其次,在压力场中扣除其时间平均场P,得到脉动压力场p*:
p*=p-P.
(5)
将式(2)、近似脉动速度(4)和脉动压力(5)代入方程组(1)中,注意到平均量亦满足方程组(1),同时注意到脉动基函数φki自动满足方程组(1)中的连续性方程.将“≈”全部用“=”表示,于是可得谱空间中的Navier-Stokes方程的脉动速度控制方程与初边值条件:
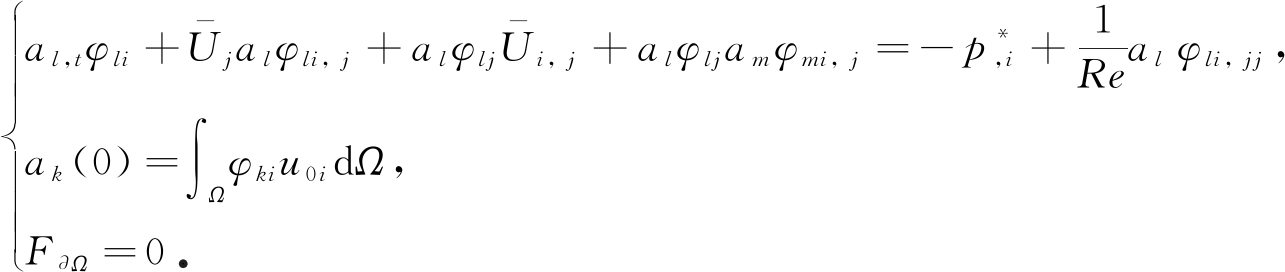
(6)
对方程组(6)中第一式构造Galerkin投影方程,在投影时引入边界条件:
(7)
其中(akφki)b的具体形式由边界条件决定,得到满足边界条件的Galerkin投影方程
(8)
其中

(9)
至此,偏微分方程定解问题(6)便转化为常微分方程(动力系统)定解问题:
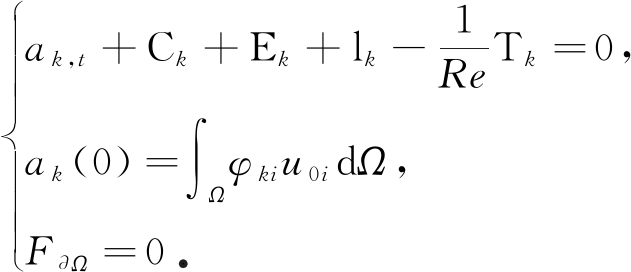
(10)
需要着重说明的是,上述定解问题中,边界条件通过积分项Ck,Ek,lk和Tk中边界处的Qi和边界附近的导数Qi, j,Qi, jj与内部流场耦合起来.动力系统方程求解完毕后,内部速度场由基函数及其系数给出,而边界处的速度由边界条件给出.
下面结合基函数的不可压缩条件,建立基函数不可压缩性目标泛函:
(11)
同时,引入罚函数μ来转化正交性约束条件,使之与目标泛函 J 共同组成广义目标泛函Jg:
(12)
其中
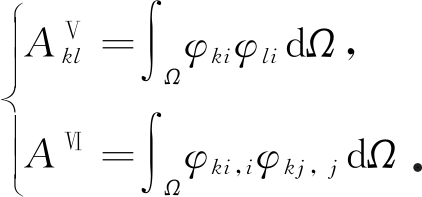
(13)
通过对方程(12)的变分运算,得到广义目标泛函梯度方程、梯度方程与动力系统方程共同组成 Navier-Stokes方程的脉动速度方程的最优动力系统模型方程.
1) 关于ak,t的脉动速度的动力系统方程
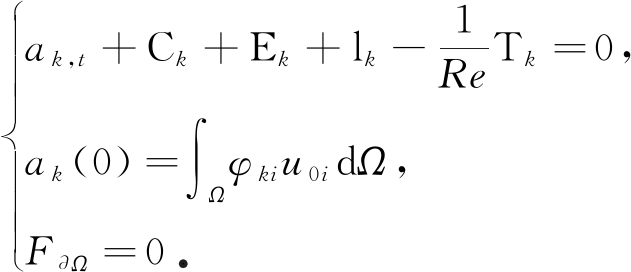
(14)
2) 广义目标泛函梯度方程
在Ω内,
(15)
在边界∂Ω上,
φkj, j ni=0.
(16)
上述最优动力系统模型可用任何优化算法进行求解,本文采用共轭梯度优化算法[9]进行求解.
1.2 边界条件
根据王金城等[7]提出的方法,并排双方柱绕流的脉动问题的边界条件F∂Ω如下(数值实现的细节请参见文献[7],在此不再赘述):
1) 右边界 脉动速度为零,可按无滑移边界处理;
2) 左边界 连续出流边界;
3) 前后上下边界 滑移边界.
2 脉动最优动力系统的数值分析
2.1 并排双方柱绕流算例和POD分析
本小节中,以并排双方柱绕流问题为例,进行Navier-Stokes方程的脉动速度方程的最优动力系统的流场分析.

(a) 速度模值云图 (b) 带状流线
(a) The contour of velocity magnitude(b) Ribboned streamlines
图1 t=700.0时粗糙流场
Fig. 1 The coarse velocity field at t=700.0

图2 时均速度模值的云图 图3 前10阶脉动POD基的能量占比
Fig. 2 The contour of the average velocity magnitude Fig. 3 The energy ratios of the first 10 fluctuation POD bases
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
整个计算域的无量纲尺寸为Ω=25.0×4.0×10.0.右边界由方柱和来流共同组成(更准确地说,它是由五个部分组成,即两个被视作方柱的无滑移部分和三个被视作来流的给定入流速度部分),方柱部分为无滑移边界条件,方柱的特征尺寸为1.0,两个方柱无量纲间距为1.0;非方柱部分为入流边界条件,无量纲来流速度为uB=(1.0, 0.0, 0.0).出口边界为连续出流边界条件.流向四周的边界皆为滑移边界条件.Reynolds数Re为200.
该算例通过 NASA-VOF3D[10]程序计算.粗糙网格数为 50×8×20,无量纲网格尺寸为Δx=Δy=Δz=0.5,无量纲时间步长为Δt=0.01.
无量纲时刻t=700.0时,双方柱绕流已经充分发展(图1),可以很明显地看到周期性脱落的K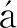 rm
rm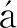 n涡街.因此,以此为时间起点开始计算此粗糙的流动数据库的时间平均速度场,对t=700.0~740.0时间段的流动数据库进行时间平均(时均场如图2所示),然后在t=700.0~740.0时间段内的200个时间截面的数据库中,同时减去刚刚生成的时均场,进而得到这200个时间截面的脉动速度场.接下来,用这200个脉动速度场来合成脉动速度的POD基[11].
n涡街.因此,以此为时间起点开始计算此粗糙的流动数据库的时间平均速度场,对t=700.0~740.0时间段的流动数据库进行时间平均(时均场如图2所示),然后在t=700.0~740.0时间段内的200个时间截面的数据库中,同时减去刚刚生成的时均场,进而得到这200个时间截面的脉动速度场.接下来,用这200个脉动速度场来合成脉动速度的POD基[11].
POD基的特征值对应了它所包含的能量,一般阶数越低的POD基所包含的能量越多,如表1和图3所示.与文献[7]中的速度全量(未扣除时均场的速度)的POD基能量分布相比,第一阶脉动基函数的能量占比确实更低了,也就是说,能量在脉动基函数中的分布更为均匀.脉动POD基的截断阶数的选择要取决于能量以及速度场的拟合程度.因为前6阶脉动基捕获了近乎100%的能量,因此我们拟采用前6阶脉动基函数来拟合原始脉动流场和构造脉动最优动力系统.
表1 脉动POD基能量分布
Table 1 The distribution of energy of fluctuation POD bases

orderenergy of kth basis ek/%energy of first k bases ek/%144.827 24044.827 240243.840 95388.668 19335.155 301 093.823 49445.092 375 098.915 86950.515 387 199.431 25760.512 078 299.943 33570.027 714 199.971 04980.027 439 999.998 48990.000 734 899.999 224100.000 723 699.999 947

图4 Jg的收敛曲线
Fig. 4 The convergence curve of Jg
2.2 近似全局最优脉动速度基
采用双尺度全局最优化方法[5]获得脉动最优基.首先,将前6阶脉动基插值到密一倍的网格上,密网格尺寸为Δx′=Δy′=Δz′=0.25.然后,将这些密的脉动基函数作为迭代初始基,代入共轭梯度优化算法进行计算,即可得到近似全局脉动最优基![]() 图4展示了式(12)中的广义目标泛函值Jg的收敛曲线,该值反映了对全局最优的脉动速度不可压缩性和脉动基函数正交性的逼近程度.
图4展示了式(12)中的广义目标泛函值Jg的收敛曲线,该值反映了对全局最优的脉动速度不可压缩性和脉动基函数正交性的逼近程度.
如图5所示,脉动最优基不再包含平均场的信息,前两阶脉动最优基![]() 的周期结构非常明显,而高阶脉动最优基的结构呈“U”字形,且比较相似.
的周期结构非常明显,而高阶脉动最优基的结构呈“U”字形,且比较相似.

(a) 第一阶 (b) 第二阶
(a) The 1st order (b) The 2nd order
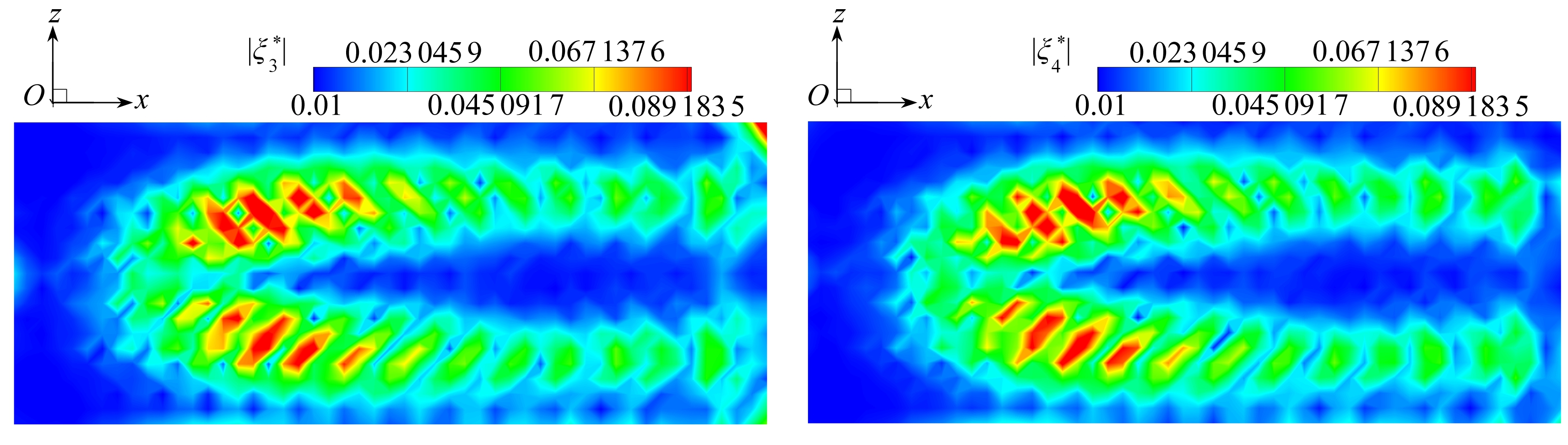
(c) 第三阶 (d) 第四阶
(c) The 3rd order (d) The 4th order

(e) 第五阶 (f) 第六阶
(e) The 5th order (f) The 6th order
图5 流向中截面上的脉动最优基模值云图
Fig. 5 The contours of the magnitudes of fluctuation optimal bases on the streamwise mid-section
2.3 脉动最优基对流场的拟合
用前6阶脉动最优基来构建脉动速度方程的最优动力系统,结合最优动力系统的各阶系数,可以得到拟合的近似脉动速度场.图6表明脉动最优动力系统的近似脉动速度结果是能与数据库的脉动速度匹配上的,其中包括了脉动速度场的发展速度的匹配.

(a) t=700.0时脉动最优动力系统(b) t=700.0时数据库
(a) The optimal dynamical system for t=700.0 (b) The database for t=700.0
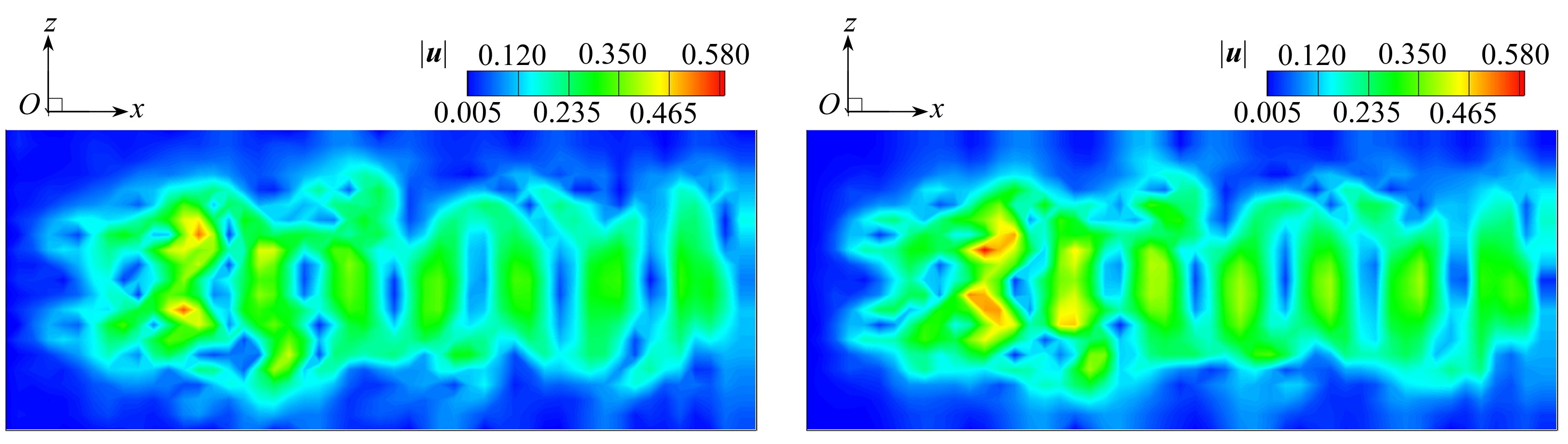
(c) t=715.0时脉动最优动力系统(d) t=715.0时数据库
(c) The optimal dynamical system for t=715.0 (d) The database for t=715.0
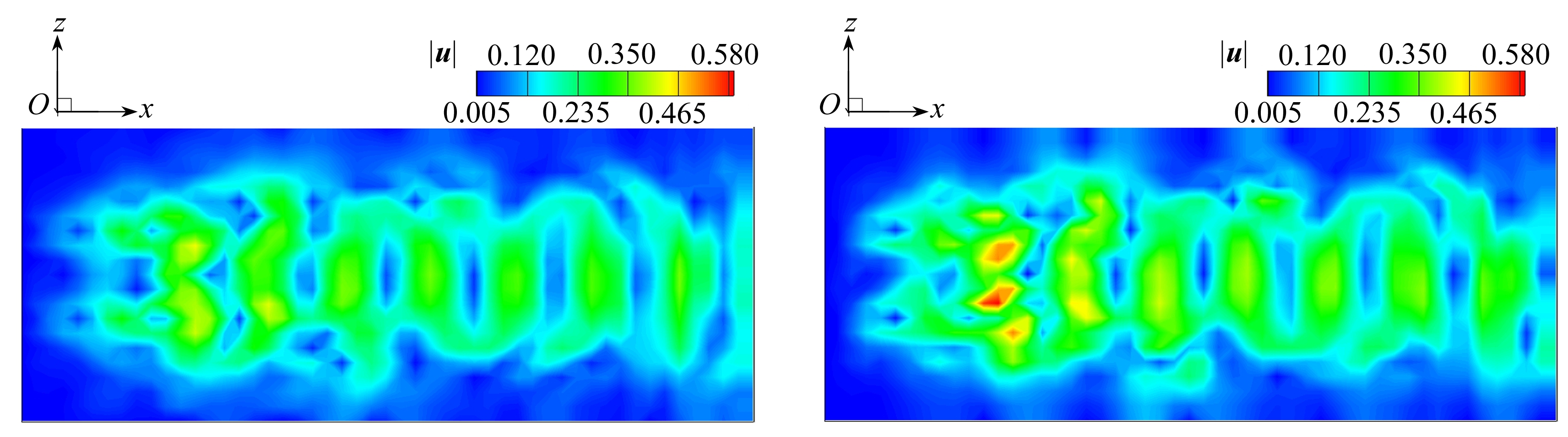
(e) t=739.8时脉动最优动力系统(f) t=739.8时数据库
(e) The optimal dynamical system for t=739.8 (f) The database for t=739.8
图6 脉动最优动力系统脉动速度模值和数据库脉动速度模值比较
Fig. 6 The comparison of the fluctuation velocity magnitudes of the optimal dynamical system and the database

(a) t=700.0时脉动最优动力系统(b) t=700.0时数据库
(a) The optimal dynamical system for t=700.0 (b) The database for t=700.0
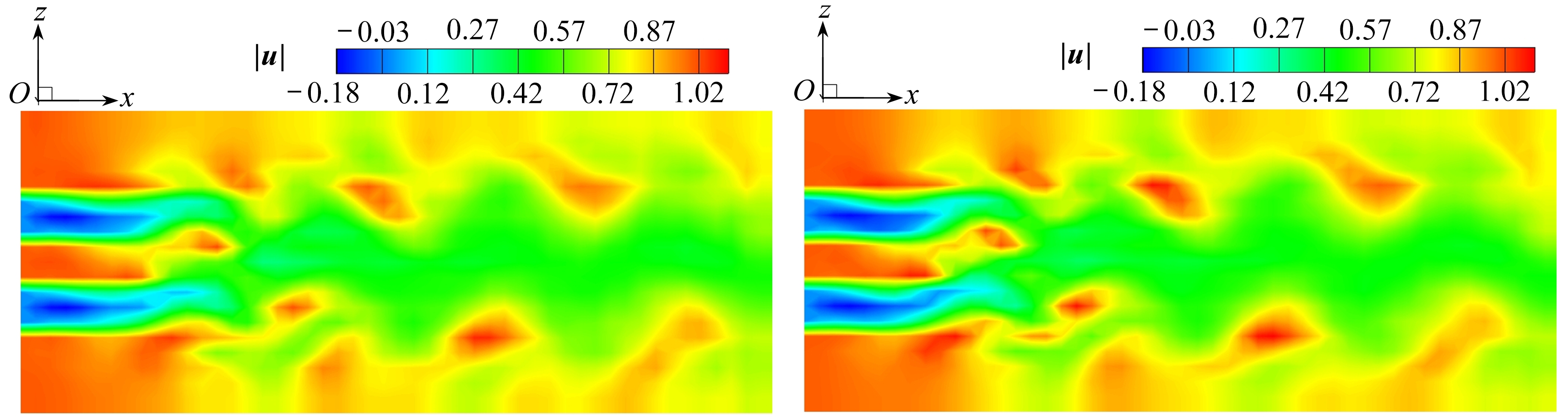
(c) t=715.0时脉动最优动力系统(d) t=715.0时数据库
(c) The optimal dynamical system for t=715.0 (d) The database for t=715.0

(e) t=739.8时脉动最优动力系统(f) t=739.8时数据库
(e) The optimal dynamical system for t=739.8 (f) The database for t=739.8
图7 脉动最优动力系统速度模值和数据库速度模值比较(速度全量)
Fig. 7 The comparison of the velocity magnitudes of the optimal dynamical system and the database(total speed)
为了进一步验证脉动最优动力系统的有效性, 将近似脉动速度叠加上时均速度场(图2), 得到近似的速度全量(如图7所示).可以发现, 脉动最优动力系统的近似速度全量也能与数据库的速度全量比对上, 包括演化的速度.因此再一次印证了脉动最优动力系统的有效性和可靠性.
3 脉动速度的最优动力系统的动力学特性
下面对不可压缩Navier-Stokes方程中的脉动速度方程最优动力系统的相空间轨道、Poincaré截面、功率谱、Lyapunov指数集和分岔等特性进行分析.
3.1 脉动最优动力系统的相空间轨道
首先,依次观测阶数相邻的三个脉动最优动力系统的三维轨迹,可以发现各个低维子系统的相轨迹经历短暂的无规律运动后,逐渐收敛到某一固定轨道上(如图8所示).
其次,依次观测阶数相邻的两个最优动力系统的二维轨迹,可以看出,二维轨迹与三维轨迹类似,轨迹逐渐收敛到一固定轨道(如图9所示).
接下来,观察脉动最优动力系统的长期动力学行为,长期行为的三维轨迹和二维轨迹分别如图10、图11所示.从图10和图11中可见,脉动最优动力系统子系统的长期动力学行为是一系列的极限环,反映出了脉动最优动力系统的周期性动力学特性,呼应了图6和图7中的周期性流动结构.

(a) a1-a2-a3 (b) a2-a3-a4

(c) a3-a4-a5 (d) a4-a5-a6 (e) a5-a6-a1
图8 脉动最优动力系统的三维相空间轨道
Fig. 8 Three-dimensional phase portaits of the fluctuation optimal dynamical systems
3.2 脉动最优动力系统的Poincaré截面
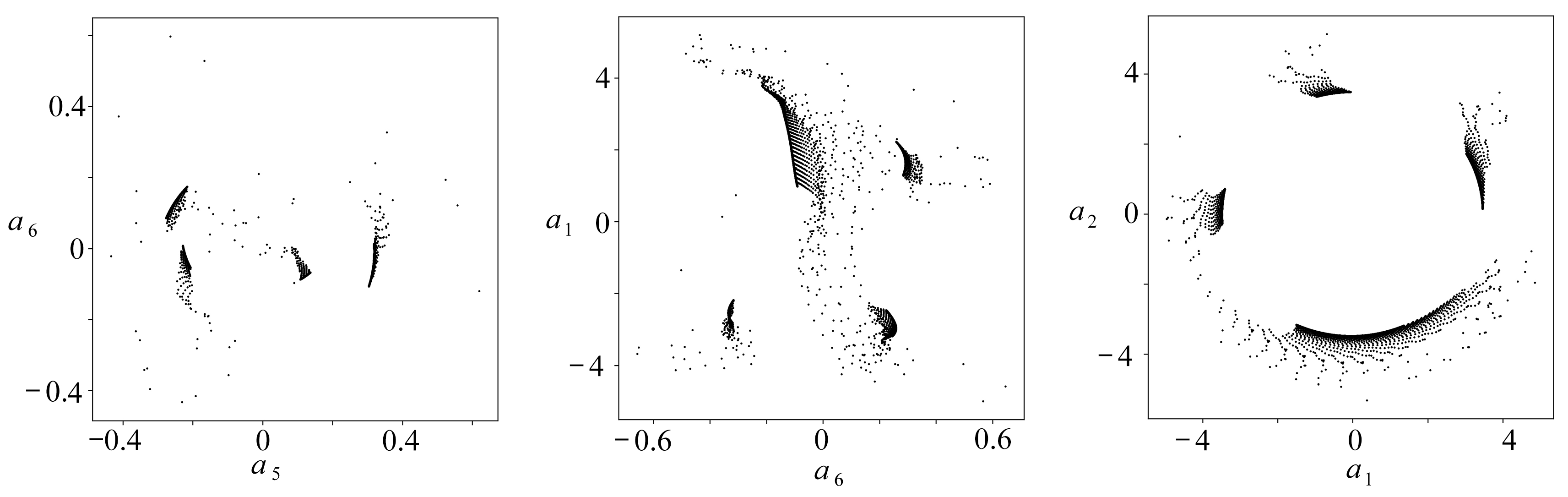
Poincaré截面是研究高维动力系统的有效手段.图12是脉动最优动力系统在六个典型相平面上的 Poincaré截面,可见各个Poincaré截面的点都有比较集中的汇集区域(深色区域),呼应了在相轨迹(图10和图11)中所观察到的极限环结构.

(a) a1-a2 (b) a2-a3(c) a3-a4

(d) a4-a5 (e) a5-a6(f) a6-a1
图9 脉动最优动力系统的二维相空间轨道
Fig. 9 Two-dimensional phase portaits of the fluctuation optimal dynamical sytems

(a) a1-a2-a3 (b) a2-a3-a4

(c) a3-a4-a5 (d) a4-a5-a6 (e) a5-a6-a1
图10 脉动最优动力系统的长期三维相空间轨道
Fig. 10 Three-dimensional long-term phase portaits of the fluctuation optimal dynamical systems
3.3 脉动最优动力系统的Lyapunov指数
Lyapunov指数在分析动力系统的整体动力学特性上具有重要作用.
采用文献[7]中的方法对脉动最优动力系统在t=0.0~12 000.0无量纲时间段内的Lyapunov指数集进行分析.假设动力系统起始时间为t=0.0,结果如图13所示,六个Lyapunov指数分别为0.025 351 9,0.025 353 0,0.022 122 7,0.022 116 9,0.010 058 8和0.007 574 4,即全为正,此系统是不稳定的,与低维子系统的极限环长期动力学行为不相符,说明从系统低维子系统的长期动力学特性为极限环这一事实出发,并不能得到整个系统的长期动力学特性也为极限环的结论.

(a) a1-a2 (b) a2-a3(c) a3-a4

(d) a4-a5 (e) a5-a6(f) a6-a1
图11 脉动最优动力系统的长期二维相空间轨道
Fig. 11 Two-dimensional long-term phase portaits of the fluctuation optimal dynamical sytems
3.4 脉动最优动力系统的分岔特性
下面研究最优动力系统随Reynolds数变化的分岔特性. 分岔图14展示了a6的分岔特性,图中的点代表t=400.0~2 200.0无量纲时间段内,最优动力系统轨迹与a1=0相平面相交时,在该Poincaré截面上的a6值,无量纲时间步长为0.2.图14(a)给出了Re=200~1 400之间的最优动力系统分岔特性, Re步长取2;图14(b)给出了Re=400~450之间的最优动力系统分岔特性,Re步长取0.1.
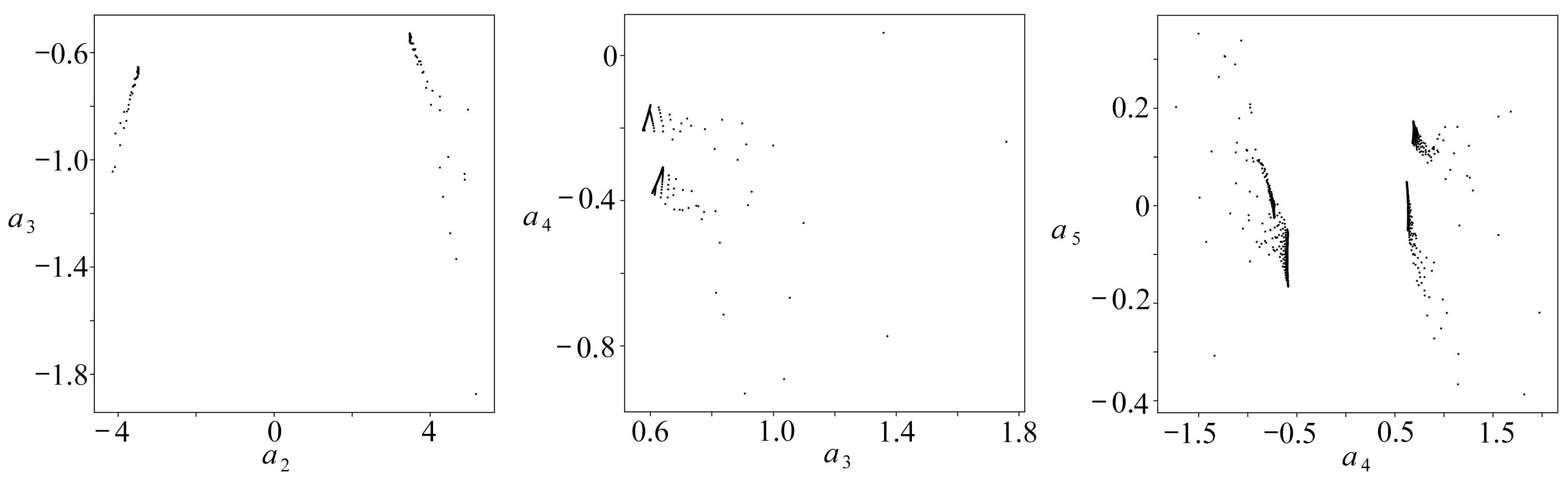
(a) 相平面a1=0 (b) 相平面a2=0 (c) 相平面a3=0
(a) The phase plane of a1=0(b) The phase plane of a2=0(c) The phase plane of a3=0
(d) 相平面a4=0 (e) 相平面a5=0 (f) 相平面a6=0
(d) The phase plane of a4=0(e) The phase plane of a5=0(f) The phase plane of a6=0
图12 脉动最优动力系统的六个典型Poincaré截面
Fig. 12 Six typical Poincaré sections of the fluctuation optimal dynamical systems

图13 脉动最优动力系统Lyapunov指数集的演化
Fig. 13 The evolution of the Lyapunov exponent spectrum of fluctuation optimal dynamical sytems

(a) Re=200~1 400 (b) Re=400~450
图14 脉动最优动力系统分岔图
Fig. 14 The bifurcation diagrams of the fluctuation optimal dynamical systems
由图14(a)可见,随着Re从初始值200开始增大,脉动最优动力系统的长期行为逐渐变得复杂,不再是极限环;从分辨率更高的图14(b)可以看出,脉动最优动力系统从Re=410开始出现类似倍周期分岔的行为,但这一分岔并不稳定,是间歇性出现的.
3.5 脉动最优动力系统的功率谱分析
下面采用文献[7]中的功率谱分析的方法来对脉动速度的最优动力系统的结果进行分析.取无量纲时间t=700.0~20 700.0的脉动最优动力系统时间序列,一共100 000个点.假设动力系统时间序列的总时长为1,频率范围取为0~0.5,结果如图15所示,其中的横坐标和纵坐标都是对数坐标.由图15可知,随着各阶功率谱阶数的升高,主频的个数也随之增加,例如,a1和a2的功率谱只有一个主频,a3和a4有两个主频,而a5和a6有三个主频,表明高阶脉动最优动力系统的周期性动力学行为比低阶系统更为复杂.

(a) a1的功率谱 (b) a2的功率谱
(a) The power spectrum of a1 (b) The power spectrum of a2
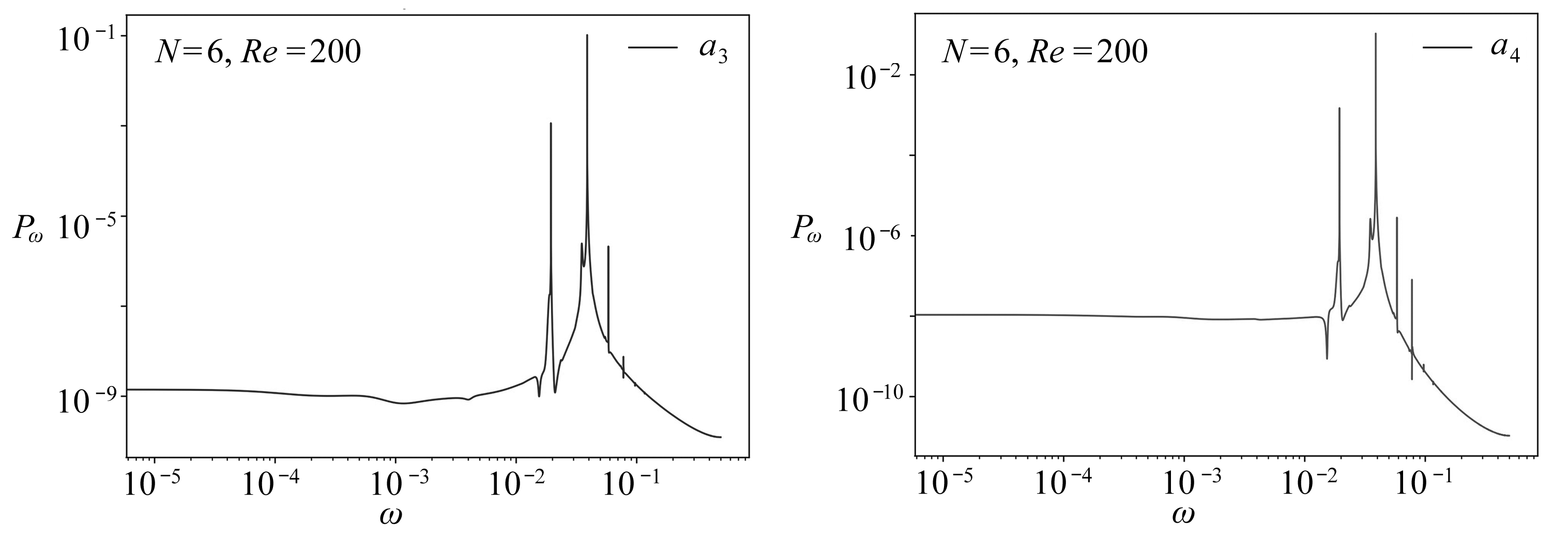
(c) a3的功率谱 (d) a4的功率谱
(c) The power spectrum of a3 (d) The power spectrum of a4

(e) a5的功率谱 (f) a6的功率谱
(e) The power spectrum of a5 (f) The power spectrum of a6
图15 脉动最优动力系统的功率谱
Fig. 15 The power spectrums of the portraits of fluctuation optimal dynamical systems
4 结 论
本文基于Navier-Stokes方程的脉动速度方程,提出了脉动最优动力系统建模理论.数值计算了并排双方柱绕流,并构建了此流动的脉动最优动力系统,通过对其动力学特性(相空间轨道、分岔特性、功率谱和Lyapunov指数集等)的分析,发现脉动最优动力系统的低维子系统的长期动力学行为是极限环,且随着Reynolds数的增加,脉动最优动力系统出现间歇性的类倍周期分岔特性.因此Navier-Stokes方程的脉动速度方程的最优动力系统确实能描述蕴藏在脉动速度场中复杂的动力学特性.
[1] WU C J. Large optimal truncated low-dimensional dynamical systems[J]. Discrete & Continuous Dynamical Systems: A, 1996, 2(4): 559-583.
[2] WU C J, SHI H S. An optimal theory for an expansion of flow quantities to capture the flow structures[J]. Fluid Dynamics Research, 1995, 17(2): 67-85.
[3] 吴锤结, 赵红亮. 不依赖数据库的最优动力系统建模理论及其应用[J]. 力学学报, 2001, 33(3): 289-300.(WU Chuijie, ZHAO Hongliang. A new database-free method of constructing optimal low-dimensional dynamical systems and its application[J]. Chinese Journal of Theoretical and Applied Mechanics, 2001, 33(3): 289-300.(in Chinese))
[4] WU C J, WANG L. A method of constructing a database-free optimal dynamical system and a global optimal dynamical system[J]. Science in China Series G: Physics, Mechanics & Astronomy, 2008, 51(7): 905-915.
[5] PENG N F, GUAN H, WU C J. Research on the optimal dynamical systems of three-dimensional Navier-Stokes equations based on weighted residual[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59(4): 644-701.
[6] PENG N F, GUAN H, WU C J. Optimal dynamical systems of Navier-Stokes equations based on generalized helical-wave bases and the fundamental elements of turbulence[J]. Science China: Physics, Mechanics & Astronomy, 2016, 59(11): 114713. DOI: 10.1016/S1007-5704(96)90007-6.
[7] 王金城, 齐进, 吴锤结. 不可压缩Navier-Stokes方程最优动力系统建模和分析[J]. 应用数学和力学, 2020, 41(1): 1-15.(WANG Jincheng, QI Jin, WU Chuijie. Analysis and modelling of optimal dynamical systems of incompressible Navier-Stokes equations[J]. Applied Mathematics and Mechanics, 2020, 41(1): 1-15. (in Chinese))
[8] 黄克智, 薛明德, 陆明万. 张量分析[M]. 北京: 清华大学出版社, 2003. (HUANG Kezhi, XUE Mingde, LU Mingwan. Tensor Analysis[M]. Beijing: Tsinghua University Press, 2003.(in Chinese))
[9] 叶庆凯, 王肇明. 优化与最优控制中的计算方法[M]. 北京: 科学出版社, 1986.(YE Qingkai, WANG Zhaoming. Computational Methods of Optimization and Optimum Control[M]. Beijing: Science Press, 1986.(in Chinese))
[10] TORREY M D, MJOLSNESS R C, STEIN L R. NASA-VOF3D: a three-dimensional computer program for incompressible flows with free surfaces[R]. Nasa Sti/Recon Technical Report N, 1987.
[11] SIROVICH L. Turbulence and the dynamics of coherent structures, part Ⅲ: dynamics and scaling[J]. Quarterly of Applied Mathematics, 1987, 45(3): 583-590.