引 言
由于太空为失重的环境,为了对航天员进行地面模拟训练,训练中心往往也需要建立失重的环境,对产品性能、出舱活动、舱外作业[1-2]等一系列过程进行评估.失重模拟最常用的方式为水下模拟失重,为了在水下模拟失重的效果,通常需要把水下使用的训练服、设备都近似配成中性浮力状态[3-6],以使得受试者在操作过程中所感受的状态类似太空中的状态.
为了实现水下训练服的中性浮力,一方面要保证重力和浮力大小相等,同时要保证质心和浮心位置完全重合在一起.但理论上的完全相等和重合是无法实现的,实际应用中需要保证达到一定的误差范围.保证质心和浮心位置重合,比保证重力和浮力大小相等的实现难度更大.目前水下训练服的配平方法如下[7-9]:服装上有多个确定位置的配重袋,每个配重袋可加的配重块数量有不同的上限限制,根据不同的配平目标,分别在不同的配重袋中加入一定数量的配重块,通过尝试调整配重块的分配,最终达到满足目标的配重方案,所以浮力配平过程就是确定各配重袋中配重块数量的过程.由于多次尝试对操作者有一定的经验要求,在不同配重目标或者训练服状态改变时,配平目标的实现又需要一定时间的尝试和摸索.
现有的浮力配平方式,主要基于长时间的水下配平操作经验.本文从数值优化的角度出发,使用数学模型来描述浮力配平过程,通过寻找最优解的方式,来寻找满足需求的最佳配平方案.
1 浮力配平的数学描述
水下训练服浮力配平目标如下:
1) 随遇平衡状态[7] 保证重力和浮力大小相等,同时保证质心和浮心完全重合在一起,或者很接近.理论上,此时水下训练服可以以任一姿态悬浮,在较小外力作用下,可以360°旋转.
2) 特定角度下的稳定平衡状态 保证重力和浮力大小相等,还需保证水下训练服的特定倾角,满足受试人员着水下训练服时的特定作业姿态.由于有一定的姿态要求,也就是对质心和浮心之间相对位置的要求.为了能够达到较长时间地稳定在该工作姿态,此时质心和浮心距离越远该姿态越稳定.距离越远时,服装绕转动点转动所需的转矩越大,偏离平衡状态后,恢复到初始状态的反作用力越大.
水下训练服的空间坐标系为OXYZ,如图1所示,X轴垂直胸部朝前,Z轴平行于服装高度方向,Y轴由坐标系右手法则确定,其中原点O为水下服两侧固定安装点的连线中心.坐标系OX0Y0Z0为重力坐标系,和OXYZ坐标系原点重合,Z0平行于重力方向.Cm为质心位置,Cf为浮心位置.
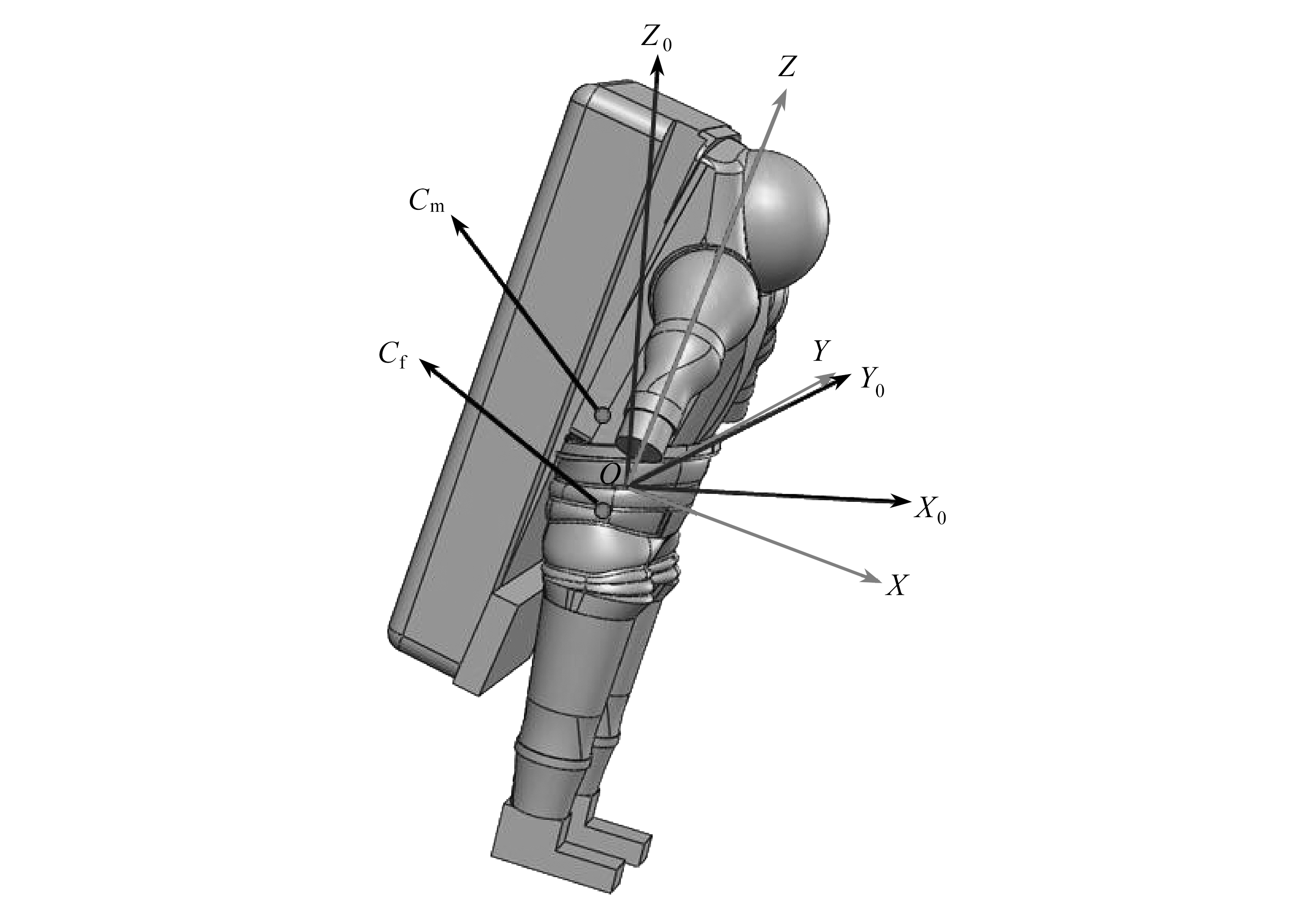
图1 水下训练服及其坐标系示意图
Fig. 1 Schematic diagram of the underwater training spacesuit and its coordinate system
水下训练服质量为M,由两部分组成[7,9]:一部分包括服装本体、人体,固定配重可由ma表示,另一部分为活动配重可表示为mb,所受浮力为F,
M=ma+mb, F=∑Fi,
(1)
式中,i为组成水下训练服的各个部分.
坐标系OXYZ中,质心坐标为Cm(xm,ym,zm),浮心坐标为Cf(xf,yf,zf);坐标系OX0Y0Z0中,质心坐标为Cm0(xm0,ym0,zm0),浮心坐标为Cf0(xf0,yf0,zf0).
水下训练服悬浮的姿态由质心和浮心的相对位置决定.最终的稳定悬浮姿态,在坐标系OX0Y0Z0中满足浮心Cf0(xf0,yf0,zf0)在质心Cm0(xm0,ym0,zm0)的正上方,即
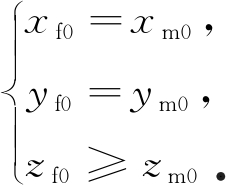
(2)
按图1所示坐标系,定义绕Y轴旋转的角度为俯仰角,绕Z轴旋转的角度为偏航角,绕X轴旋转的角度为滚摆角.对于特定倾角的稳定平衡状态,要求俯仰角为某一特定角度,滚摆角在一定误差范围内,偏航角对水下训练服的倾斜作业姿态没有影响.
2 浮力配平问题简化
对该浮力配平过程进行如下简化:
1) 初始条件给定的水下训练服各组成部分的质量、浮力、质心、浮心坐标认为是准确的,不考虑其误差;
2) 各活动配重袋的质心认为是常数,也就是每个配重袋的质心不随该配重袋中配重块数量的变化而变化;
3) 忽略活动配重块对浮心位置的影响,也就是认为训练服整体的浮心是固定的,不随配重块配平方案的变化而变化.
所以浮力配平的过程就是满足重力浮力允差、在一定姿态约束条件下,各个配重袋中配重块数量分配的问题,是一个约束条件下的整数非线性规划问题.本文基于分支定界算法,对该整数非线性规划问题进行优化计算.
3 整数非线性规划模型
服装坐标系OXYZ中,质心坐标为Cm(xm,ym,zm),浮心坐标为Cf(xf,yf,zf).若x=[x1
x2 x3 … xi]T, xi为第i个配重袋中配重块的数量,m=[m1 m2 m3 … mi], mi为第i个配重袋中单块配重块的质量,则mb=m·x; Cmi(xmi,ymi,zmi)为第i个配重袋的质心位置.
随遇平衡状态下,该问题可以描述为
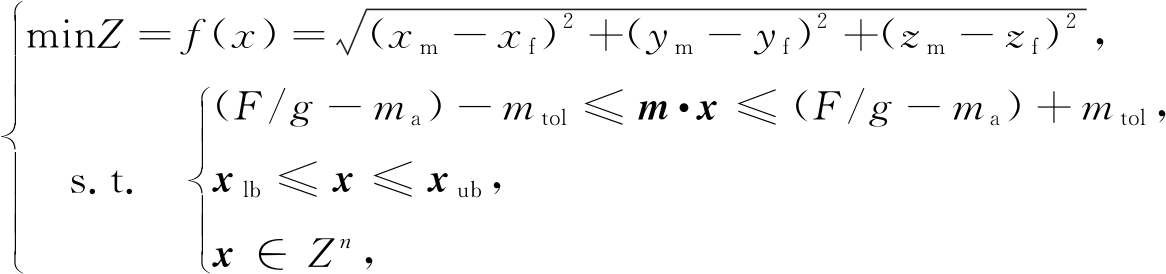
(3)
其中,mtol为重力和浮力之间的允差,xlb,xub分别为配重块数量的上下限,质心和浮心之间的距离最小作为优化的目标函数.由于添加的质量块的重量不是连续的,所以不可能达到配重后,重力和浮力刚好相等,只能给定一个质量的误差范围,用不等式表示.
特定角度下的稳定平衡状态,为了能够较长时间地稳定在该工作姿态,此时质心和浮心距离越远该姿态越稳定.特定角度下的稳定平衡状态,可以描述为

(4)
其中,向量P为质心到浮心的向量CmCf, α为目标俯仰角,αtol为俯仰角的允差,βtol为滚摆角的允差,PZ为平行于服装坐标系OXYZ中Z轴的单位向量,PXOZ,PYOZ分别为向量P投影到XOZ平面和YOZ平面的向量,〈PXOZ,PZ〉表示向量PXOZ和PZ的夹角,〈PYOZ,PZ〉表示向量PYOZ和PZ的夹角.
质心和浮心之间的距离最大作为优化的目标函数.式(4)中,对于未知量x,第一、二个约束为线性约束,第三、四个约束为非线性约束.
式(3)和(4)都可以认为是一个整数非线性规划问题.
假设有最小化的整数非线性规划问题A,与之相对应的松弛(不考虑整数约束的条件)问题为B.
由于问题A的可行域内有有限个整数解,对于很小规模问题穷举法是可行的,而对于规模较大的问题穷举法是不可行的,因为穷举法的计算量是随决策变量的增加呈指数增加.非线性整数规划问题中,分支定界算法有广泛的应用[10-12].
分支定界算法的思路[13-15]如下:
不考虑整数约束,求解相应的松弛问题(不考虑整数约束的条件).通过非线性优化可以获得相应的最优解,记为x*(0).若求得的最优解x*(0)就是整数解,则该整数解就是整数非线性规划问题的最优解;否则对原问题不断分割可行解空间,划分子问题(称为分支);并为每个子集内解的值计算一个下界或上界(称为定界);对凡是界限超出已知可行解对应函数值的那些子集,不再做进一步分支(称为剪支);逐步减小可行域的上界和增大可行域的下界,缩小搜索范围,最终获得最优的整数解.
4 浮力配平方案计算
水下训练服的相关初始参数如下:
Cm=[155.717 -7.322 61.064 5] mm, Cf=[143.64 0.17 78.05] mm,
ma=199.058 kg, F/g=240 kg.
则有
m=[0.46 0.46 0.46 0.46 0.46 0.46 0.46 0.46 0.46 0.46
0.8 0.8 0.8 0.8] kg,
xlb=[0 0 0 0 0 0 0 0 0 0 0 0 0 0],
xub=[8 8 9 24 24 15 15 15 15 15 7 7 7 7].
各配重袋的相关参数如表1所示.
表1 各配重袋相关参数
Table 1 Relevant parameters of each counterweight bag
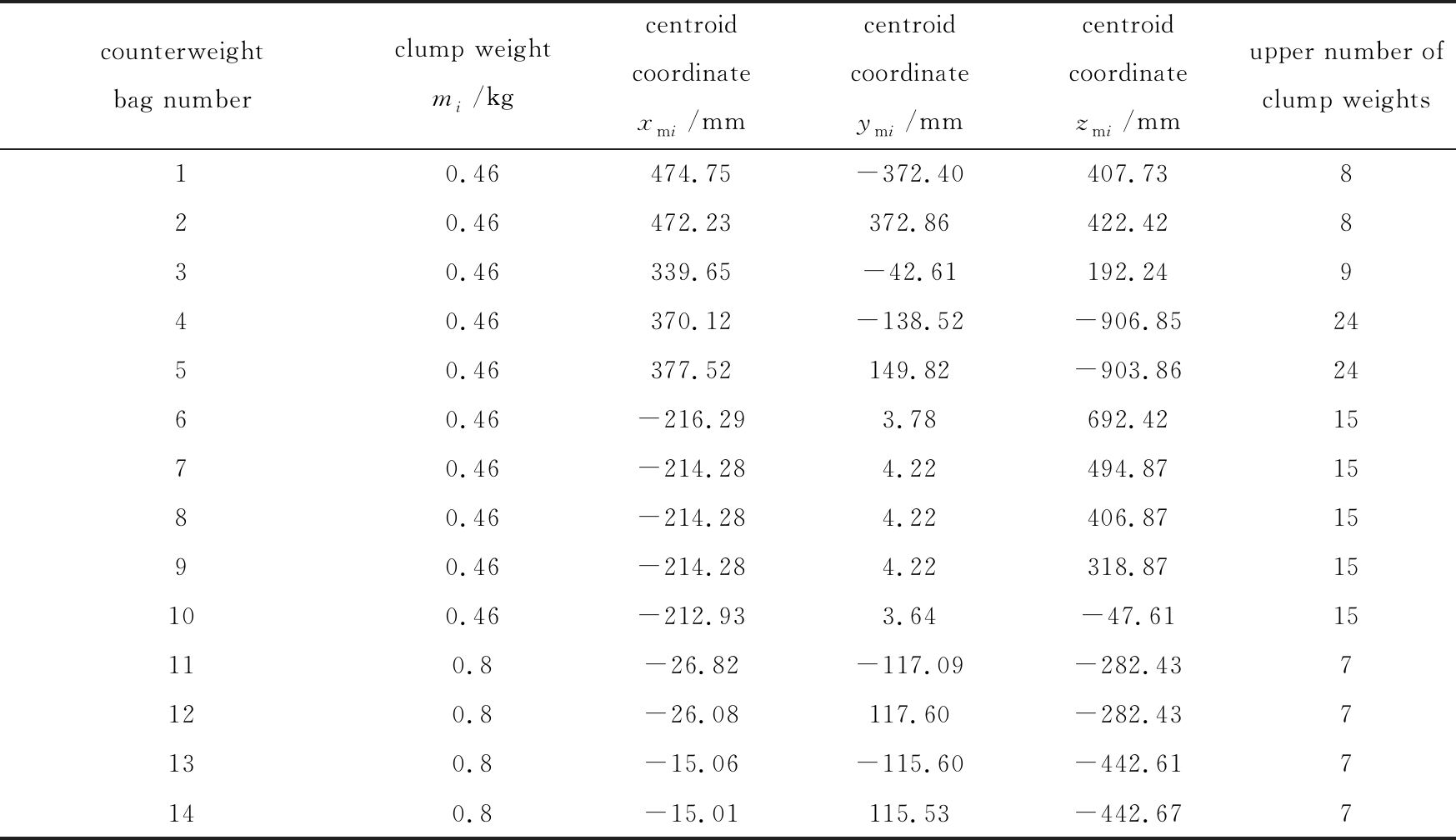
counterweight bag numberclump weight mi/kgcentroid coordinate xmi/mmcentroid coordinate ymi/mmcentroid coordinate zmi/mmupper number of clump weights10.46474.75-372.40407.73820.46472.23372.86422.42830.46339.65-42.61192.24940.46370.12-138.52-906.852450.46377.52149.82-903.862460.46-216.293.78692.421570.46-214.284.22494.871580.46-214.284.22406.871590.46-214.284.22318.8715100.46-212.933.64-47.6115110.8-26.82-117.09-282.437120.8-26.08117.60-282.437130.8-15.06-115.60-442.617140.8-15.01115.53-442.677
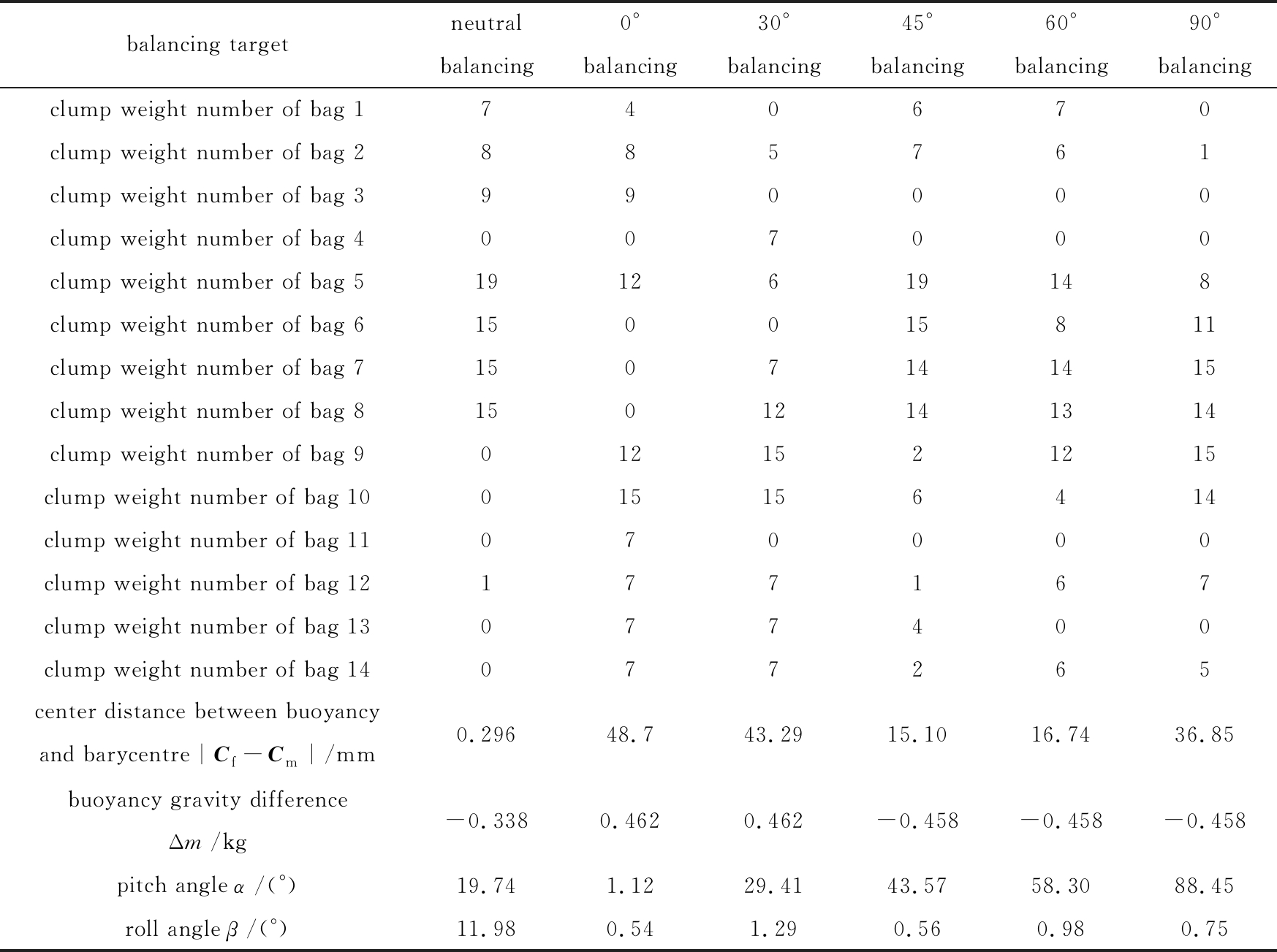
表2 不同目标下的最优配平方案
Table 2 The optimal balancing schemes under different targets
balancing targetneutral balancing0° balancing30° balancing45° balancing60° balancing90° balancingclump weight number of bag 1740670clump weight number of bag 2885761clump weight number of bag 3990000clump weight number of bag 4007000clump weight number of bag 51912619148clump weight number of bag 6150015811clump weight number of bag 71507141415clump weight number of bag 815012141314clump weight number of bag 90121521215clump weight number of bag 10015156414clump weight number of bag 11070000clump weight number of bag 12177167clump weight number of bag 13077400clump weight number of bag 14077265center distance between buoyancy and barycentre |Cf-Cm|/mm0.29648.743.2915.1016.7436.85buoyancy gravity difference Δm/kg-0.3380.4620.462-0.458-0.458-0.458pitch angle α/(°)19.741.1229.4143.5758.3088.45roll angle β/(°)11.980.541.290.560.980.75
相应的允差范围取mtol=0.5 kg,αtol=2°, βtol=2°时,根据第3节中整数非线性规划的计算,可以得到随遇平衡状态和特定角度下的稳定平衡状态的最优配重分配方案如表2所示.
如表2所示,随遇平衡状态浮心和质心距离0.296 mm,可以满足360°旋转的需求;特定角度下的稳定平衡状态角度误差都在相应的角度允差2°范围内,0°,30°,45°,60°,90°的配平方案,可以满足实际水下使用需求.
在其他不同的姿态约束条件下,同样可以通过上述方法得到相应的配平方案.实际计算过程中,在给定的约束范围内,可能不存在满足要求的整数解,此时通过放大角度允差范围的约束来实现最优方案的求解.通过调整优化目标函数和不同的配平允差条件,可以得到同一俯仰角条件下的多种配平方案.
5 结 论
本文基于分支定界算法的整数非线性规划,提出了一种可用于水下训练服浮力配平的有效计算方法.由于数学模型建立过程存在一定的简化和近似,且初始条件的数据获取存在一定的误差,数值计算结果和实际情况会存在一定差异.
在给定初始条件下,针对随遇平衡状态和特定角度下(0°,30°,45°,60°,90°)的稳定平衡状态的需求,计算得到了满足需求的最优配平方案,可以满足实际水下使用要求.
针对不同的配平对象、配平目标都能通过本文的方法实现,仅需要给定准确的初始条件,就可以高效准确地得到相应的配平方案.对于不同结构的水下训练服或其他类似需要配平的场合,不同的配平目标都有较好的指导意义.
[1] 曾磊, 孙鹏飞, 陈明, 等. 空间机械臂水下试验及其关键技术综述[J]. 载人航天, 2016, 22(1): 45-54.(ZENG Lei, SUN Pengfei, CHEN Ming, et al. Review of underwater test and key technologies of space manipulator[J]. Manned Spaceflight, 2016, 22(1): 45-54.(in Chinese))
[2] 齐乃明, 张文辉, 高九州, 等. 空间微重力环境地面模拟试验方法综述[J]. 航天控制, 2011, 29(3): 95-100.(QI Naiming, ZHANG Wenhui, GAO Jiuzhou, et al. The primary discussion for the ground simulation system of spatial microgravity[J]. Aerospace Control, 2011, 29(3): 95-100.(in Chinese))
[3] 马爱军, 卢来洁, 张磊, 等. 美国的中性浮力设备及其应用[J]. 载人航天, 2012, 18(4): 19-25.(MA Aijun, LU Laijie, ZHANG Lei, et al. American neutral buoyancy facility and its applications[J]. Manned Spaceflight, 2012, 18(4): 19-25.(in Chinese))
[4] 于喜海, 陈金盾, 孙海龙, 等. 失重模拟技术的发展及其比较研究[J]. 环境技术, 1998, 2: 22-28.(YU Xihai, CHEN Jindun, SUN Hailong, et al. The current situation of weightlessness simulation technology and its comparative investigation[J]. Environment Simulation Technology, 1998, 2: 22-28.(in Chinese))
[5] 成致祥. 中性浮力微重力环境模拟技术[J]. 航天器环境工程, 2000, 1: 1-6.(CHENG Zhixiang. Weightless environment simulation techniques of neutral buoyancy[J]. Spacecraft Environment Engineering, 2000, 1: 1-6.(in Chinese))
[6] 冯庆义, 李俊峰, 王天舒. 水下模拟失重动力学研究综述[J]. 力学与实践, 2004, 26(3): 10-15.(FENG Qingyi, LI Junfeng, WANG Tianshu. Research on dynamics of underwater weightlessness simulation[J]. Mechanics in Engineering, 2004, 26(3): 10-15.(in Chinese))
[7] 马爱军, 张磊, 刘巍, 等. 水槽训练航天服中性浮力配平方法[J]. 载人航天, 2008, 2: 1-3.(MA Aijun, ZHANG Lei, LIU Wei, et al. Method of neutral buoyancy balancing of underwater training spacesuit[J]. Manned Spaceflight, 2008, 2: 1-3.(in Chinese))
[8] 张磊, 刘海波. 水下训练航天服中性浮力配平仿真方法[J]. 系统仿真技术及其应用, 2015, 16: 38-40.(ZHANG Lei, LIU Haibo. Simulation methods of neutral buoyancy of underwater training spacesuit[J]. System Simulation Technology & Application, 2015, 16: 38-40.(in Chinese))
[9] 张磊, 马爱军, 卢来洁, 等. 水下训练航天服固定配重设计仿真[J]. 航天医学与医学工程, 2015, 28(3): 218-222.(ZHANG Lei, MA Aijun, LU Laijie, et al. Design and simulation of fixed balance weight for underwater training spacesuit[J]. Space Medicine & Medical Engineering, 2015, 28(3): 218-222.(in Chinese))
[10] 马艳利, 高岳林. 一类非线性整数规划问题的切平面分支定界算法[J]. 兰州文理学院学报(自然科学版), 2014, 28(2): 1-6.(MA Yanli, GAO Yuelin. A cutting plane branch and bound algorithm for solving nonlinear integer programming problems[J]. Journal of Lanzhou University of Arts and Science(Natural Science Edition), 2014, 28(2): 1-6.(in Chinese))
[11] 刘俊梅, 高岳林. 非线性混合整数规划问题的改进差分进化算法[J]. 工程数学学报, 2010, 27(6): 967-974.(LIU Junmei, GAO Yuelin. Improved differential evolution algorithm for nonlinear mixed-integer programming problems[J]. Chinese Journal of Engineering Mathematics, 2010, 27(6): 967-974.(in Chinese))
[12] 于战科, 倪明放, 汪泽焱, 等. 整数线性规划的改进分支定界算法[J]. 计算机应用, 2011, 3(2): 36-38.(YU Zhanke, NI Mingfang, WANG Zeyan, et al. Revised branch-and-bound algorithm for integer linear programming[J]. Journal of Computer Applications, 2011, 3(2): 36-38.(in Chinese))
[13] CHAN D Y, KU C Y, LI M C. A method to improve integer linear programming problem with branch and bound procedure[J]. Applied Mathematics and Computation, 2006, 179(2): 484-493.
[14] LI L, WANG C F, TENG C X. The approximate algorithm of global optimization for a sort of nonlinear bilevel mixed integer programming problem[J]. Systems Engineering: Theory & Practice, 2002, 22(4): 19-25.
[15] 吴亮红, 王耀南, 陈正龙. 求解混合整数非线性规划问题的改进差分进化算法[J]. 小型微型计算机系统, 2007, 28(4): 666-669.(WU Lianghong, WANG Yaonan, CHEN Zhenglong. Modified differential evolution algorithm for mixed-integer nonlinear programming problems[J]. Journal of Chinese Computer Systems, 2007, 28(4): 666-669.(in Chinese))