引 言
海水循环冷却系统广泛应用于石油化工、火力发电、工农业生产等领域,海水无填料冷却塔将海水作为冷却介质,缓解了淡水资源紧缺的问题[1].在工作过程中,气流与海水液滴发生相对运动,液滴之间相互碰撞,出现聚合、分离以及破碎等结果[2-4],冷却塔内海水液滴的分布状态不同,流动状态不同,进而冷却塔的冷却性能有所差异.对海水液滴碰撞过程进行研究和分析,能够为冷却塔的设计改进提供参考依据,具有重要的指导意义.
冷却塔中海水液滴的碰撞过程是一个多尺度、多物理的非线性问题.从20世纪60年代至今,国内外学者针对液滴碰撞过程已经开展了部分研究:Adam等[5]进行水滴碰撞实验,条理地总结了二元水滴的碰撞过程,但所得图像不够清晰.Qian等[6]对氮气中正十四烷液滴碰撞过程进行实验研究,总结出液滴碰撞结果类型图.Brazier-Smith等[7]总结实验现象,建立了纯水液滴聚合与分离两种碰撞结果的临界模型,然而对于其他物性液滴的碰撞结果预测有较大误差.相较于实验而言,数值模拟能更好地展示液滴混合状况以及内部流场变化等微观信息.Nikolopoulos等[8-11]数值模拟了液滴对心碰撞过程,观察到液滴黏度越大,二元液滴碰撞更容易聚合达到稳定状态.夏盛勇等[12]通过直接数值模拟,初步总结了三氧化二铝液滴碰撞结果模型.梁伟等[13]开展了气体介质中海水液滴碰撞过程模拟研究,得到了200 μm直径海水液滴碰撞结果分布图,但缺乏流场结构分析,未对碰撞过程影响因素进行讨论.目前,液滴碰撞过程的研究多以水液滴、高黏度液滴以及碳氢液滴为研究对象[14-21],海水液滴碰撞过程研究相对较少,其碰撞结果预测模型还有待完善.
本文利用FLUENT开展了常温常压下等尺寸二元海水液滴对心碰撞直接数值研究,在文献[13]工作的基础上,对液滴碰撞过程流场结构及流动机理进行分析,研究了不同液滴直径和不同海水浓度对碰撞过程的影响,得到了对心碰撞过程聚合和自反分离两种结果的临界We,总结出海水液滴碰撞结果诺模图.
1 数值计算方法与模型
1.1 控制方程
海水无填料冷却系统中的液滴碰撞过程是一个涉及多尺度、非线性问题的复杂流动过程,流体的黏性和表面张力对碰撞过程有很大影响.假设流体为不可压缩常黏度流体,不考虑能量传递,相关控制方程见文献[13].
对于碰撞液滴气液交界面的捕捉,采用VOF方法,其通过求解单独的动量方程和处理穿过区域流体的容积比,每个网格单元的物性变量共享,能高效进行各相间的稳态或瞬态处理,其守恒性好、计算精度高.模拟算例应用VOF方法对气液相界面进行追踪.定义网格内气液两相的体积分数.α为液相在计算网格中的体积率,各个网格对应的密度与黏度表示如下:
ρ(α)=αρl+(1-α)ρg,
(1)
μ(α)=αμl+(1-α)μg,
(2)
其中,ρl,μl,ρg,μg分别表示液体和气体的密度和黏度.
描述液滴碰撞结果的无量纲数除文献[13]述及的Reynolds数,Re;Weber数,We;碰撞参数,x;尺寸比,Δ;还有Ohnesorge数,Oh,其表达式如下:
(3)
其中,ρ为液滴密度,σ为液滴表面张力系数,μ是液滴动力黏度系数,D0为碰撞液滴直径,本文仅研究等尺寸二元液滴对心碰撞过程,尺寸比为1,碰撞参数为0.
本文采用二维轴对称模型进行计算, 计算域范围随海水液滴直径改变而更新, 取(3D0×1.5D0)~(12D0×6D0);二元液滴相距0.25D0.外部气体为常温常压下空气.利用动态网格自适应技术对网格加密.几何模型及网格如图1所示.

图1 几何模型及自适应网格
Fig. 1 The geometry and adaptive mesh of the calculation model diagram
2 计 算 结 果
为了证明数值模型的可靠性,本文从文献[6]中选取g工况进行数值模拟,相关物性参数设置与文献相同.将模拟结果与实验结果对比,如图2所示.观察到相同时刻,液滴在碰撞过程中的形变情况吻合度较好,故认为本文计算模型适于研究液滴碰撞过程.
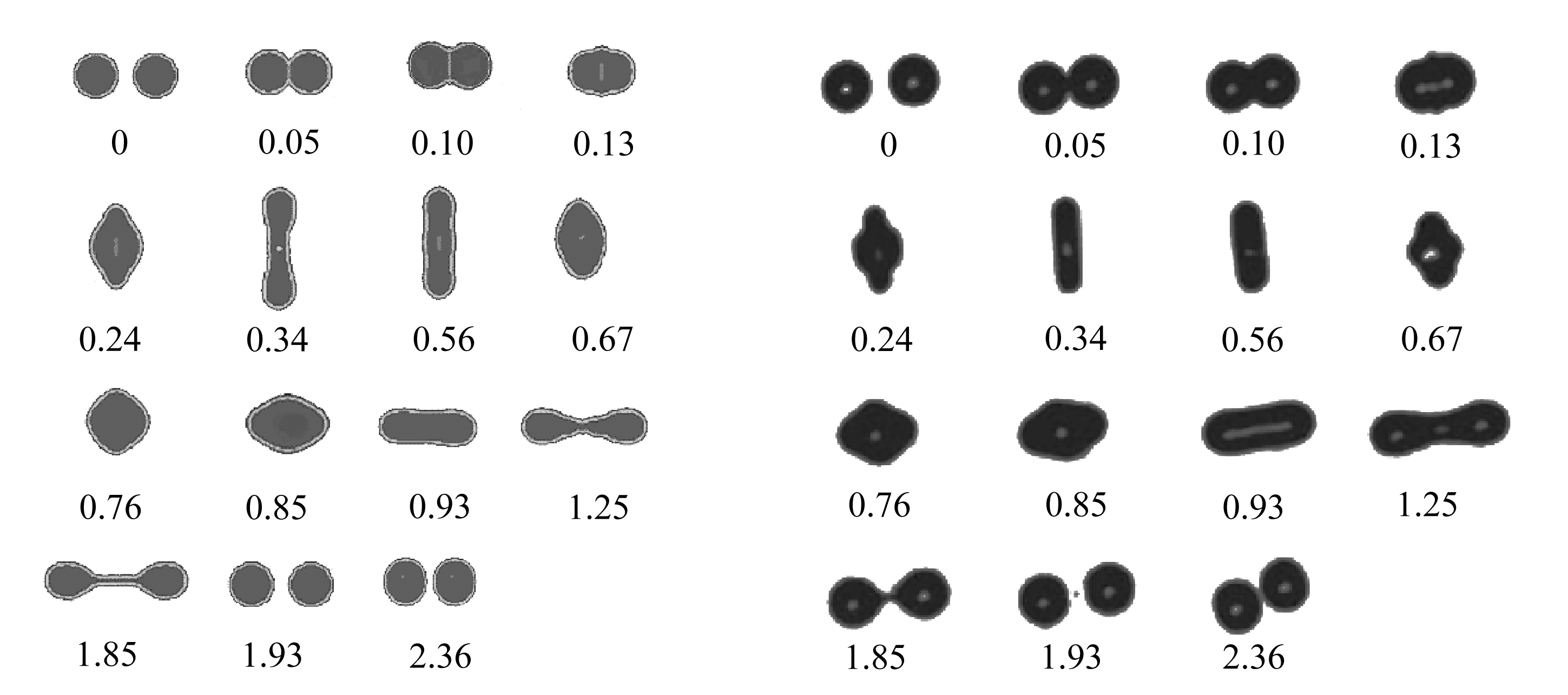
(a) 模拟结果 (b) 实验结果
(a) The simulation results (b) The experimental results
图2 数值计算方法有效性验证(单位: ms)
Fig. 2 The verification of the numerical method(unit: ms)
3 计算结果及分析
3.1 二元海水液滴对心碰撞过程
二元液滴对心碰撞一般会导致聚合、反弹、分离和飞溅等多种结果,当二元液滴以极其微小的速度相互靠近时,两者之间的空气逐渐被挤压,直至完全排出,两液滴无限靠近.当球面距离靠近到几百埃的距离时,急剧增加的Van der Waals力会克服其他作用力将两个液滴拉近至融合.当液滴速度增加时,两液滴之间的压强增大,两个液滴之间会产生一层气体膜,阻止液滴进一步靠近,此时液滴动能减小,一部分转化成表面能,另一部分由于液滴黏性力影响消耗掉,液滴的速度不足以使二者继续相互靠近,最终发生反弹.当液滴速度进一步增加,两液滴的动能不能够全部被抵消,发生聚合,速度继续增大,最终聚合后的液滴会发生自反分离.当液滴速度非常大时,液滴迅速相撞聚合,并且在速度垂直方向上被挤压成一层薄薄的液体膜,由于毛细不稳定作用,液滴发生破碎、飞溅,生成许多伴随细小液滴.对于海水液滴对心碰撞过程,目前只观察到聚合和自反分离两种结果类型.
3.1.1 聚合
直径为200 μm的二元海水液滴对心碰撞后聚合的过程如图3所示.两液滴在0.03 ms时开始接触,二者之间的压强增大,气膜压力升高.随后由各自的球型边缘逐渐开始融合,在0.05 ms时基本聚合成一个圆柱状大液滴,中间气膜区域被完整包裹在内,由于表面张力和黏性力的束缚,液滴动能被消耗,相对速度减小.随后,液滴径向拉细拉长,液滴中心的气膜不断收缩,形成球型小气泡.液滴的动能在0.29 ms时趋于零,大部分转化为液滴的表面能,此时液滴径向变形量到达最大值.随着时间增加,中间液桥连接部位被拉得足够细,致使中间的气泡被撕裂,气体流出,但是表面张力和黏性力限制了上下两部分继续径向分离.随之液滴逐渐径向收缩,缓慢恢复球型状态,由于表面张力的作用,液滴表面能降低并缓慢转化为动能,其中一部分表面能随着黏性作用被耗散.在0.63 ms时,动能的作用小于表面张力和液滴黏性力的约束作用,液滴轴向拉伸量达到最大值,此后液滴逐渐轴向收缩.之后径向与轴向反复振荡,且由于表面张力作用,振荡幅度逐渐变小,直至液滴形变趋于稳定,形成聚合结果.

图3 海水液滴对心碰撞聚合类型(We=22, Oh=0.007 9)(单位: ms)
Fig. 3 Seawater droplets coalescence after head-on collision(We=22, Oh=0.007 9)(unit: ms)
图4给出了液滴径向拉伸变形时的压力云图,当两个液滴相互靠近时,液滴内部的压力迅速增大,两液滴接触发生径向拉伸.从图中发现,压力分布由液滴中心向两端递减, 在压差作用下, 海水液滴继续由中心向两端流动, 液滴继续拉伸, 海水液滴中心气泡撕破, 气体流出,至0.29 ms时达到最大径向拉伸量.

图4 0.26 ms时海水液滴压力云图(We=22, Oh=0.007)
Fig. 4 The pressure contour of seawater droplets at 0.26 ms(We=22, Oh=0.007)
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
图5给出了液滴径向拉伸变形时的速度矢量图,液滴中心速度最低,接近于0,由液滴中心向两端速度先增加后降低,液滴由轴向收缩变为径向拉伸,液滴内部由水平方向到中心流动变为由中心到径向方向流动,由于表面张力作用,速度在接近径向两端之前达到最大值,随后速度逐渐减小,动能转化为表面能,至达到最大径向变形量.此间,在液滴四周形成四个速度矢量小漩涡,且对称性较好.随后液滴开始径向收缩,速度分布及大小与径向拉伸变形时趋势较为一致,之后液滴反复振荡至聚合状态.
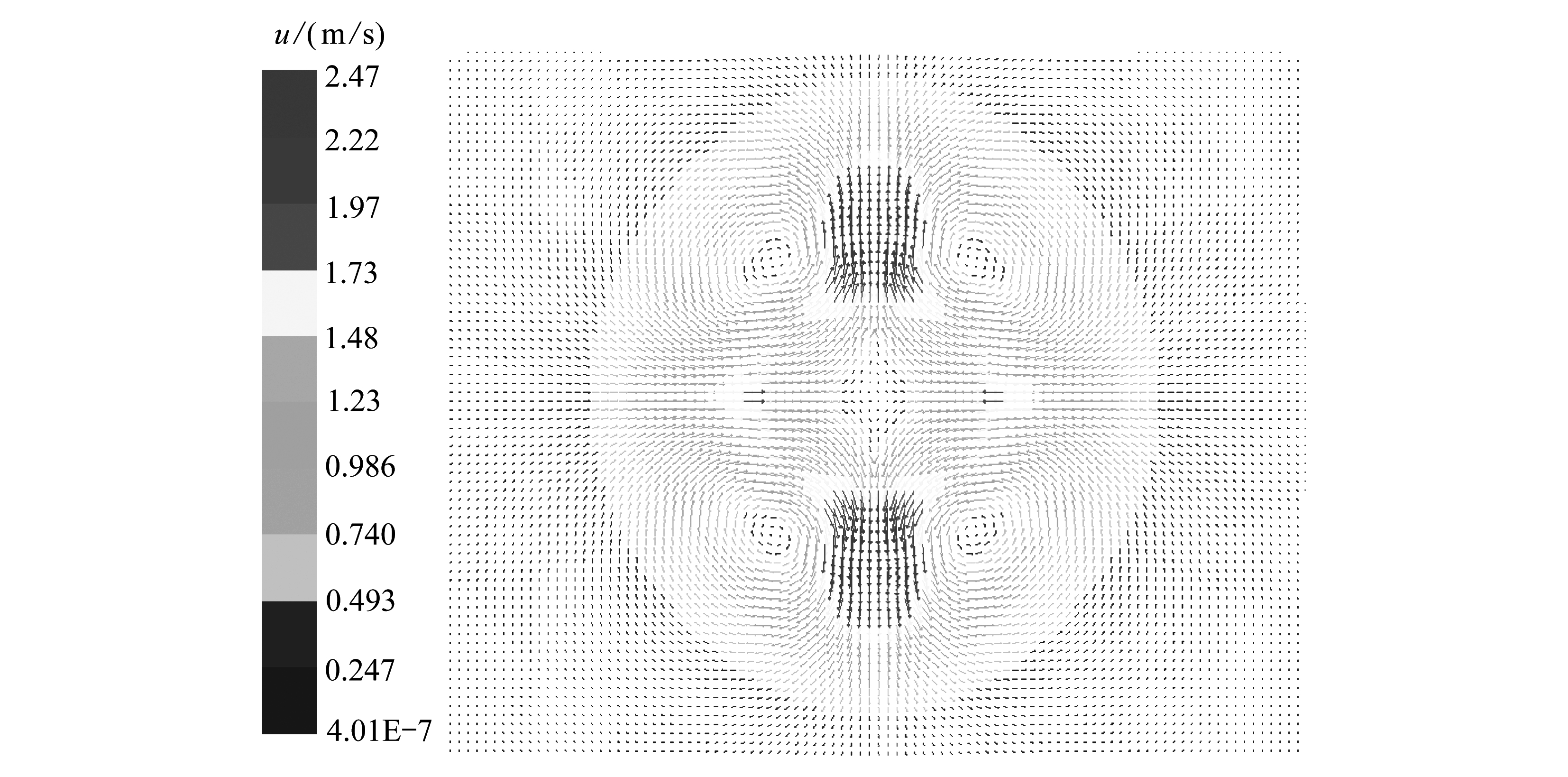
图5 0.26 ms时海水液滴速度矢量图(We=22, Oh=0.007 9)
Fig. 5 The velocity vector field of seawater droplets at 0.26 ms(We=22, Oh=0.007 9)
3.1.2 自反分离
不同We下直径为200 μm的二元海水液滴对心碰撞的自反分离过程如图6所示.两液滴相撞后形成一个圆盘状液滴,中心被拉薄,径向拉伸成哑铃状,达到最大拉伸变形.径向收缩的液滴在压力差影响下转为轴向拉伸,液滴变成长圆柱型,继续轴向拉伸,液滴中间液桥被不断拉细,乃至撕裂,之后由于表面张力作用,形成两个乃至多个子代液滴.
当We为23时,如图6(a)所示.液滴分离前的碰撞变形过程与聚合过程前期相似,在0.02 ms开始接触.液滴在0.28 ms时达到最大径向拉伸量,圆盘状液滴,中心气泡发生破裂,气体流出.此后液滴逐渐从径向收缩转变为轴向拉伸状态,中心液桥部分在0.55 ms时被拉得细长,由于液滴动能作用,液滴逐渐由中间部位向两端聚集,足够打破表面张力的约束作用,中间液桥发生断裂,发生自反分离,最终形成的两个主液滴粒径基本一致.
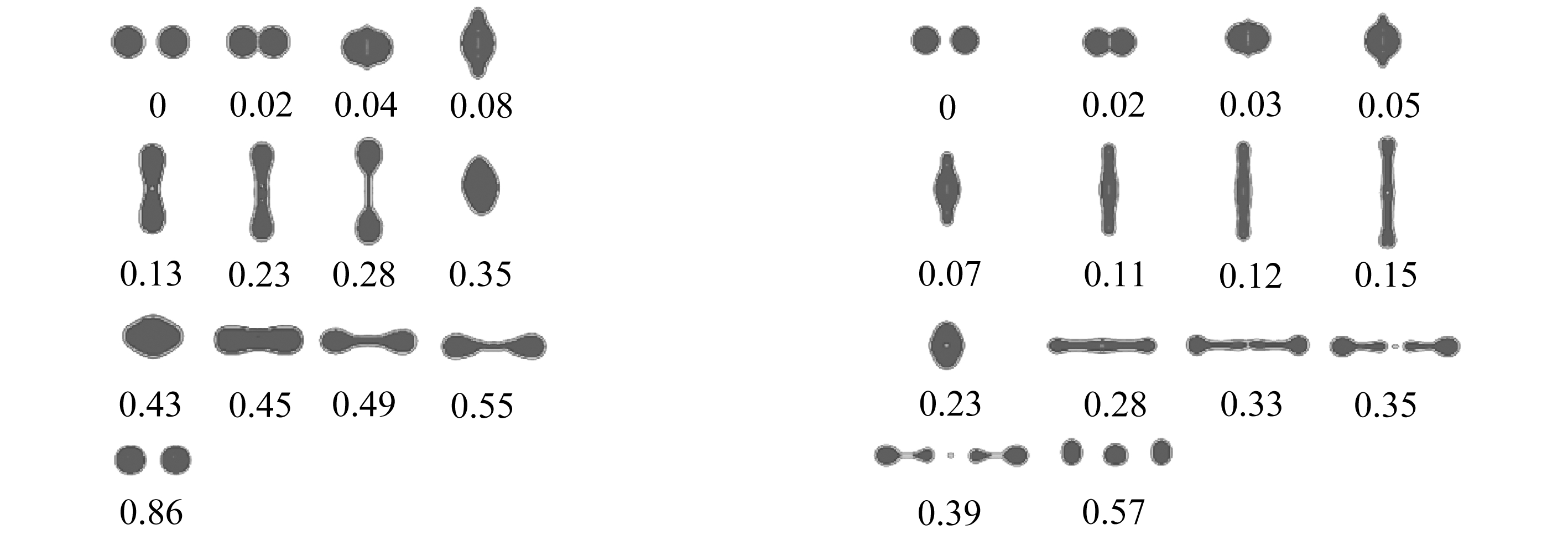
(a) We=23 (b) We=80
图6 海水液滴对心碰撞自反分离类型(Oh=0.007 9)(单位: ms)
Fig. 6 Seawater droplets reflexive separation after head-on collision(Oh=0.007 9)(unit: ms)
我们认为聚合与自反分离的临界We为22.当We=80时,如图6(b)所示.聚合时间提前,液滴轴向拉伸程度增加.0.28 ms时,液桥中间部位粗细程度大于两侧,部分较细的液桥部位发生断裂,两端的液滴发生分离,随之两端液滴逐渐增大.断裂后的细小液滴继续相互靠近,与中间微小的伴随液滴合并形成略大的伴随液滴.笔者在此前的工作中针对不同We下海水液滴对心碰撞过程进行了多组模拟分析,发现随着We增大,液滴开始接触时刻明显缩短,液滴达到最大形变量的时间随之变短,液滴的中间部位被拉伸得更薄,自反分离时刻提前,生成伴随液滴的数目相应增多,轴向分布范围也相应扩大(具体参见文献[13]).

(a) We=28 (b) We=29

(c) We=80 (d) We=100
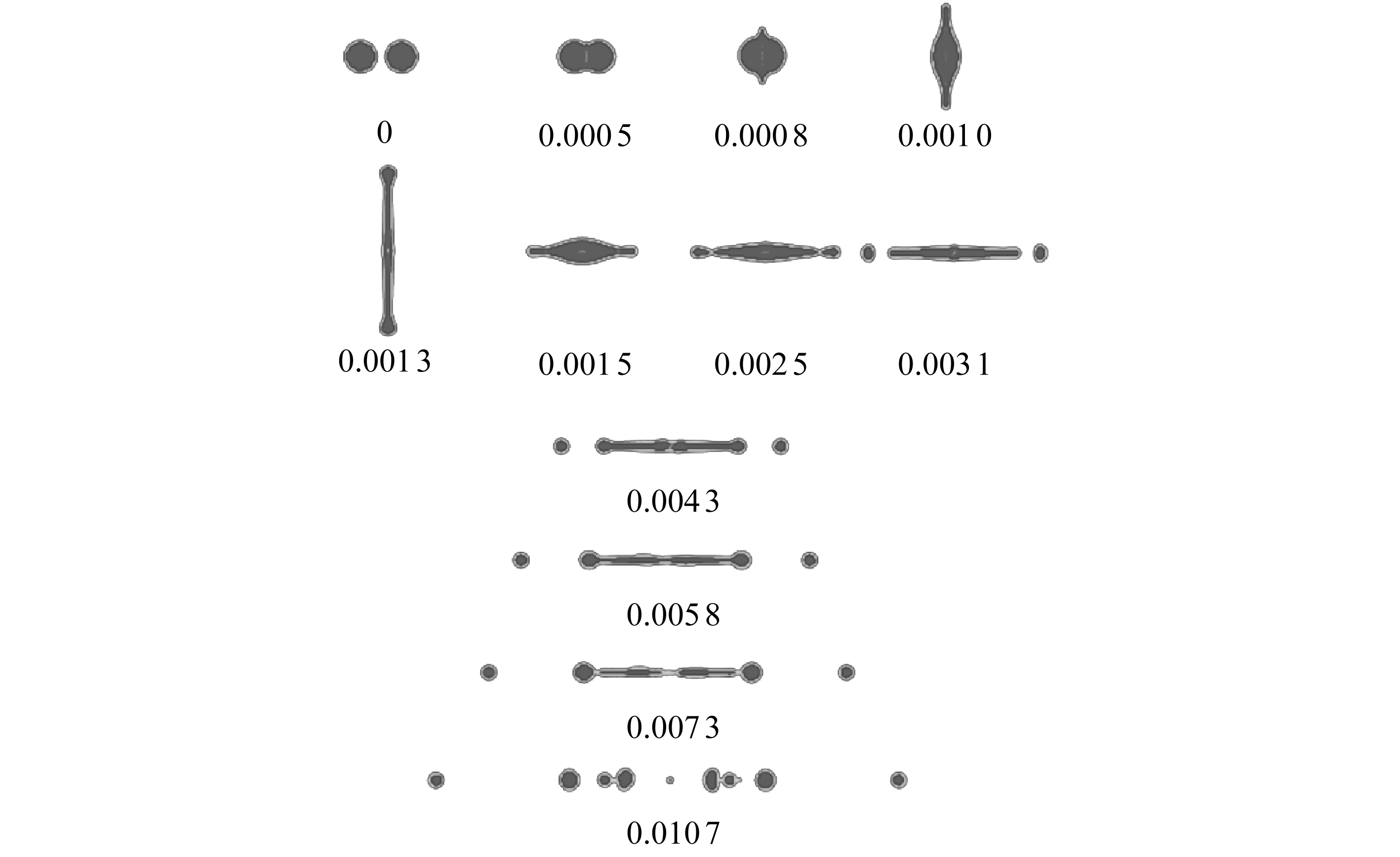
(e) We=200
图7 海水液滴对心碰撞过程(Oh=0.025)(单位: ms)
Fig. 7 Head-on collision of seawater droplets(Oh=0.025)(unit: ms)
3.2 不同液滴直径对碰撞过程的影响
由于海水冷却塔内雾化效果的影响,塔内海水液滴直径不尽相同,液滴与液滴的碰撞规律也会有所差别,对于二元海水液滴的对心碰撞过程,主要受We值和Oh值影响.当液滴直径改变时,Oh值相应改变.直径20 μm的海水液滴碰撞结果类型如图7所示,与前面所述的碰撞过程相比,液滴碰撞过程特征时间明显缩短.聚合与自反分离两种碰撞结果类型的临界We为28,且分离后在原先液桥中心部位产生了一个粒径非常小的伴随液滴.随着We继续增大,产生的伴随液滴数量增加.当We=80时,中间液桥部位在0.011 0 ms时断裂产生三个伴随液滴,在随后变形过程中,由于动能与表面能相互作用,液桥中心两侧的两个大粒径伴随液滴与距离较远的两端主液滴发生合并,最后液滴自反分离结果产生两个较大的主液滴和中间一个粒径非常小的伴随液滴.当We=100时,速度增加,动能增加,液滴轴向所受作用力影响,自反分离结果产生三个伴随液滴,依旧对称分布在中间微小液滴两侧,且两侧伴随液滴直径与两端主液滴的直径相近.随We继续增加,动能增加,液滴碰撞结果产生的伴随液滴数量增加,部分伴随液滴的直径大于两端的主液滴.

(a) We=13 (b) We=14(c) We=50
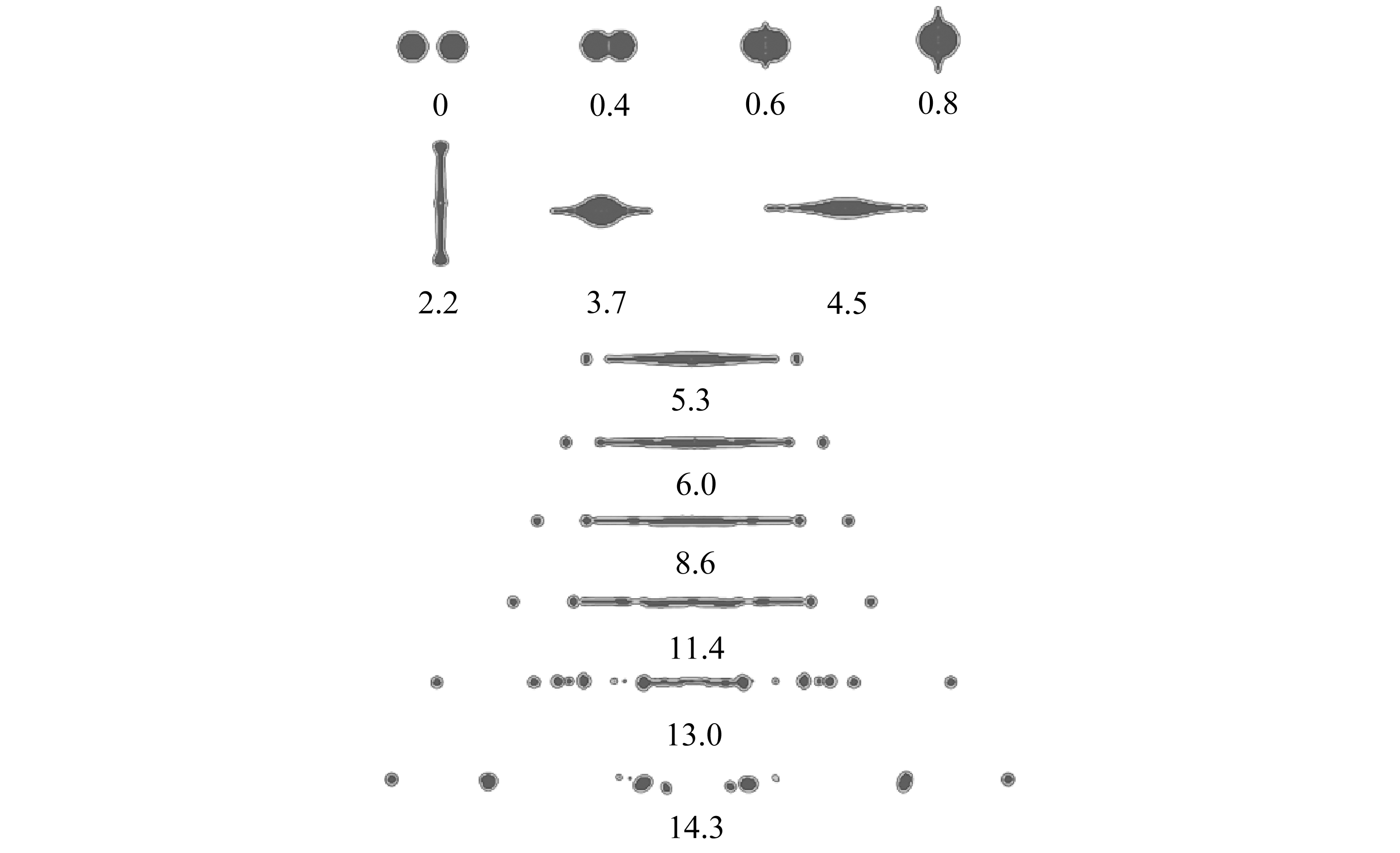
(d) We=200
图8 海水液滴对心碰撞过程(Oh=0.002 5)(单位: ms)
Fig. 8 Head-on collision of seawater droplets(Oh=0.002 5)(unit: ms)
直径为2 000 μm的海水液滴碰撞结果类型如图8所示,与此前分析的液滴碰撞情况相比,两个液滴从开始接触到聚合拉伸到最大形变量的时间明显变长,最终达到稳态结果类型所需时间显著变长.观察到两种结果类型的临界We为13,且此时没有产生伴随液滴.当速度增加,随着We增大,生成伴随液滴的数目也会增加,当We=200时经过自反分离过程产生了八个伴随液滴.
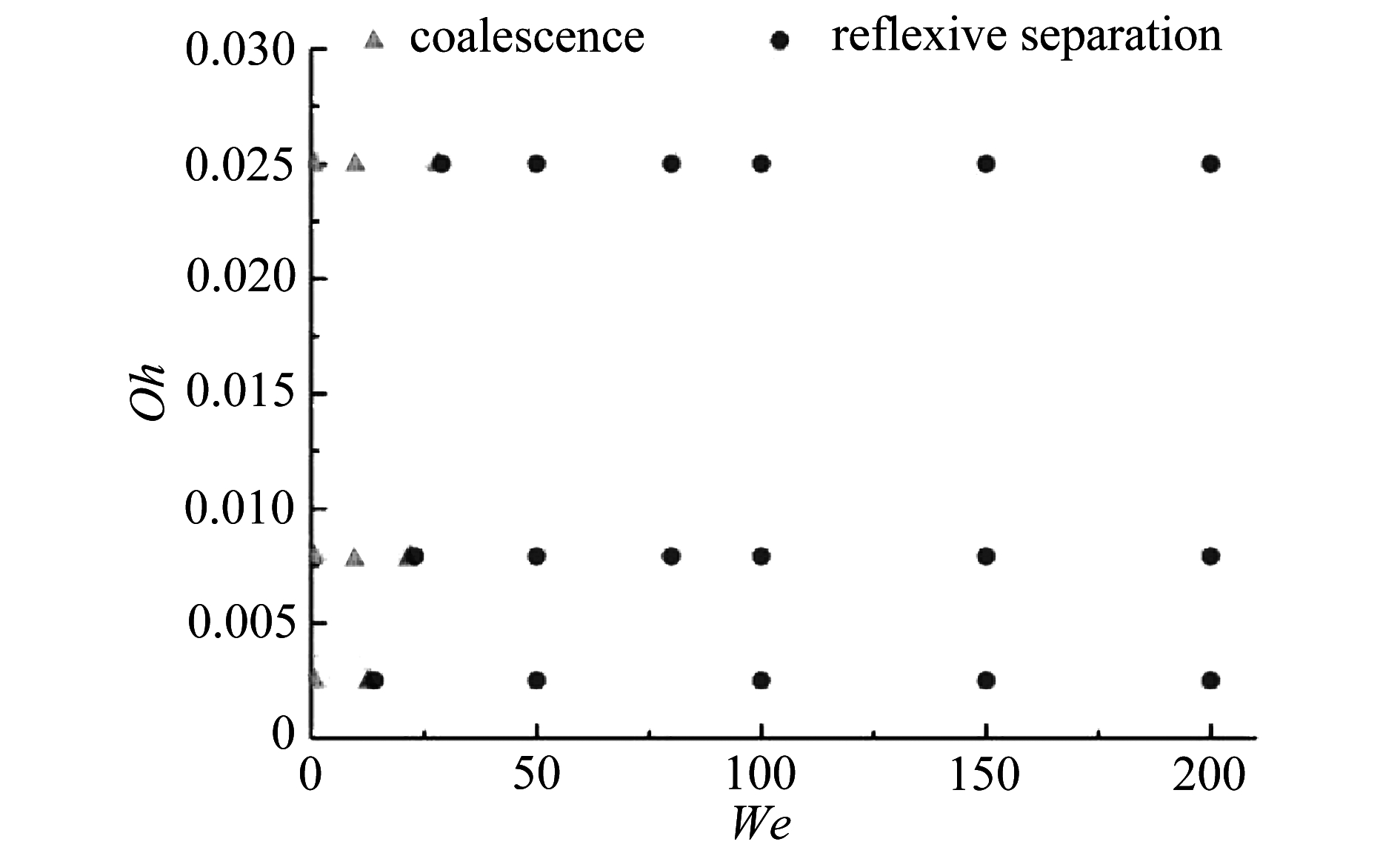
图9 不同Oh下海水液滴碰撞结果分布图
Fig. 9 Head-on collision regimes of seawater droplets for various Ohnesorge numbers
对比20 μm,200 μm(详细碰撞过程见文献[13]),2 000 μm三种不同直径的海水液滴碰撞过程,液滴的变形情况几乎没有改变,碰撞过程的机理也没有差异,但三种液滴直径对应的Oh依次减小,二元液滴相互接触到达到稳定状态的时间明显不同,随液滴直径的增大,由于动能、表面能及黏性力的影响,液滴碰撞特征时间明显推迟,最终达到稳定状态所需的时间也会明显延长,液滴对心碰撞两种结果类型的临界We逐渐降低,分别为28,22,13,聚合后的液滴开始分离所需的速度降低.不同Oh下海水液滴碰撞结果诺模图如图9所示.
3.3 不同海水浓度对碰撞过程的影响
海水冷却塔工作过程中,由于部分水蒸发,使得塔内整体海水浓度升高,相应海水的物性参数会有所改变,进而影响冷却塔整体的冷却效果,研究海水浓度的影响规律是十分有必要的.进行了常温常压下直径为200 μm纯水液滴和浓缩两倍浓度的海水液滴碰撞情况数值模拟,与文献[13]中海水液滴的碰撞过程相对比,相关物性参数如表1所示.
表1 纯水液滴及浓缩两倍海水液滴物性参数
Table 1 Properties of pure water droplets and 2-fold concentrated seawater droplets

phasedensity ρl/(kg/m3)dynamic viscosity μl/(Pa·s)surface tension coefficient σ/(N/m)pure water9.956×1028.940×10-47.173×10-22-fold concentrated seawater1.103×1031.045×10-37.359×10-2
二元纯水液滴碰撞过程如图10所示,同样得到了相同的两种碰撞类型.

(a) We=19 (b) We=20

(c) We=100
图10 纯水液滴碰撞过程(单位: ms)
Fig. 10 Head-on collision of pure water droplets(unit: ms)
同海水液滴相比,理论机制与变形过程基本类似,液滴接触及最终达到稳定状态所需时间不同,观察到两种碰撞结果的临界We为19,较海水低.随着We增大,逐渐产生伴随液滴,当We=100时,生成两个直径较大的伴随液滴及一个直径很小的中心伴随液滴.当We相同时,纯水液滴碰撞过程生成的较大伴随液滴直径明显更大.
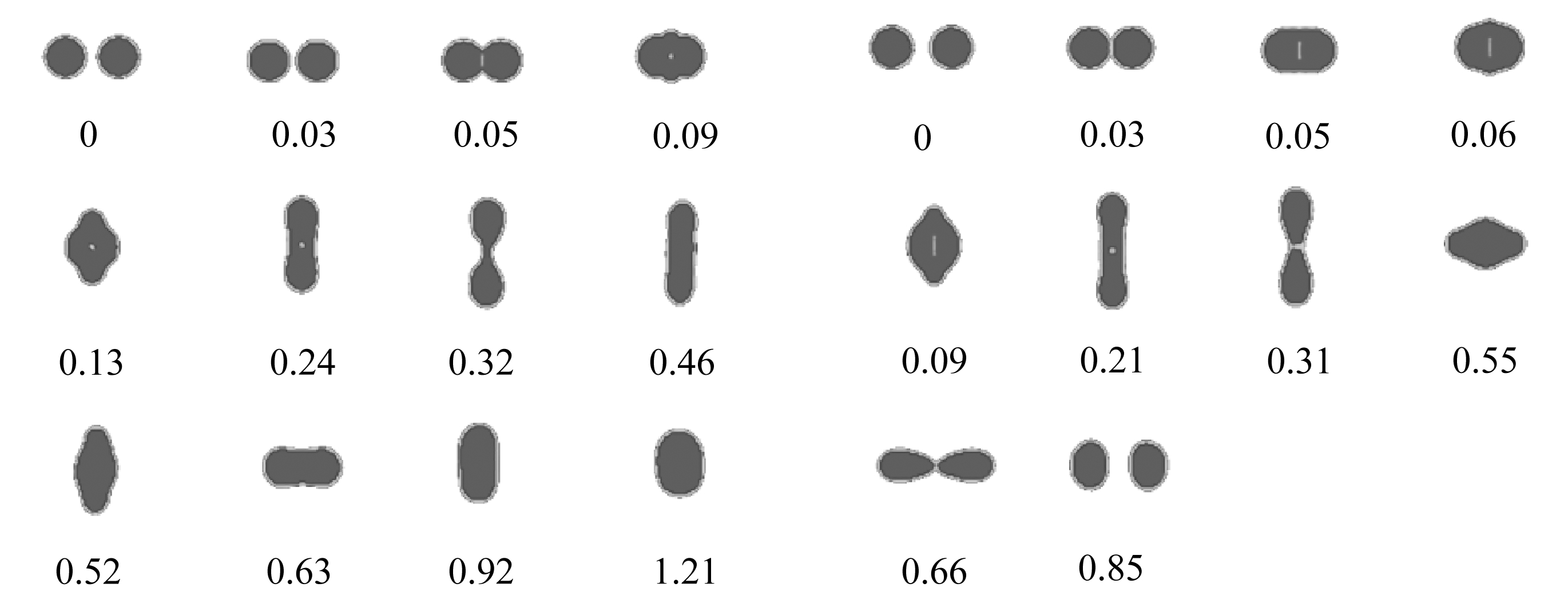
(a) We=24(b) We=25
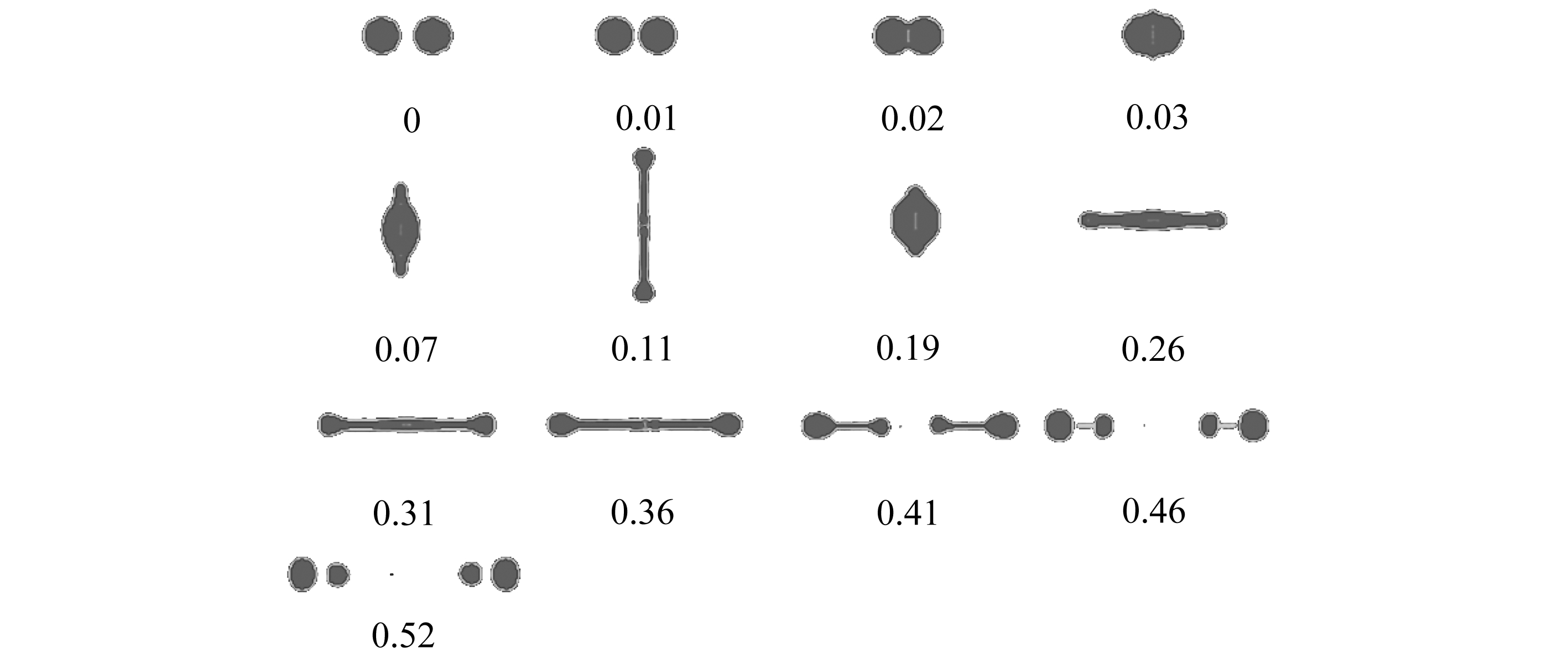
(c) We=100
图11 浓缩两倍的海水液滴碰撞过程(单位: ms)
Fig. 11 Head-on collision of 2-fold concentrated seawater droplets(unit: ms)
浓缩两倍的二元海水液滴碰撞情况如图11所示,同样获得了两种碰撞类型,其临界We为24.碰撞机制及碰撞变形过程基本没有差别.当We=100时,自反分离过程生成了两大一小三个伴随液滴,它们的直径比海水液滴碰撞过程产生的伴随液滴直径略小.
根据纯水、海水及浓缩两倍浓度海水液滴的密度、黏度、表面张力系数、直径等参数计算得到Oh值分别为0.007 5,0.007 9和0.008 2,观察到其对心碰撞过程两种结果类型的临界We依次为19,22,24.
4 结 论
本文对二元液滴对心碰撞机制进行了分析, 阐述了数值模拟方法, 并对数值计算模型进行了可靠性验证, 开展了常温常压下等尺寸二元海水液滴对心碰撞过程数值研究.主要结论如下:
1) 通过开展不同We下海水液滴对心碰撞过程数值模拟,得到了聚合和自反分离两种液滴碰撞结果类型.
2) 在径向拉伸过程中,碰撞中心区域的速度和边缘区域的速度趋于零,液滴四周形成四个速度矢量小漩涡,且对称性良好.
3) 对直径为20,200,2 000 μm的海水液滴对心碰撞过程进行数值研究,得到两种碰撞结果的临界We分别为28,22,13.随液滴直径的增大,碰撞特征时间明显推迟,液滴最终达到稳定状态所需的时间明显延长.
4) 直径均为200 μm的纯水、海水以及浓缩两倍浓度海水液滴的两种碰撞结果的临界We分别为19,22,24.海水浓度增加,Oh值增加,临界We增大,碰撞过程中聚合区域逐渐增大,诺模图中自反分离区域逐渐向高We方向转移,液滴达到自反分离状态所需要的动能增加.
5) 总结出不同Oh下海水液滴碰撞结果诺模图,随着Oh降低,海水液滴碰撞过程两种类型的临界We相应变小,仅需要较低的速度,液滴就会发生分离.
[1] 齐晓霓. 无填料冷却塔的理论与实验研究[D]. 博士学位论文. 上海: 上海交通大学, 2008.(QI Xiaoni. Research on the shower cooling tower[D]. PhD Thesis. Shanghai: Shanghai Jiao Tong University, 2008.(in Chinese))
[2] KOLLAR L E, FARZANEH M, KAREV A R. Modeling droplet collision and coalescence in an icing wind tunnel and the influence of these processes on droplet size distribution[J]. International Journal of Multiphase Flow, 2005, 31(1): 69-92.
[3] PARK J Y, BLAIR L M. The effect of coalescence on drop size distribution in an agitated liquid-liquid dispersion[J]. Chemical Engineering Science, 1975, 30(9): 1057-1064.
[4] FAETH G M. Current status of droplet and liquid combustion[J]. Progress in Energy and Combustion Science, 1977, 3(4): 191-224.
[5] ADAM J R, LINDBLAD N R, HENDRICKS C D. The collision, coalescence, and disruption of water droplets[J]. Journal of Applied Physics, 1968, 39(11): 5173-5180.
[6] QIAN J, LAW C K. Regimes of coalescence and separation in droplet collision[J]. Journal of Fluid Mechanics, 1997, 331(1): 59-80.
[7] BRAZIER-SMITH P R, JENNINGS S G, LATHAM J. The interaction of falling water drops: coalescence[J]. Proceedings of the Royal Society of London, 1972, 326(1566): 393-408.
[8] NIKOLOPOULOS N, NIKAS K S, BERGELES G. A numerical investigation of central binary collision of droplets[J]. Computers & Fluids, 2009, 38(6): 1191-1202.
[9] NIKOLOPOULOS N, THEODORAKAKOS A, BERGELES G. Off-centre binary collision of droplets: a numerical investigation[J]. International Journal of Heat and Mass Transfer, 2009, 52(19/20): 4160-4174.
[10] NIKOLOPOULOS N, BERGELES G. The effect of gas and liquid properties and droplet size ratio on the central collision between two unequal-size droplets in the reflexive regime[J]. International Journal of Heat and Mass Transfer, 2011, 54(1/3): 678-691.
[11] NIKOLOPOULOS N, STROTOS G, NIKAS K S, et al. The effect of Weber number on the central binary collision outcome between unequal-sized droplets[J]. International Journal of Heat and Mass Transfer, 2012, 55(7/8): 2137-2150.
[12] 夏盛勇, 胡春波. 三氧化二铝液滴对心碰撞直接数值模拟[J]. 应用数学和力学, 2014, 35(4): 377-388.(XIA Shengyong, HU Chunbo. Direct numerical simulation of head-on binary collision of aluminum oxide droplets[J]. Applied Mathematics and Mechanics, 2014, 35(4): 377-388.(in Chinese))
[13] 梁伟, 齐晓霓, 尹强, 等. 气体介质中海水液滴碰撞过程数值模拟[J]. 应用数学和力学, 2018, 39(11): 1236-1245.(LIANG Wei, QI Xiaoni, YIN Qiang, et al. Numerical simulation of seawater droplets collision in gaseous environment[J]. Applied Mathematics and Mechanics, 2018, 39(11): 1236-1245.(in Chinese))
[14] ASHGRIZ N, POO J Y. Coalescence and separation in binary collisions of liquid drops[J]. Journal of Fluid Mechanics, 1990, 221(221): 183-204.
[15] BRENN G, KOLOBARIC V. Satellite droplet formation by unstable binary drop collisions[J]. Physics of Fluids, 2006, 18(8): 087101.
[16] PLANCHETTE C, LORENCEAU E, BRENN G. The onset of fragmentation in binary liquid drop collisions[J]. Journal of Fluid Mechanics, 2012, 702: 5-25.
[17] ZHANG P, LAW C K. An analysis of head-on droplet collision with large deformation in gaseous medium[J]. Physics of Fluids, 2011, 23(4): 042102.
[18] TANG C L, ZHANG P, LAW C K. Bouncing, coalescence, and separation in head-on collision of unequal-sized droplets[J]. Physics of Fluids, 2012, 24(2): 022101.
[19] LIU D, ZHANG P, LAW C K, et al. Collision dynamics and mixing of unequal-size droplets[J]. International Journal of Heat and Mass Transfer, 2013, 57(1): 421-428.
[20] ORME M. Experiments on droplet collisions, bounce, coalescence and disruption[J]. Progress in Energy & Combustion Science, 1997, 23(1): 65-79.
[21] WILLIS K D, ORME M. Binary droplet collisions in a vacuum environment: an experimental investigation of the role of viscosity[J]. Experiments in Fluids, 2003, 34(1): 28-41.