引 言
我国是发展中国家，国民经济发展在相当长一段时间内仍将依赖于能源与矿产资源的开发和利用．煤炭作为我国的主体能源，其在一次性能源结构中占到70%左右[1-2]，且在今后相当长的时间内，煤炭在我国一次性能源结构中仍会占据不可替代的重要地位．在煤矿工程实际中往往遇到一系列连续弯曲岩层——褶皱构造，且褶皱构造中赋存着相当比例的煤炭资源，煤矿的开采不可避免地受到弯曲岩层不同程度的影响，这一点在煤矿实际生产中早已证实．与水平层状岩层相比，弯曲岩层的特征不仅仅有曲率，而且在褶皱构造中存在水平构造应力．在弯曲岩层中开采煤层时，覆岩变形规律与水平层状岩层中的变形规律不尽相同．因此，煤层开采后弯曲岩层中覆岩变形成为科学研究亟待解决的重点内容之一．
曲率对结构构件的应力分析已是经典课题，在结构力学方面,研究文献表明研究者正在不断改进他们的计算方法．最早有两种理论方法可用于曲梁和曲杆的应力分析：Winckler的材料强度理论[3]和Timoshenko的弹性公式[4]．Winckler的强度理论主要给出了细梁环向应力的解析表达式，对于厚曲梁却不适用．改进的Timoshenko弹性理论已成为与修正的Winckler理论对比分析的一个参考标准．Chianese和Erdlac给出了沿直径方向两个集中力压缩作用下圆内应力分布的无穷级数通解[5]．Bagci提出了一个在弯矩和集中力同时作用下考虑曲率影响的曲梁应力强度，但它是一个近似解答，因为应力状态被任意假设为平面应力状态[6-8]．Tutuncu提出了极坐标下基于应力函数的等截面窄曲梁的平面应力分析解答[9]．Sloboda和Honarmandi开发了一个适用于非矩形截面曲梁的弹性基本方法，但是边界条件却只能承受荷载条件[10]．钟万勰等将Hamilton体系引入到弹性平面条形区域问题中，并研究了在辛几何空间中正交归一及展开等性质，将问题化为本征值和本征向量的求解，但该方法存在约当型链断绝的缺陷[11-12]．
就弹性力学方法而言，应力函数公式已经成功地应用于曲梁分析[13]，但边界条件只能是应力边界条件的形式．当边界约束为径向或环向位移(应变)条件时，应力函数方法不能取得令人满意的解答．而另一方面，直接的位移参数方法只涉及到从两个偏微分平衡方程中找出两个位移参数(径向位移和环向位移)．但是，从两个变系数的二阶偏微分方程中解出两个位移参数是非常困难的事情，尤其是当边界条件为位移条件和应力条件的混合边值类型时．由于结构力学大多数实际问题的边界条件是混合边值类型，因此，传统的方法对于求解混合边值问题是不准确的，也不可靠[14-17]．
实际应用中大多数问题都是混合边值类型．这些结构的设计和分析主要是用数值计算的方法来完成的．在各种方法中，有限单元法(FEM)和有限差分法(FDM)是最主要的数值方法．FEM在各个方面得到了广泛的应用，特别是在曲线结构中[18-21]．Gangan指出FEM的计算误差会随着弯曲变形的增加而增大[22]．FDM在结构构件应力分析方面的准确性比FEM的精度更高[23-24]，这一点已经得到证实．近年来，一些研究人员在使用FDM对二维、三维结构的应力分析方面产生了新的兴趣[25-28]．与传统计算方法相比，基于势函数的FDM在预测边界条件过渡区域的应力更加合理．FDM在自然科学和工程领域内边值问题方面的应用，特别是在由二阶偏微分方程控制的边值问题方面，不断出现改进的求解方法[29-33]．
本文引入适用于极坐标下曲梁的位移函数，得出曲梁的偏微分控制方程和用位移函数表示位移分量、应力分量的表达式；在此基础上，采用差分原理进行数值计算，应用曲梁理论分析弯曲岩层中煤层开采后覆岩的位移和应力分布规律．
1 用位移函数表示的曲梁弹性解答
1.1 位移函数的控制方程
用极坐标求解平面应变问题时，由弹性理论[3-4]中的平衡方程、物理方程和几何方程，可在不计体力的情况下分析得出：
(1a)
(1b)
式中,ur，uθ分别表示径向位移和环向位移；r，θ分别表示径向坐标和环向坐标；μ为Poisson比．
式(1)是极坐标下平面应变弹性问题用位移分量求解的控制方程，满足式(1)和边界条件的位移分量应该是问题的精确解答．但是，式(1)是变系数的椭圆型偏微分方程，与此同时，边界条件往往是应力边界条件和位移边界条件的混合模式，因此，该问题精确解答在理论上是不容易得到的．如果想要获得解答，需要将式(1)和边界条件中两个变量的形式转化为一个变量的形式．
为了将控制方程中的两个变量ur和uθ用一个变量来表示，这里引入位移函数ψ(r,θ)，定义如下：
(2a)
(2b)
系数αi(i=1,2,3,…,12)是材料常数[26]．
将式(2)代入到式(1)，用位移函数表示的控制方程如下：
(3a)
(3b)
这里，用两个控制方程求解一个变量ψ(r,θ)时，需要合理选取某些系数αi(i=1,2,3,…,12)，使得两个控制方程中的一个方程为多余的方程．从数学角度来讲，就是要求式(3)中的一个方程能够自动满足等式．但是，从式(3)中可以看出，位移函数ψ(r,θ)的偏导数不全部为0．因此，要想实现两个控制方程中一个方程为自动满足等式，必须要求其中一个方程的系数全部为0．
设式(3a)自动满足等式，而式(3b)则为位移函数ψ(r,θ)的控制方程．由式(3a)的全部系数为0，得到位移函数ψ(r,θ)的控制方程为
(4)
式(4)给出了极坐标下平面弹性问题用位移函数控制方程的表达式，可以得出位移函数控制方程是与弹性模量E、Poisson比μ等材料常数无关的偏微分方程．
设式(3b)自动满足等式，而式(3a)则为位移函数ψ(r,θ)的控制方程．由式(3b)的全部系数为0，得出的位移函数控制方程与式(4)完全相同．即，用位移函数表示的控制方程是唯一的．
1.2 用位移函数表示的位移分量和应力分量
想要求解位移函数控制方程式(4)，需要知道弹性体的位移边界条件和应力边界条件．但是，弹性体的位移边界条件往往是已知的位移、应力边界条件往往是已知的载荷，因此，需要将弹性体的已知位移和已知载荷表示为位移函数的偏导数形式．
极坐标下平面应变弹性问题的位移分量为径向位移ur和环向位移uθ，应力分量为径向应力σr、环向应力σθ和剪应力τrθ．
位移分量表达式为
(5a)
(5b)
应力分量表达式为
(6a)
(6b)
(6c)
1.3 差分原理
1.3.1 控制方程的差分格式
位移函数控制方程适用于求解域内的离散点，由9部分组成：位移函数1～4阶的8个偏导数和它本身．控制方程中各个偏导数均采用中心差分公式，截断误差为O(h2)或O(k2)，差分原理如图1所示，得出求解域内离散点处控制方程的差分方程：
ξ1ψ(i+2, j)+ξ2ψ(i+1, j+1)+ξ3ψ(i+1, j)+ξ2ψ(i+1, j-1)+
ξ4ψ(i, j+2)+ξ5ψ(i, j+1)+ξ6ψ(i, j)+ξ5ψ(i, j-1)+
ξ4ψ(i, j-2)+ξ7ψ(i-1, j+1)+ξ8ψ(i-1, j)+
ξ7ψ(i-1, j-1)+ξ9ψ(i-2, j)=0，
(7)
式中
ξ2=rih2k2(2ri-3h),
ξ4=h4,
ξ7=rih2k2(2ri+3h),
h，k分别为r方向、θ方向的网格长度．
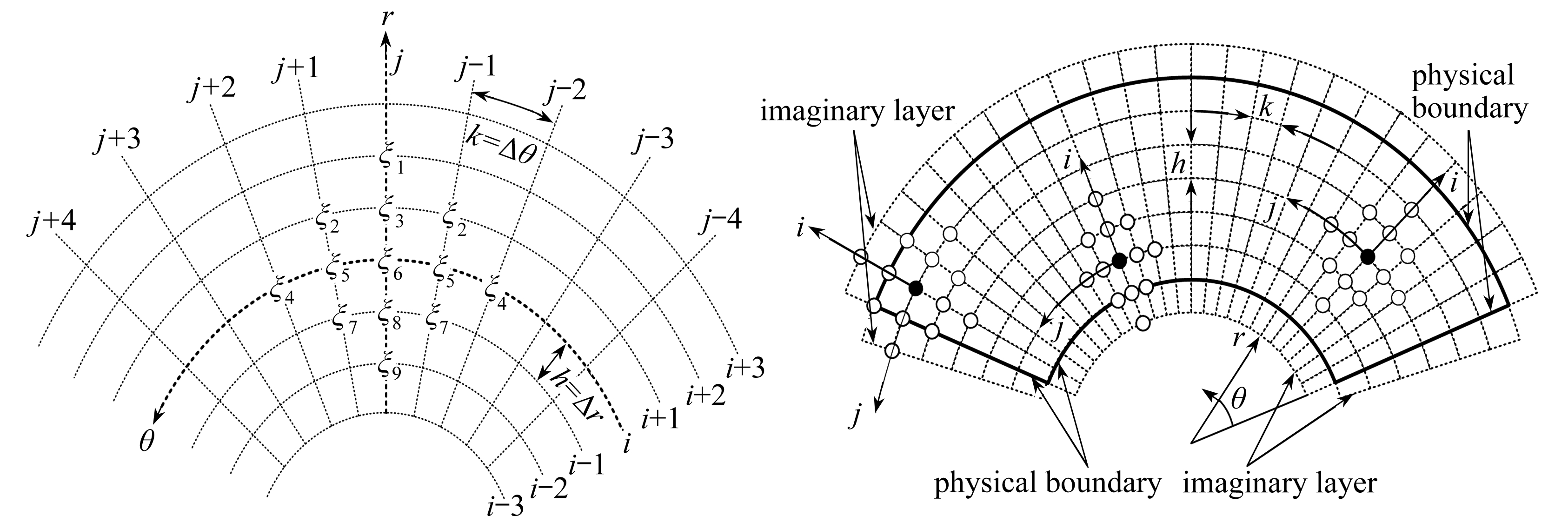
图1 控制方程的有限差分原理
Fig. 1 The finite difference scheme of the governing equation
1.3.2 位移分量的差分格式
对于径向位移ur，在不同区域的边界上，采用不同的差分公式，包括：r方向和θ方向的向前差分、向后差分的混合模式，这里给出4种径向位移ur的差分格式，差分原理如图2所示．
(a) r-向前差分，θ-向前差分
ur(i, j)=a1ψ(i+2, j+2)-4a1ψ(i+2, j+1)+3a1ψ(i+2, j)-
4a1ψ(i+1, j+2)+16a1ψ(i+1, j+1)-12a1ψ(i+1, j)+
(3a1-b1)ψ(i, j+2)-(12a1-4b1)ψ(i, j+1)+
(9a1-3b1)ψ(i, j)；
(8a)
(b) r-向前差分，θ-向后差分
ur(i, j)=-3a1ψ(i+2, j)+4a1ψ(i+2, j-1)-a1ψ(i+2, j-2)+
12a1ψ(i+1, j)-16a1ψ(i+1, j-1)+4a1ψ(i+1, j-2)-
(9a1-3b1)ψ(i, j)+(12a1-4b1)ψ(i, j-1)-
(3a1-b1)ψ(i, j-2)；
(8b)
(c) r-向后差分，θ-向前差分
ur(i, j)=-(3a1+b1)ψ(i, j+2)+(12a1+4b1)ψ(i, j+1)-
(9a1+3b1)ψ(i, j)+4a1ψ(i-1, j+2)-16a1ψ(i-1, j+1)+
12a1ψ(i-1, j)-a1ψ(i-2, j+2)+
4a1ψ(i-2, j+1)-3a1ψ(i-2, j)；
(8c)
(d) r-向后差分，θ-向后差分
ur(i, j)=(9a1+3b1)ψ(i, j)-(12a1+4b1)ψ(i, j-1)+
(3a1+b1)ψ(i, j-2)-12a1ψ(i-1, j)+16a1ψ(i-1, j-1)-
4a1ψ(i-1, j-2)+3a1ψ(i-2, j)-
4a1ψ(i-2, j-1)+a1ψ(i-2, j-2)，
(8d)
式中
对于环向位移uθ，这里采用中心差分法计算偏导数，差分原理如图3所示．
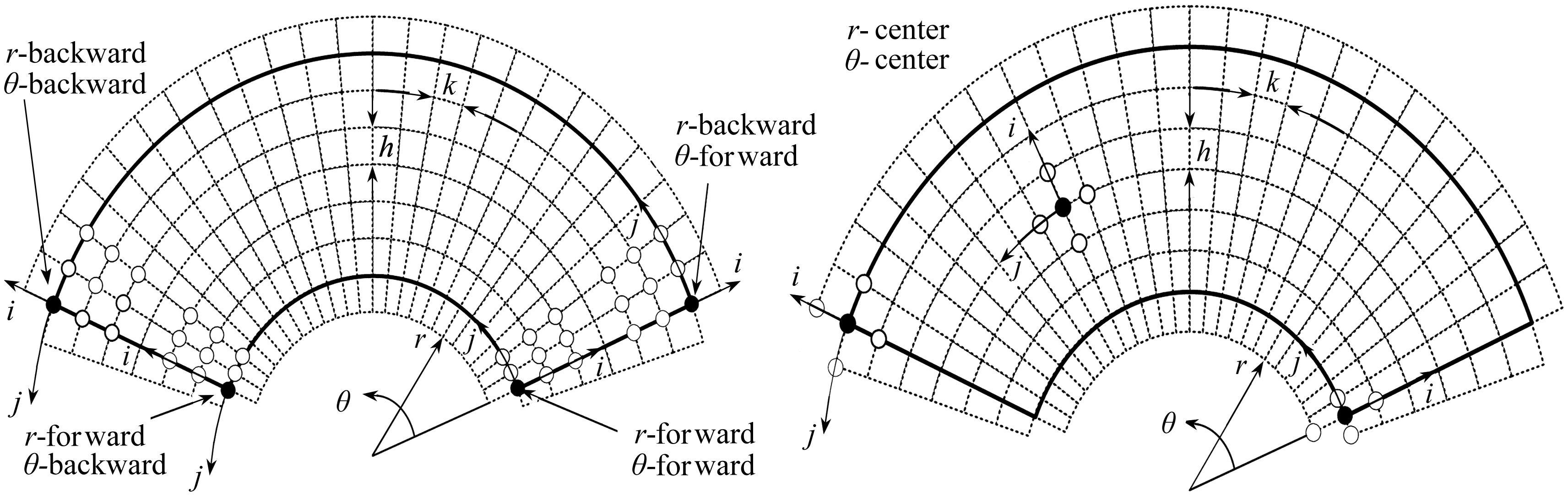
图2 径向位移差分原理 图3 环向位移差分原理
Fig. 2 The finite difference scheme of the Fig. 3 The finite difference scheme of the radial displacement circumferential displacement
uθ(i, j)=(a2+c2)ψ(i+1, j)+b2ψ(i, j+1)+
(-2a2-2b2+d2)ψ(i, j)+b2ψ(i, j-1)+(a2-c2)ψ(i-1, j)，
(9)
式中
1.3.3 应力分量的差分格式
这里采用中心差分、向前差分和向后差分混合使用的方式来计算应力分量中的偏导数，给出3种应力分量的差分格式．需要说明的是，3种应力的差分格式分为：r中心差分-θ向前差分、r中心差分-θ向后差分、r向前差分-θ中心差分、r向后差分-θ中心差分等情况．但在计算过程中，为了保证计算域涉及的节点不超出虚边界，对某些偏导数的差分采用混合差分格式，径向应力和环向应力的差分原理如图4所示，剪应力的差分原理如图5所示．
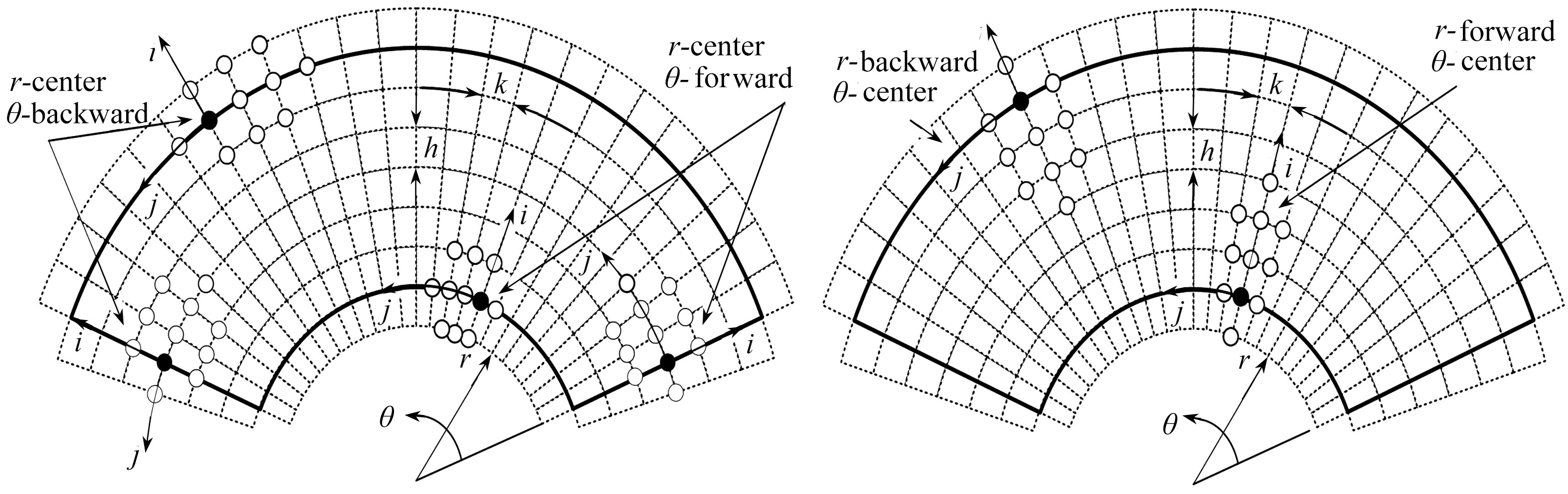
图4 径向应力和环向应力差分原理图5 剪应力差分原理
Fig. 4 The finite difference scheme of the radial Fig. 5 The finite difference scheme and circumferential stresses of the shear stress
1) 径向应力分量σr的差分方程
(a) r-中心差分，θ-向前差分
σr(i, j)=(-A1-C1)ψ(i+1, j+2)+(4A1+4C1)ψ(i+1, j+1)+
(-3A1-3C1)ψ(i+1, j)-B1ψ(i, j+3)+(2A1+6B1)ψ(i, j+2)+
(-8A1-12B1+D1)ψ(i, j+1)+(6A1+10B1)ψ(i, j)+
(-3B1-D1)ψ(i, j-1)+(-A1+C1)ψ(i-1, j+2)+
(4A1-4C1)ψ(i-1, j+1)+(-3A1+3C1)ψ(i-1, j)；
(10a)
(b) r-中心差分，θ-向后差分
σr(i, j)=(3A1+3C1)ψ(i+1, j)+(-4A1-4C1)ψ(i+1, j-1)+
(A1+C1)ψ(i+1, j-2)+(3B1+D1)ψ(i, j+1)+
(-6A1-10B1)ψ(i, j)+(8A1+12B1-D1)ψ(i, j-1)+
(-2A1-6B1)ψ(i, j-2)+B1ψ(i, j-3)+(3A1-3C1)ψ(i-1, j)+
(-4A1+4C1)ψ(i-1, j-1)+(A1-C1)ψ(i-1, j-2)，
(10b)
式中
2) 环向应力分量σθ的差分方程
(a) r-中心差分，θ-向前差分
σθ(i, j)=(-A2-C2)ψ(i+1, j+2)+(4A2+4C2)ψ(i+1, j+1)+
(-3A2-3C2)ψ(i+1, j)-B2ψ(i, j+3)+(2A2+6B2)ψ(i, j+2)+
(-8A2-12B2+D2)ψ(i, j+1)+(6A2+10B2)ψ(i, j)+
(-3B2-D2)ψ(i, j-1)+(-A2+C2)ψ(i-1, j+2)+
(4A2-4C2)ψ(i-1, j+1)+(-3A2+3C2)ψ(i-1, j)；
(11a)
(b) r-中心差分，θ-向后差分
σθ(i, j)=(3A2+3C2)ψ(i+1, j)+(-4A2-4C2)ψ(i+1, j-1)+
(A2+C2)ψ(i+1, j-2)+(3B2+D2)ψ(i, j+1)+
(-6A2-10B2)ψ(i, j)+(8A2+12B2-D2)ψ(i, j-1)+
(-2A2-6B2)ψ(i, j-2)+B2ψ(i, j-3)+
(3A2-3C2)ψ(i-1, j)+(-4A2+4C2)ψ(i-1, j-1)+
(A2-C2)ψ(i-1, j-2)，
(11b)
式中
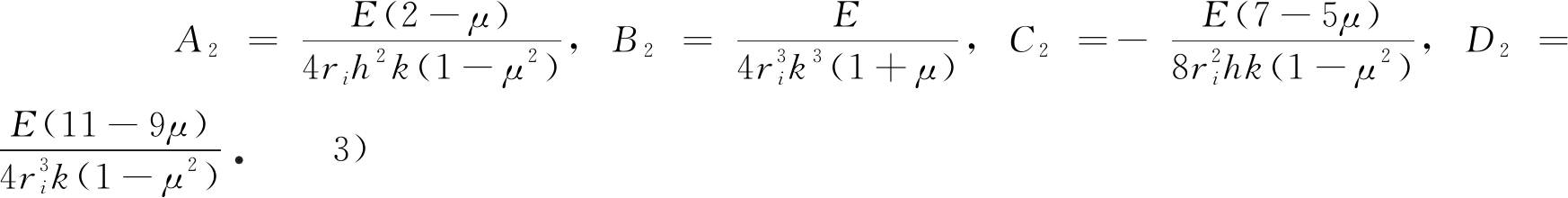剪应力τrθ的差分方程
(a) r-向前差分，θ-中心差分
τrθ(i, j)=-A3ψ(i+3, j)-B3ψ(i+2, j+1)+(6A3+2B3)ψ(i+2, j)-
B3ψ(i+2, j-1)+4B3ψ(i+1, j+1)+
(-12A3-8B3+C3+E3)ψ(i+1, j)+4B3ψ(i+1, j-1)+
(-3B3+D3)ψ(i, j+1)+(10A3+6B3-2C3-2D3+F3)ψ(i, j)+
(-3B3+D3)ψ(i, j-1)+(-3A3+C3-E3)ψ(i-1, j)；
(12a)
(b) r-向后差分，θ-中心差分
τrθ(i, j)=(3A3+C3+E3)ψ(i+1, j)+(3B3+D3)ψ(i, j+1)+
(-10A3-6B3-2C3-2D3+F3)ψ(i, j)+(3B3+D3)ψ(i, j-1)-
4B3ψ(i-1, j+1)+(12A3+8B3+C3-E3)ψ(i-1, j)-
4B3ψ(i-1, j-1)+B3ψ(i-2, j+1)-(6A3+2B3)ψ(i-2, j)+
B3ψ(i-2, j-1)+A3ψ(i-3, j)，
(12b)
式中
2 弯曲岩层中的应用
2.1 研究对象
根据弯曲岩层的形态、应力场特征，建立了弯曲岩层中煤层开采的示意图，如图6所示．为了理论研究的可行，这里将弯曲岩层的形态简化为圆弧形．工作面由开切眼位置仰采推进，煤层开采后，采场覆岩的平衡状态遭到破坏，应力重新分布；另一方面，采场覆岩开始变形下沉、破断及运动，将影响采场工作面安全生产．本文的研究对象为采空区的上覆岩层．
2.2 数值计算模型
图7为弯曲岩层数值计算的平面应变模型．模型的内外半径分别为rib和rob；模型的两端分别为切眼和工作面支撑处，简化为固定铰支座边界条件，因为在实际工程中岩层是可以发生转动的；内边界为采空区，无应力和位移边界条件；外边界为应力边界条件，承受上覆岩层的垂直应力q和水平构造应力λq,λ为构造应力系数；切眼位置与水平线之间的夹角θi称为开采部位；工作面与切眼之间的夹角θe称为推进角度；岩层厚度为st．
在使用位移函数法求解计算模型时，求解域内的离散点应满足位移函数控制方程，求解域的边界条件应满足边界条件，如表1所示．对于4个角点，传统的计算方法为在4个角点上一般使用4个边界条件中的两个，这样求解出的应力，特别是固定端拐角区域的应力与实际应力状态有较大的差别．而本文在可用的4个边界条件中只满足3个，见表2，其余一个被看作是多余的，这样与实际应力状态有较小的差别．岩层的物理力学性质见表3．
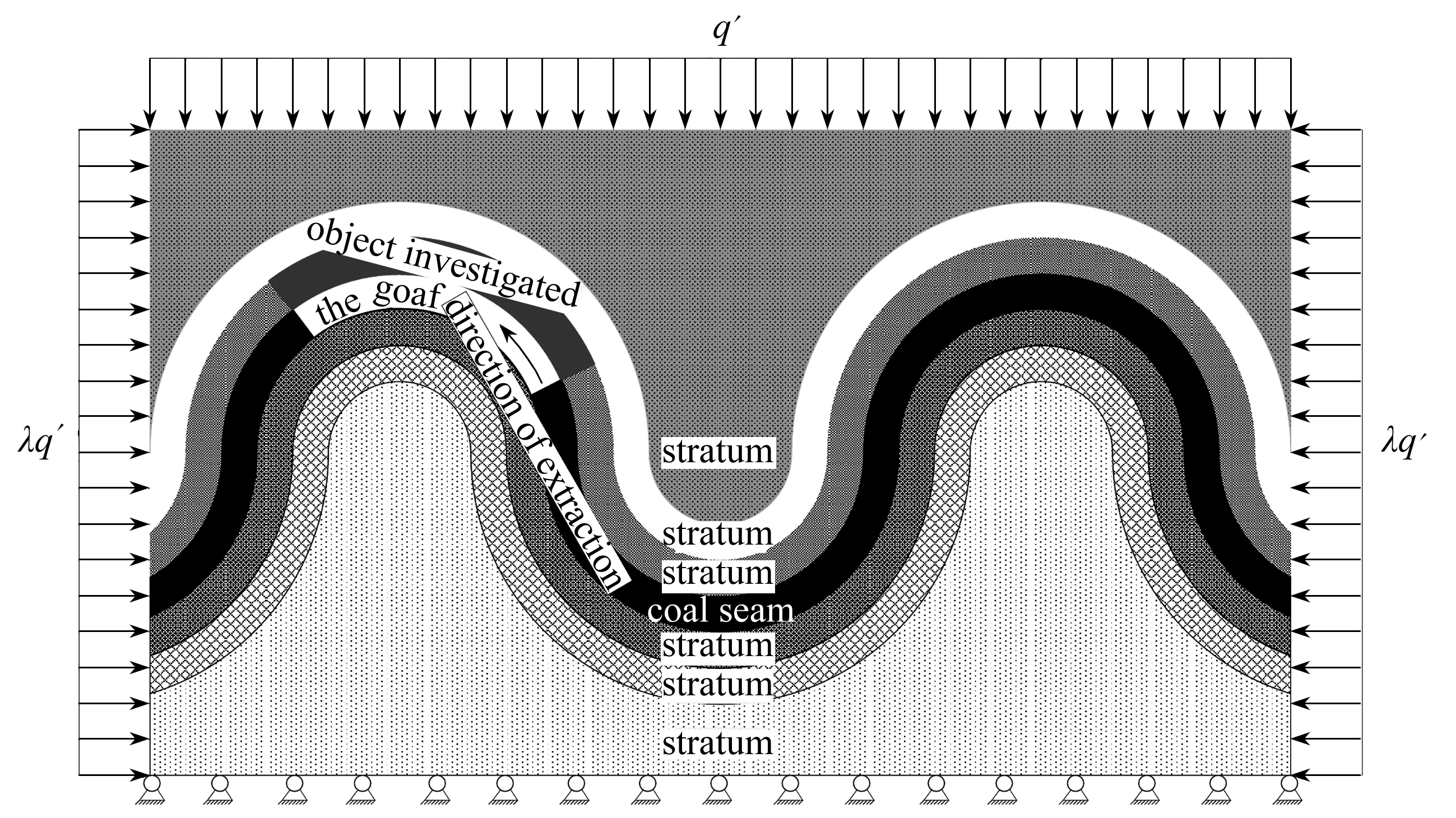
图6 弯曲岩层中煤层开采示意图
Fig. 6 Schematic diagram of coal seam mining in bending rock
计算模型中径向网格长度为0.5 m、环向网格长度为1°．以开采部位θi=0°，推进角度θe=120°，岩层厚度st=20 m为例说明计算的可行性．网格的实节点个数为121×41=4 961，边界的虚节点个数为121×2+41×2=324，每个节点上都有未知的位移函数值ψi, j，这样，总共有5 285个未知数；另一方面，求解域内的离散点个数为119×39=4 641， 这些离散点处可以列出4 641个代数方程(位移函数控制方程的差分方程)， 实边界上的每个节点(角点处的节点除外)可以列出两个代数方程(位移边界条件或应力边界条件的差分方程)， 这些节点处可以列出119×2×2+39×2×2=632个代数方程， 角点处的每个节点可以列出3个代数方程(两个位移边界条件和一个应力边界条件的差分方程)， 即可以列出3×4=12个代数方程， 这样， 总共可以列出5 285个代数方程．因此，代数方程的个数与未知数的个数相等，可以通过编制程序解出全部未知的位移函数值ψi, j,从而可进一步得出计算模型的位移和应力．采用MATLAB软件进行编写程序和求解计算．
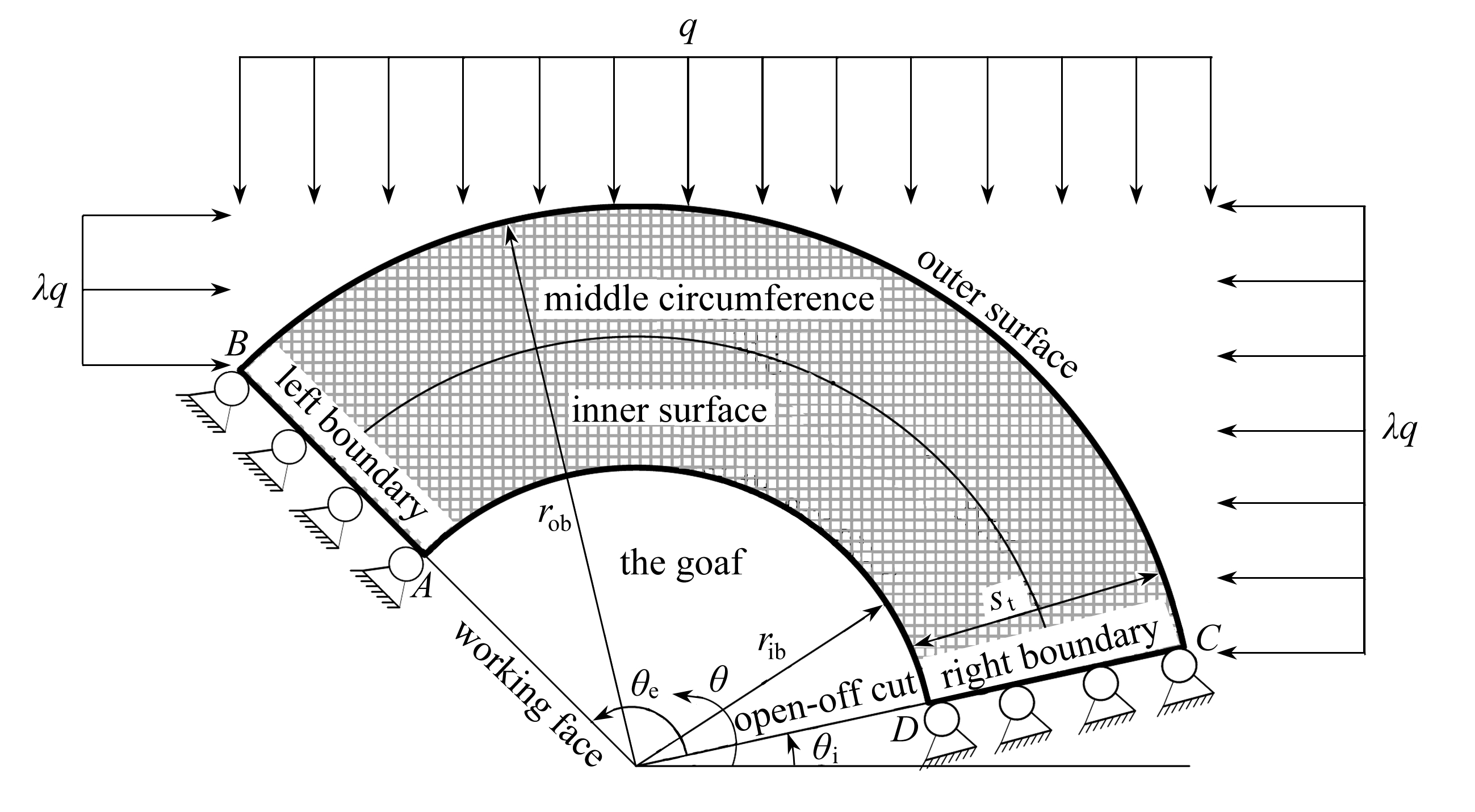
图7 弯曲岩层数值计算模型
Fig. 7 The numerical calculation model for a bending stratum
表1 计算模型的边界条件
Table 1 Boundary conditions of the domain for the numerical model
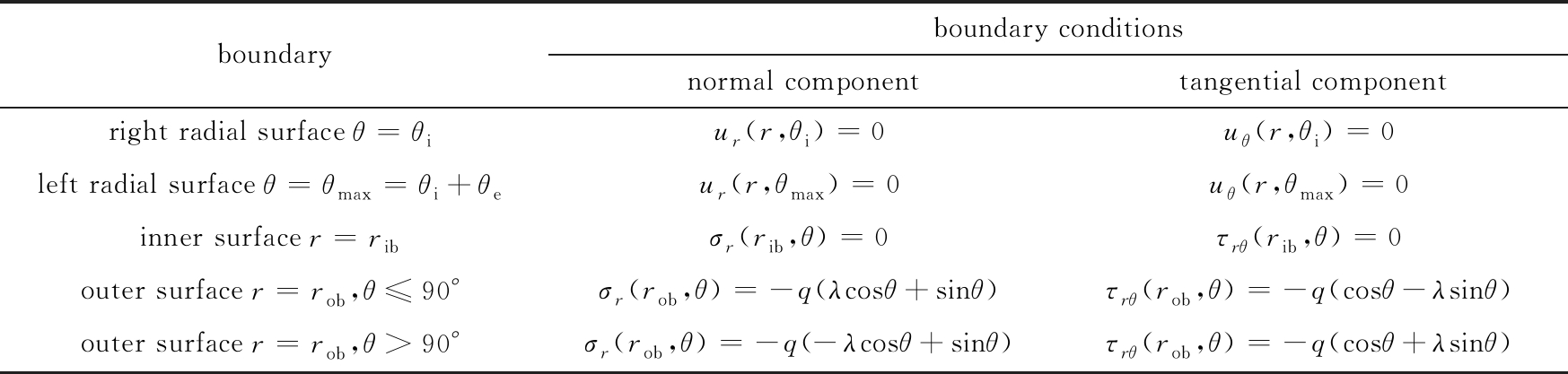
boundaryboundary conditionsnormal componenttangential componentright radial surface θ=θiur(r,θi)=0uθ(r,θi)=0left radial surface θ=θmax=θi+θeur(r,θmax)=0uθ(r,θmax)=0inner surfacer=ribσr(rib,θ)=0τrθ(rib,θ)=0outer surface r=rob,θ≤90°σr(rob,θ)=-q(λcosθ+sinθ)τrθ(rob,θ)=-q(cosθ-λsinθ)outer surface r=rob,θ>90°σr(rob,θ)=-q(-λcosθ+sinθ)τrθ(rob,θ)=-q(cosθ+λsinθ)
表2 4个角点处的边界条件
Table 2 Boundary conditions at the four corner nodes of the domain in the numerical model
corner nodegiven boundary conditionsused conditionsboundary condition valuesA ur,uθ,σr,τrθ ur,uθ,τrθ ur=0;uθ=0;τrθ=0B ur,uθ,σr,τrθ ur,uθ,τrθ ur=0;uθ=0;τrθ=0C ur,uθ,σr,τrθ ur,uθ,τrθ ur=0;uθ=0;τrθ=0D ur,uθ,σr,τrθ ur,uθ,τrθ ur=0;uθ=0;τrθ=0
表3 岩层物理力学性质
Table 3 Physical and mechanical properties of rock strata
modulus of elasticity E/GPaPoisson’s ratio μdensity of rock ρ/(kg·m-3)350.252 500
2.3 弯曲覆岩位移分布特征
以曲率半径rib=20 m，构造应力系数λ=1.8，采深md=1 000 m，推进角度θe=120°，开采部位θi=0°，岩层厚度st=20 m为例，分析数值计算模型的位移．
2.3.1 径向位移分布特征
模型内边界和外边界的径向位移沿环向的分布曲线如图8所示．由图8可以得出，弯曲岩层在外载荷作用下，边界角点处的径向位移为0，符合边界条件．内边界和外边界径向位移曲线呈下凸形状，且均表现为负值，说明在工作面的推进过程中上覆岩层产生下沉变形，主要集中在15°～105°范围内产生明显下沉变形．在θ<60°的范围内，外边界的径向位移大于内边界的径向位移；而在θ>60°的范围内，外边界的径向位移略小于内边界的径向位移，但两者差别不大．
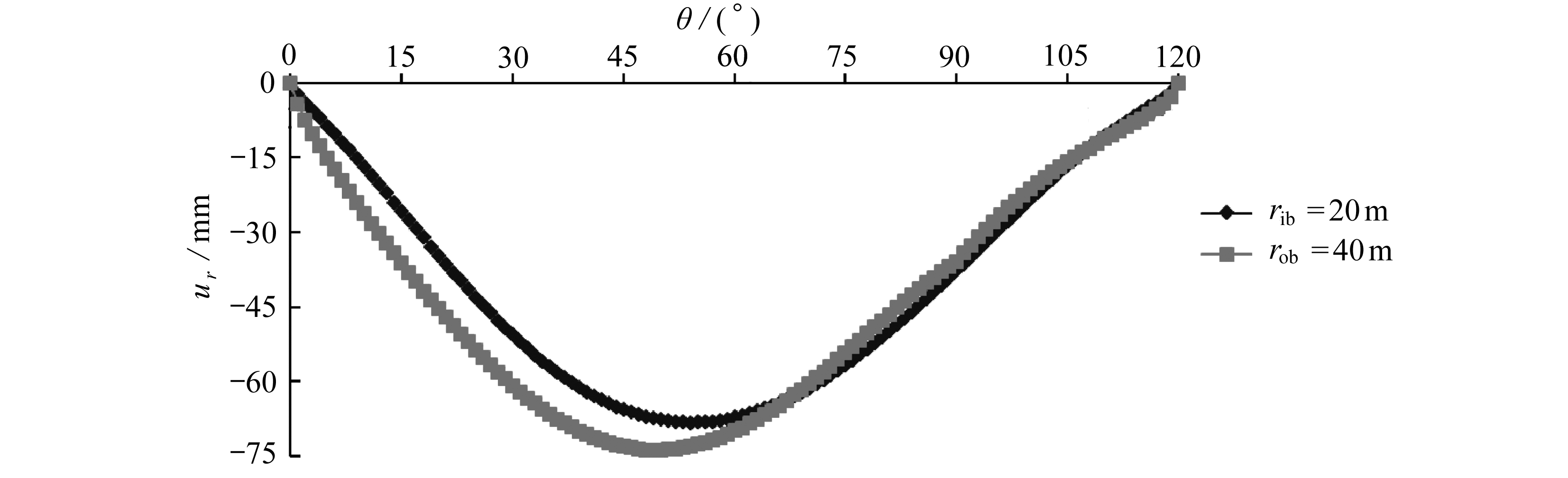
图8 径向位移沿环向的分布曲线
Fig. 8 The distribution of radial displacements on inner and outer surfaces along circumferential directions
模型不同截面上径向位移沿径向的分布曲线如图9所示．由图9可以得出，在θ=30°,45°,60°这3个截面上，径向位移沿径向由内边界向外边界逐渐增大；而在θ=75°,90°,105°这3个截面上，径向位移沿径向由内边界向外边界逐渐减小，但减小趋势变化不大．另一方面，在θ=45°,60°两个截面上的径向位移均大于60 mm，其他截面上的径向位移均小于60 mm，说明在45°～60°范围内的覆岩下沉变形最大，在工作面推进过程中应多注意观测，必要时采取相应措施减小沉降变形．
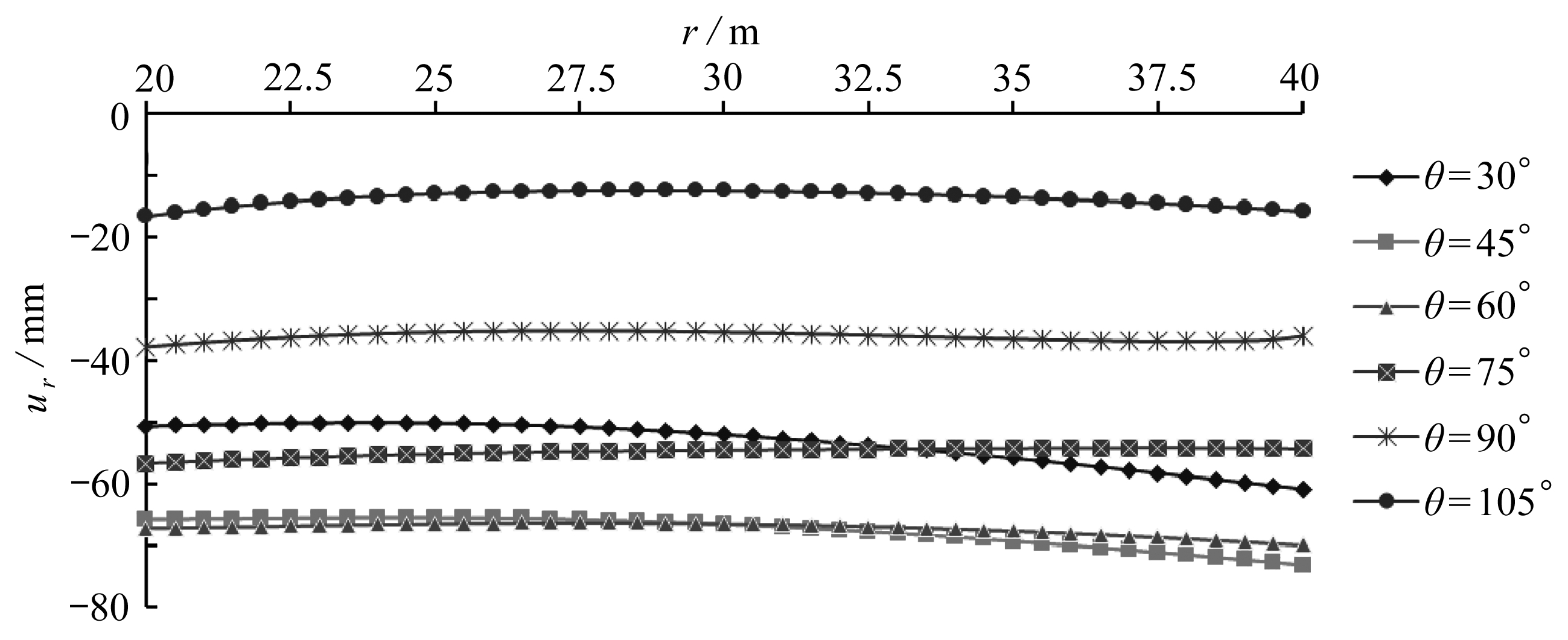
图9 不同截面上径向位移沿径向的分布曲线
Fig. 9 The distribution of radial displacements along radial directions on 6 different sections
2.3.2 环向位移分布特征
模型内边界和外边界的环向位移沿环向的分布曲线如图10所示．由图10可以得出，弯曲岩层在外载荷作用下，尽管内边界和外边界的环向位移沿环向分布曲线形状不尽相同，但是环向位移沿环向分布既有负值也有正值，且环向位移正值占主要部分，说明在工作面的推进过程中上覆岩层沿环向有的产生压缩，有的产生拉伸，且以拉伸为主．由于岩石属于脆性材料，不抗拉伸，因此，对于内边界而言在60°～105°范围内的岩层较容易产生拉伸破坏；对于外边界而言在30°～90°范围内的岩层较容易产生拉伸破坏．
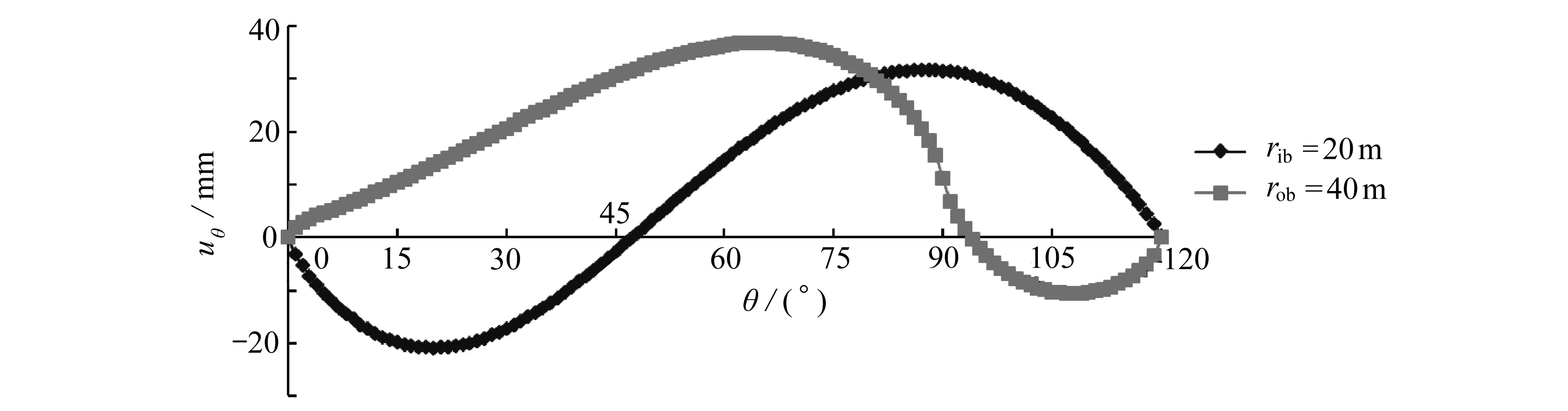
图10 环向位移沿环向的分布曲线
Fig. 10 The distribution of circumferential displacements on inner and outer surfaces along circumferential directions
模型不同截面上环向位移沿径向的分布曲线如图11所示．由图11可以得出，在θ=30°,45°两个截面上，环向位移沿径向先减小后增大，即一部分处于压缩状态，另一部分处于拉伸状态；θ=60°,75°两个截面上，环向位移沿径向均为正值，且呈增大趋势；而在θ=90°,105°两个截面上，环向位移沿径向呈减小趋势．不难看出，在θ=60°～90°的截面上，模型内边界和外边界的环向位移沿径向均为正值，岩层处于拉伸状态，说明在工作面推进过程中应多观测这些截面，避免产生拉伸破坏．
2.4 弯曲覆岩应力分布特征
以曲率半径rib=20 m，构造应力系数λ=1.8，采深md=1 000 m，推进角度θe=120°，开采部位θi=0°，岩层厚度st=20 m为例，分析数值计算模型的应力．
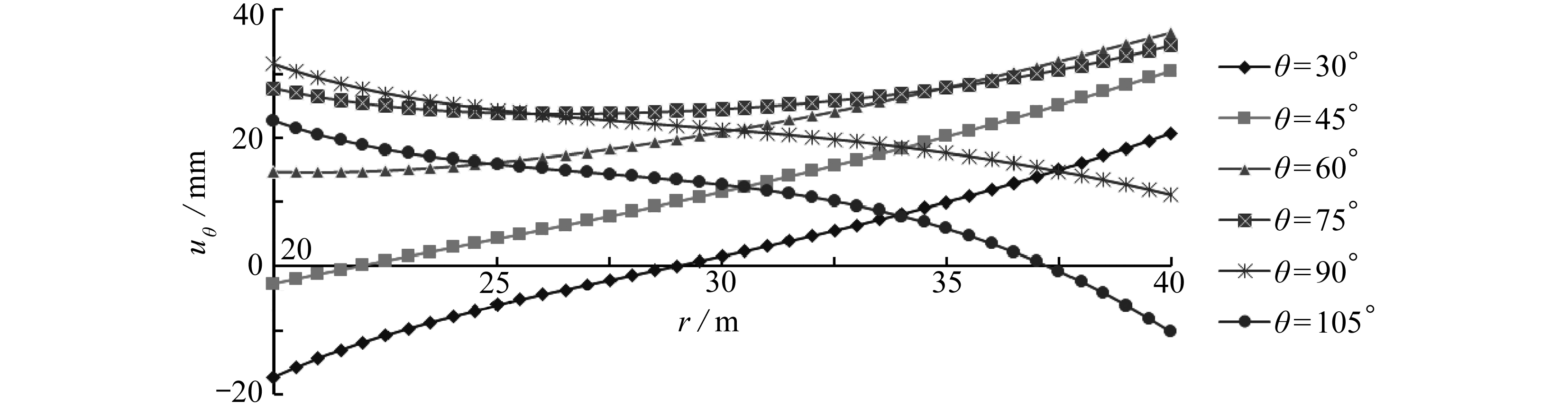
图11 不同截面上环向位移沿径向的分布曲线
Fig. 11 The distribution of circumferential displacements along radial directions on 6 different sections
2.4.1 径向应力分布特征
图12给出了计算模型中线上径向应力σr沿环向的分布情况．可以得出，径向应力沿环向分布不均匀，在0°～17°范围内径向应力随θ的增加而增大，在18°～69°范围内径向应力随θ的增加而减小，在70°～92°范围内径向应力随θ的增加而增大，在93°～120°范围内径向应力随θ的增加而减小，最大径向应力在θ=15°附近．由此可以得出，离切眼不远处径向应力将达到峰值．图13给出了不同截面上径向应力σr沿径向的分布情况．径向应力σr沿径向由内边界向外边界呈逐渐增大趋势，与其他截面相比，在θ=45°的截面上径向应力沿径向增加较快，表明越靠近切眼的截面上径向应力增加越快，且径向应力值越大，反之，则径向应力增加较慢，且径向应力值较小．值得注意的是，所有截面在r=20 m处，即内边界上，径向应力值均为0，表明计算结果符合内边界的径向应力边界条件．
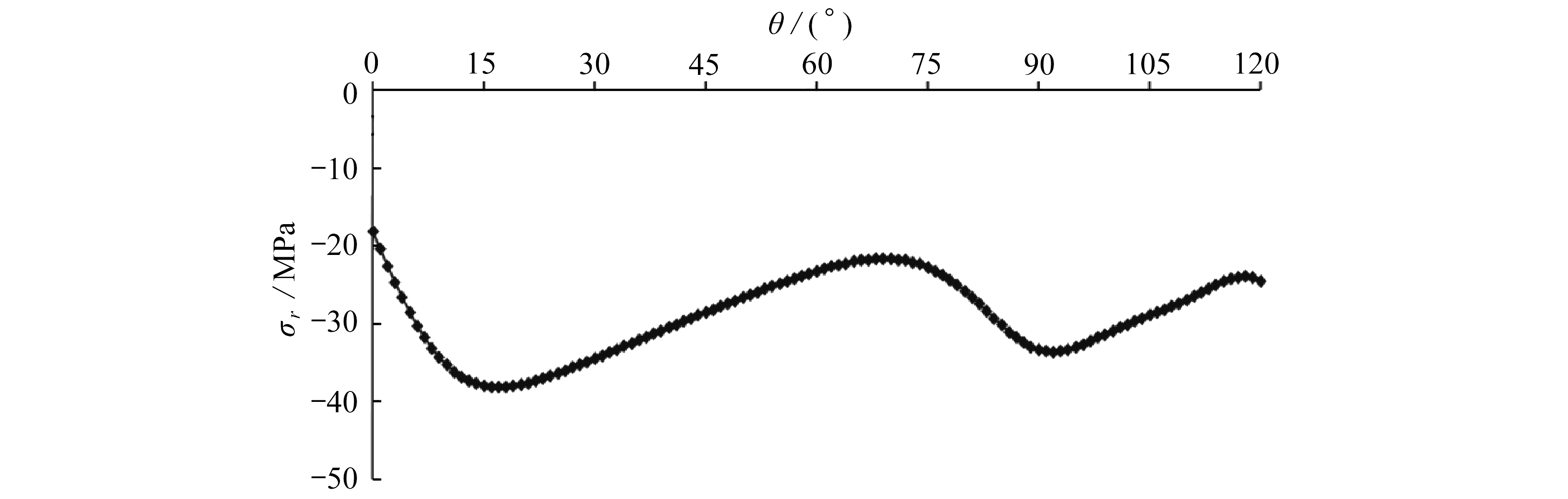
图12 中线上径向应力沿环向的分布曲线
Fig. 12 The distribution of radial stresses along the middle circumference
2.4.2 环向应力分布特征
图14给出了计算模型中线上环向应力σθ沿环向的分布情况．可以得出，环向应力沿环向分布不均匀，在0°～25°范围内环向应力随θ的增加而减小，在26°～90°范围内环向应力随θ的增加而增大，在91°～120°范围内径向应力随θ的增加而减小，最大环向应力在θ=90°附近．由此可以得出，工作面后方不远处环向应力将达到峰值，由于环向应力容易引起岩层环向压缩破断，因此，在开采过程中应多观测工作面后方的环向破断现象．图15给出了不同截面上环向应力σθ沿径向的分布情况．角度低于90°的截面上环向应力沿径向由内边界向外边界逐渐增大，而角度高于90°的截面上环向应力沿径向由内边界向外边界逐渐减小，例如：在θ=75°的截面上，内边界上的环向应力为40.99 MPa，外边界上的环向应力却高达91.28 MPa；而在θ=105°的截面上，环向应力从内边界到外边界降低了约70%．需要注意的是，在θ=75°～105°的截面上内边界附近环向应力较大，容易引起上覆岩层环向压缩破断，造成顶板事故等灾害，在工作面推进过程中应多观测，必要时采取相应的措施，避免灾害事故发生．
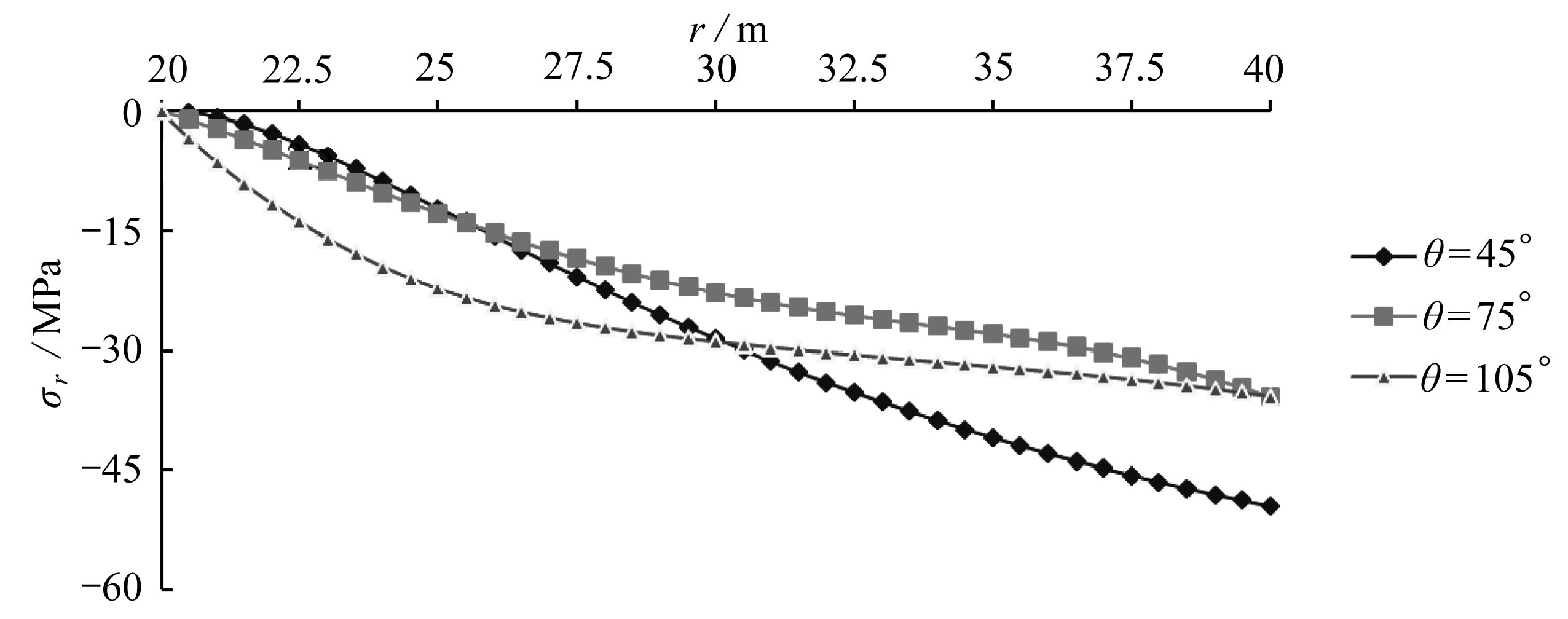
图13 不同截面上径向应力沿径向的分布曲线
Fig. 13 The distribution of radial stresses on 3 different sections
图14 中线上环向应力沿环向的分布曲线
Fig. 14 The distribution of circumferential stresses along the middle circumference
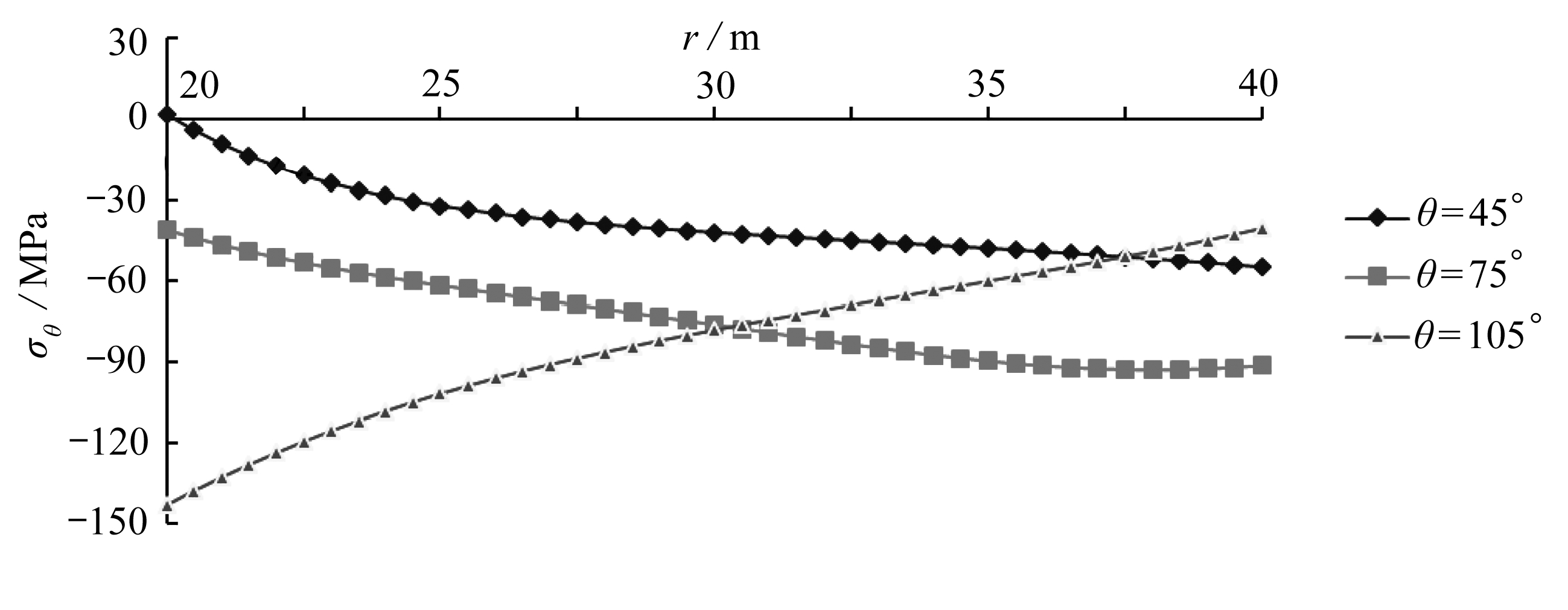
图15 不同截面上环向应力沿径向的分布曲线
Fig. 15 The distribution of circumferential stresses on 3 different sections
2.4.3 剪应力分布特征
图16给出了计算模型中线上剪应力τrθ沿环向的分布情况．可以得出，剪应力沿环向有正值也有负值，分布不均匀．在0°～42°范围内剪应力为负值，且在该范围内剪应力随θ的增加呈先增大后减小的趋势；在43°～120°范围内剪应力为正值，在该范围内剪应力随θ的增加也呈先增大后减小的趋势．在60°～105°范围内剪应力相对平稳，变化不大，但是剪应力的峰值却在θ=10°附近，由此可以得出，离切眼不远处剪应力将达到峰值．图17给出了不同截面上剪应力τrθ沿径向的分布情况．对于小角度的截面，例如θ=45°,75°的截面上剪应力沿径向由内边界向外边界基本上逐渐增大；而对于高角度的截面，例如θ=105°的截面上剪应力沿径向由内边界向外边界先增大后减小为0，然后剪应力变为负数，剪应力数值反向增大．值得注意的是， 所有截面在r=20 m处， 即内边界上， 剪应力值均为0， 表明计算结果符合内边界的剪应力边界条件．
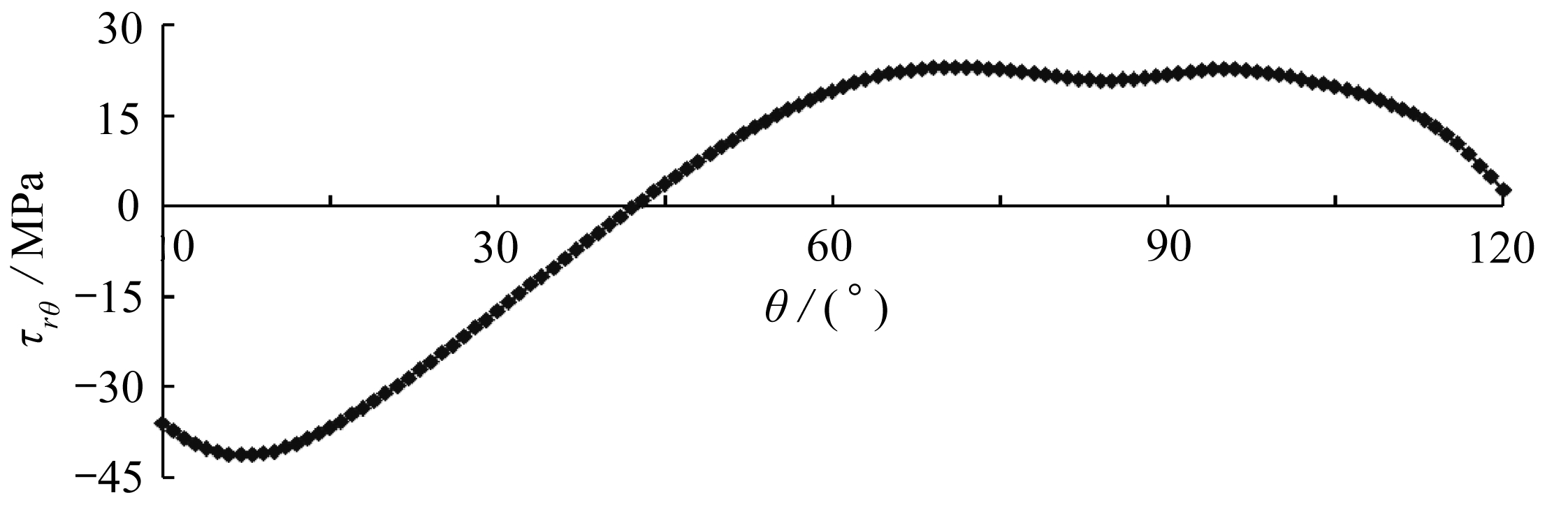
图16 中线上剪应力沿环向的分布曲线
Fig. 16 The distribution of shear stresses along the middle circumference
图17 不同截面上剪应力沿径向的分布曲线
Fig. 17 The distribution of shear stresses on 3 different sections
3 结 论
本文运用理论分析和数值计算的方法， 研究了基于位移函数法的曲梁弹性理论， 并将该理论运用到弯曲岩层中， 分析了弯曲岩层中煤层开采后上覆岩层的变形与应力， 取得如下主要结论：
1) 通过引入位移函数，得到了极坐标下平面弹性问题位移函数控制方程．通过理论分析、推导，得到了用位移函数表示的位移分量和应力分量．在此基础上，采用差分原理编制程序．
2) 煤层开采后弯曲覆岩的径向位移沿环向呈下凸形状，说明工作面的开采过程中上覆岩层产生下沉变形；弯曲岩层环向位移沿环向既有负值也有正值，且环向位移正值占主要部分．径向应力沿环向分布不均匀，且距离切眼不远处径向应力将达到峰值，径向应力沿径向由内边界向外边界逐渐增大．环向应力沿环向分布也不均匀，较大的环向应力容易引起环向破断．剪应力沿环向的分布也不均匀，距离切眼不远处剪应力将达到峰值，对于小角度的截面上剪应力沿径向由内边界向外边界基本上逐渐增大．
致谢 本文作者衷心感谢菏泽学院科研项目(XY17KJ03；XY19BS23)和菏泽学院培育项目(XYPY02)对本文的资助．
[1] 虎维岳, 何满潮. 深部煤炭资源及开发地质条件研究现状与发展趋势[M]. 北京: 煤炭工业出版社, 2008.(HU Weiyue, HE Manchao. The Present Situation and Development Trend for Deep Coal Resources and the Development of Geological Conditions[M]. Beijing: Coal Industry Publishing House, 2008.(in Chinese))
[2] 何满朝, 钱七虎. 深部岩体力学基础[M]. 北京: 科学出版社, 2010.(HE Manchao, QIAN Qihu. Mechanical Foundation for Deep Rock Mass[M]. Beijing: Science Press, 2010.(in Chinese))
[3] ODEN J T, RIPPERGER E A. Mechanics of Elastic Structures[M]. 2nd ed. New York: McGraw-Hill Book Company, 1981.
[4] TIMOSHENKO S P, GOODIER J N. Theory of Elasticity[M]. New York: McGraw-Hill Book Company, 1979.
[5] CHIANESE R B, ERDLAC R J. The general solution to the distribution of stresses in a circular ring compressed by two forces acting along a diameter[J]. The Quarterly Journal of Mechanics and Applied Mathematics, 1988, 41(2): 239-247.
[6] BAGCI C. A new unified strength of materials solution for stresses in curved beams and rings[J]. Journal of Mechanical Design, 1992, 114(2): 231-237.
[7] BAGCI C. Exact elasticity solutions for stresses and deflections in curved beams and rings of exponential and T-sections[J]. Journal of Mechanical Design, 1993, 115(3): 346-358.
[8] COOK R D. Circumferential stress in curved beams[J]. Journal of Aplied Mechanics, 1992, 59(1): 224-225.
[9] TUTUNCU N. Plane stress analysis of end-loaded orthotropic curved beams of constant thickness with applications to full rings[J]. Journal of Mechanical Design, 1998, 120(2): 368-374.
[10] SLOBODA A, HONARMANDI P. Generalized elasticity method for curved beam stress analysis: analytical and numerical comparison for a lifting hook[J]. Mechanics Based Design of Structures and Machines, 2007, 35(3): 319-332.
[11] 钟万勰, 徐新生, 张洪武. 弹性曲梁问题的直接法[J]. 工程力学, 1996, 13(4): 1-8.(ZHONG Wanxie, XU Xinsheng, ZHANG Hongwu. On a direct method for the problem of elastic curved beams[J]. Engineering Mechanics, 1996, 13(4): 1-8.(in Chinese))
[12] 李锐, 田宇, 郑新然, 等. 求解弹性地基上自由矩形中厚板弯曲问题的辛-叠加方法[J]. 应用数学和力学, 2018, 39(8): 875-891.(LI Rui, TIAN Yu, ZHENG Xinran, et al. A symplectic superposition method for bending problems of free-edge rectangular thick plates resting on elastic foundations[J]. Applied Mathematics and Mechanics, 2018, 39(8): 875-891.(in Chinese))
[13] 侯永康, 段树金, 安蕊梅. 满足断裂过程区裂纹张开位移条件应力函数的半解析解法[J]. 应用数学和力学, 2018, 39(8): 979-988.(HOU Yongkang, DUAN Shujin, AN Ruimei. A semi-analytical method for stress functions meeting crack opening displacements in fracture process zones[J]. Applied Mathematics and Mechanics, 2018, 39(8): 979-988.(in Chinese))
[14] DURELLI A J, RANGANAYAKAMMA B. Parametric solution of stresses in beams[J]. Journal of Engineering Mechanics, 1989, 115(2): 401-415.
[15] AHMED S R, IDRIS A B M, UDDIN M W. Numerical solution of both ends fixed deep beams[J]. Computers & Structures, 1996, 61(1): 21-29.
[16] AHMED S R, KHAN M R, ISLAM K M S, et al. Investigation of stresses at the fixed end of deep cantilever beams[J]. Computers & Structures, 1998, 69(3): 329-338.
[17] 姚晓东, 张元海. 基于抽象翘曲位移函数的箱形梁剪力滞效应分析[J]. 应用数学和力学, 2018, 39(12): 1351-1363.(YAO Xiaodong, ZHANG Yuanhai. Analysis of shear lag effects in box girders based on abstract warping displacement functions[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1351-1363.(in Chinese))
[18] COOK R D. Axisymmetric finite element analysis for pure moment loading of curved beams and pipe bends[J]. Computers & Structures, 1989, 33(2): 483-487.
[19] RATTANAWANGCHAROEN N, BAI H, SHAH A H. A 3D cylindrical finite element model for thick curved beam stress analysis[J]. International Journal for Numerical Methods in Engineering, 2004, 59(4): 511-531.
[20] RICHARDS T H, DANIELS M J. Enhancing finite element surface stress predictions: a semi-analytic technique for axisymmetric solids[J]. The Journal of Strain Analysis for Engineering Design, 1987, 22(2): 75-86.
[21] SMART J. On the determination of boundary stresses in finite elements[J]. The Journal of Strain Analysis for Engineering Design, 1987, 22(2): 87-96.
[22] GANGAN P. The curved beam/deep arch/finite ring element revisited[J]. International Journal for Numerical Methods in Engineering, 1985, 21(3): 389-407.
[23] DOW J O, JONES M S, HARWOOD S A. A new approach to boundary modeling for finite difference applications in solid mechanics[J]. International Journal for Numerical Methods in Engineering, 1990, 30(1): 99-113.
[24] RANZI G, GARA F, LEONI G, et al. Analysis of composite beams with partial shear interaction using available modelling techniques: a comparative study[J]. Computers & Structures, 2006, 84(13/14): 930-941.
[25] AHMED S R, NATH S K D, UDDIN M W. Optimum shapes of tire-treads for avoiding lateral slippage between tires and roads[J]. International Journal for Numerical Methods in Engineering, 2005, 64(6): 729-750.
[26] AHMED S R, HOSSAIN M Z, UDDIN M W. A general mathematical formulation for finite-difference solution of mixed-boundary-value problems of anisotropic materials[J]. Computers & Structures, 2005, 83(1): 35-51.
[27] HOSSAIN M Z, AHMED S R, UDDIN M W. Generalized mathematical model for the solution of mixed-boundary-value elastic problems[J]. Applied Mathematics and Computation, 2005, 169(2): 1247-1275.
[28] XU W, LI G. Finite difference three-dimensional solution of stresses in adhesively bonded composite tubular joint subjected to torsion[J]. International Journal of Adhesion and Adhesives, 2010, 30(4): 191-199.
[29] NATH S K D, AHMED S R. A displacement potential-based numerical solution for orthotropic composite panels under end moment and shear loading[J]. Journal of Mechanics of Materials and Structures, 2009, 4(6): 987-1004.
[30] MCCORQUODALE P, COLELLA P, GROTE D P, et al. A node-centered local refinement algorithm for Poisson’s equation in complex geometries[J]. Journal of Computational Physics, 2004, 201(1): 34-60.
[31] DING H, SHU C. A stencil adaptive algorithm for finite difference solution of incompressible viscous flows[J]. Journal of Computational Physics, 2006, 214(1): 397-420.
[32] MIN C, GIBOU F, CENICEROS H D. A supra-convergent finite difference scheme for the variable coefficient Poisson equation on non-graded grids[J]. Journal of Computational Physics, 2006, 218(1): 123-140.
[33] BIENIASZ L K. Experiments with a local adaptive grid h-refinement for the finite-difference solution of BVPs in singularly perturbed second-order ODEs[J]. Applied Mathematics and Computation, 2008, 195(1): 196-219.