引 言
圆柱壳结构是一种重要的承载构件，其在冲击载荷作用下的动力屈曲一直是研究的热点问题之一，国内外学者对受轴向冲击弹性圆柱壳的动力屈曲进行了大量研究.黄承义等[1]根据实验结果，采用Lagrange方法分析了有限长薄圆柱壳在余弦冲击载荷作用下的弹性脉冲动力屈曲.沈惠申[2]计及壳体非线性前屈曲变形和初始几何缺陷，研究了湿热环境对复合材料层合圆柱薄壳在轴向压缩作用下屈曲和后屈曲行为的影响.顾红军等[3]、张善元等[4]对薄壁圆柱壳的轴向动力屈曲进行了实验与理论研究，分析了轴向冲击下薄壁圆柱壳的屈曲行为.徐新生等[5-6]研究了半无限长弹性圆柱壳的屈曲机理,并发现轴向应力波的传播和反射对屈曲起着重要作用.Karagiozova等[7-8]基于轴向冲击产生的应力波效应，研究了圆柱壳的动态塑性屈曲及动态渐进屈曲现象，并通过实验研究了冲击速度和材料特性对动态屈曲响应的影响.马建青等[9]考虑轴向、扭转耦合应力波在圆柱壳中的传播，对弹性长圆柱壳动态屈曲问题进行了探讨.桂夷斐等[10]对阶梯圆柱壳在轴向冲击载荷作用下的屈曲进行了研究，考虑到应力波的传播、反射以及在分界面处的反射和透射，分析了波传播时间以及结构几何特性对屈曲临界载荷的影响.几种不同支承条件下圆柱壳的屈曲特点也被许多学者讨论[11-12].Tovstik等[13]为了得到能预测不同端部支承条件下的临界载荷以及屈曲模态的近似表达式，采用渐进法进行了大量的屈曲分析.Wang等[14]和Zhang等[15]采用波传播方法来预测具有不同边界条件的有限长度圆柱壳的特性.王颖泽等[16]针对包含有界边界的轴对称结构受热冲击作用的广义热弹性问题进行了研究分析，得到了有限厚度圆柱壳热冲击问题的广义热弹性解.
工程实践中，弹性介质中的圆柱壳有着广泛的应用，土木建筑等领域经常遇到弹性地基中的圆柱壳型构件，理想的约束环境很难准确地描述其连接特征.考虑圆柱壳的弹性约束环境，引入径向弹簧来模拟弹性介质，通过调节径向弹簧的刚度值，可以很好地模拟圆柱壳型构件的环境特征.本文在前人研究圆柱壳的基础上，通过调节径向弹簧的刚度模拟弹性介质的刚度变化，讨论圆柱壳在弹性介质中的动力屈曲.研究在轴向阶跃载荷作用下应力波传播及反射对弹性介质中的圆柱壳动力屈曲的影响，将圆柱壳分成两段，如图1所示，分界面将圆柱壳分成两个区域，设未嵌入弹性介质中的圆柱壳部分为区域Ⅰ，嵌入弹性介质中的圆柱壳部分为区域Ⅱ，分别进行建模并求解.考虑边界条件和相容条件，求得相应的屈曲分叉条件.计算分析弹性介质中的圆柱壳临界屈曲载荷与应力波波阵面到达圆柱壳的位置、径向刚度、壳体未嵌入弹性介质部分的长度与总长之比(以下简称长度比例)的关系.
图1 弹性介质中的圆柱壳
Fig. 1 A cylindrical shell embedded in an elastic medium
1 控制方程及求解
如图1所示为弹性介质中的圆柱壳，总长为L，壁厚为h，中面半径为r，弹性模量为E，Poisson比为ν.建立柱坐标系，x,θ,z分别表示轴向、周向和径向坐标，w表示壳体中面上的点沿z轴方向的位移.区域Ⅰ所在的壳体部分长为L1，径向弹簧刚度为k，Pw=kw，表示轴向单位长度上的径向作用力.根据弹性圆柱壳屈曲的Hamilton变分原理，分别建立圆柱壳区域Ⅰ、Ⅱ的径向位移控制方程[17]如式(1)、(2)所示：
(1)
(2)
其中D=Eh3/(12(1-ν2))，Nx是圆柱壳所受轴向载荷，壳体端部受轴向阶跃载荷冲击时，圆柱壳中应力波以纵波的形式传播，应力波传播波阵面位置xe，反射波波阵面位置xr，ce为波速.本文主要讨论弹性介质中的圆柱壳受轴向冲击后，应力波从冲击端传播到固定端，并经固定端反射回冲击端的情况.对于理想弹性圆柱壳应力波传播和反射过程中，轴向力可描述为
(3)
对于区域Ⅰ，令W=w/r,X=x/r,T=cet/r,P=Nx/(Eh),ξ2=h2/(3r2(1-ν2))，代入式(1)可将其无量纲化为如下形式:
(4)
令
W(X,θ,T)=Φ(X,T)Ψ(θ,T)，
(5)
考虑函数Ψ(θ,T)的边界连续条件(θ=0和θ=2π)有
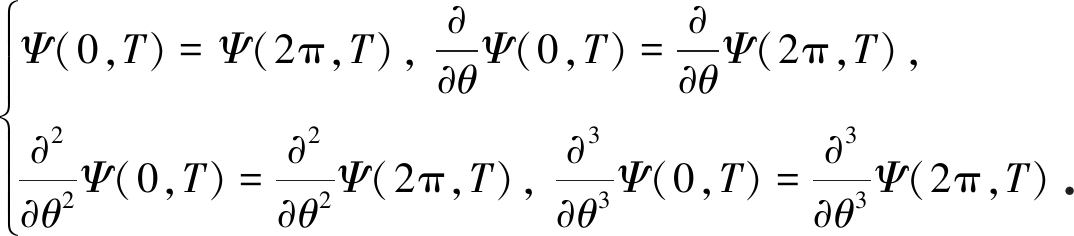
(6)
求出满足式(6)的Ψ(θ,T)的通解为
Ψ(θ,T)=e1cos(η1θ)+e2sin(η1θ),
(7)
其中
为屈曲对应的环向波数，即屈曲阶数，n=0表示圆柱壳屈曲环向截面形状为圆形，即轴对称屈曲；n为其他值(n=1,2,…)表示非轴对称屈曲，对应的圆柱壳屈曲环向截面形状为三角形或其他多边形形状，而非圆形.将式(5)和式(7)代入式(4)，得到关于Φ(X,T)满足的方程为
(8)
对于区域Ⅱ，令
经相同的处理方法得到关于Φ(X,T)满足的方程为
(9)
其中
采用无量纲参数，圆柱壳总长为1，冲击端处X=0，固定端处X=1，令λ=L1/L，求解式(8)和式(9)可得到Φ(X,T)的通解为
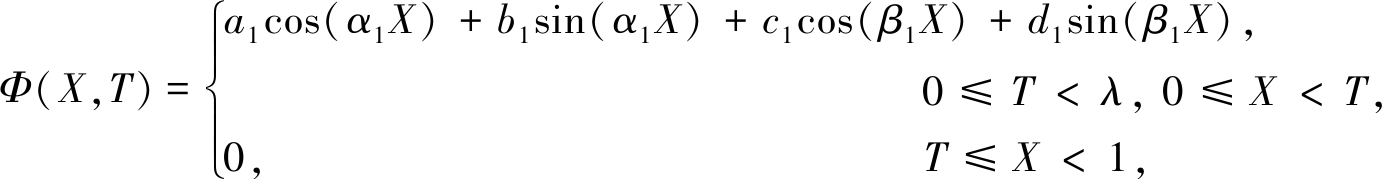
(10)
(11)
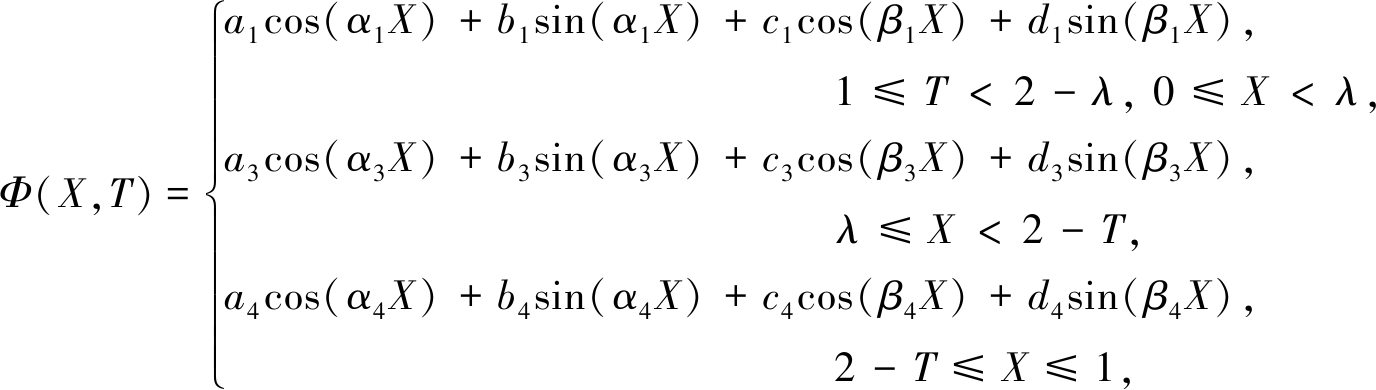
(12)
(13)
其中
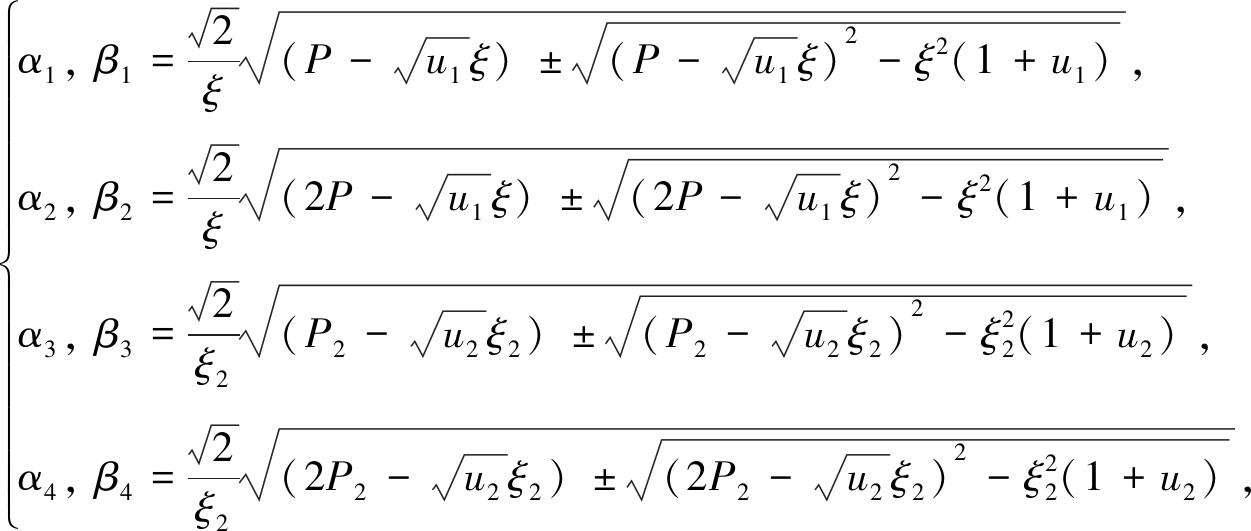
通解中ak,bk,ck,dk(k=1,2,3,4)是时间T的函数.令
为无量纲刚度，则
轴向力Nx无量纲化后成为P隐含在Φ(X,T)的通解中.式(10)～(13)分别为应力波反射前波阵面未通过分界面、反射前波阵面通过了分界面、反射后波阵面未通过分界面、反射后波阵面通过了分界面4个阶段Φ(X,T)的通解，代入接下来的边界条件、波阵面以及分界面的相容条件，可以得到圆柱壳的分叉条件.
2 边界条件及相容条件
应力波反射前弹性介质中的圆柱壳可分为应力波扰动区和非扰动区，在应力波扰动区W(X,θ,T)要满足端部边界条件、分界面及波阵面的相容条件.应力波反射后波阵面将壳体分成反射波扰动区和非扰动区，W(X,θ,T)也要满足端部边界条件、分界面及波阵面相容条件.
2.1 边界条件
考虑冲击端部自由、非冲击端部固支(C-F)，有
也可写成
(14)
(15)
2.2 相容条件
由于应力波反射前波阵面未通过分界面这一阶段，圆柱壳的边界条件和波阵面相容性条件均与弹性介质无关，因此接下来只分析应力波反射前波阵面通过了分界面、反射后波阵面未通过分界面、反射后波阵面通过了分界面3个阶段圆柱壳的相容条件.
2.2.1 应力波反射前波阵面到达区域Ⅱ
此时L1/ce≤t<L/ce，应力波反射前波阵面通过分界面后，波阵面应满足连续性条件：
(16)
考虑分界面处的相容条件,有
(17)
2.2.2 反射波波阵面到达区域Ⅱ
此时L/ce≤t<(2L-L1)/ce，反射波波阵面未通过分界面，反射波波阵面应满足应力波波阵面连续性条件：
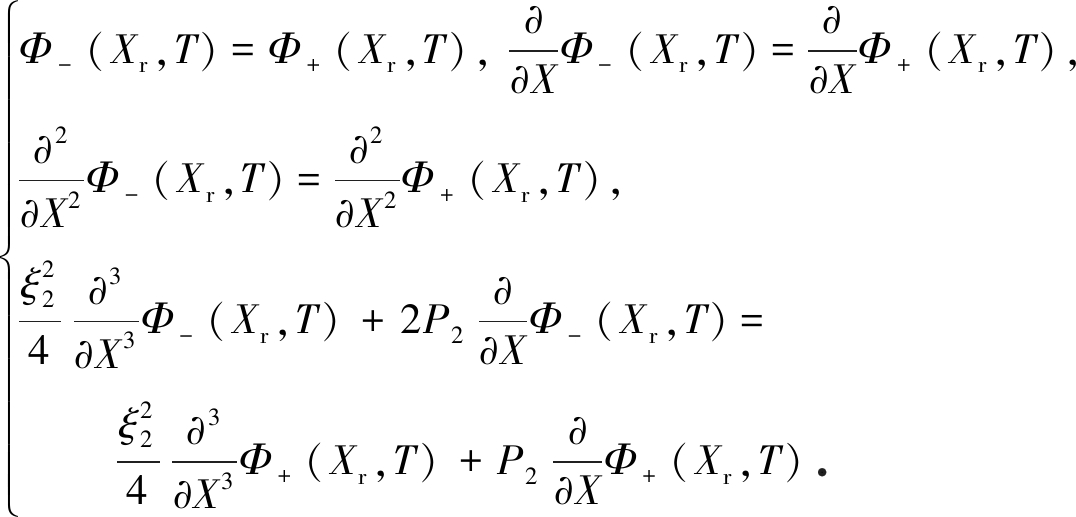
(18)
考虑分界面处的相容条件，有
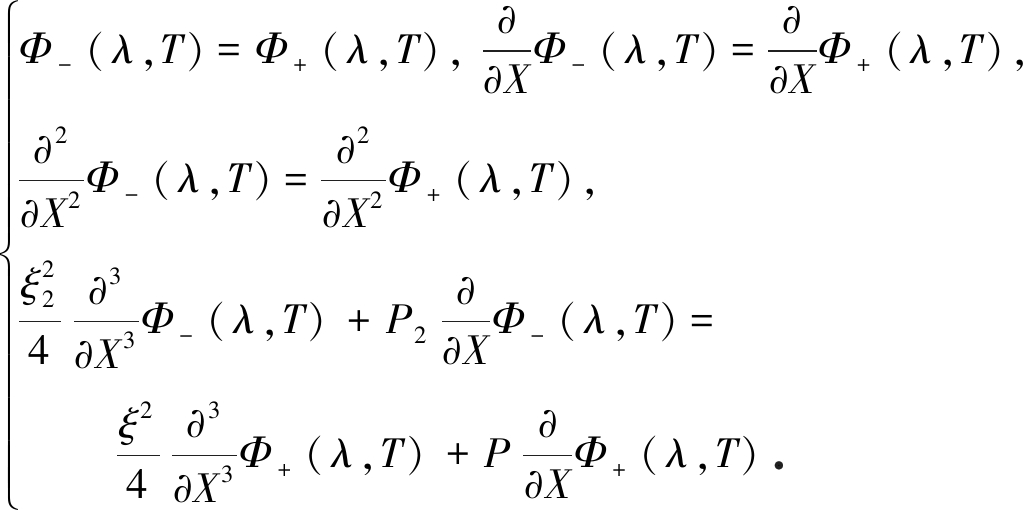
(19)
2.2.3 反射波波阵面到达区域Ⅰ
此时(2L-L1)/ce≤t≤2L/ce，反射波波阵面通过分界面，反射波波阵面应满足应力波波阵面连续性条件：
(20)
考虑分界面处的相容条件,有
(21)
3 分 叉 条 件
分叉意味着在轴向阶跃载荷作用下壳体不能维持在径向平衡位置附近的微小形变，即圆柱壳满足边界条件、分界面处连续性条件和应力波波阵面相容条件的情况下，受应力波扰动产生径向大变形.接下来对应力波传播以及发生反射后的屈曲分叉进行研究.
3.1 L1/ce≤t<L/ce
将边界条件式(14)和相容条件式(16)、(17)代入式(11)的Φ(X,T)通解，可得
A1C1=0,
(22)
其中
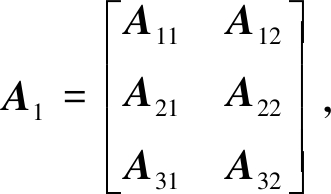
(23)
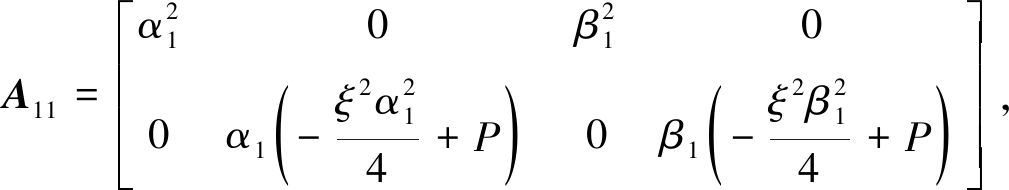
(24)
A12=A21=02×4,
(25)
(26)
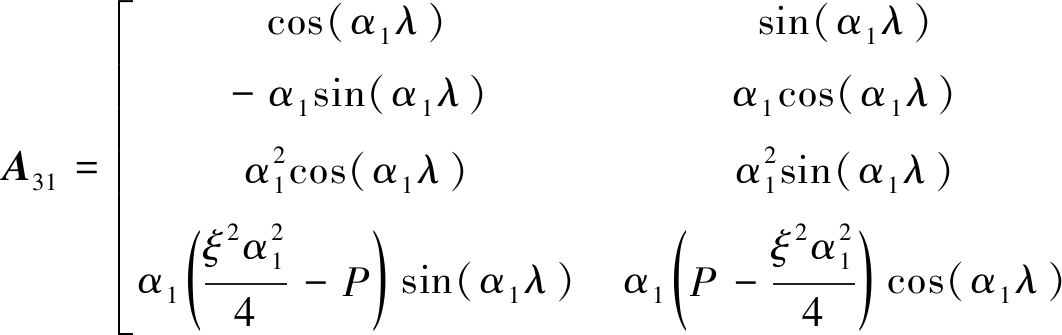
(27)
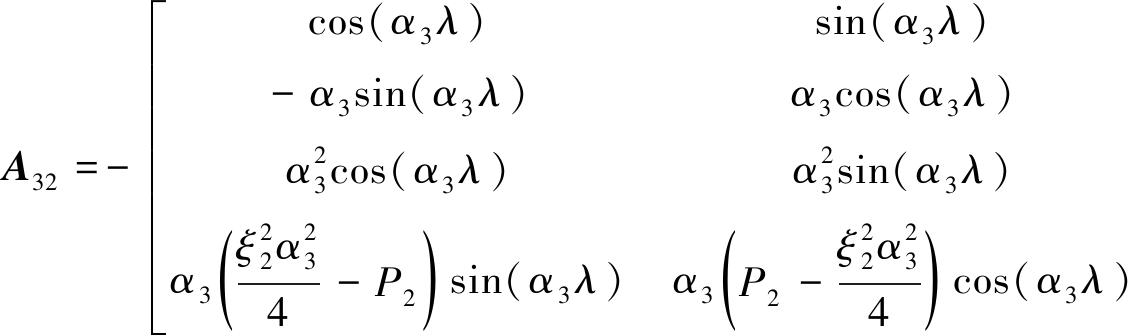
(28)
C1=[a1,b1,c1,d1,a3,b3,c3,d3]T.
(29)
若C1=0，由式(11)中Φ(X,T)表达式可知Φ(X,T)=0，则W(X,θ,T)=Φ(X,T)Ψ(θ,T)=0，说明屈曲现象将不发生.圆柱壳发生屈曲时产生径向大变形，此时W(X,θ,T)≠0，所以式(22)有非零解的条件即分叉条件是
|A1|=0.
(30)
3.2 L/ce≤t<(2L-L1)/ce
将边界条件式(14)、(15)和相容条件式(18)、(19)代入式(12)的Φ(X,T)通解，可得
A2C2=0,
(31)
其中C2=[a1,b1,c1,d1,a3,b3,c3,d3,a4,b4,c4,d4]T，A2为12×12的矩阵，上式有非零解的条件即分叉条件是
|A2|=0.
(32)
3.3 (2L-L1)/ce≤t≤2L/ce
同样的方法可得
A3C3=0,
(33)
其中C3=[a1,b1,c1,d1,a2,b2,c2,d2,a4,b4,c4,d4]T，得到A3为12×12的矩阵，有分叉条件:
|A3|=0.
(34)
4 数值计算结果及分析
弹性介质中的圆柱壳冲击端部自由，非冲击端部固支，受轴向阶跃载荷作用发生屈曲的临界载荷可由分叉条件得到.对于不同周向阶数n有许多分支，分支的高低反映了轴向的屈曲阶数.在以下的计算中，ξ表示圆柱壳的壁厚与中面半径比，λ表示长度比例，
表示无量纲的径向刚度.
令ξ=0.05,λ=0.5，图2(a)是由式(30)得到的应力波反射前波阵面通过分界面后，圆柱壳屈曲临界载荷随应力波波阵面位置的变化曲线(左图取n=0，右图取n=1)，每阶取前三支曲线进行分析.图2(b)、2(c)分别是由式(32)、(34)得到的应力波反射后，圆柱壳屈曲临界载荷随波阵面位置的变化曲线，这里取n=0，且只取其中一支进行分析.
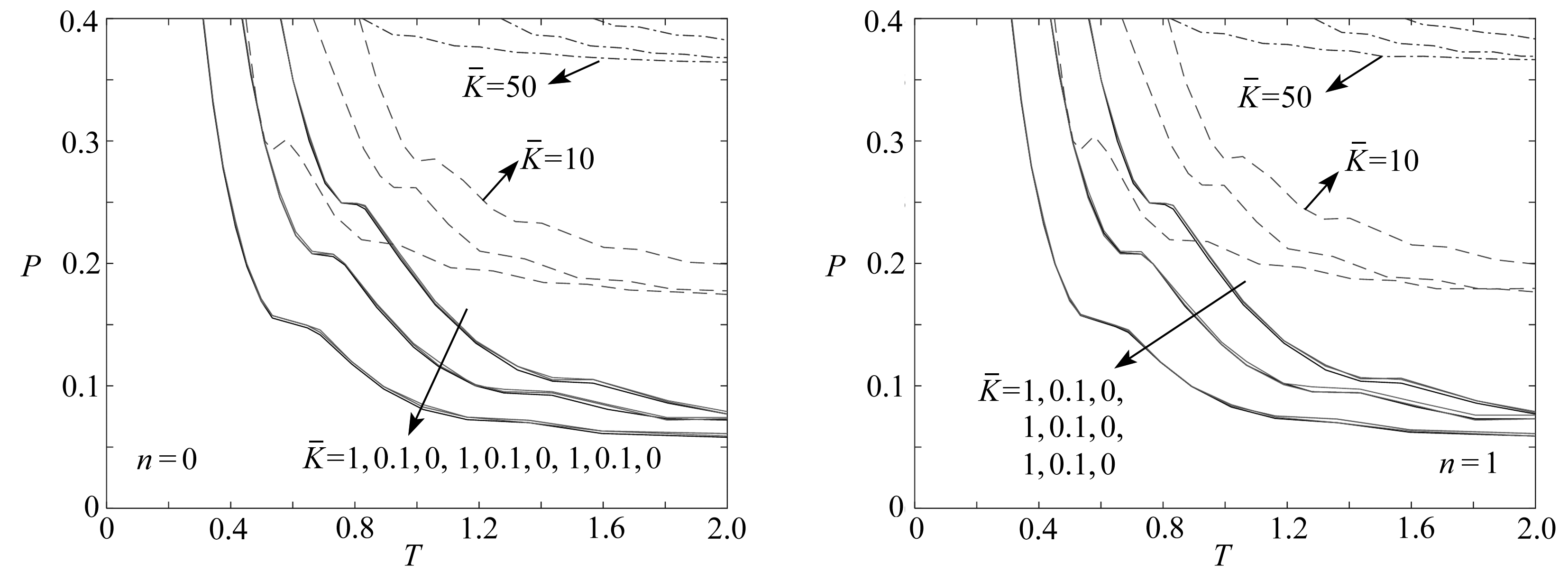
(a) 应力波反射前波阵面到达区域Ⅱ
(a) The wave fronts arrive at region Ⅱ before reflection
(b) 反射波波阵面到达区域Ⅱ (c) 反射波波阵面到达区域Ⅰ
(b) The wave fronts arrive at region Ⅱ after reflection (c) The wave fronts arrive at region Ⅰ after reflection
图2 轴向屈曲临界载荷与波阵面位置的关系
Fig. 2 Axial critical buckling loads with time of wave front propagation
从图2(a)可以看出，在径向刚度相同的情况下，n=0和n=1所对应的屈曲临界载荷随波阵面位置的变化关系规律一致，即弹性介质中的圆柱壳发生轴对称和非轴对称屈曲的规律一致.从图2(a)、2(b)、2(c)分别可以看出，应力波反射前波阵面通过分界面后、反射波波阵面通过分界面前、反射波波阵面通过分界面后各阶段，随着波传播时间的增加临界载荷逐渐降低.即弹性介质中的圆柱壳受轴向冲击，应力波传播再经固定端反射，随着波传播时间的增加临界载荷逐渐降低.还可以看出，波传播时间一定时，随着径向刚度增大，屈曲临界载荷增大，即圆柱壳的径向刚度越大越难屈曲，但当无量纲的径向刚度小于1时径向刚度的改变对圆柱壳屈曲几乎没有影响.
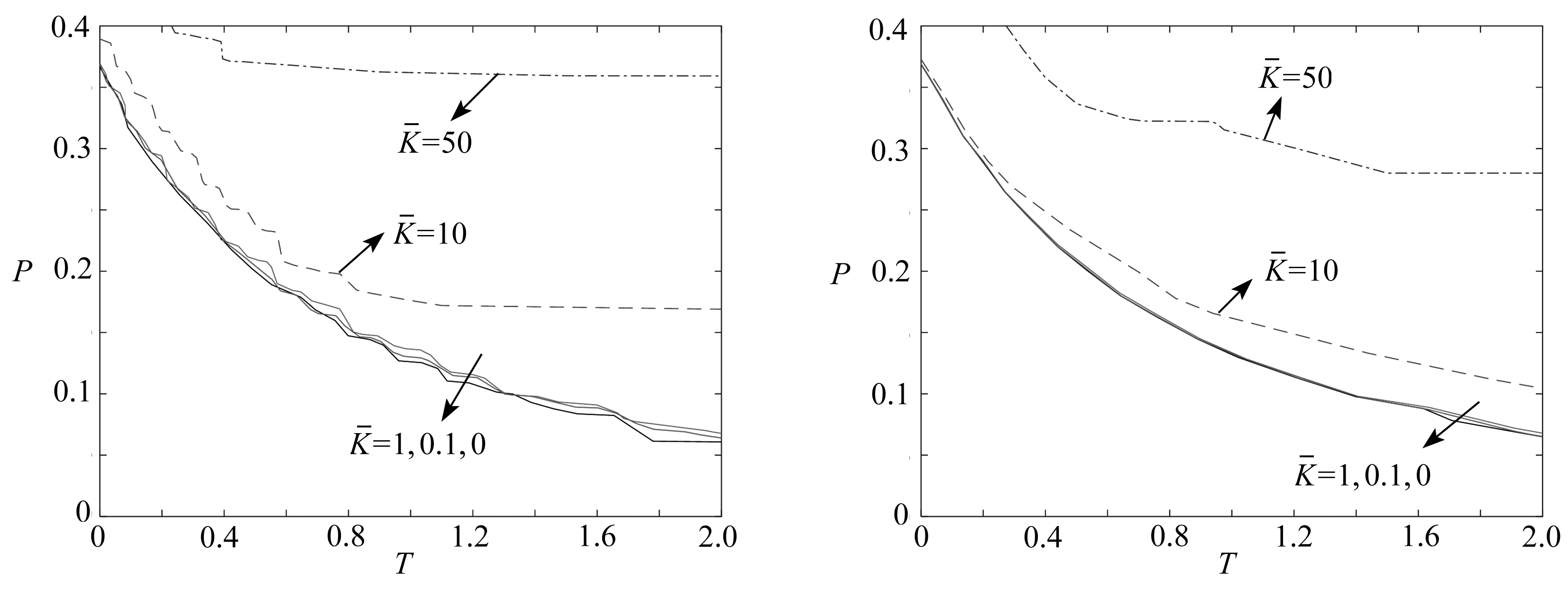
令ξ=0.05，λ=0.5，图3(a)、3(b)、3(c)是将T=0.75(表示在时刻T，应力波波阵面到达圆柱壳某一位置,此处代表反射前波阵面通过分界面后)、T=1.25(此处代表反射波未通过分界面)、T=1.75(此处代表反射波通过了分界面)，分别代入式(30)、(32)、(34)得到的屈曲临界载荷与无量纲径向刚度的关系，每阶取前三支曲线进行分析.
(a) T=0.75 (b) T=1.25 (c) T=1.75
图3 轴向屈曲临界载荷与无量纲径向刚度的关系
Fig. 3 Axial critical buckling loads with the dimensionless radial stiffness
从图3可以看出，当径向刚度较小时，临界载荷随径向刚度的增大明显增大.当无量纲径向刚度大于10，图3(a)中临界载荷增长缓慢，图3(b)、3(c)中临界载荷持续增长.结合图2可知，屈曲临界载荷随着径向刚度的增大经历了增长缓慢、增长迅速以及增长较慢3个阶段.
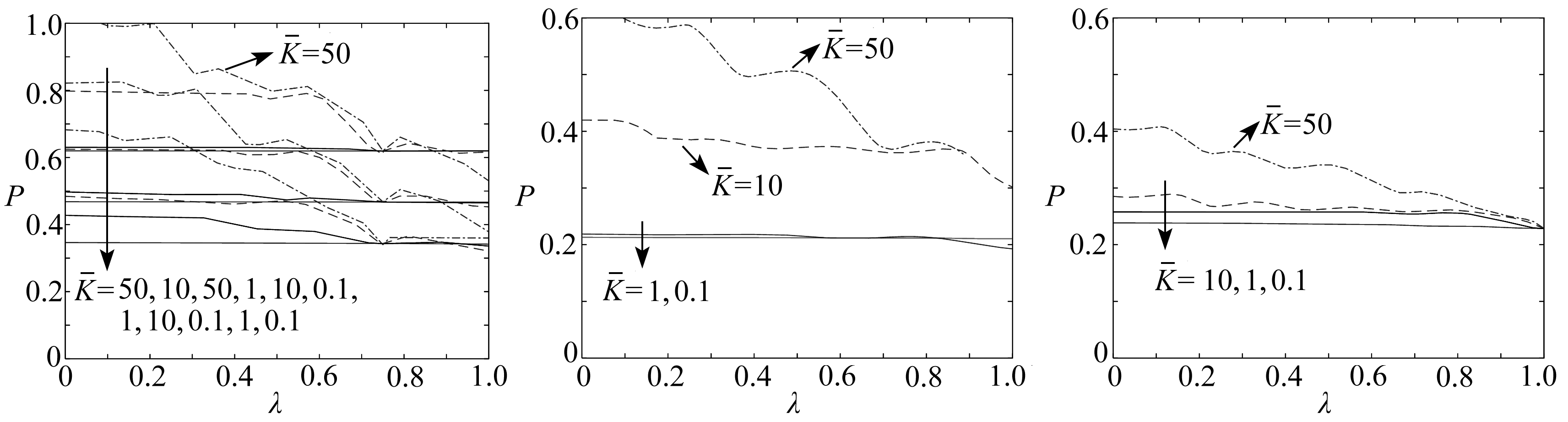
令ξ=0.05，n=0，图4(a)是由式(30)得到的应力波反射前波阵面通过分界面后，屈曲临界载荷随长度比例的变化曲线，取前三支曲线进行分析；图4(b)、4(c)分别是由式(32)、(34)得到的应力波反射后屈曲临界载荷随长度比例的变化曲线，只取其中一支进行分析.
(a) T=0.75 (b) T=1.25 (c) T=1.75
图4 轴向屈曲临界载荷与长度比例的关系
Fig. 4 Axial critical buckling loads with the length proportion
从图4可以看出，应力波反射前波阵面通过了分界面、反射后波阵面未通过分界面、反射后波阵面通过了分界面3个阶段，随着长度比例增大临界载荷都降低，即圆柱壳嵌入弹性介质部分越深越难屈曲.还可以看出，径向刚度越大，临界载荷随长度比例的变化趋势越明显.
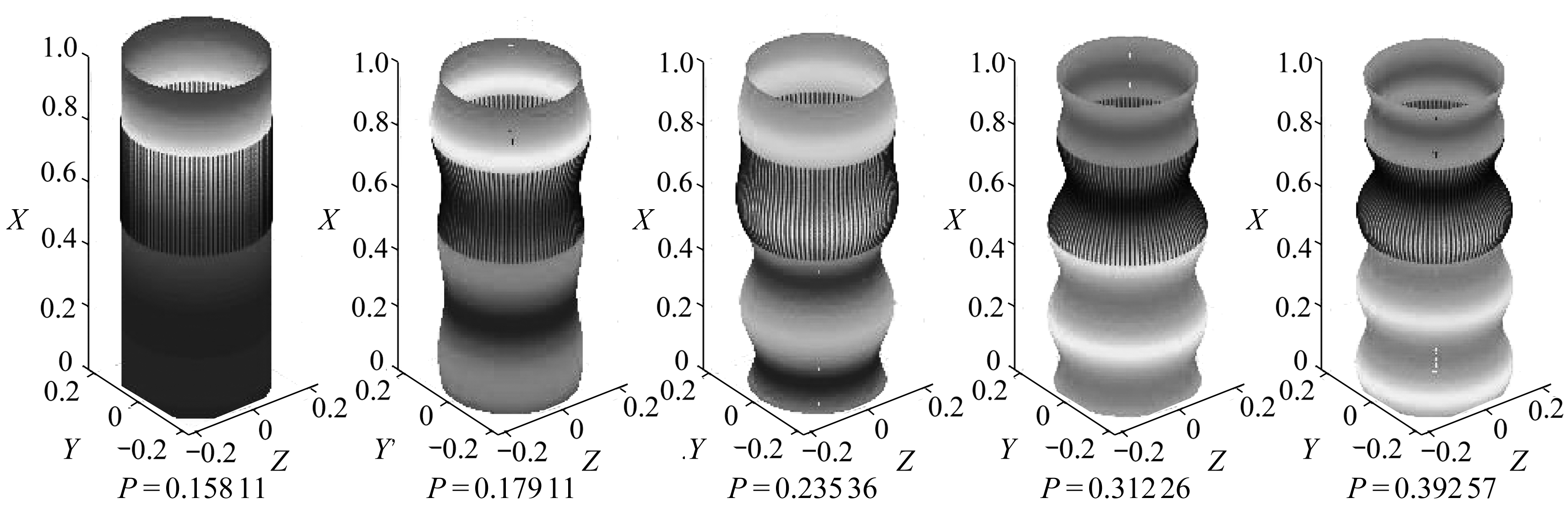
分别固定
图5根据式(30)给出了不同临界载荷对应的屈曲模态，圆柱壳下端为冲击端(下同).
(a) 不同分支临界载荷对应的屈曲模态
(a) The axial buckling models for different critical loads
(b) 不同周向阶数临界载荷对应的的屈曲模态
(b) The circumferential buckling models for different critical loads
图5 T=0.8时圆柱壳屈曲模态
Fig. 5 Buckling models for shells, T=0.8
从图5可以看出，圆柱壳在临界载荷作用下，应力波反射前，波阵面通过分界面后，分支数较大的模态沿母线的屈曲波数也越多，即临界载荷增大，轴向屈曲波数增加.随着周向阶数的增高，临界荷载增大，周向的屈曲波数也增加，且轴向屈曲模态数的增加引起的临界载荷变化量比周向屈曲模态数的增加引起的临界载荷变化量要大.还可以看出屈曲仅发生在应力波传播区域.
(a) 不同分支临界载荷对应的屈曲模态
(a) The axial buckling models for different critical loads
(b) 不同周向阶数临界载荷对应的的屈曲模态
(b) The circumferential buckling models for different critical loads
图6 T=1.2时圆柱壳屈曲模态
Fig. 6 Buckling models for shells, T=1.2
(a) 不同分支临界载荷对应的屈曲模态
(a) The axial buckling models for different critical loads
(b) 不同周向阶数临界载荷对应的的屈曲模态
(b) The circumferential buckling models for different critical loads
图7 T=1.7时圆柱壳屈曲模态
Fig. 7 Buckling models for shells, T=1.7
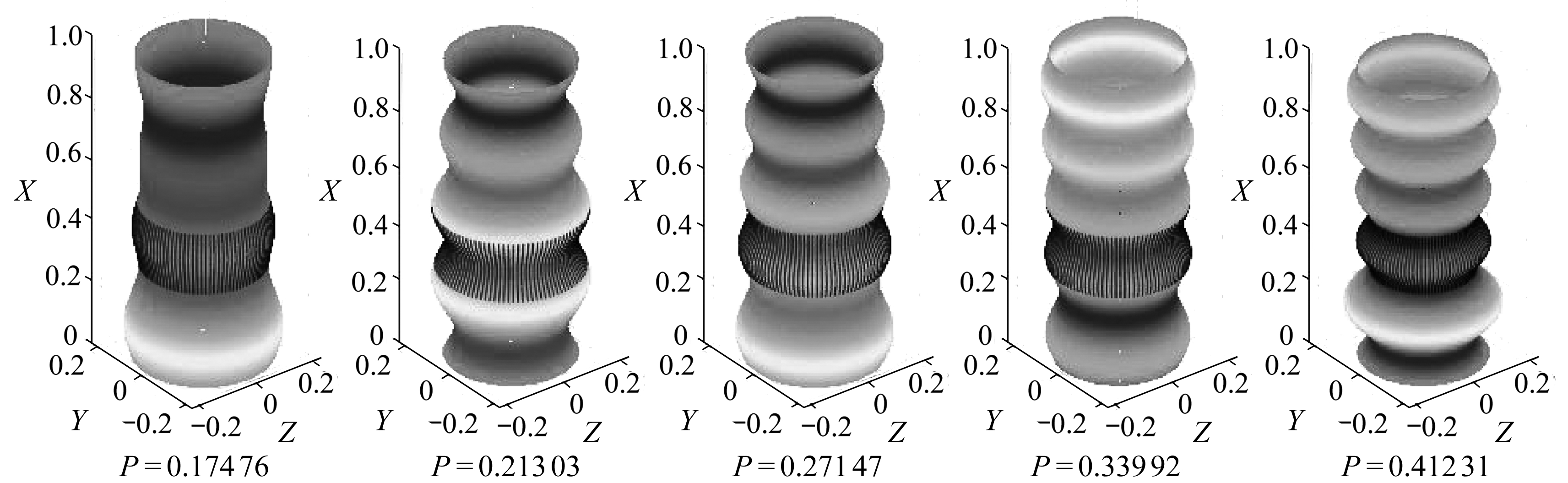
分别固定
图6根据式(32)给出了不同临界载荷对应的屈曲模态.
从图6可以看出，圆柱壳在临界载荷作用下，反射波通过分界面前，分支数较大的模态，沿母线的屈曲波数也越多, 即临界载荷增大，轴向屈曲波数增加.随着周向阶数的增高，临界荷载增大，周向的屈曲波数也增加,且轴向屈曲模态数的增加引起的临界载荷变化量比周向屈曲模态数的增加引起的临界载荷变化量要大.还可以看出在临界载荷较小时屈曲先发生在反射端部，随着分支数增大，屈曲覆盖整个圆柱壳区域.
分别固定
图7根据式(34)给出了不同临界载荷对应的屈曲模态.
从图7可以看出，圆柱壳在临界载荷作用下，反射波通过分界面之后，轴向各阶屈曲模态数的增加引起的临界载荷变化量比周向各阶屈曲模态数的增加引起的临界载荷变化量要大.还可以看出若反射波波阵面通过分界面后，壳体发生的屈曲始终覆盖整个圆柱壳区域.
5 结 论
对于弹性介质中的圆柱壳，受阶跃载荷作用时，考虑冲击端部自由，非冲击端部为固支的情况.计算分析了应力波通过了分界面但未发生反射、应力波经固定端发生反射后，圆柱壳临界屈曲载荷分别与波阵面传播位置、径向刚度、长度比例的关系.计算结果表明：
1) 弹性介质中的圆柱壳发生轴对称和非轴对称屈曲的规律一致.弹性介质中的圆柱壳受轴向冲击，应力波反射前波阵面通过分界面后、反射波波阵面通过分界面前、反射波波阵面通过分界面后各阶段，随着波传播时间的增加临界载荷逐渐降低.
2) 圆柱壳嵌入弹性介质部分越深、弹性介质的刚度越大，越难屈曲.
3) 弹性介质中的圆柱壳受轴向冲击，屈曲临界载荷随着弹性介质刚度的增大经历了增长缓慢、增长迅速以及增长较慢3个阶段.
4) 弹性介质中圆柱壳受轴向冲击发生屈曲，轴向屈曲模态数的增加引起的临界载荷变化量比周向屈曲模态数的增加引起的临界载荷变化量要大.应力波反射前波阵面通过分界面后，屈曲仅发生在在应力波传播区域；反射波波阵面通过分界面前，临界载荷较小时屈曲先发生在反射端部，随着周向阶数增大，屈曲覆盖整个圆柱壳区域；反射波波阵面通过分界面后，壳体发生的屈曲始终覆盖整个圆柱壳区域.
[1] 黄承义, 刘土光, 郑际嘉. 圆柱壳在径向冲击载荷作用下的弹性脉冲屈曲[J]. 应用数学和力学, 1996, 17(8): 735-741.(HUANG Chengyi, LIU Tuguang, ZHENG Jijia. Elastic pulse buckling of cylindrical shells under radial impulsive loading[J]. Applied Mathematics and Mechanics, 1996, 17(8): 735-741.(in Chinese))
[2] 沈惠申. 湿热环境中复合材料层合圆柱薄壳的屈曲和后屈曲[J]. 应用数学和力学, 2001, 22(3): 228-238.(SHEN Huishen. Buckling and postbuckling of laminated thin cylindrical shells under hygrothermal environments[J]. Applied Mathematics and Mechanics, 2001, 22(3): 228-238.(in Chinese))
[3] 顾红军, 赵国志, 陆廷金, 等. 轴向冲击下薄壁圆柱壳的屈曲行为的实验研究[J]. 振动与冲击, 2004, 23(4): 58-59.(GU Hongjun, ZHAO Guozhi, LU Tingjin, et al. Buckling of thin-wall cylindrical shell under axial impact[J]. Journal of Vibration and Shock, 2004, 23(4): 58-59.(in Chinese))
[4] 张善元, 张涛. 圆柱壳的轴向动力屈曲、参数共振与混沌运动[J]. 振动与冲击, 2010, 29(12): 34-38.(ZHANG Shanyuan, ZHANG Tao. Axial dynamic buckling parametric resonance and chaotic motion of a closed cylindrical shell[J]. Journal of Vibration and Shock, 2010, 29(12): 34-38.(in Chinese))
[5] 徐新生, 张耀光. 弹性圆柱壳在应力波下的动态屈曲[J]. 河南大学学报, 1997, 27(1): 1-5.(XU Xinsheng, ZHANG Yaoguang. Dynamic buckling of elastic cylindrical shells under the stress wave[J]. Journal of Henan University, 1997, 27(1): 1-5.(in Chinese))
[6] XU X S, MA Y, LIM C W, et al. Dynamic buckling of cylindrical shells subject to an axial impact in a symplectic system[J]. International Journal of Solids and Structures, 2006, 43(13): 3905-3919.
[7] KARAGIOZOVA D, JONES N. Influence of stress waves on the dynamic progressive and dynamic plastic buckling of cylindrical shells[J]. International Journal of Solids and Structures, 2001, 38(38/39): 6723-6749.
[8] KARAGIOZOVA D, ALVES M. Transition from progressive buckling to global bending of circular shells under axial impact, part Ⅰ: experimental and numerical observations[J]. International Journal of Solids and Structures, 2004, 41(5/6): 1565-1580.
[9] 马建青, 徐新生. 耦合载荷冲击下圆柱壳的动态屈曲[J]. 应用数学和力学, 2014, 35(5): 510-522.(MA Jianqing, XU Xinsheng. Dynamic buckling of cylindrical shells under coupled impact loads[J]. Applied Mathematics and Mechanics, 2014, 35(5): 510-522.(in Chinese))
[10] 桂夷斐, 马建敏. 阶梯圆柱壳在轴向冲击载荷作用下的屈曲计算分析[J]. 振动与冲击, 2019, 38(1): 200-205.(GUI Yifei, MA Jianmin. Buckling of step cylindrical shells under axial impact load[J]. Journal of vibration and shock, 2019, 38(1): 200-205.(in Chinese))
[11] 徐新生, 苏先樾, 王仁. 轴向应力波与弹塑性材料圆柱壳的动力屈曲[J]. 中国科学, 1995, 25(2): 166-173.(XU Xinsheng, SU Xianyue, WANG Ren. Dynamic elastic-plastic buckling of circular cylindrical shells under axial impact[J]. Science China, 1995, 25(2): 166-173.(in Chinese))
[12] WANGR, HAN M B, HUANG Z P, et al. An experimental study on the dynamic axial plastic buckling of cylindrical shells[J]. International Journal of Impact Engineering, 1983, 1(3): 249-256.
[13] TOVSTIK P, SMIRNOV A. Asymptotic Methods in the Buckling Theory of Elastic Shells[M]. Singapore: World Scientific, 2001.
[14] WANG C, LAI J C S. Prediction of natural frequencies of finite length circular cylindrical shells[J]. Applied Acoustics, 2000, 59(4): 385-400.
[15] ZHANG X M, LIU G R, LAM K Y. Vibration analysis of thin cylindrical shells using wave propagation approach[J]. Journal of Sound and Vibration, 2001, 239(3): 397-403.
[16] 王颖泽, 王谦, 刘栋, 等. 有限厚度圆柱壳热冲击问题的广义热弹性解[J]. 应用数学和力学, 2016, 37(6): 644-654.(WANG Yingze, WANG Qian, LIU Dong, et al. Generalized solution to the thermoelastic problem of finite-thickness hollow cylinders subjected to thermal shock[J]. Applied Mathematics and Mechanics, 2016, 37(6): 644-654.(in Chinese))
[17] 周军帅. 哈密顿体系下圆柱壳的动态和热屈曲研究[D]. 硕士学位论文. 大连: 大连理工大学, 2011.(ZHOU Junshuai. A study of dynamic and thermal buckling of circular cylindrical shells in the Hamiltonian system[D]. Master Thesis. Dalian: Dalian University of Technology, 2011.(in Chinese))