引 言
国际上多刚体系统动力学在机构动力学领域的应用已形成经典理论[1-3],但是曲柄摇杆机构的歧运动位仍值得研究.当曲柄为从动件体时,在连杆与曲柄共线的位置,由于压力角为90°而容易出现运动不确定现象,该位置可称为歧运动位.当从动件静止时,如果无论摇杆驱动力矩多么大也不能令机构运动,则该歧运动位可称为卡位.
卡位也称为死点[1],与在优化问题设计空间当中的点表示设计方案的概念相一致.自从1925年由Alt提出之后,有解析法研究文献:《四杆急回机构的分析计算》(李克涵. 铁道研究院运输所, 1983)、《按Krmin综合曲柄摇杆机构的解析法》(蒋学全. 陕西工学院论文,69号)、《用解析法设计满足K、φ、rmin要求的曲柄摇杆机构》(朱建平. 洛阳建材工业专科学校, 1985)[4] 等.文献[1]提到L’Hopital法则求解0/0型不定式用于运动歧点运动学参数的被零除问题,但是没有推导公式,也没有证明不定式类型,其中的习题也没有提及.虽然国外多体动力学仿真软件已实现商业化,如ADAMS、RecurDyn,但是,未见关于卡位运动学参数的计算公式.可见,卡位的运动学问题还没有解决.该问题阻挡了以曲柄为从动件的程序化运动学研究.
曲柄摇杆机构在机械领域得到普遍应用,以其作为主机构的机器具有结构简单、可靠性强、易损件少、操作维修方便等优点,比如游梁式抽油机[5]的主机构.摇杆外伸端带有圆弧形结构,称为驴头,该圆弧缠绕钢丝绳并悬吊抽油杆柱.悬点对应于摇杆外伸端在上极限位置时抽油杆柱与该圆弧相切的点,驴头圆弧部分的竖直切线为悬点的运动轨迹.悬点运动是抽油杆柱系统的运动输入,对冲程损失、出油量、能耗等具有重要的影响,其无冲击准确解是许多课题的研究基础.
电机的变频驱动技术日新月异,设计摇杆的理想运动规律,反推出曲柄的运动规律,然后据此提供电机的控制率可获得理想的悬点运动.目前尚存在以下两个问题:
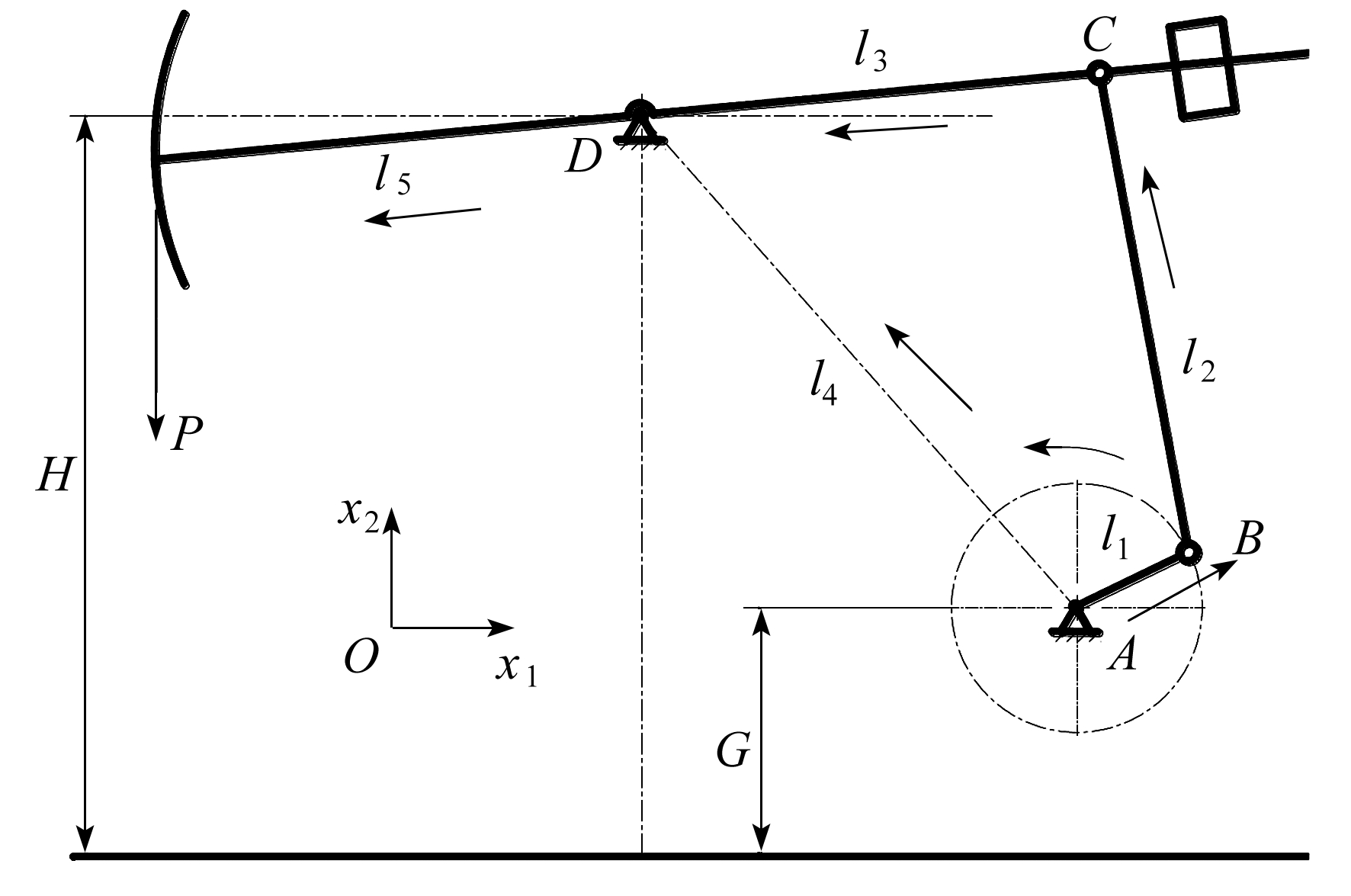
图1 机构运动简图
Fig. 1 The mechanism motion diagram
1) 没有对矢量方程及其从动件运动参数高阶时间导数的探讨.而高阶时间导数具有重大的数学意义,对于定性分析机构的运动学和动力学问题至关重要,可通过矢量方程投影方程组的求导与求解获得.
2) 机构卡位的运动学参数求取.在该位置,从动曲柄或滑块与连杆共线,从动件受力方向与运动方向相互垂直,压力角为90°、传动角为0°.如果处于静止状态,无论多么大的驱动力都不能驱使其运动.曲柄为主动件的运动学研究没有卡点,可实现程序化[6].曲柄为从动件的运动学研究却因卡点而难以实现程序化.在该位置会因被零除而计算失败.
本文主要针对如图1所示的曲柄摇杆机构(游梁式抽油机主机构)开展研究.
1 摇杆主动的矢量投影方程组求解
在图1中,以曲柄回转中心为坐标原点,以水平向右和竖直向上分别为两个坐标轴的正方向,建立x1Ox2直角坐标系.l1,l2,l3,l4,l5分别为曲柄、连杆、摇杆(游梁后臂)、机架、游梁前臂的长度,θ1,θ2,θ3,θ4,θ5=θ3分别为上述构件体的位置角,即与x1轴正方向的夹角.H为摇杆转动中心距地面的高度,G为坐标原点距地面的高度.
取转动副之间的连线为表达各构体姿态的矢量,由坐标原点指向摇杆铰接点为表达固定体姿态的矢量.根据各构体之间的连接关系,可列出以下矢量方程(N=2):
l1+l2+l3=l4.
(1)
矢量方程的各矢量组成封闭的多边形[7].对于N维矢量方程,可由图解法求出N个未知量.
将矢量方程式(1)分别向x1轴和x2轴投影,将已知项都放在等号右边,可得矢量方程投影的方程组:
(2)
将式(2)两式移项,使等号左边均为θ1的三角函数.将两式平方后求和,可根据正、余弦函数的平方和公式消去θ2,从而获得θ1的三角函数方程:
2l1(l4cos θ4-l3cos θ3)cos θ1+2l1(l4sin θ4-l3sin θ3)sin θ1=
(3)
也可消去θ1而获得θ2的三角函数方程.
在摇杆的两个极限位置,曲柄与连杆在同一条直线上.机架、摇杆及该线段组成三角形,根据各构体长度,在摇杆的两个极限位置处,θ3为
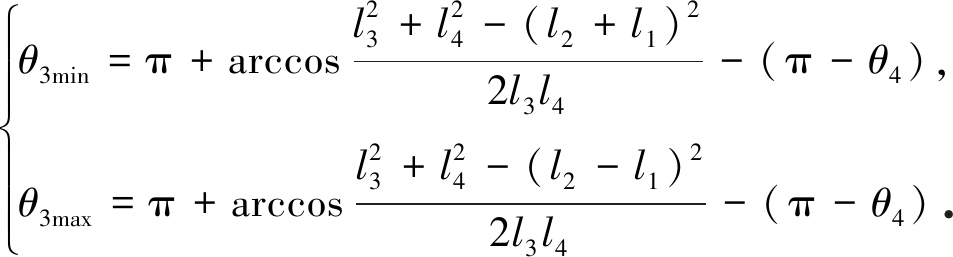
(4)
设摇杆按照正弦变化规律摆动,周期为T,即
(5)
根据式(3),由基于谐波合成与分解原理的角度求解方法[8]可得
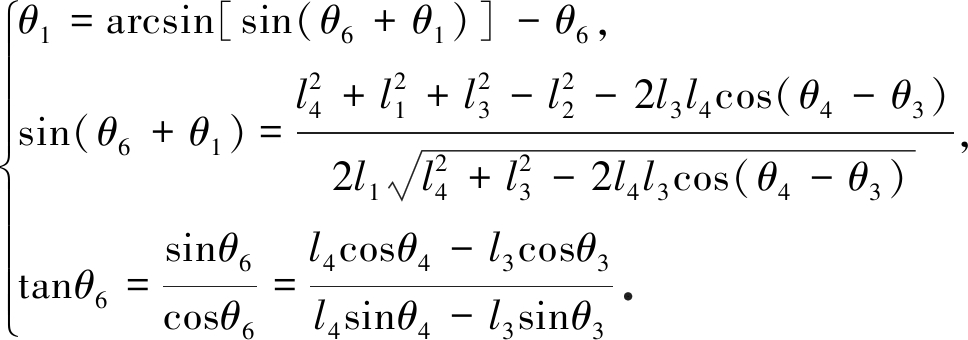
(6)
由于曲柄整周转动,须设定范围.如果θ1<0,令
θ1=θ1+2π;
(7)
如果θ1>2π,令
θ1=θ1-2π.
(8)
设曲柄逆时针转动(正向),根据运动的连续性,如果上一时刻θ1大于式(6)并且不在0°过渡处(两者之差大于1.5π除外),则令
θ1=π-arcsin[sin(θ6+θ1)]-θ6.
(9)
通常, 将式(6)、 (9)全部算出, 然后综合考虑实际情况进行取舍, 以免出现运动不连续现象.
根据式(2),可得θ2的正弦、余弦函数的符号与数值,可确定θ2.
将式(2)对时间求一阶和二阶导数,可得
(10)
(11)
在摇杆上(右)极限位置,θ1=θ2,在摇杆下(左)极限位置,θ1=θ2+π,机构均处于卡位.式(10)、(11)所示角速度和角加速度的分母为0.如果进行程序化运动学参数计算,在该位置会出现被零除而被迫终止运算的现象.可进行判断延迟而避免,但是,理论性不足.
(角)位移的高阶导数没有刚体转动动力学方程(Euler方程)及平动动力学方程(Newton第二定律)的支持,通常被研究者忽略.但是,其理论意义和实践价值重大,比如三阶导数(急动度[9])在高阶逐步积分法研究当中,往往是希望获取的值;在机床刀具运动规律和凸轮廓线设计当中,为延缓刀具老化、避免从动件频跳、减小噪声和磨损而要求三阶导数没有突变.
理论上,式(2)可以对时间进行无限次求导而获得从动件位置角的任意阶导数.如果曲柄为主动件,则进行三阶和四阶求导,可得

(12)
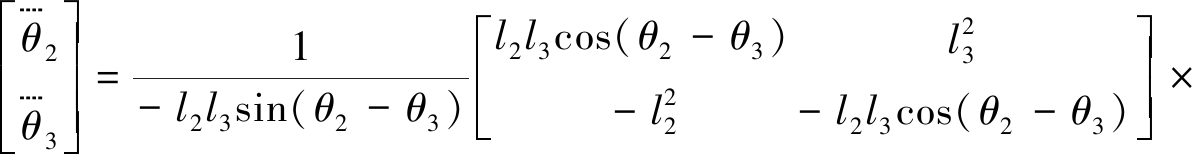

(13)
如果摇杆为主动件,可得相似的结果.在卡位仍然分母为0.
2 卡位的运动学研究
在图1中,以连杆BC为研究对象,取C为基点,令B相对于C的相对速度为vBC,则B点的速度为
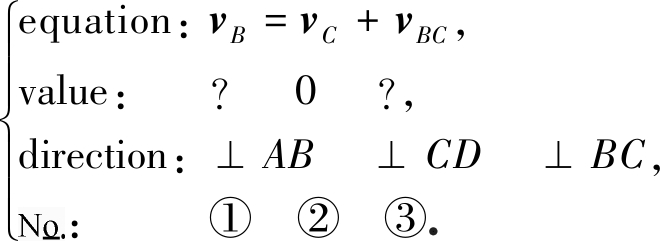
(14)
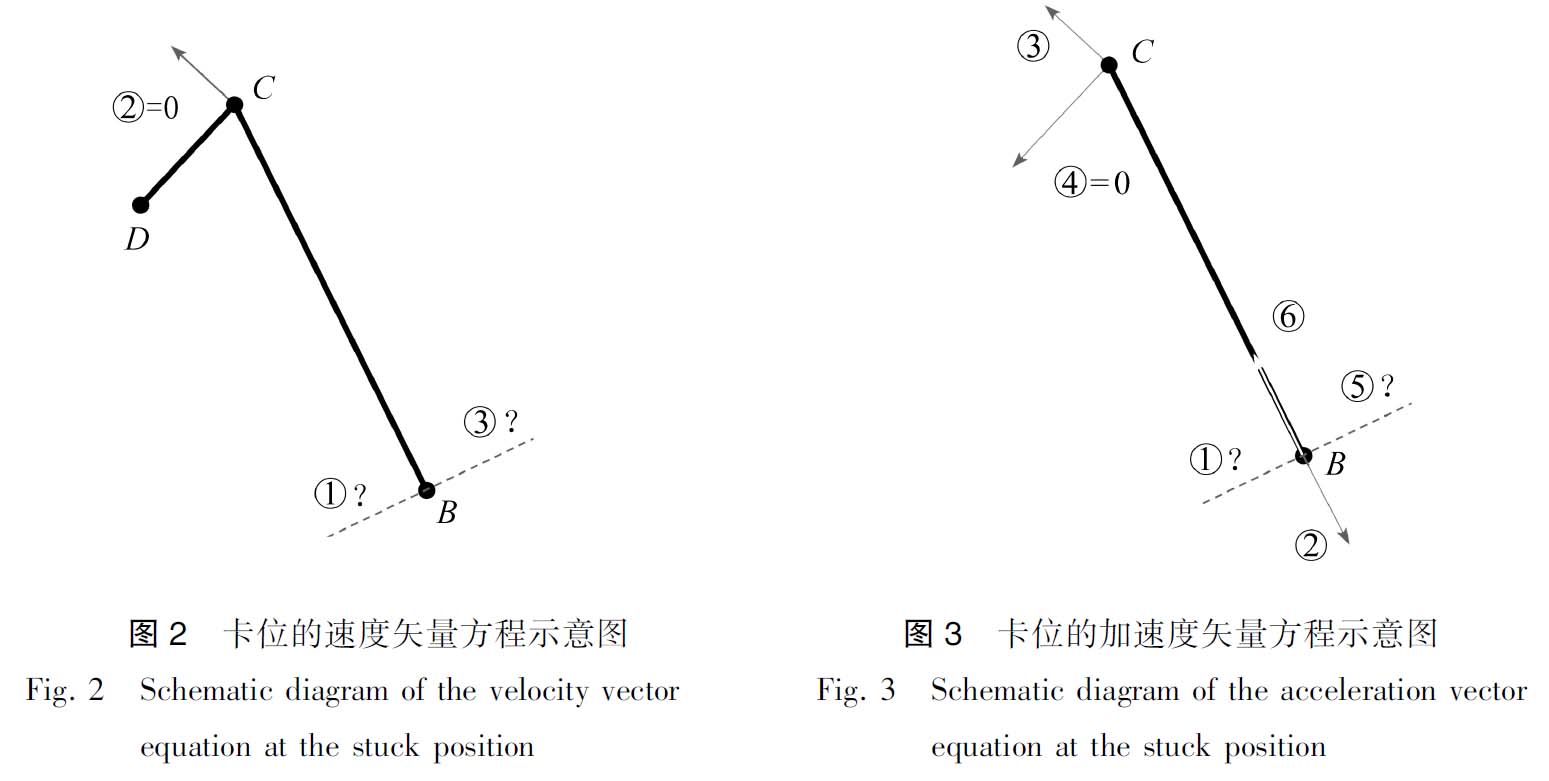
从各矢量大小和方向的分析结果看,存在两个未知量,可由矢量方程图解法求取.但是,在卡位,两个未知量共线(见图2),难以求取,只能获得以下关系式:

(15)
式中,±,∓的上符号对应于摇杆上(右)极限的卡位,两者方向相反;下符号对应于摇杆下(左)极限的卡位,两者方向相同.由瞬心法及其三心定理也可求得上述结果.
式(10)系数的分母为0,分子也为0,属于0/0型未定式,可根据L’Hopital法则将分子和分母分别求导获得该未定式的值.因此,有
(16)
由于![]() 上式的第二项为0.将式(15)代入式(16),在摇杆上(右)、下(左)极限所对应的卡位:
上式的第二项为0.将式(15)代入式(16),在摇杆上(右)、下(左)极限所对应的卡位:
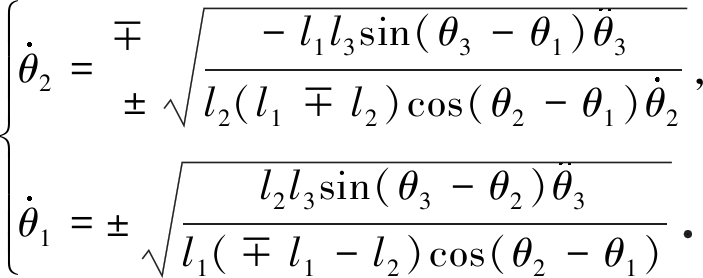
(17)
根据运动的连续性或沿切向的力学分析,如果曲柄逆时针运动,则二次根号外取上面的符号;如果对应于摇杆上(右)极限,则二次根号内取上面的符号.
令B相对于C的相对加速度为aBC,则B点的加速度为
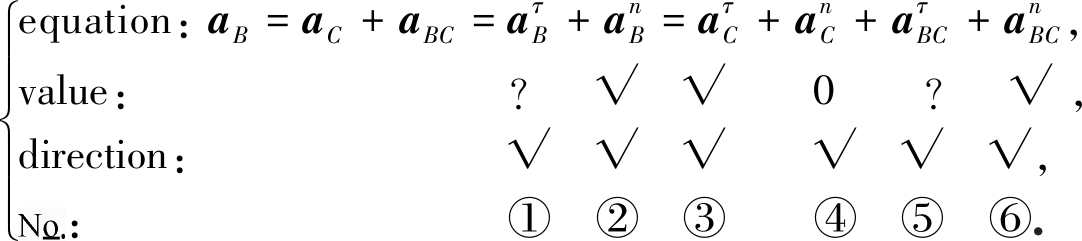
(18)
从各矢量的大小和方向分析结果看,存在两个未知量.在卡位,两个未知量共线(见图3),难以用矢量方程图解法求出.
根据垂直于连杆方向的分量之和为0,可得
(19)
由图3可知,在卡位,式(11)的分子恰好为矢量②、③、④、⑥在连杆长度方向上的投影之和,为0.式(11)为0/0型的未定式,可由L’Hopital法则求值,得
令曲柄逆时针转动,摇杆上(右)、下(左)极限所对应卡位的![]() 和
和![]() 分别为
分别为
(20)
(21)
3 程序化计算机仿真
3.1 结构参数及仿真参数
针对图1所示的曲柄摇杆机构,设相关参数如表1所示.
表1 结构参数和仿真参数
Table 1 Structure and simulation parameters

parameterl1/ml2/ml3/ml4/ml5/mvalue0.863.433.034.283.53parameterH/mG/mt/sΔT/sT/svalue5.982.47200.0115
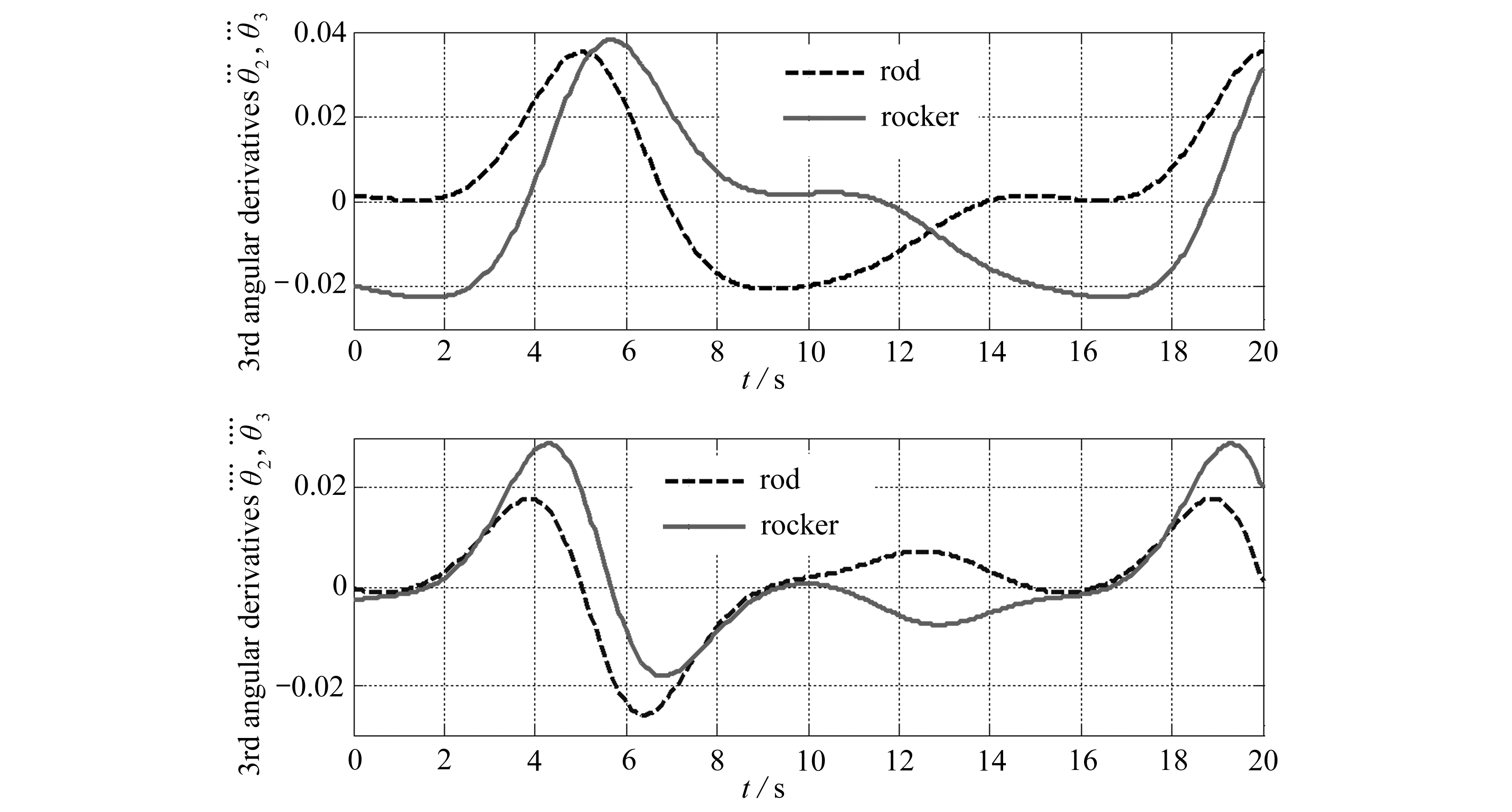
图4 曲柄匀速转动的连杆和摇杆位置角的三、四阶导数
Fig. 4 The 3rd- and 4th-order angular derivatives of the rod and rocker with uniform rotation of the crank
3.2 曲柄匀速转动的从动件位置角高阶导数
取θ1=0为初始位置,则
(22)
从动连杆和摇杆位置角的三、四阶导数如图4所示.实线为从动摇杆的参数,虚线为从动连杆的参数.经验算,上述结果满足矢量投影方程组的各阶导数式.
3.3 摇杆为主动件的仿真结果
取摇杆的运动规律为式(5),曲柄和连杆的运动规律分别如图5所示.

图5 摇杆正弦规律摆动的从动连杆和曲柄运动规律
Fig. 5 The motion rule of the driven rod and crank with a sinusoidal swing rocker
在3.75, 11.25, 18.75 s,机构出现卡位,θ1分别为![]() 分别为
分别为![]() 分别为-0.012 774,-0.009 728 2,-0.012 774 rad/s2,运动参数平滑过渡,没有突变.
分别为-0.012 774,-0.009 728 2,-0.012 774 rad/s2,运动参数平滑过渡,没有突变.
从动件的运动明显不是简谐运动,从动曲柄的角加速度出现多个峰值.
4 结 论
1) 本文所用数学知识主要有矢量投影、矢量方程、链式求导法则、导数的乘法法则、L’Hopital法则、三角函数关系式等.对矢量投影方程组多次求导获得了位置角高阶导数.经检验,方程组求导与求解的顺序不影响最终结果,先求导后求解与先求解后求导的结果一样.
2) 基于L’Hopital法则求0/0未定式极限的卡位运动学参数求解方法,可使曲柄从动件的机构运动学和动力学计算机仿真算法的程序化研究顺利开展.
3) 在曲柄从动件连续运动的过程中,虽然存在卡点位置,但是卡点不卡,没有速度和加速度突变现象,既没有刚性冲击也没有柔性冲击.该结论可解释两个现象.以曲柄滑块机构为主机构的内燃机虽然主动件滑块的往复运动具有惯性力较大、给机构造成的冲击明显等恶劣的动力学特性,但是仍获得了广泛的应用[10].作为功率传递零件,从动曲柄轴和偏心轮获得了广泛的应用.
4) 在卡位处,本文根据运动连续性确定下一时刻的位置.如果恰好从动曲柄的角速度为0,则需要根据受力情况分析.如果在运动过程当中考虑摩擦力[11-12]的作用,则卡位之后的运动将更加复杂.即使从动曲柄的角速度不为0,外力也有可能给从动件造成刚性冲击而改变其运动方向.
致谢 本文作者衷心感谢中国石油大学胜利学院教学改革研究基金(JG201725)对本文的资助.
[1] VINOGRADOV O. Fundamentals of Kinematics and Dynamics of Machines and Mechanisms[M]. Boca Raton: CRC Press, 2000.
[2] EDWARD J H. Computer Aided Analysis and Optimization of Mechanical System Dynamics[M]. Berlin: Springer, 1984.
[3] PARVIZ E N. Computer-Aided Analysis of Mechanical Systems[M]. New Jersey: Prentice Hall, 1988.
[4] 李学荣, 吴培芳. ALT法设计曲柄摇杆机构[J]. 齐齐哈尔轻工学院学报, 1988, 4(3): 47-52.(LI Xuerong, WU Peifang. The ALT means of designing oscillation-crank mechansis[J]. Journal of Qiqihaer Institute of Light Industry, 1988, 4(3): 47-52.(in Chinese))
[5] 游晓燕. 常规式游梁抽油机改造成斜井抽油机分析[J]. 机械设计与制造工程, 2002, 31(3): 82-83.(YOU Xiaoyan. Reconstruct ion of the pump with inclined oil well from the common beam-moving one[J]. Mechanical Design and Manufacturing Engineering, 2002, 31(3): 82-83.(in Chinese))
[6] 李春明. 闭环结构的降维违约修正方法[J]. 中国石油大学学报(自然科学版), 2008, 32(2): 93-96.(LI Chunming. Reduced dimension constraint violation correction method for multibody system with loop[J]. Journal of the China University of Petroleum(Edition of Natural Science), 2008, 32(2): 93-96.(in Chinese))
[7] 李春明, 尹晓丽, 贠平利, 等. 某机械曲柄滑块机构的动力学及相关问题研究[J]. 德州学院学报, 2019, 35(6): 40-46.(LI Chunming, YIN Xiaoli, YUN Pingli, et al. Crank slider mechanism dynamics and its related problem of a machine[J]. Journal of Dezhou University, 2019, 35(6): 40-46.(in Chinese))
[8] 李春明, 李万腾, 刘庆, 等. 受弯矩作用中心轮的受力分析方法[J]. 德州学院学报, 2017, 33(4): 50-53.(LI Chunming, LI Wanteng, LIU Qing, et al. Force analysis method of the center wheel with bending moment load[J]. Journal of Dezhou University, 2017, 33(4): 50-53.(in Chinese))
[9] 李岩汀, 徐绩青, 许锡宾, 等. 结构动力响应中急动度的计算[J]. 应用数学和力学, 2017, 38(8): 922-931.(LI Yanting, XU Jiqing, XU Xibin, et al. A numerical method for calculation of structural jerk responses[J]. Applied Mathematics and Mechanics, 2017, 38(8): 922-931.(in Chinese))
[10] 刘晓昂, 上官文斌, 吕兆平. 三缸发动机悬置系统设计方法的研究[J]. 振动工程学报, 2016, 29(5): 804-813.(LIU Xiaoang, SHANGGUAN Wenbin, LÜ Zhaoping. Design methods of the powertrain mounting system with three cylinders engine[J]. Journal of Vibration Engineering, 2016, 29(5): 804-813.(in Chinese))
[11] 李春明. 摩擦力分类及压杆失效的新概念[J]. 制造业自动化, 2015, 37(23): 85-86, 91.(LI Chunming. The new conception of the friction classification and the stressed pole failure[J]. Manufacturing Automation, 2015, 37(23): 85-86, 91.(in Chinese))
[12] 赵雪芬, 李星. 一维六方准晶非周期半平面的有限摩擦接触问题[J]. 应用力学学报, 2018, 35(1): 8-14, 223.(ZHAO Xuefen, LI Xing. The frictional contact problem for aperiodical half-plane in one-dimensional hexagonal quasicrystals[J]. Chinese Journal of Applied Mechanics, 2018, 35(1): 8-14, 223.(in Chinese))