引 言
工程材料和结构在循环载荷和冲击载荷作用下往往会出现缺陷，如微孔洞和微裂纹[1-3]，从而在局部位置产生高应力集中或者发生应力奇异，极大降低了材料和结构的强度性能[4-6].孔边多裂纹的问题也是普遍存在的：飞机内部结构中会出现共线孔多裂纹平板疲劳裂纹扩展寿命的研究问题[7]；孔边多裂纹构型可为生物力学中骨移植界面提供力学模型等[8].对于宏观尺度时孔边裂纹的断裂力学问题，国内外许多学者进行了广泛研究，如孔边裂纹的静强度问题[9-11]和孔边裂纹的动应力问题[12-14].随着现代科技的发展，材料学家可以从微观层面设计出具有周期分布的微结构材料[15].因此，对圆孔边周期性多裂纹模型的研究具有重要的科学价值与工程意义.
当缺陷的尺寸为纳米量级时，非均匀材料的细观场和断裂性能受表面效应的影响，表现出显著的尺寸效应[16-17].Gurtin-Murdoch表面弹性理论模型[18-20]通过引入界面应力，给出了合理表征纳米尺度缺陷表面效应的数学表达，广泛用于纳米尺度夹杂、孔洞和裂纹问题的强度性能研究.Luo等[21]运用复变函数理论和保角映射技术，对纳米椭圆夹杂的反平面问题进行了研究;Pinyochotiwong等[22]研究了表面弹性半空间的刚性无摩擦压痕问题;Kim等[23]研究了反平面剪切变形中表面弹性对Ⅲ型裂纹问题的影响;肖俊华等[24]研究了纳米正三角形孔边裂纹问题的断裂特性;Xiao等[25]讨论了含有纳米缺陷正交各向异性体的界面应力问题;Wang等[26]对双材料各向异性体界面裂纹进行了分析;Kim等[27]研究了面内变形时表面性能对双材料界面裂纹的影响;Kim等[28]研究了反平面变形时表面性能对双材料界面裂纹的影响;Xu等[29]讨论了反平面剪切载荷作用时表面/界面应力对无限区域内纳米夹杂和纳米裂纹相互作用的影响;肖俊华等[30]对开裂椭圆孔的断裂力学特性进行了研究.
本文基于Gurtin-Murdoch表面弹性理论[18-20]和保角映射技术，研究了纳米尺度孔边均布径向多裂纹问题的断裂力学问题;给出了孔洞和裂纹周围的应力场表达式和裂纹尖端的应力强度因子的解析解；讨论了应力强度因子的尺度效应以及裂纹数量、裂纹/孔径比和缺陷表面性能对应力强度因子的影响.
1 模型与基本方程
图1为纳米尺度孔边均布多裂纹问题的示意图，远场受均匀反平面剪切载荷
图中实线表示n=3，实线和虚线一共表示n=6，n为裂纹数量.圆孔半径为R，孔洞区域用Ωc表示，基体区域用Ωm表示，缺陷的边界用S表示，裂纹长L，下标c、m分别表示孔洞和基体材料.
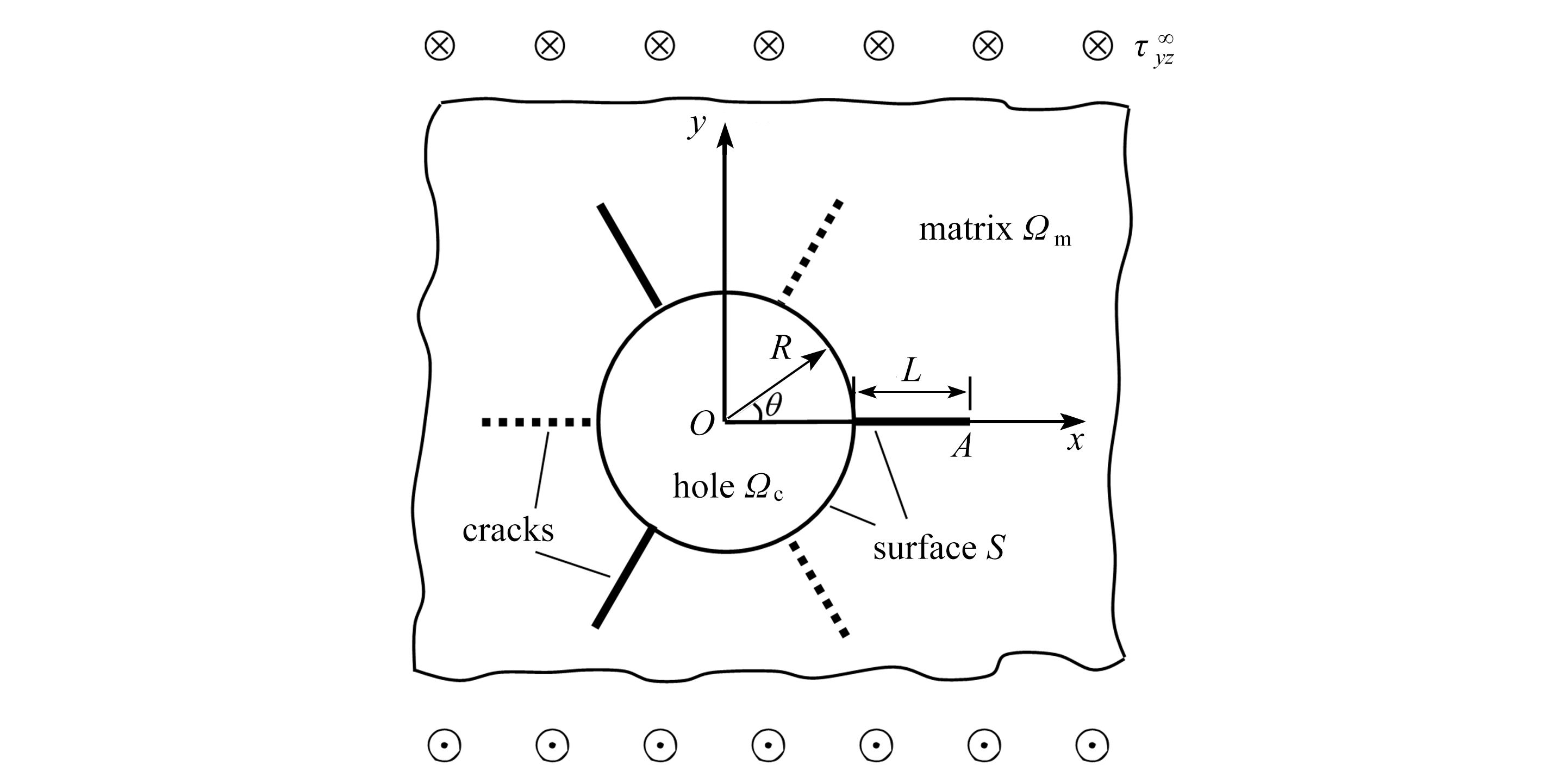
图1 纳米尺度孔边均布径向多裂纹示意图
Fig. 1 Schematic diagram of radial multi cracks at the nanometer scale
基体内的平衡方程和物理方程如下：
(1)
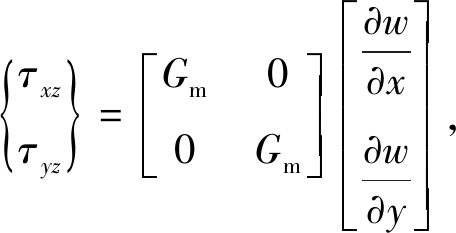
(2)
其中w=w(x,y)表示纵向位移.
由复变弹性理论可知，复平面内各点的纵向位移和应力分量可用一个解析函数φ(z)来表示：
(3)
τxz-iτyz=Gmφ′(z)，
(4)
τrz-iτθz=Gmeiθφ′(z)，
(5)
式中τrz和τθz分别表示柱坐标系下的两个切应力分量；z=x+iy，i为虚数单位.
基于Gurtin-Murdoch表面弹性理论[18-20]，缺陷的表面被视为一个无厚度但仍有自身物理性能的弹性层.由于表面效应的影响，缺陷表面上的位移边界条件和应力边界条件如下：
wc(t)=wm(t)， t∈S，
(6)
(7)
式中μs为表面弹性常数;t(ρ,θ)=ρeiθ为缺陷边界上的点的极坐标;
为表面应变分量.
2 分析与解答
将图1所示圆孔边多裂纹的圆孔外部分保角变换为图2所示的半径为R的圆外部分，映射函数为[31]
(8)
(9)
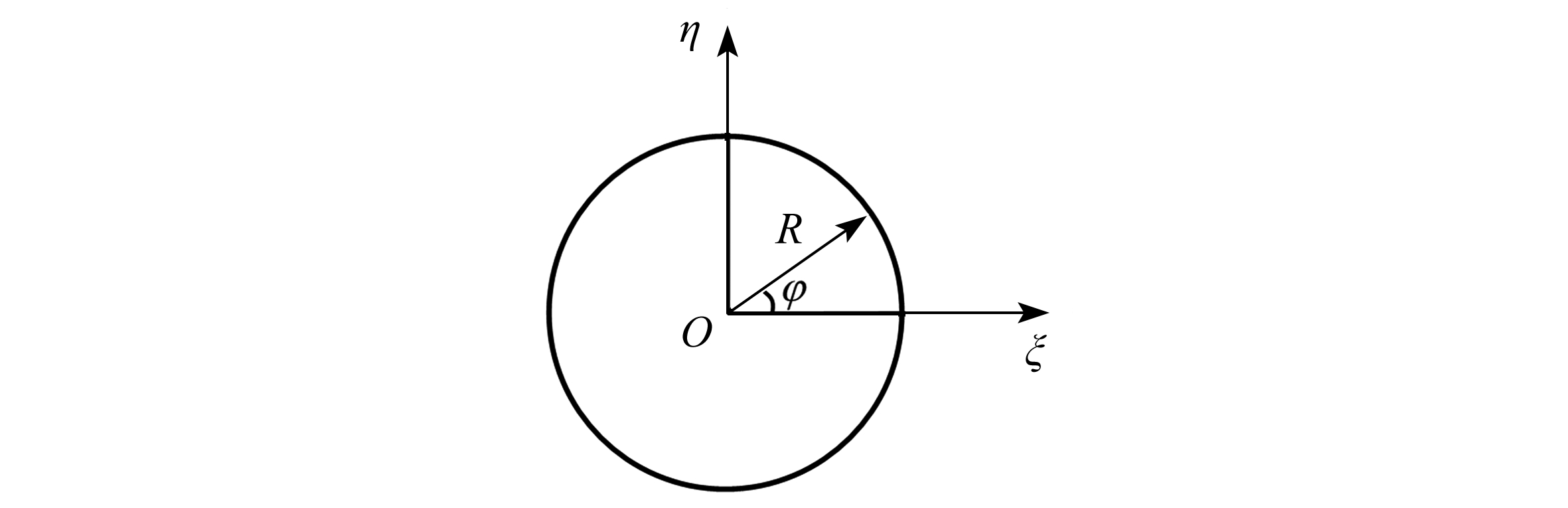
图2 保角映射(ζ平面, ζ=ξ+iη)
Fig. 2 Conformal mapping (ζ plane, ζ=ξ+iη)
将解析函数φ(z)在ζ平面内展开成Laurent级数形式[32]：
(10)
式中a*和ak为待定常数.
经分析，取下述有限项级数形式就可以得到问题的解析解：
φc(ζ)=Aζ, within the circle,
(11)
(12)
式中A,B1,B-1为复常数.
利用远场边界条件，由式(4)和(12)可得
(13)
由表面边界条件(6)和(7)得
(14)
(15)
联立式(13)～(15)可得
(16)
(17)
由式(4)、(11)～(13)、(16)和(17)可得基体内部的应力表达式为
(18)
其中ω′(ζ)表示映射函数ω(ζ)的一阶导数：
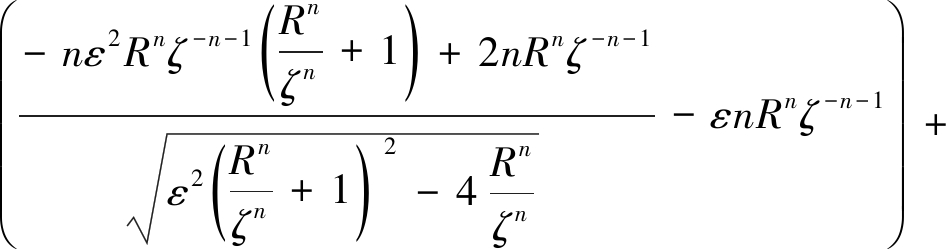
(19)
在图1所示z平面内定义裂纹尖端的Ⅲ型应力强度因子如下：
(20)
其中 z0=R+L.
将式(18)代入式(20)，在ζ平面内可得
(21)
注意到当裂纹数量n及λ=L/R给定时ω′(R)=0，对式(21)运用L’Hopital法则，可得
(22)
其中L′=R+L表示等效裂纹长度,
(23)
经比较，当本文的裂纹数量n分别取值1和2时，式(23)分别与文献[33]和[34]的结果一致.
若不考虑缺陷的表面效应，令μs=0，式(23)退化为
(24)
经比较，式(24)与文献[31]的纯弹性情形结果一致.
3 算例与讨论
根据文献可知，纳米缺陷的表面弹性常数μs的量级为1 N/m，数值可以是正值也可以是负值[21]，定义表面性能参数α=μs/Gm.
算例1 图3给出了无量纲应力强度因子
随孔径R的变化曲线，其中裂纹数n分别取3，6和9， α取为±2×10-10 m，λ=L/R=1.
由图3可以看出，不考虑表面效应时(α=0，经典断裂理论)，无量纲应力强度因子与缺陷的尺寸无关；考虑表面效应(α≠0)且孔径R<15 nm时，无量纲应力强度因子存在尺寸依赖效应；随着孔径的增加，负表面弹性常数时无量纲应力强度因子单调减小，正表面弹性常数时无量纲应力强度因子单调增加；随着孔径尺寸逐渐增大，尺寸依赖效应逐渐消失，无量纲应力强度因子趋近于经典断裂理论解.
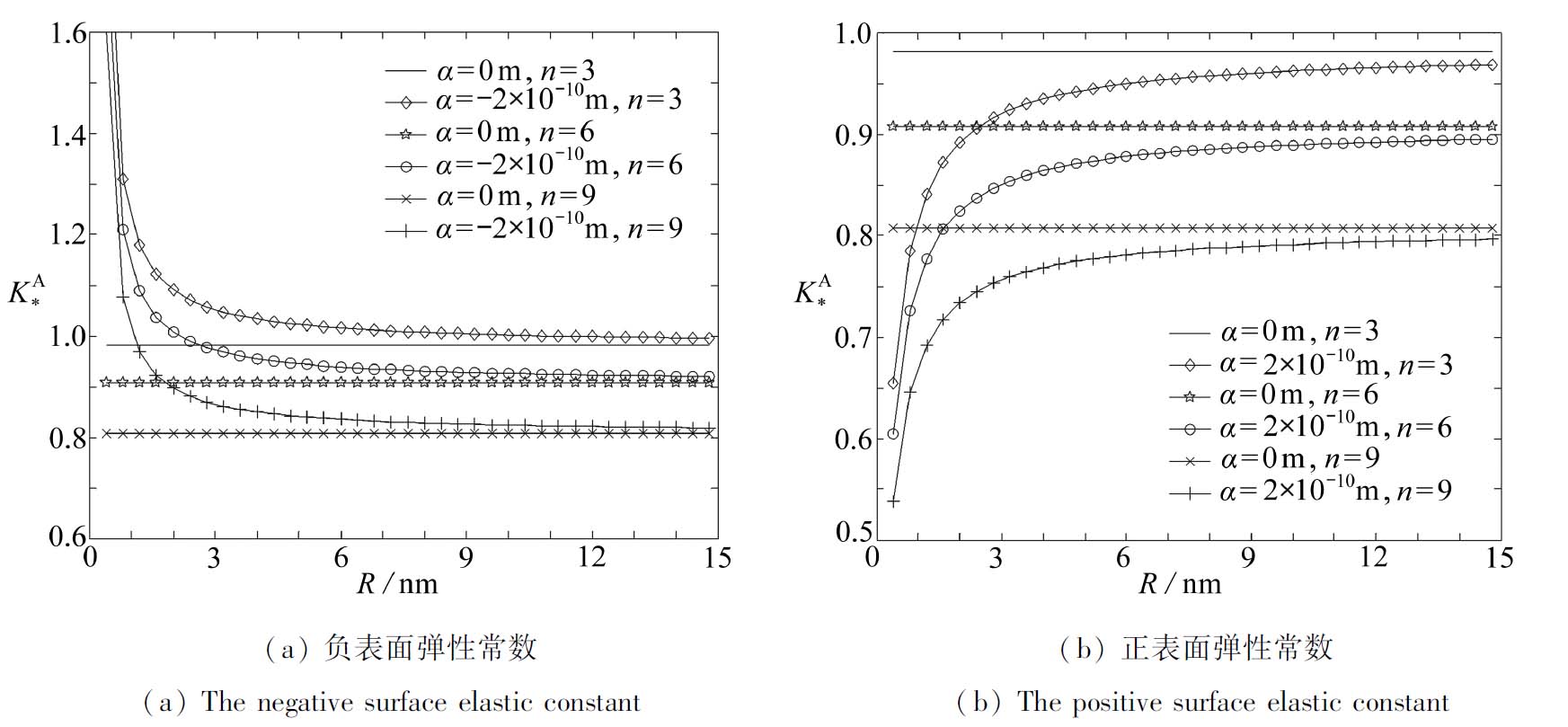
图3 不同裂纹数量时应力强度因子随孔径的变化
Fig. 3 Variations of the stress intensity factor with the hole size under different crack numbers
算例2 图4给出了不同裂纹/孔径比时无量纲应力强度因子随裂纹数的变化曲线，其中孔径R=5 nm，λ=L/R取值分别为0.3，0.5和0.8，α=2×10-10 m.
图4中显示，无论λ=L/R取值如何，无量纲应力强度因子在裂纹数n=3时取得最大值，而后随着裂纹数量的增加逐渐减小.尽管不同λ值时所达到的峰值不同，但是当n>20时,值受λ的影响可以忽略.
算例3 图5给出了无量纲应力强度因子随裂纹/孔洞相对尺寸的变化曲线，其中裂纹数n=3，L=5 nm.
由图5可知，随着lg(L/R)的增大，当参数α取不同值时，无量纲应力强度因子变化趋势不同：当α=-2×10-10 m时，单调增大，且增速越来越快；当α=2×10-10 m时，先增大后减小；当α=0 m时，缓慢增加至定值.图中还显示，当lg(L/R)<0时，无论是否考虑表面效应，无量纲应力强度因子相差不大；但是当lg(L/R)>0时，表面效应对的影响越来越大.
图4 不同裂纹/孔径比时应力强度因子随裂纹数的变化
Fig. 4 Variations of the stress intensity factor with the crack number under different crack/hole radius ratios
算例4 图6给出了不同表面性能时无量纲应力强度因子随裂纹数的变化曲线，其中R=5 nm，λ=0.5.
图6中显示，无量纲应力强度因子随着裂纹数量的增加非单调变化，但表面效应对无量纲应力强度因子的影响几乎保持不变，没有随着裂纹数量的增加有明显的增强或者减弱.
4 结 论
本文基于表面弹性理论和复变弹性方法， 研究了纳米尺度孔边均布径向多裂纹问题的断裂力学问题， 给出了孔洞和裂纹周围的应力场和裂纹尖端的应力强度因子解析表达.主要结论如下：
1) 当圆孔和裂纹的尺寸在纳米量级时，应力强度因子具有非常明显的尺寸效应；正负表面弹性常数对应力强度因子的影响趋势相反；随着缺陷尺寸的增大，尺寸效应逐渐减小.无论是否考虑表面效应(α≠0,α=0)，无论λ取值如何，裂纹数n=3时应力强度因子取得最大值.
2) 裂纹数n、裂纹/孔径比λ和表面性能参数α对应力强度因子的影响规律不同：
随着裂纹数n的增加，应力强度因子先增加后减小，裂纹数量达到一定值之后，裂纹/孔径比λ对应力强度因子的影响可以忽略.
当L<R时，不同表面性能时的应力强度因子相差不大，说明小的裂纹/孔径比屏蔽了表面效应对应力强度因子的影响；当L>R时，表面效应对应力强度因子的影响显著，正表面弹性常数时应力强度因子逐渐减小，负表面弹性常数时应力强度因子迅速增加；不考虑表面效应时，应力强度因子趋于定值.
当裂纹/孔径比λ给定时，无论是否考虑表面效应，应力强度因子随着裂纹数的增加先增后减，但表面效应对无量纲应力强度因子的影响几乎保持不变，没有随着裂纹数量的增加有明显的增强或者减弱.
[1] 邢帅兵, 王强胜, 生月, 等. 圆形杂质对裂纹扩展的影响[J]. 应用数学和力学, 2019, 40(2): 189-199.(XING Shuaibing, WANG Qiangsheng, SHENG Yue, et al. Effect of circular inhomogeneity on crack propagation[J]. Applied Mathematics and Mechanics, 2019, 40(2): 189-199.(in Chinese))
[2] 余建星, 李修波, 谭玉娜, 等. 管道表面蚀坑-裂纹的应力强度因子分析[J]. 天津大学学报(自然科学与工程技术版), 2019, 52(5): 522-528.(YU Jianxing, LI Xiubo, TAN Yuna, et al. Analysis of the stress intensity factor of a pipeline surface with a pit-crack[J]. Journal of Tianjin University(Science and Technology), 2019, 52(5): 522-528.(in Chinese))
[3] 陈长征, 王琳琳, 周勃, 等. 基于红外热像技术的风力机微裂纹叶片研究[J]. 太阳能学报, 2019, 40(2): 417-421.(CHEN Changzheng, WANG Linlin, ZHOU Bo, et al. Study on microcrack of wind turbine blade based on infrared thermography technology[J]. Acta Energiae Solaris Sinica, 2019, 40(2): 417-421.(in Chinese))
[4] HAJIMOHAMADI M, GHAJAR R. An analytical solution for the stress field and stress intensity factor in an infinite plane containing an elliptical hole with two unequal aligned cracks[J]. Applied Mathematics and Mechanics(English Edition), 2018, 39(8): 1103-1118.
[5] 张俊, 靳莹, 熊涛. 集中力作用下多铁性板状复合材料的断裂分析[J]. 应用数学和力学, 2018, 39(12): 1390-1399.(ZHANG Jun, JIN Ying, XIONG Tao. Fracture analysis on multiferroic composite plates under concentrated forces[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1390-1399.(in Chinese))
[6] 彭俊, 蔡明, 荣冠, 等. 裂纹闭合应力及其岩石微裂纹损伤评价[J]. 岩石力学与工程学报, 2015, 34(6): 1091-1100.(PENG Jun, CAI Ming, RONG Guan, et al. Stress for crack closure and its application to assessing stress-induced microcrack damage[J]. Chinese Journal of Rock Mechanics and Engineering, 2015, 34(6): 1091-1100.(in Chinese))
[7] 李政鸿, 徐武, 张晓晶, 等. 多孔多裂纹平板的疲劳裂纹扩展试验与分析方法[J]. 航空学报, 2018, 39(7): 149-157.(LI Zhenghong, XU Wu, ZHANG Xiaojing, et al. Experimental and analytical analyses of fatigue crack growth in sheets with multiple holes and cracks[J]. Acta Aeronautica et Astronautica Sinica, 2018, 39(7): 149-157.(in Chinese))
[8] 郭俊宏, 于静. 多场耦合材料断裂力学[M]. 北京: 科学出版社, 2015.(GUO Junhong, YU Jing. Multi-Field Coupling Material Fracture Mechanics[M]. Beijing: Science Press, 2015.(in Chinese))
[9] GUO J H, LU Z X. Anti-plane analysis of multiple cracks originating from a circular hole in a magnetoelectroelastic solid[J]. International Journal of Solids and Structures, 2010, 14/15(47): 1847-1856.
[10] GUO J H, LU Z X. Exact solution of four cracks originating from an elliptical hole in one-dimensional hexagonal quasicrystals[J]. Applied Mathematics and Computation, 2011, 217(22): 9397-9403.
[11] WANG Y J, GAO C F. The mode Ⅲ cracks originating from the edge of a circular hole in a piezoelectric solid[J]. International Journal of Solids and Structures, 2008, 45(16): 4590-4599.
[12] HASSAN A, SONG T S. Dynamic anti-plane analysis for two symmetrically interfacial cracks near circular cavity in piezoelectric bi-materials[J]. Applied Mathematics and Mechanics (English Edition), 2014, 35(10): 1261-1270.
[13] 宋天舒, 李冬. 压电体中孔边Ⅲ型界面裂纹的动应力强度因子[J]. 力学学报, 2010, 42(6): 1219-1224.(SONG Tianshu, LI Dong. Dynamic stress intensity factor for interfacial cracks of mode Ⅲ on a circular cavity in piezoelectric bimaterials[J]. Chinese Journal of Theoretical and Applied Mechanics, 2010, 42(6): 1219-1224.(in Chinese))
[14] 张乐乐. 纳米复合材料中表面/界面效应对动应力的影响[D]. 硕士学位论文. 石家庄: 石家庄铁道大学, 2011.(ZHANG Lele. Effect of surface/interface on the dynamic stress in nano composites[D]. Master Thesis. Shijiazhuang: Shijiazhuang Tiedao University, 2011.(in Chinese))
[15] 杨娟. 压电效应下一维六方准晶中孔边多裂纹反平面断裂问题研究[D]. 博士学位论文. 宁夏: 宁夏大学, 2015.(YANG Juan. Study on anti-plane fracture problems of multiple cracks emanating from a hole in one-dimensional hexagonal quasicrystals with piezoelectric effects[D]. PhD Thesis. Ningxia: Ningxia University, 2015.(in Chinese))
[16] 肖俊华, 徐耀玲. 纳米夹杂复合材料的有效反平面剪切模量研究[J]. 固体力学学报, 2011, 32(3): 287-292.(XIAO Junhua, XU Yaoling. Study on the effective anti-plane shear modulus of nano inhomogeneity composite materials[J]. Chinese Journal of Solid Mechanics, 2011, 32(3): 287-292.(in Chinese))
[17] 沈海军. 纳米科技概论[M]. 北京: 国防工业出版社, 2007.(SHEN Haijun. Introduction to Nanotechnology[M]. Beijing: National Defense Industry Press, 2007.(in Chinese))
[18] GURTIN M E, MURDOCH A I. A continuum theory of elastic material surfaces[J]. Archive for Rational Mechanics and Analysis, 1975, 57(4): 291-323.
[19] GURTIN M E, MURDOCH A I. Surface stress in solids[J]. International Journal of Solids and Structures, 1978, 14(6): 431-440.
[20] GURTIN M E, WEISSMULLER J, LARCHE F. A general theory of curved deformable interfaces in solids at equilibrium[J]. Philosophical Magazine A: Physics of Condensed Matter Structure Defects and Mechanical Properties, 1998, 78(5): 1093-1109.
[21] LUO J, WANG X. On the anti-plane shear of an elliptic nano inhomogeneity[J]. European Journal of Mechanics A: Solids, 2009, 28(5): 926-934.
[22] PINYOCHOTIWONG Y, RUNGAMORNART J, SENJUNTICHAI T. Analysis of rigid frictionless indentation on half-space with surface elasticity[J]. Procedia Engineering, 2011, 14: 2403-2410.
[23] KIM C I, SCHIAVONE P, RU C Q. The effects of surface elasticity on an elastic solid with mode-Ⅲ crack: complete solution[J]. Journal of Applied Mechanics, 2010, 77(2): 021011-1-7. DOI: 10.1115/1.3177000.
[24] 肖俊华, 韩彬, 徐耀玲, 等. 考虑表面弹性效应时正三角形孔边裂纹反平面剪切问题的断裂力学分析[J]. 固体力学学报, 2017, 38(6): 530-536.(XIAO Junhua, HAN Bin, XU Yaoling, et al. Fracture analysis of cracked equilateral triangular hole with surface elasticity effect under antiplane shear[J]. Chinese Journal of Solid Mechanics, 2017, 38(6): 530-536.(in Chinese))
[25] XIAO J H, SHI C F, XU Y L, et al. Interface stress of orthotropic materials with a nanodefect under antiplane shear loading[J]. Journal of Mechanics of Materials and Structures, 2016, 11(5): 491-504.
[26] WANG X, ZHOU K. Interface cracks with surface elasticity in anisotropic bimaterials[J]. International Journal of Solids and Structures, 2015, 59: 110-120.
[27] KIM C I, SCHIAVONE P, RU C Q. Effect of surface elasticity on an interface crack in plane deformations[J]. Proceedings Mathematical Physical & Engineering Science, 2011, 467(2136): 3530-3549.
[28] KIM C I, SCHIAVONE P, RU C Q. The effects of surface elasticity on a mode-Ⅲ interface crack[J]. Archives of Mechanics, 2011, 63(3): 267-286.
[29] XU J Y, DONG C Y. Surface and interface stress effects on the interaction of nano-inclusions and nano-cracks in an infinite domain under anti-plane shear[J]. International Journal of Mechanical Sciences, 2016, 111/112: 12-23.
[30] 肖俊华, 徐耀玲, 张福成. 基于表面弹性理论的开裂椭圆孔断裂力学研究[J]. 固体力学学报, 2019, 40(1): 82-89.(XIAO Junhua, XU Yaoling, ZHANG Fucheng. Fracture mechanics of cracked elliptical hole based on surface elasticity theory[J]. Chinese Journal of Solid Mechanics, 2019, 40(1): 82-89.(in Chinese))
[31] GUO J H, LU Z X. The fracture behavior of multiple cracks emanating from a circular hole in piezoelectric materials[J]. Acta Mechanica, 2010, 215(1/4): 119-134.
[32] MUSKHELISHVILI N I. Some Basic Problems of the Mathematical Theory of Elasticity[M]. Groningen: Noordhoff, 1953.
[33] 肖俊华, 崔友强, 徐耀玲, 等. 纳米尺度孔边裂纹裂尖Ⅲ型应力强度因子研究[J]. 中国机械工程, 2018, 29(19): 2347-2352.(XIAO Junhua, CUI Youqiang, XU Yaoling, et al. Study on mode Ⅲ stress intensity factor at tip of nano cracks emanating from a circular hole[J]. China Mechanical Engineering, 2018, 29(19): 2347-2352.(in Chinese))
[34] XIAO J H, XU Y L, ZHANG F C. An analytic solution for problem of two symmetrical edge cracks emanating from a circular hole with surface effect under antiplane shear[J]. Acta Mechanica, 2018, 229(12): 4915-4925.