引 言
近年来，由于波形钢腹板组合箱梁具有轻质、经济、高效等多方面的优越性而在工程中得到了迅速的推广和发展，国内外学者也对其进行了大量的理论分析和试验研究[1-3]，其中包括对波形钢腹板箱梁扭转效应的研究.蔡千典等[4]认为，波形钢腹板的纵向刚度相比于混凝土顶底板而言非常小，故在偏心荷载作用下，扭转产生的变形不可忽略.李宏江等[5]指出，在偏载作用下，波形钢腹板箱梁的扭转翘曲正应力约占对称弯曲正应力的35%～45%，占有相当大的比例，这意味着波形钢腹板箱梁因自身特点，其扭转畸变效应更为突出，在设计中必须充分考虑.徐勋等[6]分析了薄壁箱梁剪力流的组成和分布，研究了悬臂板对于整个箱梁截面扭转和畸变的影响，发现悬臂板使闭口箱梁翘曲应力发生应力重分布，使剪切变形的影响增大，且随着悬臂长度的增大而增大.对于大跨度预应力箱梁桥而言，混凝土顶底板所承受的应力相应更大，因而使其翼缘板开裂的可能性也增大，故更需要对混凝土悬臂板的受力性能进行精细化分析[7-8]，才能有效避免危害.张元海[9]提出了一种对闭口薄壁杆件约束扭转时的纯扭转剪应力和约束扭转剪应力的正确表达，澄清了剪应力的计算问题.扭转剪应力的正确计算，也是合理计算主应力的基础，且有利于控制箱梁翼缘板的面内主拉应力.因此，研究波形钢腹板箱梁悬臂部分的扭转剪应力对于实际工程具有重要的参考价值.
本文在对悬臂部分的约束扭转剪应力计算中，依然沿用的是苏联学者Umanskii提出的第二理论，针对有些文献在计算该部分扭转剪应力时存在的不合理性，本文将进行改进并进行合理计算.
1 波形钢腹板的力学性能
1.1 纵向表观弹性模量
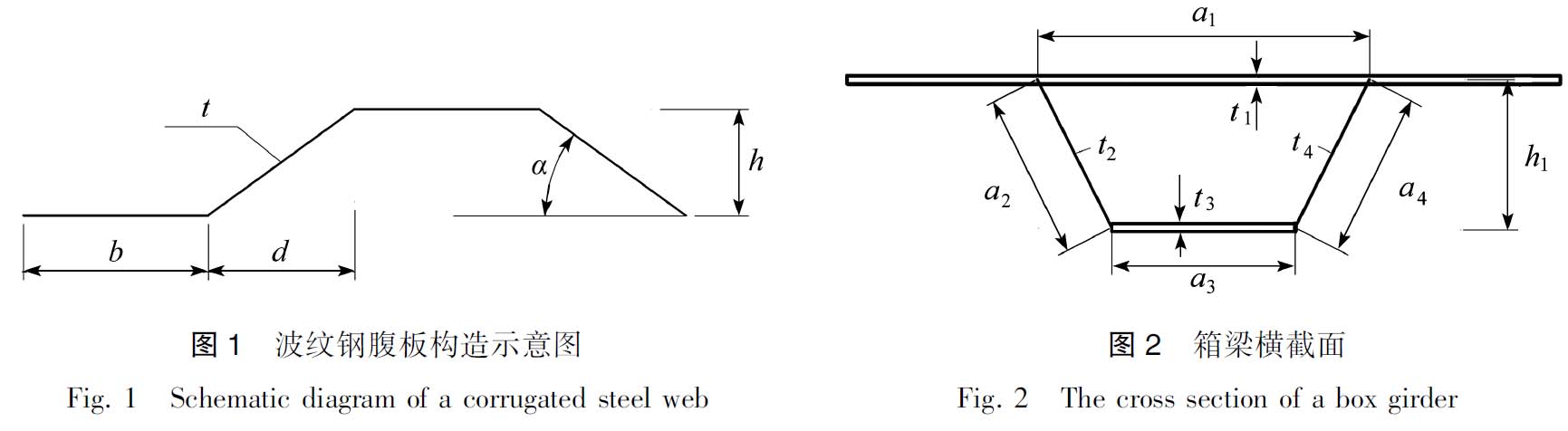
考虑到波形钢腹板的褶皱效应，波形钢腹板在沿桥轴线方向可自由伸缩变形[4,10]，其轴向刚度很小，故一般不考虑波形钢腹板在结构中的纵向抗弯作用，而纵向表观弹性模量Ex是在平面钢板弹性模量Eo的基础上考虑板厚t、波高h及波纹形状系数ζ的影响.对于图1所示波纹钢腹板，可得到其纵向表观弹性模量的表达式为
(1)
式中，t，b，h，α详见图1.
1.2 波形钢腹板的有效剪切模量及等效换算
由于波形钢腹板波折状的存在，其有效剪切模量Ge要比钢板的剪切模量Go在数值上小些.其有效剪切模量Ge的计算公式[11]为
Ge=Go(b+d)/(b+dsec α),
(2)
式中，Go=Eo/[2(1+ν)],ν为钢板的Poisson比.
由于箱梁在扭转时主要承受剪应力，根据能量守恒，可以采用钢与混凝土剪切模量的比，对混凝土腹板截面和波形钢腹板截面进行换算.这里将钢腹板截面换算成混凝土截面，则换算后的截面厚度为
(3)
式中，tg为波形钢腹板的厚度，tc为波形钢腹板换算为混凝土腹板后的厚度，Gc为混凝土的剪切模量.
1.3 波形钢腹板箱梁的修正抗扭惯性矩
根据文献[2]，对于图2所示的波形钢腹板箱梁横截面，其修正的抗扭惯性矩为
(4)
式中,α为修正系数,α=0.400(h1/b1)-0.060≥0，h1为波形钢腹板高度，b1为箱室宽度，A为箱室截面所包围的面积，ns为波形钢腹板有效剪切模量与混凝土剪切模量的比值，a1，a2，a3，a4，t1，t2，t3，t4详见图2.
2 约束扭转剪应力分析
图3所示为任意形式的波形钢腹板组合箱梁的等效薄壁微元体简图，根据微元体的平衡条件,由纵向即z方向的合力为0，可得
(5)
式中，
为截面扭转翘曲剪流，s为沿壁厚中线的坐标，σω为截面扭转翘曲正应力，t为壁厚，z为沿轴向即沿跨径方向的坐标.
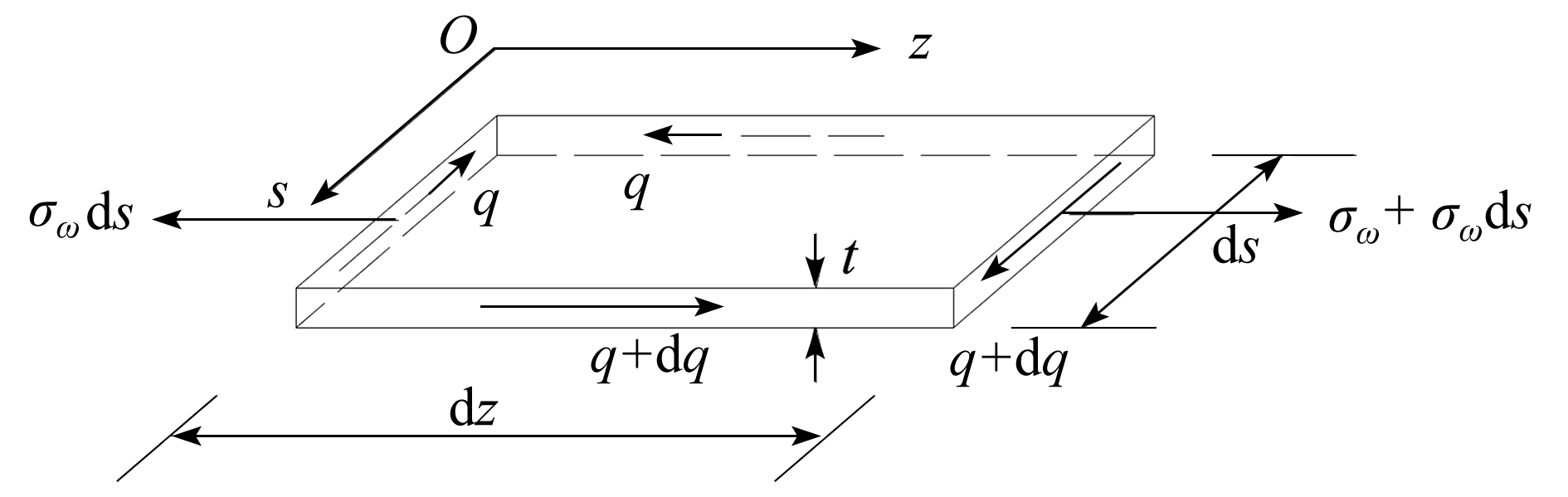
图3 等效微元体的应力状态
Fig. 3 The stress state of an equivalent microelement
根据Umanskii第二理论可知，翘曲正应力表达式为
将其代入式(5)中，任选一起始点，定为s=0，积分到s,可得翘曲剪流为
(6)
亦即
(7)
式中,
为闭口截面广义扇形坐标，E为弹性模量，β(z)表示截面的翘曲函数，qω0为起始点s=0处约束扭转的剪流，qω为二次剪流，
为截面扇形静
和qω分别为
(8)
(9)
由几何方程和刚周边假设，可得
(10)
(11)
式中，u为约束扭转翘曲位移，q为扭转总剪流，G为剪切模量，θz为绕z轴的扭转角函数，ρ为扭转中心到薄壁任一点处切线的垂直距离，u0为s起始点处的约束扭转翘曲位移.
按式(11)计算起始点的翘曲位移，则由u=u0，可得下式：
(12)
式中，Ω为壁厚中心线所围成的面积的2倍.
薄壁组合结构在约束扭转中，总剪流Mz由两部分组成，即
(13)
(14)
再将式(13)代入式(12)中， 并与式(14)联立， 可证得翘曲剪流自平衡， 并可得到下列的基本关系：
(15)
(16)
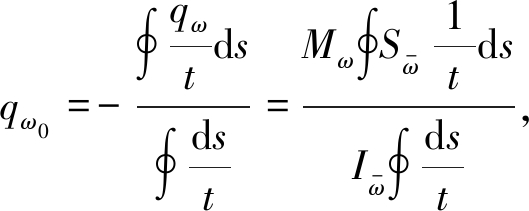
(17)
式中，qs为自由扭转剪流，Ms为自由扭转扭矩，Mω为翘曲扭转扭矩，
为广义主扇形惯性矩.将式(7)、(15)、(16)和(17)联立可求得翘曲剪流为
(18)
其中
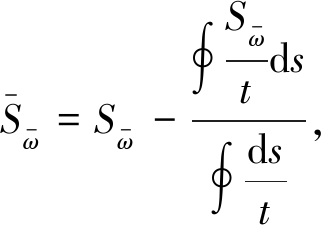
(19)
式中，
为广义主扇形静矩.
约束扭转时的总剪流为自由扭转剪流和纵向翘曲应力变化引起的翘曲剪流之和，即总剪流表达式为
(20)
在计算约束扭转的翘曲剪应力时，考虑到顶板的悬臂部分属于开口部分[12-13]，故这部分的计算应按照开口杆件计算，则s坐标的起算点应取在悬臂板的自由端.值得指出的是，在计算悬臂板的广义主扇形坐标时，s坐标的起始点必须与计算闭口部分时采用同一个起始点，这样才能保证开口和闭口部分的纵向翘曲位移协调.此外，计算开口悬臂部分的广义主扇形坐标时，不计带
的项.
薄壁截面扇形静矩按式(8)计算，因壁厚均为t，故断面静矩为
面积的累计值与壁厚的乘积.对于带悬臂板的一般箱形截面，其扇形静矩的分布如图4(a)所示，在薄壁截面扇形静矩基础上，可按照式(19)计算出广义主扇形静矩，其分布如图4(b)所示.
在式(20)表达的薄壁截面约束扭转总剪流公式中，第一项自由扭转剪流计算时，对于开口部分是不涉及的.严格而言，在开口部分的断面中还存在沿壁厚线性分布的Saint-Venant剪应力，但这里研究的是壁厚中线的剪应力，故沿壁厚线性分布的Saint-Venant剪应力可忽略不计.从而，自由扭转剪应力计算式为
(21)
翘曲剪应力
综合式(18)和式(21)可知，约束扭转时的总剪应力为τ=τs+τω，其分布如图4(c).由于悬臂板自由端不受约束，故扭转剪应力应为0.
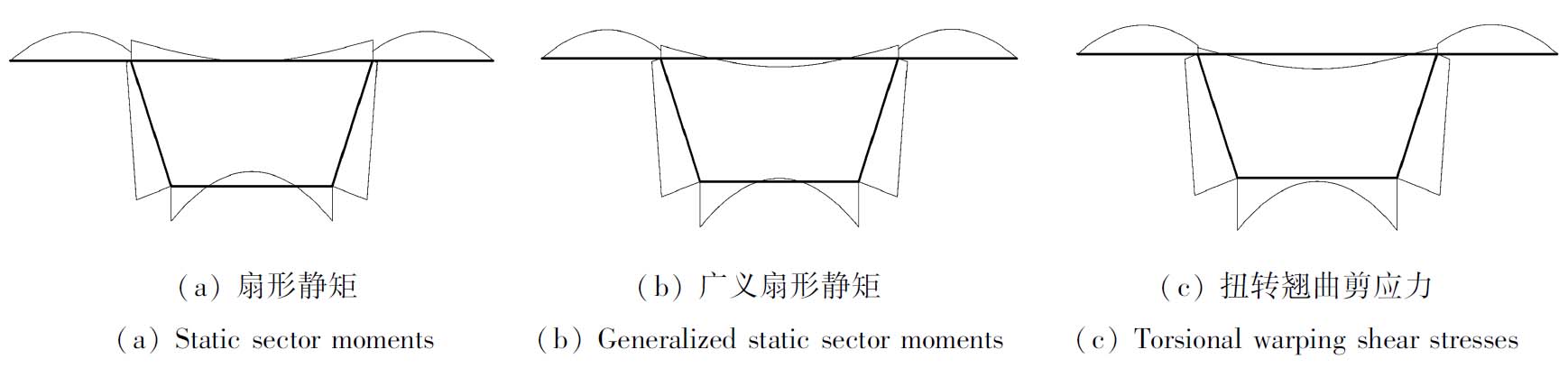
图4 扇形静矩及翘曲剪应力分布
Fig. 4 Distributions of static sector moments and warping shear stresses
对于波形钢腹板组合箱梁，因材料不同，使混凝土顶底板和钢腹板的计算分析有所不同.由于波形钢腹板的纵向表观弹性模量Ex非常小，可认为翘曲变形较大，但产生的翘曲剪应力很小.这时，可视为只有自由扭转产生的剪应力，可得混凝土截面的扭转剪应力τc和波形钢腹板截面的剪应力τo分别为
(22)
(23)
3 约束扭转正应力
根据Umanskii闭口薄壁杆件约束扭转理论的基本假定，可用广义翘曲和主扇形坐标表达约束扭转时的纵向位移，从而可得约束扭转正应力.计算横截面的翘曲正应力时，考虑到波形钢腹板的波折形状的影响，以及混凝土和波形钢腹板材料及结构受力的不同，可得扭转翘曲正应力的计算公式如下[10]：
(24)
式中,nc=Ec/Ex,σωc为混凝土顶底板的扭转翘曲正应力，σωo为波形钢腹板的扭转翘曲正应力，
为约束扭转双力矩.事实上，波形钢腹板的翘曲正应力很小.
建立约束扭转微分方程时，需先利用变形条件建立β(z)和θ(z)的关系式，再根据总扭矩为自由扭转扭矩和约束扭转扭矩之和，可推导出箱梁关于θ(z)的约束扭转微分方程为
(25)
式中，μ为截面约束系数， μ=1-Jd/Jρ， Jρ为极惯性矩， θ(z)为扭转角函数， m为分布外扭矩集度.
根据截面的边界条件，采用初参数法，即可求得θ(z)，β′(z)，B(z)及Mz(z)的函数，其中Mz(z)为总扭矩，由自由扭转扭矩Ms和翘曲扭矩Mω两部分组成，分别按下式计算：
Ms=GJdθ′(z)，
(26)
(27)
对解微分方程得到的函数θ(z)求一次导数后，代入式(26)中，可得自由扭转扭矩；同理，对函数B(z)求一次导数，代入式(27)中，得到翘曲扭转扭矩.再由式(20)求得总剪流后，即可得到扭转剪应力τ.
4 算 例 分 析
选取文献[10]中的简支波形钢腹板组合箱梁为算例，荷载及跨度如图5(a)所示，计算跨径L=7.5 m，横断面如图5(b)所示，顶板厚度t1=0.112 5 m,底板厚度t3=0.11 m,波形钢腹板厚度为0.003 m,波形钢腹板的波纹形状如图5(c)所示,b=0.063 m,d=0.05 m,h=0.038 m,在跨中截面顶板与钢腹板交界处施加竖向偏心荷载p=20 kN，偏心距e=0.419 5 m，集中扭矩Mk=pe.材料特性：混凝土弹性模量Ec=3.4×104 MPa，Poisson比νc=1/6；钢腹板弹性模量Eo=2.1×104 MPa,Poisson比ν=0.3.
图5 简支箱梁模型简图(单位: mm)
Fig. 5 Schematic diagram of the simply supported box girder(unit: mm)
根据波形钢腹板的力学特性，将波形钢腹板截面换算成混凝土截面，可计算出波形钢腹板的纵向表观弹性模量Ex =0.002 8Eo,波形钢腹板的剪切模量Ge=7.242×104 MPa,换算后的截面厚度为tc=0.014 9 m.由扭转中心的计算方法可得，扭转中心位于顶板中点下方0.045 448 8 m处，可求得广义主扇形坐标如图6所示，根据扭转特性的计算方法可进一步求得各项截面特性参数，列于表1中，其中
为以扭转中心为极点的广义主扇形惯性矩，
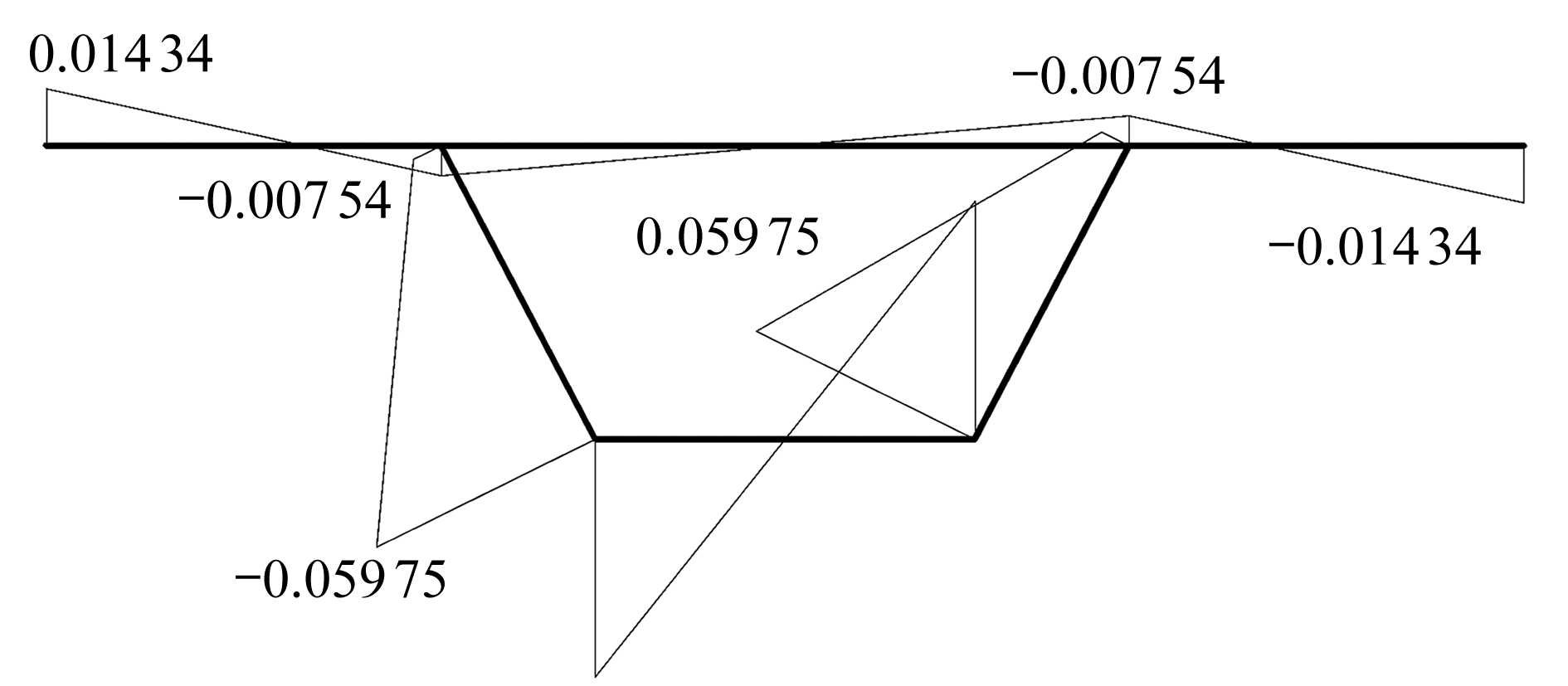
图6 广义主扇形坐标
单位: m2)
Fig. 6 Generalized principal sector coordinates 
m2)
表1 扭转几何特性参数
Table 1 Parameters of torsional geometry
parameterIω-A/m6Jd/m4Jρ/m4μk/m-1value6.820 1×10-53.735 5×10-37.272 6×10-30.486 63.378 7
以跨中左截面为例进行截面剪应力计算，利用初参数法求得该截面的双力矩和翘曲扭矩:
在图6的基础上，可求得扇形静矩
和广义主扇形静矩
分别如图7和图8所示，从而可得跨中截面翘曲扭转剪应力，如图9所示.
为了便于验证本文关于约束扭转剪应力的计算值及其分布规律的合理性，本文采用壳单元建立简支波形钢腹板箱梁的ANSYS计算模型，结构承受的跨中集中扭转荷载通过在跨中腹板位置处施加一对反对称集中力来实现，有限元应力提取点在板件厚度的中心线上.在横截面上的剪应力与正应力大小均呈对称分布，故这里只取一半分析.有限元数值提取位置点分别为①、②、③、④、⑤、⑥和⑦，如图5(b)所示，ANSYS有限元计算模型的具体数值列于表2中，并将有限元数值用点的形式连同本文理论计算结果一并绘于图9中，以便比较.
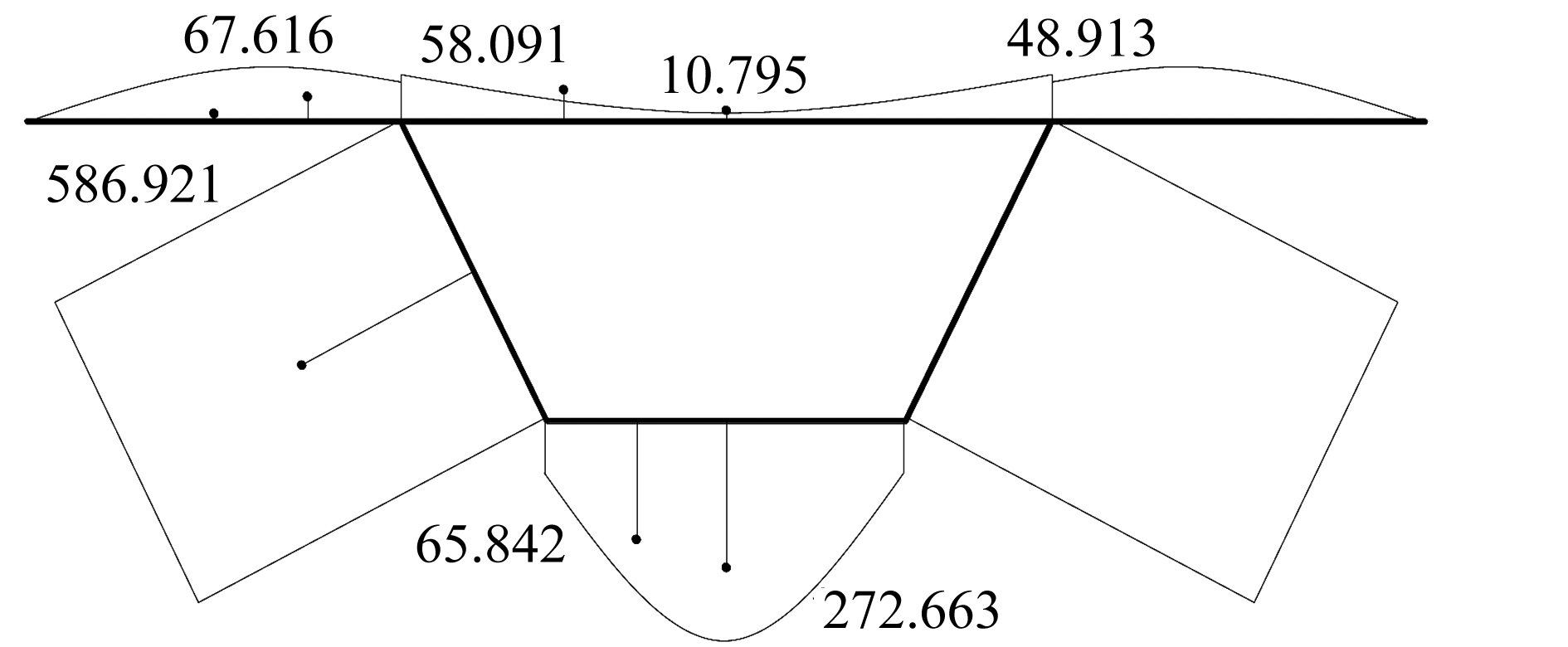
图9 跨中截面扭转剪应力(单位: kPa)
Fig. 9 Torsional shear stresses of the mid-span section(unit: kPa)
表2 剪应力的有限元计算值(单位: Pa)
Table 2 Finite element calculation values for shear stresses(unit: Pa)
①④⑤⑦ANSYS result1.159 2×1021.231 0×1042.934 2×1051.810 2×105
从图9中可以看出，有限元数值与本文的剪应力理论计算值有相似的变化和分布规律，悬臂自由端处扭转剪应力为0，随着计算点逐渐向悬臂板内部靠近，剪应力数值逐渐增大.随着计算点从底板中点向底板与腹板连接处靠近，有限元数值也是从较大值逐渐变化到较小值，与本文理论计算的剪应力分布规律一致.总之，本文理论计算结果与有限元计算结果总体上吻合较好，表明本文的计算方法是合理的.需要指出的是，本文计算的横截面剪应力结果及分布与文献[10]中有明显差异.在文献[10]及其他一些文献中[14,16]，在悬臂开口部分的扇形静矩、广义主扇形静矩和剪应力分布曲线显示，在悬臂板自由端处都有数值，这显然是不合理的.本文在悬臂自由端的计算值都为0，完全符合剪力流在悬臂部分的分布规律[6,15]，因此，本文的计算结果更为合理.
5 结 论
1) 本文基于薄壁杆件约束扭转分析的周边不变形理论，分析了波形钢腹板箱梁剪力流的组成和分布，推导了波形钢腹板箱梁的混凝土顶底板及波形钢腹板两种不同材料的约束扭转剪力流计算公式.
2) 通过对具体算例的扭转剪应力计算，发现在跨中横截面上，腹板的剪应力值最大，其次是底板中心处；腹板上的扭转剪应力几乎是底板中心处剪应力的两倍，表明波形钢腹板在抗扭中能够发挥重要作用.
3) 通过算例的有限元分析与理论计算结果的比较，发现本文关于约束扭转剪应力的计算更符合剪应力的一般变化规律，特别是本文计算的箱梁悬臂部分的剪应力分布与有限元结果的变化趋势一致，在一定程度上完善了波形钢腹板箱梁的约束扭转解析理论.
[1] SAYED-AHMED E Y. Behaviour of steel and(or) composite girders with corrugated steel webs[J]. Canadian Journal of Civil Engineering, 2001, 28(4): 656-672.
[2] 李宏江. 波形钢腹板预应力混凝土组合箱梁扭转与畸变研究进展[J]. 建筑结构学报, 2017, 38(7): 59-67.(LI Hongjiang. Review on torsion and distortion in prestressed concrete box girders with corrugated steel webs[J]. Journal of Building Structures, 2017, 38(7): 59-67.(in Chinese))
[3] RACHED E F. Non-uniform warping including the effects of torsion and shear forces, part Ⅰ: a general beam theory[J]. International Journal of Solids and Structures, 2007, 44(18/19): 5912-5929.
[4] 蔡千典, 冉一元. 波形钢腹板预应力结合箱梁结构特点的探讨[J]. 桥梁建设, 1994, 24(1): 26-30.(CAI Qiandian, RAN Yiyuan. Discussion on structural characteristics of corrugated steel web prestressed box girder[J]. Bridge Construction, 1994, 24(1): 26-30.(in Chinese))
[5] 李宏江, 叶见曙, 万水, 等. 波形腹板箱梁的扭转与畸变分析及试验研究[J]. 桥梁建设, 2003, 33(6): 1-4.(LI Hongjiang, YE Jianshu, WAN Shui, et al. Analysis and experimental study of torsion and distortion of box girder with corrugated steel webs[J]. Bridge Construction, 2003, 33(6): 1-4.(in Chinese))
[6] 徐勋, 叶华文, 强士中. 带悬臂板薄壁箱梁的扭转和畸变分析[J]. 铁道学报, 2015, 37(10): 83-91.(XU Xun, YE Huawen, QIANG Shizhong. Torsion and distortion analysis of thin-walled box girder with cantilever flanges[J]. Journal of the China Railway Society, 2015, 37(10): 83-91.(in Chinese))
[7] 项海帆. 高等桥梁结构理论[M]. 2版. 北京:人民交通出版社, 2013.(XIANG Haifan. Advanced Theory of Bridge Structures[M]. 2nd ed. Beijing: China Communications Press, 2013.(in Chinese))
[8] 郭金琼, 房贞政, 郑振. 箱形梁设计理论[M]. 2版. 北京: 人民交通出版社, 2008.(GUO Jinqiong, FANG Zhenzheng, ZHENG Zhen. Design Theory of Box Girder[M]. 2nd ed. Beijing: China Communications Press, 2008.(in Chinese))
[9] 张元海. 闭口薄壁杆件的约束扭转剪应力分析[J]. 兰州交通大学学报, 2008, 27(4): 1-3.(ZHANG Yuanhai. Study on the shear stress of thin-walled member with closed section under restrained torsion[J]. Journal of Lanzhou Jiaotong University, 2008, 27(4): 1-3.(in Chinese))
[10] 杨丙文, 黎雅乐, 万水, 等. 波形钢腹板箱梁的扭转应力分析[J]. 华南理工大学学报(自然科学版), 2012, 40(2): 19-22.(YANG Bingwen, LI Yale, WAN Shui, et al. Stress analysis of box girder with corrugate steel webs under torsion[J]. Journal of South China University of Technology (Natural Science Edition), 2012, 40(2): 19-22.(in Chinese))
[11] JOHNSON R P, CAFOLLA J. Corrugated webs in plate girders for bridge[J]. Proceedings of the Institution of Civil Engineers, Structures and Buildings, 1997, 122(2): 157-164.
[12] 包世华, 周坚. 薄壁杆件结构力学[M]. 北京: 中国建筑工业出版社, 2006.(BAO Shihua, ZHOU Jian. Structural Mechanics of Thin-Walled Members[M]. Beijing: China Construction Industry Press, 2006.(in Chinese))
[13] 黄剑源. 薄壁构件的扭转分析(上册)[M]. 北京: 中国铁道出版社, 1983.(HUANG Jianyuan. Torsional Analysis of Thin-Walled Members(Vol 1)[M]. Beijing: China Railway Publishing House, 1983.(in Chinese))
[14] 狄谨, 周绪红, 游金兰, 等. 波纹钢腹板预应力混凝土组合箱梁抗扭性能[J]. 长安大学学报(自然科学版), 2009, 29(3): 58-63.(DI Jin, ZHOU Xuhong, YOU Jinlan, et al. Torsional property of prestressed concrete composite beam with corrugated steel webs[J]. Journal of Chang’an University (Natural Science Edition), 2009, 29(3): 58-63.(in Chinese))
[15] GUO Z H. A unified theory of thin-walled elastic structures[J]. Journal of Structural Mechanics, 1981, 9(2): 179-197.
[16] 胡建华, 刘海波, 狄瑾. 波形钢腹板PC组合箱梁扭转性能分析[J]. 中外公路, 2017, 37(3): 118-123.(HU Jianhua, LIU Haibo, DI Jin. Torsional analysis of PC box girder with corrugated steel webs[J]. Journal of China & Foreign Highway, 2017, 37(3): 118-123.(in Chinese))