引 言
在文献中对非标准条件ui(x1,x2,x3,T)-δui(x1,x2,x3,0)=h(x)(其中δ是一个非零常数)的研究已经持续了很长一段时间.Showalter[1]引入这个条件对热传导方程的Cauchy问题进行了正则化.Clark和Oppenheimer[2]证明了时间向后的非适定热传导问题在这种条件下是适定的.Ames和Payne[3]研究了当h(x)=0时，在半无限的圆柱内时间向后的热传导方程解的渐近行为,并且他们在文献[4]中获得了具有非标准条件的时间向后的热传导方程的连续依赖性.
特别地,我们注意到在非标准条件下,文献[5]推导了在一个柱体上的热传导方程解的空间衰减界,文献[6]获得了非标准Navier-Stokes和Stokes方程的Dirichlet边界值问题关于时间t的衰减估计.这种类型的空间衰减性和连续依赖性研究可以看作Saint-Venant原理型的研究.著名的Saint-Venant原理是由Saint-Venant[7]提出的一个数学和力学原理,这个原理一经提出就引起了流体方程领域内的广泛研究[8-13].这些研究的目的就是建立流体方程组的空间衰减估计.
在空间衰减性的相关研究中,普遍的做法是假设方程组的解必须在远离有限端的无穷远处趋近于零.经典的二择一定理不必假设方程组的解在无限端趋近于零,而是证明方程组的解随距有限端的距离的增大要么呈指数(多项式)增长要么呈指数(多项式)衰减,关于二择一定理的详细论述可以参见文献[14-19].受文献[5]的启发,本文将研究一个在非标准条件下更加复杂的Stokes系统，利用微分不等式技术,在参数δ的适当范围上,推导非标准Stokes系统的二择一结果.
本文的结构如下：第1节将给出一些准备工作；第2节将推导要使用的一些基本不等式;第3节将推导本文的主要结果;第4节将推导全能量的上界;最后是本文的总结.
1 准 备 工 作
令R表示三维区域上的半无限柱体,并且它的横截面D是坐标平面x1Ox2上一个有界充分光滑的区域,x3坐标轴平行于柱体的母线,即
R={(x1,x2,x3)|(x1,x2)∈D, x3≥0}.
∂D表示D的边界,z是x3轴上的一个动点.Rz和Dz分别记为
Rz={(x1,x2,x3)|(x1,x2)∈D, x3≥z≥0},
Dz={(x1,x2,x3)|(x1,x2)∈D, x3=z},
显然 R=R0, D=D0.
本文用下标中的逗号表示求导,重复英文下标表示从1～3求和,重复希腊字母表示从1～2求和,例如
本文研究了以下非标准Stokes方程[20]:
ui,t-Δui+p,i=0, in R×[0,T],
(1)
ui,i=0, in R×[0,T],
(2)
其中i=1,2,3.在R的侧面上假设
ui=0, on ∂D×(0,∞)×[0,T];
(3)
在R的有限端假设
ui(x1,x2,0,t)=gi(x1,x2,t), in D×[0,T],
(4)
其中gi是大于零的连续函数且
初始条件为
ui(x1,x2,x3,T)=δui(x1,x2,x3,0), in R,
(5)
其中δ是一个非零常数.同时gi(x1,x2,t)满足兼容性条件:
gi(x1,x2,T)=δgi(x1,x2,0), in D,
gi(x1,x2,t)=0, on ∂D×[0,T].
首先给出几个在本文中常用的引理.
引理1[21] 设w是一个定义在平面区域D上的Dirichlet可积函数,并且w|∂D=0.则
(6)
其中λ1是问题
的最小特征值.
引理2[22] 设D是Lipschitz平面区域,w是D上的可微函数，满足
则存在向量函数φ=(φ1,φ2)满足
以及存在一个依赖于D大于零的常数C使得
(7)
2 基本不等式
在本节首先定义一个“能量不等式”,然后推导出一个关于此“能量不等式”的一个二阶微分不等式.
1) 首先,定义
(8)
应用分部积分以及方程(1)～(5),可得
所以
(9)
为了控制式(9)右边的第二项,可以参考文献[23]所用的方法.利用式(2)和(3),可得对∀z* >0,有
此式表明u3在R的每一个截面上的积分都是相等的.假设g3(x1,x2,t)满足
(10)
所以根据引理2,存在向量函数φ满足
所以,有
再利用分部积分,可得
(11)
现在定义一个“能量表达式”：
(12)
结合式(9),可得E1(z)的另外一个表达式：
(13)
对式(13)求导,可得
(14)
接下来,推导式(12)所定义的|E1(z)|的上界.
利用Hölder不等式、Young不等式以及引理1和引理2,由式(12)可得
(15)
(16)
(17)
把式(15)～(17)代入式(12),有
(18)
2) 再定义
(19)
与式(13)的推导类似,可得
(20)
现在定义一个“能量表达式”：
(21)
类似于式(13)的推导,应用分部积分以及利用方程(1)～(5),可得
对上式求导,可得
(22)
采取和式(15)～(17)类似的方法,由式(21)可得
(23)
记E(z)为
E(z)=E1(z)+E2(z).
(24)
结合式(14)和(22),可得
利用引理1,有
(25)
或者
(26)
记
为了确保μ1, μ2, μ3大于零,要求δ2>max{e-T, e-λ1T, e-2λ1T/(1+λ1)}.对式(25)和(26)从z0到z积分,可得
E′(z)-E′(z0)=
E″(ξ)dξ≥
(27)
E′(z)-E′(z0)≤
(28)
结合式(18)、(23)和(24),可得
(29)
结合式(25)、(27)和(29),可得
|E(z)|≤m1[E′(z)-E′(z0)]+m2E″(z), z≥0,
(30)
其中
式(30)就是本节取得的基本结果,下一节将利用式(30)来讨论非标准Stokes方程组的二择一结果.
3 二择一结果
在本节中我们将分两种情形来考虑“能量表达式”,通过对式(30)进行分析,从而得到本文的主要结果.
情形1 如果存在一个z1≥0,使得E′(z1)>0.
由式(29)可知E″(z)≥0,所以对所有的z≥z1,有E′(z)>0.又因为
E(z)≥E(z1)+E′(z1)(z-z1), z≥z1,
所以E(z)必然在z≥z1上的某一个点之后全大于零.因此存在z0(z0≥z1)使得E(z0)>0且E′(z0)>0.所以E′(z)≥E′(z)-E′(z0).因此式(30)可以写为
E(z)≤m1E′(z)+m2E″(z), z≥z0.
(31)
由式(31)可得
(32)
其中
(33)
对式(32)从z0到z积分,可得
E′(z)+m4E(z)≥e-m3z0[E′(z0)+m4E(z0)]em3z, z≥z0.
(34)
再次对式(34)从z0到z积分,可得
(35)
这就表明如果E′(z)在某点z1处大于零,|E(z)|随z→∞呈指数式增长.
情形2 如果∀z>0，E′(z)都是小于零的.在此条件下,分两种情况来讨论.
(a) 若∃z0≥0, 使得E(z0)<0.由于E″(z)≥0,所以E′(z0)≤E′(z)<0, z≥z0. 因此,E(z)≤E(z0)<0, z≥z0.于是由式(30)可得
-E(z)≤m1[E′(z)-E′(z0)]+m2E″(z), z≥z0.
(36)
于是可得
(37)
即
(38)
其中
对式(38)从z0到z积分,可得
-E′(z)-m6E(z)≤-[E′(z0)+m6E(z0)]e-m5(z-z0)-
(39)
这就表明当z→∞时，-E′(z)指数式衰减于-m1/(m2m5)E′(z0).对式(25)从z到∞积分,可得
(40)
结合式(39)和(40),有
(41)
(b) 若对所有的z≥0,有E(z)>0.所以由式(30)并取z0=0,可得
E(z)≤m1[E′(z)-E(0)]+m2E″(z), z≥0.
(42)
与式(37)类似,可得
即
(43)
对式(43)从0到z积分,可得
(44)
这就表明当z→∞时，-E′(z)指数式衰减于-m1/(m2m4)E′(0).于是在式(25)中从z到∞积分,则
(45)
结合式(44)和(45)，可得
(46)
我们把上述结果总结为以下定理.
定理1 假设u是定义在一个半无穷柱体上的非标准Stokes方程(1)～(5)的解,
且初始条件中参数δ满足δ2>max{e-T, e-λ1T, e-2λ1T/(1+λ1)}.则当z→∞时，u,
u,u,t的L2积分要么呈指数式增长要么呈指数式衰减.具体可以叙述为: 对式(24)所定义的E(z),如果存在一个z1≥0,使得E′(z1)>0,则式(35)成立;如果对∀z≥0,E′(z)≤0,但是∃z0>0使得E(z0)<0,则式(41)成立;如果对∀z≥0,E′(z)≤0且E(z)≥0,则式(46)成立.
显然,要使得式(46)有意义,还需要推导E(0)和E′(0)的显式上界,我们必须证明E(0)和E′(0)可以由已知数据项控制.由于这个过程稍微有些复杂,我们把这个证明过程放到下一节进行.
4 全能量估计
本节中我们将推导当方程组的解衰减时E(0)和E′(0)的上界.由于E′(z)当z→∞时指数式衰减,所以对式(26)从0到∞积分,可得
再注意到m4(见式(33))的定义可知
(47)
记
(48)
其中ν是一个大于零的待定常数以及
wi(x1,x2,x3,t)=gi(x1,x2,t)e-σx3, σ>0, i=1,2,3.
显然wi和ui具有相同的边界条件.利用散度定理以及方程(1)～(5),有
(49)
利用Schwarz不等式,有
(50)
其中ε1, ε2是任意的大于零的常数.利用引理1,有
(51)
由于δ2>max{e-T, e-λ1T, e-2λ1T/(1+λ1)},所以
然后取ε1=(2/3)ν, ν=2/5, ε2=1/4,由式(51)可得
(52)
其中
再由三角不等式,由式(52)可得
(53)
即
(54)
所以
J(u)≤8[2J(w)+Q(w)].
(55)
再由式(47)可知
-E′(0)≤C，
(56)
其中C为常数.由式(44)可得
在上式中从z到∞积分,可得
(57)
在式(57)中取z=0并利用式(56)以及注意到m3,m4的定义,可得
E(0)≤m1[-E′(0)]+
(58)
5 总 结
本文考虑了在一个柱体上的非标准Stokes流体方程,获得了解的二择一结果.我们希望本文的研究会给读者带来一些研究的灵感,在此领域还可以继续对N-S方程、Boussinesq方程组等进行类似的研究,由于这些方程组中具有非线性项或耦合了温度,研究将具有一定难度,结果会更复杂.此外,目前关于二维柱体区域上的非标准流体方程的研究成果在文献中也比较少,因此把本文的研究结果和思路推广到二维柱体上也是一个重要的研究方向.
致谢 本文作者衷心感谢广东财经大学华商学院校内学术类科研项目(2019HSXS05)对本文的资助.
[1] SHOWALTER R E. Cauchy problem for hyper-parabolic partial differential equations[J]. North-Holland Mathematics Studies, 1985, 110: 421-425.
[2] CLARK G, OPPENHEIMER C. Quasireversibility methods for non-well-posed problems[J]. Electronic Journal of Differential Equations, 1994, 8: 1-9.
[3] AMES K A, PAYNE L E. Asymptotic behavior for two regularizations of the Cauchy problem for the backward heat equation[J]. Mathematical Models and Methods in Applied Sciences, 1998, 8: 187-202.
[4] AMES K A, PAYNE L E. Continuous dependence on modeling for some well-posed perturbations of the backward heat equations[J]. Journal of Inequalities and Applications, 1999, 3: 51-64.
[5] AMES K A, PAYNE L E, SCHAEFER P W. On a nonstandard problem for heat conduction in a cylinder[J]. Applicable Analysis, 2004, 83: 125-133.
[6] PAYNE L E, SCHAEFER P W, SONG J C. Some nonstandard problems in viscous 
ow[J]. Mathematical Methods in the Applied Sciences, 2004, 27: 2045-2053.
[7] DE SAINT-VENANT A J C B. Mémoire sur la exion des prismes[J]. Journal de Mathématiques Pures et Appliquées, 1856, 1(2): 89-189.
[8] LIN C, PAYNE L E. Spatial decay bounds in time dependent pipe ow of an incompressible viscous fluid[J]. SIAM Journal on Applied Mahematics, 2004, 65(2): 458-475.
[9] HORGAN C O, PAYNE L E, WHEELER L T. Spatial decay estimates in transient heat equation[J]. Quarterly of Applied Mathematics, 1984, 42: 119-127.
[10] HAMEED A A, HARFASH A J. Continuous dependence of double diffusive convection in a porous medium with temperature-dependent density[J]. Basrah Journal of Science, 2019, 37: 1-15.
[11] 王欣, 郭科. 一类非凸优化问题广义交替方向法的收敛性[J]. 应用数学和力学, 2018, 39(12): 1410-1425. (WANG Xin, GUO Ke. Convergence of the generalized alternating direction method of multipliers for a class of nonconvex optimization problems[J]. Applied Mathematics and Mechanics, 2018, 39(12): 1410-1425. (in Chinese))
[12] 李远飞, 郭连红. 具有边界反应Brinkman-Forchheimer型多孔介质的结构稳定性[J]. 高校应用数学学报, 2019, 34(3): 315-324. (LI Yuanfei, GUO Lianhong. Structural stability on boundary reaction terms in a porous medium of Brinkman-Forchheimer type[J]. Applied Mathematics: a Journal of Chinese Universities, 2019, 34(3): 315-324. (in Chinese))
[13] 李远飞. 大尺度海洋大气动力学三维黏性原始方程对边界参数的连续依赖性[J]. 吉林大学学报(理学版), 2019, 57(5): 1-7. (LI Yuanfei. Continuous dependence on boundary parameters for three-dimensional viscous primitive equation of large-scale ocean atmospheric dynamics[J]. Journal of Jilin University(Science Edition), 2019, 57(5): 1-7. (in Chinese))
[14] HORGAN C O, PAYNE L E. Phragmén-Lindelöf type results for harmonic functions with nonlinear boundary conditions[J]. Archive for Rational Mechanics and Analysis, 1993, 122: 123-144.
[15] LIN C H, PAYNE L E. A Phragmén-Lindelöf alternative for a class of quasilinear second order parabolic problems[J]. Differential and Integral Equations, 1995, 8: 539-551.
[16] LIN C H, PAYNE L E. Phragmén-Lindelöf type results for second order quasilinear parabolic equation in R2[J]. Zeitschrift für Angewandte Mathematik und Physik Zamp, 1994, 45: 294-311.
[17] LIU Y, LIN C H. Phragmén-Lindelöf type alternative results for the Stokes flow equation[J]. Mathematical Inequalities and Applications, 2006, 9(4): 671-694.
[18] LESEDUARTE M C, QUINTANILLA R. Phragmén-Lindelöf alternative for the Laplace equation with dynamic boundary conditions[J]. Journal of Applied Analysis and Computation, 2017, 7(4): 1323-1335.
[19] PAYNE L E, SCHAEFER P W. Some Phragmén-Lindelöf type results for the biharmonic equation[J]. Zeitschrift für Angewandte Mathematik und Physik ZAMP, 1994, 45: 414-432.
[20] AMES K A, PAYNE L E, SONG J C. On two classes of nonstandard parabolic problems[J]. Journal of Mathematical Analysis and Applications, 2005, 311: 254-267.
[21] BANDLE C. Isoperimetric Inequalities and Their Applications[M]. London: Pitman Press, 1980.
[22] BABU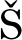
KA I, AZIZ A K. Survey lectures on the mathmitical foundations of the 
nite element method[M]//The Mathmetical Foundation of the Finite Element Method With Application to Partial Differential Equation. New York: Academic Press, 1972.
[23] AMES K A, PAYNE L E, SCHAEFER P W. Spatial decay estimates in time-dependent stokes flow[J]. SIAM Journal on Mathematical Analysis, 1993, 24: 1395-1413.