引 言
随着人类不断地探索宇宙天体和空间、开发受控聚变能源、发展工程技术,磁流体力学这门新兴学科应运而生.磁流体力学理论可以用来研究和解释天体物理现象,还能制造磁流体发电机应用到社会生产实践.早在1919年,Larmor就提出了太阳发电机的概念来解释太阳这样的旋转天体为何具有磁场[1].1934年,Cowling在研究太阳磁场时发现并证明了轴对称运动不能维持轴对称子午磁场[2],这是第一个无发电机效应的理论——Cowling定理.1937年,Ferraro提出了理想轴对称等离子体的等旋转定理[3],Hartmann分析了两无限大平板之间的磁流体流动[4].1942 年,Alfvén在应用电磁感应定律研究太阳等离子体时提出了磁冻结的概念[5].1953年到1956年,Shercliff研究了绝缘固壁内充分发展的磁流体流动[6-7].1980年,Rädler提出了平均场电动力学理论,发展了一套湍流发电机理论[8].近些年来,对可控热核反应原理和装置的探索促进了国内外学者磁流体力学的研究[9-13].本文研究的是带有源项的广义Chaplygin气体磁流体Euler方程组,它的一维形式具体如下：
(1)
其中β是常数.P,ρ,u,B和μ分别表示压强、密度、 速度、 磁感强度和磁导率.P,B满足
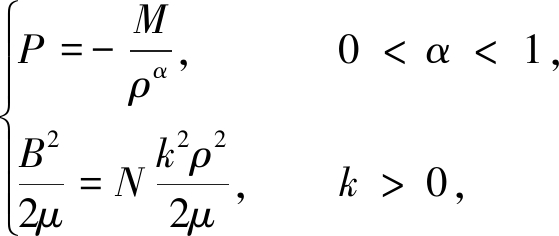
(2)
其中M,N是正实数.
当压力和磁感强度同时消失时,方程组(1)变为零压流输运方程组:
(3)
关于该方程组的Riemann问题请参看文献[14].输运方程最早被用来研究热力学系统,它可以用来描述低温下粒子的运动[15-17].
如果只是磁感强度消失,方程组(1)变为非齐次广义Chaplygin气体Euler方程组:
(4)
关于该方程组的Riemann问题请参看文献[18].广义Chaplygin气体模型是经典的天体力学暗能量模型,其在探索宇宙起源和研究占宇宙总质量96%的暗物质时有很重要的作用,关于广义Chaplygin气体Euler方程组在文献[19-24]有详细研究.
本文考虑方程组(1)、(2)Riemann解的极限,所用到的Riemann初值为
(5)
其中,u-,ρ-,u+,ρ+均为常数,采用Faccanoni和Mangeney[25]引进的速度变换
v(x,t)=u(x,t)-βt
(6)
得到方程组(1)、(2)的解.当压力和磁感强度同时消失时,方程组(3)的Riemann解中会出现质量集中和真空现象.但当磁感强度消失时,方程组(5)的Riemann解中只会出现质量集中现象.在研究方程组(1)、(2)Riemann解的极限情形时需要运用特征值分析法和相平面分析法[26-33],并得到以下定理.
定理1 当M,N→0,方程组(1)、(2)的Riemann解收敛到方程组(3)的Riemann解.
1) 当u->u+,两个激波解收敛到方程组(3)的δ-激波解；
2) 当u-<u+,两个疏散波解收敛到方程组(3) 的两个接触间断和一段中间状态为真空的解.
定理2 当N→0,方程组(1)、(2)的Riemann解收敛到方程组(4)的Riemann解.
1) 当
两个激波解收敛到方程组(4)的δ-激波解；
2) 当(u+,ρ+)∈Ⅰ: (u-,ρ-),两个疏散波解收敛到方程组(4)相应的两个疏散波解,未出现真空情形.
本文的结构如下：在第1节和第2节中分别简要叙述了方程组(3)和(4)带初始条件(5)的Riemann解.第3节给出方程组(1)、(2)带初始条件(5) 的Riemann解.第4节研究了压力和磁感强度同时消失时δ- 激波和真空状态的形成.第5节研究了仅磁感强度消失时δ-激波的形成并说明未出现真空状态的原因.第6节对第4节和第5节的物理现象运用数值实验进行了模拟和验证.第7节对全文的研究进行总结.
1 零压流输运方程组(3)的Riemann问题
这一节将简单叙述方程组(3)带初始条件(5)的解[14].
由式(6),方程组(3)可以转化为齐次方程组：
(7)
对于一个给定的负状态(u-,ρ-),接触间断曲线和δ-激波分别满足以下情况：
1) 接触间断满足
(8)
2) δ-激波满足广义Rankine-Hugoniot条件,[ρ]表示ρ-ρ-，
(9)
其中w(t)和uδ(t)=vδ+βt分别表示δ-激波的权和波速,(x,w)(0)=(0,0).
由式(9)可得
(10)
2 非齐次广义Chaplygin气体Euler方程组的Riemann问题
本节将简单叙述方程组(4)带初始条件(5)的Riemann解[18],不失一般性,取M=1.
由式(6),方程组(5)可以转化为齐次方程组：
(11)
对于一个给定的负状态(u-,ρ-),疏散波曲线、激波曲线和δ-激波分别满足以下情况：
1) 疏散波曲线满足
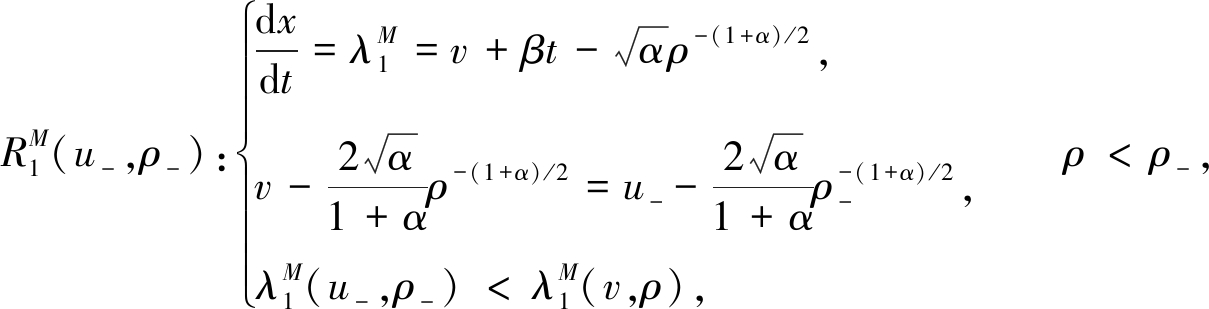
(12)
和
(13)
2) 激波曲线满足
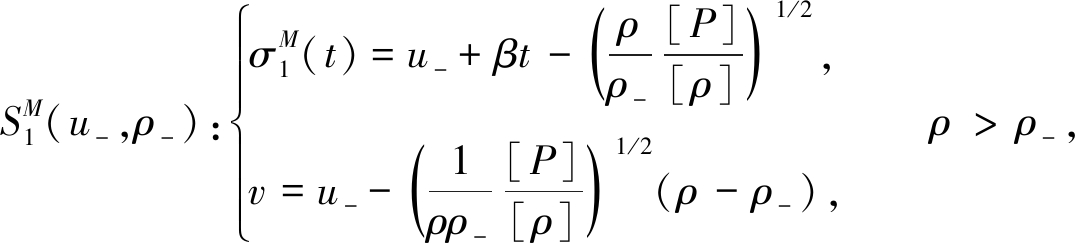
(14)
和
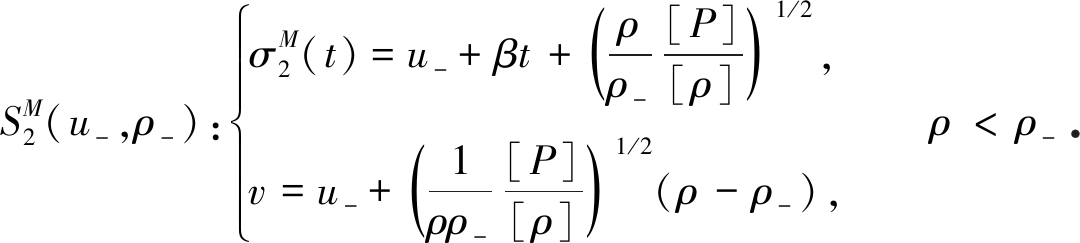
(15)
3) δ-激波满足广义Rankine-Hugoniot条件:
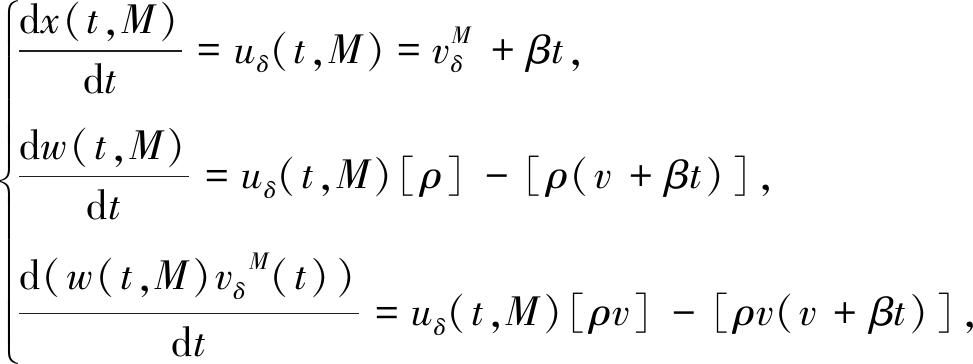
(16)
其中(x,w)(0,M)=0,w(t,M)和
分别表示δ-激波的权和波速，
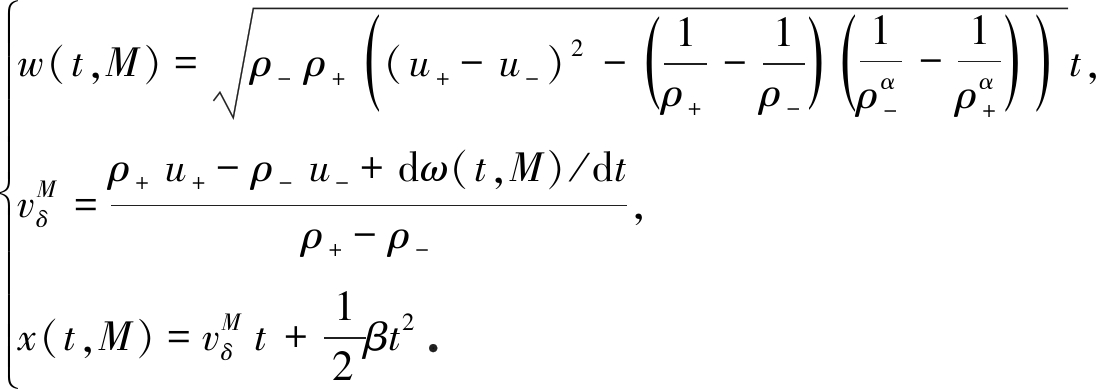
(17)
根据文献[18],得到
此时相平面被分成Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ五个区域,解的相平面见图1.
图1 非齐次广义Chaplygin气体Euler方程组的相平面
Fig. 1 Phase planes of the non-homogeneous generalized Chaplygin gas Euler equations
3 非齐次广义Chaplygin气体磁流体Euler方程组的Riemann解
本节将研究方程组(1)、(2)的Riemann解,关于不含源项的情况请参看文献[34].
由式(6),方程组(1)、(2)可以转化为齐次方程组：
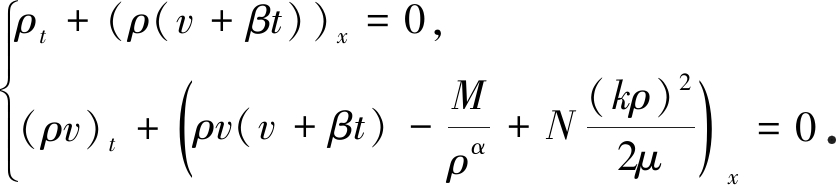
(18)
方程组(18)有两个特征值
其中P′=αρ-α-1.对应的两个右特征向量分别是
由于0<α<1,可得
所对应的特征区域是真正非线性的,相应的基本波是疏散波和激波.
对于一个给定的负状态(u-,ρ-),疏散波曲线满足
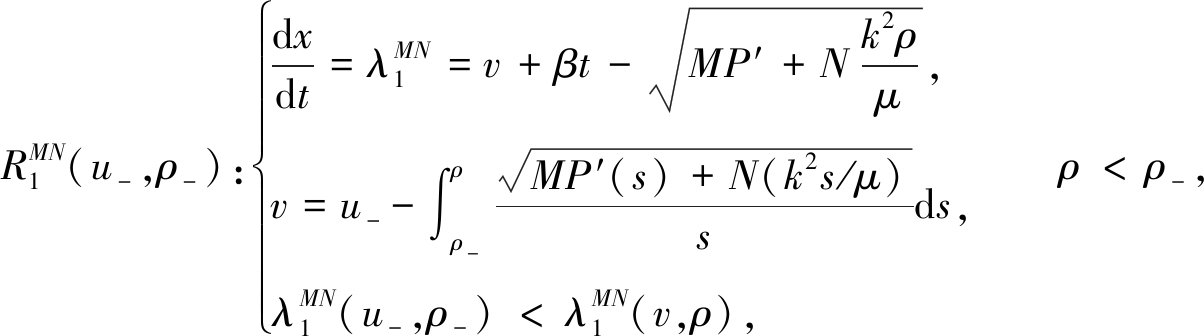
(19)
和
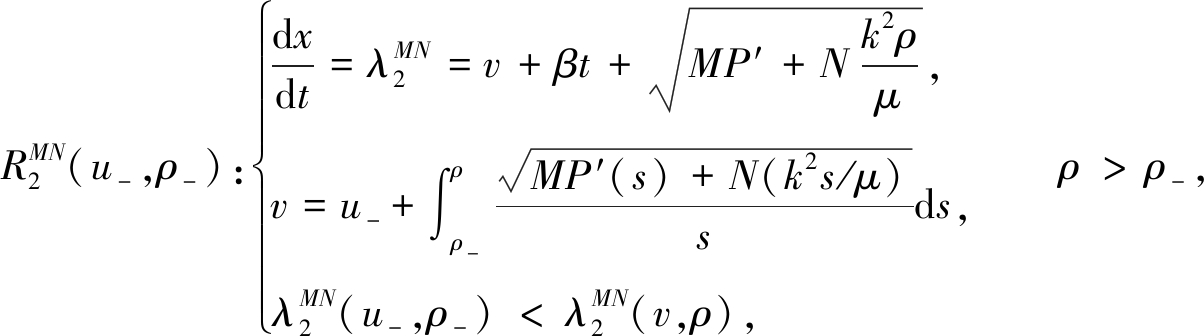
(20)
其中
P′(s)=αs-α-1.
由方程组(18),可得Rankine-Hugoniot条件：
(21)
激波满足如下熵条件:
λi(ρ)<σi(ρ,ρ-)<λi(ρ-), i=1,2.
(22)
由式(21)、(22)可得激波曲线的表达式:
对于一个给定的负状态(u-,ρ-),激波曲线满足
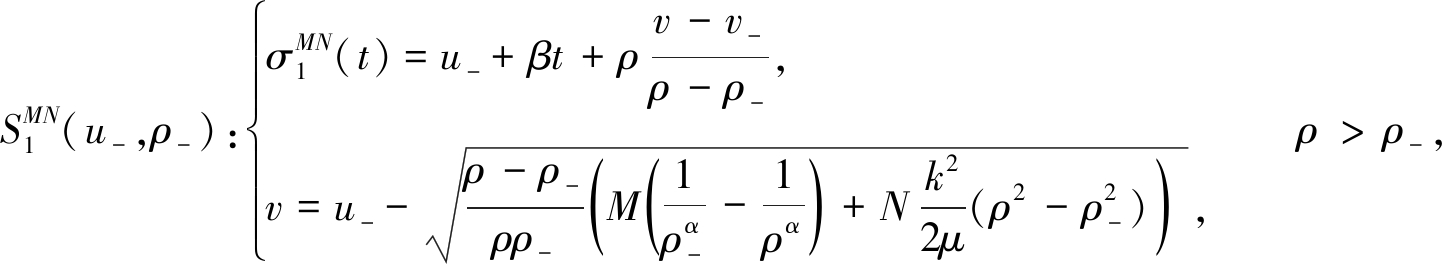
(23)
和
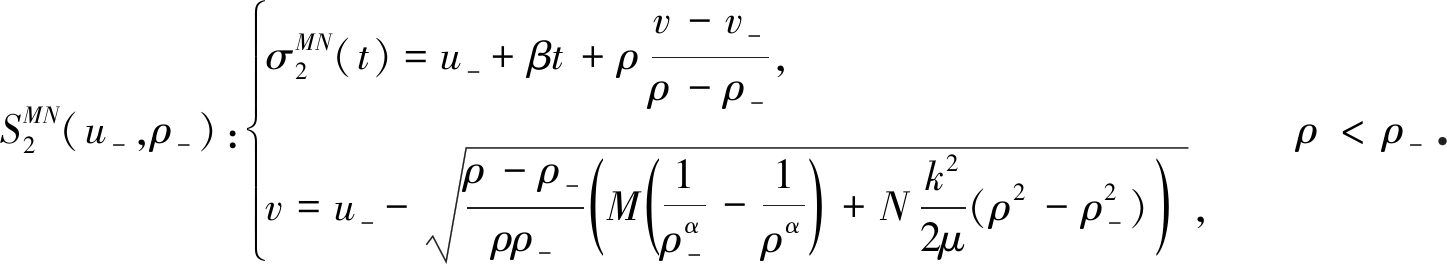
(24)
在相平面上,给定一负状态(u-,ρ-),由式(19)、(20)、(23)和(24)可以画出相应的曲线
和
此时相平面被分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个区域(见图2).
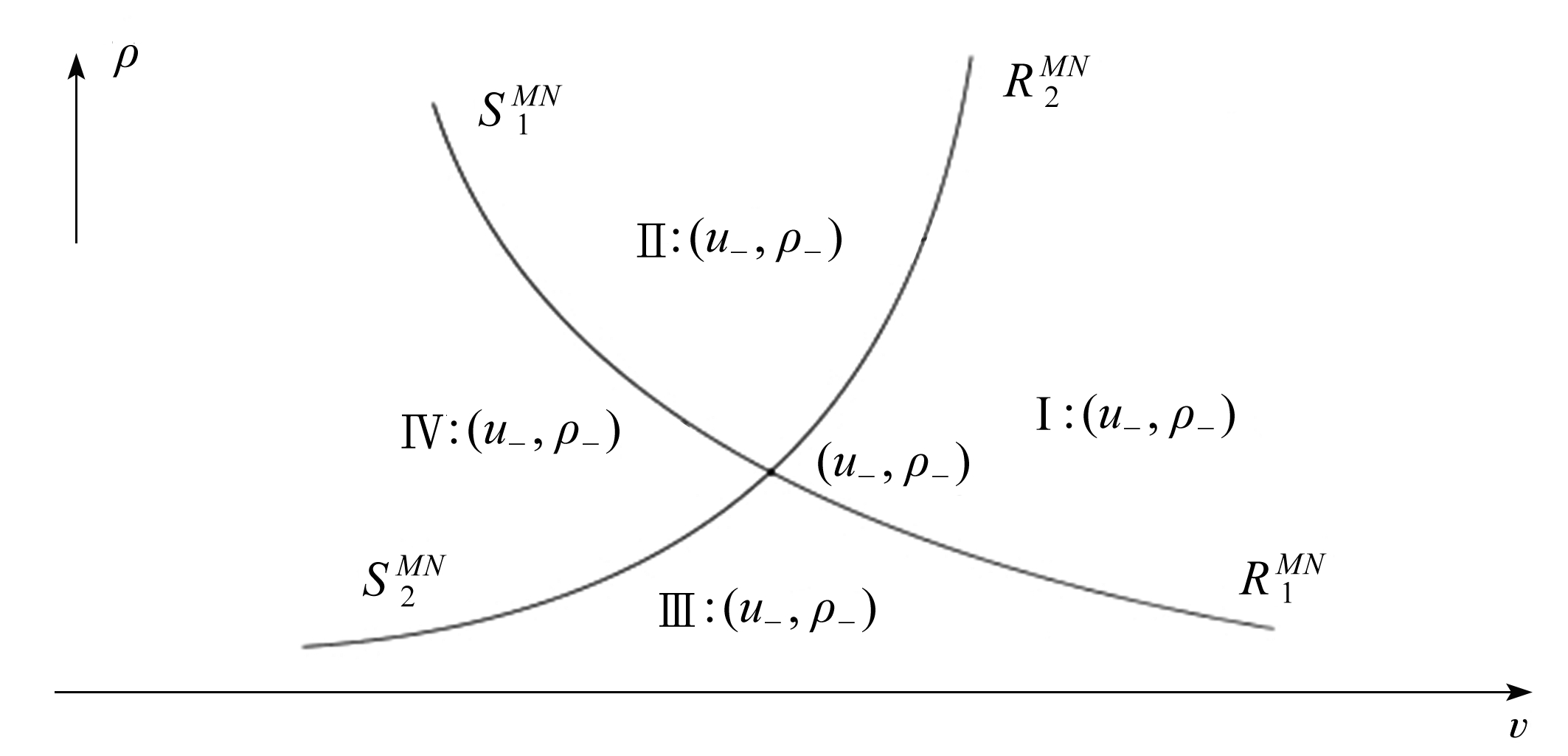
图2 非齐次广义Chaplygin气体磁流体Euler方程组的相平面
Fig. 2 Phase planes of the non-homogeneous generalized Chaplygin gas magnetic fluid Euler equations
综上,由式(6),对于任意给定的(u+,ρ+),得到方程组(1)、(2)的Riemann解如下：
① (u+,ρ+)∈Ⅰ:(u-,ρ-)，
② (u+,ρ+)∈Ⅱ:(u-,ρ-)，
③ (u+,ρ+)∈Ⅲ:(u-,ρ-)，
④ (u+,ρ+)∈Ⅳ:(u-,ρ-)，
其中
表示中间状态.
4 当M,N→0时δ-激波和真空状态的形成
这一节将主要研究压力和磁感强度同时消失时方程组(1)、(2)Riemann解的极限,主要考虑δ-激波和真空状态的形成.
4.1 δ-激波的形成
当(u+,ρ+)∈Ⅳ:(u-,ρ-)时,u->u+,对于任给的M,N>0,激波曲线
连接(u-,ρ-)和
激波曲线
连接
和(u+,ρ+)，具体如下：
(25)
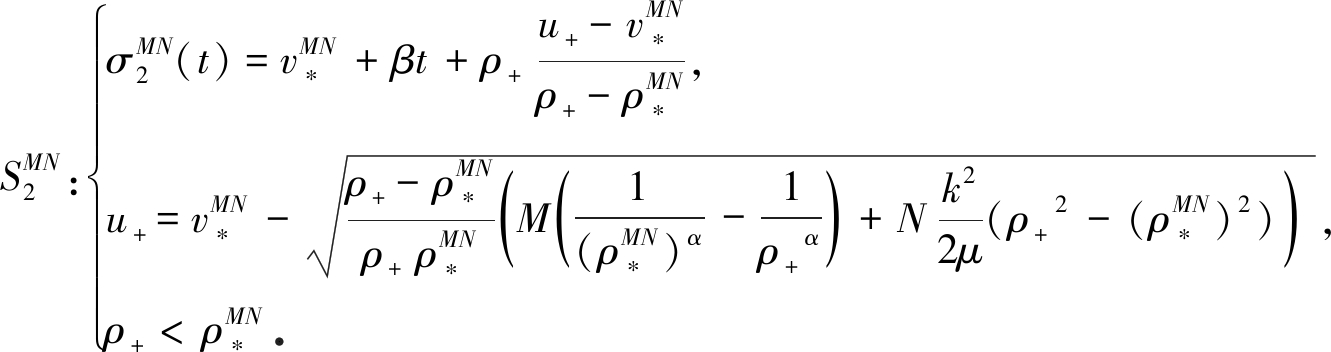
(26)
引理
证明 将式(25)、(26)中的第二个式子相加消去未知量
得
(27)
运用反证法,假设
其中A是一个正实数,由式(27)可得limM,N→0(u+-u-)=0,这与前提条件u+<u-相矛盾.那么引理得证.
引理
证明 根据引理1,由式(27)计算整理后就可得引理成立.
引理
证明 根据引理1,由式(25)、(26)的第一个式子可得
根据引理1和引理2,由式(25)的第二个式子可得
引理得证.
引理4
其中
证明 由式(21)的第一个式子,可得
(28)
由式(28)和引理3得
(29)
由式(29)得
(30)
同理,根据式(21)的第二个式子可以得到
引理得证.
这些引理表明M,N→0时,中间状态的密度趋于无穷大,解中会出现质量集中现象,方程组(1)、(2)的两个激波解收敛到零压流输运方程组(3)的δ-激波解.
4.2 真空状态的形成
当(u+,ρ+)∈Ⅰ:(u-,ρ-)时,u-<u+,对于任给的M,N>0,疏散波曲线
连接(u-,ρ-)和疏散波曲线
连接和(u+,ρ+),具体如下：
(31)
(32)
引理
证明 首先,考虑如下的积分：
(33)
由式(31)～(33)得
(34)
运用反证法, 假设引理不成立, 那么存在一个常数K∈(0,min(ρ-,ρ+)),使得
由式(34),可得limM,N→0(u+-u-)≤0,这与前提条件u+>u-相矛盾.引理得证.
该引理表明M,N→0时,中间状态的密度趋于零,会产生真空状态.另外,由式(31)、(32),易知方程组(1)、(2)的疏散波解收敛到零压流输运方程组(3)相应的接触间断解J.
5 当N→0时δ-激波的形成
这一节将研究磁感强度消失时方程组(1)、(2)Riemann解的极限,主要考虑δ-激波的形成和未产生真空的原因.
5.1 δ-激波的形成
不失一般性,取M=1,通过以下引理可以说明δ-激波的形成.
引理6 当
时,存在一个N0,使得N∈(0,N0)时(u+,ρ+)∈Ⅳ:(u-,ρ-).
证明 只要找到符合引理的N0即可.由式(23)、(24),得
当ρ>ρ-时,N减小dv/dρ增大.若(u+,ρ+)∈Ⅳ:(u-,ρ-),则
移项得
则
当(u+,ρ+)∈Ⅳ:(u-,ρ-)时,激波曲线连接(u-,ρ-)和激波曲线连接和(u+,ρ+)，具体如下：
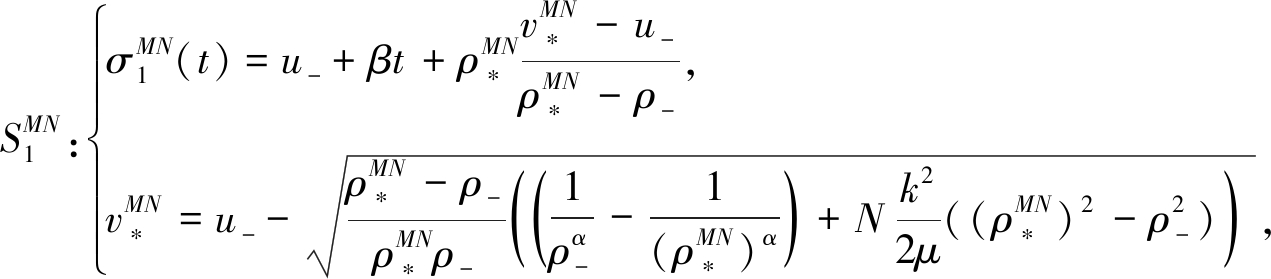
(35)
(36)
由式(35)、(36),得
(37)
其中
引理
且
证明 运用反证法,假设
由式(37),得
这与前提条件
矛盾,则
再假设
由式(37)得
因为u-和u+是给定的,所以u--u+是一个有限数,这样就形成了一个矛盾.引理得证.
引理
证明 由式(35)、(36),得
由式(37)得
则
引理9
其中
证明 由式(21)的第一个式子,可得
(38)
由式(38)和引理8得
(39)
由式(39)得
(40)
同理,由式(21)的第二个式子可以得到
综上,引理得证.
这些引理表明N→0时,中间状态的密度趋于无穷大,解中会出现质量集中现象,方程组(1)、(2)的激波解收敛到非齐次广义Chaplygin气体Euler方程组(4)的δ-激波解.
图3表明了当
且磁感强度趋于零时物理平面的变化，两条激波合成一条δ-激波.图4表明了当磁感强度趋于零时相平面的变化，解的区域划分由四个变成了五个.
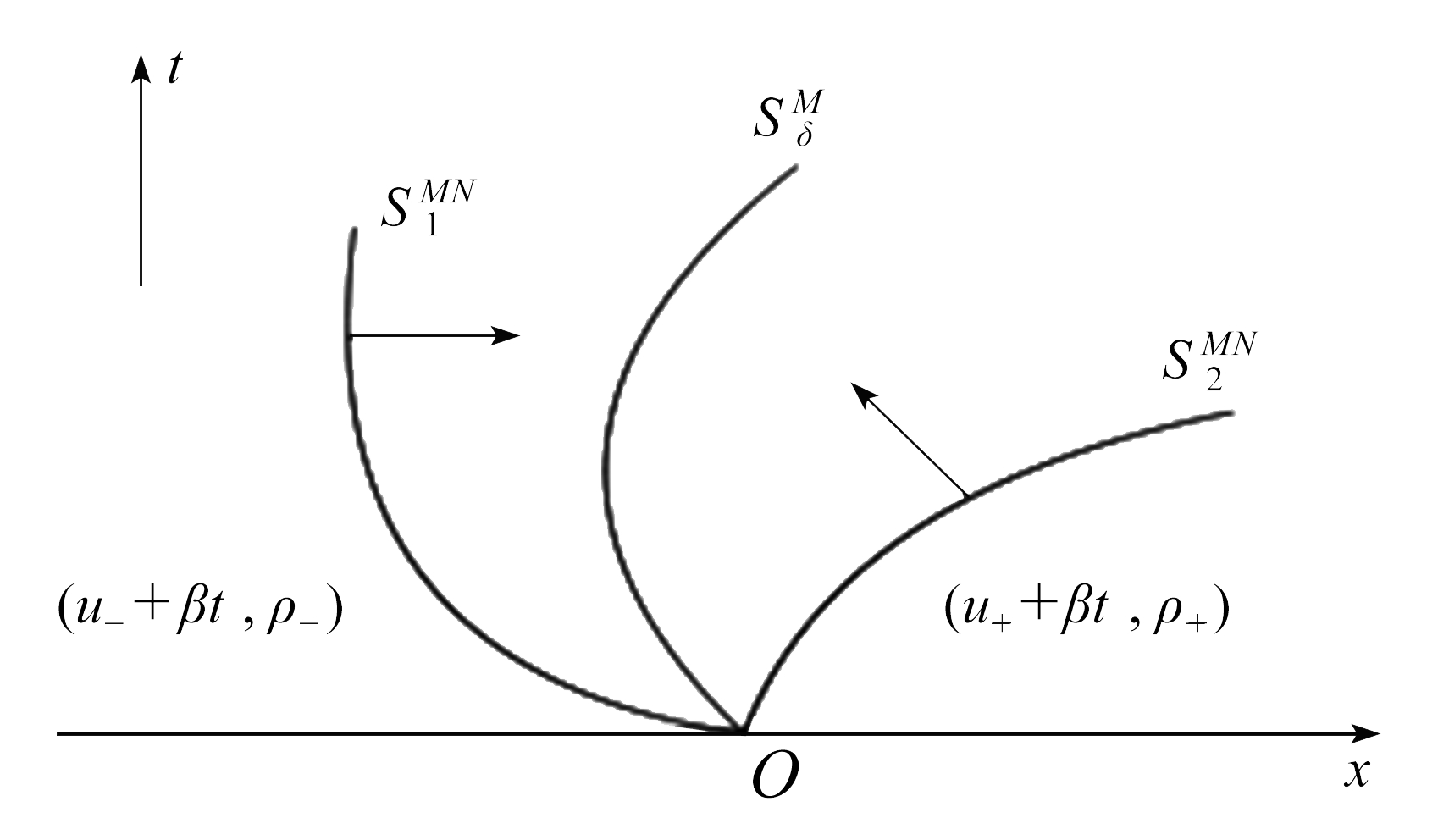
图3 物理平面的变化(箭头表示变化情况)
Fig. 3 Changes in the physical plane (arrows indicate changes)
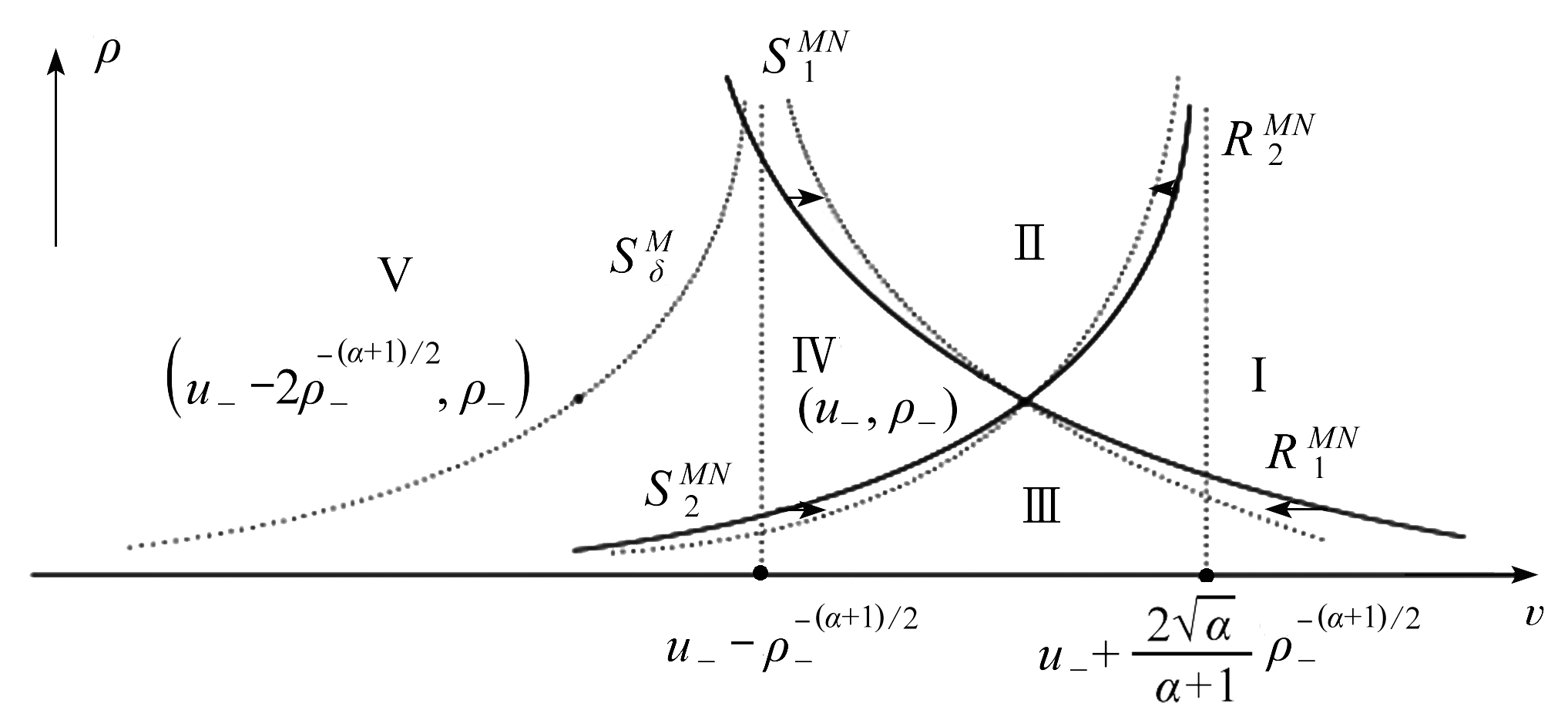
图4 相平面的变化(虚线表示变化后的情况)
Fig. 4 Changes in the phase plane(dotted lines show the situation after change)
5.2 当N→0时区域Ⅰ未出现真空
当(u+,ρ+)∈Ⅰ:(u-,ρ-)时,若是中间状态,则(u-,ρ-) 和由疏散波曲线连接,和(u+,ρ+)由疏散波曲线连接，具体如下：
(41)
(42)
引理
证明 运用反证法,假设
由式(41)、(42),可得
(43)
由式(43)可得
根据比较判别法可知,
这两个瑕积分发散，则
因为u-和u+是给定的,所以u--u+是一个有限数,这样就形成了一个矛盾.引理得证.
这些引理表明N→0时,中间状态的密度不会变成零,不会产生真空状态.另外,由式(41)、(42),易知方程组(1)、(2)的疏散解收敛到非齐次广义Chaplygin气体Euler方程组(4)相应的疏散波解
和
6 数 值 实 验
为验证上述结论的正确性,这一节中将运用Lax-Friedrichs差分格式对之前的内容进行数值模拟.对于等离子体,由于温度极高,磁化率几乎为零,因此磁导率μ在数值实验中取值为1,为了简单起见,k取值为
取值为0.5,β取值为1.
1) 为了验证4.1小节中δ-激波的形成,给定如下的初值：
(44)
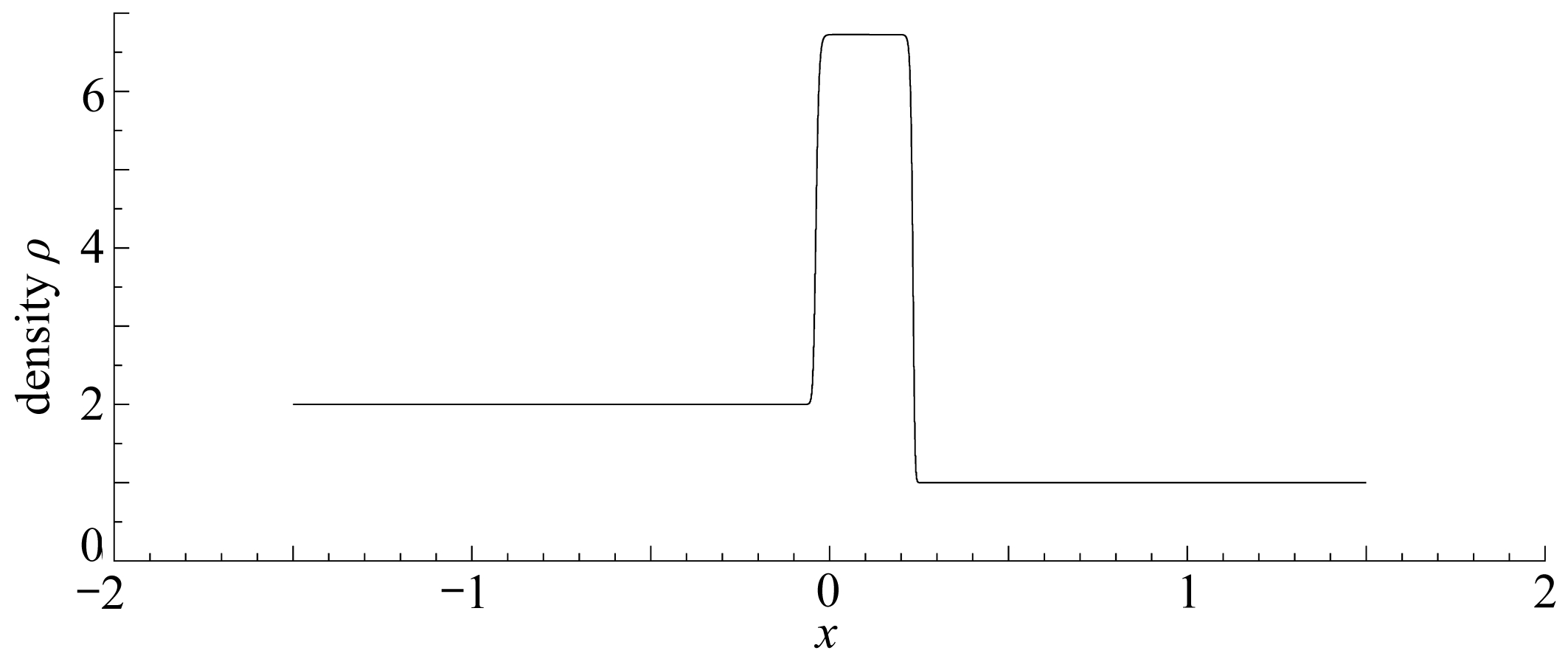
(a) M=1, N=1, t=0.1
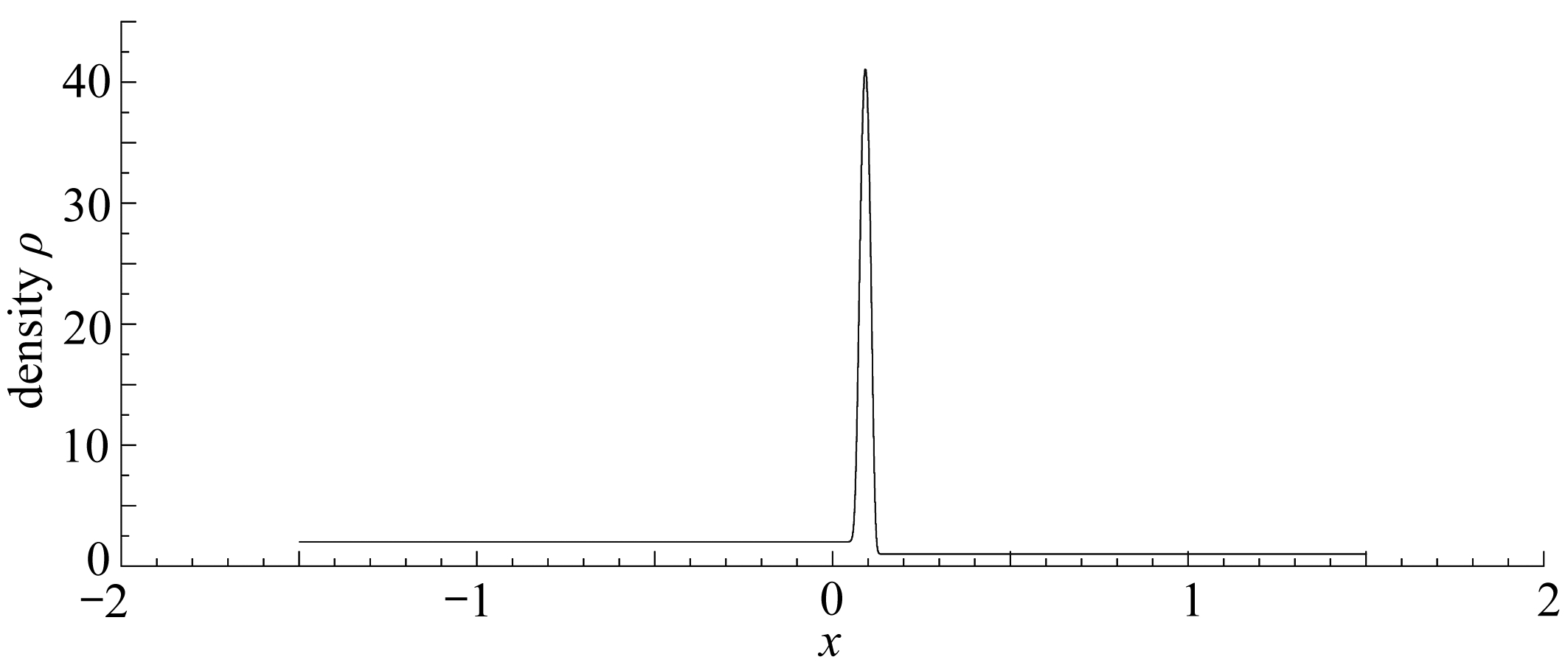
(b) M=0.01, N=0.01, t=0.1
图5 压力和磁感强度同时趋于零时出现质量集中现象
Fig. 5 Mass concentration appears when the pressure and the magnetic induction approach zero
根据4.1小节中的条件,给定负状态和正状态,使得(u+,ρ+)∈Ⅳ: (u-,ρ-), 当M=1,N=1时,由图5(a)可以看出中间状态的密度相对于初值并没有出现多大变化;而对于相同的初值,取M=0.01,N=0.01时,由图5(b)可以清晰地看出，中间状态的密度相对而言出现的变化比图5(a)要大得多.从图5(a)和图5(b)的比较中可以看出，压力和磁感强度同时趋于零时中间状态的密度变得越来越大,出现了质量集中现象.
2) 为了验证4.2小节中真空状态的形成,给定如下的初值：
(45)
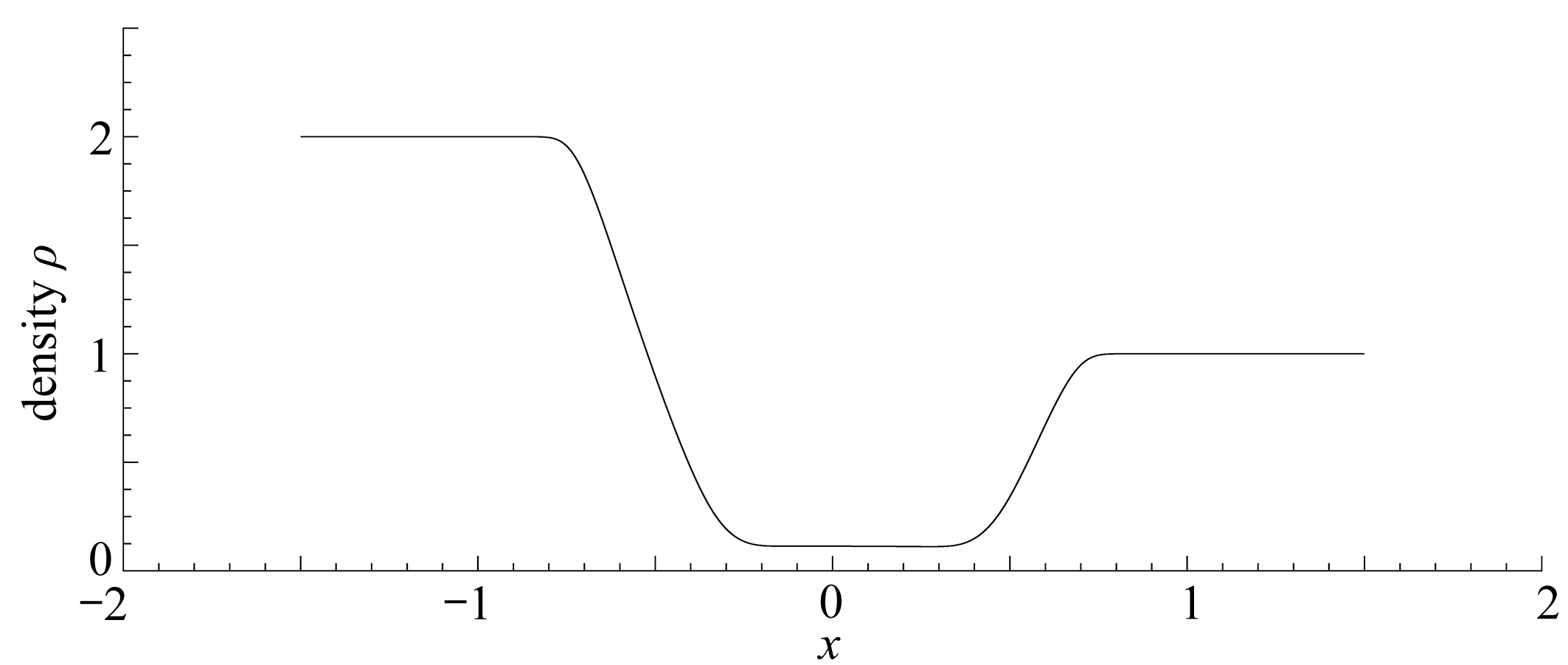
(a) M=1, N=1, t=0.1
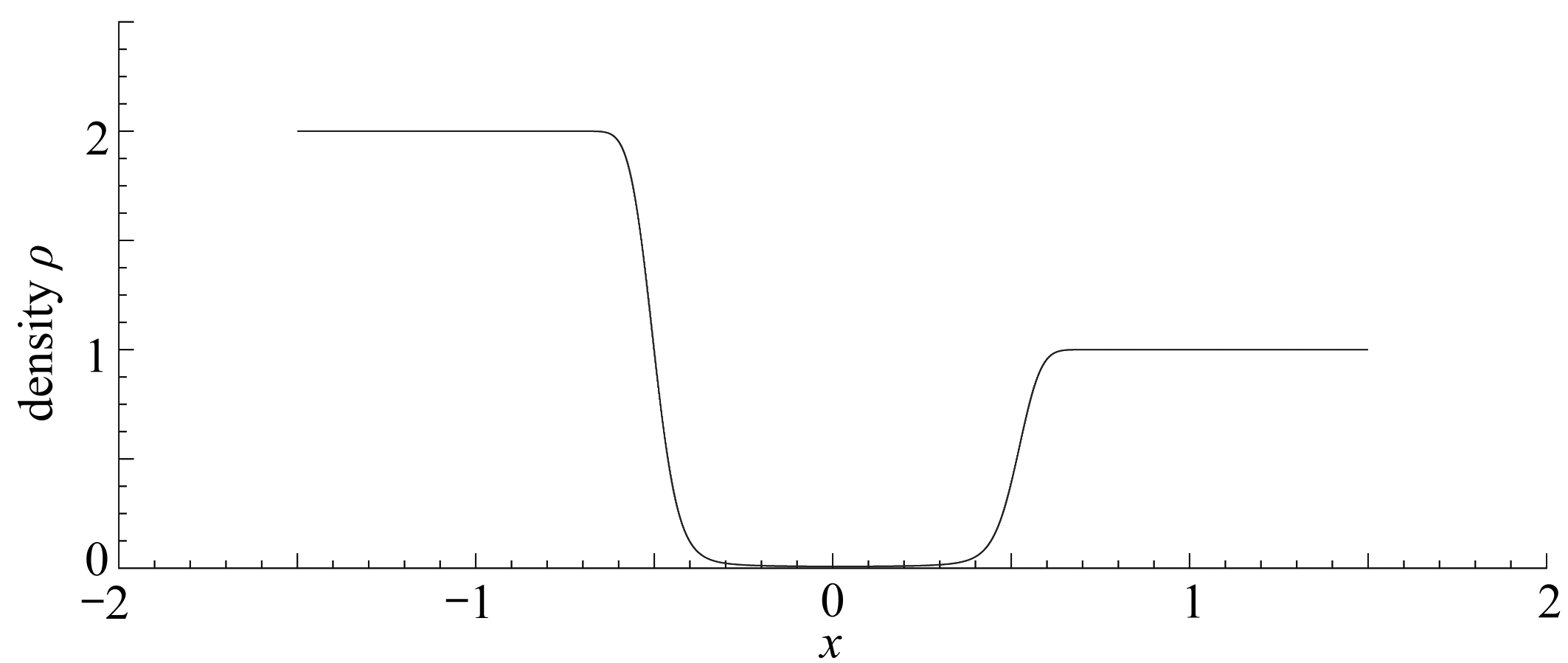
(b) M=0.01, N=0.01, t=0.1
图6 压力和磁感强度同时趋于零时出现真空现象
Fig. 6 Vacuum appears when the pressure and the magnetic induction approach zero
根据4.2小节中的条件,给定负状态和正状态,使得(u+,ρ+)∈Ⅰ: (u-,ρ-),当M=1,N=1时,由图6(a)可以看出中间状态的密度与零还保持着一定距离；而对于相同的初值,取M=0.01,N=0.01时,由图6(b)可以清晰地看出中间状态的密度几乎与横坐标轴重合.比较图6(a)和图6(b)可以看出，压力和磁感强度同时趋于零时中间状态的密度也会趋近于零,这意味着产生了真空现象.
3) 为了验证5.1小节中δ-激波的形成,给定如下的初值:
(46)
(a) M=1, N=1.5, t=0.1
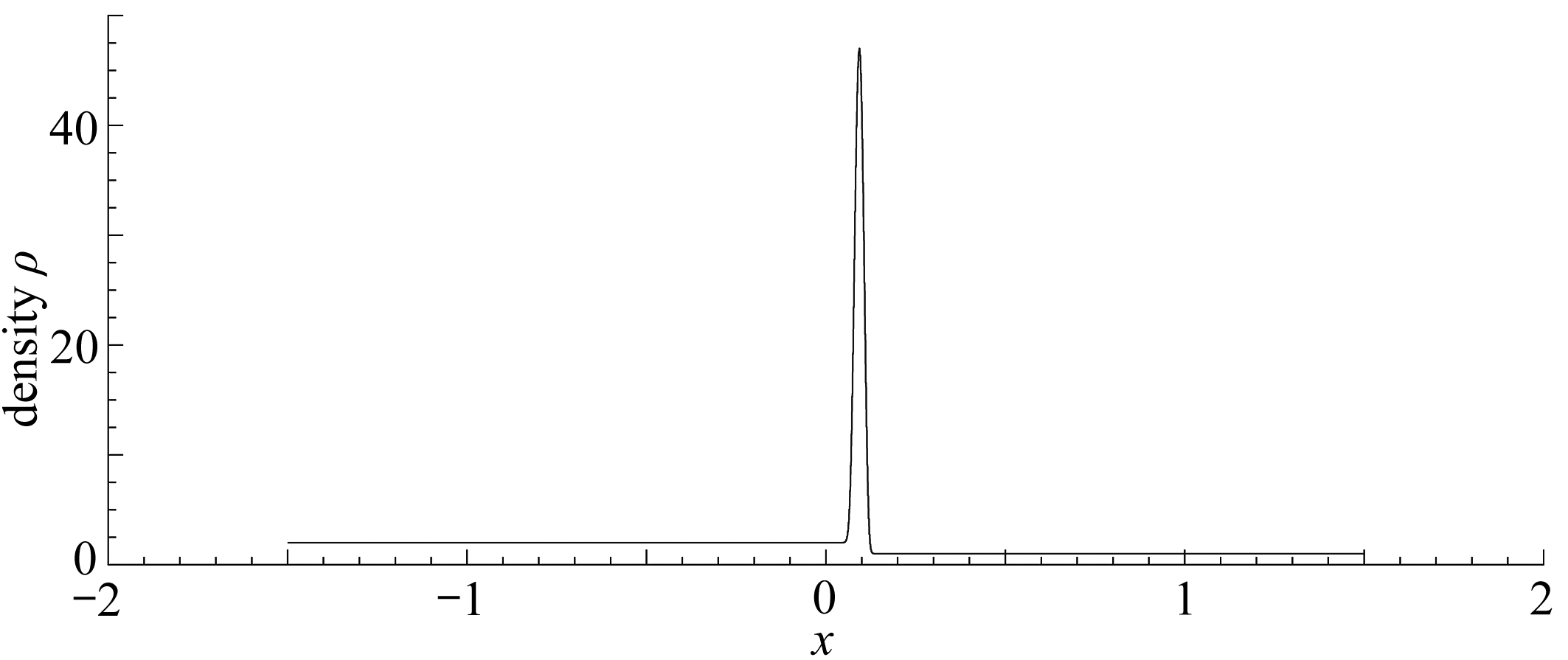
(b) M=1, N=0.001, t=0.1
图7 磁感强度趋于零时出现质量集中现象
Fig. 7 Mass concentration appears when the magnetic induction approach zero
根据5.1小节中的条件,给定负状态和正状态,使得当M=1,N=1.5时,由图7(a)可以看出中间状态的密度相对于初值并没有出现多大变化;而对于相同的初值,取M=1,N=0.001时,由图7(b)可以清晰地看出中间状态的密度相对而言出现的变化比图7(a)要大得多.比较图7(a)和图7(b)可以看出，压力和磁感强度同时趋于零时，Ⅳ：(u-,ρ-)中间状态的密度变得越来越大,出现了质量集中现象.
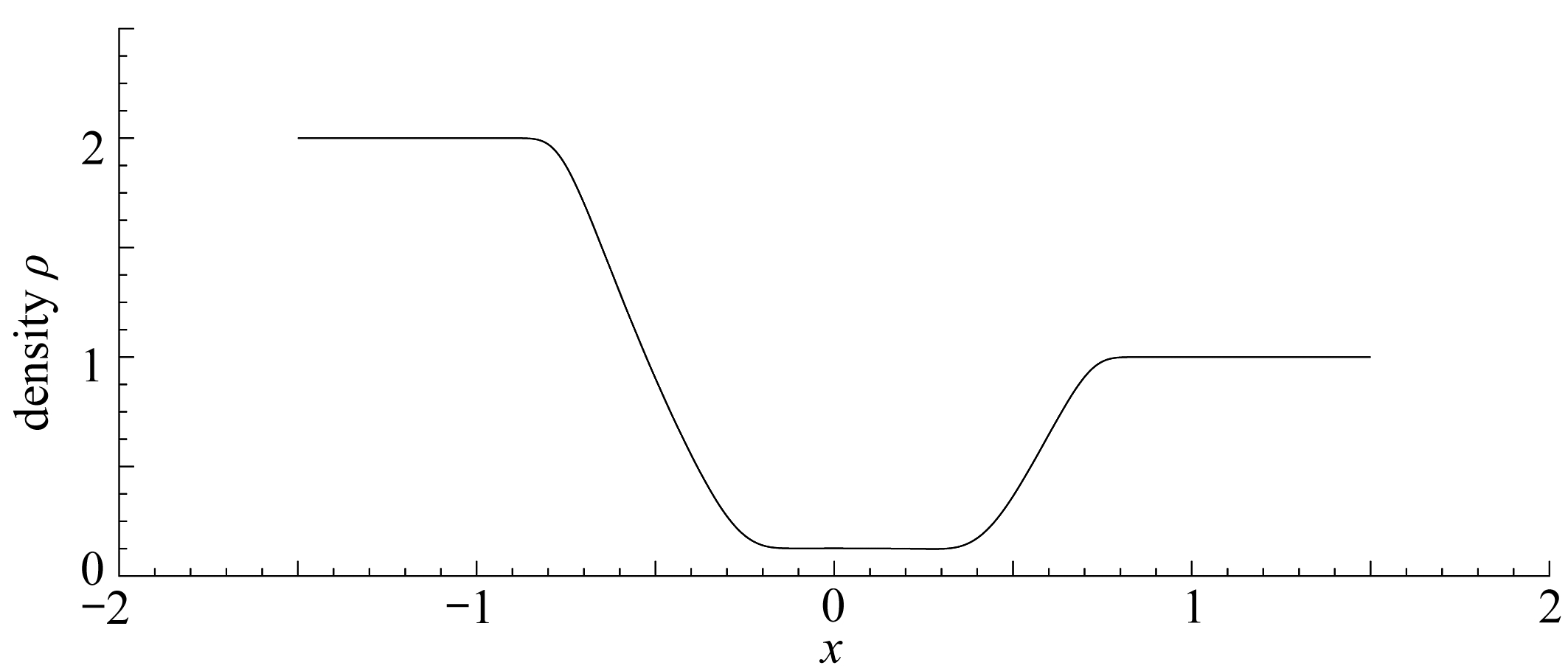
(a) M=1, N=1.5, t=0.1
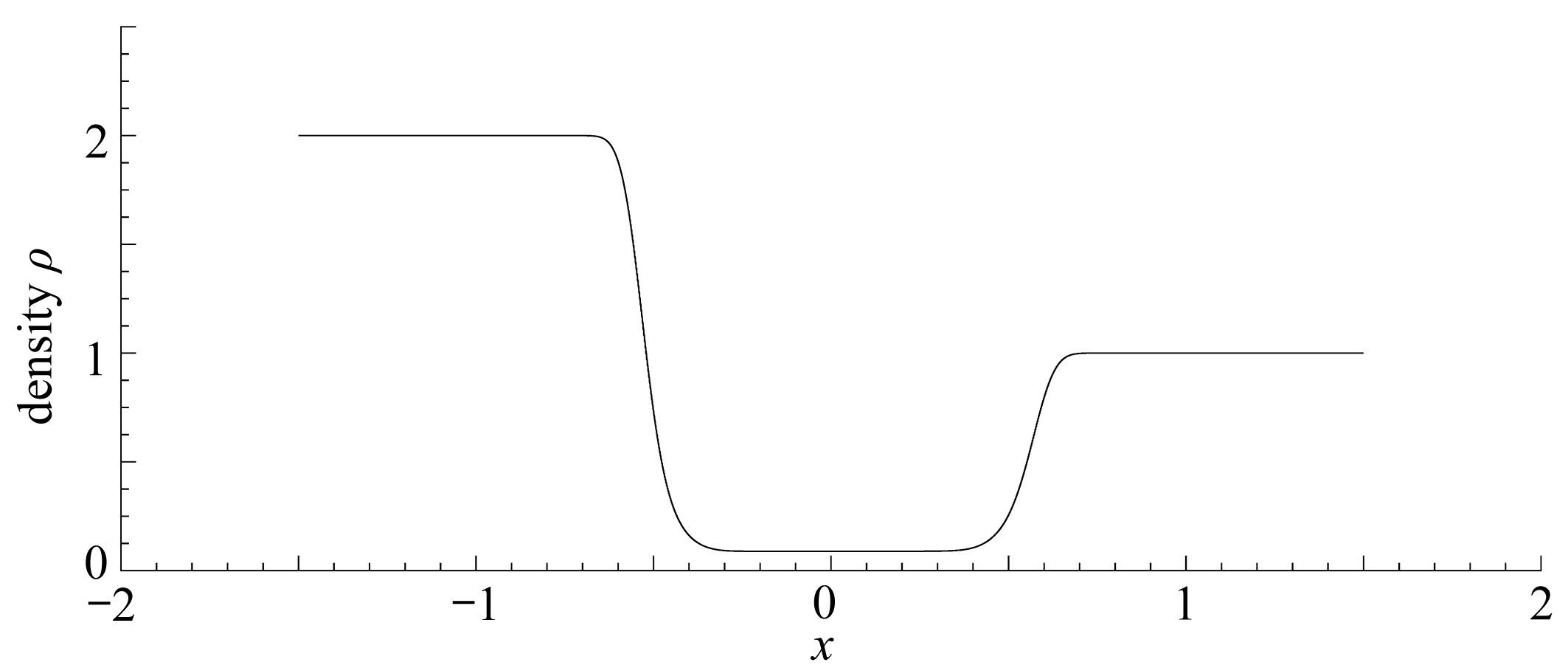
(b) M=1, N=0.001, t=0.1
图8 磁感强度趋于零时未出现真空现象
Fig. 8 Vacuum doesn’t occur when the magnetic induction approach zero
4) 为了验证5.2小节中未出现真空状态,给定如下的初值:
(47)
根据5.2小节中的条件,给定负状态和正状态,使得(u+, ρ+)∈Ⅰ: (u-, ρ-).当M=1, N=1.5时,由图8(a)可以看出中间状态的密度没有达到零；而对于相同的初值,取M=1,N=0.001时,由图8(b)可以清晰地看出中间状态的密度还是没有达到零.从图8(a)和图8(b)的比较中可以看出，磁感强度趋于零时中间状态的密度达不到零,这意味着不会出现真空现象.
7 结 论
本文以质量守恒定律和动量守恒定律为基础建立了磁流体Euler方程组,运用特征分析和相平面分析方法,分析了压力与磁感强度同时消失和仅磁感强度消失后的情形,并用数值实验验证了压力与磁感强度同时消失和仅磁感强度消失后这些情形.本文工作凸显了压力和磁场对磁流体的影响,不仅对天体物理中很多物理现象例如太阳风做出了合理解释,更为等离子体物理中运用受控核聚变来提取氢的同位素氘提供了一些思路.
[1] LARMOR J. How could a rotating body such as the sun become a magnet[J]. Reports of the British Association, 1919, 87: 159-160.
[2] COWLING T G. Thestability of gaseous stars[J]. Monthly Notices of the Royal Astronomical Society, 1934, 94: 768-782.
[3] FERRARO V C A. The non-uniform rotation of the sun and its magnetic fiel[J]. Monthly Notices of the Royal Astronomical Society, 1937, 97: 458-472.
[4] HARTMANN J. Theory of the laminar flow of an electrically conductive liquid in a homogeneous magnetic field[J]. Mathematisk-Fysiske Meddelelser, 1937, 6: 1-28.
[5] ALFVÉN H. On the cosmogony of the solar system[J]. Stockholms Observatoriums Annaler, 1942, 14(2): 85-100.
[6] SHERCLIFF J A. Steady motion of conducting fluids in pipes under transverse magneticfields[J]. Mathematical Proceedings of the Cambridge Philosophical Society, 1953, 49: 136-144.
[7] SHERCLIFF J A. The flow of conducting fluids in circular pipes under transversemagnetic fields[J]. Journal of Fluid Mechanics, 1956, 1(6): 644-666.
[8] R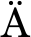
DLER K H. Mean-field approach to spherical dynamo models[J]. Astronomische Nachrichten, 1980, 301(3): 101-129.
[9] XU B, LI B Q, STOCK D E. An experimental study of thermally induced convection of molten gallium in magnetic fields[J]. International Journal of Heat and Mass Transfer, 2006, 49(13/14): 2009-2019.
[10] SMITH D L, PARK J H, LYUBLINSKI I. Progress in coating development for fusion systems[J]. Fusion Engineering and Design, 2002, 61/62: 629-641.
[11] YING A Y, GAIZER A A. The effects of imperfect insulator coatings on MHD and heat transfer in rectangular ducts[J]. Fusion Engineering and Design, 1994, 27: 634-641.
[12] LIU Y J, SUN W H. Elementary wave interactions in magnetogasdynamics[J]. Indian Journal of Pure and Applied Mathematics, 2016, 47(1): 33-57.
[13] LIU Y J, SUN W H. Riemann problem and wave interactions in magnetogasdynamics[J]. Journal of Mathematical Analysis and Applications, 2013, 397(2): 454-466.
[14] SHEN C. The Riemann problem for the pressureless Euler system with the Coulomb-like friction term[J]. IMA Journal of Applied Mathematics, 2016, 81(1): 76-99.
[15] SHENG W C, ZHANG T. The Riemann problem for the transportation equations in gas dynamics[J]. Memoirs of the American Mathematical Society, 1999, 137: 654.
[16] WEINAN E, RYKOV Y G, SINAI Y G. Generalized variational principles, global weak solutions and behavior with random initial data for systems of conservation laws arising in adhesion particle dynamics[J]. Communications in Mathematical Physics, 1996, 177(2): 349-380.
[17] SHANDARIN S F, ZELDOVICH Y B. Large-scale structure of the universe: turbulence, intermittency, structures in a self-gravitating medium[J]. Review of Modern Physics, 1989, 61(2): 185-220.
[18] SUN M N. The exact Riemann solutions to the generalized Chaplygin gas equations with friction[J]. Communications in Nonlinear Science and Numerical Simulation, 2016, 36: 342-353.
[19] BRENIER Y. Solutions with concentration to the Riemann problem for the one-dimensional Chaplygin gas equations[J]. Journal of Mathematical Fluid Mechanics, 2005, 7(3): 326-331.
[20] CHEN S X, QU A F. Two-dimensional Riemann problems for Chaplygin gas[J]. SIAM Journal on Mathematical Analysis, 2012, 44(3): 2146-2178.
[21] GUO L H, LI T, PAN L J,et al. The Riemann problem with delta initial data for the one-dimensional Chaplygin gas equations with a source term[J]. Nonlinear Analysis: Real World Applications, 2018, 41: 588-606.
[22] SHEN C. The Riemann problem for the Chaplygin gas equations with a source term[J]. Zeitschrift fǜr Angewandte Mathematik und Mechik, 2016, 96(6): 681-695.
[23] GUO L H, SHENG W C, ZHANG T. The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system[J]. Communications on Pure & Applied Analysis, 2010, 9(2): 431-458.
[24] WANG G D. The Riemann problem for one dimensional generalized Chaplygin gas dynamics[J]. Journal of Mathematical Analysis and Applications, 2013, 403(2): 434-450.
[25] FACCANONI G, MANGENEY A. Exact solution for granular flows[J]. International Journal for Numerical and Analytical Methods, 2012, 37: 1408-1433.
[26] CHEN G Q, LIU H L. Formation of δ-shocks and vacuum states in the vanishing pressure limit of solutions to the Euler equations for isentropic fluids[J]. SIAM Journal on Mathematical Analysis, 2003, 34(4): 925-938.
[27] LI J Q. Note on the compressible Euler equations with zero temperature[J]. Applied Mathematics Letters, 2001, 14(4): 519-523.
[28] SHEN C. The limits of Riemann solutions to the isentropic magnetogasdynamics[J]. Applied Mathematics Letters, 2011, 24(7): 1124-1129.
[29] CHEN J J, SHENG W C. The Riemann problem and the limit solutions as magnetic field vanishes to magnetogasdynamics for generalized Chaplygin gas[J]. Communications on Pure & Applied Analysis, 2018, 17(1): 127-142.
[30] SHENG W C, WANG G J, YIN G. Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes[J]. Nonlinear Analysis: Real World Applications, 2015, 22: 115-128.
[31] YANG H C, WANG J H. Delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations for modified Chaplygin gas[J]. Journal of Mathematical Analysis and Applications, 2014, 413(2): 800-820.
[32] SHEN C, SUN M N. Formation of delta shocks and vacuum states in the vanishing pressure limit of Riemann solutions to the perturbed Aw-Rascle model[J]. Journal of Differential Equations, 2010, 249(12): 3024-3051.
[33] GUO L H, LI T, YIN G. The limit behavior of the Riemann solutions to the generalized Chaplygin gas equations with a source term[J]. Journal of Mathematical Analysis and Applications, 2017, 455(1): 127-140.
[34] 尹淦, 谢娇艳. 广义Chaplygin气体磁流体力学方程组的Riemann问题[J]. 应用数学与计算数学学报, 2013, 27(4): 508-516.(YIN Gan, XIE Jiaoyan. Riemann problem for generalized Chaplygin magnetogasdynamics equations[J]. Communication on Applied Mathematics Computation, 2013, 27(4): 508-516.(in Chinese))