引 言
Allee效应[1-2]是由著名的生态学家Allee于20世纪30年代提出来的，他指出: 生物种群的群聚现象有利于种群的增长、存活，每个生物种群都有自己的最适密度，过分稀疏、拥挤都可能阻碍种群的生长.Allee效应可能是由诸多因素引起的，包括寻找配偶的困难、近亲繁殖、对捕食者的防御以及扩散消耗等.脊椎动物、无脊椎动物、植物等有机体[3-5]都可能存在Allee效应，当种群数量变大时Allee效应就消失了.Allee效应对濒危生物的管理、种群的开发利用以及物种的引入至关重要.
自Allee效应被提出后，生态种群的Allee效应一直是生态学及生物数学领域内一个倍受关注的热点研究问题.许多专家学者尝试着用数学模型来研究种群的Allee效应，文献[5-6]建立了具有Allee效应的单种群模型; 文献[7-8]将Allee效应引入到多种群模型中.然而，应用非光滑Filippov系统来研究种群Allee效应的文献很少，本文正是关注于Allee阈值对生物种群行为的影响，建立由Allee阈值诱导的非光滑Filippov生态切换模型，并从理论和数值上研究模型的动力学行为.
本文的结构如下: 第1节将建立具有Allee效应的Filippov捕食模型; 第2节重点介绍Filippov系统的基本理论、相关定义及其子系统的动力学性质; 第3节从理论上对模型的滑动区域、滑动动力学及各类平衡点的存在性进行系统分析; 第4节从数值上研究模型的滑动分支、全局动力学行为等; 最后给出相应的生物意义解释.
1 模 型 建 立
基于文献[9]提出的Leslie-Gower捕食模型，考虑到食饵种群具有附加Allee效应，文献[10] 建立了具有Allee效应的Leslie-Gower捕食模型:
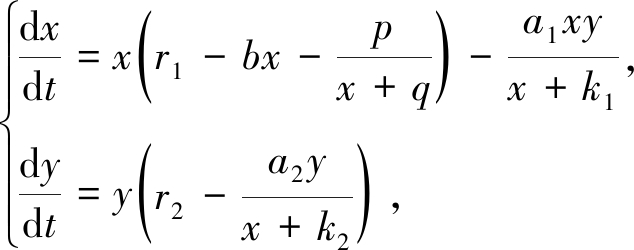
(1)
其中x(t)和y(t)分别代表食饵和捕食者在时间t的种群密度; r1和r2分别表示食饵和捕食者的内禀增长率，b为食饵种群的种内抑制率，a1和a2分别代表食饵转化成捕食者的最大生物转化率和生物转化率，k1和k2表示半饱和常数; p/(x+q)为附加Allee效应，其中p和q为Allee效应常数; 假设所有参数均为正常数.
Allee效应只有在食饵密度小于Allee阈值xET时才发生，而当食饵密度大于Allee阈值xET时，食饵种群将不会发生Allee效应，于是便得到了如下模型(即文献[9]考虑的情形):
(2)
因此，联系模型(1)和(2)，本文建立了具有附加Allee效应的非光滑Filippov捕食模型:
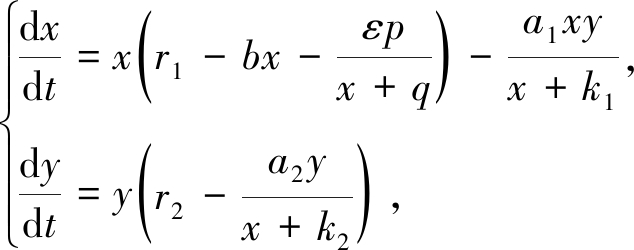
(3)
其中
(4)
2 预 备 知 识
2.1 Filippov系统的相关理论及定义
定义二维空间
和函数H(Z)=x-xET,并作如下记号：
则模型(3)及(4)可以写成一般的非光滑Filippov系统[11-17]：
(5)
其中
同时，定义不连续的切换面
将区域G1与G2分开.为了研究模型(5)在切换面Σ上的性质，需要采用凸组合[11]或Utkin等度控制[12]方法.由文献[11]的相关定义可得
FG(Z)=λ(Z)FG1(Z)+[1-λ(Z)]FG2(Z),
(6)
其中
(7)
或定义
FG(Z)=[1-λ(Z)]FG1(Z)+λ(Z)FG2(Z),
其中
另外，Filippov系统的滑动模式动力学可由
决定.
现在，本文参考文献[11-14]，给出了Filippov系统平衡点的相关定义.
定义1(伪平衡点) 若平衡点Z*是Filippov系统(5)滑动模式动力学上的点，且满足关系式(6)和(7)，则称Z*为Filippov系统(5)的伪平衡点.
定义2(边界平衡点) 若Filippov系统(5)的平衡点Z*满足如下条件之一：
FG1(Z*)=0, H(Z*)=0;
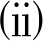FG2(Z*)=0, H(Z*)=0,
则称Z*为Filippov系统(5)的边界平衡点.
定义3(切点) 若Filippov系统(5)的平衡点Z*满足如下条件之一:
FG1H(Z*)=0, Z*∈ΣS；
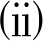FG2H(Z*)=0, Z*∈ΣS，
则称Z*为Filippov系统(5)的切点.
定义4(真、假平衡点) 若Filippov系统(5)的平衡点Z*满足如下条件之一：
FG1(Z*)=0, H(Z*)<0；
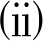FG2(Z*)=0, H(Z*)>0,
则称Z*为Filippov系统(5)的真平衡点.
若Z*满足如下条件之一：
FG1(Z*)=0, H(Z*)>0；
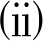FG2(Z*)=0, H(Z*)<0，
则称Z*为Filippov系统(5)的假平衡点.
2.2 子系统的动力学行为
当x(t)<xET时，Filippov系统(5)的动力学行为由子系统(1)决定，文献[10]通过无量纲变化将系统(1)转化成如下系统：
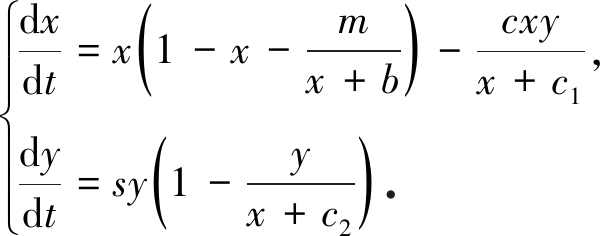
(8)
文献[10]对系统(8)的动力学行为进行了深入细致的分析，本文主要考虑0<m<b的情形(弱Allee效应)，为了方便叙述引理，作记号:
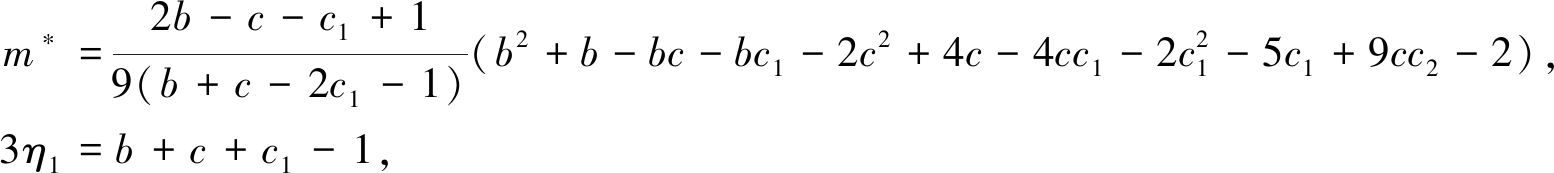3η2=bc+bc1+cc2+m-b-c1, η3=bcc2+c1(m-b),
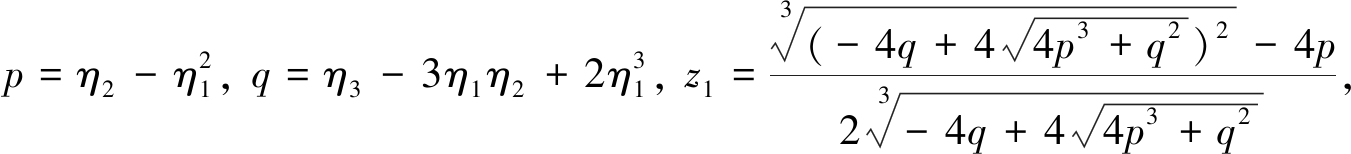
μ1=1+b+c1+bc1+c2+cc1-2m-bc-2cc2-2c,
μ2=-cc2+b-m+2bc1-2bc+b2-cc1+c2c2+c2b-bm+cm-b2c-
引理1 如果系统(8)满足如下条件之一:
2c1+1-c-b>0, 0<m
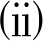2c1+1-c-b<0, 0<m*<m<b,
则系统(8)存在唯一的正平衡点
进一步地，如果
则系统(8)的正平衡点
的Hopf分支发生在
处.
当x(t)>xET时，Filippov系统(5)的动力学行为由子系统(2)决定.基于文献[9]的主要研究结果，本文给出了如下引理.
引理2 子系统(2)存在三个边界平衡点(0,0),(r1/b1,0),(0,r2k2/a2). 若r1k2a1<r1k1a2,则系统存在唯一的正平衡点(x*,y*).进一步地，如果
2a1L1<r1k1, k1<2k2, 4(r1+b1k1)<a1
成立，则正平衡点(x*,y*)是全局渐近稳定的，其中
3 滑动模态及平衡点
由式(7)中λ(Z)的定义，可得
求解不等式0≤λ(Z)≤1可得
为了叙述的方便，作如下记号:
根据预备知识中关于ΣS的定义，可得Filippov系统(5)的滑线区域为
(9)
接下来，应用Utkin等度控制方法[12]来研究Filippov系统(5)在滑线ΣS上的动力学性质，由H(Z)=0可得
对于上述方程关于ε求解得
由Utkin等度控制方法可得Filippov系统(5)在滑线ΣS上滑动模式动力学微分方程为
(10)
下文将继续探讨Filippov系统(5)各类平衡点的存在性.
伪平衡点 由定义1可知Filippov系统(5)存在唯一的伪平衡点Ep(xET,yp)，其中
边界平衡点 由定义2可知Filippov系统(5)的边界平衡点需满足如下方程:
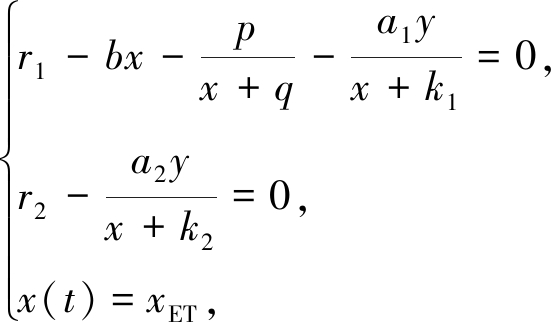
(11)
或
(12)
对于方程组(11)，若ymin=yp,则Filippov系统(5)存在边界平衡点Eb(xET,ymin)；
对于方程组(12),若ymax=yp, 则Filippov系统(5)存在边界平衡点Eb(xET,ymax).
切点 由定义3可知Filippov系统(5)的切点需满足如下方程:
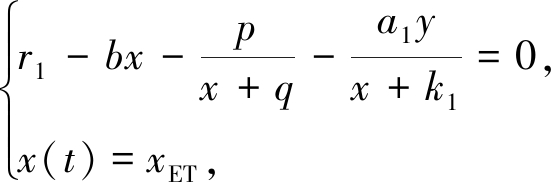
(13)
或
(14)
求解上述方程组可得，Filippov系统(5)存在切点Et(xET,ymin)或Et(xET,ymax).
真、假平衡点 由子系统的动力学行为相关预备知识可知，子系统(1)至多存在两个正平衡点，记为E11(x11,y11)和E12(x12,y12),在此假设x11<x12. 因此对子系统(1)的真、假平衡点概括如下:
若x12>xET,则子系统(1)存在两个假平衡点
和
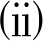若x11<xET,则子系统(1)存在两个真平衡点
和
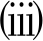若x11<xET<x12,则子系统(1)存在一个真平衡点和一个假平衡点
类似地，子系统(2)至多存在一个正平衡点，记为E21(x21,y21). 则对子系统(2)的真、假平衡点概括为:
若x21<xET,则子系统(2)存在一个假平衡点
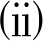若x21>xET,则子系统(2)存在一个真平衡点
此外，本文还给出两个子系统的等倾曲线方程.子系统(1)的垂直和水平等倾曲线方程分别为
子系统(2)的垂直和水平等倾曲线方程分别为
4 滑动分支及全局动力学行为
通过对Filippov系统(5)滑动区域、滑动模态动力学及平衡点的研究可知: Filippov系统(5)存在伪平衡点、真平衡点、假平衡点、边界平衡点等多种平衡点，当一些重要参数发生微小变化时，可能会引起一系列滑动模态及平衡点分支现象.下面，本文将通过数值方法来研究Filippov系统(5)的滑动分支及全局动力学行为.
首先，选择Allee阈值xET作为分支参数来研究Filippov系统(5)的滑动模态分支，同时固定其他参数为r1=4,r2=3,b=0.1,q=0.1,a1=0.5,a2=0.9,k1=2,k2=2.如图1所示，随着xET的逐渐变化，Filippov系统(5)的滑线段长度、伪平衡点的存在发生了迅速变化.特别地，当Allee效应常数p不同时，Filippov系统(5)的滑线段长度和伪平衡点个数变化趋势也不同.通过对比图1(a)与1(b)发现Filippov系统(5)的滑动模态对Allee效应常数p相当敏感，当p较大时，即Allee效应较强时，Filippov系统(5)滑线段上的伪平衡点个数增多，而滑线上的伪平衡点会使Filippov系统的动力学行为变得更加复杂.这说明了Allee效应的强度可使种群的动态变得不稳定，不利于濒危生物种群的管理.
(a) p=10
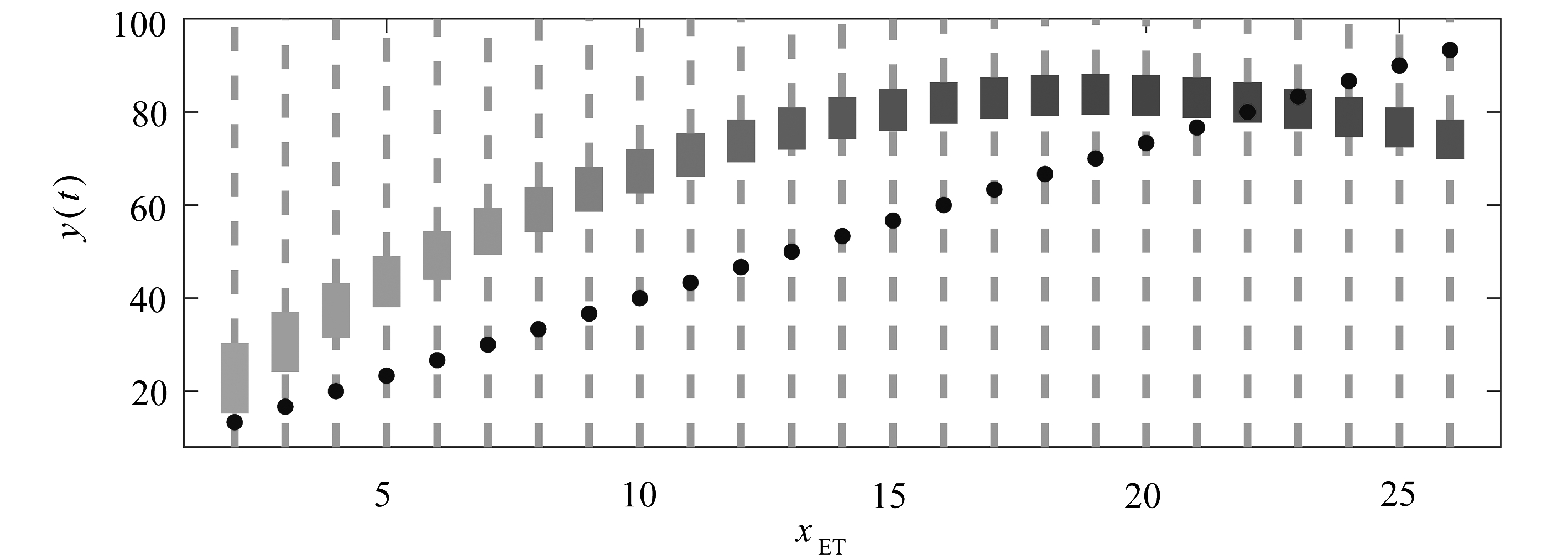
(b) p=4
图1 Filippov系统(5)的滑动模态分支
Fig. 1 Sliding mode bifurcation of Filippov system (5)
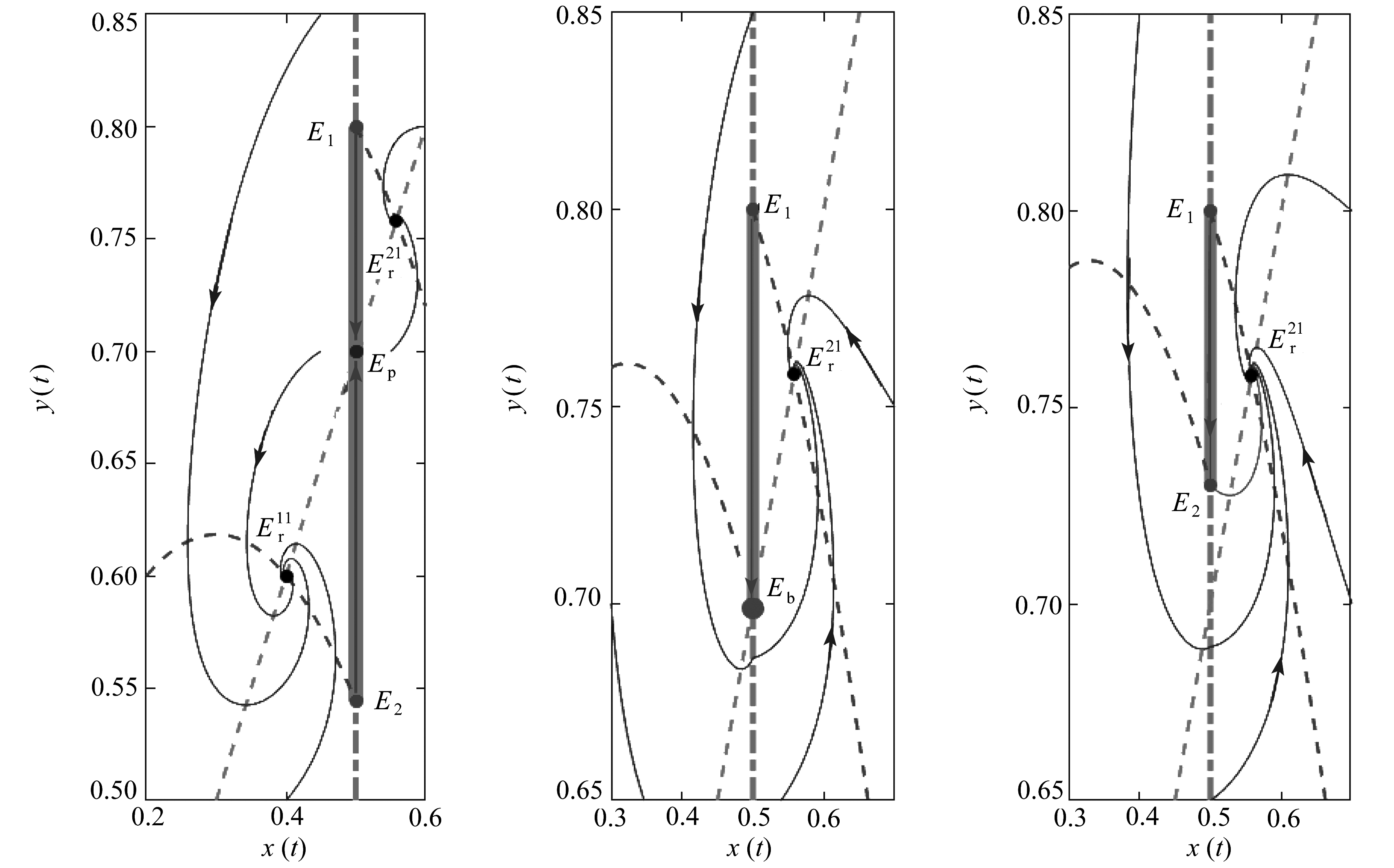
(a) q=1 (b) q=3.3 (c) q=5
图2 Filippov系统(5)的边界焦点分支
Fig. 2 Boundary focus bifurcation of Filippov system (5)
接下来，选择以Allee常数q为分支参数来研究Filippov系统(5)的边界焦点分支，其他参数为r1=1,r2=0.125,a1=0.5,a2=0.125,k1=0.3,k2=0.2,b=1,p=0.24,xET=0.5.当q较小时，Filippov系统(5)的两个子系统(1)和(2)分别存在一个稳定的真平衡点(焦点)和
同时系统还存在一个稳定的伪平衡点Ep,如图2(a)如示.当q增大到3.3时，即图2(b)所示情形，子系统(1)的焦点与系统的伪平衡点Ep碰撞成一点，即边界平衡点Eb, 此时Filippov系统(5)发生了边界焦点分支.进一步增大q到图2(c)所示情形，边界平衡点Eb突然消失，系统所有的轨线趋于子系统(2)的真平衡点(焦点)
最后，本文研究了Filippov系统(5)的全局动力学行为.如图3所示，选取所有参数值为r1=1,r2=0.08,a1=0.5,a2=0.08,k1=0.3,k2=0.2,b=1,p=0.24,q=0.4,xET=0.5.子系统存在一个不稳定的真平衡点(焦点)和一个稳定的标准周期解(极限环)Γ. 同时，Filippov系统(5)在滑线上存在一个稳定的伪平衡点Ep. 此外，从图3还可以看出: 子系统(2)存在一个稳定的真平衡点(焦点)
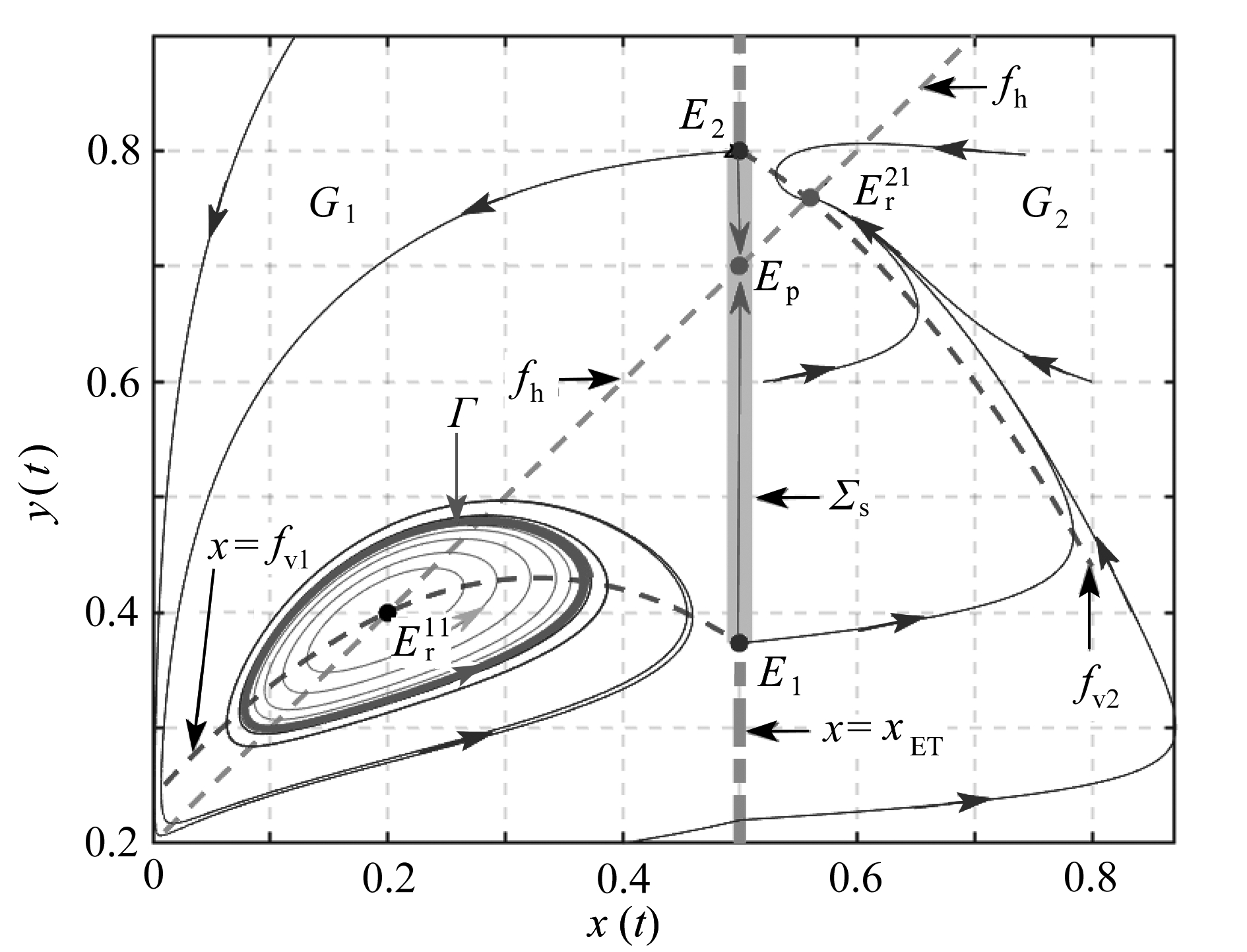
图3 Filippov系统(5)的全局动力学行为
Fig. 3 Global dynamic behaviors of Filippov system (5)
5 结 论
本文在一类具有Allee效应的Leslie-Gower捕食模型的基础上，考虑到Allee阈值对种群Allee效应的影响，建立了一类具有附加Allee效应的非光滑Filippov捕食系统.综合运用Filippov系统的基本理论与研究方法，从理论上研究了Filippov系统(5)的滑动区域、滑动动力学和各类平衡点的存在性.同时用数值分析技巧研究了该系统的滑动模态分支、 边界焦点分支及全局动力学行为.研究发现: Allee效应的强度可使种群的动态不稳定， 不利于濒危生物种群的管理.
然而，本文仅考虑了附加Allee效应对种群生态的影响.事实上，诸如气候的多变、环境的不确定等随机因素也可能会对生物种群带来重要影响.因此，考虑这些随机因素，建立复杂的混合动力学模型来研究Allee效应对种群生态的影响，探讨在Allee效应条件下混合动力系统的生态学解释，这将是一项非常有意义的工作.今后我们将重点关注这方面的研究.
[1] ALLEE W C. Animal Aggregations: a Study in General Sociology[M]. Chicago: Chicago University Press, 1931.
[2] ALLEE W C, PARK O, EMERSON A E, et al. Principles of Animal Ecology[M]. Philadelphia: Saunders Company, 1949.
[3] DENNIS B. Allee effects: population growth, critical density, and the chance of extinction[J]. Natural Resource Modeling, 1989, 3(4): 481-538.
[4] MCCARTHY M A. The Allee effect, finding mates and theoretical models[J]. Ecological Modelling, 1997, 103(1): 99-102.
[5] STEPHENS P A, SUTHERLAND W J. Consequences of the Allee effect for behaviour, ecology and conservation[J]. Trends in Ecology & Evolution, 1999, 14(10): 401-405.
[6] BOUKAL D S, BEREC L. Single-species models of the Allee effect: extinction boundaries, sex ratios and mate encounters[J]. Journal of Theoretical Biology, 2002, 218(3): 375-394.
[7] WANG W X, ZHANG Y B, LIU C. Analysis of a discrete-time predator-prey system with Allee effect[J]. Ecological Complexity, 2011, 8(1): 81-85.
[8] YU T, TIAN Y, GUO H, et al. Dynamical analysis of an integrated pest management predator-prey model with weak Allee effect[J]. Journal of Biological Dynamics, 2019, 13(1): 218-244.
[9] AZIZ-ALAOUI M A, OKIYE M D. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes[J]. Applied Mathematics Letters, 2003, 16(7): 1069-1075.
[10] CAI Y L, ZHAO C D, WANG W M, et al. Dynamics of a Leslie-Gower predator-prey model with additive Allee effect[J]. Applied Mathematical Modelling, 2015, 39(7): 2092-2106.
[11] FILIPPOV A F. Differential Equations With Discontinuous Right-Hand Sides[M]. Dordrecht: Kluwer Academic Publishers, 1988.
[12] UTKIN V I, GULDNER J, SHI J X. Sliding Model Control in Electromechanical Systems[M]. London: Taylor Francis Group, 2009.
[13] KUZNETSOV YU A, RINALDI S, GRAGNANI A. One parameter bifurcations in planar Filippov systems[J]. International Journal of Bifurcation and Chaos, 2003, 13(8): 2157-2188.
[14] DI BERNARDO M, BUDD C J, CHAMPNEYS A R, et al. Bifurcations in nonsmooth dynamical systems[J]. SIAM Review, 2008, 50(4): 629-701.
[15] KRIVAN V. On the Gause predator-prey model with a refuge: a fresh look at the history[J]. Journal of Theoretical Biology, 2011, 274(1): 67-73.
[16] TANG S Y, LIANG J H, XIAO Y N, et al. Sliding bifurcations of Filippov two stage pest control models with economic thresholds[J]. SIAM Journal on Applied Mathematics, 2012, 72(4): 1061-1080.
[17] TANG S Y, LIANG J H. Global qualitative analysis of a non-smooth Gause predator-prey model with a refuge[J]. Nonlinear Analysis: Theory, Methods & Applications, 2013, 76: 165-180.