引 言
随着旅游行业的迅速发展,机场旅客的比例相较于在其他交通体系所占的比例逐年递增[1].航空公司为了应对未来的发展,缓解机场现有航站楼旅客流量饱和状态[2],新增设卫星厅以改善原有航站楼登机口不足的压力,但同时对中转旅客的航班衔接会产生一定的影响.因此,合理优化分配登机口,使中转旅客流程时间最短是目前需要解决的问题.
对于登机口分配问题国内外学者主要采用人工智能和数学规划等方法.人工智能法能较好地将航班和机位信息转化为“知识表达”,但存在专家系统推理结果受推理规则影响较大的不足[3-4].数学规划法可将实际问题进行具体量化,Babic等[5]建立了机位分配模型,Mangoubi等[6]在Babic等的基础上研究了中转旅客的问题.但上述研究只考虑旅客在航站楼内的距离最小化,并未研究中转旅客在航站楼和卫星厅之间的距离.
单纯的航班-登机口的优化分配问题已经被解决[7].但在优化分配登机口的同时考虑旅客步行距离最短、机场现有资源使用率最高[8-9]的影响,一直是航空公司关注的热点问题.本文以2018年第十五届“华为杯”中国研究生数学建模竞赛F题为依据,针对在航站楼和卫星厅之间如何合理优化分配登机口以减少中转旅客流程时间的问题,分别构建了登机口优化分配网络模型和多目标优化模型,为航班飞行计划提供参考.
1 基 本 假 设
1) 在航班正常运转的前提下,假设对2018年1月20日到达或20日出发的航班和旅客进行分析不影响本文研究结论的普遍适用性;
2) 在航班及登机口符合实际情况的前提下,假设航班-登机口分配调度方案是在一定约束下的优化方案.
2 定义与记号
2.1 定义
1) 转场,到达航班和出发航班,称之为转场;
2) 最短流程时间,中转旅客从前一航班的到达至后一航班的出发之间的流程所用的最短时间.
2.2 记号
Xwi,Xni分别表示航站楼T使用宽型登机口和窄型登机口的数量(下标w表示宽机体,n表示窄机体);Ywj,Ynj分别表示卫星厅S使用宽型登机口和窄型登机口的数量;A1,A2,A3分别代表航站楼T中一个宽型登机口可停靠宽体飞机的架次、一个宽型登机口可停靠窄体飞机的架次和一个窄型登机口可停靠窄体飞机的架次;B1,B2,B3分别代表卫星厅S中一个宽型登机口可停靠宽体飞机的架次、一个宽型登机口可停靠窄体飞机的架次和一个窄型登机口可停靠窄体飞机的架次.
3 问题的提出
本文主要针对航站楼旅客流量的饱和状态,通过增设卫星厅对中转旅客的航班衔接问题进行解决,从而为航空公司航班规划的调整提供参考依据[7].图1为航班及其停靠示意图.
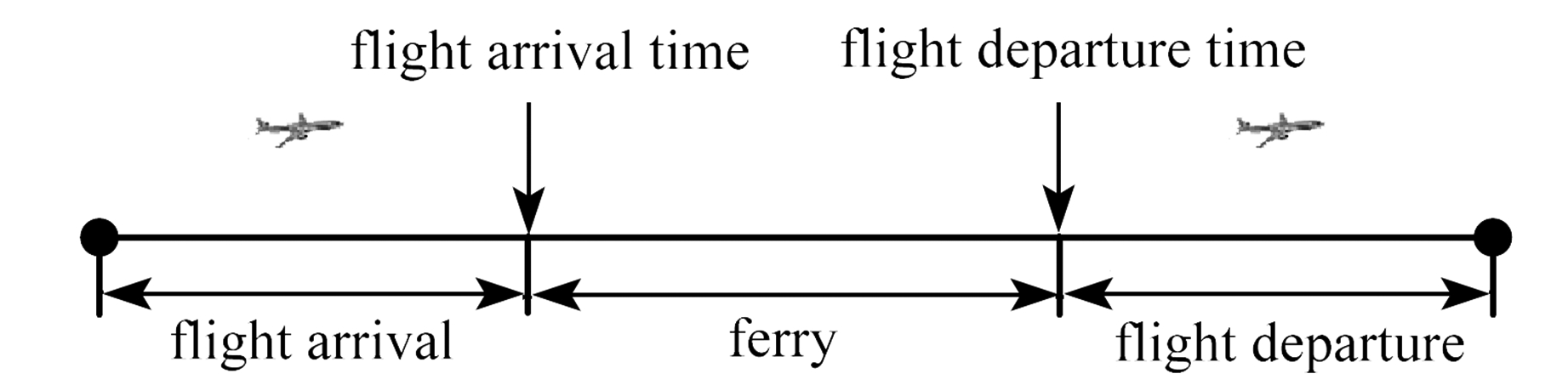
图1 航班及其停靠示意图
Fig. 1 Flight and its docking diagram
针对此,本文主要解决的问题如下:
(A) 在尽可能多分配航班到合适的登机口的基础上,最小化被使用登机口数量的问题;
(B) 充分考虑最小化中转旅客最短流程时间,确定最小化被使用登机口的数量.
4 问题的分析
针对问题(A),只考虑航班-登机口分配.航站楼T和卫星厅S共有登机口69个.其中,航站楼T有28个登机口,卫星厅S有41个登机口.为最小化被使用登机口的数量,建立单目标优化模型.以使用登机口数量最少为优化目标,以登机口允许机型限制、登机口航班停靠最小间隔限制、每架飞机转场的到达和出发两个航班必须分配在同一登机口进行为约束条件,建立单目标优化模型,以最大流理论建立登机口分配模型,该模型可最大程度上最小化被使用登机口的数量.
针对问题(B),在问题(A)的基础上加入旅客换乘因素.要求最小化中转旅客的总体最短流程时间.如题所述,可对已给出数据进行相关性分析,获取满足此问题所需的确切数据,以计算中转旅客最短流程时间.以登机口的使用数量最少为优化目标,以登机口允许机型限制、登机口航班停靠最小间隔限制、每架飞机转场的到达、中转旅客流程时间最短和出发两个航班必须分配在同一登机口进行为约束条件,建立双目标优化模型,可采用加权组合法或目标约束法对建立的模型进行求解.该模型可最大限度地解决中转旅客流程时间以及登机口数量最小化问题.
5 数学模型的建立
此实际问题共有69个登机口,303架航班,每个航班的登机口起用和停用时间已知.卫星厅S与航站楼T相对位置如图2所示.

图2 卫星厅S与航站楼T相对位置示意图
Fig. 2 Schematic diagram of the relative positions of satellite hall S and terminal T
5.1 问题(A)的解答
5.1.1 登机口分配优化的网络模型
本题以登机口数量最少为优化目标,建立单目标优化模型,采用最大流理论建立登机口分配模型.构建登机口分配网络图[1,10-12]步骤如下:
步骤1 根据航班到达和离开时间的顺序,每个航班被视为网络图上的一个节点,时间间隔设置为45 min,两个航班通过箭头线连接,方向指向时间晚的航班.根据此规则,所有节点都连接起来形成网络图,从网络图起点到终点的每条有向线路上的所有节点,都是可以安排在同一个登机口的航班组合.
步骤2 通过在节点上标记到达和离开时间来形成具有多个起点和多个终点的无环路网络图.
以2018年1月20日到达或20日出发的部分航班和旅客信息按上述设计网络图的方法构建如图3的网络图.

图3 登机口分配网络图
Fig. 3 Network diagram of gate assignment
5.1.2 基于整数线性规划理论求解
本题以使用登机口数量最少为优化目标,以登机口允许机型限制、登机口航班停靠最小间隔限制、每架飞机转场的到达和出发两个航班必须分配在同一登机口进行为约束条件,建立目标函数和约束条件如下:
min Z=Xwi+Xni+Ywj+Ynj,
(1)
s.t.
A1Xwi+A2Xwi+A3Xni+B1Ywj+B2Ywj+B3Ynj≥304,
Xwi+Ywj≤23,
Xni+Ynj≤46,
A1Xwi+A2Xwi+B1Ywj+B2Ywj≥49,
A3Xni+B3Ynj≥254,
A1Xwi+A2Xwi≥91,
B1Ywj≥39,
Xwi≤10,
Xni≤18,
Ywj≤13,
Ynj≤28,
其中i∈1,2,3,…,28; j∈1,2,3,…,41.由此可得A1,A2,A3,B1,B2,B3优先级如表1所示,即为
表1 A1,A2,A3,B1,B2,B3优先级
Table 1 Priority of A1, A2, A3, B1, B2, B3
number of aircraftsA1A2A3B1B2B3priority of each type12/35/61/21/61/3
对于问题(A)的求解步骤: ① 依据I-I(国际到国际)、I-D(国际到国内)、D-I(国内到国际)、D-D(国内到国内)将航班路线分配到航站楼T和卫星厅S; ② 根据题目建立目标函数与约束条件; ③ 基于整数线性规划[13-15]理论,利用MATLAB求解最优解; ④ 将得到的最优解与实际过程结果进行比较,并验证其合理性与最优性.图4为问题(A)MATLAB程序算法流程图.
登机口分配结果如表2、表3所示.
表2 登机口分配结果
Table 2 Gate assignment results

projectwide-body gate in terminal Tnarrow-body gate in terminal Twide-body gate in satellite hall Snarrow-body gate in satellite hall Ssumnumber60102642
表3 各登机口可停靠机型分配结果
Table 3 Assignment results of the dockable plane types for each gate

projectnumber of planes accommodable by terminal Tnumber of planes accommodable by satellite hall Swide gatenarrow gatewide gatenarrow gatetype of planesA1A2A3B1B2B3number511742010
由上可知:一共分配到的最小登机口数量共42个,航站楼T中的宽型登机口6个,卫星厅S中宽体登机口10个,卫星厅S中窄体登机口26个.同时航站楼T中的宽型登机口中可停靠宽体机5架,窄体机11架,窄型登机口可停靠窄体机7架;卫星厅S中的宽型登机口中可停靠宽体机4架,窄体机20架,窄型登机口可停靠窄体机10架.

图4 问题(A)程序算法流程图
Fig. 4 The flow chart of the algorithm for problem(a)
5.2 问题(B)的解答
5.2.1 基于双目标的登机口分配优化模型
多目标优化是在给定的约束范围[16-17]内求多个目标的最值,一般形式如下[18-23]:
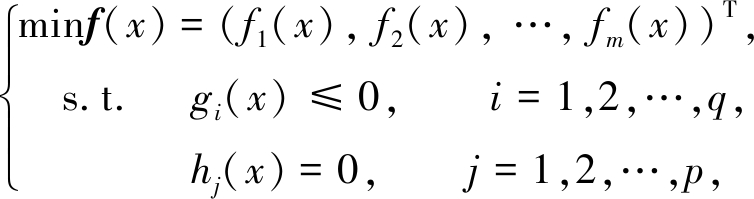
(2)
式中,x表示n维的决策向量即x=(x1,x2,…,xn)∈X⊂R,X为n维的决策空间; f表示目标函数;g表示不等式约束函数;h表示等式约束函数[23-24].
多目标优化的方法一般有加权组合法和目标约束法,其具体模型[24]如式(3)和(4):
(3)
式中,λ表示权重系数,正则化后的权重系数需要满足λi≥0且![]()
(4)
式中,ε表示函数的下界.
5.2.2 基于双目标登机口优化模型的求解
根据本题提供的数据, 经分析, 表4中包含20日到达或20日出发航班中所需的最短流程时间和捷运乘坐次数.其中, 每一项的第一个数是最短流程时间(min), 第二个数是捷运乘坐次数.
表4 旅客最短流程时间/捷运乘坐次数
Table 4 Minimum process time for passengers/number of MRT rides
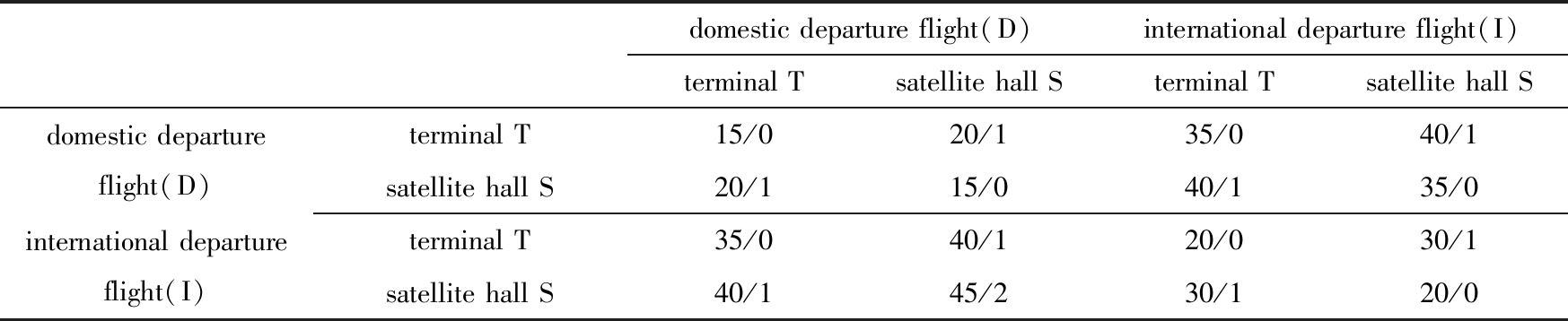
domestic departure flight(D)international departure flight(I)terminal Tsatellite hall Sterminal Tsatellite hall Sdomestic departure flight(D)terminal T15/020/135/040/1satellite hall S20/115/040/135/0international departure flight(I)terminal T35/040/120/030/1satellite hall S40/145/230/120/0
在此问题中,以登机口的使用数量最少为优化目标,以登机口允许机型限制、登机口航班停靠最小间隔限制、每架飞机转场的到达、中转旅客流程时间最短和出发两个航班必须分配在同一登机口进行为约束条件.于是,建立目标函数和约束条件:
min Z=Xwi+Xni+Ywj+Ynj,
(5)
(6)
s.t.
A1Xwi+A2Xwi+A3Xni+B1Ywj+B2Ywj+B3Ynj≥304,
Xwi+Ywj≤23,
Xni+Ynj≤46,
A1Xwi+A2Xwi+B1Ywj+B2Ywj≥49,
A3Xni+B3Ynj≥254,
A1Xwi+A2Xwi≥91,
B1Ywj≥39,
Xwi≤10,
Xni≤18,
Ywj≤13,
Ynj≤28,
其中,i∈1,2,3,…,28; j∈1,2,3,…,41.由此可得A1,A2,A3,B1,B2,B3优先级如表5所示, 即为
表5 A1,A2,A3,B1,B2,B3优先级
Table 5 Priority of A1, A2, A3, B1, B2, B3
number of aircraftsA1A2A3B1B2B3piority of each type12/35/61/21/61/3
MATLAB算法求解流程如图5所示.
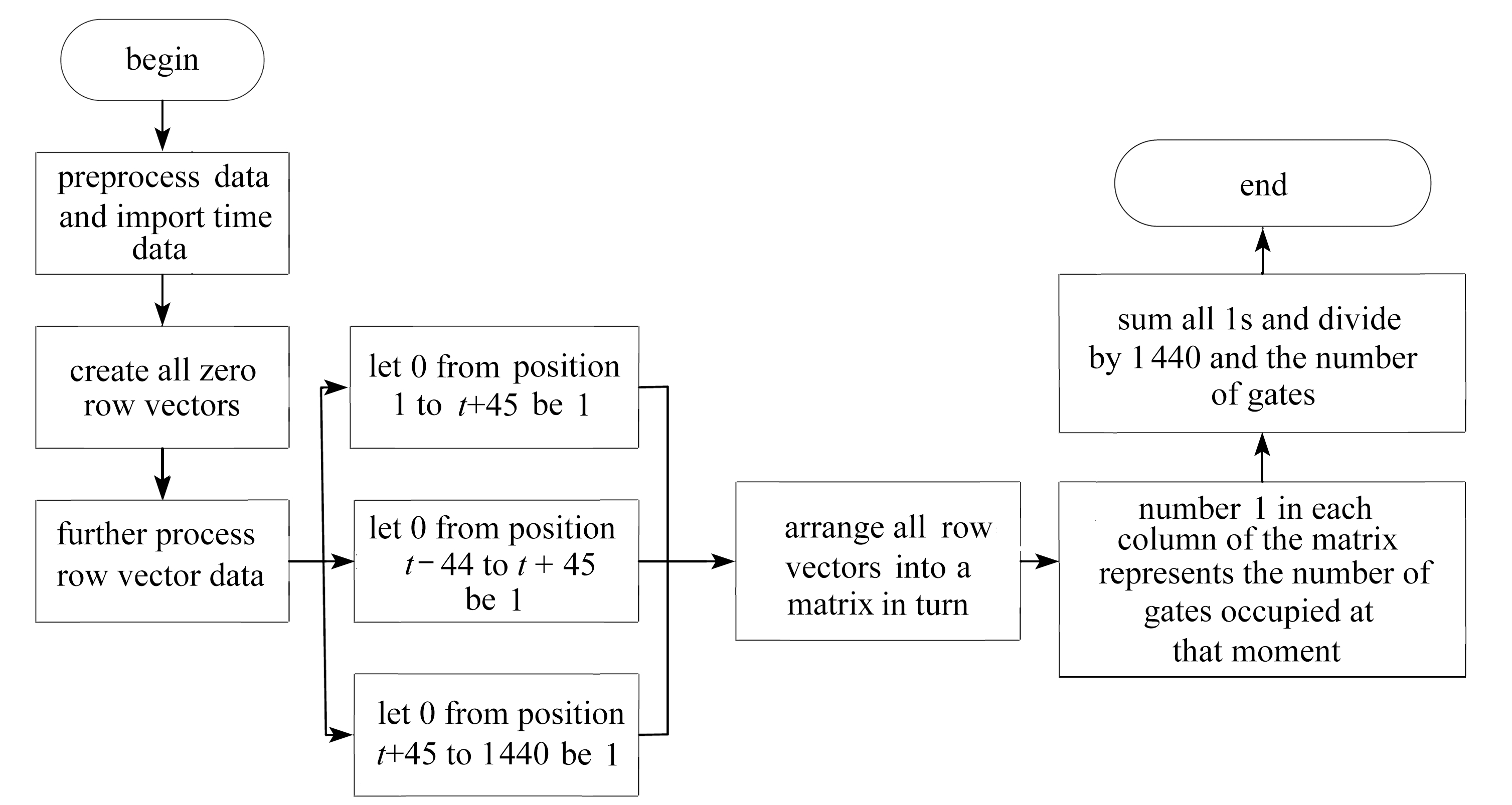
图5 问题(B)程序算法流程图
Fig. 5 The flow chart of the algorithm for problem(b)
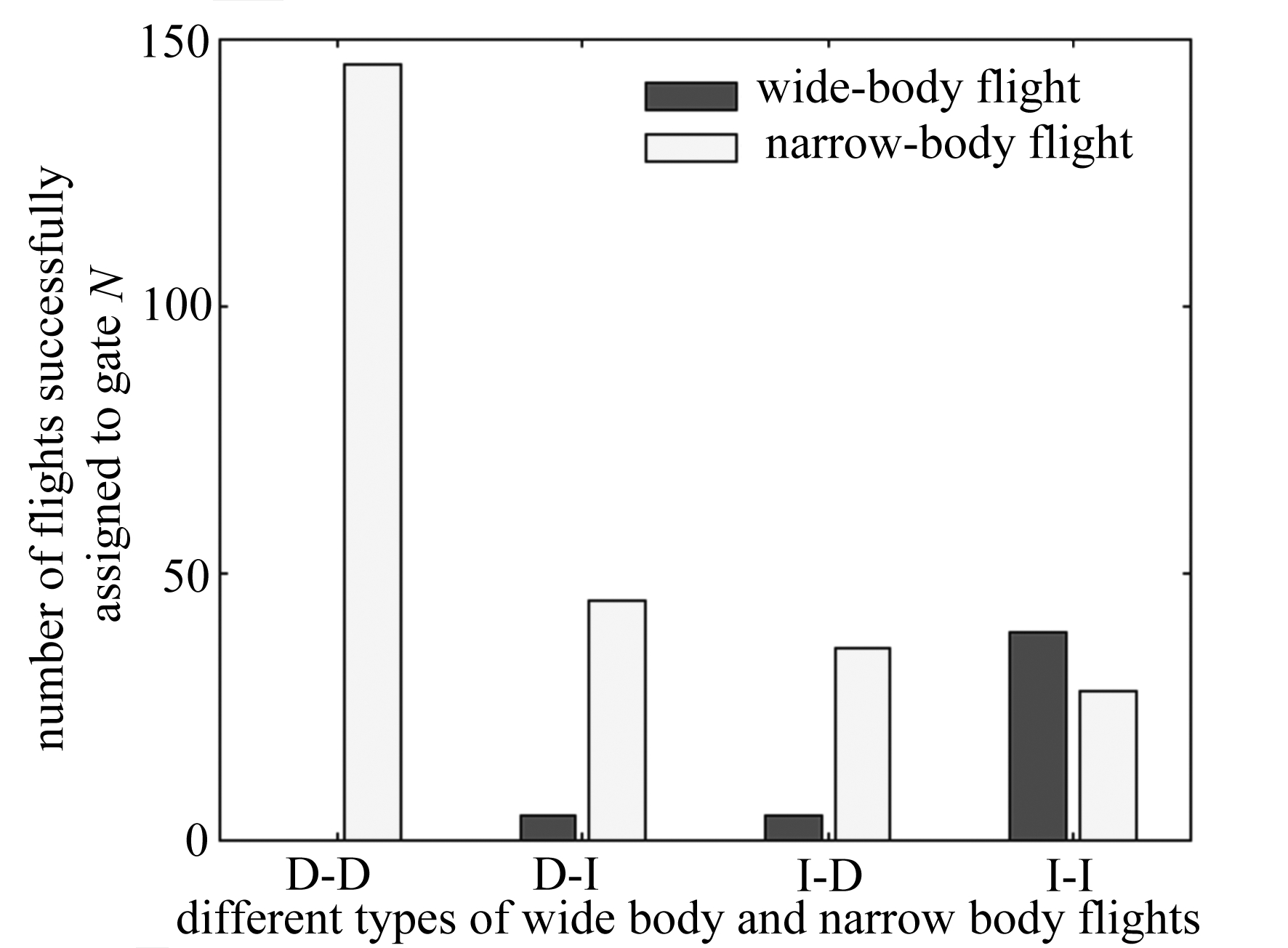
图6 成功分配到登机口的航班数量
Fig. 6 The number of flights successfully assigned to the gate
运行结果分析可知:20日到达或20日出发的航班中,成功分配到登机口的航班数量为303架,其中I-I的航班数量中宽体机为39架,窄体机为28架;I-D的航班数量中宽体机为5架,窄体机为36架;D-I的航班数量中宽体机为5架,窄体机为45架;国内到国内D-D的航班数量中窄体机为145架.图6为成功分配到登机口的航班数量.图7为成功分配到登机口的宽体机和窄体机的航班比例.
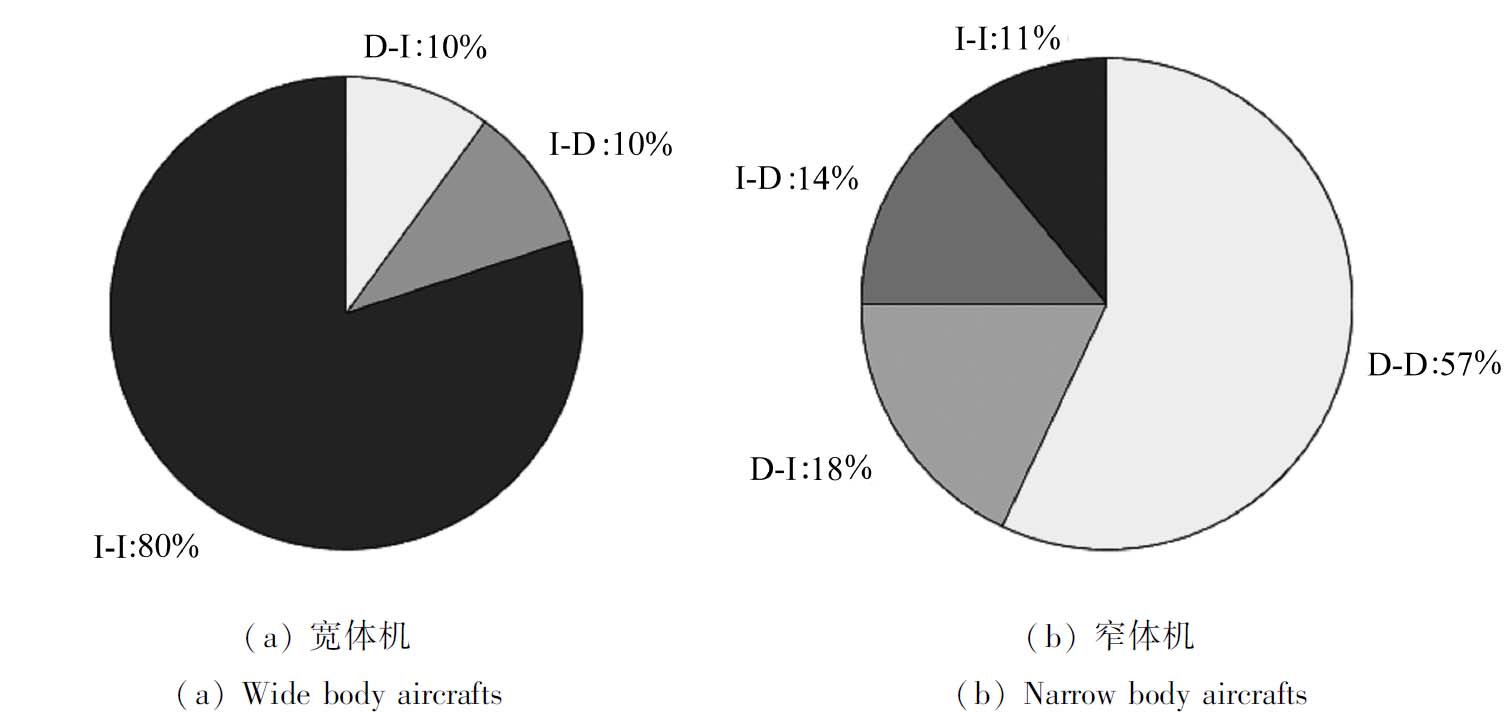
图7 成功分配到登机口的航班比例
Fig. 7 Proportions of flights successfully assigned to the gate
6 模型的评价与探讨
本文研究了机场新增航站楼对登机口分配的影响,构建了登机口优化分配网络模型和多目标优化模型.通过加权组合法或目标约束法对模型进行求解,依据2018年第十五届“华为杯”中国研究生数学建模竞赛F题提供的权威数据进行本模型验证,计算结果表明,该模型在新增航站楼的情况下,利用42个登机口即可实现303架航班正常运转.
本文从理论上计算了登机口分配的优化算法,减少了中转旅客最短流程时间,提高了现有登机口的效率,这对机场更合理、科学地制定登机口的分配具有重要的理论和实际意义.但仍存在航班延误、旅客上下飞机时间等实际情况影响,在下一步的研究中则应对这些理论和方法进行考虑.
致谢 本文作者衷心感谢陕西省光电测试与仪器技术重点实验室开放基金(2015SZSJ-60-3)对本文的资助.
[1] 王志清. 民航旅客运输便捷工程及其流程优化方法研究[D]. 博士学位论文. 南京: 南京航空航天大学, 2006.(WANG Zhiqing. Research on the convenient engineering of air transportation and its process optimization[D]. PhD Thesis. Nanjing: Nanjing University of Aeronautics and Astronautics, 2006.(in Chinese))
[2] LIU S, CHEN W H, LIU J Y. Robust assignment of airport gates with operational safety constraints[J]. International Journal of Automation and Computing, 2016, 13(1): 31-41.
[3] JO G S, JUNG J J, YANG C Y. Expert system for scheduling in an airline gate allocation[J]. Expert Systems With Applications, 1997, 13(4): 275-282.
[4] LAM S H, CAO J M, FAN H. Development of an intelligent agent for airport gate assignment[J]. Journal of Air Transportation, 2002, 7(2): 103-114.
[5] BABIC O, TEODOROVIC D, TOSIC V. Aricarft stand assignment to minimize walking[J]. Journal of Transportation Engineering, 1984, 110(3): 55-56.
[6] MANGOUBI R S, MATHAISEL DENNIS F X. Optimizing gate assignments at airport terminals[J]. Transportation Science, 1985, 19(2): 173-189.
[7] BOURAS A, GHALEB M A, SURYAHATMAJA U S, et al. The airport gate assignment problem: a survey[J]. The Scientific World Journal, 2014(1): 859-923.
[8] SU Y Y, SRIHARI K. A knowledge-based aircraft gate assignment advisor[J]. Computers and Industrial Engineering, 1993, 25(2): 123-126.
[9] BIHR R. A conceptual solution to the aircraft gate assignment problem using 0, 1 linear programming[J]. Computers and Industrial Engineering, 1990, 19(3): 280-284.
[10] 李耐毅. 机场登机口分配仿真及优化[D]. 硕士学位论文. 南京: 南京航空航天大学, 2013.(LI Naiyi. Airport gate assignment simulation and optimization[D]. Master Thesis. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013.(in Chinese))
[11] 王志清, 商红岩, 宁宣熙. 机场登机口优化调度算法及实证[J]. 南京航空航天大学学报, 2007, 39(6): 819-823.(WANG Zhiqing, SHANG Hongyan, NING Xuanxi. Assignment algorithm for airport gate and its application[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2007, 39(6): 819-823.(in Chinese))
[12] 郑志武, 刘军政, 刘文萍, 等. 天津机场登机口分配仿真与优化策略研究[J]. 现代商贸工业, 2017(6): 186-187.(ZHENG Zhiwu, LIU Junzheng, LIU Wenping, et al. Study on simulation and optimization strategy of boarding port assignment in tianjin airport[J]. Modern Business Trade Industry, 2017(6): 186-187.(in Chinese))
[13] 赵又群, 刘英杰, 李小龙. 基于滚动时域混合整数线性规划的汽车紧急避让问题求解方法[J]. 应用基础与工程科学学报, 2014, 22(5): 1010-1017.(ZHAO Youqun, LIU Yingjie, LI Xiaolong. Vehicle emergency collision avoidance based on receding horizon mixed and integer linear programming[J]. Journal of Basic Science and Engineering, 2014, 22(5): 1010-1017.(in Chinese))
[14] 陈国华. 整数线性规划投资组合模型的直接搜索算法求解[J]. 应用数学与计算数学学报, 2011, 25(1): 119-126.(CHEN Guohua. Direct search algorithm to integer linear programming portfolio selection model[J]. Communication on Applied Mathematics and Computation, 2011, 25(1): 119-126.(in Chinese))
[15] 徐永琳, 巫青山, 林川. 递归回溯法求解整数线性规划及MATLAB实现[J]. 兰州文理学院学报(自然科学版), 2014, 28(4): 1-5.(XU Yonglin, WU Qingshan, LIN Chuan. Recursive backtracking method to solve the integer linear programming and implementation of MATLAB[J]. Journal of Lanzhou University of Arts and Science (Natural Sciences), 2014, 28(4): 1-5.(in Chinese))
[16] ASCO A, ATKIN J A D, BURKE E K. An evolutionary algorithm for the over-constrained airport baggage sorting station assignment problem[J]. Lecture Notes in Computer Science, 2012, 7673: 32-41.
[17] ASCO A, ATKIN J A D, BURKE E K. An analysis of constructive al-gorithms for the airport baggage sorting station assignment problem[J]. Journal of Scheduling, 2014, 17(6): 601-619.
[18] 左海超, 蔡翔, 冯霞. 机场航班行李分拣站合理分配仿真研究[J]. 计算机仿真, 2018, 35(9): 52-58.(ZUO Haichao, CAI Xiang, FENG Xia. Simulation research on assignment of baggage sorting station for airport flights[J]. Computer Simulation, 2018, 35(9): 52-58.(in Chinese))
[19] 衡红军, 晏晓东, 王芳, 等. 基于多目标优化的机场行李运输车辆调度问题研究[J]. 计算机应用与软件, 2017, 34(2): 87-92.(HENG Hongjun, YAN Xiaodong, WANG Fang, et al. Research on scheduling of airport baggage transport vehicles based on multi-objective optimization[J]. Computer Applications and Software, 2017, 34(2): 87-92.(in Chinese))
[20] 秦易达. 基于模糊多目标优化的飞机排班问题研究[D]. 硕士学位论文. 天津: 中国民航大学, 2014.(QIN Yida. Fleet assignment problem research based on fuzzy multi-objective optimization[D]. Master Thesis. Tianjin: Civil Aviation University of China, 2014.(in Chinese))
[21] 卫东选. 基于运行安全的机场停机位分配问题研究[D]. 博士学位论文. 南京: 南京航空航天大学, 2010.(WEI Dongxuan. Study on airport gate assignment problem based-on operational safety[D]. PhD Thesis. Nanjing: Nanjing University of Aeronautics and Astronautics, 2010.(in Chinese))
[22] 刘文华. 资源有限下的机场近停机位综合调度问题及其算法研究[D]. 硕士学位论文. 北京: 清华大学, 2010.(LIU Wenhua. Analysis and algorithm study on multicriteria airport limited frontal stands assignment[D]. Master Thesis. Beijing: Tsinghua University, 2010.(in Chinese))
[23] 张宝亮. 基于多目标的乘务员排班问题的研究[D]. 硕士学位论文. 天津: 中国民航大学, 2010.(ZHANG Baoliang. The research on aircrew scheduling for multi-objective optimization[D]. Master Thesis. Tianjin: Civil Aviation University of China, 2010.(in Chinese))
[24] 吴鑫辉, 黄高明, 高俊. 一种不等式状态约束最优滤波算法[J]. 西安电子科技大学学报, 2013, 40(1): 148-154.(WU Xinhui, HUANG Gaoming, GAO Jun. Approach for optimal filtering of the nonlinear system with inequality constraints[J]. Journal of Xidian University(Natural Science), 2013, 40(1): 148-154.(in Chinese))