引 言
众所周知,凸性在优化问题、变分不等式等相关问题中扮演着重要的角色.然而,凸性是一个非常强的概念,实际上,许多优化问题不能满足凸性假设.因此,弱化凸性是十分必要的.Hanson[1]引入了不变凸集和不变凸函数,在此基础上,许多学者提出了不同的广义凸性并建立了最优性条件[2-8].在上述文献中,一些作者在Rn和线性空间中建立了最优性条件,怎样推广上述文献中的结果是有意义的.为了代替线性空间的凸性,Rapcs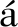 k[9]在Riemann流形上引入了测地凸性的概念,保证了光滑非线性优化问题的局部和全局性质.Pini[10] 在Riemann流形上引入了不变凸函数,Mititelu[11]对文献[10]中的结果进行了推广.Barani和Pouryayevali[12] 研究了Riemann流形上的测地不变凸集和测地预不变凸函数,从而推广了测地凸集和测地凸函数.为了进一步推广Riemann流形上的测地不变凸集和测地预不变凸函数的概念,Agarwal等[13] 引入了α-不变凸集和α-预不变凸函数,并证明了在适当条件下最优性问题全局极小解的存在条件.Chen等[14] 在Riemann流形上定义了一类B-预不变凸和B-不变凸函数,进一步研究了测地伪(拟)B-预不变函数和测地伪(拟)B-不变凸函数,并讨论了这些函数之间的关系.
k[9]在Riemann流形上引入了测地凸性的概念,保证了光滑非线性优化问题的局部和全局性质.Pini[10] 在Riemann流形上引入了不变凸函数,Mititelu[11]对文献[10]中的结果进行了推广.Barani和Pouryayevali[12] 研究了Riemann流形上的测地不变凸集和测地预不变凸函数,从而推广了测地凸集和测地凸函数.为了进一步推广Riemann流形上的测地不变凸集和测地预不变凸函数的概念,Agarwal等[13] 引入了α-不变凸集和α-预不变凸函数,并证明了在适当条件下最优性问题全局极小解的存在条件.Chen等[14] 在Riemann流形上定义了一类B-预不变凸和B-不变凸函数,进一步研究了测地伪(拟)B-预不变函数和测地伪(拟)B-不变凸函数,并讨论了这些函数之间的关系.
另一方面,向量变分不等式的解和向量优化问题的解之间存在着紧密联系.Mishra和Wang[15]建立了向量变分不等式与非光滑向量优化问题之间的关系.肖刚等[16]在Riemann流形上利用不变凸性和测地凸函数,讨论了向量变分不等式的解与向量优化问题的解之间的关系.陈胜兰和方长杰[17]在Riemann流形上,在不变凸性或不变单调性假设下建立了广义向量似变分不等式与非光滑向量优化问题的关系.
受上述文献的启发,本文在Riemann流形上研究了向量变分不等式及向量优化问题.首先,在Riemann流形上给出ρ-(η,d)-B不变凸函数、ρ-(η,d)-B伪不变凸函数和ρ-(η,d)-B拟不变凸函数的概念.其次,在这些广义凸性条件下研究了变分不等式的解和向量优化问题的解的关系.最后,建立向量优化问题的Kuhn-Tucker充分性条件.
1 预 备 知 识
本文中,以M来表示在TpM上定义了Riemann度量〈·,·〉p的m维Riemann流形,其中TpM表示M在点p∈M处的切空间.相应的范数定义为‖·‖p,TM=∪p∈MTpM是M的切丛,![]() 为TpM的对偶空间.M上的分段光滑曲线γ:[a,b]→M的长度定义为
为TpM的对偶空间.M上的分段光滑曲线γ:[a,b]→M的长度定义为
L(γ)![]()
![]() ‖γ′(t)‖γ(t)dt.
‖γ′(t)‖γ(t)dt.
(1)
M上任意两点p,q∈M之间的距离定义为
d(p,q)=inf{L(γ)|γ(a)=p,γ(b)=q}.
(2)
对任意M上的向量场X和Y, XY表示Levi-Civita联络.设γ为光滑曲线,若γ的切向量γ′沿γ是平行的,即
XY表示Levi-Civita联络.设γ为光滑曲线,若γ的切向量γ′沿γ是平行的,即 dγ(t)/dtdγ(t)/dt=0,称曲线γ为M上的测地线.在M上,若p和q是测地线γ上的任意两点,则L(γ) = d(p,q).设p∈M,v∈TpM,指数映射expp: TpM→M定义为
dγ(t)/dtdγ(t)/dt=0,称曲线γ为M上的测地线.在M上,若p和q是测地线γ上的任意两点,则L(γ) = d(p,q).设p∈M,v∈TpM,指数映射expp: TpM→M定义为
expp(v)=γ(1),
(3)
其中测地线γ:[0,1]→M满足γ(0)=p和γ′(0)=v.
定义1[18] 设M为Riemann流形,函数f:M→R在x∈dom f上满足局部Lipschitz条件,f在x∈dom f上以v∈TxM为方向的广义方向导数定义为
定义2[19] 设M为Riemann流形,函数f:M→R在x∈dom f上满足局部Lipschitz条件, f在x处的广义次梯度定义为
定义3[20] 设M为Riemann流形,K⊆M是测地凸集,称f:K→R为测地凸函数,如果∀x,y∈K,∀t∈[0,1],
f[expx(tv)]≤tf[expx(v)]+(1-t)f[expx(0)],
其中γ(t)![]() expx(tv),t∈[0,1]是满足expx(0)=x和expx(v)=y的唯一测地线.
expx(tv),t∈[0,1]是满足expx(0)=x和expx(v)=y的唯一测地线.
定义4[12] 设M为Riemann流形,K⊆M,函数η:K×K→TM满足η(y,x)∈TxM,∀x∈K,∀y∈K.称K为不变凸集,若对于任意两点x,y∈K有t∈[0,1],expx[tη(y,x)]∈K. 定义5 设M为Riemann流形,K⊆M, f:K→R是在x∈dom f上满足局部Lipschitz条件的可微函数,若存在η:K×K→TM,d:K×K→R+,b:M×M→R+和ρ∈R+:
 ∀x,y∈K,∀ζ∈∂f(x)满足
∀x,y∈K,∀ζ∈∂f(x)满足
f(y)-f(x)≥b(y,x)〈η(y,x),ζ〉+ρd2(y,x),
则称函数f在K上是ρ-(η,d)-B不变凸的.若不等式严格成立,则f在K上称为严格ρ-(η,d)-B不变凸函数.
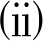 ∀x,y∈K,∃ζ∈∂f(x)满足
∀x,y∈K,∃ζ∈∂f(x)满足
b(y,x)〈η(y,x),ζ〉+ρd2(y,x)≥0 ⟹ f(y)≥f(x),
则称函数f在K上是ρ-(η,d)-B伪不变凸的.若不等式严格成立,则f在K上称为严格ρ-(η,d)-B伪不变凸函数.
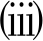 ∀x,y∈K,∃ζ∈∂f(x)满足
∀x,y∈K,∃ζ∈∂f(x)满足
f(y)≤f(x) ⟹ b(y,x)〈η(y,x),ζ〉+ρd2(y,x)≤0,
则称函数f在K上是ρ-(η,d)-B拟不变凸的.若不等式严格成立,则f在K上称为严格ρ-(η,d)-B拟不变凸函数.
注1 当ρ=0时,定义5退化为文献[14]中的定义8; 当ρ=0且b(y,x)=1时,定义5退化为文献[16]中的定义5.下面的例子被用作描述定义5中的ρ-(η,d)-B不变凸函数.
例1 设K⊆M,K={eiθ|0≤θ≤π/2},对任意的x=eiθ和y=eiφ,定义
f(x)=f(eiθ)![]() θ2,
θ2,
η(y,x)=η(eiφ,eiθ)![]() (φ-θ)ieiθ,
(φ-θ)ieiθ,
b(y,x)=b(eiφ,eiθ)![]()
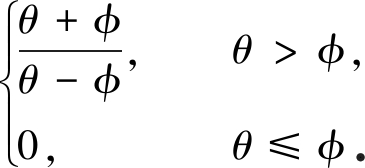
定义M上的测地线为
γx,y(t)![]() (cos((1-t)φ+tθ),sin((1-t)φ+tθ)),
(cos((1-t)φ+tθ),sin((1-t)φ+tθ)),
按照式(1)和(2)所定义K上点x和点y的距离函数d(y,x),取ρ=1/2.
当θ>φ时,有
f(y)-f(x)-b(y,x)〈η(y,x),ζ〉-ρd2(y,x)=
当θ≤φ时,有
f(y)-f(x)-b(y,x)〈η(y,x),ζ〉-ρd2(y,x)=
因此f是K上的ρ-(η,d)-B不变凸函数.
2 变分不等式与向量优化问题
文献[16]在Riemann流形上,利用测地凸函数和不变凸集的概念和性质,研究了变分不等式与向量优化问题解之间的关系.本节将研究变分不等式与向量优化问题近似解之间的关系.
设M为Riemann流形,K⊆M是关于η:K×K→TM的不变凸集,考虑如下向量优化问题:
向量函数f: K→Rm称为ρ-(η,d)-B(伪,拟)不变凸函数,若其每个分量都是ρ-(η,d)-B(伪,拟)不变凸函数.定义∂f![]() ∂f1×∂f2×…×∂fm,ζ=(ζ1,ζ2,…,ζm)∈∂f(x),ζi∈∂fi,i=1,2,…,m.〈η(y,x),ζ〉=(〈η(y,x),ζ1〉,〈 η(y,x),ζ2〉,…,〈η(y,x),ζm〉).ρ=(ρ1,ρ2,…,ρm)和ρi∈R+.定义指标集I={1,2,…,m},对任意x,y∈Rm:
∂f1×∂f2×…×∂fm,ζ=(ζ1,ζ2,…,ζm)∈∂f(x),ζi∈∂fi,i=1,2,…,m.〈η(y,x),ζ〉=(〈η(y,x),ζ1〉,〈 η(y,x),ζ2〉,…,〈η(y,x),ζm〉).ρ=(ρ1,ρ2,…,ρm)和ρi∈R+.定义指标集I={1,2,…,m},对任意x,y∈Rm:
 x=y ⟺ xi=yi, ∀i∈I;
x=y ⟺ xi=yi, ∀i∈I;
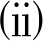 x>y ⟺ xi>yi, ∀i∈I;
x>y ⟺ xi>yi, ∀i∈I;
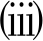 x≥y ⟺ xi≥yi, ∀i∈I且x≠y;
x≥y ⟺ xi≥yi, ∀i∈I且x≠y;
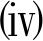 x≥y ⟺ xi≥yi, ∀i∈I.
x≥y ⟺ xi≥yi, ∀i∈I.
定义6 设![]() 是局部Lipschitz函数, ∀x∈K, ∀ζ∈∂f(x*),满足
是局部Lipschitz函数, ∀x∈K, ∀ζ∈∂f(x*),满足
 b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)≥0,则称x*∈K是向量似变分不等式(VVLI)的解;
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)≥0,则称x*∈K是向量似变分不等式(VVLI)的解;
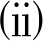 b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)>0,则称x*∈K是弱向量似变分不等式(WVVLI)的解;
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)>0,则称x*∈K是弱向量似变分不等式(WVVLI)的解;
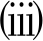 b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)+ε≥0,则称x*∈K是向量似变分不等式(AVVLI)的ε-近似解;
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)+ε≥0,则称x*∈K是向量似变分不等式(AVVLI)的ε-近似解;
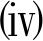 b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)+ε>0,则称x*∈K是弱向量似变分不等式(AWVLI)的ε-近似解.
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)+ε>0,则称x*∈K是弱向量似变分不等式(AWVLI)的ε-近似解.
定义7 设![]() 满足
满足
![]() 则称y为VOP的有效解;
则称y为VOP的有效解;
![]() 则称y为VOP的弱有效解;
则称y为VOP的弱有效解;
![]() 则称y为VOP的ε-有效解;
则称y为VOP的ε-有效解;
![]() 则称y为VOP的ε-弱有效解.
则称y为VOP的ε-弱有效解.
注2 ∀x∈K,若y是VOP的有效解,则y一定是VOP的ε-有效解.反之不成立,反例如下.
例2 设K⊆M,K={eiθ|0≤θ≤π/2}, f(x)=(f1(x), f2(x)),其中fi:K→R(i=1,2)定义如下:
f1(x)=f(eiθ)=sin θ+θ2, ∀θ∈[0,π/2],
f2(x)=f(eiθ)=-cos θ, ∀θ∈[0,π/2].
取φ=0,θ∈(0,π/2],则
f(eiθ)-f(ei·0)=(sin θ+θ2-sin φ-φ2,cos φ-cos θ)>0.
因此,ei·0为VOP的有效解.显然,ei·0也是VOP的ε-有效解.反之,令ε=(π/9,π/9),θ∈(0,π/2],则
f(eiθ)-f(ei(π/18))+ε=
因此,y=ei(π/18) 是VOP的ε-有效解.然而,y=ei(π/18)不是VOP的有效解.
定理1 设K⊆M, f: M→Rm是满足局部Lipschitz条件的严格ρ-(η,d)-B拟不变凸函数,若x*∈K是VVLI的解,则x*是VOP的有效解.
证明 假设x*不是VOP的有效解,则存在x∈K使得![]() 即
即
f(x)<f(x*).
(4)
由于f是严格ρ-(η,d)-B拟不变凸函数和式(4),则存在ζ∈∂f(x*)使得
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)<0,
与x*∈K是VVLI的解矛盾,从而x*是VOP的有效解.
□
定理2 设![]() 是满足局部Lipschitz条件的ρ-(η,d)-B 不变凸函数,若x*∈K是AWVLI的ε-近似解,则x*是VOP的ε-有效解.
是满足局部Lipschitz条件的ρ-(η,d)-B 不变凸函数,若x*∈K是AWVLI的ε-近似解,则x*是VOP的ε-有效解.
证明 假设x*不是VOP的ε-有效解,则存在x∈K使得
f(x)≤f(x*)-ε.
(5)
由于f是ρ-(η,d)-B不变凸函数和式(5),则
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)+ε≤0, ∀ζ∈∂f(x*),
与x*∈K是AWVLI的ε-近似解矛盾,从而x*是VOP的ε-有效解.
□
定理3 设![]() 是满足局部Lipschitz条件的严格ρ-(η,d)-B不变凸函数,若x*∈K是AVVLI的ε-近似解,则x*是VOP的ε-弱有效解.
是满足局部Lipschitz条件的严格ρ-(η,d)-B不变凸函数,若x*∈K是AVVLI的ε-近似解,则x*是VOP的ε-弱有效解.
证明 假设x*不是VOP的ε-弱有效解,则存在x∈K使得
f(x)<f(x*)-ε.
(6)
由于f是严格ρ-(η,d)-B不变凸函数和式(6),则
b(x,x*)〈η(x,x*),ζ〉+ρd2(x,x*)+ε<0,
与x*∈K是AVVLI的ε-近似解矛盾,从而x*是VOP的ε-弱有效解.
□
3 最优性条件
设M为Riemann流形,K⊆M是关于η:K×K→TM的不变凸集,考虑如下带不等式约束的优化问题:
其中f:K→R和gi:K→R(j∈J)都是K上的 ρ-(η,d)-B不变凸函数.假设优化问题P的解集非空,定义为S![]() {x∈D|f(x)≤f(y),∀y∈D}.∀z∈D,记J(z)={j∈J|gj(z)=0}. 定理4 对于问题P,设b(y,x)=c,其中c为非负常数,则可行集D和解集S都是关于η的不变凸集,其中η满足(1-λ)η(x,expx[λη(y,x)])=(-λ)η(y,expx[λη(y,x)]).
{x∈D|f(x)≤f(y),∀y∈D}.∀z∈D,记J(z)={j∈J|gj(z)=0}. 定理4 对于问题P,设b(y,x)=c,其中c为非负常数,则可行集D和解集S都是关于η的不变凸集,其中η满足(1-λ)η(x,expx[λη(y,x)])=(-λ)η(y,expx[λη(y,x)]).
证明 首先证明可行集D是关于η的不变凸集.设x,y∈D,则需证expx[λη(y,x)] D.假设expx[λη(y,x)]∉D,则存在j0∈J使得
gj0(expx[λη(y,x)])>0.
(7)
由式(7),有
gj0(expx[λη(y,x)])>gj0(x),
(8)
和
gj0(expx[λη(y,x)])>gj0(y).
(9)
由式(8)和(9),有
λ[gj0(x)-gj0(expx[λη(y,x)])]+
(1-λ)[gj0(y)-gj0(expx[λη(y,x)])]<0.
(10)
另一方面,因为gj(x)在K上是ρ-(η,d)-B不变凸函数,从而
gj0(x)-gj0(expx[λη(y,x)])≥
b(x,expx[λη(y,x)])〈η(x,expx[λη(y,x)]),ζ〉+
ρd2(x,expx[λη(y,x)]),
(11)
gj0(y)-gj0(expx[λη(y,x)])≥
b(y,expx[λη(y,x)])〈η(y,expx[λη(y,x)]),ζ〉+
ρd2(y,expx[λη(y,x)]).
(12)
由式(11)和(12),则有
λ[gj0(x)-gj0(expx[λη(y,x)])]+
(1-λ)[gj0(y)-gj0(expx[λη(y,x)])]≥
λρd2(x,expx[λη(y,x)])+(1-λ)ρd2(y,expx[λη(y,x)])≥0.
(13)
式(13)与式(10)矛盾,因此,D是关于η的不变凸集.
同理可证解集S是关于η的不变凸集.
□
定理5 对于问题P,假设f:K→R和gj:K→R(j∈J)在S上都是ρ-(η,d)-B不变凸函数.设z∈S,若存在![]() 使得
使得
(14)
μjgj(z)=0, ∀j∈J,
(15)
则z是问题P的最优解.
证明 假设z不是问题P的最优解,则存在x∈S使得
f(x)<f(z).
(16)
由于f在S上是ρ-(η,d)-B不变凸函数,则有
f(x)-f(z)≥b(x,z)〈η(x,z),ζ〉+ρd2(x,z), ∀ζ∈∂f(z).
(17)
另一方面,由式(14),存在![]() 使得
使得
(18)
由式(17)和(18)有
(19)
式(19)与式(16)矛盾,因此,z是问题P的最优解.
□
定理6 对于问题P,设z∈S,假设f:K→R和 gj:K→R(j∈J)在S上都是ρ-(η,d)-B不变凸函数.若存在![]() 使得
使得
(20)
μjgj(z)=0, ∀j∈J
(21)
成立,则![]() 且
且![]() 在S上是常数,其中
在S上是常数,其中![]()
![]() {j∈J(z)|μj>0}.
{j∈J(z)|μj>0}.
证明 由式(20),存在![]() 和
和![]() 使得
使得
(22)
另一方面,∀x∈S且z∈S,有f(x)=f(z),由f是ρ-(η,d)-B不变凸函数,则
0=f(x)-f(z)≥b(x,z)〈η(x,z),ζ〉+ρd2(x,z), ∀ζ∈∂f(z),
即
〈η(x,z),ζ〉≤0, ∀ζ∈∂f(z).
显然
(23)
由式(22)和(23),有
进一步有
(24)
又由gj(x)在S上是ρ-(η,d)-B不变凸函数,则
因此
(25)
由式(24)和(25),则
显然,![]() 因此,
因此,![]() 所以,
所以,![]() 在S上是常数.
在S上是常数.
□
4 结 论
本文主要对Riemann流形上的优化问题进行了研究.包括利用广义方向导数在Riemann流形上定义了ρ-(η,d)-B不变凸函数、ρ-(η,d)-B伪不变凸函数和ρ-(η,d)-B拟不变凸函数,给出了变分不等式的解与Riemann流形上向量优化问题解之间的关系,建立了优化问题的Kuhn-Tucker充分条件等.然而这方面的研究仍需要深入和拓广: 1) 在进一步讨论优化问题其解集的性质的基础上,如何在本文提出的广义凸性假设下,利用广义导数和次微分等非光滑分析工具对优化问题的解集进行等价刻画; 2) 如何在本文提出的广义凸性假设下,研究带不等式约束的向量优化问题的Mond-Weir对偶问题,并得到相应的结果.
致谢 本文作者衷心感谢重庆理工大学研究生创新项目(ycx20192083)对本文的资助.
[1] HANSON M A. On sufficiency of the Kuhn-Tucker conditions[J]. Journal of Mathematical Analysis and Applications, 1981, 80(2): 545-550.
[2] GULATI T R, ISLAM M A. Sufficiency and duality in multiobjective programming involving generalized F-convex functions[J]. Journal of Mathematical Analysis and Applications, 1994, 183(1): 181-195.
[3] CROUZEIX J P, LEGAZ J E M, VOLLE M. Generalized Convexity, Generalized Monotonicity: Recent Results[M]. Springer Science and Business Media, 2013.
[4] CAMBINI A, MARTEIN L. Generalized Convexity and Optimization: Theory and Applications[M]. Springer Science and Business Media, 2008.
[5] GUDDER S, SCHROECK F. Generalized convexity[J]. SIAM Journal on Mathematical Analysis, 2012, 11(6): 984-1001.
[6] 陈望, 周志昂. 基于改进集的带约束集值向量均衡问题的最优性条件[J]. 应用数学和力学, 2018, 39(10): 1189-1197.(CHEN Wang, ZHOU Zhiang. Optimality conditions for set-valued vector equilibrium problems with constraints involving improvement sets[J]. Applied Mathematics and Mechanics, 2018, 39(10): 1189-1197.(in Chinese))
[7] 黄应全. 关于向量值D-半预不变真拟凸映射的刻画[J]. 应用数学和力学, 2018, 39(3): 364-370.(HUANG Yingquan. Characterizations of D-properly semi-prequasi-invex mappings[J]. Applied Mathematics and Mechanics, 2018, 39(3): 364-370.(in Chinese))
[8] 杨玉红, 李飞. 非光滑半无限多目标优化问题的最优性充分条件[J]. 应用数学和力学, 2017, 38(5): 526-538.(YANG Yuhong, LI Fei. Sufficient optimality conditions for nonsmooth semi-infinite multiobjective optimization problems[J]. Applied Mathematics and Mechanics, 2017, 38(5): 526-538.(in Chinese))
[9] RAPCS K T. Smooth Nonlinear Optimization in Rn[M]. USA: Springer, 1997.
K T. Smooth Nonlinear Optimization in Rn[M]. USA: Springer, 1997.
[10] PINI R. Convexity along curves and indunvexity[J]. Optimization, 1994, 29(4): 301-309.
[11] MITITELU S. Generalized invexity and vector optimization on differentiable manifolds[J]. Differential Geometry: Dynamical Systems, 2001, 3(1): 21-31.
[12] BARANI A, POURYAYEVALI M R. Invex sets and preinvex functions on Riemannian manifolds[J]. Journal of Mathematical Analysis and Applications, 2007, 328(2): 767-779.
[13] AGARWAL R P, AHMAD I, IQBAL A, et al. Generalized invex sets and preinvex functions on Riemannian manifolds[J]. Taiwanese Journal of Mathematics, 2012, 16(5): 1719-1732.
[14] CHEN S L, HUANG N J, O’REGAN D. Geodesic B-preinvex functions and multiobjective optimization problems on Riemannian manifolds[J]. Journal of Applied Mathematics, 2014, 2014: 1-12.
[15] MISHRA S K, WANG S Y. Vector variational-like inequalities and non-smooth vector optimization problems[J]. Nonlinear Analysis: Theory, Methods & Applications, 2006, 64(9): 1939-1945.
[16] 肖刚, 肖红, 刘三阳. 黎曼流形上的向量似变分不等式与向量优化问题[J]. 安徽大学学报(自然科学版), 2009, 33(3): 5-8.(XIAO Gang, XIAO Hong, LIU Sanyang. Vector variational-like inequalities and vector optimization problems on Riemannian manifolds[J]. Journal of Anhui University(Natural Science Edition), 2009, 33(3): 5-8.(in Chinese))
[17] 陈胜兰, 方长杰. 黎曼流形上的广义向量似变分不等式和向量优化问题[J]. 四川师范大学学报(自然科学版), 2016, 39(3): 332-336.(CHEN Shenglan, FANG Changjie. Generalized vector variational-like inequality and vector optimization problem on Riemannian manifolds[J]. Journal of Sichuan Normal University(Natural Science), 2016, 39(3): 332-336.(in Chinese))
[18] LI C, MORDUKHOVICH B S, WANG J H, et al. Weak sharp minima on Riemannian manifolds[J]. SIAM Journal on Optimization, 2011, 21(4): 1523-1560.
[19] 肖刚, 刘三阳. 黎曼流形上非可微多目标规划的必要最优性条件[J]. 吉林大学学报(理学版), 2008, 46(2): 209-213.(XIAO Gang, LIU Sanyang. Necessary optimality conditions of nondifferentiable-multiobjective programming on Riemannian manifolds[J]. Journal of Jilin University(Science Edition), 2008, 46(2): 209-213.(in Chinese))
[20] AZAGRA D, FERRERA J, LOPEZMESAS F. Nonsmooth analysis and Hamilton-Jacobi equations on Riemannian manifolds[J]. Journal of Functional Analysis, 2003, 220(2): 304-361.