引 言
水中悬浮隧道(submerged floating tunnel,SFT)是利用支撑系统的作用来平衡结构重力与浮力的差值,悬浮于水下一定深度的全封闭新型交通结构形式[1-2].由于悬浮隧道自身具备的经济、环保、受外界环境干扰小等优点,使其拥有非常广泛的应用前景.
为推动悬浮隧道工程的实践应用,国内外学者对其在不同荷载(波浪、地震、冲击、爆炸等)情况下的动力响应进行了广泛的研究.在波浪荷载方面:Hiroshi[3]研究了悬浮隧道在海水波浪荷载作用下不同锚固形式的性能;麦继婷等[4]分析了作用在悬浮隧道上的波浪荷载随波浪入射角、隧道放置深度和表面流速的变化情况;Remseth等[5]通过建立流固耦合有限元模型,研究了流固相互作用下悬浮隧道的随机动力响应.在研究进程中,将悬浮隧道简化为梁模型已成为一种公认的研究方法.在地震荷载方面:Martinelli 等[6]以拟建的千岛湖悬浮隧道设计方案为模型,提出了一种基于中值伪加速度谱来获取响应谱的新方法,编程实现了悬浮隧道非线性地震响应时程分析;Fogazzi等[7]采用有限元软件建立悬浮隧道模型,进行了地震激励下的动力响应分析;Chen等[8]基于有限元软件采用大质量法计算了悬浮隧道地震动力响应.在冲击荷载方面:葛斐等[9]采用等效质量法研究了悬浮隧道在冲击荷载作用下的动力响应,并通过有限元分析模型进行了验证;项贻强等[10]基于Hamilton原理建立了悬浮隧道在冲击荷载作用下的振动方程,探讨了锚索刚度、倾角、动水阻尼和结构浮重比对管体冲击响应的影响;Luo等[11]基于SPH-FEM耦合法建立了潜艇撞击悬浮隧道的模型,研究了碰撞过程中的能量转化、撞击力和隧道内人体的损伤情况.
近些年来,关于水下爆炸荷载作用下悬浮隧道的动力响应问题日益得到学者们的关注.在此方面,王刚等[12]采用Fourier级数对位移和作用力进行展开的方法分析了圆柱壳的弹塑性行为,得到了水下圆柱壳在爆炸冲击载荷下动力响应的规律;罗刚等[13]利用有限元软件建立了悬浮隧道在近场非接触爆炸荷载作用的计算模型,分析了锚索支撑体系、炸药量和爆心距离对悬浮隧道结构动力响应的影响;Hong等[14]以韩国Honam-Jeju连岛工程悬浮隧道方案为依托,利用有限元软件研究了潜艇爆炸荷载作用下悬浮隧道(简化为连续弹性支承梁)的动力响应.尽管这些研究揭示了悬浮隧道在水下爆炸荷载下的部分动力响应规律,但是关于悬浮隧道在爆炸荷载下动力响应的研究仍然较少,且多集中在有限元数值模拟方面.因此,本文针对爆炸荷载作用下的悬浮隧道,采用理论推导的方式分析其响应规律.
1 计 算 假 定
悬浮隧道结构一般由悬浮在水下一定深度的管体结构、水下基础、支撑系统、管段连接装置、驳岸接头等组成,如图1、2所示.
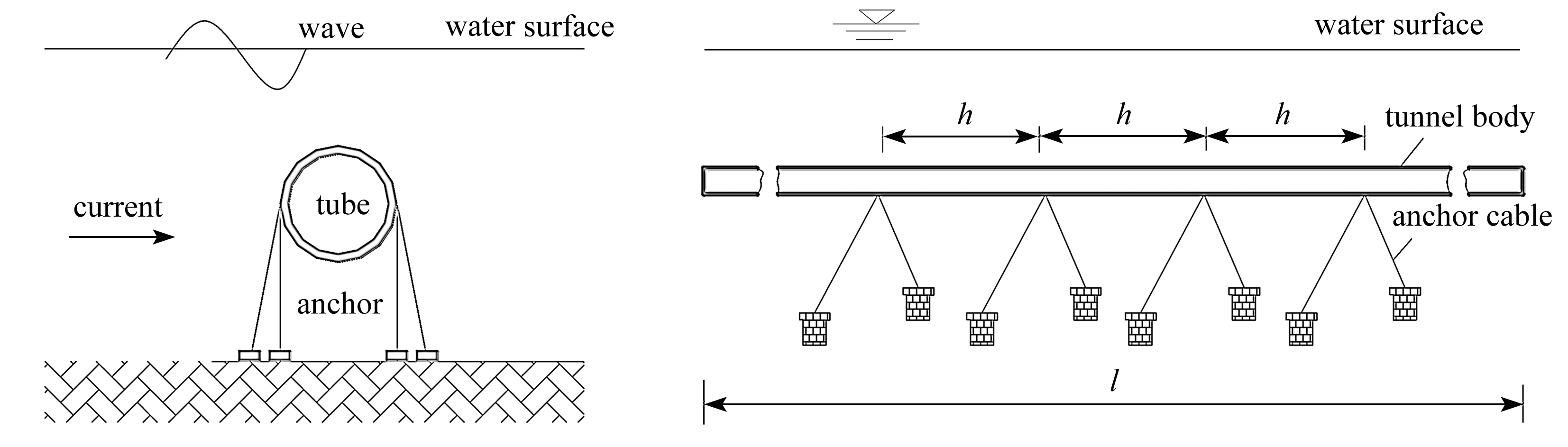
图1 悬浮隧道模型横向示意图 图2 悬浮隧道模型纵向示意图
Fig.1 Schematic cross-section diagram Fig.2 Schematic longitudinal diagram of the SFT model of the SFT model
根据Saint-Venant原理[15],当连续梁的长度大于静力反应的临界长度时,超过临界长度之外的荷载对结构的影响可忽略不计.因此,本文选取锚索支撑式悬浮隧道的一段,将锚索简化为弹簧,悬浮隧道简化为弹性支承梁[16],探究其在爆炸荷载下的动力响应,具体如图3所示.并作出如下假定: 1) 计算爆炸荷载作用时,只考虑冲击波的作用; 2) 忽略爆炸过程中的能量损失,只考虑动能与势能的转化; 3) 悬浮隧道管体为等截面、等刚度的Bernoulli-Euler梁.
2 运动微分方程
2.1 荷载建立
根据美国水面武器中心(NSWC)在综合大量水下爆炸实验数据而提出的公式,计算水下爆炸冲击波[17]:
pm=K0(W1/3/R)α,
(1)
式中,pm为水中冲击波超压峰值(MPa);W为TNT当量(kg);R为爆心距(m);K0和α为TNT炸药水中爆炸的相似常数和系数,分别取52.4,1.13.
冲击波荷载的特征是在极短的时间内上升到峰值随后迅速衰减到0,然后有数值很小的负相压力,这种冲击荷载一般可以采用线性规律进行简化表示[18]:
(2)
式中,pm同式(1);θ为水中冲击波正相压力的持续时间;p(t)为水中冲击波压力时程函数.
根据式(1),水下某点的冲击波超压值与其距爆心的距离R有关.如图3,为了便于后续推导,本文通过计算梁端两点(a,c)和跨中一点(b)的荷载峰值对其空间分布进行简化,得到梁的水下爆炸荷载公式:
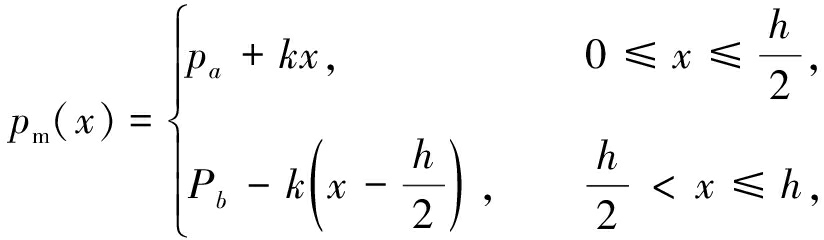
(3)
(4)
式中,pa,pb为由式(1)计算出的a,b两点冲击波超压峰值,k=2(pb-pa)/h,h为梁的全长.
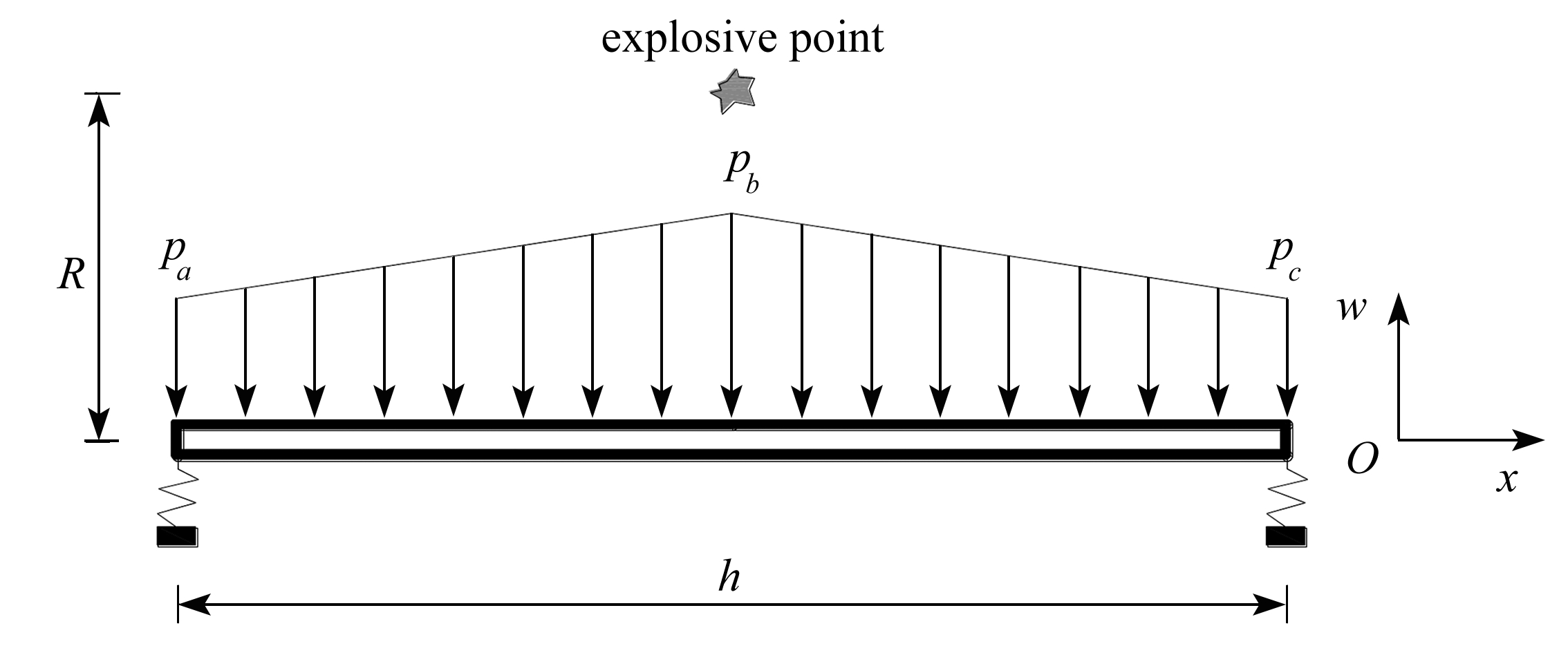
图3 爆炸荷载及隧道模型简化示意图
Fig.3 Schematic diagram of the simplified blast load and the tunnel model
考虑锚索对悬浮隧道管体的张力,将锚索简化为支撑弹簧,弹簧的竖向刚度为K,等效锚索竖向刚度为κ=K/h,h为锚索的间距,则单位长度悬浮隧道所受到的张力为κw,w为梁的竖向位移.
悬浮隧道在爆炸荷载作用下产生剧烈的振动,必然带动周围水体共同运动从而反作用于管体,因此需要考虑因管体运动引起的流体作用.如果流体在某一点处的速度和加速度已知,则可以通过Morison方程即式(5)计算出流体的作用力,其中方程的第一项是流体作用引起的拖拽力,第二项是流体作用引起的惯性力.
(5)
式中,ρ为流体密度,D为管体外径,CD为拖拽力系数,Cm为附加质量系数,CD和Cm的取值与水中结构物的形状有关,在此取CD=0.7,Cm=1.0[19].
式(5)中的第一项带有绝对值符号,为了后续计算方便又可以写为式(6)的形式[20]:
(6)
式中,γ为失速参数,Ω0为角频率.在静止的流体中Ω0为结构振动的角频率,γ为结构振动幅值的函数,与结构的平均截面拖拽力系数CD有关.悬浮隧道周围的流体作用可以看作是二维的绕流,对于二维绕流的情况,Ω0为漩涡脱落的角频率,Ω0=2πSrU/D,Sr为Strouhal数,是表征流体绕流特征的一个参数,U为流体的平均速度,γ是常数,Sr和γ分别取0.2,0.8[21].
2.2 微分方程的建立与求解
对于图3水中爆炸荷载作用下的弹性支撑梁,考虑上述荷载后,根据d’Alembert原理可得悬浮隧道的运动微分方程为
(7)
式中,EI为梁截面的抗弯刚度;cs为悬浮隧道的黏滞阻尼系数;cf为流体的附加阻尼,![]() 为管体的平均位移;ms为梁截面单位长度的质量;mf为流体的附加质量,mf=cmπD2ρ/4.假定此处的阻尼为Rayleigh阻尼,具有振型的正交性,为了便于公式的简化,在下列公式推导中令m=ms+mf,c=cs+cf.
为管体的平均位移;ms为梁截面单位长度的质量;mf为流体的附加质量,mf=cmπD2ρ/4.假定此处的阻尼为Rayleigh阻尼,具有振型的正交性,为了便于公式的简化,在下列公式推导中令m=ms+mf,c=cs+cf.
对于式(7)可采用Galerkin法进行求解,得到的解可表示为
(8)
式中,梁的振型函数φn(x)=sin(nπx)/h,qn(t)为广义坐标函数.将式(8)代入式(7)并对方程的两边同乘以φm(x),然后对隧道的全长h进行积分,根据振型的正交性化简整理,可得
(9)
式中
为爆炸荷载函数pm(x)积分化简后的结果.
根据简化后的悬浮隧道物理模型,可确定该方程的初始条件:
(10)
由式(9)和(10)可得广义坐标q(t):
qn(t)=e-At/2[F1cos(Ωt)+F2sin(Ωt)]+F3+F4t,
(11)
式中
当t>θ后,爆炸冲击作用结束,悬浮隧道做自由振动,其位移函数为w*(x,t),初始条件为
(12)
根据式(11)和(12)解得q*(t)为
(13)
式中
3 SFT爆炸动力响应参数分析
悬浮隧道受到水下爆炸冲击波的作用而发生剧烈的振动,影响振动的主要因素有爆心距、炸药量以及锚索的刚度,因此本文将对以上3个主要因素进行讨论.
3.1 模型取值
由于悬浮隧道尚处于研究阶段,无建成实例,本文参考国内外待建悬浮隧道的设计参数进行分析,相关指标如表1.
表1 SFT的设计参数
Table 1 The design parameters of SFT

parametertunnel lengthl/manchor cable spaceh/manchor cable stiffnessK/(N/m)modulus of elasticityE/Patunnel outer diameterD/mtunnel inner diameterd/mmass per unit lengthms/(kg/m)value1 0002005×1053.2×101012.6010.00124.69
水下爆炸荷载的持续时间极短(10-2~10-3 s)[24],往往很短的时间内就能达到峰值,考虑海水的阻尼取爆炸荷载,正向持续时间为θ=0.08 s.
3.2 高阶振型的影响分析
很多学者在研究悬浮隧道的动力响应时,只考虑了一阶振型[25-26],这是因为一阶振型在结构振动中起主要作用而高阶振型能量占比太低对整个结构振动影响不大.据此,本文将取前三阶振型进行讨论,以验证在爆炸荷载作用下,只考虑一阶振型的合理性.
根据上文推导的公式,计算出悬浮隧道前3阶振型在强迫振动阶段和自由振动阶段管体最不利位置处的位移得到图4、5.如图4,在受到爆炸荷载后的瞬间,3种振型产生的位移都急剧增加,t=0.08 s时达到了该阶段峰值,1,2,3阶振型的位移分别为0.178 9,0.081 1,0.135 0 m,总体而言该阶段位移值较小.
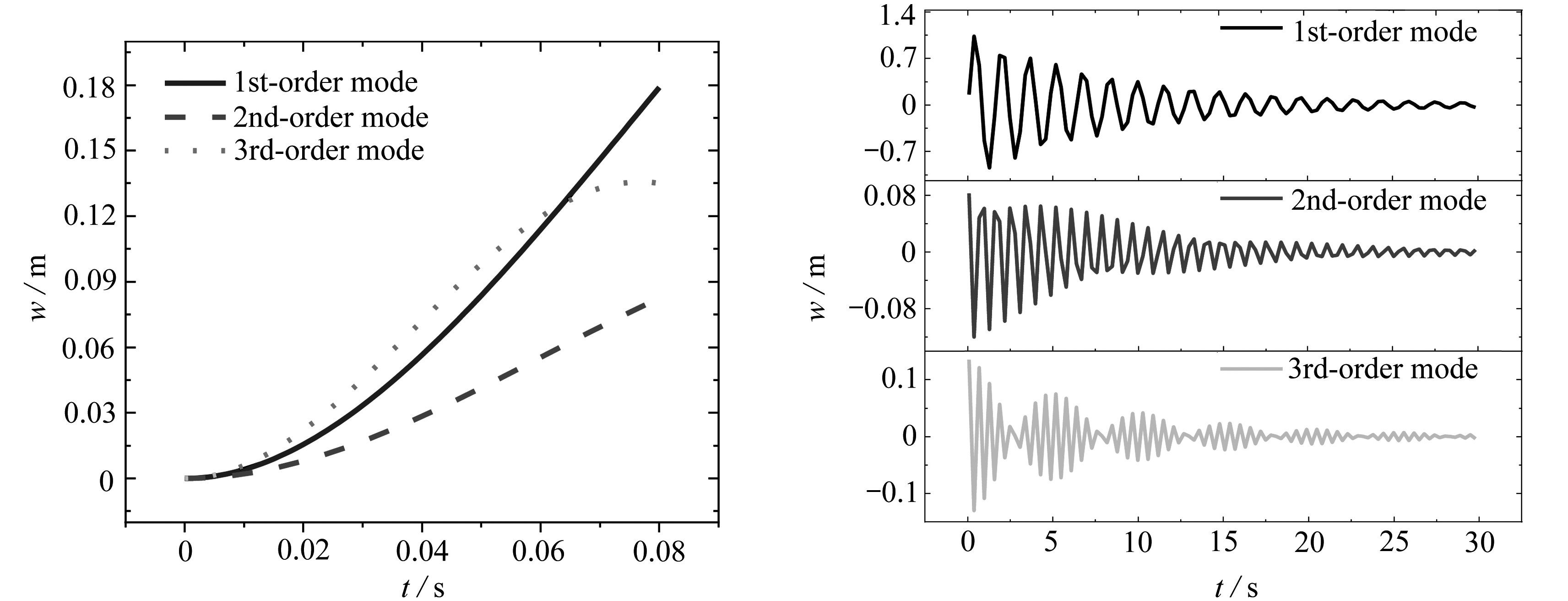
图4 不同振型下SFT强迫振动位移时程曲线 图5 不同振型下SFT自由振动位移时程曲线
Fig.4 The forced vibration displacement time histories Fig.5 The free vibration displacement time histories
of SFT under different modes of SFT under different modes
如图5,当作用时间t>0.08 s时,进入自由振动阶段,在该阶段管体出现最大位移,1,2,3阶振型的最大位移分别为1.036 2,0.119 2,0.135 0 m,对3种振型的峰值位移进行叠加,计算出各自所占总体的比例分别为80.3%,9.2%和10.5%.由此可知一阶振型在悬浮隧道振动过程中起主要作用,只取一阶振型进行讨论是合理的,因此在下文中将针对悬浮隧道的一阶振型动力响应进行讨论.
3.3 爆心距对运动学参数影响分析
为了研究爆心距对悬浮隧道爆炸冲击动力响应的影响规律,选取炸药量为20 kg,爆心距为10,20,30 m的3种工况,分析爆心距对结构动力响应的影响,取受冲击损伤最严重的情况——隧道跨中位移进行分析.计算所得的管体位移、速度、加速度如图6~9所示.
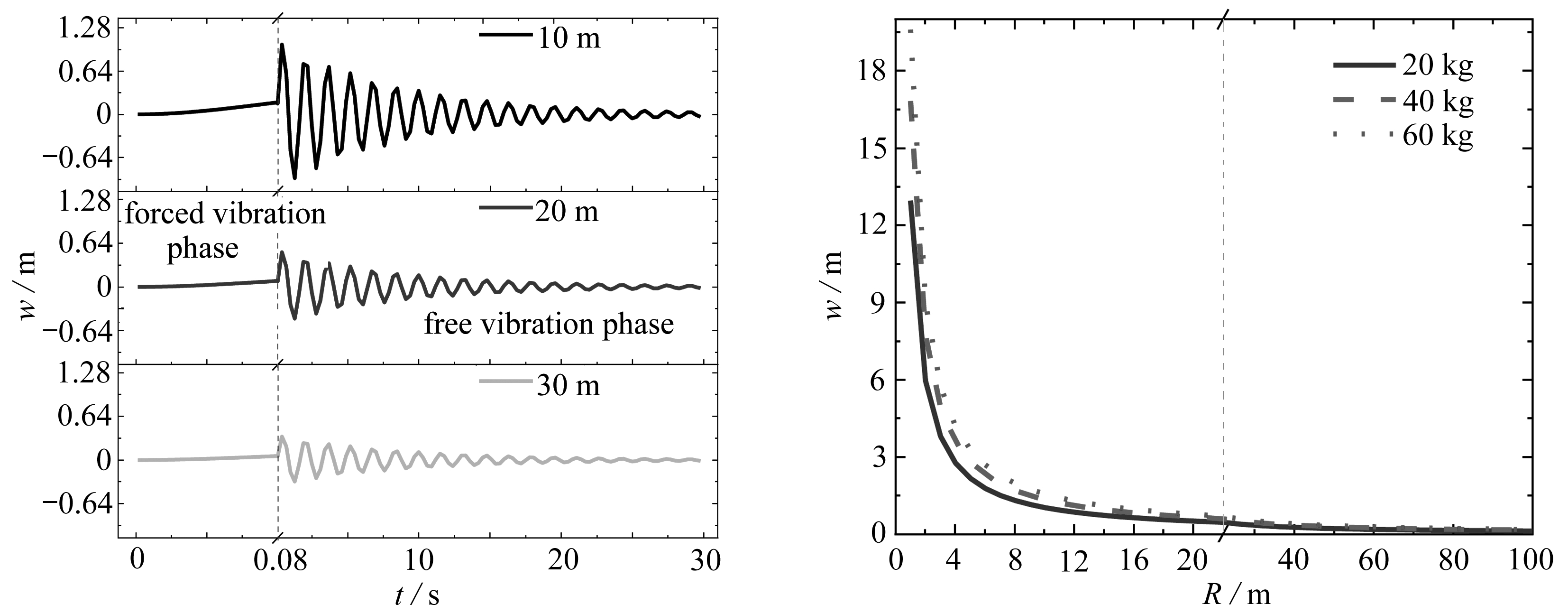
图6 不同爆心距下SFT的位移时程曲线 图7 不同炸药量下SFT峰值位移与爆心距的关系曲线
Fig.6 The displacement time histories of SFT Fig.7 The maximum displacement-blasting distance
under different blasting distances curves under different explosive quantities
如图6,当t=0.08 s时,冲击波达到最大值,由于水和结构的阻尼导致结构响应具有滞后性,此时结构不能及时响应;当t=0.38 s时,结构跨中位移达到最大值,10,20,30 m爆心距所对应的跨中最大位移分别为1.036 2,0.510 3,0.346 2 m,相比10 m工况,20 m和30 m工况跨中最大位移分别下降了50.7%和66.6%.继续计算可以得到爆心距与最大位移之间的关系如图7所示,从图中可知随爆心距的增加,隧道最大位移近似呈反比例下降趋势.
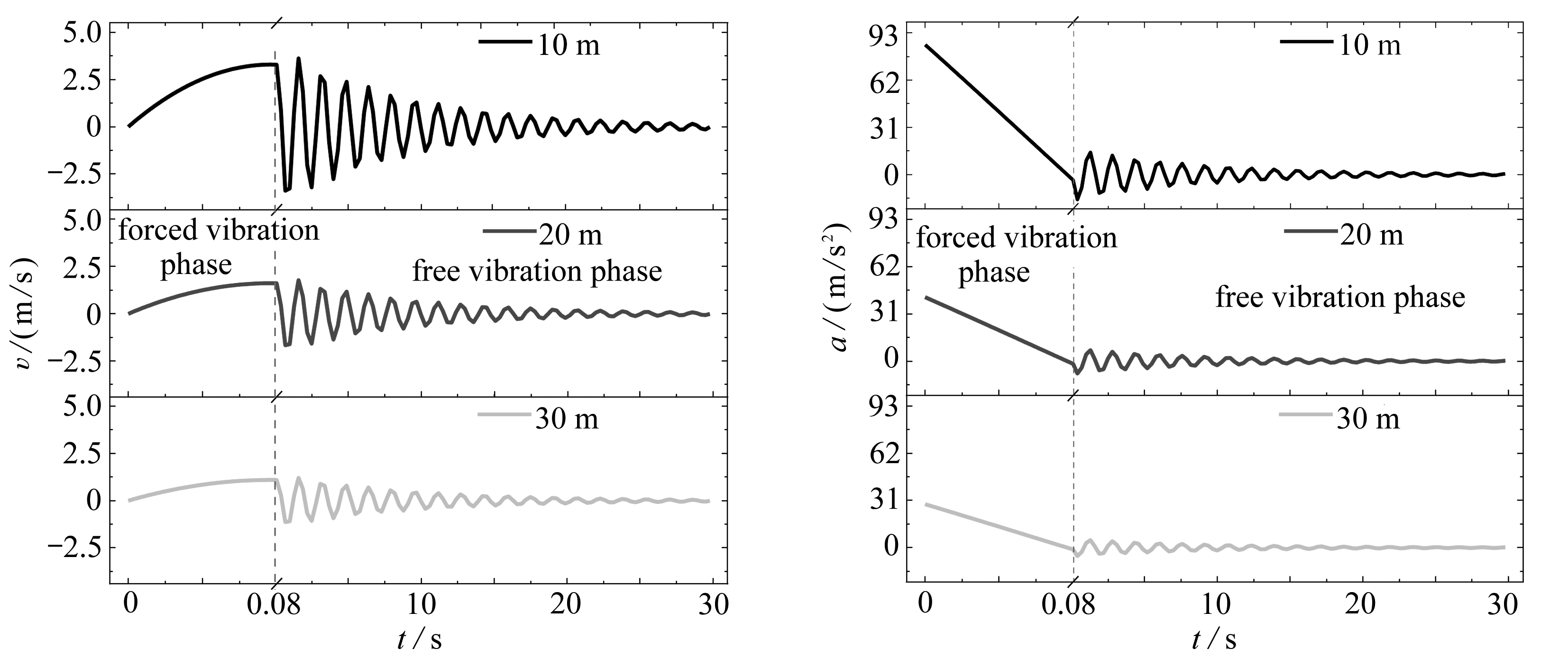
图8 不同爆心距下SFT自由振动速度时程曲线 图9 不同爆心距下SFT自由振动加速度时程曲线
Fig.8 The velocity time histories of SFT Fig.9 The acceleration time histories of SFT
under different blasting distances under different blasting distances
如图8,速度时程曲线与位移时程曲线相似,10,20,30 m爆心距对应的跨中最大速度分别为3.620 8,1.783 6,1.209 7 m/s,远超过规范《爆破安全规程》(GB6722—2014)中一般混凝土结构10~20 cm/s的限值,与文献[13]中通过数值模拟的结论基本一致.如图9,加速度最大值出现在爆炸瞬间,10,20,30 m爆心距对应的峰值加速度分别为85.288 9,41.464 9,28.494 0 m/s2.在悬浮隧道运营期间内部会有过往的行人和车辆,爆炸冲击振动对人体健康损伤的评价方法常采用容许加速度法,由参考文献[27]可知坐姿有约束的情况下允许的垂直和水平加速度为150 m/s2,可以判断本次3种工况是相对安全的.
3.4 炸药量对运动学参数影响分析
为研究炸药量对管体动力响应的影响规律,分别选取爆心距为10 m,炸药量为20,40,60 kg的3种工况,分析炸药量对结构动力响应的影响.计算所得的管体位移、速度、加速度如图10~13所示.
如图10所示,3种炸药量下悬浮隧道的峰值位移同样出现在自由振动阶段,在t=0.38 s出现峰值,20,40,60 kg这3种工况对应的结构跨中最大位移分别为1.036 3,1.345 4,1.567 5 m,与20 kg相比,40 kg和60 kg的峰值位移分别增加了29.8%,51.3%.可以发现随着炸药量的增加,最大位移的增量逐渐减小,这表明随着炸药量的增加爆炸冲击波在水中传播能量损失也随之增加.继续计算可以得到不同爆心距下炸药量与隧道最大位移的关系曲线,如图11,从图中可知随着炸药量的增加,隧道最大位移近似呈低阶幂函数上升趋势.
如图12所示,3种工况下的跨中速度峰值分别为3.620 8,4.701 1,5.476 8 m/s,这已远远超出《爆破安全规程》中的限值,与20 kg的工况相比,40 kg和60 kg的炸药量引起的跨中速度峰值分别增加了1.080 3 m/s和1.856 0 m/s.如图13所示,20,40,60 kg这3种工况下的跨中加速度峰值分别为85.288 9,110.733 7,129.005 3 m/s2,与20 kg炸药量相比,40 kg和60 kg的峰值加速度分别增加了25.444 8 m/s2和43.716 4 m/s2.继续计算可以得到在当炸药量为89.55 kg时,管体的最大加速度就达到了150 m/s2的限值.
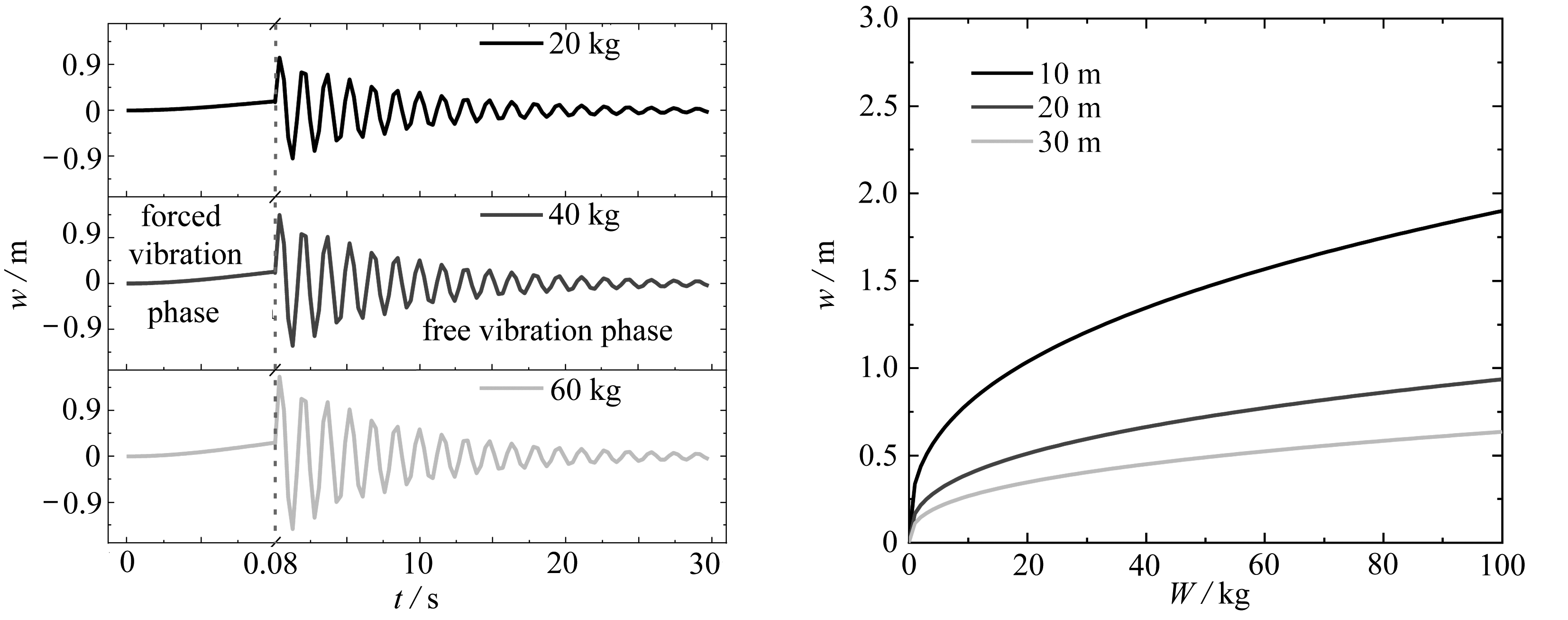
图10 不同炸药量下SFT位移时程曲线 图11 不同爆心距下SFT最大位移与炸药量关系曲线
Fig.10 The displacement time histories of SFT Fig.11 The maximum displacement-explosive
under different explosive quantities quantity curves of SFT under different
blasting distance
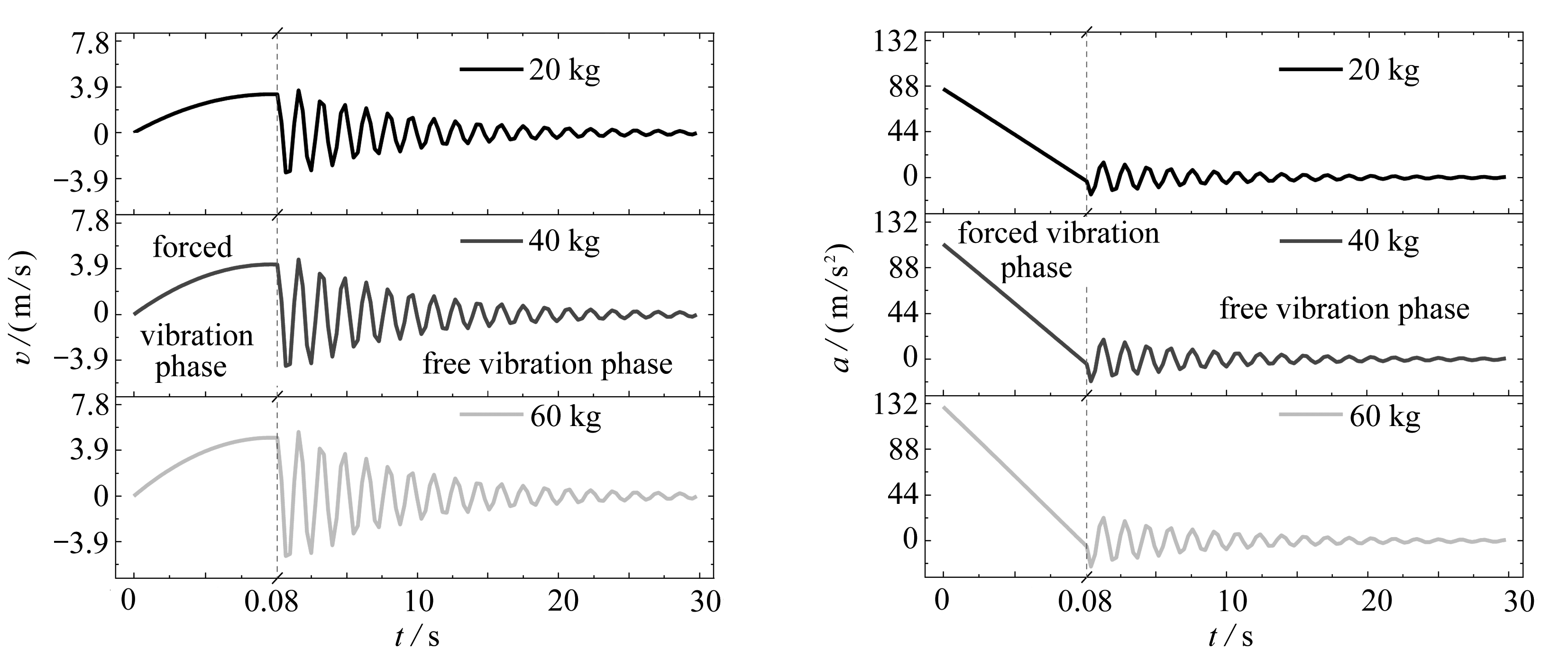
图12 不同炸药量下SFT速度时程曲线 图13 不同炸药量下SFT加速度时程曲线
Fig.12 The velocity time histories of SFT Fig.13 The acceleration time histories of SFT
under different explosive quantities under different explosive quantities
3.5 锚索竖向刚度对管体位移的影响分析
当锚索的直径为122 mm时,锚索竖向刚度的取值约为5×105 N/m,通过改变锚索的直径和钢材可以使锚索的刚度增大.为了分析锚索刚度对悬浮隧道的动力响应影响规律选择不同的锚索竖向刚度进行计算,得到的结果如图14~17所示.
如图14,在强迫振动阶段不同锚索刚度对管体的位移影响不大,在自由振动阶段不同锚索刚度明显地改变了位移振动曲线的两个参数——振幅和频率.3种锚索刚度对应的自由振动阶段的最大位移分别为1.040 9,0.489 6,0.143 2 m,相对于5×105 N/m的锚索刚度,5×106 N/m和5×107 N/m的位移分别下降了53.0%和86.2%,由此可见锚索能够显著地抑制悬浮隧道的振动.图15中计算了爆炸荷载固定时锚索刚度与最大位移的关系,从中可以发现锚索刚度在较大和较小时对最大位移的影响都不明显,但其存在一个高效作用区间,当刚度在区间内能显著地改变隧道管体的位移.
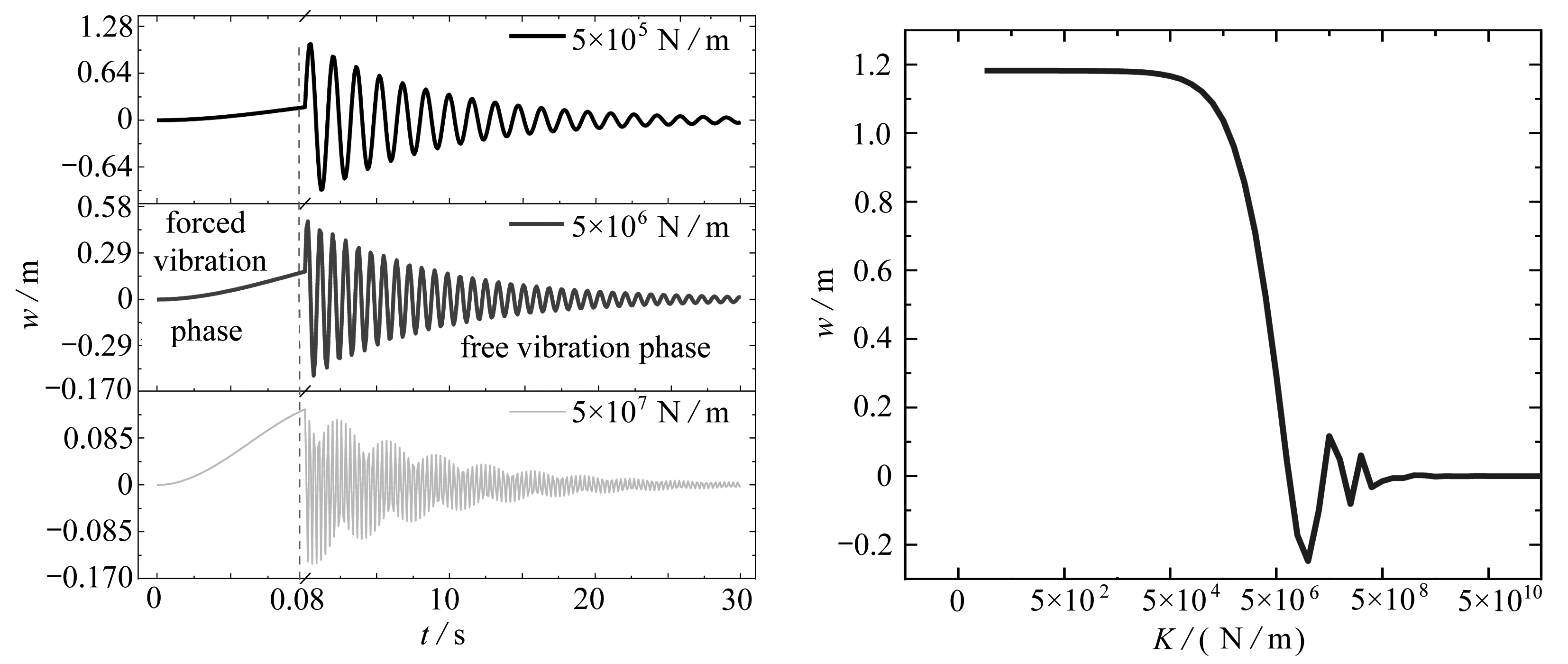
图14 不同锚索刚度下SFT位移时程曲线 图15 锚索刚度与最大位移的关系曲线
Fig.14 The displacement time histories of SFT Fig.15 The anchor cable stiffness-maximum
under different anchor cable stiffnesses displacement curves
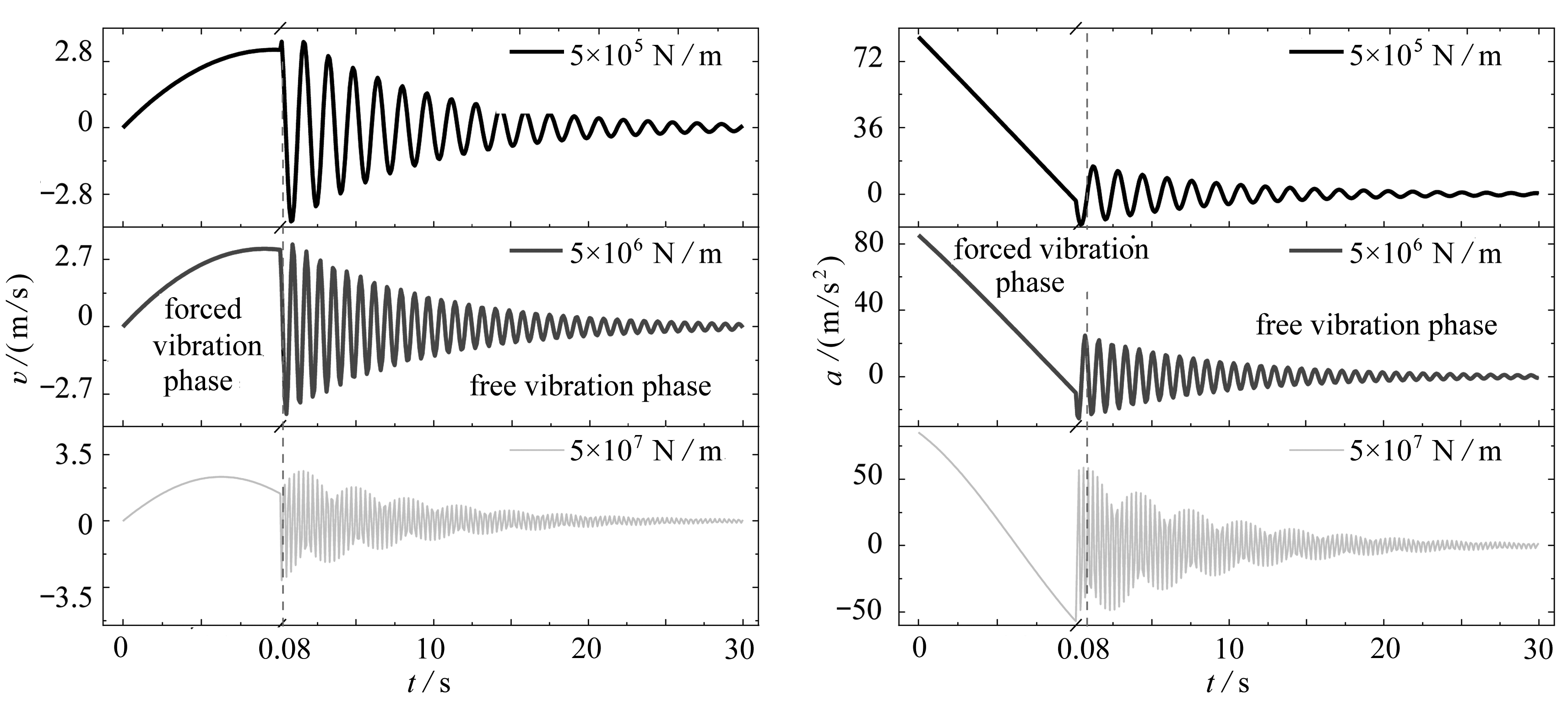
图16 不同锚索刚度下SFT速度时程曲线图17 锚索刚度下SFT加速度时程曲线
Fig.16 The velocity time histories of SFT Fig.17 The acceleration time histories of SFT under different anchor cable stiffnesses under different anchor cable stiffnesses
如图16,锚索刚度对悬浮隧道强迫振动与自由振动的速度具有显著影响.在强迫振动阶段,随锚索刚度的增加最大速度逐渐减小,3种工况下的最大速度为3.290 9,3.134 4,2.330 3 m/s.此外,在该阶段最值出现的时间前移,对比图17中强迫振动的加速度曲线可知,是因为加速度在较大锚索刚度下快速衰减造成的.在自由振动阶段,随锚索刚度增加,3种工况下的最大速度为3.953 1,3.505 4,3.132 7 m/s,为整个振动过程的最大速度,相对于5×105 N/m的锚索刚度,5×106 N/m和5×107 N/m的速度分别下降了11.3%和20.8%,显然锚索刚度对速度的影响不及对位移的影响.
4 结论与展望
本文通过建立和求解爆炸荷载作用下悬浮隧道的简化模型,结合一个悬浮隧道待建工程进行参数分析,得到以下结论:
1) 爆心距对悬浮隧道位移、速度、加速度影响显著,相同炸药量下的悬浮隧道,动力响应随爆心距的增加而减小.就位移而言随着爆心距的增加,隧道最大位移近似呈反比例下降趋势,与10 m爆心距相比,20 m和30 m工况下位移分别下降了50.7%,66.6%.
2) 炸药量对悬浮隧道位移、速度、加速度的影响显著,相同爆心距下的悬浮隧道,动力响应随炸药量的增加而增加.就位移而言,隧道最大位移近似呈低阶幂函数上升趋势,与20 kg炸药量相比,40 kg和60 kg的峰值位移分别增加了29.8%,51.3%.
3) 锚索刚度对悬浮隧道位移、速度、加速度的影响显著,相同爆炸荷载的悬浮隧道,位移随锚索刚度的增加而减小.与5×105 N/m的锚索刚度相比,5×106 N/m和5×107 N/m的位移分别下降了53.0%和86.2%.但锚索的刚度存在高效作用区间,当刚度在区间内能显著地改变隧道管体的位移,当刚度处在区间外(或大或小时)对位移的影响都不明显.
4) 本文的数据和结论为锚索式悬浮隧道的设计和建造提供了理论参考,但所研究的模型忽略了波浪力、气泡脉动压力等因素,计算结果不能全面地反映悬浮隧道的动力响应.因此,下一步将进一步探讨爆炸荷载和多种荷载耦合作用下的悬浮隧道动力响应机理,期望对悬浮隧道可能遭遇的灾害事件展开全面的研究.
[1] 项贻强, 陈政阳, 杨赢.悬浮隧道动力响应分析方法及模拟的研究进展[J].中国公路学报, 2017, 30(1): 69-76.(XIANG Yiqiang, CHEN Zhengyang, YANG Ying.Research development of method and simulation for analyzing dynamic response of submerged floating tunnel[J].China Journal of Highway and Transport, 2017, 30(1): 69-76.(in Chinese))
[2] DONNA A.Chapter 10 submerged floating tunnels: a concept whose time has arrived[J].Tunnelling and Underground Space Technology, 1997, 12(2): 317-336.
[3] HIROSHI K.Evaluation of wave force acting on submerged floating tunnels[J].Procedia Engineering, 2010, 4: 99-105.
[4] 麦继婷, 杨显成, 关宝树.悬浮隧道在波浪作用下的动力响应分析[J].铁道工程学报, 2007, 24(3): 45-49.(MAI Jiting, YANG Xiancheng, GUAN Baoshu.Dynamic response analysis of the submerged floating tunnel subjected to wave[J].Journal of Railway Engineering Society, 2007, 24(3): 45-49.(in Chinese))
[5] REMSETH S, LEIRA B J, OKSTAD K M, et al.Dynamic response and fluid/structure interaction of submerged floating tunnels[J].Computers & Structures, 1999, 72(4): 659-685.
[6] MARTINELLI L, BARBELLA G, FERIANI A.A numerical procedure for simulating the multi-support seismic response of submerged floating tunnels anchored by cables[J].Engineering Structures, 2011, 33(10): 2850-2860.
[7] FOGAZZI P, PEROTTI F.The dynamic response of seabed anchored floating tunnels under seismic excitation[J].Earthquake Engineering & Structural Dynamics, 2015, 29(3): 273-295.
[8] CHEN W, HUANG G.Seismic wave passage effect on dynamic response of submerged floating tunnels[J].Procedia Engineering, 2010, 4(1): 217-224.
[9] 葛斐, 董满生, 惠磊, 等.水中悬浮隧道锚索在波流场中的涡激动力响应[J].工程力学, 2006, 23(S1): 217-221.(GE Fei, DONG Mansheng, HUI Lei, et al.Vortex-induced vibration of submerged floating tunnel tethers under wave and current effects[J].Engineering Mechanics, 2006, 23(S1): 217-221.(in Chinese))
[10] 项贻强, 晁春峰.悬浮隧道管体及锚索耦合作用的涡激动力响应[J].浙江大学学报(工学版), 2012, 46(3): 409-415.(XIANG Yiqiang, CHAO Chunfeng.Vortex-induced dynamic response for combined action of tube and cable of submerged floating tunnel[J].Journal of Zhejiang University(Engineering Science), 2012, 46(3): 409-415.(in Chinese))
[11] LUO G, PAN S K, ZHANG Y L, et al.Response analysis of submerged floating tunnel hit by submarine based on smoothed-particle hydrodynamics[J].Shock and Vibration, 2019, 6: 1-12.
[12] 王刚, 陈铁云.圆柱壳在水下径向爆炸载荷下的弹塑性动力响应[J].上海交通大学学报, 1997, 31(11): 106-111.(WANG Gang, CHEN Tieyun.Elastoplastic dynamic response of a cylindrical shell to underwater radial explosive loading[J].Journal of Shanghai Jiaotong University, 1997, 31(11): 106-111.(in Chinese))
[13] 罗刚, 潘少康, 周晓军, 等.水下非接触爆炸冲击作用下悬浮隧道动力响应[J].中国公路学报, 2018, 31(6): 244-253.(LUO Gang, PAN Shaokang, ZHOU Xiaojun, et al.Dynamic response of a submerged floating tunnel during non-contact underwater explosions[J].China Journal of Highway and Transport, 2018, 31(6): 244-253.(in Chinese))
[14] HONG K Y, LEE G H.Collision analysis of submerged floating tunnel by underwater navigating vessel[J].IABSE Symposium Report, 2014, 27(5): 369-377.
[15] 孔超群.圣维南原理研究工作综述[J].力学季刊, 1990, 11(3): 35-40.(KONG Chaoqun.Research summary of Saint-Venant’s principle[J].Chinese Quarterly of Mechanics, 1990, 11(3): 35-40.(in Chinese))
[16] SATO M, KANIE S, MIKAMI T.Mathematical analogy of a beam on elastic supports as a beam on elastic foundation[J].Applied Mathematical Modelling, 2008, 32(5): 688-699.
[17] 王振宇.水下爆炸作用下结构的动态响应分析[D].博士学位论文.哈尔滨: 哈尔滨工程大学, 2008.(WANG Zhenyu.Dynamic response analysis of structure under underwater explosion[D].PhD Thesis.Harbin: Harbin Engineering University, 2008.(in Chinese))
[18] 刘福林.简支弹塑性梁受冲击波作用时的动力响应的权余解法[J].机械强度, 1989, 11(1): 48-52.(LIU Fulin.The residual weight method for dynamic response of elastic support beam subjected to shock wave[J].Mechanical Strength, 1989, 11(1): 48-52.(in Chinese))
[19] 张嫄, 董满生, 唐飞.冲击荷载作用下水中悬浮隧道的位移响应[J].应用数学和力学, 2016, 37(5): 483-491.(ZHANG Yuan, DONG Mansheng, TANG Fei.Displacement responses of submerged floating tunnels under impact loads[J].Applied Mathematics and Mechanics, 2016, 37(5): 483-491.(in Chinese))
[20] FACCHINETTI M L, LANGRE E D, BIOLLEY F.Coupling of structure and wake oscillators in vortex-induced vibrations[J].Journal of Fluids & Structures, 2004, 19(2): 123-140.
[21] SRINIL N, ZANGANEH H.Modelling of coupled cross-flow/in-line vortex-induced vibrations using double Duffing and van der Pol oscillators[J].Ocean Engineering, 2012, 53: 83-97.
[22] 陈建云, 王变革, 孙胜男.悬浮隧道锚索的涡激动力响应分析[J].工程力学, 2007, 24(10): 186-192.(CHEN Jianyun, WANG Biange, SUN Shengnan.Analysis of vortex-induced dynamic response for the anchor cable of submerged floating tunnel[J].Engineering Mechanics, 2007, 24(10): 186-192.(in Chinese))
[23] 董满生, 张嫄, 唐飞, 等.等间距移动荷载作用下水中悬浮隧道管体的位移响应[J].应用力学学报, 2016, 33(5): 760-765.(DONG Mansheng, ZHANG Yuan, TANG Fei, et al.Displacement response of submerged floating tunnel tube due to moving loads of constant intervals[J].Chinese Journal of Applied Mechanics, 2016, 33(5): 760-765.(in Chinese))
[24] 吴成, 廖莎莎, 李华新, 等.水下爆炸的一些声学特性分析[J].北京理工大学学报, 2008, 28(8): 719-722.(WU Cheng, LIAO Shasha, LI Huaxin, et al.Analysis of acoustic characteristics for he charge underwater explosion[J].Transactions of Beijing Institute of Technology, 2008, 28(8): 719-722.(in Chinese))
[25] 刘立名, 余建星, 王磊.基于非线性理论的海底管跨涡激共振可靠性研究[J].天津大学学报, 2001, 38(1): 31-35.(LIU Liming, YU Jianxing, WANG Lei.Reliability research on vortex induced resonance of submarine pipeline span based on nonlinear theory[J].Journal of Tianjin University, 2001, 38(1): 31-35.(in Chinese))
[26] 秦银刚, 周生国, 周晓军.多跨悬浮隧道合理支撑间距分析[J].铁道工程学报, 2008, 25(3): 78-81.(QIN Yingang, ZHOU Shengguo, ZHOU Xiaojun.Analysis of the reasonable support length for multi-spans submerged floating tunnel[J].Journal of Railway Engineering Society, 2008, 25(3): 78-81.(in Chinese))
[27] 黄建松, 华宏星, 周建鹏.水下爆炸引起舰船冲击人体损伤生物力学模型研究进展[J].医用生物力学, 2008, 23(4): 321-326.(HUANG Jiansong, HUA Hongxing, ZHOU Jianpeng.Progress of human mathematical model to study ship shock injury by underwater explosion[J].Journal of Medical Biomechanics, 2008, 23(4): 321-326.(in Chinese))