引 言
随着世界油气资源需求量日益增大,海洋油气资源的开采逐渐由浅海向深海领域发展.立管是进行深海石油天然气开采必不可少的设备,也是采油平台结构中最薄弱的环节之一[1],由于涡激振动(VIV)造成的疲劳损坏可能会导致立管结构的失效和重大事故的发生,因此海洋立管涡激振动的非线性动力学分析具有重要的理论和工程意义.
近些年,对海洋立管的涡激振动在实验[2-4]和数值仿真[5-9]方面已有了较为广泛的研究.关于立管涡激振动的理论研究主要基于3种半经验模型[10]:强迫力系统模型、水弹性系统模型和耦合系统模型.这些模型都是基于实验数据得到的,其中前两类模型是第三类模型的简化.由于耦合系统模型能够准确地预测涡激振动的锁频现象,因此得到了广泛的应用.Birkhoff和Zarantanello[11]首次提出了非线性振子模型的概念.随后,Bishop和Hassan[12]在此基础上提出了用van der Pol振子方程来模拟尾流作用于圆柱上的流体力.Srinil等[13]使用双Duffing-van der Pol振子来预报两向耦合的涡激振动响应,该模型可以较成功地预报出两向涡激振动的振幅响应,并且从振幅随约化速度递增和递减曲线中发现跳跃和滞后现象.文献[14-18]通过对柔性管涡激振动偏微分方程进行高阶Galerkin离散,采用直接数值积分法求解系统响应进而分析涡激振动中多模态相互作用的现象.然而完全基于数值计算的方法,难以全面揭示立管系统涡激共振时的分岔现象以及各阶模态的作用效果,需要采用解析方法进一步分析.
因为尾流振子的非线性,高阶Galerkin离散方程较为复杂,在解析分析立管多模态涡激振动时存在困难.涉及解析分析时,多针对双模态离散模型.比如,唐友刚等[19]采用多尺度法得到了仅考虑立管前两阶模态的涡激振动模型的近似解析解;Wang[20]对双模态离散系统特征值问题进行分析,研究了分布力作用下两端简支输油管道的颤振失稳问题.相比于单模态离散模型,立管涡激振动双模态简化模型既能够部分反映系统多模态振动特性,又便于进行理论分析,在研究立管动力学分岔及多模态相互作用机理方面具有非常重要的价值,值得深入分析.
本文利用van der Pol尾流振子模型描述流体的作用,采用加速度耦合模型,建立深海立管涡激振动的非线性动力学方程组,基于二阶Galerkin离散将该偏微分方程组简化为一组常微分方程;采用谐波平衡法分析流速变化对立管振动幅值和频率的影响,使用Poincaré映射方法和Lyapunov指数法研究流速变化引起立管涡激振动行为的分岔现象;根据谐波平衡法所得频率对系统概周期区域频率成分进行预测.
1 深海立管涡激振动模型及求解
1.1 运动方程
如图1所示,考虑顶张力立管的涡激振动.立管底端铰接在万向节上,顶部通过张紧器与平台连接,立管模型可简化为具有弯曲刚度的Euler-Bernoulli梁.
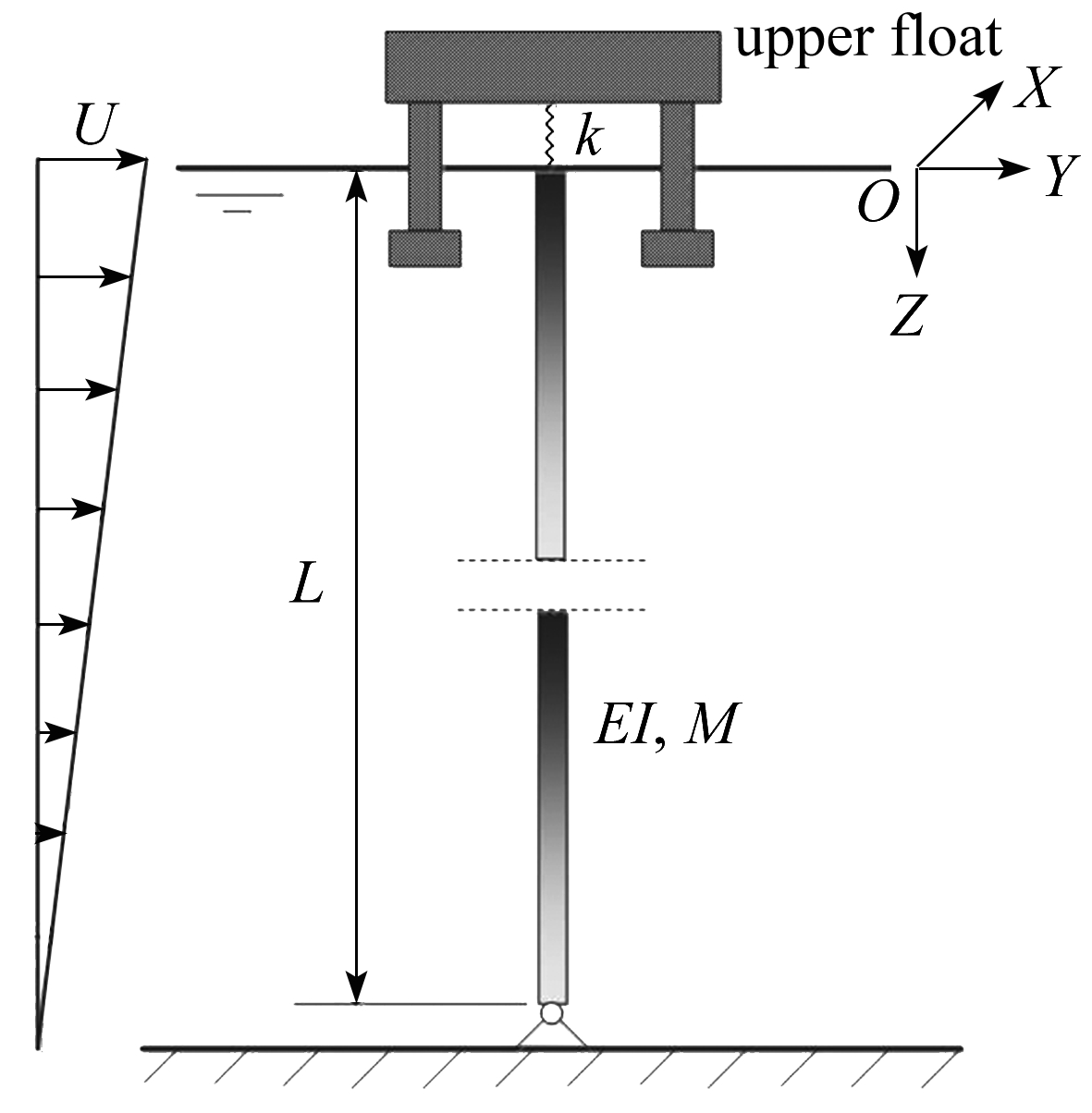
图1 海洋立管模型示意图
Fig.1 The marine riser model
立管涡激振动动力学的研究表明,立管在横流向的振动比顺流向振动大一个数量级,因此仅考虑横流向振动.作用在立管上的流体升力可用van der Pol尾流振子描述,则有
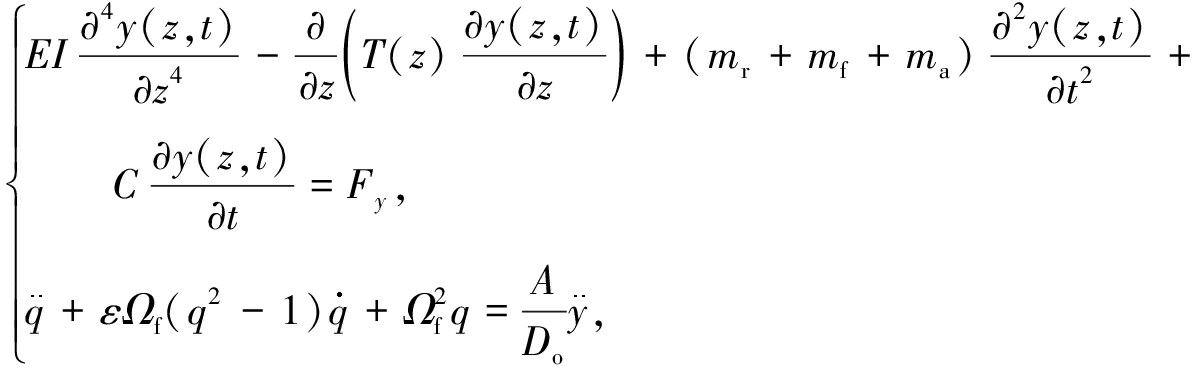
(1)
式中y(z,t)表示立管横向位移;EI为抗弯刚度;T(z)为顶张力;mr,mf和ma分别表示单位长度立管质量、立管内流体质量和附加质量;C为结构阻尼;Fy是流体对立管的作用力;变量q表示局部流体对结构的瞬时升力系数CL与结构静态横向升力系数CL0之比,有q=2CL/CL0;Ωf是涡泄频率,有Ωf=2πSrUf/Do,Sr是Strouhal数;A,ε为试验测定的耦合系数.
立管单位长度质量为

(2)
式中ρs,ρf和ρw分别为立管材料密度、内部流体密度和海水密度,Ca为附加质量系数,Do为立管外径,d为立管内径.
立管轴向有效张力为
T(z)=Asg(ρs-ρw)(ftopL-z),
(3)
式中ftop是顶张力系数,As为立管截面面积,有![]() 是顶张力立管的长度.
是顶张力立管的长度.
流体对立管的作用力为
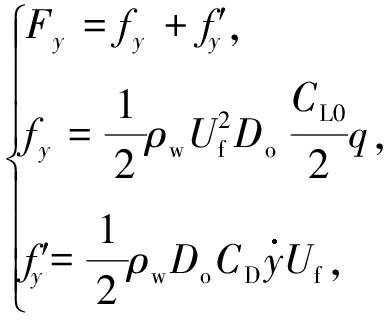
(4)
式中fy表示立管横向振动的涡激升力,f′y表示流体产生的非线性阻尼力,CD是阻力系数.
采用线性剪切流模型,假设海平面最大流速为U,海底最小流速为0,流速从海平面到海底线性减小,则立管管身不同位置处的海流速度为
(5)
为分析方便引入无量纲变量,![]() 方程(1)可转化为如下形式:
方程(1)可转化为如下形式:
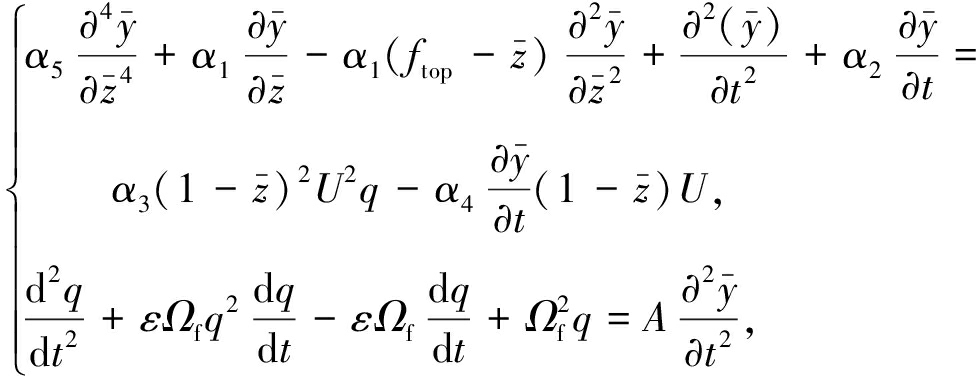
(6)
式中
立管的边界条件为
(7)
1.2 二阶Galerkin离散
根据Galerkin离散方法,原始的偏微分方程(6)可离散为一组常微分方程.综合考虑分析难度和讨论的流速范围,本文对系统进行二阶离散,设解有如下形式:
(8)
其中![]() 为满足相应位移边界条件和力边界条件的模态函数;hi(t),Hi(t)分别为立管和van der Pol振子对应的离散系统的广义坐标,表示在系统整体响应中各阶模态函数所占权重.将式(8)代入方程(6)中,得离散后的深海立管耦合系统的运动方程为
为满足相应位移边界条件和力边界条件的模态函数;hi(t),Hi(t)分别为立管和van der Pol振子对应的离散系统的广义坐标,表示在系统整体响应中各阶模态函数所占权重.将式(8)代入方程(6)中,得离散后的深海立管耦合系统的运动方程为
(9a)
(9b)
(9c)
(9d)
离散系统中各系数具体表达式在附录中给出.
1.3 谐波平衡法求解系统响应
立管涡激振动离散方程(9)是自治的四自由度耦合方程,周期解具有时移不变性,不失一般性,可设方程(9)的解为如下形式:
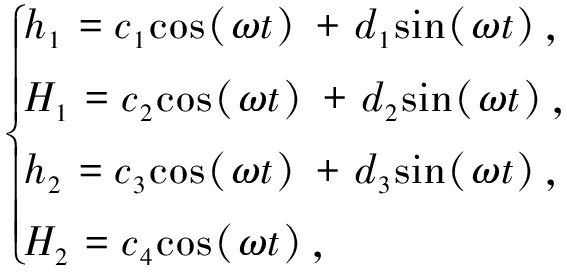
(10)
其中ci(i=1,2,3,4),di(i=1,2,3),ω为待求量.
立管一阶模态广义坐标h1的幅值为![]() 尾流振子一阶模态广义坐标H1的幅值为
尾流振子一阶模态广义坐标H1的幅值为![]() 立管二阶模态广义坐标h2的幅值为
立管二阶模态广义坐标h2的幅值为![]() 尾流振子二阶模态广义坐标H2的幅值为r4=c4.
尾流振子二阶模态广义坐标H2的幅值为r4=c4.
根据谐波平衡法,将设解(10)代入微分方程式(9),只考虑一阶谐波平衡,令方程两侧cos(ωt)和sin(ωt)前系数相等,得如下代数方程组:
β11c1+β12c3-β13c2-β14c4-β15d1ω-β16d3ω-c1ω2=0,
(11a)
β11d1+β12d3-β13d2+β15c1ω+β16c3ω-d1ω2=0,
(11b)
β21c1+β22c3-β23c2-β24c4-β25d1ω-β26d3ω-c3ω2=0,
(11c)
β21d1+β22d3-β23d2+β25c1ω+β26c3ω-d3ω2=0,
(11d)
(11e)
(11f)
(11g)
β45c4ω+Ad3ω2-β410c2ω+β49d2=0.
(11h)
本文以100 m长API X65级钢材制顶张力立管的涡激振动为算例,计算和分析立管的振动特性.对上文讨论的非线性代数方程组(11)进行编程求解,给定流速及适当初始条件,可得对应ci,di,ω的值,逐步改变流速即可得到系统周期解随流速变化曲线,进而对系统分岔现象进行分析.立管参数如表1[21-22]所示.
表1 计算模型参数
Table 1 Calculation model parameters

parametervalueriser length L/m100elastic modulus E/Pa2.1×1011outside diameter Do/m0.325inside diameter d/m0.305 material density ρs/(kg/m3)7 850seawater density ρw/(kg/m3)1 025internal fluid densityρf/(kg/m3)900top tension coeffcient ftop1.3structural damping C/(N·s/m)0.05additional mass coeffcient Ca1.0structural static lift coefficient CL00.3resistance coefficient CD1.2Strouhal number Sr0.2coupling coefficient A12coupling coefficient ε0.3
2 立管耦合系统分岔分析
谐波平衡法是处理复杂非线性系统动力学问题常用的一种半解析分析方法,多用于周期解求解,但稳定性分析不便.Poincaré映射方法作为一种数值分析方法,具有较广泛的应用.Lyapunov指数分析法是一种定量分析的方法,根据Lyapunov指数的值可判断吸引子的类型.为此采用这3种方法分析流速导致的系统动力学分岔现象.
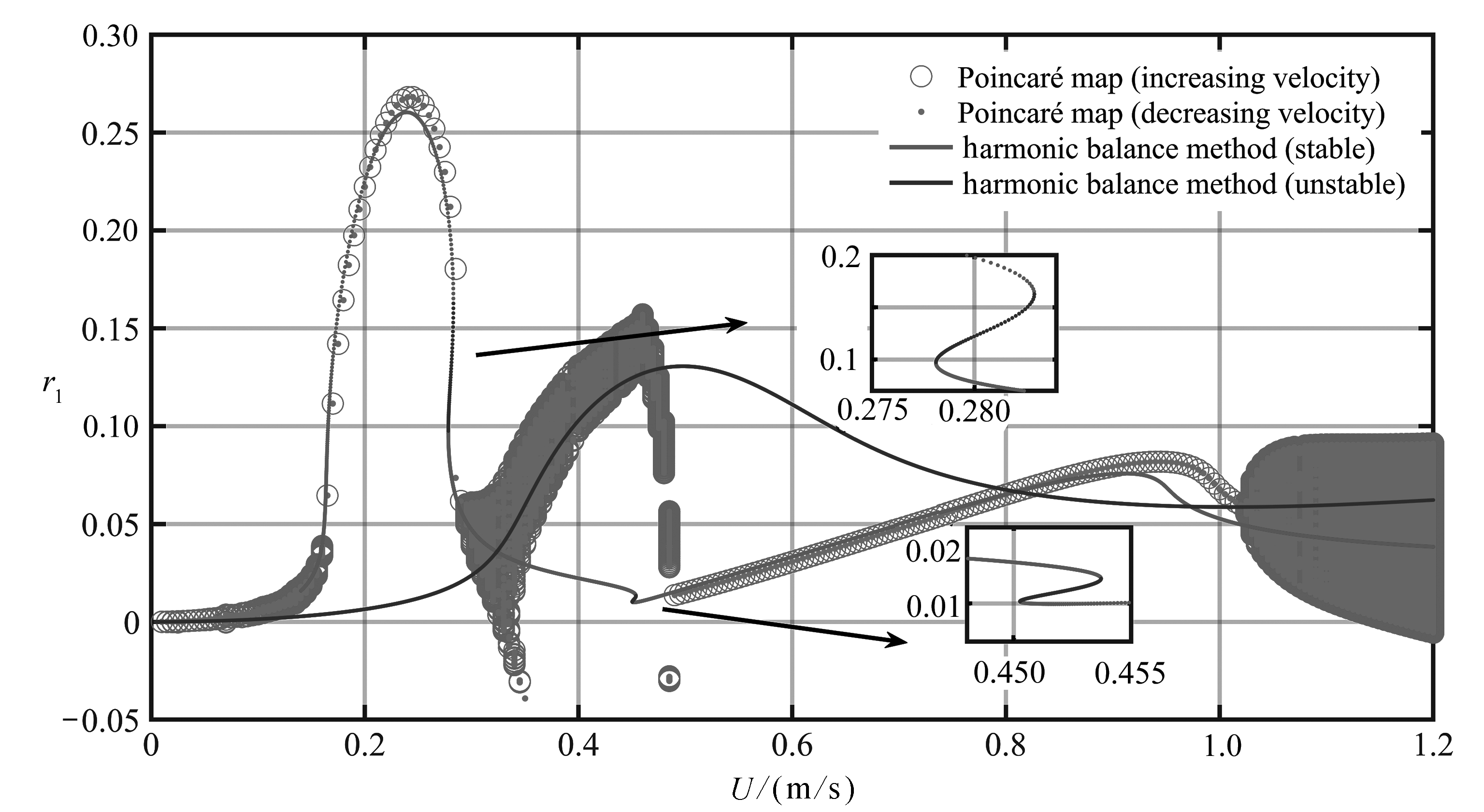
对1.3小节中非线性代数方程组(11)求解,得到两个解支,分别是图2中谐波平衡法稳定解支与不稳定解支.从稳定解支曲线可以看出,随着流速的增加,立管各阶模态广义坐标幅值呈现先增大后减小再增大再减小的趋势,出现了涡激共振现象.在该图所示的速度范围内,系统出现两个涡激共振区, 一阶涡激共振区U1=0.163~0.285 m/s和二阶涡激共振区U2=0.453~1.015 m/s.从图2局部放大图中可以看出, 在一阶涡激共振区右侧U=0.285 m/s附近系统存在两个鞍结分岔点,这两个分岔点之间的解是不稳定的,两个分岔点对应的流速区域内系统出现双稳态现象;同样地,在二阶涡激共振区左侧U=0.453 m/s附近也存在双稳态现象.
(a) 立管一阶模态广义坐标幅值
(a) The first-order generalized coordinates of the riser

(b) 立管二阶模态广义坐标
(b) The second-order generalized coordinates of the riser
图2 流速对响应幅值特征的影响
Fig.2 Effects of velocity on response amplitude characteristics
利用Poincaré映射方法计算了立管一阶、二阶模态广义坐标无量纲振动位移极大值r1,r3随流速变化的分岔图,如图2所示,圆圈和圆点分别表示流速递增和递减过程中Poincaré分岔图计算结果.从图2中可以看出,在表面流速区间U=0~0.163,0.285~0.488,1.015~1.2 m/s内的任一流速下立管一阶、二阶模态广义坐标幅值的极大值出现多个值,对应分岔图中一列点,系统表现为概周期运动;在涡激共振区U=0.21~0.285,0.488~1.015 m/s内的任一流速下立管一阶、二阶模态广义坐标幅值极大值只有一个,对应分岔图中一个点,系统表现为周期运动;并且在0.285 m/s流速附近模态广义坐标幅值极大值出现跳跃现象和滞后现象,与谐波平衡法稳定解一阶涡激共振区右侧双稳态区域一致.值得注意的是,在一阶涡激共振区U=0.167~0.21 m/s流速范围内,立管一阶模态广义坐标幅值极大值只有一个, 表现为一倍周期运动, 而立管二阶模态广义坐标幅值极大值出现3个, 表现为1∶3内共振的三倍周期运动.
对比两种方法所得结果可知,在一阶涡激共振区内,谐波平衡法稳定解与数值(Poincaré映射)周期解拟合较好,在二阶涡激共振区,两种方法所得结果基本一致,但稍有偏差,数值周期解稍大于谐波平衡法稳定解,这是由于谐波平衡法计算时只考虑了一阶谐波,故存在误差.
系统存在8个Lyapunov指数,图3所示为系统前三大的Lyapunov指数,分别用σ1,σ2,σ3表示.在流速U=0~0.163,0.285~0.488,1.015~1.2 m/s区间内时, 系统有两个Lyapunov指数等于0, 其余均小于0, 说明吸引子为稳定二维环面,系统响应是准周期的.在区间U=0.163~0.285,0.488~1.015 m/s内时,系统只有一个Lyapunov指数等于0,其余均小于0,说明吸引子为稳定极限环,系统响应是周期的,与图2中Poincaré映射方法分析结果相一致.从图3中还可以看出并未出现Lyapunov指数大于0的情况,可知系统不会出现混沌运动.

图3 系统的Lyapunov指数谱
Fig.3 The Lyapunov exponent spectrum of the system
3 立管双模态非线性响应特征
综合考虑流速、系统固有频率等因素的影响,定义了无量纲量约化速度Ur对立管涡激振动行为进行分析,其具体表达式为
(12)
其中U表示海平面最大流速,fn表示系统的固有频率,Do表示立管直径.图4给出了约化速度下系统响应频率特征.
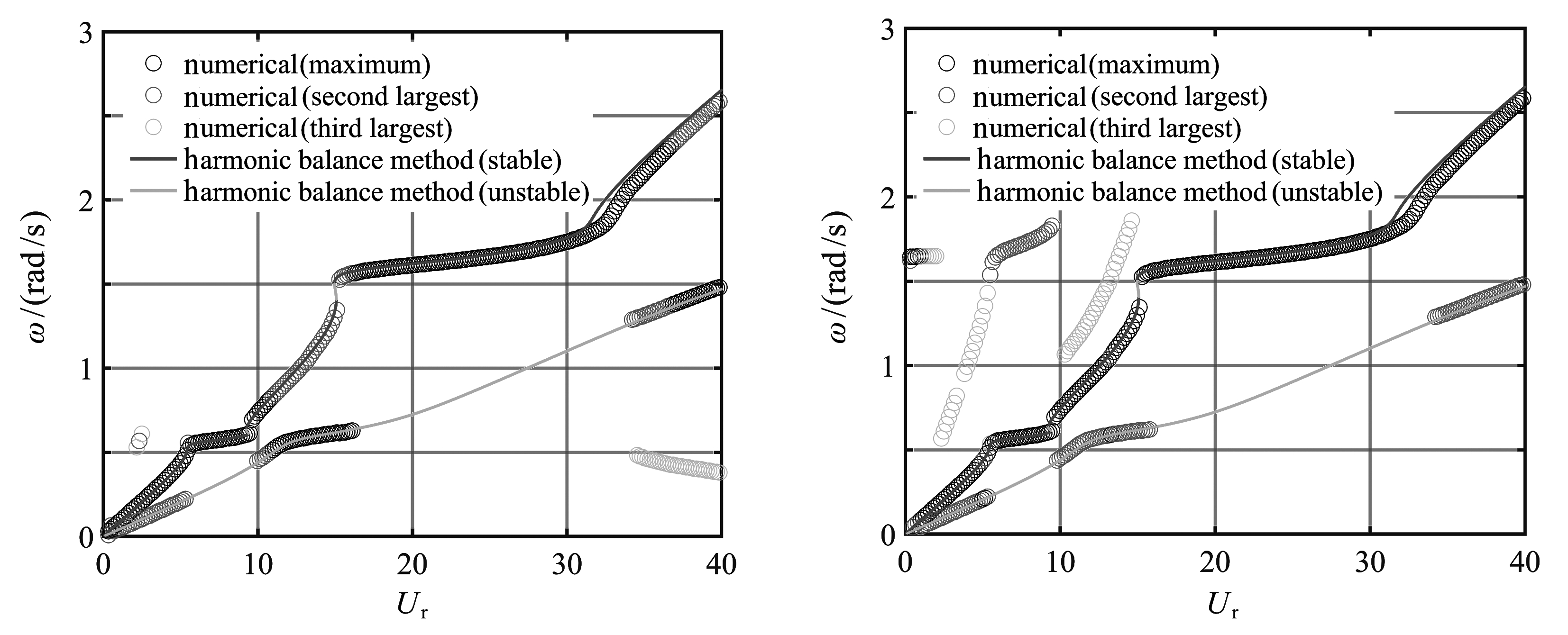
为了分析立管不同运动性态的特点,揭示立管多模态相互作用机理,对数值计算得到的系统响应进行了幅值谱分析,提取主要频率成分及其幅值,分析流速变化的影响.图4(a)、(b)分别给出了立管一阶、二阶模态广义坐标响应的分析结果.同时图中还给出了由谐波平衡法求解得到频率结果以便比较.图4(a)、(b)中由深至浅的圆圈分别表示幅值谱分析中的幅值最大频率成分、幅值第二大频率成分和幅值第三大频率成分,深色线和浅色线分别表示谐波平衡法计算所得稳定周期解频率和不稳定周期解频率.
从图4中可以看出,随着流速的增加,系统的频率逐渐增大,而且在涡激共振区域频率变化缓慢.谐波平衡法所得稳定解支频率要大于不稳定解支.在涡激共振区内,立管一阶模态广义坐标数值结果所得频率成分只有一个,且与谐波平衡法稳定解支上的频率相一致,系统表现为周期运动.在涡激共振区域外,数值结果至少含有两个频率成分,最主要的两个频率成分分别与谐波平衡法稳定解支和不稳定解支上的频率相一致,系统表现为概周期运动.数值结果中,立管二阶模态广义坐标在一阶涡激共振区出现两个频率成分,且两个频率成分比值接近1∶3,所以认为在一阶锁频区域系统表现为1∶3内共振的三倍周期运动,且最大频率成分与谐波平衡法稳定解相一致,在二阶涡激共振区域和非锁频区域,立管二阶模态广义坐标频率特征及分岔特性与立管一阶模态广义坐标下的情况相同.
由于非线性的影响,立管一阶、二阶模态广义坐标在同一流速下的主要频率成分有差别.从图4(a)中可以看出,在概周期运动区域Ur=11~16,35~40内,数值计算所得立管一阶模态广义坐标最大频率成分与谐波平衡法不稳定解支一致,第二大频率成分与谐波平衡法稳定解支一致;从图4(b)中可以看出,相同流速区间内,数值计算所得立管二阶模态广义坐标最大频率成分与谐波平衡法稳定解一致,第二大频率成分与谐波平衡法不稳定解一致.因此,谐波平衡法求得系统周期响应的频率能够很好地预测涡激振动概周期解的频率成分.
立管一阶模态广义坐标在概周期运动区域Ur=2~2.5,35~40,立管二阶模态广义坐标在概周期运动区域Ur=0~15,出现谐波平衡法解以外的频率成分.这些频率一部分近似等于谐波平衡法所得频率的三倍,是由谐波平衡法两个解支衍生出来的;另一部分频率集中于结构固有频率附近.
需要指出,图4还表明系统响应从周期(涡激共振)到概周期的变化都伴随着新的频率成分突然出现.从分岔图角度看属于周期解的Hopf分岔现象,与文献[10]中弹性支撑管道频率锁定到解锁的机制有本质区别.
(a) 立管一阶模态广义坐标(b) 立管二阶模态广义坐标
(a) The first-order generalized coordinates of the riser(b) The second-order generalized coordinates of the riser
图4 流速对响应频率特征的影响
Fig.4 Velocity effects on response frequency characteristics
4 结 论
本文采用van der Pol尾流振子模型,基于两阶Galerkin离散,研究了线性剪切流作用下,顶张力立管涡激振动特性.分别采用谐波平衡法、Poincaré映射方法和Lyapunov指数法对系统的动力学分岔行为进行分析,所得结论如下:
1) 对比谐波平衡法与Poincaré映射方法所得结果,发现谐波平衡法所得周期解中频率较低的一个解支是不稳定的;从系统稳定解随流速变化规律可以看出,立管涡激振动出现两个共振区域;在一阶涡激共振区右侧和二阶涡激共振区左侧出现双稳态现象.
2) 从系统Poincaré映射分岔图和Lyapunov指数谱图中可以发现,随着流速的增加,立管的振动在周期运动和概周期运动间多次转换,但未出现混沌运动.
3) 系统数值解概周期响应的最主要的两个频率成分分别对应谐波平衡法得到的稳定与不稳定周期解的频率.
4) 双模态涡激响应从周期到概周期运动的转换,属于周期解的Hopf分岔现象而非通常认为的频率解锁.共振机理和普适性问题还有待进一步研究.
附 录
[1] 冯钰钦, 艾志久, 艾雨.考虑流体升力作用的海洋钻井隔水管变形特性分析[J].应用数学和力学, 2016, 37(1): 48-59.(FENG Yuqin, AI Zhijiu, AI Yu.Analysis on deformation properties of marine risers under fluid lift forces[J].Applied Mathematics and Mechanics, 2016, 37(1): 48-59.(in Chinese))
[2] CHAPLIN J R, BEARMAN P W, HUARTE F J H, et al.Laboratory measurements of vortex-induced vibrations of a vertical tension riser in a stepped current[J].Journal of Fluids and Structures, 2005, 21(1): 3-24.
[3] LIE H, KAASEN K E.Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow[J].Journal of Fluids and Structures, 2006, 22(4): 557-575.
[4] SONG J N, LU L, TENG B, et al.Laboratory tests of vortex-induced vibrations of a long flexible riser pipe subjected to uniform flow[J].Ocean Engineering, 2011, 38(11/12): 1308-1322.
[5] HUANG Z, DENG Z, LIU D, et al.Numerical simulation for VIV of a long flexible cylinder in the time domain[J].Ships and Offshore Structures, 2018, 13(1): 214-227.
[6] WILLDEN R H J, GRAHAM J M R.Multi-modal vortex-induced vibrations of a vertical riser pipe subject to a uniform current profile[J].European Journal of Mechanics, 2004, 23(1): 209-218.
[7] FU B, ZOU L, WAN D.Numerical study on the effect of current profiles on vortex-induced vibrations in a top-tension riser[J].Journal of Marine Science and Application, 2017, 16(4): 473-479.
[8] LI Y, GUO S, CHEN W.Analysis on multi-frequency vortex-induced vibration and mode competition of flexible deep-ocean riser in sheared fluid fields[J].Journal of Petroleum Science & Engineering, 2018, 163: 378-386.
[9] 万德成, 端木玉.深海细长柔性立管涡激振动数值分析方法研究进展[J].力学季刊, 2017, 38(2): 179-196.(WAN Decheng, DUANMU Yu.A recent review of numerical studies on vortex-induced vibrations of long slender flexible risers in deep sea[J].Chinese Quarterly of Mechanics, 2017, 38(2): 179-196.(in Chinese))
[10] PAÏDOUSSIS M P, PRICE S J, LANGRE E.Fluid-Structure Interactions: Cross-Flow-Induced Instabilities[M].New York: Cambridge University Press, 2010.
[11] BIRKHOFF G, ZARANTONELLO E H.Jets, Wakes and Cavities[M].New York: Academic Press, 1957.
[12] BISHOP R E D, HASSAN A Y.The lift and drag forces on a circular cylinder oscillating in a flowing fluid[J].Proceedings of the Royal Society of London, 1964, 277(1368): 51-75.
[13] SRINIL N, ZANGANEH H.Modelling of coupled cross-flow/in-line vortex-induced vibrations using double Duffing and van der Pol oscillators[J].Ocean Engineering, 2012, 53: 83-97.
[14] PAVLOVSKAIA E, KEBER M, POSTNIKOV A, et al.Multi-modes approach to modelling of vortex-induced vibration[J].International Journal of Non-Linear Mechanics, 2016, 80: 40-51.
[15] SRINIL N.Multi-mode interactions in vortex-induced vibrations of flexible curved/straight structures with geometric nonlinearities[J].Journal of Fluids and Structures, 2010, 26(7/8): 1098-1122.
[16] MENG S, ZHANG X Q, CHE C D, et al.Cross-flow vortex-induced vibration of a flexible riser transporting an internal flow from subcritical to supercritical[J].Ocean Engineering, 2017, 139: 74-84.
[17] HE F, DAI H, HUANG Z, et al.Nonlinear dynamics of a fluid-conveying pipe under the combined action of cross-flow and top-end excitations[J].Applied Ocean Research, 2017, 62: 199-209.
[18] WANG Y C, WU Z Q, ZHANG X Y.Vortex-induced vibration response bifurcation analysis of top-tensioned riser based on the model of variable lift coefficient[J].Mathematical Problems in Engineering, 2018, 2018: 6491517.DOI: 10.1155/2018/6491517.
[19] 唐友刚, 朱龙欢, 李杨青.深海顶张式立管组合参激共振的非线性振动分析[J].天津大学学报, 2015, 48(9): 811-816.(TANG Yougang, ZHU Longhuan, LI Yangqing.Nonlinear vibration analysis of combination parametric resonance for TTRs in deep water[J].Journal of Tianjin University, 2015, 48(9): 811-816.(in Chinese))
[20] WANG L.Flutter instability of supported pipes conveying fluid subjected to distributed follower forces[J].Acta Mechanica Solida Sinica, 2012, 25(1): 46-52.
[21] 唐友刚, 邵卫东, 张杰.深海顶张力立管参激-涡激耦合振动响应分析[J].工程力学, 2013, 30(5): 282-286.(TANG Yougang, SHAO Weidong, ZHANG Jie.Dynamic response analysis for coupled parametric vibration and vortex-induced vibration of top-tensioned riser in deep-sea[J].Engineering Mechanics, 2013, 30(5): 282-286.(in Chinese))
[22] VIOLETTE R, LANGRE E D, SZYDLOWSKI J.Computation of vortex-induced vibrations of long structures using a wake oscillator model:comparison with DNS and experiments[J].Computers & Structures, 2007, 85(11): 1134-1141.