引 言
管束结构流致振动问题一直备受关注，流致振动将对结构完整性产生不利影响．流体引起管子的小幅运动可能使管子与相邻结构发生碰撞、摩擦，在管子表面形成微小的损伤．流体引起的强烈振动可使管子发生塑性变形甚至断裂[1]．管束流致振动存在三种作用机理：湍流抖振(turbulent buffeting)、涡激振动(vortex-induced vibration)和流弹失稳(fluidelastic instability)．湍流抖振是管子在湍流作用下发生的小幅随机振动．涡激振动指管子表面的周期性漩涡脱落诱发的共振．流弹失稳是指当流速超过某一临界值后，管子振幅突然增大，运动发生失稳．此时流体力对管子做功大于结构阻尼耗散掉的能量，同时流体力受管子运动影响强烈．在几种管束结构的流致振动机理中，流弹失稳最为危险，可能使管子在短时间内产生较大的磨损，甚至发生弯折、断裂．
流弹失稳研究的重点之一在于建立流体力模型，确定与管子运动相关的流体力的具体形式．Lever[2]的流道(streamtube)理论将管束之间的流场分为流道和尾迹区，在流道内利用Bernoulli方程求解压力，考虑管子运动对流道面积的影响，得到了与运动相关的流体力模型．聂清德等[3]结合风洞实验对Lever的理论模型进行研究，结果表明管子受到的流体力受其运动影响强烈．Price和Paidoussis[4]的准稳态(quasi-steady)理论认为管子的运动相当于改变了流体和管子之间的相对速度，把管子放置在一系列不同位置下并测量流体力系数，然后结合人为选取的延迟时间来表示流体力的非定常效应，建立起准非稳态(quasi-unsteady)流体力模型．准非稳态模型中的流体力系数是管子位移和速度的线性函数，Price和Valerio[5]后来用高阶多项式对流体力系数测量结果进行拟合，将非线性引入到流体力模型中．蒋天泽等[6]基于两相流试验测量了流体力系数，将准稳态模型拓展应用于两相流的情况．Chen等[7]的非稳态(unsteady)理论给出的流体力是管子与其相邻管的位移、速度、加速度的线性组合形式．Meskell[8]让管子在流场中自由运动，利用管子的运动和流体力实测数据结合力状态映射法[9]建立起了流体力和管子位移、速度之间的函数关系．
数值仿真技术的发展为流弹稳定性研究提供了一种新的途径．利用计算流体力学模拟管束间流场可得到管子受到的流体力，然后利用计算结构动力学模拟管子受流体力作用下的运动情况．冯志鹏等[10]利用双向流固耦合算法和动网格技术研究了3×3正方形排列管束结构的流致振动特性．吴皓等[11]对正方形排列管束结构的流致振动过程进行了数值模拟研究，讨论了不同流速下传热管的运动特征，通过不断调整入口流速计算得到管束流弹失稳临界流速．以上研究主要是采用数值方法研究管束流固耦合现象．Gillen等[12]结合准非稳态理论的假设，对管子静止在不同位置下的流场进行计算，将流体力计算结果和准非稳态理论相结合，确定了流体力模型，并对管束流弹失稳临界流速进行了预测．Hassan等[13]让管子在流场中以给定的方式运动，计算管子受到的流体力，并结合非稳态理论的流体力模型计算其中的流体力系数．这些数值研究都是基于已有理论给出的流体力模型，计算其中的未知流体力系数．本文对管子在流体力作用下运动的过程进行模拟，不依赖已有理论模型，直接以数值计算结果为基础建立了流体力模型．
1 数值模型建立与验证
1.1 管束静止绕流数值模型建立
在管束结构中，流场沿管子轴线方向的变化可以忽略[13-14]，可在二维平面内进行数值计算．本文以正三角形排列管束为研究对象，流场几何结构如图1所示，P为管子中心距，D为管子直径，流道中央有5排(每排6根)管子，上游长度为9D，下游为13D．
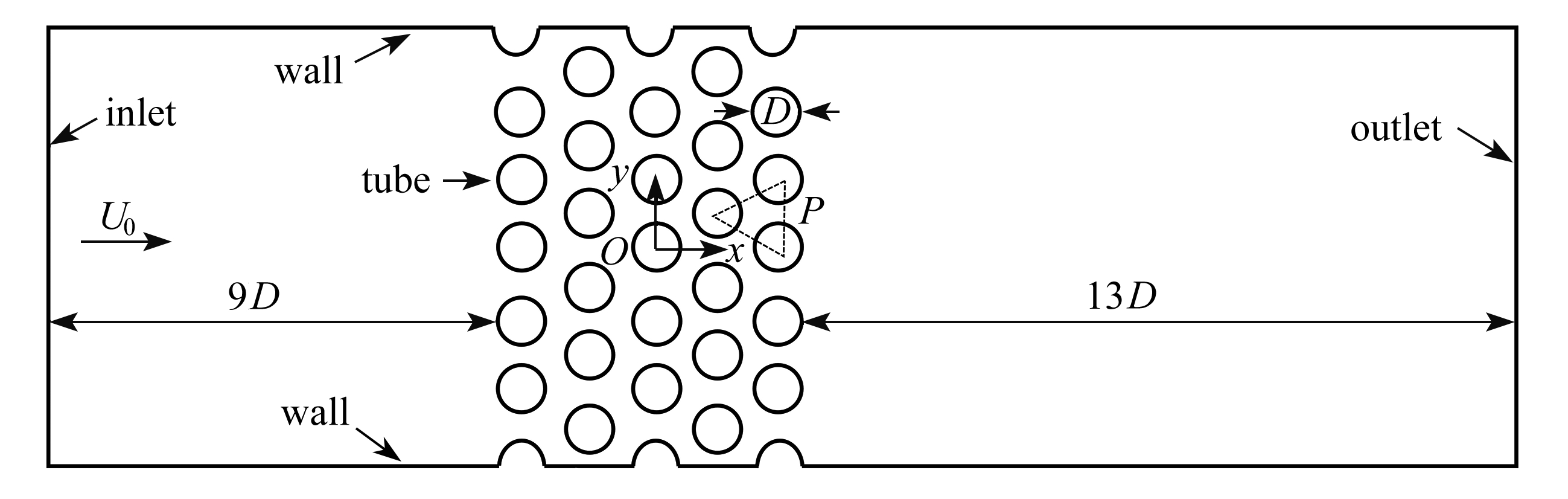
图1 流场几何结构
Fig.1 Flow field geometry
在计算核心部分管子周围采用四边形边界层网格，确保第一层网格y+<1，边界层网格厚度为1 mm．管子间隙内流道结构复杂，因此采用三角形网格对其进行网格划分，使用三角形网格也有利于后续流致振动模拟中动网格功能的实现．三角形网格的尺寸和管子表面附近边界层网格长度近似(图2)．
图2 边界层和间隙内网格
Fig.2 boundary layer and flow channel mesh
对于管束结构的流致振动问题，一般可将管子受到的流体力分为与管子运动有关的流体弹性力和与管子运动无关的湍流随机激励[8,15]．对于结构运动幅度较大的情况，湍流随机激励的效应可以忽略[8]．因此，本文用Reynolds平均法求解流场，不对湍流随机脉动进行详细模拟．Reynolds平均法对流体动量方程(N-S方程)进行时均处理，只关注平均流动，抛弃湍流的瞬时特征．管束结构内部流场本质上属于圆柱绕流问题，流场内存在逆压梯度、边界层分离、回流、再附着等现象．在湍流模型的选取方面，本文采用Realizable k-ε模型，期望能够对以上这些流动现象进行更好地模拟．流场入口为均匀速度入口边界(velocity inlet)，管束下游出口为流量出口边界(outflow)．
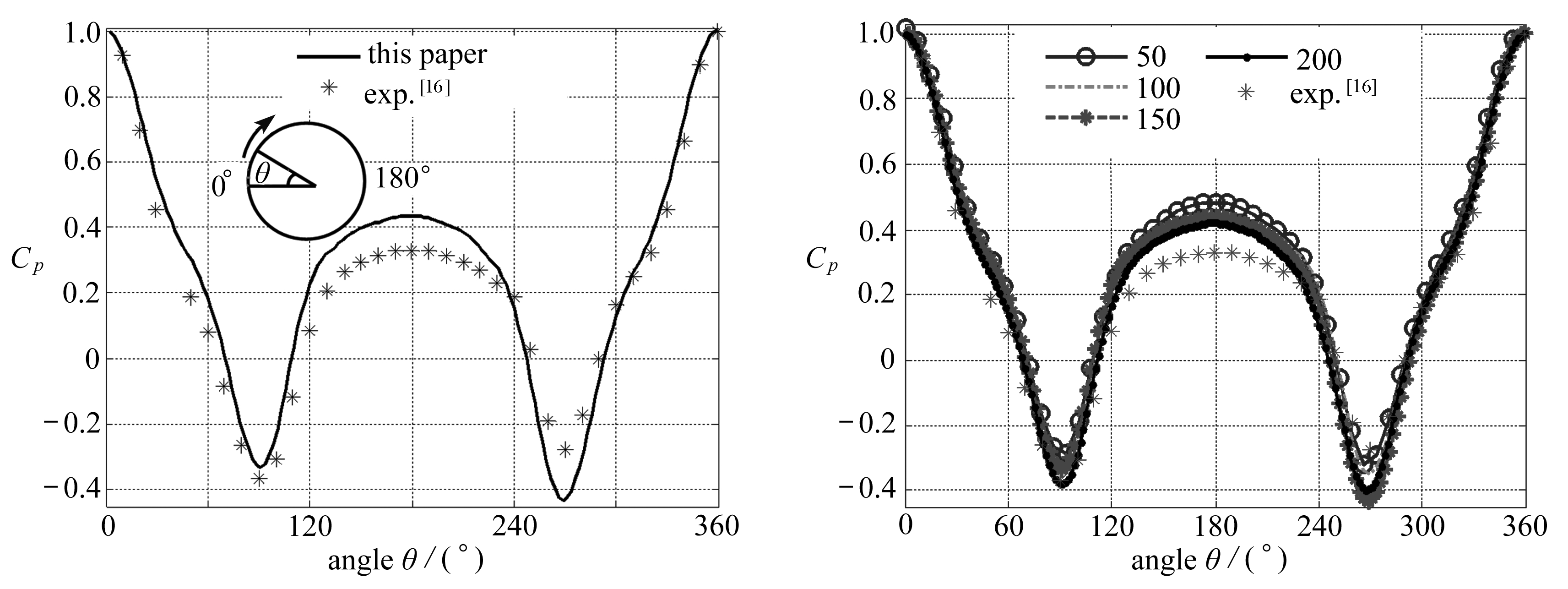
图3 U0=7 m/s,管子表面压力分布图4 网格无关性验证结果
Fig.3 U0=7 m/s, pressure distribution Fig.4 Mesh-independent calculation results
on the central tube
首先在入口流速为7 m/s的情况下进行流场模拟，并与实验结果对比，验证流场计算数值模型．待流场稳定后，提取中间管表面压力，由式(1)计算压力系数Cp：
(1)
其中，p0是驻点压力，Ug=U0P/(P-D)为间隙流速．以驻点为0°沿顺时针方向画出压力分布曲线，如图3所示．图3同时给出了Mahon等[16]的实验测量结果，可以看出，数值结果与实验结果吻合较好．
本文流场网格尺寸主要受管子表面网格尺寸控制，在边界层网格径向划分方式不变的情况下，采用不同的周向分段数划分网格，验证网格对计算结果的影响，计算结果见图4．从图4可以发现，除120°～240°这个区域(尾迹)以外，总体而言各种网格下的中间管表面压力计算结果和实验测量值都比较接近．同时，随着周向分段数越来越多(网格越来越密)，压力计算结果逐渐收敛．综合权衡计算量和结果精度，最终决定选择管子周向为150°分段做为后续网格划分标准．
1.2 流致振动模拟方法
本文以阻尼机理控制的流弹稳定性问题为研究对象，对管束中间一根管子在升力方向做单自由度运动情况下的流固耦合过程进行模拟．如图5所示，管子除了受到流体力作用，还引入了外部弹簧和阻尼力．在流致振动计算中，中间管子在流体力和结构回复力作用下自由运动．
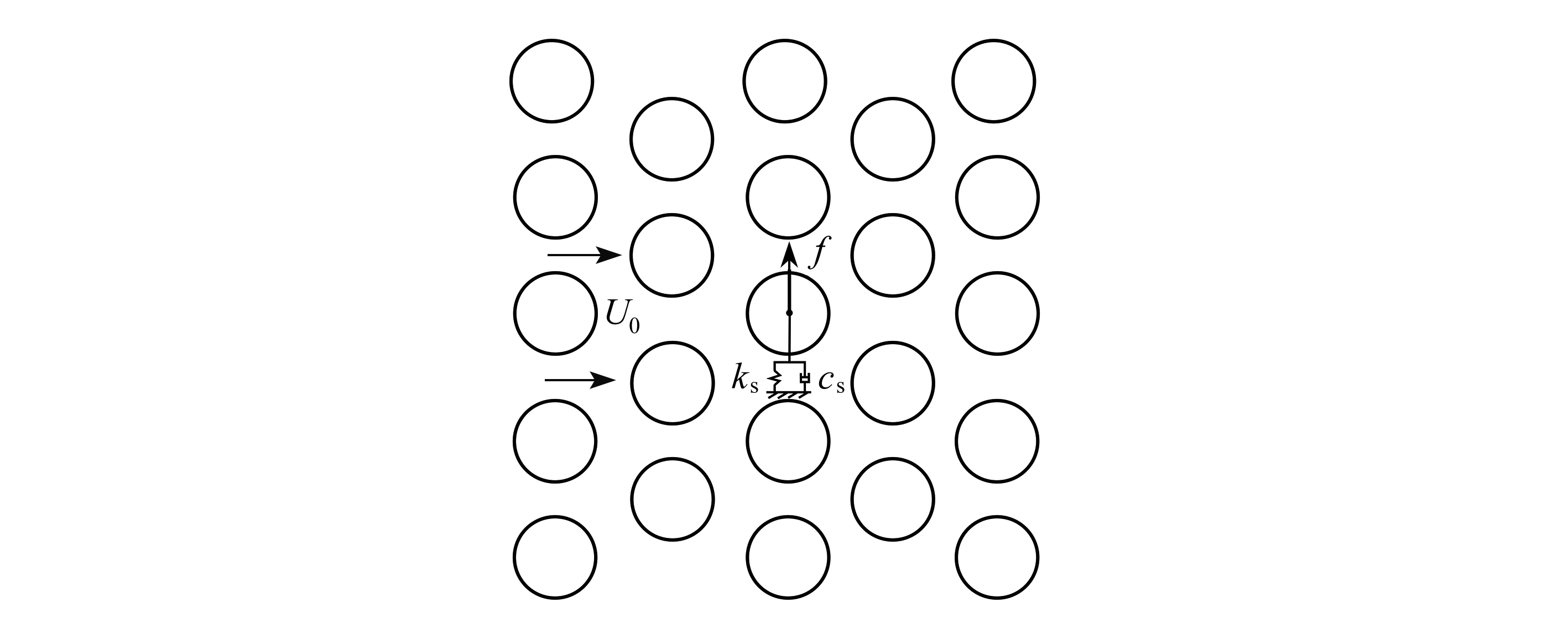
图5 管子流致振动示意图
Fig.5 The flow-induced vibration model
本文采取的流致振动模拟过程如下：在初始时刻首先让可动管子放置于远离平衡位置8.5 mm处，在初始位置进行流场计算．待流场稳定后，释放管子，开始流致振动计算，流场数值计算可以得到管子受到的流体力，利用流体力和结合动力学参数通过式(2)计算合力作用下管子的加速度:
(2)
将加速度对时间积分，求出当前时间步内管子的速度和位移，并利用管子位移计算结果更新流场网格．网格更新完成后，将计算时间向前推进，在新网格下开始流场计算，然后再计算管子的运动．
2 计 算 结 果
图6为入口流速U0=1.1 m/s时，中间管子位移时程曲线．管子从初始位置开始以固有频率(图7)做周期性衰减运动．图6同时给出了没有流体时管子的运动曲线．对比观察发现，流体的作用使管子运动衰减速度放缓．
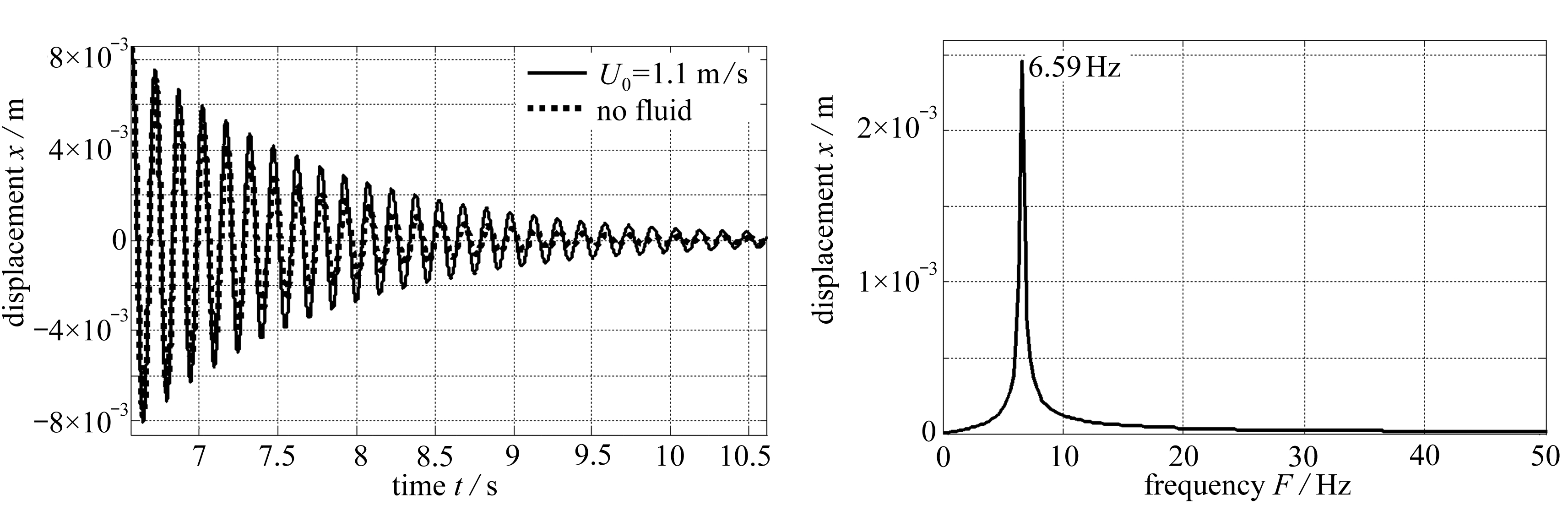
图6 U0=1.1 m/s时中间管子位移时程曲线 图7 U0=1.1 m/s时中间管子位移幅频曲线
Fig.6 The displacement time series for U0=1.1 m/s Fig.7 The displacement spectrum for U0=1.1 m/s
图8、9分别是管子受到的流体力时程和幅频曲线．从图中可知，流体力呈现周期性衰减振荡，流体力的主要频率和管子的固有频率非常接近．流体力时程最开始一段的波动不太规律，这是由于刚打开动网格进行流致振动计算时，流场的瞬态效应还比较明显，随着时间推移，流场逐渐受到管子运动的扰动，最终变成周期衰减振荡．因此，可以认为流体力波动是由管子运动引起的．此时管子运动对流场的影响更明显，原因是当前流速(U0=1.1 m/s)较小，流体携带的能量与管子自身的机械能相比还比较小．
图8 升力时程(U0=1.1 m/s)图9 升力幅频曲线(U0=1.1 m/s)
Fig.8 The fluid force time series for U0=1.1 m/s Fig.9 The fluid force time series for U0=1.1 m/s
3 流体力模型研究
管子运动方程中，流体力f的具体表达式未知．流体力和管子的运动状态相关， f应该是管子位移x、速度
和加速度
的函数．本文以空气作为实验流体，忽略流体附加质量，不考虑管子加速度对f的贡献．流体力还受流场状态控制，而这个控制量一般是指入口流速U0．因此，流体力f应该是管子位移、速度和入口流速U0这三个量的函数，记为
流体力包含流弹力和湍流力[8]，与流弹力相比，湍流力的作用可以忽略．本文采用Reynolds平均方程求解流场，得到的结果只有平均流动，流体力主要是流弹力部分，所以此处
就是流弹力．利用管子位移、速度和流体力数据可以生成力-状态图[9](图10)．
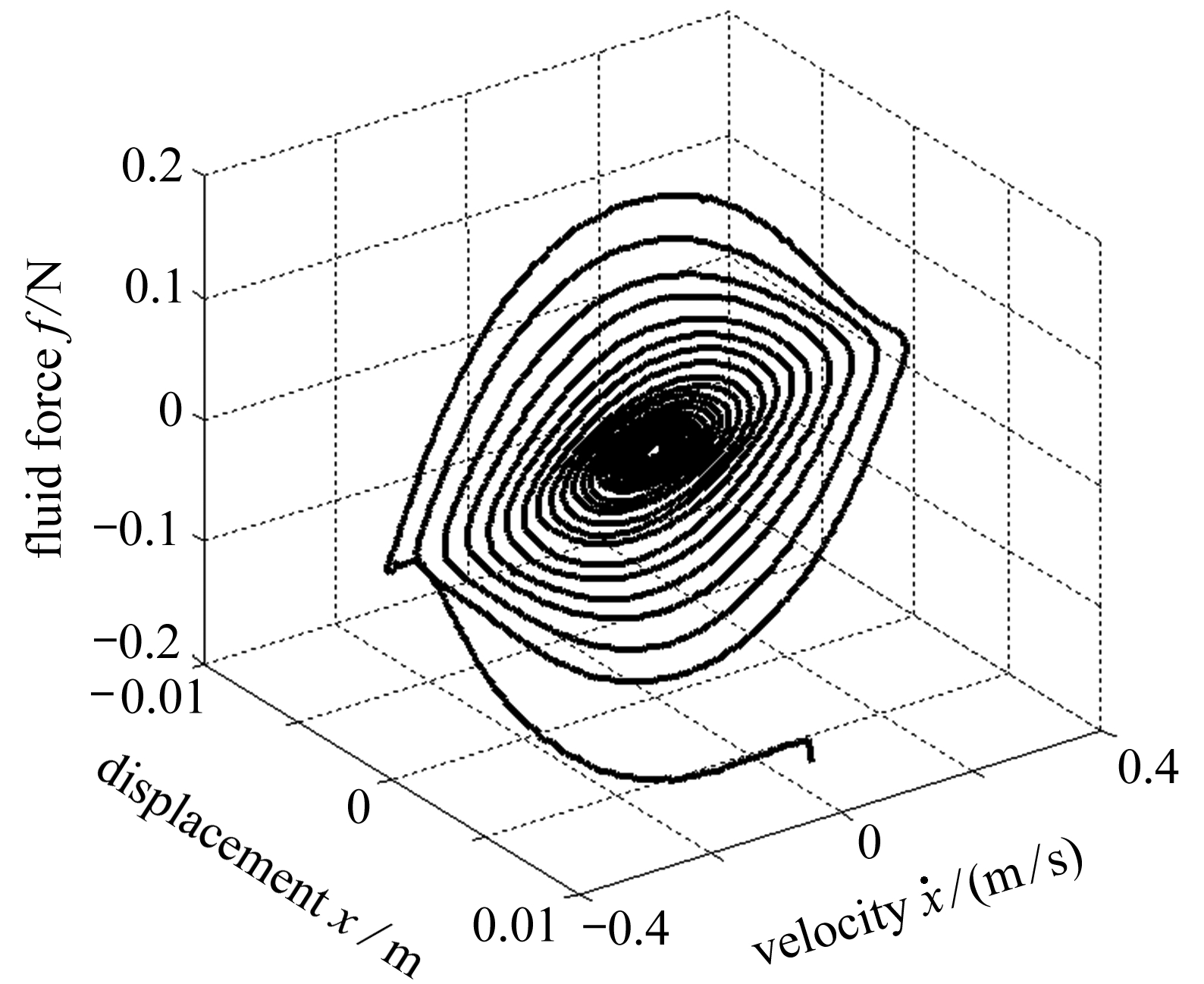
(a) 力-状态图
(a) The force-state map
(b) 力-位移图 (c) 力-速度图
(b) The force-displacement map (c) The force-velocity map
图10 力-状态图及其投影(U0=1.1 m/s)
Fig.10 Force-state map and its projections(U0=1.1 m/s)
图10(b)、10(c)分别是将力状态面向速度和位移方向投影的结果．观察发现流体力随速度和位移有近似三次多项式的关系，采用如下二元三次多项式来拟合流体力、位移、速度之间的关系：
(3)
利用式(3)结合每组入口流速工况下的流体力和运动数据，计算其中的未知流体力系数，结果见图11(图中的圆圈)．
再对流体力系数cij与入口流速U0进行拟合．对流体力系数随U0的变化趋势进行观察后决定对c10,c20,c21,c02用二次多项式拟合，将c30,c01,c11,c12,c03拟合为U0的线性函数：
(4)
最终拟合情况如图11中曲线所示，拟合参数见表1．
图11 流体力系数
Fig.11 Fluid force coefficients
表1 流体力系数对入口流速拟合系数
Table 1 Fluid force coefficients
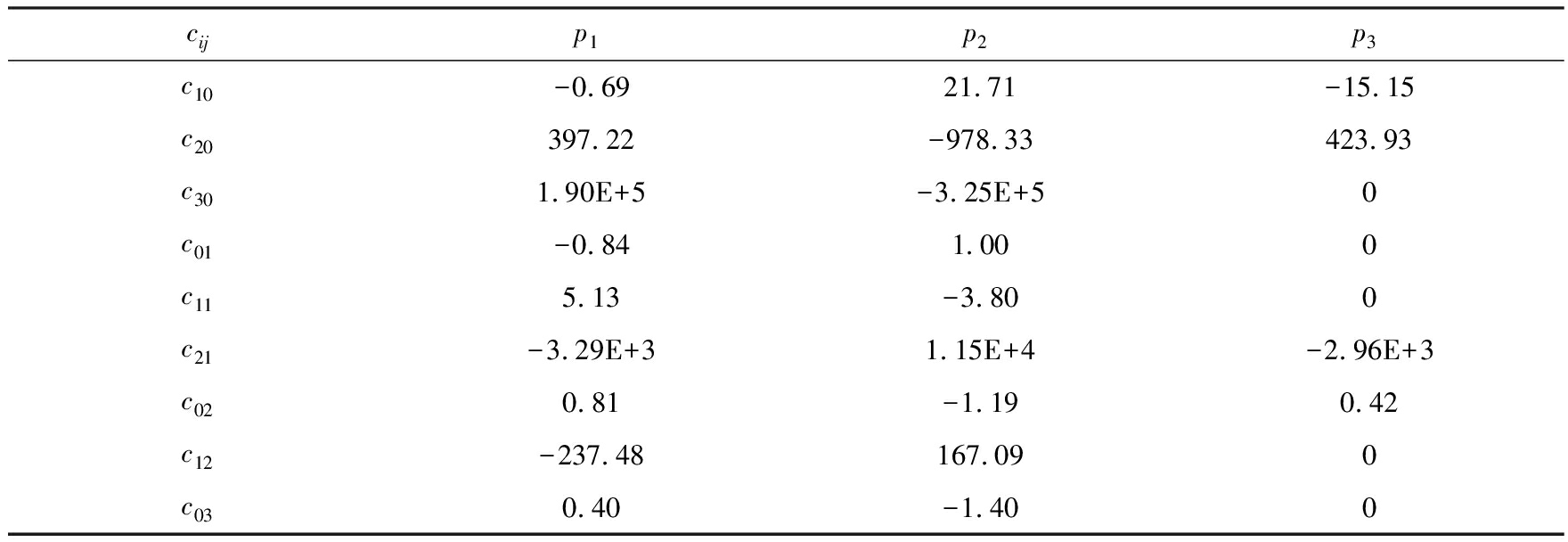
cijp1p2p3c10-0.6921.71-15.15c20397.22-978.33423.93c301.90E+5-3.25E+50c01-0.841.000c115.13-3.800c21-3.29E+31.15E+4-2.96E+3c020.81-1.190.42c12-237.48167.090c030.40-1.400
结合式(3)、(4)和表1中的系数，就可以确定流体力的具体形式．
在流体力模型(3)中，c10和c01分别是位移和速度线性项的系数，这两项的相反数分别是流体附加刚度和流体附加阻尼(因为本文是将流体力作为外载荷，把流体力移项到管子运动方程右边，其系数才是相应的附加刚度和附加阻尼等)．从图11可知，流体线性刚度系数c10为负值，其绝对值随时间逐渐增大，这相当于流体附加刚度-c10随流速逐渐增加．同理，流体附加阻尼-c01随流速不断减小．如果只考虑流体力的线性部分，最终流体阻尼将克服结构阻尼，使管子发生运动失稳．
现在利用流体力模型预测管子发生流弹失稳的临界流速，用这种方法对流体力模型进行验证．管子受到流体力和结构回复力共同作用，在一个运动周期内合外力对管子做功为
(5)
设管子位移方程为
x=Asin(ωt)．
(6)
利用流体力模型(3)结合式(6)代入式(5)，计算合力做功得
(7)
当一个运动周期内合外力对管子做功为0时，管子运动进入极限环状态．由W=0可得极限环振幅方程：
(8)
其中c03,c21和c01是随来流速度U0变化的流体力系数，也就是说方程(8)解的情况受U0影响．U0较小时，方程只有0解．U0增大并超过某一临界值后，方程(8)出现非0实根，此时管子存在多个平衡状态，方程的非0实根是相应平衡状态的振幅．调整U0，在不同系数下对方程(8)进行求解，使方程(8)首次出现非0实根的流速便是管子发生流弹失稳的临界流速．流弹失稳临界流速还受结构参数影响，改变方程(8)中结构阻尼cs的大小，可以计算不同结构情况下流弹失稳临界流速，结果如图12所示．
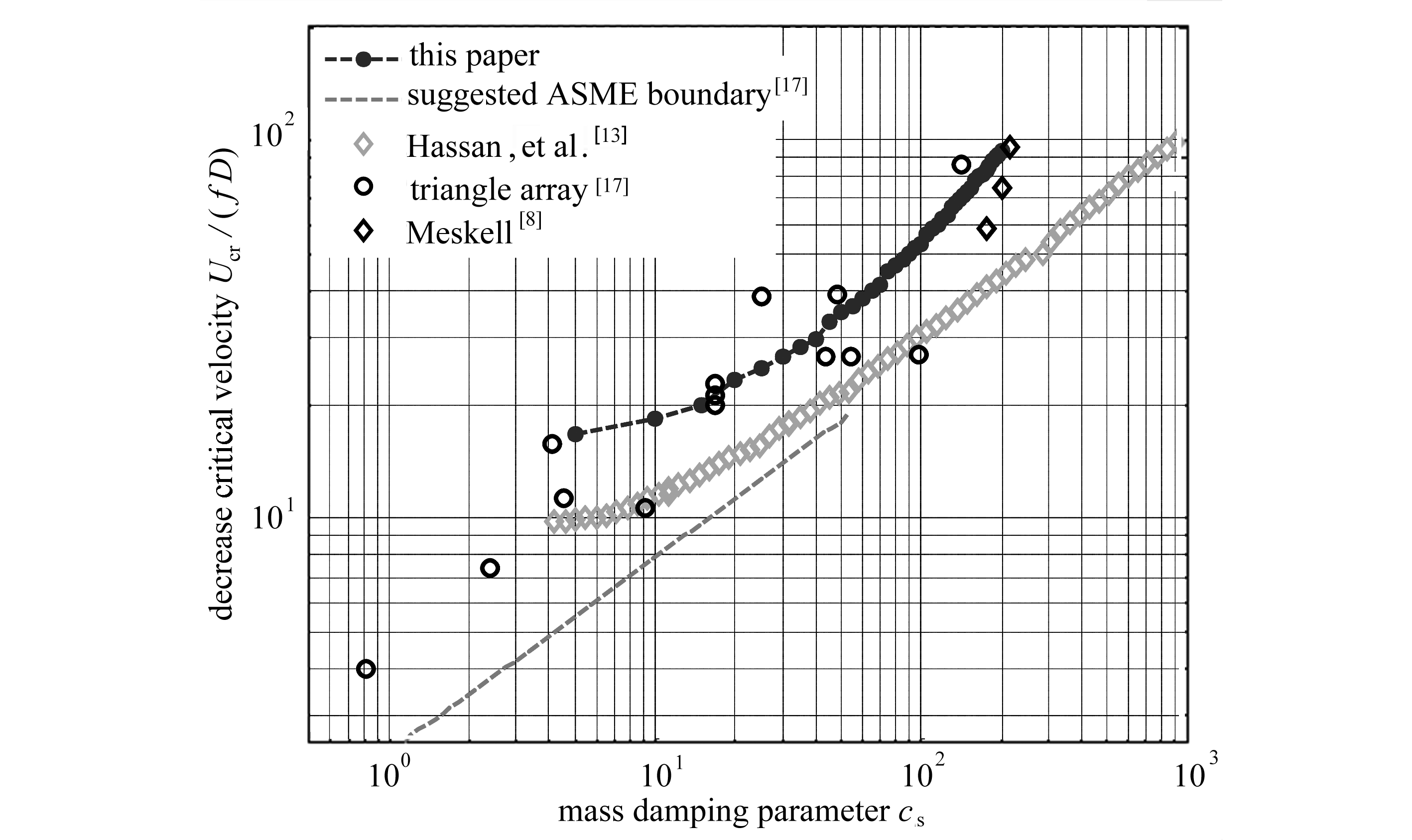
图12 临界流速随质量阻尼变化曲线
Fig.12 Comparison of the predicted critical flow velocity with the experimental data
从图12可以看出，用本文的流体力模型预测出的临界速度和文献[8,13,17]中给出的值较为接近，这说明了模型的合理性．
4 结 论
本文建立了管束结构流致振动数值仿真模型，计算得到了不同流速情况下管子受到的流体力和运动数据．确定了一种建立管束结构流弹失稳流体力模型的方法．这种方法以选定的函数作为流体力模型，结合流体力和运动数据计算流体力系数，通过拟合流体力系数和流速关系引入流速对流体力的影响，得到与管子速度、位移以及入口流速相关的流体力模型．利用本文流体力模型对管束结构在不同质量阻尼系数下的流弹失稳临界流速计算值与文献中的数值较为接近，说明了本文方法的合理性．
[1] AU-YANG M K.Flow-Induced Vibration of Power and Process Plant Components: a Practical Workbook[M].New York: ASME Press, 2001.
[2] LEVER J H.A theoretical model for fluid-elastic instability in heat exchanger tube bundles[D].PhD Thesis.Hamilton: McMaster University, 1983.
[3] 聂清德, 郭宝玉, 丁学仁, 等.换热器管束中的流体弹性不稳定性[J].力学学报, 1996, 28(2): 151-158.(NIE Qingde, GUO Baoyu, DING Xueren, et al.Fluidelastic instability of heat exchanger array[J].Chinese Journal of Theoretical and Applied Mechanics, 1996, 28(2): 151-158.(in Chinese))
[4] PRICE S J, PAIDOUSSIS M P.An improved mathematical model for the stability of cylinder rows subject to cross-flow[J].Journal of Sound and Vibration, 1984, 97(4): 615-640.
[5] PRICE S J, VALERIO N R.A non-linear investigation of single-degree-of-freedom instability in cylinder arrays subject to cross-flow[J].Journal of Sound and Vibration, 1990, 137(3): 419-432.
[6] 蒋天泽, 李朋洲, 马建中.两相横流作用下的旋转三角形管束流弹失稳研究[J].核动力工程, 2019, 39(1): 33-36.(JIANG Tianze, LI Pengzhou, MA Jianzhong.Fluidelastic instability of rotated triangle tube bundles subject to two-phase cross-flow[J].Nuclear Power Engineering, 2019, 39(1): 33-36.(in Chinese)).
[7] CHEN S S, JENDRZEJCZYK J A.Stability of tube arrays in crossflow[J].Nuclear Engineering & Design, 1983, 75(3): 351-373.
[8] MESKELL C.Identification of a non-linear model for fluidelastic instability in a normal triangular tube array[D].PhD Thesis.Dublin: Trinity College, 1999.
[9] MASRI S F, CAUGHEY T K.A nonparametric identification technique for nonlinear dynamic problems[J].Journal of Applied Mechanics, 1979, 46(2): 433-447.
[10] 冯志鹏, 张毅雄, 臧峰刚.直管束流固耦合振动的数值模拟[J].应用数学和力学, 2013, 34(11): 1165-1172.(FENG Zhipeng, ZHANG Yixiong, ZANG Fenggang, Numerical simulation of fluid-structure interaction for tube bundles[J].Applied Mathematics and Mechanics, 2013, 34(11): 1165-1172.(in Chinese))
[11] 吴皓, 谭蔚, 聂清德.正方形排布管束流体弹性不稳定性数值计算模型研究[J].振动与冲击, 2013, 32(21): 102-106.(WU Hao, TAN Wei, NIE Qingde.A numerical model for fluid elastic instability of a square tube array[J].Journal of Vibration and Shock, 2013, 32(21): 102-106.(in Chinese))
[12] GILLEN S, MESKELL C.Numerical analysis of fluidelastic instability in a normal triangular tube array[C]//ASME Pressure Vessels & Piping Conference.Prague, Czech Republic, 2009.
[13] HASSAN M, GERBER A, OMAR H.Numerical estimation of fluidelastic instability in tube arrays[J].Journal of Pressure Vessel Technology, 2010, 132(4): 041307.
[14] ROMBERG O, POPP K.Fluid-damping controlled instability in tube bundles subjected to air cross-flow[J].Flow, Turbulence and Combustion, 1998, 61: 285-300.
[15] CHEN S S.圆柱结构的流动诱发振动[M].冯振宇, 张希农, 译.北京: 石油工业出版社, 1993.(CHEN S S.Flow-Induced Vibration of Circular Cylindrical Structures[M].FENG Zhenyu, ZHANG Xinong, transl.Beijing: Petroleum Industry Press, 1993.(Chinese version))
[16] MAHON J, MESKELL C.Surface pressure distribution survey in normal triangular tube arrays[J].Journal of Fluids and Structures, 2009, 25(8): 1348-1368.
[17] KANEKO S, NAKAMURA T, INADA F, et al.Flow-Induced Vibrations Classifications and Lessons From Practical Experiences[M].Academic Press, 2014.