引 言
各向异性材料在自然界和实际工程中广泛存在,木材、晶体和碳纤维布等便是其中的典型代表.此类材料的特点是在不同方向上性能有所差异,因而在工程应用中可充分利用优选方向的性能[1].与各向同性材料相比,各向异性材料的导热系数会随方向的改变而改变,导致材料内部的温度分布情况较前者更为复杂,因此对其开展热传导分析具有重要的意义.纵观以往研究,其中不乏与此类问题有关的成果.闫相桥和武海鹏[2]建立了正交各向异性材料三维热传导问题的有限元列式.Mera等[3]采用边界元法(BEM)中不同类型的单元对各向异性材料稳态热传导问题进行了分析.刘俊俏等[4]基于BEM研究了二维各向异性功能梯度材料(FGM)的热传导问题.陈闽慷等[5]采用顺序函数法对二维非线性非稳态条件下正交各向异性材料的热传导反问题进行了研究.谢佳萱等[6]应用改进的复变量无单元Galerkin方法求解了正交各向异性介质中的热传导问题.上述工作中涉及的有限元法(FEM)、BEM和无网格法等皆为数值计算中常用的工具.FEM作为应用最广的数值方法,可应对各种复杂形状,但受单元边界须与求解域边界一致的约束,不便求解复杂的不连续及其演化问题.BEM通过降维处理问题,但由于须先得到问题的基本解,不易进行非线性分析.无网格法采用一系列点来离散物理域,无需划分单元,便于求解大变形及不连续演化等问题,但此类方法在数值积分和边界条件处理等方面存在一定的困难.此外,以上数值方法在表征裂纹时均需要采用额外的策略,如FEM和BEM需使用多重结点方法,无网格法则通常借助可视性准则和衍射法等.
20世纪90年代初,由石根华博士创立的数值流形方法[7]诞生于岩石工程领域.该方法因数学中“流形”一词而获名,其融合了FEM和非连续变形分析方法(DDA),可实现对连续和不连续问题的统一求解.NMM的主要特点为:1) 数学覆盖(类似于FEM网格)无需适应物理域内外边界形状;2) 在保持原有数学覆盖不变的情况下,采用高阶形式的局部函数便可获得高阶次的整体逼近,以达到提高解精度的目的;3) 通过合理选取局部函数可准确表征待研究问题的局部物理特性;4) 可自然描述某些物理量(如跨越裂纹面的温度场)的不连续性.经过多年的发展,NMM已在理论及应用层面取得了较多的研究成果,如文献[8-16].在热分析方面,林绍忠等[17]采用NMM分析了大体积混凝土结构的温度场及温度应力;刘泉声和刘学伟[18]提出了裂隙岩体二维不稳定温度场求解的NMM;谭育新等[19]利用正六边形NMM研究了二维各向同性材料中的稳态热传导问题;Zhang等[20-21]基于NMM对FGM稳态及瞬态热断裂问题进行了研究.
据笔者所悉,采用NMM对各向异性材料热传导的分析尚未报道.鉴于此,本文从相关问题的控制方程和边界条件出发,结合NMM的双覆盖理论,建立用于求解典型连续及不连续各向异性材料热传导问题的NMM.在验证方法可行性和精度的基础上,探讨材料属性等因素对温度场的影响规律.
1 控制方程及边界条件
考虑如图1所示的由各向异性材料组成的物理域Ω中的热传导问题,域内包含孔洞和裂纹等不连续.Ω由封闭域Γ=ΓT∪Γq围成,其中,ΓT和Γq分别为Dirichlet边界和Neumann边界.该问题的控制微分方程为
(kijT, j),i+Q=0,
(1)
其中kij(i, j=1,2)为热传导系数,应满足k12=k21且k11k22-k12k21>0,当k11≠k22且k12=0时则退化为正交各向异性;T为温度;Q为热源;下标“,i”表示对总体直角坐标xi(见图1)的一阶偏导.

图1 各向异性材料中的热传导
Fig. 1 Heat conduction in an anisotropic material
相应的边界条件为
(2)
(3)
其中![]() 和
和![]() 分别为ΓT和Γq上给定的温度和热通量;ni(i=1,2)为外法向向量分量.
分别为ΓT和Γq上给定的温度和热通量;ni(i=1,2)为外法向向量分量.
2 NMM求解各向异性热传导问题
2.1 NMM简介
NMM引入了两套覆盖系统(即数学覆盖和物理覆盖)求解物理问题.数学覆盖是由一系列允许相互重叠且形状任意的数学分片组成,无需与物理域的内外边界重合,只需完全覆盖整个物理域.物理分片由各个数学分片和物理域求交而成,所有物理分片的并集则组成物理覆盖.若干个物理分片的重叠部分便形成NMM的基本计算单元,即流形单元(以下简称单元).
鉴于NMM的离散方式异于FEM和BEM等数值方法,本文以图2为例对其进行简要说明.图2(a)为待剖分的物理域Ω=Ω1∪Ω2,采用图2(b)中由一个矩形数学分片M1和一个三角形数学分片M2组成的数学覆盖将其完全覆盖.经物理域和数学分片求交后,得到图2(c)所示的四个物理分片P1,P2,P3和P4,其中P1和P2(P3和P4)由数学分片M1(M2)和物理域产生,这四个物理分片最终生成图2(d)中的E1~E6六个单元,以E2为例,其由物理分片P1和P3求交后得到.在完成域离散的基础上,进一步定义局部近似函数并采用与FEM类似的方式便可获得NMM的离散方程及相应的近似解[8].
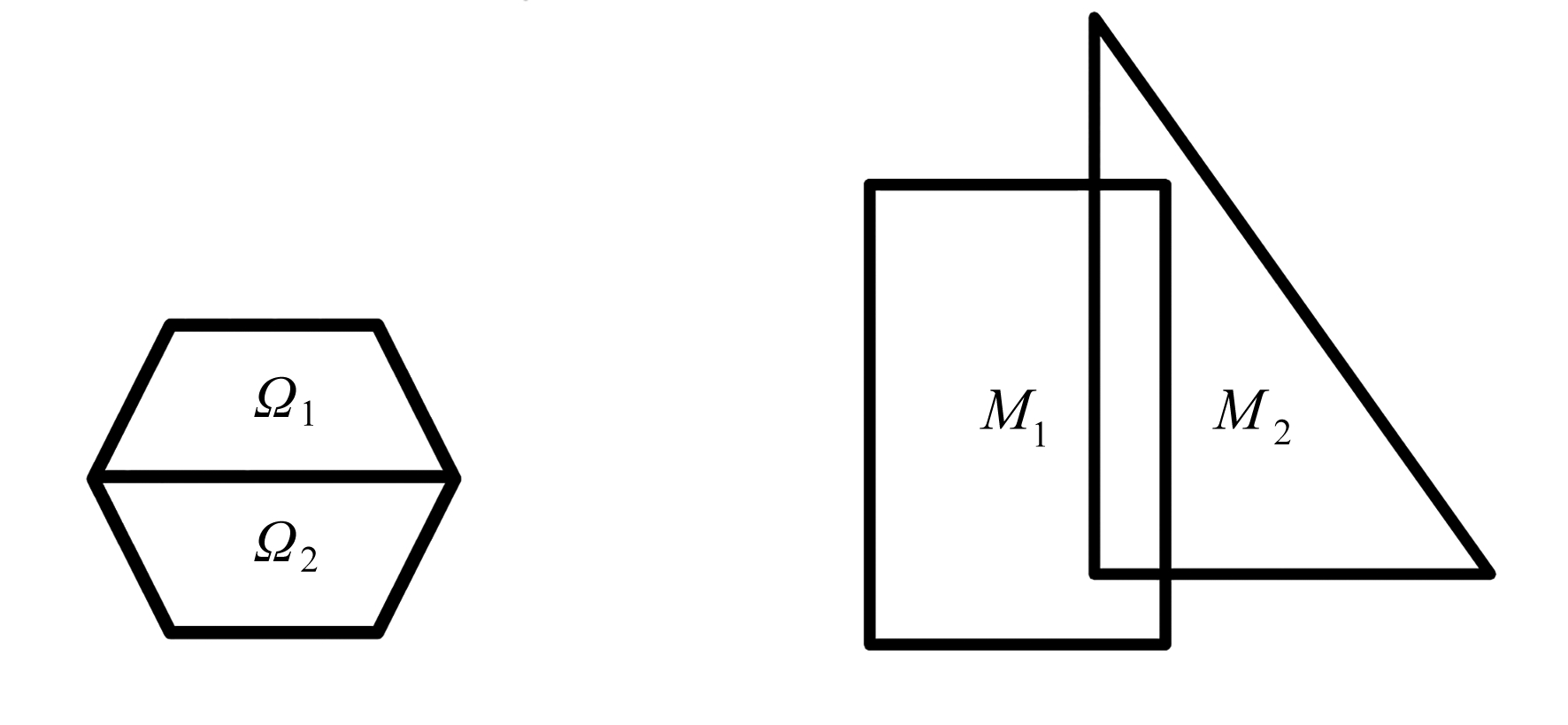
(a) 物理域 (b) 数学覆盖
(a) The physical domain(b) The mathematical cover
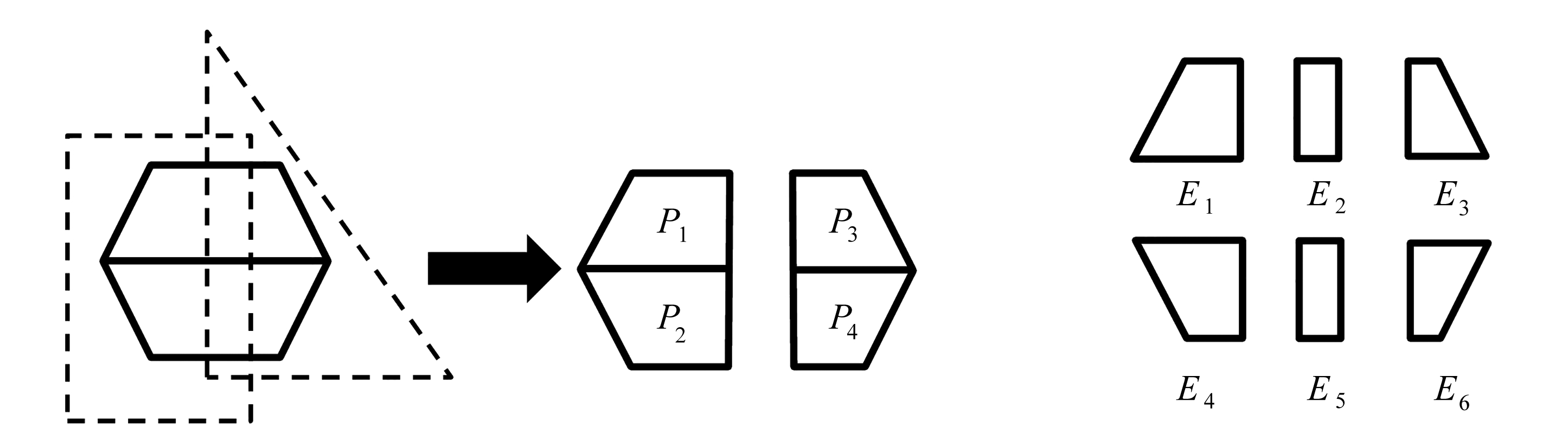
(c) 物理分片的形成过程 (d) 单元的生成
(c) Generation of physical patches (d) Generation of manifold elements
图2 NMM离散过程图示
Fig. 2 Illustration of the NMM discretization
2.2 NMM的温度场近似
由NMM的理论[7]知,定义在任一单元E上的温度场近似函数可表示为[20]
(4)
其中N为形成单元E的物理分片个数;x=(x1,x2);wI(x)为物理分片PI所对应的权函数,它继承于生成PI的数学分片MJ上定义的权函数wJ[8],且wJ应满足
(5)
此外,由于权函数具有单位分解的特性[22],对于所有包含点x的数学分片,还应满足
(6)
TI(x)为定义在PI上的局部函数,对于连续物理分片(即内部无裂纹等不连续因素的物理分片),常取为[20]
TI(x)=P(x)aI,
(7)
其中aI为定义在PI上的常规未知量列阵;P(x)为完全多项式基函数, 对于二维情况, 可表示为
(8)
对包含不连续体的物理分片,局部函数可根据不连续的属性进行合理选取.如对内部包含裂尖的物理分片(称其为奇异物理分片),局部函数可进一步取为
TI(x)=P(x)aI+Φ(x)bI,
(9)
其中bI为定义在PI上的附加未知量列阵;Φ(x)为由裂尖渐近温度场提取出的基函数,对绝热裂纹,仍采用文献[23]给出的形式,即
(10)
其中(r,θ)为位于局部直角坐标系x′1O′x′2中且以裂尖为原点的极坐标(参见图1).
2.3 NMM求解各向异性热传导问题的总体方程
根据式(1)~(3)并采用罚函数法[19]处理式(2)中的Dirichlet边界条件,得到等效积分形式为
(11)
其中![]() 和
和![]() 为任意的标量函数;λ为罚函数.
为任意的标量函数;λ为罚函数.
令![]() (δ为一阶变分)并利用Green公式对式(11)中第一个积分的前四项进行分部积分后,得到其弱形式:
(δ为一阶变分)并利用Green公式对式(11)中第一个积分的前四项进行分部积分后,得到其弱形式:
(12)
由上式可得到各向异性热传导问题的变分原理,即
δΠ(T)=0,
(13)
其中Π(T)为问题的泛函,其具体形式为
(14)
用式(4)中的Th去逼近真实温度场T,则有
δT≈δTh=wIδTI.
(15)
将式(15)代入式(12)中并考虑到未知量变分的任意性,得到NMM求解各向异性热传导问题的总体方程:
KT=F,
(16)
其中T为总体未知量列阵;K和F分别为总体热传导矩阵和等效温度载荷列阵,均由相应的单元矩阵组装而成,任一单元E对K和F的贡献分别为
(17)
(18)
其中上标T表示矩阵的转置;![]() 和
和![]() 分别为与单元E相关的物理域、温度边界和热流边界;矩阵B和G的具体形式为
分别为与单元E相关的物理域、温度边界和热流边界;矩阵B和G的具体形式为
(19)
(20)
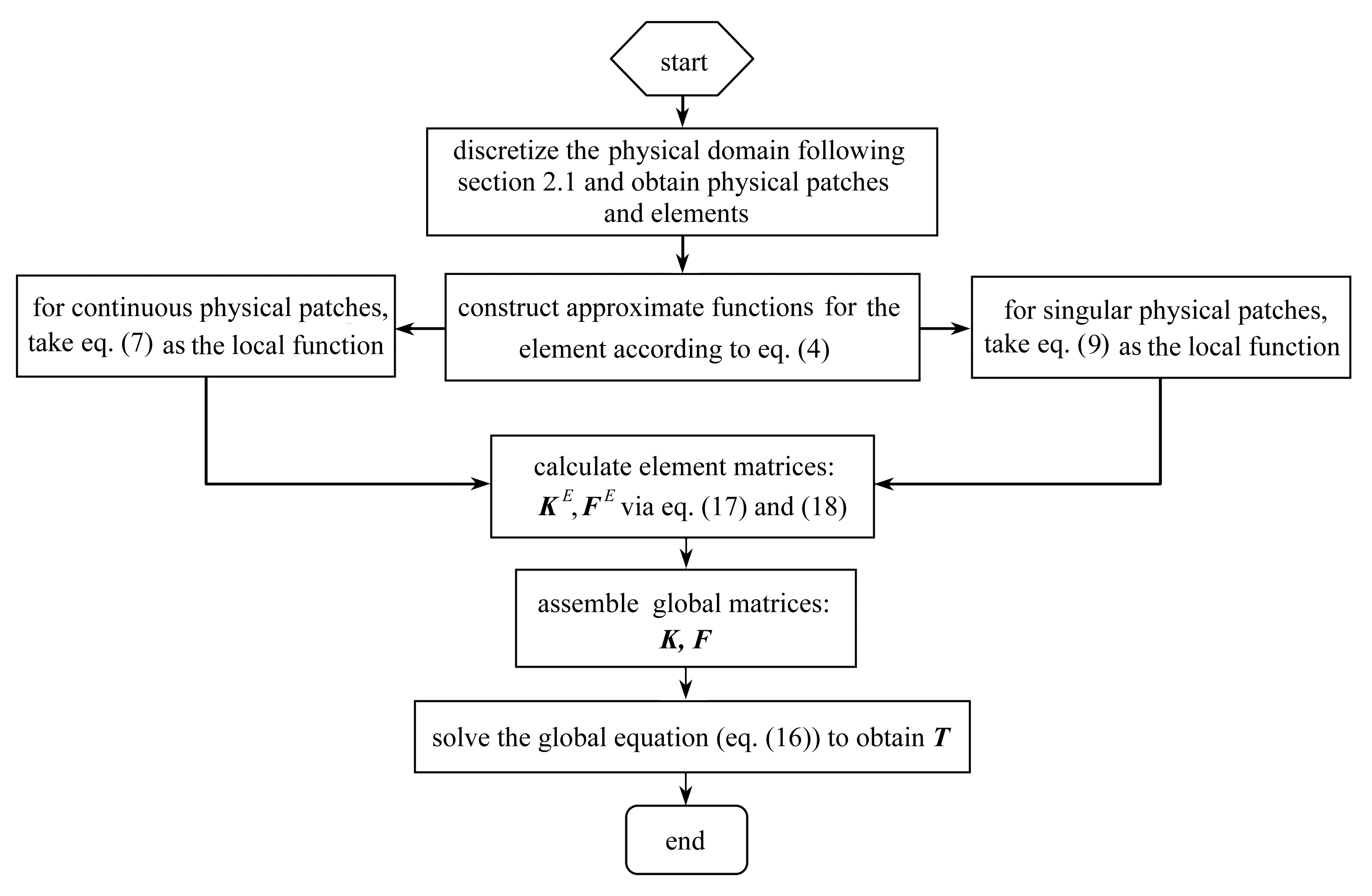
图3 NMM模拟热传导问题流程图
Fig. 3 The flowchart of the NMM for heat conduction problems
对连续物理分片,
(21)
(22)
对奇异物理分片,
(23)
(24)
基于上述讨论,本文采用C++语言编制计算程序以实现相关算法,相应的实施步骤如图3所示.
3 数 值 算 例
本节通过四个代表性算例验证本文方法的可行性与精度,并探讨典型问题中的温度场分布规律.首先对两个具有解析解的连续问题(即均质矩形板及均质圆板中的热传导问题)进行分析以探讨方法的收敛性和精度,在此基础上对两个不连续算例(即含多孔洞FGM方板和含交叉裂纹FGM方板中的热传导问题)进行仿真,分析材料参数等因素对温度场的影响.考虑到NMM中的数学覆盖可不与物理域的边界一致及规则单元的便利性,模拟中一律采用由正四边形组成的数学覆盖进行离散.式(4)中的权函数按文献[24]选取.此外,式(8)中的完全多项式基取为常数基,式(17)和(18)中的罚值λ取为1010[25].
3.1 有热源矩形板的热传导问题
考虑图4所示的有内部热源的均质正交各向异性矩形板.板尺寸L×W=1.0×0.8,k11=1,k22=4.板左侧和右侧的温度分别为![]() 和
和![]() 上、 下边界绝热, 热源强度Q(x1, x2)=x1.该问题对应的温度场解析解为[6]
上、 下边界绝热, 热源强度Q(x1, x2)=x1.该问题对应的温度场解析解为[6]
(25)

图4 物理模型 图5 h=0.05时的数学覆盖
Fig. 4 The physical model Fig. 5 The mathematical cover for h=0.05
NMM仿真时,为探讨本文方法的收敛性,选用四种尺寸分别为h=0.4,0.2,0.1,0.05的数学覆盖对平板进行剖分(h为数学单元的边长,以h=0.05的情况为例,其对应的数学覆盖见图5,其中左上角的填充区即为数学单元,四个数学单元则构成一个数学分片).图6给出了h取不同值时的离散域,相应的物理分片和单元数量列于表1.图7给出了h=0.05时的温度场分布情况,可以看出,温度场仅沿水平方向变化,此规律与式(21)中解析解的形式能很好地吻合.表2列出了h取不同值时九个测点(测点编号及坐标分别为:A(0.1, 0.08),B(0.2, 0.16),C(0.3, 0.24), D(0.4, 0.32), E(0.5, 0.40), F(0.6, 0.48), G(0.7, 0.56), H(0.8, 0.64)和I(0.9, 0.72))温度的NMM结果及对应的精确解,由表中的数据可知,随着单元尺寸的减小,计算结果逐渐逼近理论解,很好地展示了方法的收敛性及精度.
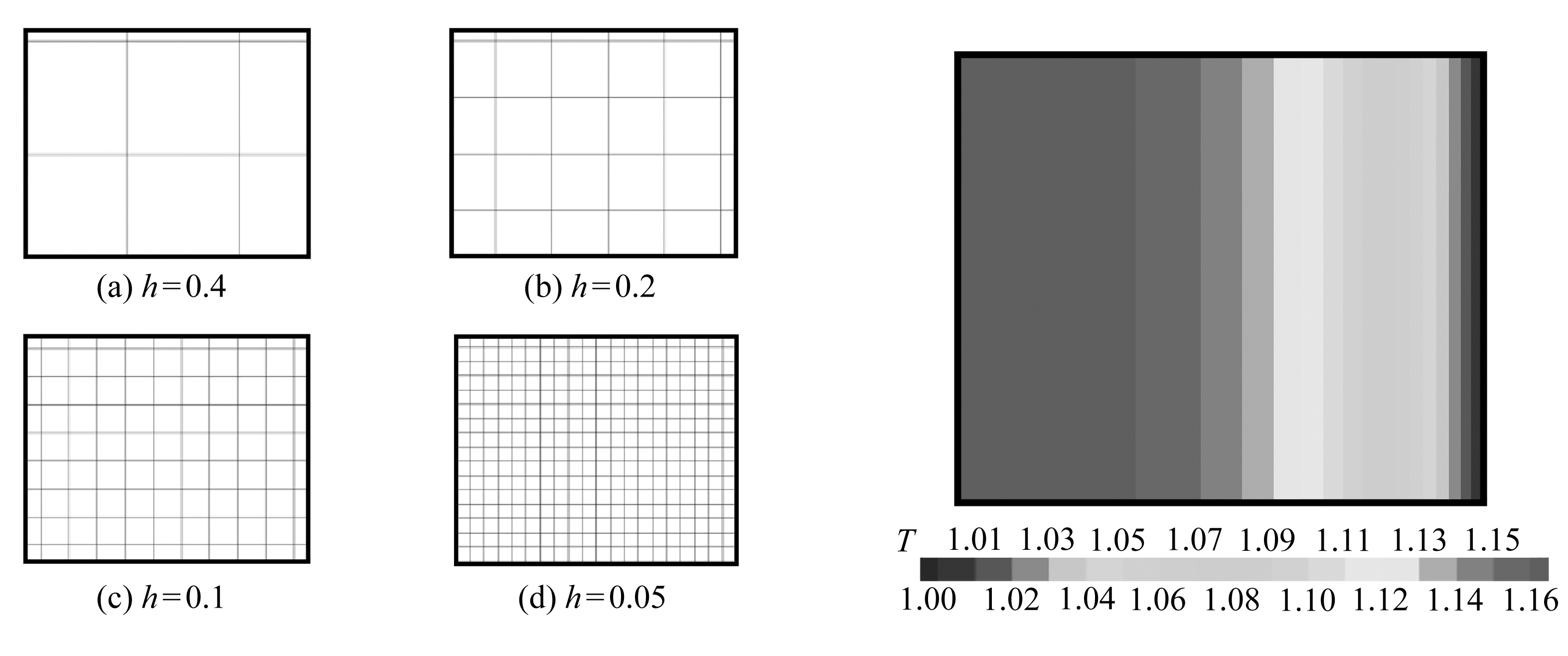
图6 数学单元尺寸取不同值时的离散域 图7 h=0.05时的温度场分布
Fig. 6 Discretized domains at different Fig. 7 Temperature distribution for h=0.05mathematical element sizes
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
表1 数学单元尺寸取不同值时物理分片和单元的个数
Table 1 Numbers of physical patches and elements at different mathematical element sizes

h0.40.20.10.05number of physical patches1642120378number of elements93099340
表2 数学单元尺寸取不同值时测点的温度
Table 2 Temperatures of measuring points at different mathematical element sizes

measuring pointh=0.4h=0.2h=0.1h=0.05analytical solutionA1.164 61.166 21.166 31.166 41.166 5B1.162 51.164 41.165 01.165 31.165 3C1.160 51.161 11.161 71.162 11.162 2D1.151 61.154 31.155 51.156 01.156 0E1.135 81.144 11.145 21.145 81.145 8F1.120 01.128 31.129 91.130 61.130 7G1.104 21.107 01.108 61.109 51.109 5H1.077 11.078 21.080 31.081 31.081 3I1.038 51.041 91.044 01.045 21.045 2
3.2 无热源圆板的热传导问题
考虑图8所示的均质各向异性圆板.板半径R=1.0,k11=5,k22=1,k12=k21=2,外边界温度![]() 与此对应的全域温度场解析解为[2]
与此对应的全域温度场解析解为[2]
(26)
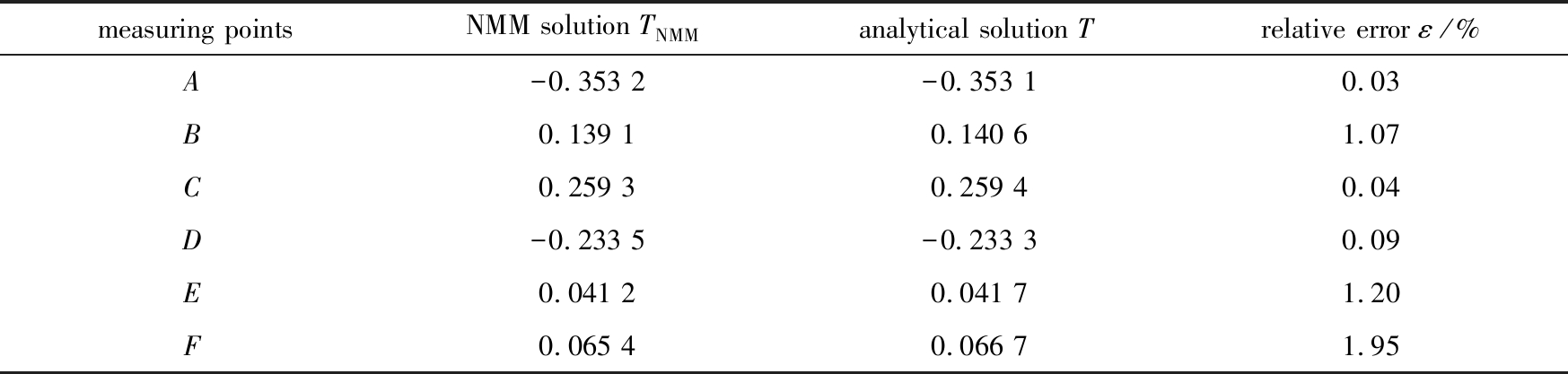
NMM模拟时,采用h=0.04的数学覆盖对板进行剖分,离散后的圆板如图9所示,其中包含2 172个物理分片和2 069个单元.图10给出了温度场的整体分布情况.表3给出了六个测点(即A(-0.5, 0.75), B(0.0, 0.75), C(0.5, 0.75), D(-0.5, 0.5), E(0.0, 0.5)和F(0.5, 0.5))温度值的NMM结果及相应的理论解,且两者最大相对误差为1.95%,可见数值解与解析解具有很好的一致性.

图8 物理模型 图9 离散域 图10 温度场分布
Fig. 8 The physical modelFig. 9 The discretized domainFig. 10 The temperature distribution
表3 不同测点的温度
Table 3 Temperatures at different measuring points
measuring pointsNMM solution TNMM analytical solution Trelative error ε/%A-0.353 2-0.353 10.03B0.139 10.140 61.07C0.259 30.259 40.04D-0.233 5-0.233 30.09E0.041 20.041 71.20F0.065 40.066 71.95
3.3 含孔洞无热源FGM板的热传导问题
为展示本文方法分析不连续热传导问题的能力,选取图11所示的含五个孔洞的FGM正交各向异性方板进行研究.板宽为L=4L0=2.0,板内两种规格的孔洞半径分别为R=0.4和r=0.2,板顶部和底部的温度分别为![]() 和
和![]() 其余边界均绝热,x1和x2方向的热传导系数k11和k22沿相应方向按指数函数变化,即
其余边界均绝热,x1和x2方向的热传导系数k11和k22沿相应方向按指数函数变化,即
k11=eβx1,
(27)
k22=eβx2,
(28)
其中β为材料梯度参数.
NMM分析时主要考察材料梯度对温度场的影响,为此,分别取β=0.2,0.4,0.6,…,1.2.数学单元尺寸h=0.04,对应的离散域见图12,其中包含2 332个物理分片和2 116个单元.图13给出了β=1的温度场等值云图,可以发现孔洞的存在对温度场具有明显的扰动作用.图14给出了梯度参数取不同值时五个测点:A(-0.5, 0.3), B(0.3, 0.5), C(-0.3, -0.5), D(0.5, -0.3)和E(0.4, 0.0)的温度变化情况,可知各测点的温度均随β的增大而减小.
3.4 含裂纹无热源FGM板的热传导问题
本例通过分析图15所示的含交叉型裂纹FGM正方形板进一步展示方法对更复杂不连续问题的模拟能力,并探讨裂纹构型对温度场的影响规律.板宽为L=2L0=2.0,各分支裂纹的长度均为a且与x1方向的倾角为φ.板左侧的温度为![]() 大小为
大小为![]() 的热流经板右侧流入域内,其余边界均绝热.k11和k22分别沿着x1和x2方向按线性函数变化,即
的热流经板右侧流入域内,其余边界均绝热.k11和k22分别沿着x1和x2方向按线性函数变化,即
k11=2x1+8,
(29)
k22=2x2+8.
(30)

图11 物理模型 图12 离散域
Fig. 11 The physical model Fig. 12 The discretized domain
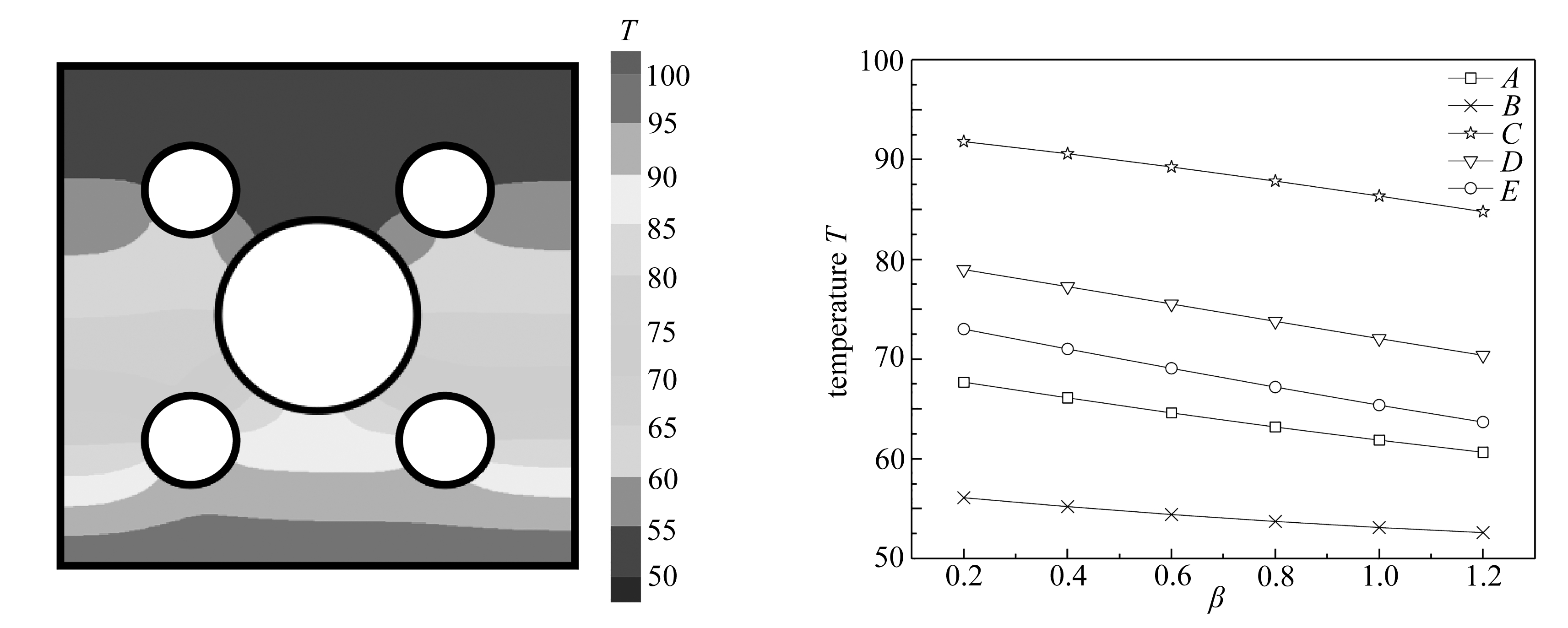
图13 β=1时的温度场分布 图14 梯度参数取不同值时测点的温度
Fig. 13 The temperature distribution for β=1 Fig. 14 Temperatures of measuring points at different graded parameters

图15 物理模型 图16 a=0.4和φ=45°时的离散域
Fig. 15 The physical model Fig. 16 The discretized domain for a=0.4 and φ=45°
NMM分析时, 取h=0.04.首先研究裂纹长度对温度的影响.令φ=45°, a=0.2,0.3,0.4,0.5,0.6.图16为a=0.4时的离散域,共包含2 784个物理分片和2 628个单元.图17给出了相应温度场的分布情况,从图中可以明显地观察到温度场在穿越各裂纹面时的跳跃,这便直观展现了NMM可自然表征场函数在跨越裂纹时不连续的优点.图18给出了五个测点:A(-0.75, 0.75),B(-0.5, 0.5),C(0.0, 0.5),D(0.5, 0.5)和E(0.75, 0.75)的NMM模拟结果,容易看出各测点的温度均随裂纹长度的增加而增大,但点A和B的温度变化不如其他点显著.

图17 a=0.4和φ=45°时的温度场分布图18 裂纹长度取不同值时测点的温度
Fig. 17 The temperature distribution for Fig. 18 Temperatures of measuring points a=0.4 and φ=45° at different crack lengths
最后讨论倾角的影响.取a=0.4,φ=15°,30°,45°,…,90°.NMM得到的测点温度值绘于图19,可以看出,点A和B的温度对倾角的变化不敏感;其他点的温度则随着倾角的增加先增大后减小,当倾角取75°时温度最高.
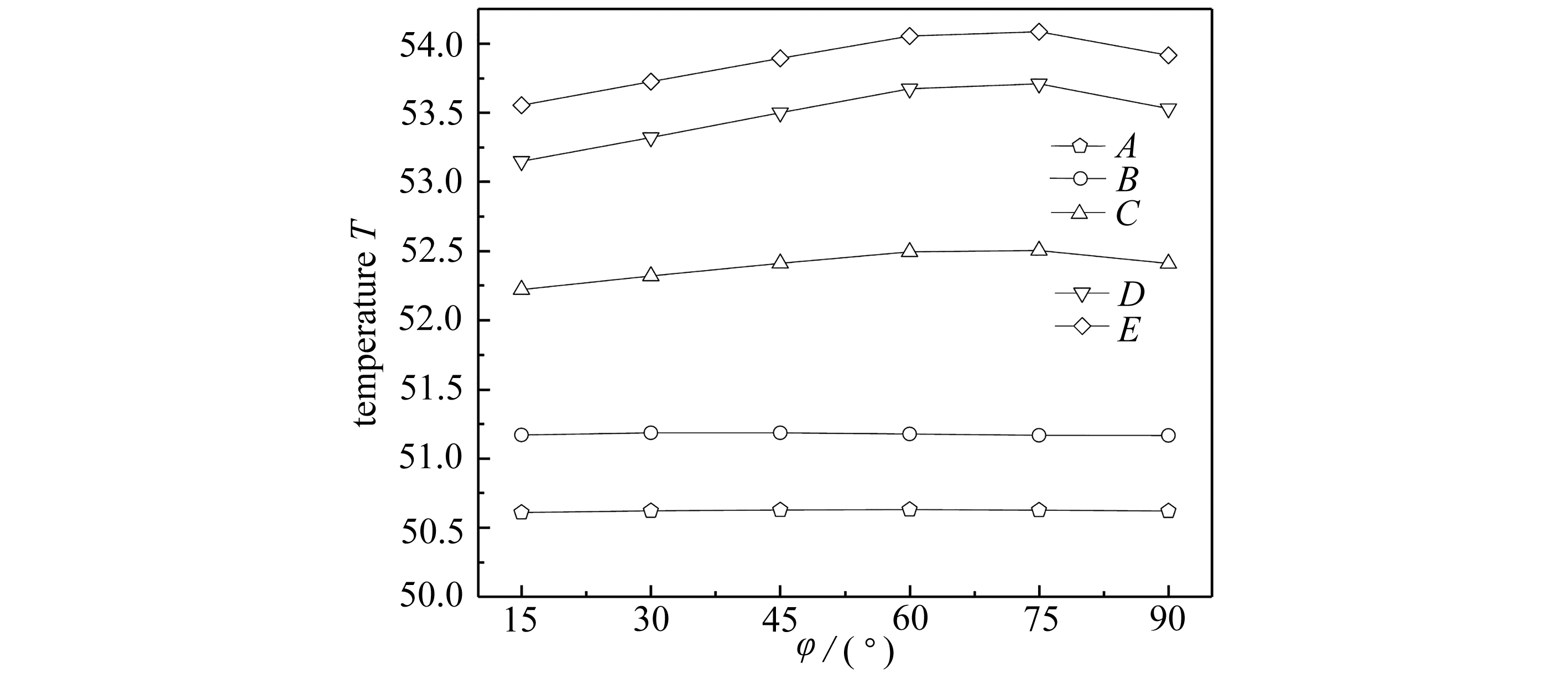
图19 倾角取不同值时测点的温度
Fig. 19 Temperatures of measuring points at different inclined angles
4 结 语
本文发展了用于求解各向异性材料稳态热传导问题的NMM.根据问题的控制微分方程、边界条件以及变分原理,导出了求解此类问题的总体离散方程.在算例测试环节,通过对具有解析解的连续问题的模拟验证了方法收敛性和精度,在此基础上进一步对含多孔洞/交叉裂纹等的不连续问题进行了仿真,探讨了材料参数和裂纹构型(如裂纹的长度和倾角)等因素对温度场的影响规律;此外,通过对裂纹问题的研究还直观展现了NMM可自然表征穿越裂纹面的温度场不连续的特点.与其他基于网格的数值方法(如FEM和BEM)相比,本文方法的明显优势在于:1) 域离散时,不必像FEM和BEM一样满足网格与求解域的所有边界一致的规定,因而无论是对易于处置的矩形边界(如算例3.1)或如算例3.2中不易操作的圆形边界甚至内部含孔洞(如算例3.3)和裂纹(如算例3.4)的物理域,均可采用均匀的数学覆盖;2) 无需采用任何附加策略(如FEM和BEM在模拟中需使用多个结点)即可以自然的方式描述某些物理量的不连续性.基于本文的工作,NMM在后续可应用于各向异性材料瞬态热传导以及热断裂等问题的研究中.
致谢 本文作者衷心感谢南昌航空大学研究生创新专项资金项目(YC2018069)对本文的资助.
[1] PRESTINI D, FILIPPINI G, ZDANSKI P S B, et al. Fundamental approach to anisotropic heat conduction using the element-based finite volume method[J]. Numerical Heat Transfer, Part B: Fundamentals, 2017, 71(4): 327-345.
[2] 闫相桥, 武海鹏. 正交各向异性材料三维热传导问题的有限元列式[J]. 哈尔滨工业大学学报, 2003, 35(4): 405-409. (YAN Xiangqiao, WU Haipeng. Finite element formulation of 3-D heat transfer in orthotropic materials[J]. Journal of Harbin Institute of Technology, 2003, 35(4): 405-409.(in Chinese))
[3] MERA N S, ELLIOTT L, INGHAM D B, et al. A comparison of boundary element method formulations for steady state anisotropic heat conduction problems[J]. Engineering Analysis With Boundary Elements, 2001, 25(2): 115-128.
[4] 刘俊俏, 苗福生, 李星. 二维各向异性功能梯度材料热传导的边界元分析[J]. 西安交通大学学报, 2013, 47(5): 77-81.(LIU Junqiao, MIAO Fusheng, LI Xing. Boundary element analysis of the two-dimensional heat conduction equation for anisotropic fuctionally graded materials[J]. Journal of Xi’an Jiaotong University, 2013, 47(5): 77-81.(in Chinese))
[5] 陈闽慷, 杜涛, 苏雪, 等. 二维非线性正交各向异性材料的瞬态热传导反问题数值方法[J]. 国防科技大学学报, 2017, 39(1): 194-198.(CHEN Minkang, DU Tao, SU Xue, et al. A numerical method for two-dimensional nonlinear transient inverse heat conduction problems for orthotropic material[J]. Journal of National University of Defense Technology, 2017, 39(1): 194-198.(in Chinese))
[6] 谢佳萱, 李冬明, 聂峰华, 等. 正交各向异性稳态热传导问题的ICVEFG方法[J]. 固体力学学报, 2019, 40(1): 74-81.(XIE Jiaxuan, LI Dongming, NIE Fenghua, et al. The ICVEFG method for steady-state heat conduction problems in orthotropic media[J]. Chinese Journal of Solid Mechanics, 2019, 40(1): 74-81.(in Chinese))
[7] SHI G H. Manifold method of material analysis[C]//Proceedings of the 9th Army Conference on Applied Mathematics and Computing. Minneapolis, Minnesota, 1991.
[8] MA G W, AN X M, ZHANG H H, et al. Modeling complex crack problems using the numerical manifold method[J]. International Journal of Fracture, 2009, 156(1): 21-35.
[9] KOUREPINIS D, PEARCE C, BICANIC N. Higher-order discontinuous modeling of fracturing in concrete using the numerical manifold method[J]. International Journal of Computational Methods, 2010, 7(1): 83-106.
[10] YANG Y T, ZHENG H. A three-node triangular element fitted to numerical manifold method with continuous nodal stress for crack analysis[J]. Engineering Fracture Mechanics, 2016, 162: 51-75.
[11] WU Z J, JIANG Y L, LIU Q S, et al. Investigation of the excavation damaged zone around deep TBM tunnel using a Voronoi-element based explicit numerical manifold method[J]. International Journal of Rock Mechanics and Mining Sciences, 2018, 112: 158-170.
[12] WU Z J, XU X Y, LIU Q S, et al. A zero-thickness cohesive element-based numerical manifold method for rock mechanical behavior with micro-Voronoi grains[J]. Engineering Analysis With Boundary Elements, 2018, 96: 94-108.
[13] YANG S K, CAO M S, REN X H, et al. 3D crack propagation by the numerical manifold method[J]. Computers & Structures, 2018, 194: 116-129.
[14] YANG Y T, TANG X H, ZHENG H, et al. Hydraulic fracturing modeling using the enriched numerical manifold method[J]. Applied Mathematical Modelling, 2018, 53: 462-486.
[15] GUO H W, ZHENG H, ZHUANG X Y. Numerical manifold method for vibration analysis of Kirchhoff’s plates of arbitrary geometry[J]. Applied Mathematical Modelling, 2019, 66: 695-727.
[16] ZHENG H, YANG Y T, SHI G H. Reformulation of dynamic crack propagation using the numerical manifold method[J]. Engineering Analysis With Boundary Elements, 2019, 105: 279-295.
[17] 林绍忠, 明峥嵘, 祁勇峰. 用数值流形法分析温度场及温度应力[J]. 长江科学院院报, 2007, 24(5): 72-75.(LIN Shaozhong, MING Zhengrong, QI Yongfeng. Thermal field and thermal stress analysis based on numerical manifold method[J]. Journal of Yangtze River Scientific Research Institute, 2007, 24(5): 72-75.(in Chinese))
[18] 刘泉声, 刘学伟. 裂隙岩体温度场数值流形方法初步研究[J]. 岩土工程学报, 2013, 35(4): 635-642.(LIU Quansheng, LIU Xuewei. Preliminary research on numerical manifold method for temperature field of fractured rock mass[J]. Chinese Journal of Geotechnical Engineering, 2013, 35(4): 635-642.(in Chinese))
[19] 谭育新, 张慧华, 胡国栋. 二维稳态热传导问题的正六边形流形元研究[J]. 应用数学和力学, 2017, 38(5): 594-604.(TAN Yuxin, ZHANG Huihua, HU Guodong. 2D steady heat conduction analysis with the regular hexagon numerical manifold method[J]. Applied Mathematics and Mechanics, 2017, 38(5): 594-604.(in Chinese))
[20] ZHANG H H, LIU S M, HAN S Y, et al. Modeling of 2D cracked FGMs under thermo-mechanical loadings with the numerical manifold method[J]. International Journal of Mechanical Sciences, 2018, 148: 103-117.
[21] ZHANG H H, LIU S M, HAN S Y, et al. The numerical manifold method for crack modeling of two-dimensional functionally graded materials under thermal shocks[J]. Engineering Fracture Mechanics, 2019, 208: 90-106.
[22] BABUSKA I, MELENK J M. The partition of unity method[J]. International Journal for Numerical Methods in Engineering, 1997, 40(4): 727-758.
[23] BAYESTEH H, AFSHAR A, MOHAMMDI S. Thermo-mechanical fracture study of inhomogeneous cracked solids by the extended isogeometric analysis method[J]. European Journal of Mechanics A: Solids, 2015, 51: 123-139.
[24] ZHANG H H, MA G W. Fracture modeling of isotropic functionally graded materials by the numerical manifold method[J]. Engineering Analysis With Boundary Elements, 2014, 38: 61-71.
[25] ZHANG H H, HAN S Y, FAN L F. Modeling 2D transient heat conduction problems by the numerical manifold method on Wachspress polygonal elements[J]. Applied Mathematical Modelling, 2017, 48: 607-620.