引 言
光滑无缝的机翼可变弯度前缘是一种新型的高升力装置.相比传统前缘缝翼,它能够显著降低飞机起降阶段的气动噪声,并满足未来层流机翼对蒙皮表面光滑程度的苛刻要求[1-5].
经过几十年的发展,业界逐渐形成了变弯度机翼前缘的基本设计方案[6-10],即通过内部机构驱动柔性蒙皮的纯弯曲变形实现前缘下垂,其机构原理如图1所示.
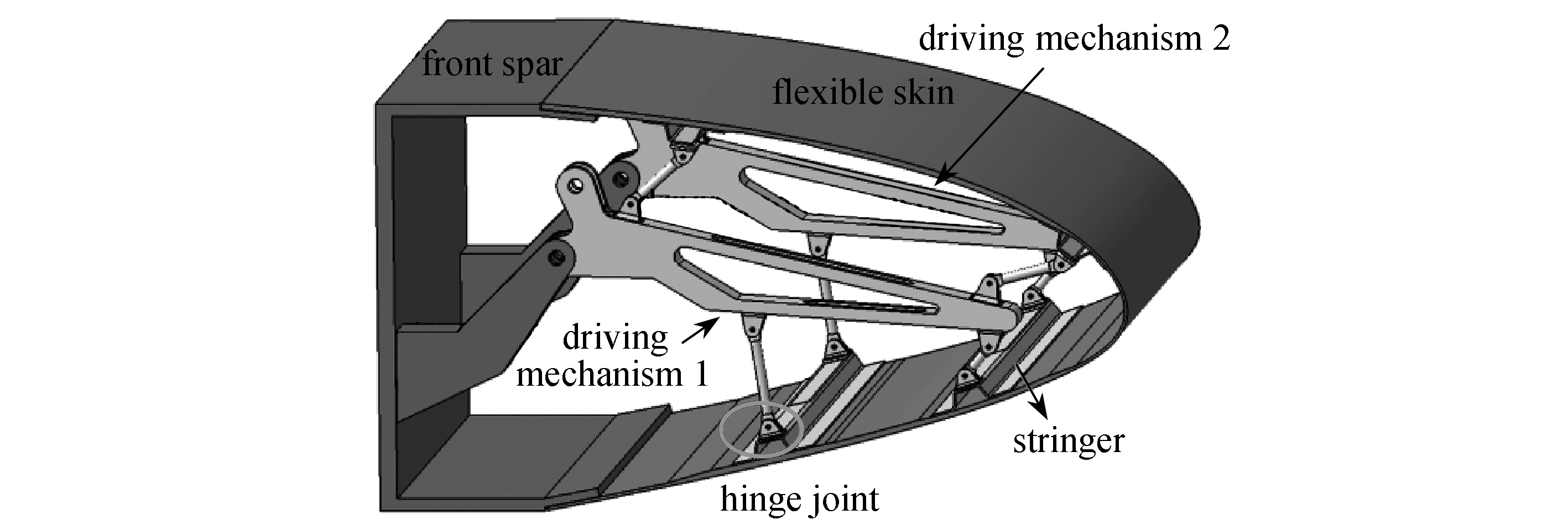
图1 变弯度前缘结构示意图
Fig. 1 Schematic diagram of the variable camber leading edge structure
前缘的变形精度对气动效率的影响较大.前期研究表明,在下垂状态下,位于前缘前端5 mm的位移偏差可造成飞机的升阻比降低10%、升力降低4.5%.变形精度受多种因素影响,包括柔性蒙皮结构的变形误差、内部机构的驱动误差、加工组装误差等[6].柔性蒙皮结构作为设计流程中的第一环节,是影响变形精度的主要因素,因此必须保证柔性蒙皮外形的高精度性.
变弯度机翼前缘柔性蒙皮的设计方法研究主要分为两个阶段,即基于二维翼型截面和三维后掠机翼的设计技术研究.
目前,基于二维翼型截面的柔性蒙皮设计方法已较为成熟.Kintscher和Monner等在SADE(2009—2011)项目中采用分层优化策略对蒙皮结构进行设计,但高耦合度变量的直接分层造成优化结果中上翼面产生较大的位移偏差,影响了前缘气流分布[7];Rudenko等使用单纯形算法对柔性蒙皮结构设计变量进行协同优化,并完成了物理样件的功能试验验证,但由于单纯形算法处理多变量优化问题时易陷入局部最优解,其变形精度未达到柔性蒙皮的性能要求[8];Wang等[11]使用NSGA-Ⅱ解决了柔性蒙皮设计变量多、优化易陷入局部最优解的问题,变形结果中平均位移偏差仅为1.1 mm,变形精度符合柔性蒙皮的性能要求.
三维后掠机翼的柔性蒙皮设计是在二维翼型基础上开展的,其难点在于需要考虑沿展向不同翼型截面间变形的相互影响,蒙皮的受力形式复杂,实现高精度外形的难度大.Vasista和Gaspari等在Novemore项目中应用Rudenko等的优化策略,完成了翼梢小翼前缘柔性蒙皮结构的设计,并取得了较好的变形结果[9],但翼梢小翼前缘的下垂目标仅为2°,弦长仅为200 mm,设计问题的难度小,易实现;Kintscher等在SARISTU项目中进行了全尺寸后掠机翼柔性蒙皮的设计、样件制造和风洞试验,但在数值模型分析中,上下翼面均产生了9 mm的位移偏差[7,10],且相关文献并未涉及具体的优化设计方法和物理试验数据.
为实现三维后掠机翼前缘的高精度外形,本文首先分析了现有方法的设计弊端,然后分别从刚度设计区域划分方式、优化模型的目标函数以及优化算法等方面进行改进,提出了一种基于改进NSGA-Ⅱ的柔性蒙皮优化设计方法,最终实现后掠机翼前缘蒙皮的精确变形.
1 现有优化设计方法的弊端及改进方法
三维后掠机翼的前缘柔性蒙皮结构包含蒙皮和长桁,其结构构型如图2所示.其中蒙皮上下根部(边1和边2)为固支,以模拟前缘与机翼前梁的连接,参考点1~8表示两套驱动机构与长桁的8个铰接点,驱动位移施加在参考点上.在面向工程应用的研究中,柔性蒙皮通常采用玻璃纤维增强复合材料(GFRP)[6-11].
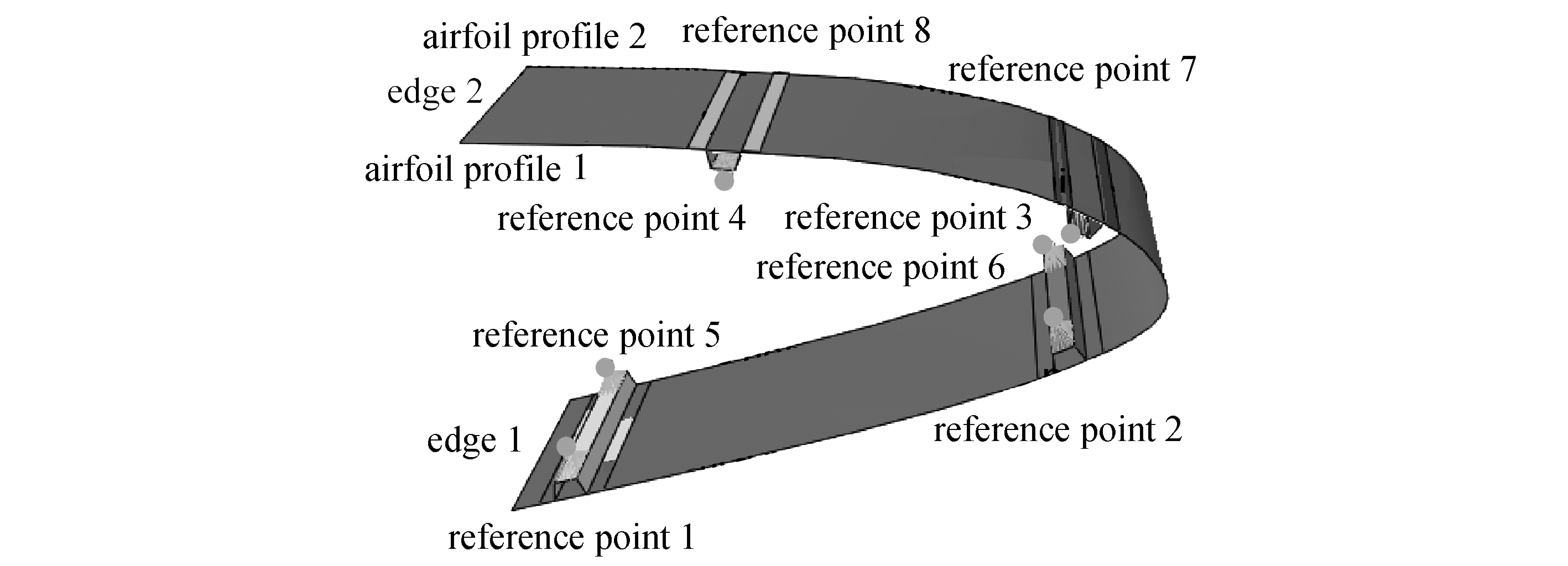
图2 后掠前缘柔性蒙皮的数值模型
Fig. 2 The numerical model for the leading edge flexible skin with a sweep angle
1.1 优化变量
柔性蒙皮的优化变量分为3类:设计区域的蒙皮厚度、长桁位置以及施加在驱动点处的驱动位移.三维后掠机翼和二维翼型优化变量的主要区别在于蒙皮厚度设计区域的划分方式,在二维翼型模型中,设计区域只需沿翼型轮廓线划分(图3(a)),然而在三维后掠机翼模型中,由于后掠角和根梢比因素的存在,需要同时沿翼型轮廓线和翼展方向进行划分(图3(b)).

(a) 二维翼型前缘 (b) 后掠机翼前缘
(a) The 2D airfoil leading edge (b) The leading edge of sweep-back wing
图3 柔性蒙皮的刚度设计区域划分方式
Fig. 3 The regional division mode of the straight leading edge flexible skin
1.2 目标函数
在二维翼型的优化设计过程中,控制翼型变形精度的目标函数为
(1)
式中,eLSE为二维翼型平面内实际变形曲线与目标曲线间的最小二乘误差(least square error),n为翼型轮廓线上形状控制点的个数,xi,yi为目标曲线中第i个形状控制点的坐标,![]() 为实际变形曲线中第i个形状控制点的坐标(图4).然而,在三维后掠机翼的蒙皮设计过程中,需要对沿翼展方向的多个翼型截面的变形精度进行控制.因此,这里的柔性蒙皮结构设计已经从二维翼型情况下的单目标优化问题升级为三维情况下的多目标优化问题.
为实际变形曲线中第i个形状控制点的坐标(图4).然而,在三维后掠机翼的蒙皮设计过程中,需要对沿翼展方向的多个翼型截面的变形精度进行控制.因此,这里的柔性蒙皮结构设计已经从二维翼型情况下的单目标优化问题升级为三维情况下的多目标优化问题.
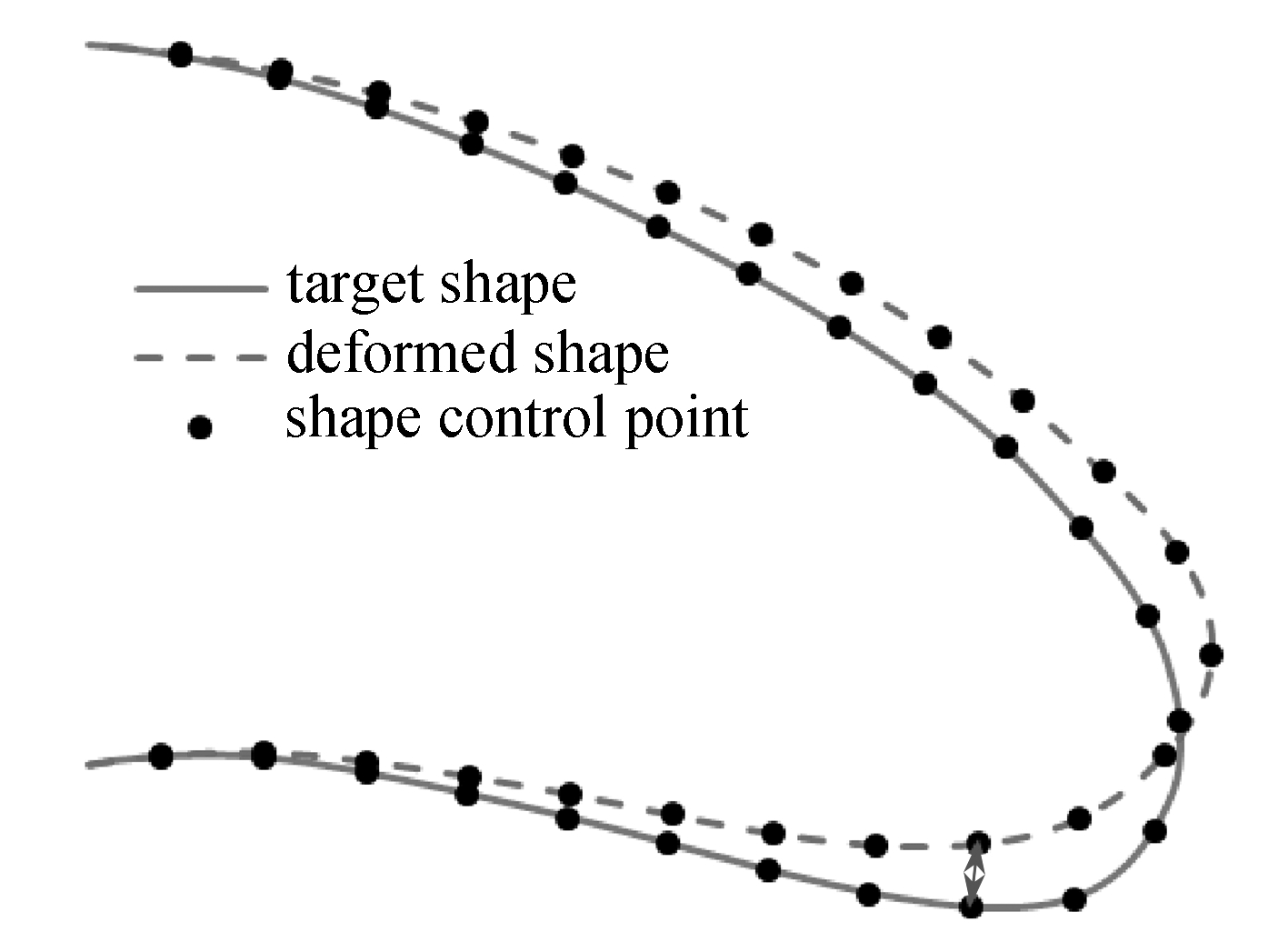
图4 LSE说明
Fig. 4 The instruction of LSE
另外,通过研究发现,仅依靠多个翼型截面的eLSE作为目标函数依旧无法获得满意的变形效果,容易出现畸形变形,如图5(a)所示.通过沿翼展方向截取不同翼型截面的变形曲线(图5(b))可以发现,畸形变形部位的曲线存在明显的“凹凸”现象.虽然此时的eLSE值较小,但是其外形无法满足气动设计要求.该现象可通过曲率值的正负变化来进行解释.图6(a)为理想变形曲线,该曲线上所有点的曲率值均为正,而图6(b)为畸形变形曲线,该曲线的曲率出现正负更替现象.因此,为解决该问题,需在原目标函数中增加负曲率点的曲率误差和.改进后的目标函数表示为
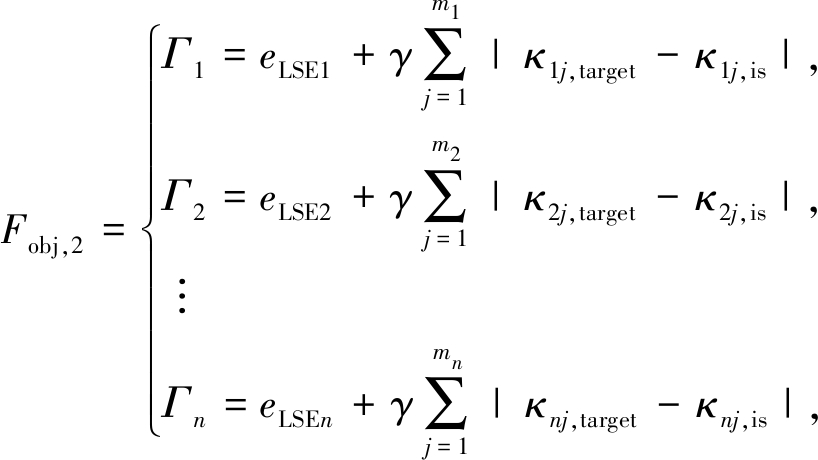
(2)
式中,Γ1~Γn分别为沿翼展方向的n个翼型截面的目标函数值,n的个数与前缘展长相关;γ为权重系数;κij,target为第i个截面中第j个负曲率点的目标曲率,κij,is为第i个截面中第j个负曲率点的实际曲率;mi表示第i个截面中负曲率点的个数.
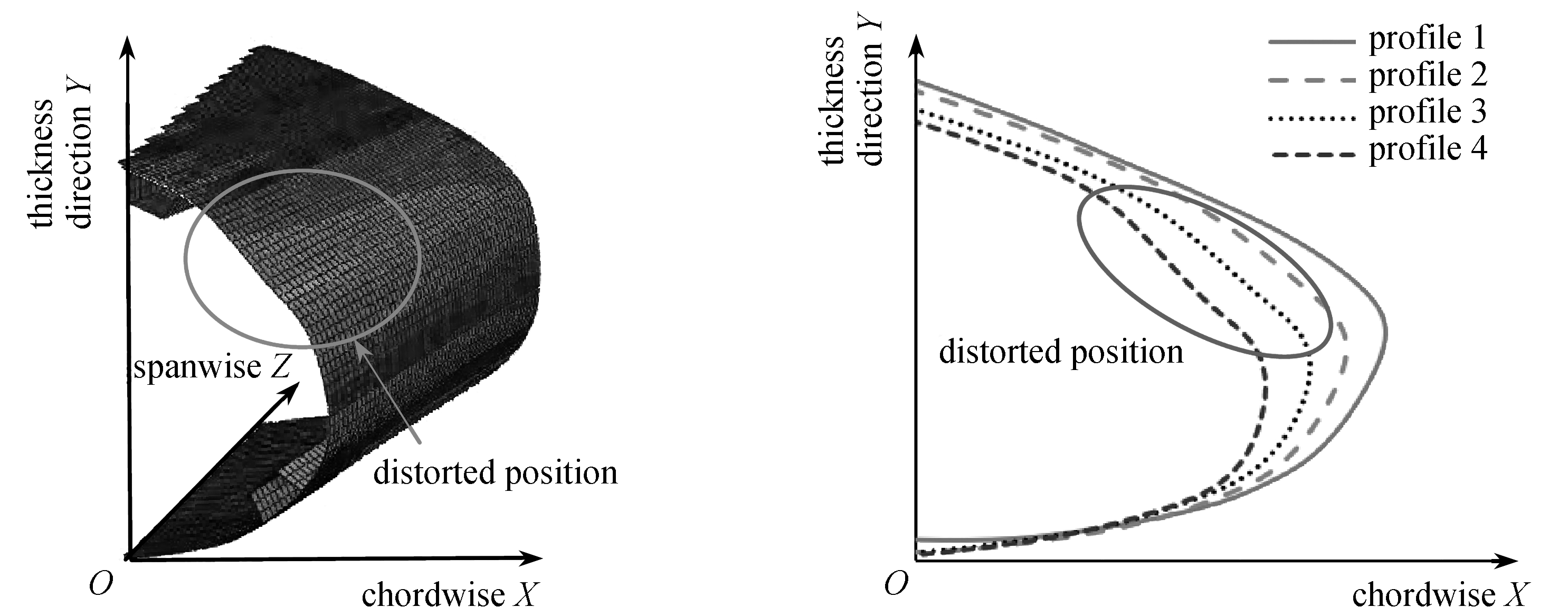
(a) 整体变形 (b) 不同翼型截面的变形曲线
(a) The overall deformation (b) The deformation curves of different profiles
图5 畸形变形示意图
Fig. 5 Diagrams of distorted deformation
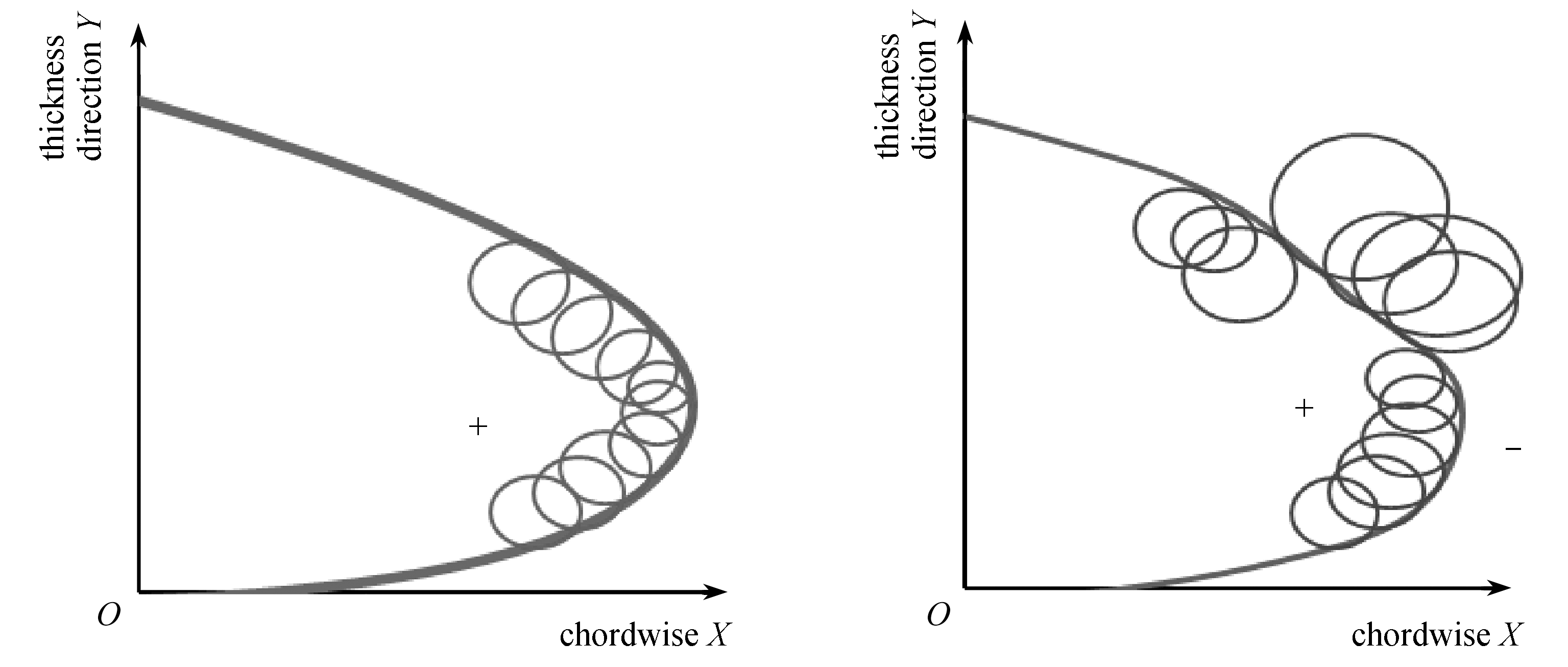
(a) 理想变形曲线 (b) 畸形变形曲线
(a) The target curv (b) The distorted deformation curve
图6 理想变形曲线与畸形变形曲线对比
Fig. 6 The comparison between the ideal deformation curve and the distorted deformation curve
1.3 优化算法
研究表明,用于二维翼型设计的多目标优化算法NSGA-Ⅱ并不适合三维后掠机翼,其优化结果无法收敛.以双目标优化问题为例,使用NSGA-Ⅱ对图2中的后掠机翼蒙皮进行优化,并选取端面1、2作为变形精度控制面,经过20代遗传,其结果如图7所示,其中圆点、方形分别表示初代和第20代种群中的第一层级个体,Γ1,Γ2分别为两个端面的目标函数值.理想的优化结果应为第一层级的大部分个体(图7中的方形数据点)集中于区域1,即优化后端面1 和2的变形误差均减小.然而实际结果是虽然Γ1均有所减小,但绝大部分的Γ2增加且幅度较大,这表明NSGA-Ⅱ未能使优化结果收敛于Γ1,Γ2同时减小的个体.
经分析发现,优化结果不理想归咎于NSGA-Ⅱ的精英个体选择方法.图8所示为优化过程中,某代种群内第一层级的所有个体,NSGA-Ⅱ根据拥挤度筛选精英个体,拥挤度大的个体优先选出,拥挤度小的个体则可能被放弃[12].拥挤度的计算方法如下[13]:首先,规定该层级中排在两端的个体(P1,P2)拥挤度为正无穷;其次,对于排在中间的个体n,则以相邻个体n-1,n+1为对角建立长方形,个体n的拥挤度为长方形的边长和(图8中a+b).也就是说,NSGA-Ⅱ对该层级个体进行筛选时,队列两端的个体具有最高的优先级,队列中间的个体能否入选则取决于它与相邻个体的距离.
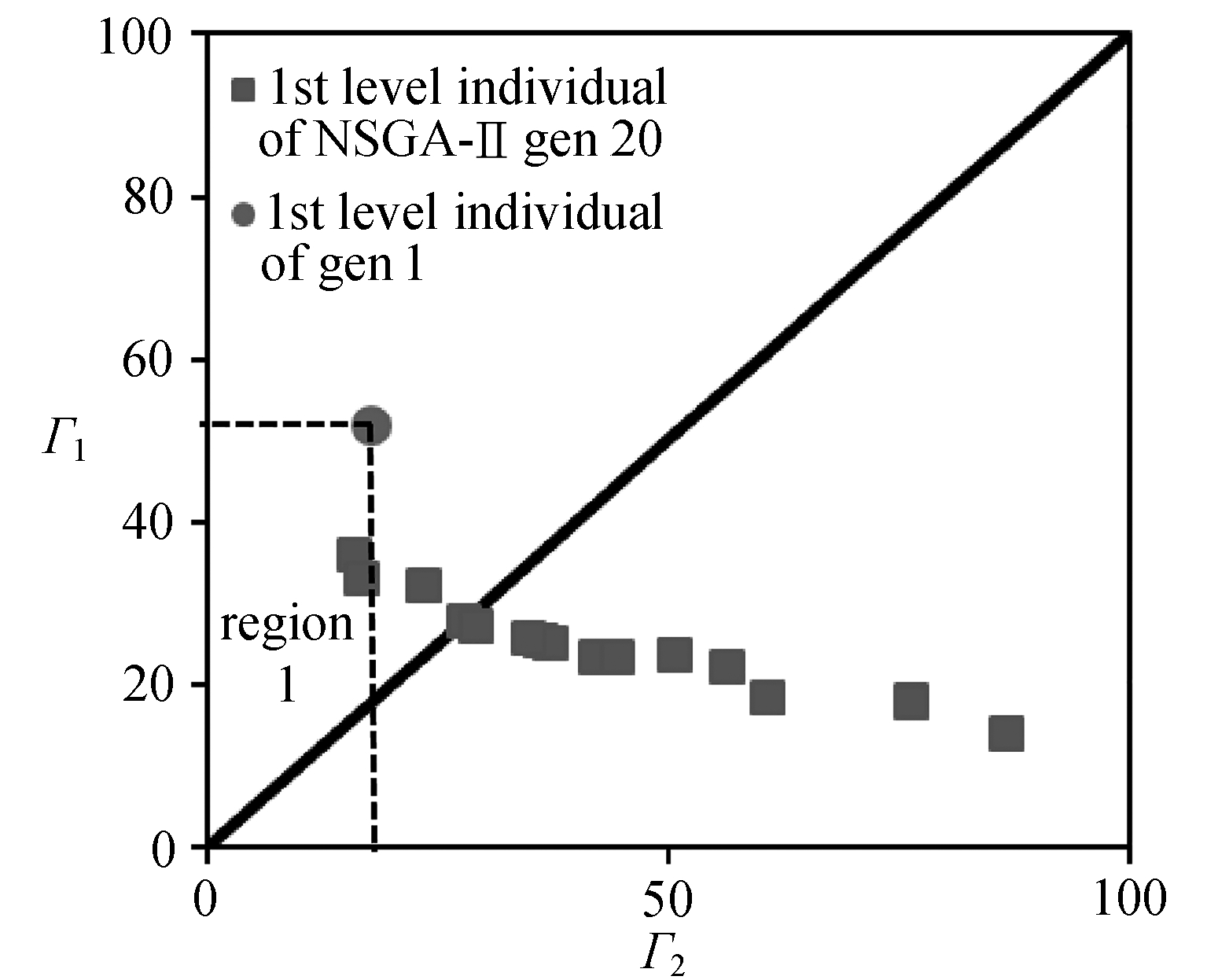
图7 NSGA-Ⅱ的优化结果
Fig. 7 Optimization results of NSGA-Ⅱ
根据以上选择方法,图8中个体P1,P2一定会被选中.然而在三维柔性蒙皮结构设计中,P1,P2恰恰代表了较差的方案,因为这类个体只能保证一个端面的变形精度高,而另一个端面的变形精度较差,应该被首先放弃.因此,需要对现有的选择方法进行修改,具体如图9所示:首先,设定距离控制参数α和权重控制参数β;其次,对同一层级内所有个体进行分类,针对目标函数Γ1,Γ2,规定|Γ1-Γ2|<α的个体为较优类个体,|Γ1-Γ2|>α的个体为普通类个体;最后,计算所有个体的拥挤度,规定较优类个体的拥挤度D=a+βb,而普通类个体的拥挤度D=a+βb-H,其中H为Γ1,Γ2的归一化标准差.至此,可通过调节参数α,β控制优化结果中两端面的变形精度差,以筛选出符合前缘变形精度要求的结构方案.
应用改进后的NSGA-Ⅱ对图2中的蒙皮结构进行优化,同样经过第20代遗传,结果如图10所示,其中三角形为第20代种群中的第一层级个体.与原优化结果相比(图10中方形),NSGA-Ⅱ改进后的优化结果呈收敛趋势,且大部分个体的Γ1,Γ2同步减小.这说明,改进后的NSGA-Ⅱ能够有效解决后掠机翼柔性蒙皮结构的优化设计问题.
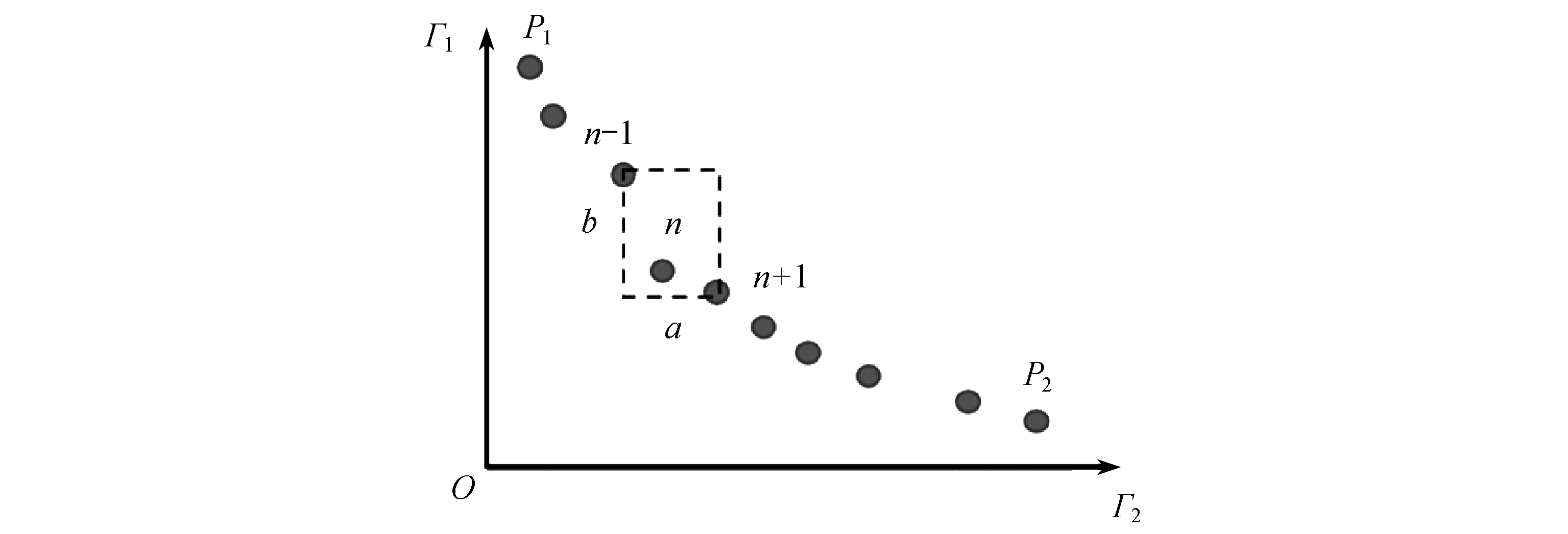
图8 NSGA-Ⅱ中拥挤度的计算方法
Fig. 8 The calculation method for the crowding degree in NSGA-Ⅱ
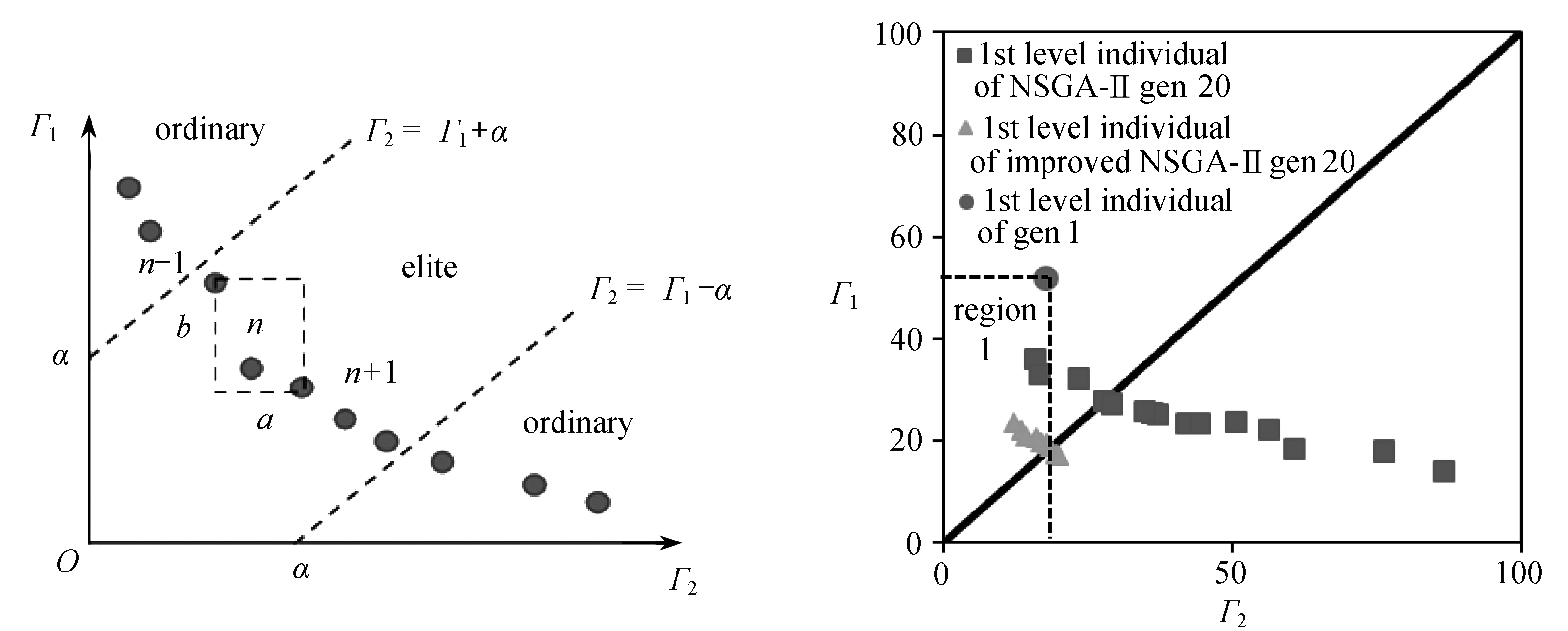
图9 改进NSGA-Ⅱ中拥挤度的计算方法 图10 改进NSGA-Ⅱ的优化结果
Fig. 9 The calculation method for the crowding Fig. 10 Optimization results of degree in modified NSGA-Ⅱ modified NSGA-Ⅱ
2 数值算例分析与试验验证
本文数值模型中的蒙皮材料使用编织GFRP,其0°和90°的拉伸模量分别为23.3 GPa和23.2 GPa,Poisson比为0.114,剪切模量为2.97 GPa.本文的参考模型为某国产远程公务机的气动验证模型(图11),其变弯度前缘后掠角为1.2°~3°.选取该模型沿翼展方向距翼根66%~69%展长处的前缘翼段为初始模型,变形部分弦长425~433 mm,轮廓周长940~956 mm,展长300 mm,变弯度前缘后掠角为1.5°,目标模型为前缘下垂17°的气动外形,初始和目标模型如图12所示.下垂状态下的气动载荷分布由CFD计算得到,并通过等效转换,在前缘变形至最终状态后,作为压强载荷施加到柔性蒙皮的有限元模型上(图13),以考察气动载荷下柔性蒙皮的变形精度.此时的速度为0.2Ma,机翼攻角为8°.该气动载荷分布暂未考虑气动弹性影响.这是由于: 1) 数值模型的蒙皮材料为GFRP,其刚度较大,在气动载荷的作用下只发生微小变形; 2) 在结构设计的初始阶段,为减小结构设计复杂程度,暂不考虑气动弹性问题.
由于该前缘翼段后掠角较小,仅在前缘前端区域沿展向进行设计区域划分.蒙皮共分为70个刚度控制区域,设置4个长桁,各长桁的位置范围及蒙皮区域划分方式如图14所示,区域A内的蒙皮厚度范围为2~3.5mm,区域B为1~2.5 mm,区域C为3.5~4.2 mm.优化模型中设计变量共90个,包括70个设计区域的蒙皮厚度、4个长桁位置和16个驱动位移;变形精度控制面为截面1~3(图12),目标函数如式(2)所示.NSGA-Ⅱ中种群个体数量为32个,交叉概率为0.9,变异概率为0.1,优化过程经过110代收敛于Γ1=3.5,Γ2=3.1,Γ3=4,此时截面1~3的eLSE分别为1.0,0.9,1.2 mm,最大位移偏差分别为2.0,2.4,4.1 mm,均出现在弯曲和剪切变形最大的前缘前端.前缘蒙皮厚度、长桁位置的优化结果及变形形状如图15所示.

图11 参考飞机的气动验证模型
Fig. 11 The aerodynamic verification model for the reference aircraft

图12 后掠前缘初始和目标模型 图13 目标变形形状的气动载荷分布状态
Fig. 12 Initial and target models for the Fig. 13 Aerodynamic load distribution on swept-back leading edge the target deformation shape
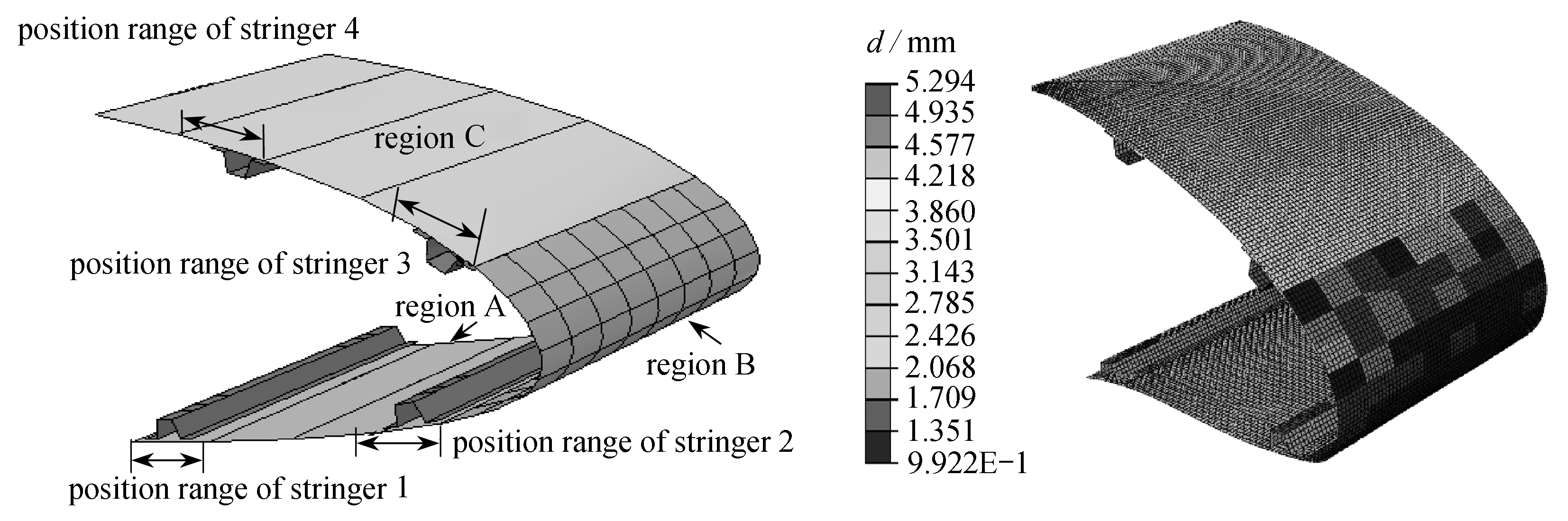
图14 区域划分方式与长桁位置范围图15 前缘蒙皮厚度优化结果及变形形状
Fig. 14 The region division mode and stringer location rangesFig. 15 The deformation results
注 为了解释图中的颜色,读者可以参考本文的电子网页版本,后同.
由图15和变形数据可知,后掠机翼前缘翼段变形精度较高,蒙皮沿展向未发生“凹凸”不平的现象,整体光滑.
变形最终状态,截面1和截面3在施加气动载荷前、后的外形形状对比如图16所示,截面1和截面3的最大位移改变量均发生在前缘前端,分别为2.1 mm和1.3 mm,平均位移改变量仅为0.3 mm和0.21 mm.由此可知,针对该结构形式,使用GFRP作为蒙皮材料时气动载荷对前缘变形结果的影响较小.
将最大位移偏差和弦长的比值作为误差考核参数,相比于SARISTU项目中的最大位移偏差9 mm[6](最大弦长、高度分别为620 mm和400 mm),本文的优化设计方法使变形误差降低了27%.
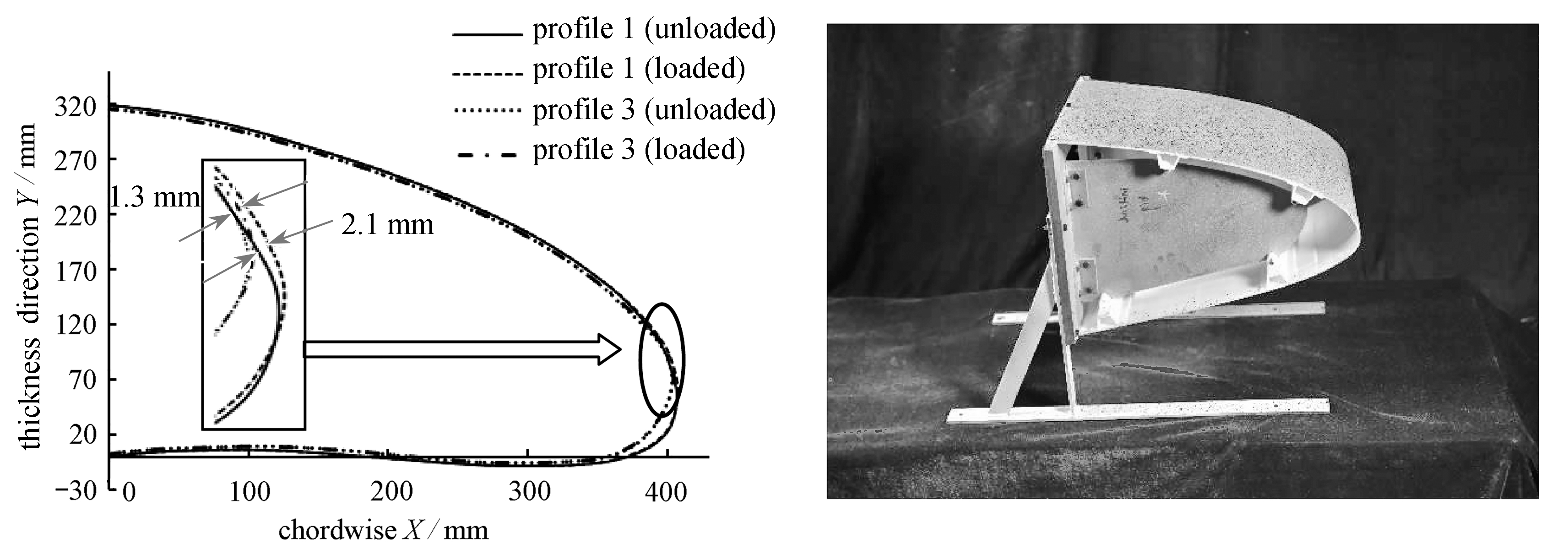
图16 截面1、3在施加气动载荷前后的变形形状对比 图17 前缘翼段的物理模型
Fig. 16 Comparison of deformation shapes of profile 1,3 before Fig. 17 The physical sample of the and after application of aerodynamic loads leading edge model
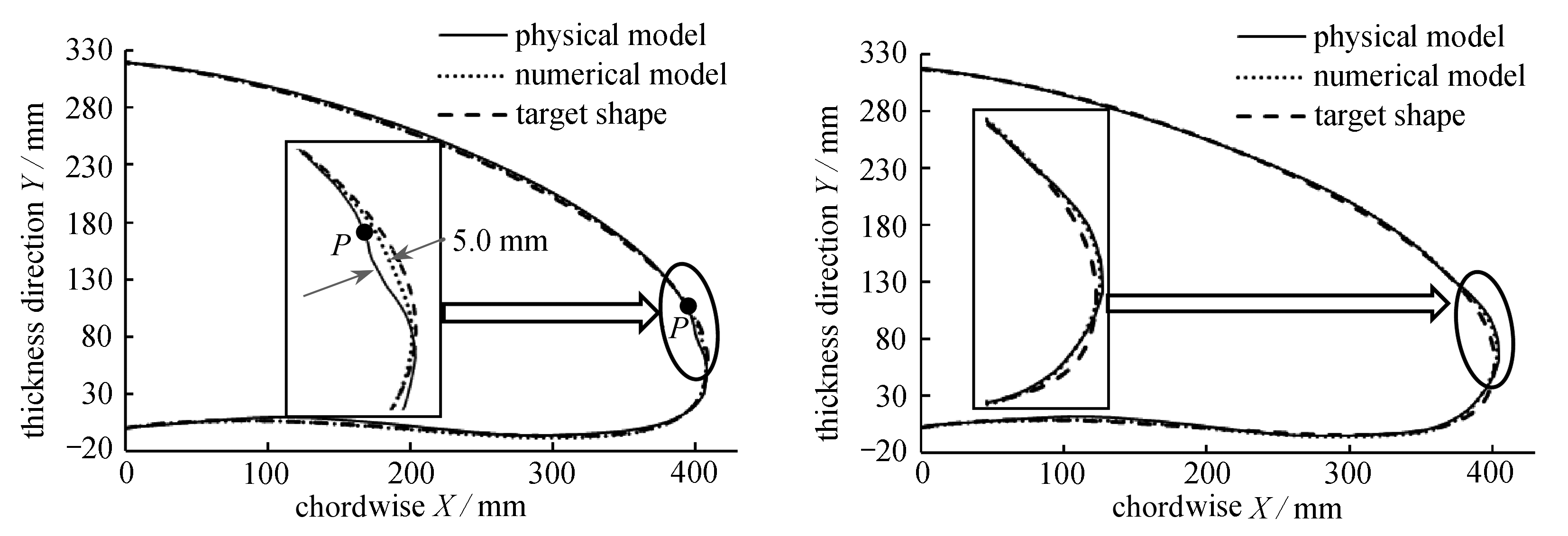
此外,前期研究结果表明,无气动载荷情况下,变形结果主要取决于蒙皮的弯曲刚度比例分布情况,与材料的力学性能参数无关[14-16].因此从成本角度出发,本文通过3D打印技术使用高韧性树脂材料进行样件制造,以验证不考虑气动载荷时柔性蒙皮结构的变形精度,其中高韧性树脂材料的拉伸弹性模量为2.8 GPa,Poisson比为0.4,剪切模量为1 GPa.物理模型如图17所示,根据设计原则,在物理模型的4个长桁上施加强制位移,截面1、3的物理变形结果与数值仿真结果(无气动载荷)、目标变形结果的对比如图18所示,其中截面1、3的物理变形结果与数值仿真结果间的eLSE为1.3 mm和0.5 mm,最大位移偏差分别为5.0 mm和1.0 mm.
(a) 截面1 (b) 截面3
(a) Profile 1 (b) Profile 3
图18 物理模型变形结果与数值仿真结果、目标形状的对比
Fig. 18 The results comparison between the physical model, the numerical model and the target shapes
由图18可知,实际变形结果与数值仿真结果、目标变形结果整体吻合度较高,尤其是截面3,即使在前缘前端,实际变形结果与数值仿真结果的最大位移偏差也只有1.0 mm.但截面1在点P处发生了凹陷,如图18(a)所示.点P处在数值仿真结果中就存在轻微凹陷,但在物理模型中凹陷现象明显加剧.这是由于点P附近为刚度薄弱区域,点P附近的蒙皮厚度为1.0 mm,而其两侧的蒙皮厚度分别为1.6 mm和2.0 mm,物理模型的加工制造误差对刚度薄弱区域的变形精度会产生较大影响.为解决该问题,可在优化结束后,对点P附近的蒙皮厚度进行单独设计.
此外,使用DIC技术测量了下翼面蒙皮外表面的最大主应变分布,物理模型与数值模型的应变分布状态整体相近(图19),但在应变最大位置(位置1)处两模型的应变数值差距较大.数值模型中,位置1的应变近似为0.023,而在物理模型中仅为0.015.这是由于在有限元模型中,没有设计各刚度控制区域的厚度过渡区,“台阶”的存在造成蒙皮变形后曲率变化较大,而在3D打印模型中,各刚度控制区域光滑连续过渡,应变减小.

图19 数值模型和物理模型的下翼面最大主应变比对
Fig. 19 The maximum principal strain comparison of the lower wing surface between the numerical model and the physical model
3 结 论
1) 本文提出了一种新的三维后掠机翼柔性蒙皮结构优化设计方法,其创新点主要体现在沿翼展方向对多个翼型进行同步优化;对目标函数进行改进从而解决了畸形变形问题;对现有NSGA-Ⅱ算法进行改进以适应三维蒙皮多目标优化求解.
2) 以大型远程飞机为研究对象,应用该方法对后掠机翼变弯度前缘蒙皮结构进行了优化设计,获得了机翼前缘在下垂状态下的高精度外形.与现有柔性蒙皮优化设计结果相比,该方法在变形精度上优势显著.
3) 经过分析总结,认为目前三维变弯度机翼前缘的设计难点主要有两点:第一是在下垂过程中,在前缘尖端部分,蒙皮沿翼型截面方向会产生较大的弯曲变形,现有材料可能无法满足变形要求;第二是随着后掠角的增大,蒙皮前缘尖端部分沿翼展方向的剪切变形会变得比较严重,无法满足变形精度要求.因此,下一步的研究方向应该是进一步改进优化策略,缓解局部严重的弯曲变形,同时沿翼展方向获得更合理的蒙皮厚度分布,避免因剪切作用导致变形精度无法满足要求.
[1] KRETH S, KÖNIG R, WILD J. Aircraft noise determination of novel wing configurations[C]//Inter-Noise. Istanbul, Türkei, 2007.
[2] 黄杰, 葛文杰, 杨方. 实现机翼前缘形状连续变化柔性机构的拓扑优化[J]. 航空学报, 2007, 29(7): 988-992.(HUANG Jie, GE Wenjie, YANG Fang. Topology optimization of the compliant mechanism for shape change of airfoil leading edge[J]. Acta Aeronautica et Astronautica Sinica, 2007, 29(7): 988-992.(in Chinese))
[3] 杨智春, 党会学, 解江. 基于动网格技术的柔性后缘自适应机翼气动特性分析[J]. 应用力学学报, 2009, 26(3): 548-553.(YANG Zhichun, DANG Huixue, XIE Jiang. Aerodynamic characteristics of flexible trailing edge adaptive wing by unstructured dynamic meshes[J]. Chinese Journal of Applied Mechanics, 2009, 26(3): 548-553.(in Chinese))
[4] 邹森, 刘勇, 王琦. 翼涡干扰前缘开孔被动控制数值研究[J]. 应用数学和力学, 2019, 40(10): 1159-1168.(ZOU Sen, LIU Yong, WANG Qi. Numerical study on passive control of wing vortex interference front opening[J]. Applied Mathematics and Mechanics, 2019, 40(10): 1159-1168.(in Chinese))
[5] SATTI R, LI Y, SHOCK R, et al. Computational aeroacoustic analysis of a high-lift configuration[C]//46th AIAA Aerospace Sciences Meeting and Exhibit. Reno Nevada, USA, 2008: 654-681.
[6] PECORA R, MAGNIFICO M, AMOROSO F, et al. Structural design of an adaptive wing trailing edge for large aeroplanes[C]//WÖLCKEN P C, PAPADOPOULOS M, eds. Smart Intelligent Aircraft Structures. Switzerland: Springer, 2016: 159-170.
[7] KINTSCHER M, WIEDEMANN M, MONNER H P, et al. Design of a smart leading edge device for low speed wind tunnel tests in the European project SADE[J]. International Journal of Structural Integrity, 2011, 2(4): 383-405.
[8] RUDENKO A, RADESTOCK M, MONNER H P. Optimization, design and structural testing of a high deformable morphing leading edge of an active blown high lift system[C]//24th AIAA/AHS Adaptive Structures Conference. San Diego, California, USA, 2016.
[9] VASISTA S, GASPARI A D, RICCI S, et al. Compliant structures-based wing and wingtip morphing devices[J]. Aircraft Engineering and Aerospace Technology, 2016, 88(5): 210-228.
[10] KINTSCHER M, GEIER S, MONNER H P, et al. Investigation of multi-material laminates for smart droop nose devices[C]//29th Congress of the International Council of the Aeronautical Sciences. St Petersburg, Russia, 2014.
[11] WANG Z G, YANG Y, SUN X S. Structural optimization of a variable camber leading edge[C]//1st EU-China Aeronautical Cooperation Workshop: INNOVATE. Glasgow, UK, 2018: 20-31.
[12] 王珑,王同光,罗源. 改进的NSGA-Ⅱ算法研究风力机叶片多目标优化[J]. 应用数学和力学, 2011, 32(6): 693-701.(WANG Long, WANG Tongguang, LUO Yuan. Improved non-dominated sorting genetic algorithm (NSGA)-Ⅱ in multi-objective optimization studies of wind turbine blades[J]. Applied Mathematics and Mechanics, 2011, 32(6): 693-701.(in Chinese))
[13] DEB K, AGRAWAL S, PRATAP A, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-Ⅱ[M]//Parallel Problem Solving From Nature PPSN VI. Springer, 2000: 849-858.
[14] LI Shuguang. Rigidities of one-dimensional laminates of composite materials[J]. Journal of Engineering Mechanics, 1996, 122(4): 371.
[15] CARRERA E, PAGANI A. Multi-line enhanced beam model for the analysis of laminated composite structures[J]. Composites Part B, 2014, 57(3): 112-119.
[16] VINSON J R, SIERAKOWSKI R L. The behavior of structures composed of composite materials[J]. Journal of Applied Mechanics, 2002, 105: 215-258.