基于AUSM分裂的二维通量分裂格式*

胡立军1， 吴世枫2， 翟 健3

(1. 衡阳师范学院 数学与统计学院， 湖南 衡阳 421002;2. 广东技术师范大学 数学与系统科学学院， 广州 510665; . 曙光信息产业(北京)有限公司， 北京 100193)

摘要： 基于对流迎风分裂思想构造的AUSM类格式具有简单、高效、分辨率高等优点,在计算流体力学中得到了广泛的应用．传统的AUSM类格式在计算界面数值通量时只考虑网格界面法向的波系,忽略了网格界面横向波系的影响．使用Liou-Steffen通量分裂方法将二维Euler方程的通量分裂成对流通量和压力通量,采用AUSM格式来分别计算对流数值通量和压力数值通量．通过求解考虑了横向波系影响的角点数值通量来构造一种真正二维的AUSM通量分裂格式．在计算一维算例时,该格式保留了精确捕捉激波和接触间断的优点．在计算二维算例时,该格式不仅具有更高的分辨率而且表现出更好的鲁棒性,可以消除强激波波后的不稳定现象．此外,在多维问题的数值模拟中,该格式大大地提高了稳定性CFL数,具有更高的计算效率．因此,它是一种精确、高效并且强鲁棒性的数值方法．

关 键 词： 可压缩流； Liou-Steffen分裂； AUSM格式； GT-AUSM格式； 鲁棒性

引 言

近几十年来,构造高分辨率、高效率和强鲁棒性的迎风格式吸引了计算流体力学工作人员的广泛关注．一类迎风格式是通量差分裂(FDS)格式,如Roe格式[1]和HLLC格式[2],其特点是耗散小、鲁棒性差,计算高速流问题时容易出现数值激波不稳定性．另一类迎风格式是通量向量分裂(FVS)格式,如 Steger-Warming格式[3]和van Leer格式[4],其特点是形式简单、鲁棒性好,但是数值耗散大,对于接触波、物质界面、剪切波、涡流以及燃烧面的分辨率低[5]．Liou和Steffen结合两类迎风格式的特点,构造了一种混合迎风格式,即AUSM(advection upstream splitting method)格式[6],并且发展成为广泛应用于湍流、多相流和磁流体力学等领域的AUSM类格式[7-10]．

在求解多维问题时,传统的迎风方法都是基于方向分裂的思路来设计的,在计算网格界面的数值通量时只考虑界面法向的波系,而忽略了横向波系的影响[11],其本质是采用一维迎风格式来计算多维数值通量．这不仅会降低格式的分辨率,而且稳定性CFL数也会减小,从而降低格式的计算效率[12]．研究人员做了大量的尝试来克服这些问题,基本的思路是在网格界面数值通量的计算中增加横向波系的影响,进而设计一种真正多维的迎风格式．

一些研究人员通过对一维迎风格式进行复杂的组合来实现数值格式的多维迎风性．例如,Rumsey等[13]构造了一种多维Roe格式来计算多维Euler方程和N-S方程,Collela[14]提出了一种多维角点输运格式,Leveque[15]设计了多维波传播算法，Saltzman[16]基于二维对流算法构造了三维迎风格式．尽管这样处理可以增加稳定性CFL数,但是经常会以求解大量的一维Riemann问题作为代价,从而大大增加单时间步的计算量．另外一些研究人员尝试去建立更加复杂的多维波传播模型来构造线性化的多维迎风格式[17-19],但是该格式只能用来计算Euler方程,很难推广到其他的守恒律系统．此外,Wendroff[20]利用HLLE格式适用于任何守恒律系统这一特性构造了一种真正多维的Riemann解法器,但是该格式引入了九个常数状态,形式非常复杂．

在文献[21]中,Balsara基于一维HLLE格式构造了一种简单高效的真正二维Riemann解法器,并将其应用到Euler方程和磁流体力学的数值模拟中．与前面的多维迎风格式不同的是,该格式具有简单的封闭形式,其算法很容易实现,具有较高的计算效率．为了克服二维HLLE格式无法捕捉接触间断和剪切波的缺陷,Balsara[22]在两个常数态之间引入一个子波系,从而构造了一种可以应用到任何守恒律系统的真正二维HLLC格式．在文献[23]中,Balsara利用相似变量来阐述多维Riemann问题,并且证明了任何一种自相似一维Riemann解法器都可以用来构造多维Riemann解法器．Dumbser和Balsara[24]对具有自相似内部结构的多维Riemann问题提出了一种求解策略,并且构造了一种可以用来求解守恒律和非守恒律问题的多维HLLI格式,其优点是在计算数值通量时不需要详细区分接触间断的方向．最近,Balsara和Nkonga[25]将HLLI格式进行推广,构造了一种具有广泛用途的多维MuSIC(multidimensional, self-similar, strongly-interacting, consistent)格式．

采用Balsara的思路,Mandal和Sharma[26]利用HLL-CPS格式的优点并且结合Zha-Bilgen分裂方法构造了一种简单高效的二维HLL格式．胡立军和袁礼[11]基于Toro-Vázquez分裂方法在二维结构网格上构造了一种真正二维的HLL Riemann解法器,Qu等[27]将其推广到了二维曲线坐标系．胡立军和袁礼[28]基于Liou-Steffen分裂方法构造了一种真正二维的HLL格式．结合通量分裂方法设计的多维迎风格式,形式简单并且计算代价小,为构造真正多维迎风格式提供了一条新的思路．

本文以传统的一维AUSM格式为基础,构造了一种形式简单的二维通量分裂格式．与其他研究人员构造的真正二维通量分裂格式不同的是,本文采用AUSM格式而不是HLL格式来计算压力通量,从而进一步减少HLL格式带来的数值耗散．全文结构如下: 第1节介绍一些预备知识,包括控制方程组和Liou-Steffen通量分裂方法；第2节详细介绍真正二维的AUSM通量分裂格式的构造过程；第3节展示数值算例的结果和分析；最后,第4节是全文的结论．

1 预 备 知 识

在这一部分,首先介绍可压缩流的控制方程组,然后介绍Liou-Steffen通量分裂方法．

1.1 控制方程组

直角坐标系下的二维Euler方程组为

(1)

式中

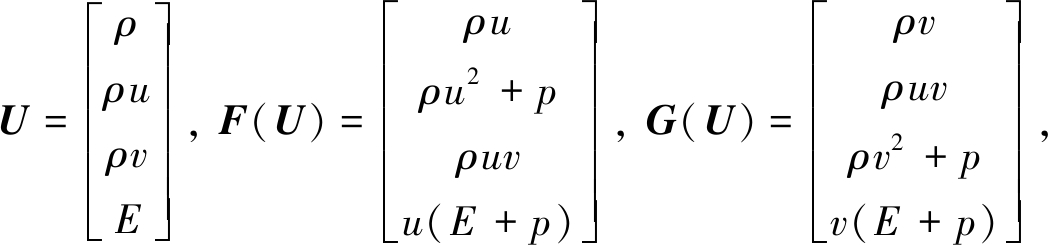
(2)

ρ为密度,u,v为x和y方向的流体速度,p为压力,E=p/(γ-1)+0.5ρ(u2+v2)为总能．状态方程为

p=(γ-1)[E-0.5ρ(u2+v2)],

(3)

本文比热比γ取1.4．

用守恒型数值方法求解式(1)：

(4)

式中,Fi+1/2, j和Gi, j+1/2为x和y方向的数值通量．

1.2 Liou-Steffen通量分裂

Liou和Steffen[6]将法向动量方程的静压项分裂出来,从而将Euler方程的通量分裂成对流项和压力项两部分．以x方向为例：

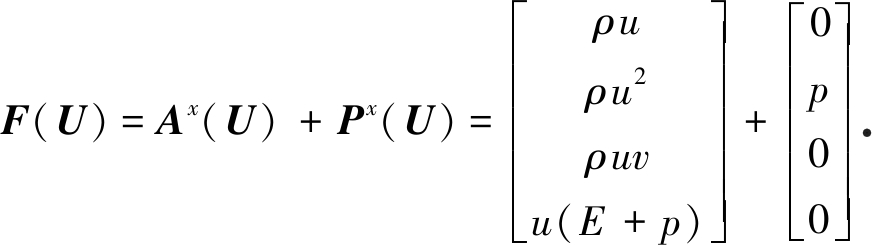
(5)

对流通量Ax(U)的Jacobi矩阵为

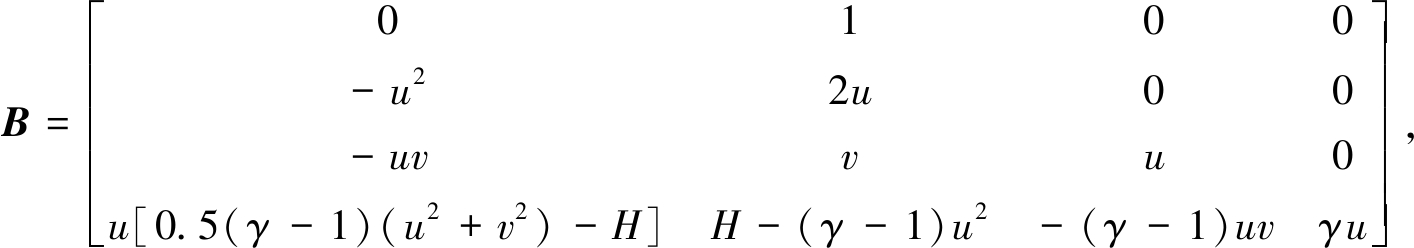
(6)

式中,H=(E+p)/ρ为总焓,B的特征值为

(7)

压力通量Px(U)的Jacobi矩阵为

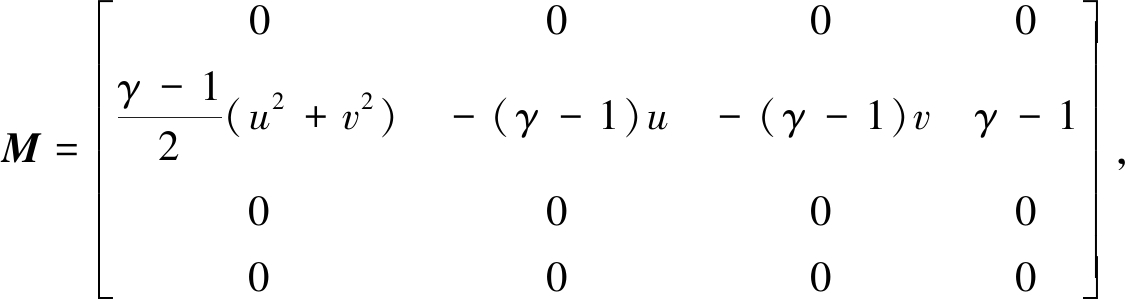
(8)

矩阵M的特征值为

(9)

2 二维AUSM通量分裂格式

这一节将详细介绍真正二维的AUSM通量分裂格式的构造过程．如图1(a)所示,将计算区域划分成二维结构化网格．以网格单元(i, j)为例,传统的一维迎风格式网格界面的数值通量通过求解由(UL,UR)构成的一维Riemann问题来获得．按照Balsara在文献[21]中构造多维迎风格式的思路,在计算界面数值通量时,不仅考虑界面中点处数值通量的贡献,还要考虑角点处由(URU,ULU,ULD,URD)所构成的二维Riemann问题对于数值通量的影响,如图1(b)所示．文中用表示界面中点处的一维数值通量,表示界面角点处的二维数值通量．

(a) 二维结构化网格[21] (b) 角点处Riemann问题的四个初态[26]
(a) The 2D structured grid[21] (b) Four initial states at the corners[26]
图1 结构化网格和角点处Riemann问题的四个初态
Fig. 1 The structured grid and four initial states at the corners

2.1 界面中点一维数值通量的计算

根据Liou-Steffen对流/压力通量分裂式(5),界面中点处的一维数值通量可以分裂成对流数值通量和压力数值通量之和：

(10)

2.1.1 中点对流数值通量

通过引入Mach数Ma=u/a,式(5)中的对流通量可以改写成

(11)

式中为当地声速．

对界面Mach数进行分裂,从而网格界面中点处的对流数值通量可以表示成

(12)

采用文献[6]中的方法来计算界面Mach数：

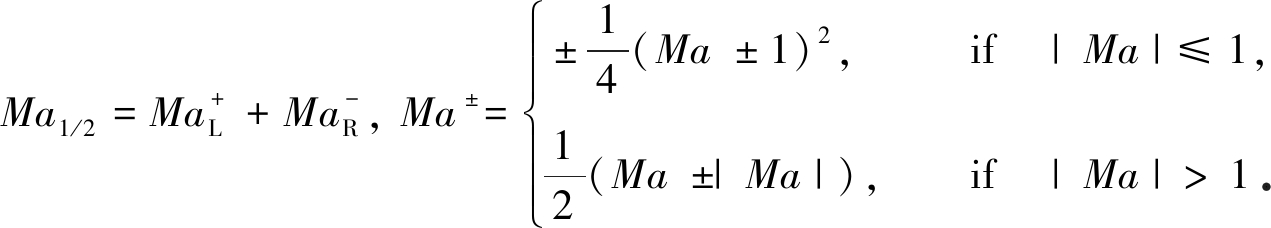
(13)

注意到,通过隐含在界面Mach数中对流速度的符号,式(12)中的数值通量是满足迎风性的．

2.1.2 中点压力数值通量

采用AUSM格式[6]来计算界面中点的压力数值通量，其值为

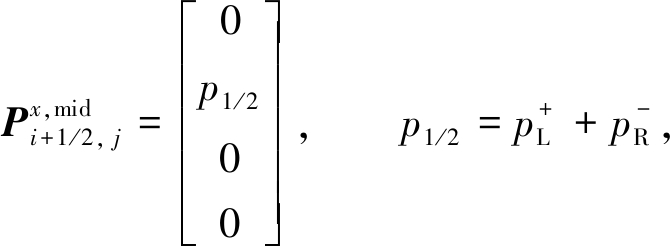
(14)

其中压力分裂采用(Ma±1)的二阶多项式展开来计算：

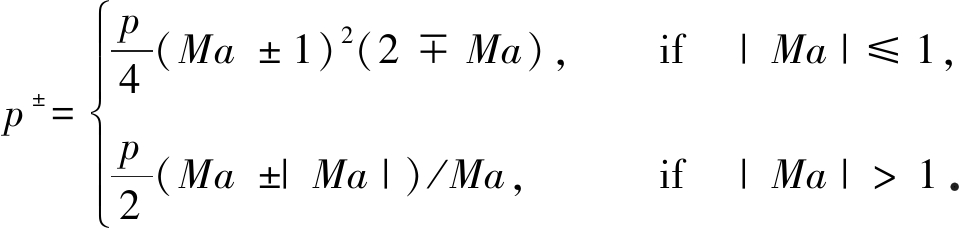
(15)

2.2 界面角点二维数值通量的计算

根据Liou-Steffen通量分裂式(5),角点处的二维数值通量可以分裂成两部分之和：

(16)

2.2.1 角点对流数值通量

使用迎风格式来求解角点处的对流数值通量．在计算中考虑角点处横向波对数值通量的贡献来实现数值格式真正二维的特性．其具体的计算公式为

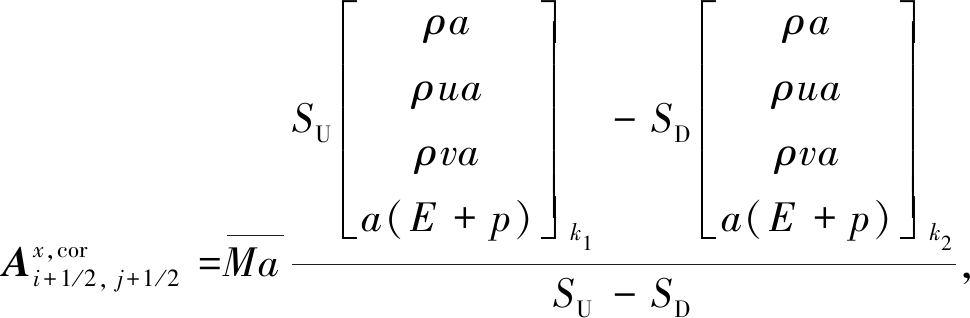
(17)

式中,平均Mach数为

(18)

根据平均Mach数的符号来选取迎风方向k1和k2：

(19)

2.2.2 角点压力数值通量

文献[28]基于Liou-Steffen通量分裂方法构造的真正二维数值格式采用HLL格式来计算压力通量,这会降低数值格式对于接触间断的分辨率．为了更好地保留一维AUSM格式能够捕捉接触间断的优点,本文中的压力数值通量使用AUSM格式而不是HLL格式来求解：

(20)

上式右端第一项为考虑了影响域面积加权的AUSM通量,其计算公式为

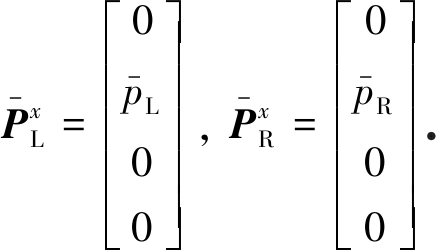
(21)

平均压力和的计算公式为

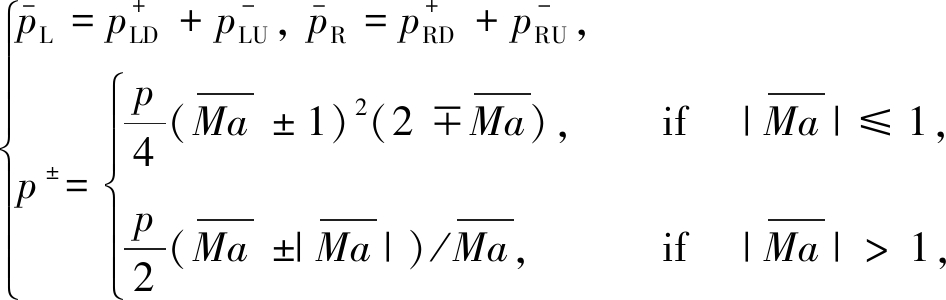
(22)

式中,平均Mach数的定义见式(18)．式(20)右端第二项为横向压力通量对角点处压力数值通量的贡献．其中,Py为y方向的压力通量,其定义为

(23)

如图1(b)所示,波速SU,SD,SL,SR分别代表沿着上、下、左、右四个方向传播的最快波速,本文按照文献[11]中的定义来计算波速．

2.3 界面数值通量

从图1(a)可知,界面(i+1/2, j)总的数值通量Fi+1/2, j由中点处的数值通量和两个角点C1和C4的数值通量和组成．利用Simpson公式[21]对这三部分通量进行求和,得到真正二维的AUSM通量分裂格式(genuinely 2D advection upstream splitting method,GT-AUSM)最终的数值通量表达式为

(24)

3 数值结果及分析

这一部分我们计算一些典型的算例来验证本文所构造的真正二维AUSM格式在数值计算中的表现,包括格式的精度、鲁棒性和计算效率．

3.1 一维算例

使用GT-AUSM格式计算存在精确解的四个一维Riemann问题,其中每个问题在数值计算中分别代表了一种特定的计算难度．计算区域[0,1]被均匀划分成200个网格,初始间断的位置x0,间断左右的初始物理状态WL和WR以及计算时间T0如表1所示．计算中使用的CFL数均为0.9．

算例1的解由两个右行的强激波和位于中间的接触间断构成,并且左边激波移动的速度非常慢．该算例通常用来检验数值格式捕捉强激波(包括慢行激波)和接触间断的能力．从图2(a)可以看到本文构造的GT-AUSM格式对于各个波系都得到了比较满意的计算结果．

算例2的解对应一个孤立静止的接触波．一般来说,高分辨率格式都能精确地分辨孤立静止的接触间断,因此该算例通常用来检验格式数值耗散的大小．从图2(b)可以看到GT-AUSM格式保留了传统AUSM格式能够精确地分辨孤立静止的接触间断的优点．

表1 四个一维Riemann问题的初始值和计算时间

Table 1 Initial data of 4 1D Riemann problems and the computation time

testWL=(ρL,uL,pL)WR=(ρR,uR,pR)x0T0RP1(5.999 24,19.597 5,460.894)(5.992 42,-6.196 33,46.095)0.40.035RP2(1.4,0.0,1.0)(1.0,0.0,1.0)0.52.0RP3(1.4,0.1,1.0)(1.0,0.1,1.0)0.52.0RP4(1.0,-2.0,0.4)(1.0,2.0,0.4)0.50.15

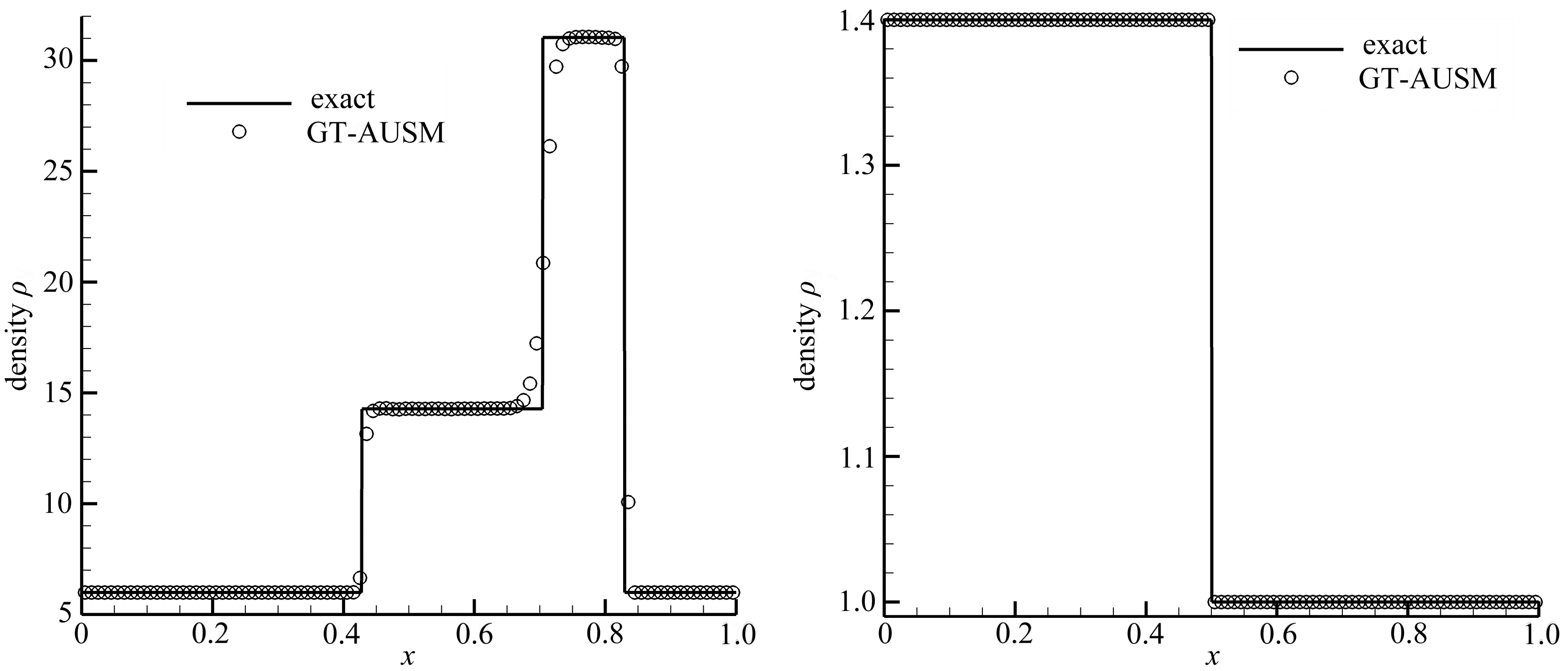
(a) 算例1的计算结果 (b) 算例2的计算结果
(a) The solutions of RP1 (b) The solutions of RP2

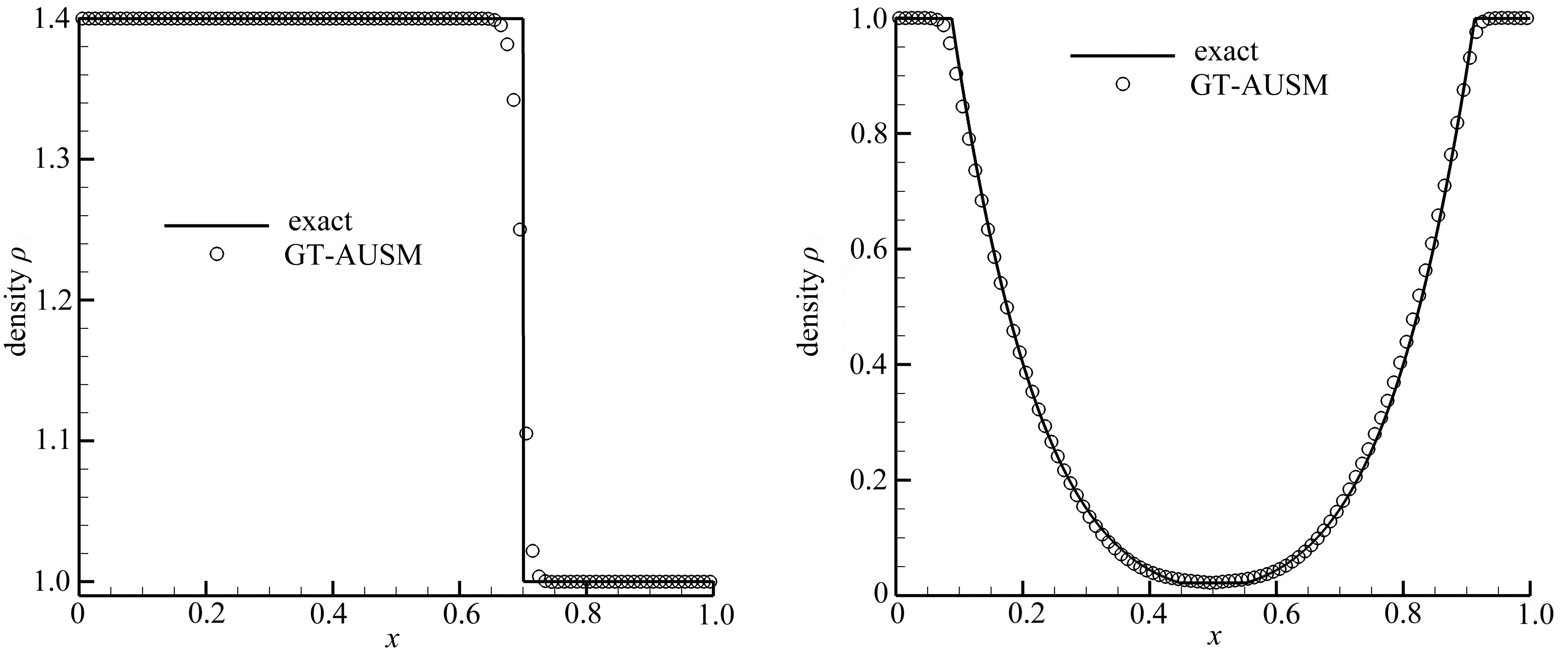
(c) 算例3的计算结果 (d) 算例4的计算结果
(c) The solutions of RP3 (d) The solutions of RP4
图2 一维Riemann问题的计算结果
Fig. 2 The solutions of 1D Riemann problems

算例3的解由一个右行的接触波构成．该算例通常用来测试数值格式分辨慢行接触间断的能力．从图2(c)可以看到GT-AUSM格式能够很好地分辨该孤立右行的接触波．

算例4的解由两个对称的稀疏波和一个接触间断构成,两个稀疏波之间的区域接近于真空,因此该算例经常用来测试数值格式计算低密度流时的表现．从图2(d)可以看到GT-AUSM格式对于该算例给出了精确的解．

3.2 二维Riemann问题

为了比较三种数值格式(GT-AUSM、一维AUSM[6]、GM-HLL-A[28])的分辨率,计算文献[29]中的二维Riemann问题．正方形区域[0,1]×[0,1]被均匀划分成400×400的正方形网格．初始条件由直线x=0.5和y=0.5所围成的四个象限内的常数状态所组成：

(25)

由于该算例没有精确解,我们使用HLLC格式在1 200×1 200的密网格下所得到的计算结果作为参考解,三种格式(GT-AUSM、AUSM、GM-HLL-A)的数值解使用400×400的粗网格来计算．数值解与参考解之间的误差定义为

(26)

其中,ρi, j为粗网格下网格单元(i, j)密度值的数值解,为密网格下网格单元(3i,3j)密度值的参考解．图3展示了计算时间T=0.3时参考解和三种格式数值解的密度轮廓图,图中画出了密度值从0.25到3.05,间隔为0.1的29条轮廓线．从图3中可以看到,参考解和数值解具有相同的波系结构,即四个接触间断沿着顺时针方向在中心盘旋出涡形结构．相比于一维AUSM格式和GM-HLL-A格式,本文构造的真正二维GT-AUSM格式对于接触间断和涡形结构的内部波纹具有更高的分辨率．表2展示了三种数值格式与参考解之间的误差,从表中可以看到,相比于一维AUSM格式和GM-HLL-A格式,本文构造的真正二维GT-AUSM格式的精度更高,其误差分别减少了9.99%和10.16%．值得注意的是,在计算中,一维AUSM格式的稳定性CFL数不能超过0.5,真正二维的GM-HLL-A格式和GT-AUSM格式的稳定性CFL数均可以取到0.95．这和文献[14]中分析的结论是相符的：真正多维的迎风格式在计算多维问题时可以提高稳定性CFL数．

表2 二维Riemann问题不同数值格式与参考解之间的误差

Table 2 Errors between different numerical schemes and the reference solution of the 2D Riemann problem

schemeerror ‖L(ρ)‖2AUSM7.125 4E-3GM-HLL-A7.138 8E-3GT-AUSM6.413 7E-3

3.3 随机扰动问题

进行数值模拟时,在初始分布和计算过程中经常会引入微小的随机扰动．扰动量随着时间的变化过程,经常用来检验数值格式的鲁棒性．为了模拟随机扰动随着时间的发展过程,构造二维平面激波随机扰动算例，Mach数为25的平面激波从左向右移动,在初始分布的物理量上增加10-6倍随机扰动：

(ρ,u,v,p)=(1.4,0,0,1)+10-6(α1,α2,α3,α4)，

(27)

其中,αk(k=1,2,3,4)是(0,1)之间的随机数,在计算中由相应的随机函数来生成．计算区域[0,120]×[0,1]被划分成2 400×20的正方形网格．图4展示了计算时间T=4时,使用一维AUSM格式和真正二维的GT-AUSM格式计算所得到的密度轮廓图．从图4中可以看到,一维AUSM格式在激波波后出现了轻微的不稳定现象,而GT-AUSM格式消除了不稳定现象,得到了清晰的激波轮廓图．值得注意的是, 在计算中, 一维AUSM格式的稳定性CFL数不能超过0.45,而GT-AUSM格式的稳定性CFL数可以取到0.95．

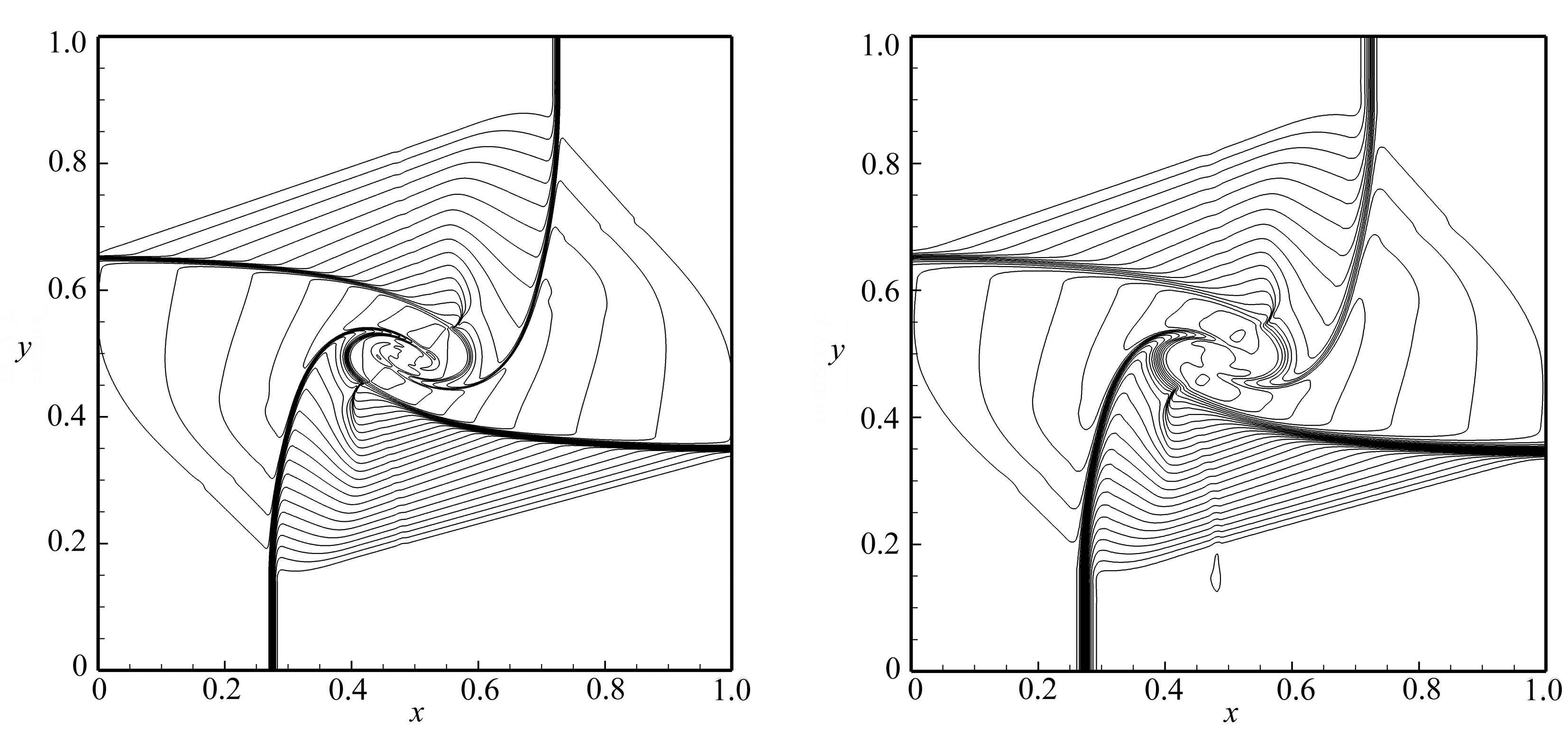
(a) HLLC格式计算的参考解 (b) AUSM格式计算的数值解
(a) The reference solution computed (b) The solution computed with the HLLC scheme with the AUSM scheme

(c) GM-HLL-A格式计算的数值解 (d) GT-AUSM格式计算的数值解
(c) The solution computed with the (d) The solution computed with the GM-HLL-A scheme GT-AUSM scheme
图3 二维Riemann问题的密度轮廓图
Fig. 3 Density contours of the 2D Riemann problem

3.4 计算效率的比较

在构造数值格式时,除了分辨率和鲁棒性,计算效率也是需要考虑的一个重要因素．本文构造的真正二维GT-AUSM格式除了要计算界面中点的数值通量还需要计算界面角点的数值通量,因此单个时间步的计算量会大于一维AUSM格式．但是GT-AUSM格式作为一种多维迎风格式在计算多维问题时可以提高稳定性CFL数[14],从而增加时间步长,减少迭代的步数,节约CPU的计算时间．表3展示了用一维AUSM格式和二维GT-AUSM格式计算二维Riemann问题(表中用“example 1”表示)和随机扰动问题(表中用“example 2”表示)的计算时间．在比较计算时间时,CFL数均取格式允许的最大值．例如,计算二维Riemann问题时,AUSM格式的CFL数取0.5,GT-AUSM格式的CFL数取0.95．从表3可以看到,相比于一维AUSM格式,GT-AUSM格式的计算效率分别提高了23.93%和28.83%,因此GT-AUSM格式在计算中具有更高的效率．

(a) AUSM格式的计算结果 (b) GT-AUSM格式的计算结果 (a) The solution computed with the AUSM scheme (b) The solution computed with the GT-AUSM scheme
图4 随机扰动问题的密度轮廓图
Fig. 4 Density contours of the random perturbation problem

表3 不同数值格式的计算效率比较

Table 3 Comparison of computational efficiencies between different numerical schemes

schemeexample 1CPU timeCFLexample 2CPU timeCFLAUSM91.65 s0.50301.16 s0.45GT-AUSM69.72 s0.95214.35 s0.95

4 结 论

基于对流迎风分裂思想构造的AUSM类格式不仅形式简单，而且可以精确捕捉一维激波和接触间断．但是在求解多维问题时,只考虑了界面法向波系对数值通量的贡献,忽视了横向波系的影响，这样不仅会减小稳定性CFL数,而且无法保证格式的鲁棒性．本文通过求解考虑了横向波系影响的角点数值通量来构造一种真正二维的AUSM通量分裂格式，并且进行了数值试验来验证格式在计算中的表现．其中一维Riemann问题的计算结果表明：本文构造的二维AUSM格式保留了一维AUSM格式可以精确捕捉一维激波和接触间断的优点．二维算例的计算结果表明,与一维AUSM格式相比,本文构造的二维AUSM格式不仅有更高的分辨率和计算效率,而且有更好的鲁棒性,可以避免强激波波后的不稳定现象．研究多维迎风格式提高分辨率和稳定性CFL数的深层次机理,构造非结构网格上的多维通量分裂格式并且将其应用到不同的守恒律系统的数值模拟中可以作为未来的研究工作．

参考文献（References）：

[1] ROE P L. Approximate Riemann solvers, parameter vectors, and difference schemes[J]. Journal of Computational Physics, 1981, 43(2): 357-372.

[2] TORO E F, SPRUCE M, SPEARES W. Restoration of the contact surface in the HLL Riemann solver[J]. Shock Waves, 1994, 4(1): 25-34.

[3] STEGER J L, WARMING R F. Flux vector splitting of the inviscid gas dynamic equations with application to finite-difference methods[J]. Journal of Computational Physics, 1981, 40(2): 263-293.

[4] VAN LEER B. Flux-vector splitting for the Euler equation[C]//8th International Conference on Numerical Methods in Fluid Dynamics. Berlin, Heidelberg: Springer-Verlag, 1982.

[5] TORO E F, V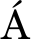ZQUEZ-CEND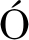N M E. Flux splitting schemes for the Euler equations[J]. Computers & Fluids, 2012, 70: 1-12.

[6] LIOU M S, JR STEFFEN C J. A new flux splitting scheme[J]. Journal of Computational Physics, 1993, 107(1): 23-39.

[7] LIOU M S. A sequel to AUSM: AUSM+[J]. Journal of Computational Physics, 1996, 129(2): 364-382.

[8] KIM K H, LEE J H, RHO O H. An improvement of AUSM schemes by introducing the pressure-based weight functions[J]. Computers and Fluids, 1998, 27(3): 311-346.

[9] KIM K H, LEE J H, RHO O H. Methods for the accurate computations of hypersonic flows Ⅰ: AUSMPW+ scheme[J]. Journal of Computational Physics, 2001, 174(1): 38-80.

[10] LIOU M S. A sequel to AUSM, part Ⅱ: AUSM+-up for all speeds[J]. Journal of Computational Physics, 2006, 214(1): 137-170.

[11] 胡立军, 袁礼. 一种基于TV分裂的真正多维Riemann解法器[J]. 应用数学和力学, 2017, 38(3): 243-264.(HU Lijun, YUAN Li. A genuinely multidimensional Riemann solver based on the TV splitting[J]. Applied Mathematics and Mechanics, 2017, 38(3): 243-264.(in Chinese))

[12] BRIO M, ZAKHARIAN A R, WEBB G M. Two-dimensional Riemann solver for Euler equations of gas dynamics[J]. Journal of Computational Physics, 2001, 167(1): 177-195.

[13] RUMSEY C B, VAN LEER B, ROE P L. A multidimensional flux function with application to the Euler and Navier-Stokes equations[J]. Journal of Computational Physics, 1993, 105(2): 306-323.

[14] COLLELA P. Multidimensional upwind methods for hyperbolic conservation laws[J]. Journal of Computational Physics, 1990, 87(1): 171-200.

[15] LEVEQUE R J. Wave propagation algorithms for multidimensional hyperbolic systems[J]. Journal of Computational Physics, 1997, 131(2): 327-353.

[16] SALTZMAN J. An unsplit 3D upwind method for hyperbolic conservation laws[J]. Journal of Computational Physics, 1994, 115(1): 153-168.

[17] ROE P L. Discrete models for the numerical analysis of time-dependent multidimensional gas dynamics[J]. Journal of Computational Physics, 1986, 63(2): 458-476.

[18] FEY M. Multidimensional upwinding, part Ⅰ: the method of transport for solving the Euler equations[J]. Journal of Computational Physics, 1998, 143: 159-180.

[19] FEY M. Multidimensional upwinding, part Ⅱ: decomposition of the Euler equations into advection equations[J]. Journal of Computational Physics, 1998, 143: 181-203.

[20] WENDROFF B. A two-dimensional HLLE Riemann solver and associated Godunov-type difference scheme for gas dynamics[J]. Computers & Mathematics With Applications, 1999, 38(1): 175-185.

[21] BALSARA D S. Multidimensional HLLE Riemann solver: application to Euler and magnetohydrodynamic flows[J]. Journal of Computational Physics, 2010, 229(6): 1970-1993.

[22] BALSARA D S. A two-dimensional HLLC Riemann solver for conservation laws: application to Euler and MHD flows[J]. Journal of Computational Physics, 2012, 231(22): 7476-7503.

[23] BALSARA D S. Multidimensional Riemann problem with self-similar internal structure, part Ⅰ: application to hyperbolic conservation laws on structured meshes[J]. Journal of Computational Physics, 2014, 277: 163-200.

[24] DUMBSER M, BALSARA D S. A new efficient formulation of the HLLEM Riemann solver for general conservative and non-conservative hyperbolic systems[J]. Journal of Computational Physics, 2016, 304: 275-319.

[25] BALSARA D S, NKONGA B. Multidimensional Riemann problem with self-similar internal structure, part Ⅲ: a multidimensional analogue of the HLLI Riemann solver for conservative hyperbolic systems[J]. Journal of Computational Physics, 2017, 346: 25-48.

[26] MANDAL J C, SHARMA V. A genuinely multidimensional convective pressure flux split Riemann solver for Euler equations[J]. Journal of Computational Physics, 2015, 297: 669-688.

[27] QU F, SUN D, BAI J Q, et al. A genuinely two-dimensional Riemann solver for compressible flows in curvilinear coordinates[J]. Journal of Computational Physics, 2019, 386: 47-63.

[28] 胡立军, 袁礼. 一种基于AUSM分裂的真正多维HLL格式[J]. 气体物理, 2016, 1(6): 22-35.(HU Lijun, YUAN Li. A genuinely multidimensional HLL Riemann solver based on AUSM splitting[J]. Physics of Gases, 2016, 1(6): 22-35.(in Chinese))

[29] SCHULZ-RINNE C W, COLLINS J P, GLAZ H M. Numerical solution of the Riemann problem for two-dimensional gas dynamics[J]. SIAM Journal of Scientific Computing, 1993, 14(6): 1394-1414.

A 2D Flux Splitting Scheme Based on the AUSM Splitting

HU Lijun1, WU Shifeng2, ZHAI Jian3

(1. College of Mathematics and Statistics, Hengyang Normal University,Hengyang, Hunan 421002, P.R.China;2. School of Mathematics and System Sciences, Guangdong Polytechnic Normal University, Guangzhou 510665, P.R.China;3. Dawning Information Industry Co., Ltd., Beijing 100193, P.R.China)

Abstract: The AUSM-type schemes based on the advection upstream splitting method have the advantages of simpleness, high efficiency and high resolution, and are widely applied in computational fluid dynamics. The traditional AUSM-type schemes only consider the normal waves to the cell interface while ignoring the influence of tangential waves to the interface in the computation of the interfacial numerical flux. The flux of 2D Euler equations was split into the convective flux and the pressure flux by means of the AUSM splitting method, and they were both computed with the modified AUSM scheme. In the solution of the numerical flux at the corners where the influence of tangential waves was considered, a genuinely 2D AUSM flux splitting scheme was constructed. In the computation of 1D numerical examples, the proposed scheme keeps the merits of capturing shocks and contact discontinuities accurately. In the computation of the 2D numerical examples, the scheme has higher resolution and better robustness, while eliminating the instability behind the strong shock waves. In addition, with the scheme the stable CFL number greatly improves and the computation efficiency rises in the simulation of multidimensional problems. Therefore, the proposed scheme makes an accurate, efficient and robust numerical method.

Key words: compressible flow; Liou-Steffen splitting; AUSM scheme; GT-AUSM scheme; robustness

*收稿日期： 2019-09-06； 修订日期：2019-11-02

作者简介： 胡立军(1985—)，男，博士(通讯作者. E-mail: hulijun@lsec.cc.ac.cn).

引用格式: 胡立军, 吴世枫, 翟健. 基于AUSM分裂的二维通量分裂格式[J]. 应用数学和力学, 2020, 41(6): 615-626.

中图分类号： O354； O241.82

文献标志码：A

DOI: 10.21656/1000-0887.400264