引 言
近年来,动力系统的多稳态越来越受到人们的关注,当系统初始条件或参数受到扰动时,其动力学状态可以从一个运动状态切换到另一个状态,我们称这种现象为多稳态共存.最常见的共存是多平衡点共存或者多周期解共存,也有一些关于概周期或者混沌共存的报道[1-2].已有研究表明,神经系统中存在着混沌共存,自连接和它连接下的三神经元耦合系统[3]呈现出两混沌共存,Hopfield型神经耦合系统存在两混沌和一周期解的三稳态共存[4].进一步地,两个Hindmarsh-Rose(HR)神经元耦合系统具有一个混沌和两周期解的三稳态共存[5],而非单调激活函数耦合下的离散型神经网络系统具有平衡态与混沌态的共存[6].带有惯性项神经元的耦合系统也存在混沌和周期解的双稳态共存[7].而事实上,混沌共存除了以上说的两混沌和其他稳态的共存,也可以是更多混沌的共存,比如三混沌共存[8],甚至是八混沌共存[9].但是目前关于系统多混沌共存的研究中,一般只给出系统混沌的相图或时间历程图,却很少有混沌路径的探讨.而事实上,混沌路径可以清楚地展现系统在参数影响下的动力学转迁过程,这不仅能够进一步佐证系统所具有的多混沌共存,从而避免因混沌的初值敏感性而错误判断混沌的个数,而且在混沌的动力学转迁过程中,能够发现更多不同种类的多动力学共存.
考虑到生物神经元在信号处理过程中所具有的电感效应,Mauro等利用RLC振荡电路提出了惯性项神经元模型[10].事实上,动物半规管中毛发细胞的膜电位就可以用一个等价的电感电路进行模拟[11].此外,惯性项的增加能够更容易地使得系统产生混沌现象[12].随后,Babcock和Westervelt考虑了惯性项神经元耦合系统,发现了系统所具有的周期解和混沌[13].此后,在考虑耦合时滞影响下,一些学者构建了惯性项神经元的时滞耦合神经系统,研究并分析了相应的动力学行为[14-15].最近,Yao等基于惯性项神经元模型,提出了具有非单调激活函数的时滞耦合神经系统,研究发现,系统可以通过两个倍周期分岔序列和一个概周期分岔序列进入三混沌共存区域[16].本文在此基础上,进一步研究发现,时滞耦合惯性项神经元系统可以出现多级倍周期分岔序列和概周期分岔序列,进一步拓展了原有的研究结果,展现了系统更加丰富的多混沌和多周期解的多稳态共存.
本文的结构如下:首先,给出了惯性项神经元耦合系统的数学模型及其相应平衡点个数的分析.其次,选择固定的系统参数,以耦合时滞τ作为参数变量,在选取不同初始条件的情况下,利用Poincaré截面展现出系统相应的倍周期分岔图,结果表明,系统具有多级倍周期分岔序列共存现象,并给出了相应的相图.然后,以同一组参数为研究对象,在不同的时滞τ区间内,展现了系统在不同初始条件下的概周期分岔序列,结果表明,系统不仅具有上述的倍周期分岔序列共存,也存在多级概周期分岔序列共存.
1 系统模型及其平衡点
时滞耦合惯性项神经元系统的数学模型如下:
(1)
其中k1,k2>0表示阻尼因子,c1,c2为神经元的耦合强度,τ>0是耦合时滞,神经元之间的激活函数为f(u)=uexp(-u2/2),它是一个有界、可微、非单调的非线性函数.事实上,这个激活函数是1999年Crespi为了提高神经网络联想的记忆存储能力而提出来的,我们称之为Crespi函数[17].此后,Li和Chen基于此激活函数构建了带有外激励的神经元模型,并讨论了系统的两混沌共存[18].针对此激活函数,Li等[19]讨论了单惯性项神经元自反馈激励下的Hopf分岔和混沌动力学.令![]() 系统(1)可以改写成如下的等效系统:
系统(1)可以改写成如下的等效系统:

(2)
为了分析系统(2)的平衡点个数, 首先令![]() 显然, 系统有一个平凡平衡点(0, 0, 0, 0), 而相应的非平凡平衡点可以记为
显然, 系统有一个平凡平衡点(0, 0, 0, 0), 而相应的非平凡平衡点可以记为![]() 并且满足方程
并且满足方程![]() 和
和![]() 事实上,由于整个方程是一个超越方程,我们无法给出相应的理论精确解,但是在固定不同的参数c1和c2时,可以利用数值计算的方法给出相应的数值解[15].
事实上,由于整个方程是一个超越方程,我们无法给出相应的理论精确解,但是在固定不同的参数c1和c2时,可以利用数值计算的方法给出相应的数值解[15].
图1为固定参数c1=5,c2选取不同值时,系统平衡点个数的变化情况(其中浅色线为![]() 深色线为
深色线为![]() 从图中可以看出,在c1=5,c2=0.1时,系统(2)只有一个平凡平衡点(0, 0, 0, 0).随着c2从0.1增长到1,平衡点个数增加到了3个,其中包括一个平凡平衡点和两个对称的非平凡平衡点,此时,系统通过叉型分岔(pitchfork bifurcation)出现了一对非平凡平衡点,如图1(b)所示.随着c2继续增大到5时,即c1=5,c2=5时,系统(2)的平衡点个数增加到7个,此时,系统的非平凡平衡点通过鞍结分岔(saddle-node bifurcation)出现了两对新的非平凡平衡点,如图1(c)所示.
从图中可以看出,在c1=5,c2=0.1时,系统(2)只有一个平凡平衡点(0, 0, 0, 0).随着c2从0.1增长到1,平衡点个数增加到了3个,其中包括一个平凡平衡点和两个对称的非平凡平衡点,此时,系统通过叉型分岔(pitchfork bifurcation)出现了一对非平凡平衡点,如图1(b)所示.随着c2继续增大到5时,即c1=5,c2=5时,系统(2)的平衡点个数增加到7个,此时,系统的非平凡平衡点通过鞍结分岔(saddle-node bifurcation)出现了两对新的非平凡平衡点,如图1(c)所示.

(a) c2=0.1 (b) c2=1 (c) c2=5
图1 固定参数c1=5,系统平衡点个数随参数c2选取不同所带来的变化
Fig. 1 Intersection points of x1=c1 f(y1) and y1=c2 f(x1) showing the number of equilibrium for fixed c1=5 in neural system (2)
2 倍周期分岔序列共存
选取系统(2)的参数为k1=1,k2=1.6,c1=5,c2=1.此时,由第1节的分析我们知道,系统(2)具有3个平衡点,分别为平凡平衡点(0, 0, 0, 0)和一对对称的非平凡平衡点.为了展现系统多级倍周期分岔的共存,选取时滞τ作为分岔参数,利用Poincaré截面x2=0,给出在不同初始条件下,参数τ变动时系统(2)的一维分岔图.数值结果表明,在不同初始条件下,系统(2)可以通过多级倍周期分岔进入不同的混沌模式,从而使得系统存在多个混沌的共存.并且,在此动力学演变过程中,系统具有周期轨道、多周期轨道以及混沌等不同运动模式的混合共存.
2.1 一级倍周期分岔序列
首先,我们展示系统(2)的一级倍周期分岔序列.选取系统初始条件为(2,-2,0,0)和(-2,2,0,0),利用Poincaré截面x2=0,给出在时滞参数为τ∈[0,6]区间内系统(2)的一维分岔图,如图2所示,系统具有两个倍周期分岔序列的共存,我们称之为一级倍周期分岔序列.从图中可以看出,当参数τ<0.9时,系统具有一对对称的单周期轨道,相应的相图如图3(a)所示,此时参数τ=0.1.随着时滞参数τ的增加,系统的单周期轨道共存演变为周期二轨道共存,如图3(b)所示,此时参数τ=1.05.进一步地,周期二轨道在时滞增加到τ=2时演变为周期四轨道,此时系统(2)具有两个周期四轨道的共存,如图3(c)所示.最后,从图2可以看出,在时滞的影响下,系统通过倍周期分岔序列进入了混沌共存,如图3(d)所示,此时参数τ=3.

图2 初始条件为(2,-2,0,0)和(-2,2,0,0)时,系统(2)在τ∈[0,6]区间内通过一级倍周期分岔进入混沌共存
Fig. 2 System (2) entering a pair of chaotic attractors for [0,6] through the 1st period-doubling bifurcation with initial conditions of (2,-2,0,0) and (-2,2,0,0)
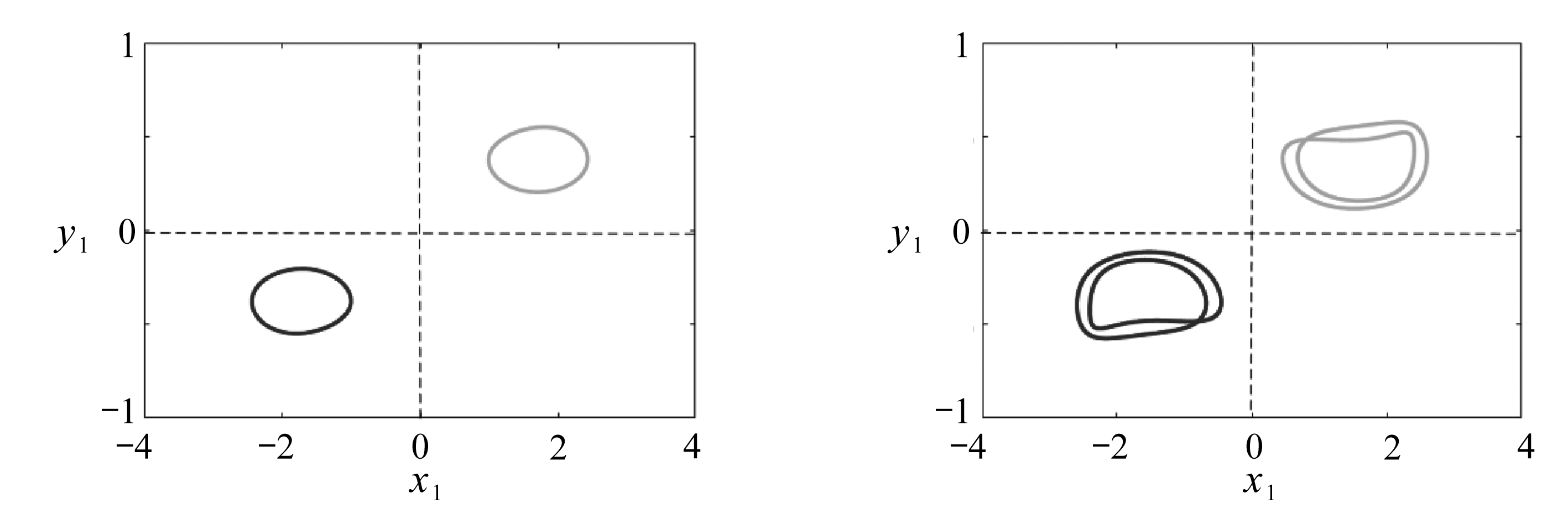
(a) τ=0.1 (b) τ=1.05

(c) τ=2 (d) τ=3
图3 在一级倍周期分岔图序列中,不同时滞参数下系统(2)的相图(其中初始条件分别为(2,-2,0,0)和(-2,2,0,0))
Fig. 3 Phase portraits of the steady state for the 1st period-doubling bifurcationunder initial conditions of (2,-2,0,0) and (-2,2,0,0)
2.2 二级倍周期分岔序列
其次,选取初始条件为(0,2.5,0,0)和(0,-2.5,0,0),利用Poincaré截面x2=0,展现在时滞参数为τ∈[3.54,9.54]区间内,系统(2)的一维分岔图,如图4所示,此时我们称之为二级倍周期分岔序列.从图中可以看出,此时的二级倍周期分岔序列完全类似于2.1小节中的一级倍周期分岔序列, 只是初始条件和时滞参数τ的区间不同.具体来看, 当参数τ在3.54<τ<6.04区间内,系统(2)具有一对对称的单周期轨道,相应的相图如图5(a)所示,此时参数选取τ=4.4.而另一方面,从2.1小节的数值结果我们知道,系统(2)在τ=3时已有一对周期轨道通过倍周期分岔进入了混沌,所以,此时系统(2)具有一对单周期轨道和一对混沌的混杂共存.
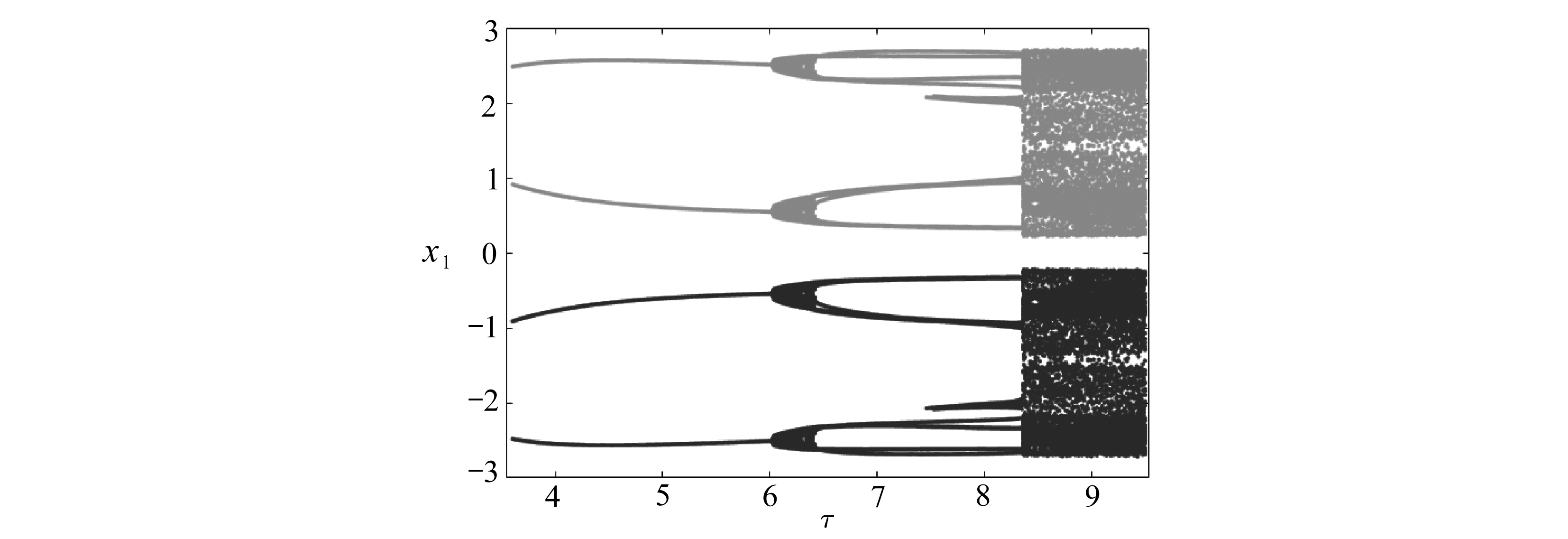
图4 初始条件分别为(0,2.5,0,0)和(0,-2.5,0,0)时,系统(2)在τ∈[3.54,9.54]区间内的二级倍周期分岔序列共存
Fig. 4 System (2) entering a pair of chaotic attractors for [3.54,9.54] through the 2nd period-doubling bifurcation with initial conditions of (0,2.5,0,0) and (0,-2.5,0,0)
进一步地,在二级倍周期分岔序列中,随着时滞参数τ的增加,系统的单周期轨道共存演变为周期二轨道共存,相应的相图如图5(b)所示,此时参数τ=6.7.同样地,由于此时系统(2)存在通过一级倍周期分岔序列进入的混沌共存,故系统具有的混杂共存动力学是一对周期二轨道和一对混沌运动的共存.类似于一级倍周期分岔序列,在二级倍周期分岔序列中,周期二轨道在时滞增加到τ=7时演变为周期四轨道,如图5(c)所示,系统存在一对周期四轨道和混沌运动的共存.最后,周期四的周期轨道在二级倍周期分岔序列中进入另一对混沌,如图5(d)所示,此时参数τ=9,系统(2)具有二对对称的混沌共存.
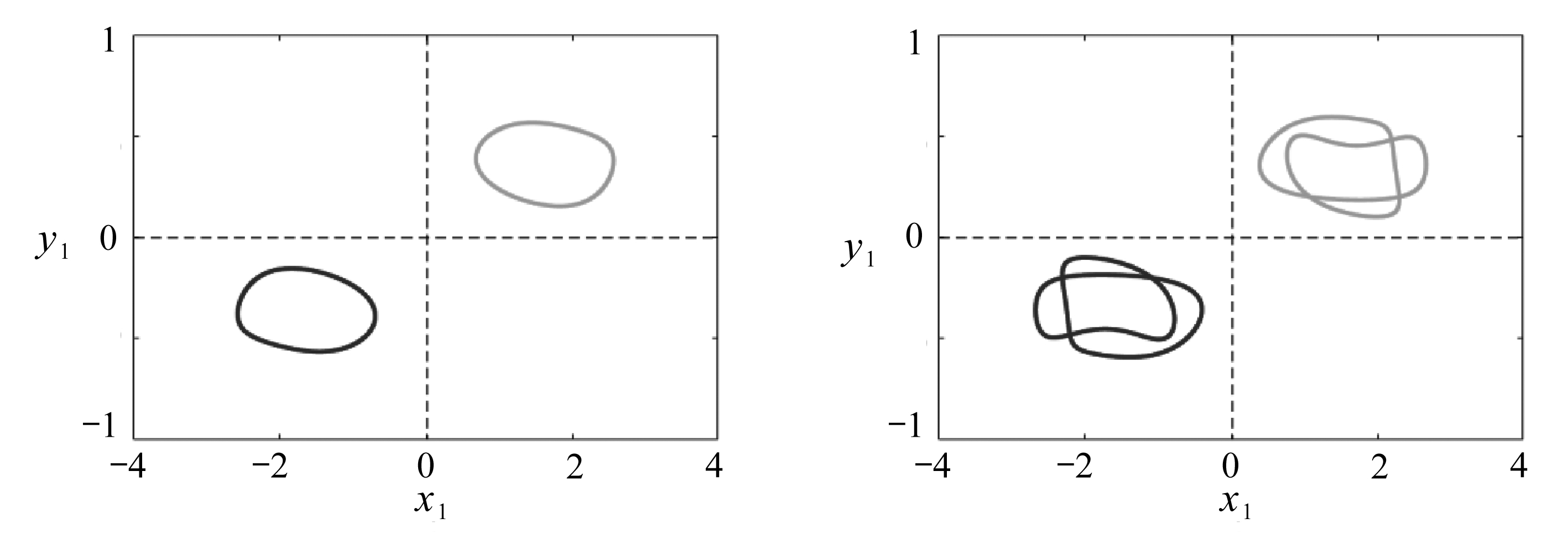
(a) τ=4.4 (b) τ=6.7
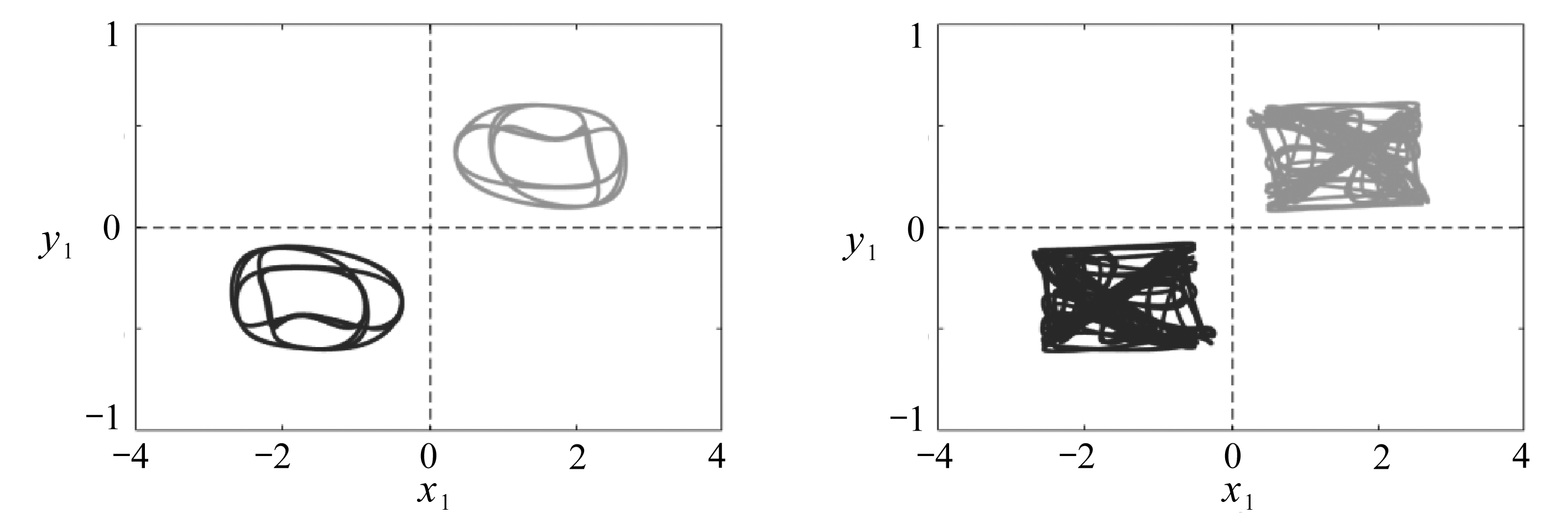
(c) τ=7 (d) τ=9
图5 二级倍周期分岔图序列中,不同时滞参数下系统(2)的相图(其中初始条件为(0,2.5,0,0)和(0,-2.5,0,0))
Fig. 5 Phase portraits of the steady state for the 2nd period-doubling bifurcation under initial conditions of (0,2.5,0,0) and (0,-2.5,0,0)
3 概周期分岔序列共存
在前一节的数值仿真中,我们发现在k1=1,k2=1.6,c1=5,c2=1的参数条件下,系统(2)可以具有不同的倍周期分岔序列共存.接下来,固定系统参数如上,即k1=1,k2=1.6,c1=5,c2=1,选择时滞τ作为分岔参数,利用Poincaré截面x2=0,选择在不同的初值条件下,数值仿真系统(2)的一维分岔图.结果表明,在不同的初始条件下,系统(2)存在着不同于倍周期分岔的概周期分岔序列,并且进一步的研究表明,类似于倍周期分岔序列共存,系统存在不同的概周期分岔序列共存,为了叙述方便,我们分别称之为一级和二级概周期分岔序列.在此动力学的演变转迁过程中,系统存在更加丰富的多运动模式共存.
3.1 一级概周期分岔序列
同样地, 类似于倍周期分岔序列, 依然选择Poincaré截面x2=0,首先展示系统(2)在参数τ∈[1.81,9.81]区间内的一级概周期分岔序列,如图6所示,此时系统的初始条件分别为(1.8,-2.4,0,0)和(-1.8,2.4,0,0).从图中可以看出,当参数1.81<τ<2.46时,系统(2)的动力学行为是位于二四象限的反对称8字型单周期轨道,相图如图7(a)所示,此时参数τ=2.随着时滞参数τ的增加,系统可以通过两个不同频率的耦合转迁至位于二四象限的概周期模式,如图7(b)所示,此时参数τ=2.7.

图6 初始条件分别为(1.8,-2.4,0,0)和(-1.8,2.4,0,0)时,系统(2)在τ∈[1.81,9.81]区间内的一级概周期分岔序列共存
Fig. 6 The 1st coexistence of quasi-periodic bifurcations for system (2) in [1.81,9.81] with initial conditions of (1.8,-2.4,0,0) and (-1.8,2.4,0,0)

(a) τ=2 (b) τ=2.7
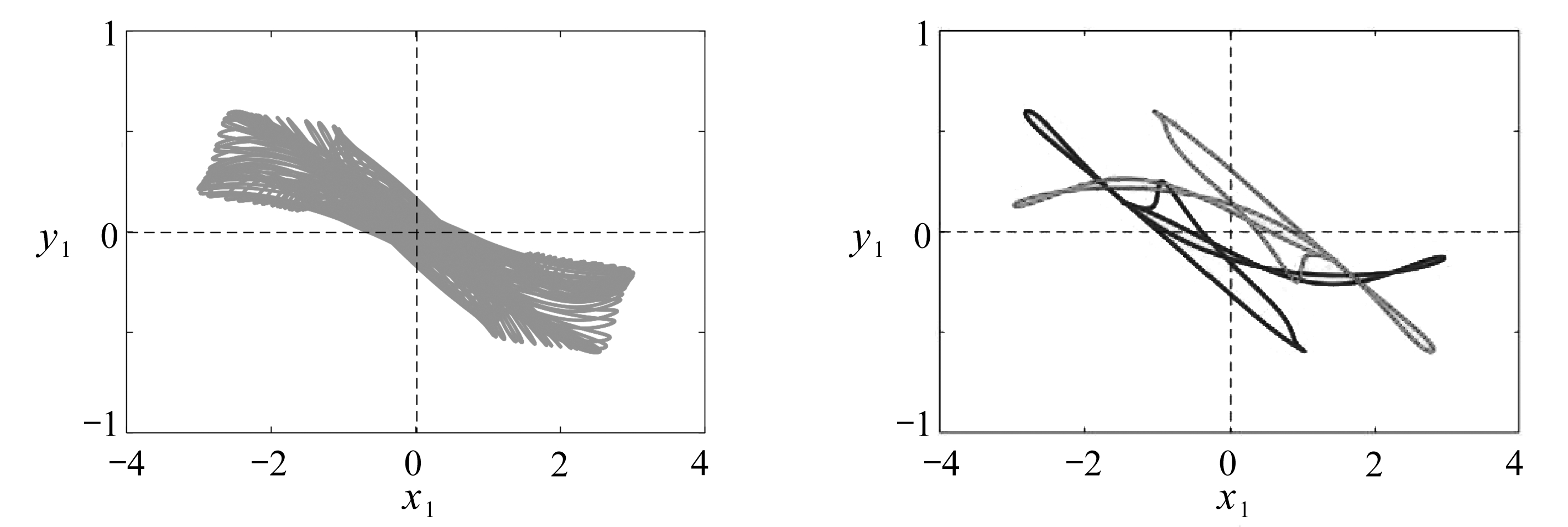
(c) τ=3.3 (d) τ=4
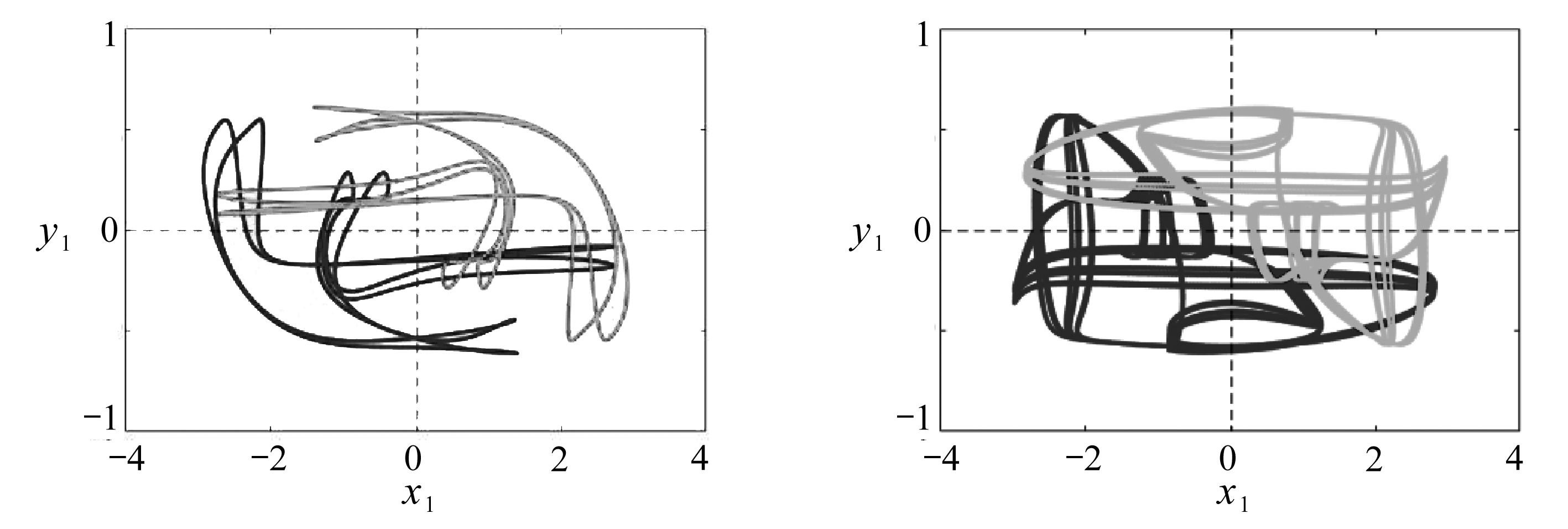
(e) τ=5 (f) τ=7
图7 一级概周期分岔图序列中,不同时滞参数下系统(2)的相图(其中初始条件为(1.8,-2.4,0,0)和(-1.8,2.4,0,0))
Fig. 7 Phase portraits of the steady state for the 1st quasi-periodic bifurcation under initial conditions of (1.8,-2.4,0,0) and (-1.8,2.4,0,0)
此外,概周期在时滞增加到τ=3.3时通过概周期的破裂演变为混沌运动,如图7(c)所示.进一步地,混沌运动模式分裂转迁至两个具有原点对称的多周期运动轨道,如图7(d)所示,此时参数τ=4.最后,多周期轨道在参数τ的进一步增大下又进入了两个具有原点对称的混沌运动模式,如图7(f)所示,此时参数τ=7.
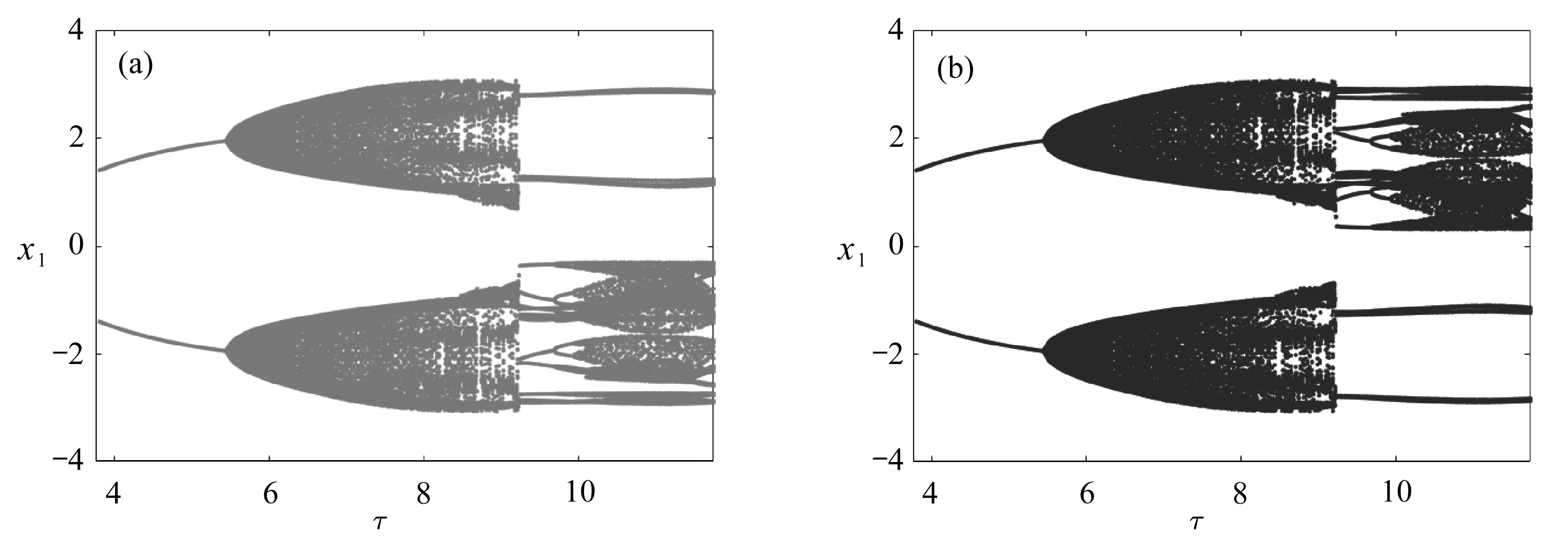
图8 初始条件分别为(3,-3,0,0)和(-3,3,0,0)时,系统(2)在τ∈[3.75,11.75]区间内的二级概周期分岔序列共存
Fig. 8 The 2nd coexistence of quasi-periodic bifurcations for system (2) in [3.75,11.75] with the initial conditions of (3,-3,0,0) and (-3,3,0,0)
3.2 二级概周期分岔序列
类似于一级概周期分岔序列,利用Poincaré截面x2=0,选取初始条件为(3,-3,0,0)和(-3,3,0,0),数值仿真出时滞参数为τ∈[3.75,11.75]区间内,系统(2)的二级概周期分岔序列,如图8所示.从图中可以看出,系统二级概周期分岔序列从拓扑结构上看,完全类似于3.1小节中的一级概周期分岔序列,只是时滞参数τ的区间选择不同.具体来看,当参数τ在3.75<τ<5.41区间内,系统(2)具有一个位于一三象限的对称8字型单周期轨道,相应的相图如图9(a)所示,此时参数τ=4.5.从相图图形上看,此时的单周期完全不同于一级概周期分岔序列中位于二四象限的反对称8字型单周期.此外,特别值得注意的是,从3.1小节的数值仿真我们知道,系统(2)在τ=4.5时已有一对通过一级概周期分岔序列得到的多周期轨道,此时系统(2)具有单周期轨道和多周期轨道的混杂共存.
进一步地,在二级概周期分岔序列中,随着时滞参数τ的增加,系统的正8字型单周期轨道演变转迁为概周期运动模式,并同样位于一三象限内,如图9(b)所示,此时参数τ=5.7.另一方面,由于系统(2)存在通过一级概周期分岔序列进入的对称混沌运动共存,故系统具有概周期和混沌运动的混杂共存动力学.类似于一级概周期分岔序列,在二级概周期分岔序列中,概周期在时滞增加到τ=8时通过概周期破裂演变为混沌运动,如图9(c)所示,此时系统存在多混沌运动共存.随着时滞的增加,混沌运动模式在二级概周期分岔序列中分裂出一对多周期,如图9(d)所示,此时参数τ=9,系统(2)具有多周期和混沌的共存.而相应的多周期运动最后进入了一对混沌运动模式,如图9(e)和9(f)所示.

(a) τ=4.5 (b) τ=5.7
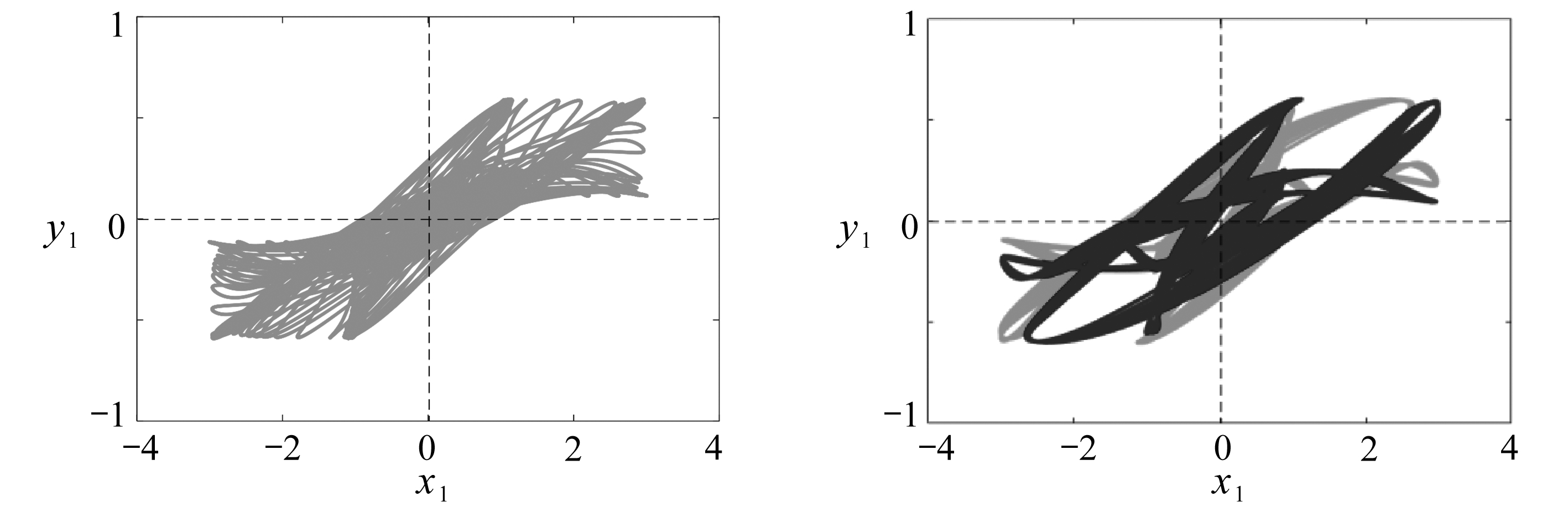
(c) τ=8 (d) τ=9
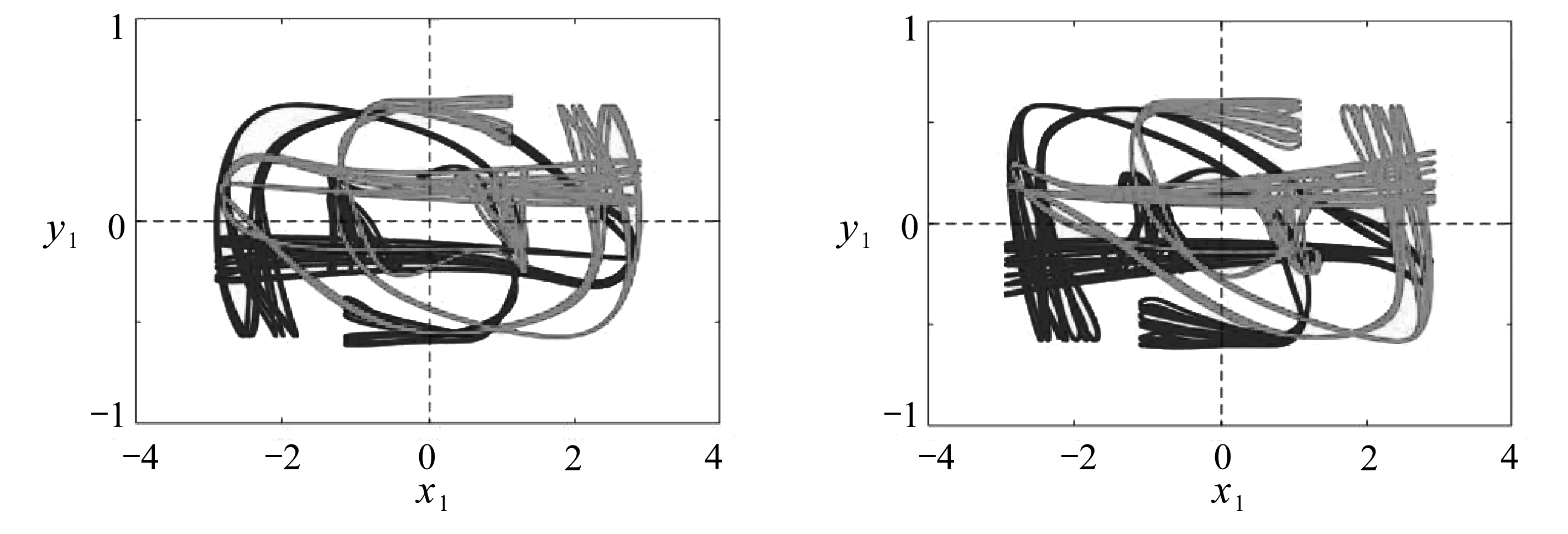
(e) τ=10 (f) τ=11
图9 二级概周期分岔图序列中,不同时滞参数下系统(2)的相图(其中初始条件为(3,-3,0,0)和(-3,3,0,0))
Fig. 9 Phase portraits of the steady state for the 2nd quasi-periodic bifurcation under initial conditions of (3,-3,0,0) and (-3,3,0,0)
4 结 论
神经网络系统中混沌共存具有十分重要的意义,在通信、语音与图像处理、模式识别以及优化与控制等方面都具有很强的应用价值.本文针对惯性项神经元模型,利用非线性激活函数,构建了时滞耦合的惯性项神经元耦合系统,在固定系统参数的情况下,以耦合时滞τ作为参数变量,选取不同初始条件,利用Poincaré截面技术展现出系统相应的倍周期分岔图.结果表明,系统存在多级的倍周期分岔序列.同样地,在同一组参数下,在不同的时滞τ区间内,展现了系统在不同初始条件下的概周期分岔序列.结果表明,系统不仅具有上述的倍周期分岔序列共存,也同时存在多级概周期分岔序列,进一步研究了耦合神经系统动力学的复杂性.
[1] PISARCHIK A N, FEUDEL U. Control of multistability[J]. Physics Reports, 2014, 540(4): 167-218.
[2] AIHARA K, TAKABE T, TOYODA M. Chaotic neural networks[J]. Physics Letter A, 1990, 144(67): 333-340.
[3] HUANG W Z, HUANG Y. Chaos, bifurcation and robustness of a class of Hopfield neural networks[J]. International Journal of Bifurcation and Chaos, 2011, 21(3): 885-895.
[4] CHEN P F, CHEN Z Q, WU W J. A novel chaotic system with one source and two saddle-foci in Hopfield neural networks[J]. Chinese Physics B, 2010, 4: 134-139.
[5] PISARCHIK A N, JAIMES-REATEGUI R, GARC A-VELLISCA M A. Asymmetry in electrical coupling between neurons alters multistable firing behavior[J]. Chaos, 2018, 28(3): 033605.
A-VELLISCA M A. Asymmetry in electrical coupling between neurons alters multistable firing behavior[J]. Chaos, 2018, 28(3): 033605.
[6] CHENG C Y. Coexistence of multistability and chaos in a ring of discrete neural network with delays[J]. International Journal of Bifurcation and Chaos, 2010, 20(4): 1119-1136.
[7] SONG Z G, XU J, ZHEN B. Multitype activity coexistence in an inertial two-neuron system with multiple delays[J]. International Journal of Bifurcation and Chaos, 2015, 25(13): 1530040.
[8] LAI Q, HUANG J N. Coexistence of multiple attractors in a new chaotic system[J]. Acta Physica Polonica B: Particle Physics & Field, 2016, 47(10): 2315-2323.
[9] JIMENEZ-LOPEZ E, GONZALEZ SALAS J S, ONTANON-GARCIA L J, et al. Generalized multistable structure via chaotic synchronization and preservation of scrolls[J]. Journal of the Franklin Institute, 2013, 350(10): 2853-2866.
[10] MAURO A, CONTI F, DODGE F, et al. Subthreshold behavior and phenomenological impedance of the squid giant axon[J]. The Journal of General Physiology, 1970, 55: 497-523.
[11] ANGELAKI D E, CORREIA M J. Models of membrane resonance in pigeon semicircular canal type Ⅱ hair cells[J]. Biological Cybernetics, 1991, 65(1): 1-10.
[12] TANI J. Proposal of chaotic steepest descent method for neural networks and analysis of their dynamics[J]. Electronics and Communications in Japan (Part 3: Fundamental Electronic Science), 1992, 75(4): 62-70.
[13] BABCOCK K L, WESTERVELT R M. Dynamics of simple electronic neural networks[J]. Physica D, 1987, 28: 305-316.
[14] SONG Z G, XU J. Stability switches and Bogdanov-Takens bifurcation in an inertial two-neuron coupling system with multiple delays[J]. Science China Technological Sciences, 2014, 57: 893-904.
[15] SONG Z G, WANG C H, ZHEN B. Codimension-two bifurcation and multistability coexistence in an inertial two-neuron system with multiple delays[J]. Nonlinear Dynamics, 2016, 85: 2099-2113.
[16] YAO S W, DING L W, SONG Z G, et al. Two bifurcation routes to multiple chaotic coexistence in an inertial two-neural system with time delay[J]. Nonlinear Dynamics, 2019, 95: 1-15.
[17] CRESPI B. Storage capacity of non-monotonic neurons[J]. Neural Networks, 1999, 12(10): 1377-1389.
[18] LI C G, CHEN G R. Coexisting chaotic attractors in a single neuron model with adapting feedback synapse[J]. Chaos, Solitons & Fractals, 2005, 23: 1599-1604.
[19] LI Chunguang, CHEN Guangrong, LIAO Xiaofeng, et al. Hopf bifurcation and chaos in a single inertial neuron model with time delay[J]. The European Physical Journal B:Condensed Matter and Complex Systems, 2004, 41: 337-343.