引 言
分数阶微积分在流体力学、控制系统、人工智能等诸多领域的应用[1-4]，引起了学者们对分数阶微积分的广泛关注．与整数阶微积分相比,分数阶微积分可以更精确地描述系统的遗传和记忆特性．基于分数阶微积分的这些特性，相关学者在神经网络中引入了分数阶微积分,从而更好地描述神经元的动态行为．针对分数阶神经网络已经出现了相关的研究背景:文献[5]给出了分数阶神经网络模型,并分析了分数阶神经网络的动力学行为．文献[6]给出了环型和中心结构的分数阶神经网络系统，讨论了该模型的分岔和混沌现象，建立了分岔条件,并给出了系统的稳定性条件．文献[7]通过整数阶神经网络和分数阶神经网络的对比,说明了分数阶神经网络比整数阶神经网络有更好的动力学行为,对系统的动力学行为描述得更加精确．文献[8]研究了分数阶神经网络的修正投影同步问题．
分数阶神经网络的稳定性分析是分数阶神经网络研究的重要课题之一，也取得了丰富的成果:如文献[9]研究了含有单侧Lipschitz条件的分数阶脉冲神经网络的全局Mittag-Leffler稳定性．文献[10]讨论了含有参数扰动的分数阶记忆电阻器神经网络的Hopfield鲁棒稳定性．文献[11]给出了含有脉冲的分数阶神经网络全局Mittag-Leffler稳定性的LMI条件．
随着人们对神经网络研究的不断深入，特别在具有约束条件的神经网络中，考虑含有时滞的分数阶神经网络具有重要的理论意义和应用价值．到目前为止，考虑含有时滞的分数阶神经网络的稳定性已经取得了若干成果:文献[12]研究了具有多重时间延迟非线性分数阶细胞神经网络的稳定性．文献[13]研究了一类基于记忆电阻器的时滞分数阶神经网络,通过构造Lyapunov泛函并应用Gronwall积分不等式，提出了一种新的保证全局Mittag-Leffler稳定性的准则．文献[14]给出了具有时滞的中立型分数阶神经网络一致稳定性的充分条件．文献[15]研究了含有时滞的分数阶Hopfield神经网络的全局稳定性．文献[16]研究了基于忆阻器的分数阶时滞复值神经网络的全局渐近稳定性．基于以上研究成果，本文将研究同时含有离散时滞及分布时滞的分数阶神经网络的渐近稳定性问题．
1 准 备 知 识
为了讨论方便,本文给出以下的记号:Rn是n维Euclid空间,Rn×n是所有n×n实矩阵的集合,I是n阶单位矩阵,UT是实矩阵或向量U的转置，‖x‖是实向量x的Euclid范数，A<0表示对称矩阵A是负定的，λmax(P)与λmin(P)表示矩阵P的最大特征值和最小特征值．
定义1[1] 设可积函数f(t)∈C[t0,+∞), α>0, 则当t>t0时,记
(1)
为函数f(t)的α阶Riemann-Liouville分数阶积分．
定义2[1] 设0≤n-1<α<n,n∈N+, f(t)具有n阶连续导数,记
(2)
为函数f(t)的α阶Caputo分数阶导数．
引理1[17] 若x(t)∈Rn是可微函数且P∈Rn×n是对称正定矩阵,则有下列不等式成立：
(3)
引理2[18] 对任意的u,v∈Rn,δ>0,则2uTv≤δuTu+(1/δ)vTv成立．
考虑分数阶时滞方程：
(4)
这里0<α≤1,xt(θ)=x(t+θ),θ∈[-r,0], f是一个连续向量函数满足f(t,0)=0．
引理3[19] 如果存在常数a1>0,a2>0,a3>0和Lyapunov函数V:Rn→R满足
a1‖x‖2≤V(x)≤a2‖x‖2,
(5)
且当V(x(t+θ))≤γV(x(t)),θ∈[-r,0],γ>1时,沿着方程(4)的α阶导数满足
(6)
则分数阶时滞方程(4)的零解是渐近稳定的．
引理4(Schur complement)[20] 对一个给定的对称矩阵S,下列说法是等价的:
(7a)
(7b)
(7c)
引理5[21] 对任意常矩阵W∈Rm×m,W=WT>0, 标量0<r(t)<r,向量函数ω:[0,r]→Rm,则有
(8)
下面主要考虑含有离散时滞和分布时滞的分数阶神经网络的渐近稳定性:
(9)
(10)
其中i∈{1,2,…,n},或等价为
(11)
D
h(y(s))ds+I，
(12)
其中
表示y(t)的α阶Caputo导数,0<α<1, n表示神经元的单位数,y(t)=[y1(t), y2(t), …, yn(t)]T∈Rn表示在时刻t的状态向量;A=diag{ai}, ai>0,i∈{1,2,…,n}, ai表示在断开网络和外部输入时第i个神经元将其电位重置为静止状态的速率；B=(bij)n×n,C=(cij)n×n,D=(dij)n×n 代表权重矩阵； f(y(t))=[f1(y1(t)), f2(y2(t)),…, fn(yn(t))]T,g(y(t))=[g1(y1(t)), g2(y2(t)), …, gn(yn(t))]T , h(y(t))=[h1(y1(t)), h2(y2(t)), …, hn(yn(t))]T表示激励函数，且f(0)=g(0)=h(0)=0;I=[I1,I2, …,In]T是神经元的输出；r1(t),r2(t)是时变时滞，且满足0≤r1(t)≤r1,0≤r2(t)≤r2．
已知系统(11)和(12)至少存在一个平衡点，可以将系统(11)和(12)的平衡点
平移到原点．通过变换x(t)=y(t)-y*将系统(11)和(12)转化为下面的形式:
(13)
(14)
其中x(t)=[x1(t),x2(t),…,xn(t)]T是变换后的系统的状态向量,且f(x(t))= f(y(t))- f(y*),g(x(t))=g(y(t))-g(y*),h(x(t))=h(y(t))-h(y*)．
2 主 要 结 果
2.1 含有离散时滞的分数阶神经网络的稳定性
考虑含有离散时滞的分数阶神经网络：
(15)
这里x(t)∈Rn,r1(t)是变时滞且满足0≤r1(t)≤r1,A是正定对角矩阵,A,B,C∈Rn×n且f(·),g(·)∈Rn, f(0)=0,g(0)=0．
为了研究系统(15),做如下假设：
(H1) 假设存在非负常数l1,l2使得对任意u,v∈Rn, f,g满足
‖f(u)- f(v)‖≤l1‖u-v‖, ‖g(u)-g(v)‖≤l2‖u-v‖．
(16)
定理1 如果条件(H1)成立,且存在常数k>0和对称正定矩阵P满足
(17)
那么分数阶时滞神经网络(15)的零解是渐近稳定的．
证明 构造一个Lyapunov函数V(t)=xT(t)Px(t), 这里P=PT>0．则
λmin(P)‖x(t)‖2≤V(t)≤λmax(P)‖x(t)‖2．
(18)
由引理1可以得到沿着方程(15)的V(t)的α阶Caputo导数:
2xT(t)P[-Ax(t)+Bf(x(t))+Cg(x(t-r1(t)))]．
(19)
又由条件(H1)和引理2有
2xT(t)PBf(x(t))≤xT(t)PBBTPx(t)+ fT(x(t))f(x(t))≤
(20)
2xT(t)PCg(x(t-r1(t)))≤
xT(t)PCCTPx(t)+gT(x(t-r1(t)))g(x(t-r1(t)))≤
(21)
所以
(22)
存在常数γ>1,当xt满足V(x(t+ξ))<γV(x(t)),ξ∈[-r1,0]时,对任意k>0有
(23)
由式(17)表明：对充分小的δ>0,γ=1+δ,有
(24)
记
(25)
λmin(-Ω)=λ0，则λ0>0．可以得到
(26)
则由引理3可知,分数阶时滞神经网络(15)的零解是渐近稳定的,定理得证．
2.2 含有分布时滞分数阶神经网络的稳定性
下面考虑含有分布时滞分数阶神经网络：
Dh(x(s))ds, 0<α≤1,
(27)
这里x(t)∈Rn,r1(t),r2(t)是时变时滞且满足0≤r1(t)≤r1,0≤r2(t)≤r2,A是正定对角矩阵,A,B,C,D∈Rn×n 且 f(·),g(·),h(·)∈Rn, f(0)=0,g(0)=0,h(0)=0．
为了研究系统(27),做如下假设：
(H2) 假设存在非负常数l1,l2,l3使得对任意u,v∈Rn, f,g,h满足
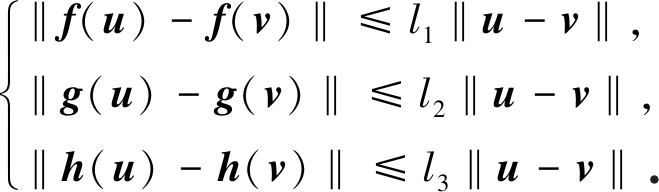
(28)
定理2 如果条件(H2)成立,且存在对称正定矩阵P和常数k1>0,k3>k2>0满足
(29)
(30)
那么分数阶时滞神经网络(27)的零解是渐近稳定的．
证明 构造一个Lyapunov函数V(t)=xT(t)Px(t)．这里P=PT>0．则
λmin(P)‖x(t)‖2≤V(t)≤λmax(P)‖x(t)‖2．
(31)
由引理1可以得到沿着方程(27)的V(t)的α阶Caputo导数：
2xT(t)P(-A)x(t)+2xT(t)PBf(x(t))+
2xT(t)PCg(x(t-r1(t)))+2xT(t)PDh(x(s))ds．
(32)
又由条件(H2)和引理2有
2xT(t)PBf(x(t))≤xT(t)PBBTPx(t)+ fT(x(t))f(x(t))≤
(33)
2xT(t)PCg(x(t-r1(t)))≤
xT(t)PCCTPx(t)+gT(x(t-r1(t)))g(x(t-r1(t)))≤
(34)
2xT(t)PDh(x(s))ds≤
(35)
存在常数γ>1,当V(x(t+ξ))<γV(x(t)),ξ∈[-r,0]时,这里r=max(r1,r2)，对任意k1,k2>0时,有
k1[γx(t)TPx(t)-xT(t-r1(t))Px(t-r1(t))]+
k2[γx(t)TPx(t)-xT(s)Px(s)]ds≤
(36)
由式(29)和(30)表明对充分小的δ>0,γ=1+δ,有
(37)
(38)
记
(39)
(40)
λmin(-Φ)=μ0,λmin(-Θ)=ω0, 则μ0>0,ω0>0．可以得到
(-ω0)(‖x(t)‖2+‖x(s)‖2)ds≤
-μ0‖x(t)‖2．
(41)
则由引理3可知,分数阶时滞神经网络(27)的零解是渐近稳定的,定理得证．
3 数 值 例 子
例1 考虑含有离散时滞的分数阶神经网络系统:
(42)
其中
这里
f(x(t))=(sin x1,sin x2)T,
显然l1=1,l2=1/2．取k=1,P=I2，直接计算得到
且有
根据引理4(Schur引理)可知式(17)成立,这表明系统(42)的解是渐近稳定的．
下面的图像是在初值x1=0.1×(t+1),x2=0.1×(t+1),t∈[-1,0]时,α=0.5,
f(x(t))=(sin x1,sin x2)T,
r1(t)=1>0，
这些条件下对系统(42)解的数值模拟(见图1和图2)．算法参考了文献[22]．
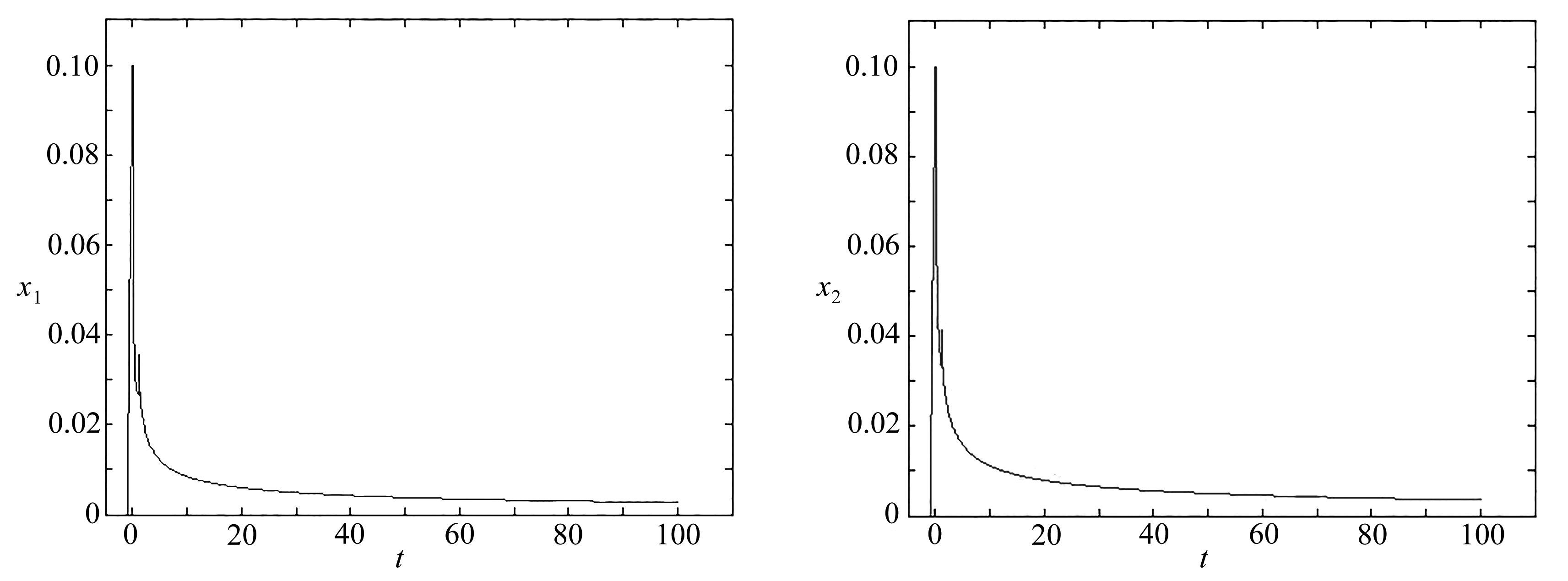
图1 方程(42)的x1状态轨迹 图2 方程(42)的x2状态轨迹
Fig. 1 The x1 state trace of eq. (42) Fig. 2 The x2 state trace of eq. (42)
下面给出不满足定理1的判定条件时,分数阶时滞神经网络的解的数值模拟．
例2 考虑含有离散时滞的分数阶神经网络系统:
(43)
其中
这里
f(x(t))=(sin x1,sin x2)T,
显然l1=1,l2=1/2．取k=1,P=I2,直接计算得到且有
不是负定矩阵．
下面的图像是在初值x1=0.1×(t+1)，x2=0.1×(t+1),t∈[-1,0],α=0.5,r1(t)=1时,对系统(43)解的数值模拟(见图3和图4)．
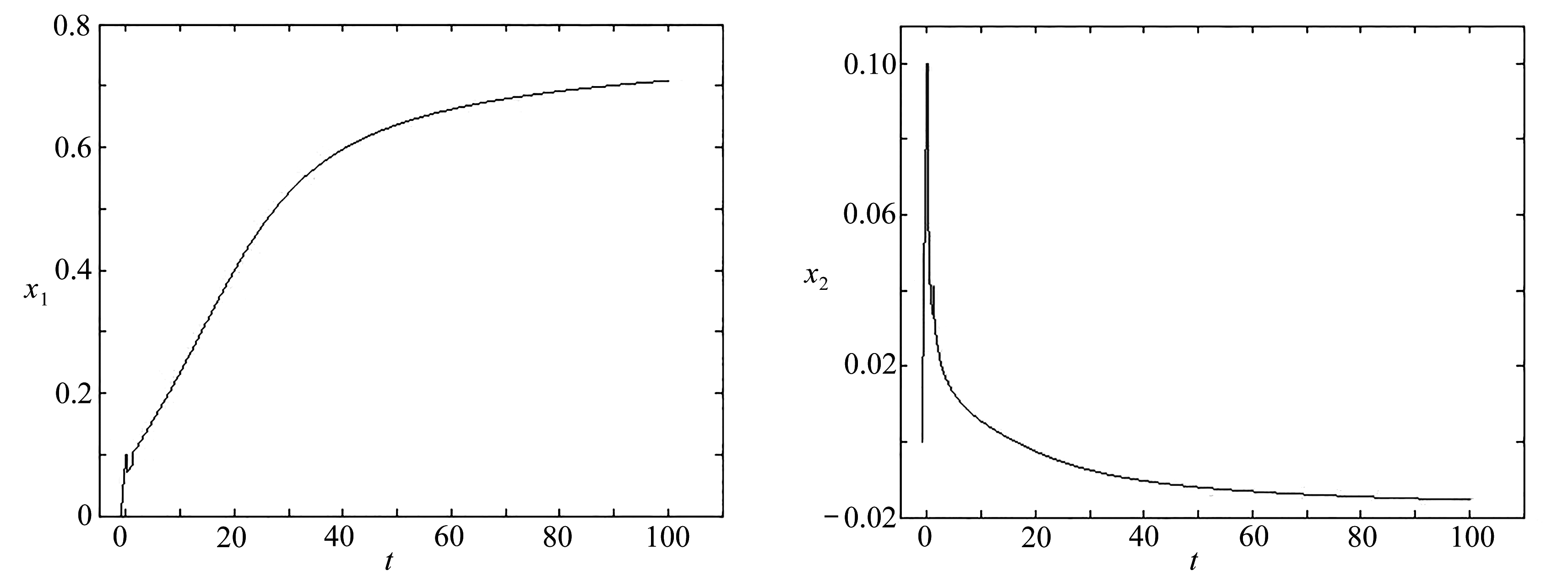
图3 方程(43)的x1状态轨迹 图4 方程(43)的x2状态轨迹
Fig. 3 The x1 state trace of eq. (43) Fig. 4 The x2 state trace of eq. (43)
由系统(43)的数值模拟结果可知系统(43)的解不是渐近稳定的．
例3 考虑含有离散时滞和分布时滞的分数阶神经网络系统：
Dh(x(s))ds, 0<α≤1,
(44)
其中
这里r1(t)>0,r2(t)=0.5sin2t≤0.5=r2且
f(x(t))=(sin x1,sin x2)T,
h(x(s))=(tanh x1(s),tanh x2(s))T．
显然l1=1,l2=1/2,l3=1．这里取k1=k2=1,k3=2,P=I2，直接计算得到
且有
显然(k2-k3)P=-I2<0,且r2l32I-k2P=-0.5I2<0．
根据引理4(Schur引理)可知,式(29)和(30)成立,这表明系统(44)的解是渐近稳定的．
下面的图像是在初值x1=1×(t+0.5)，x2=1×(t+0.5),t∈[-0.5,0],α=0.5,r1(t)=r2(t)=0.5时,对系统(44)解的数值模拟(见图5和图6)．
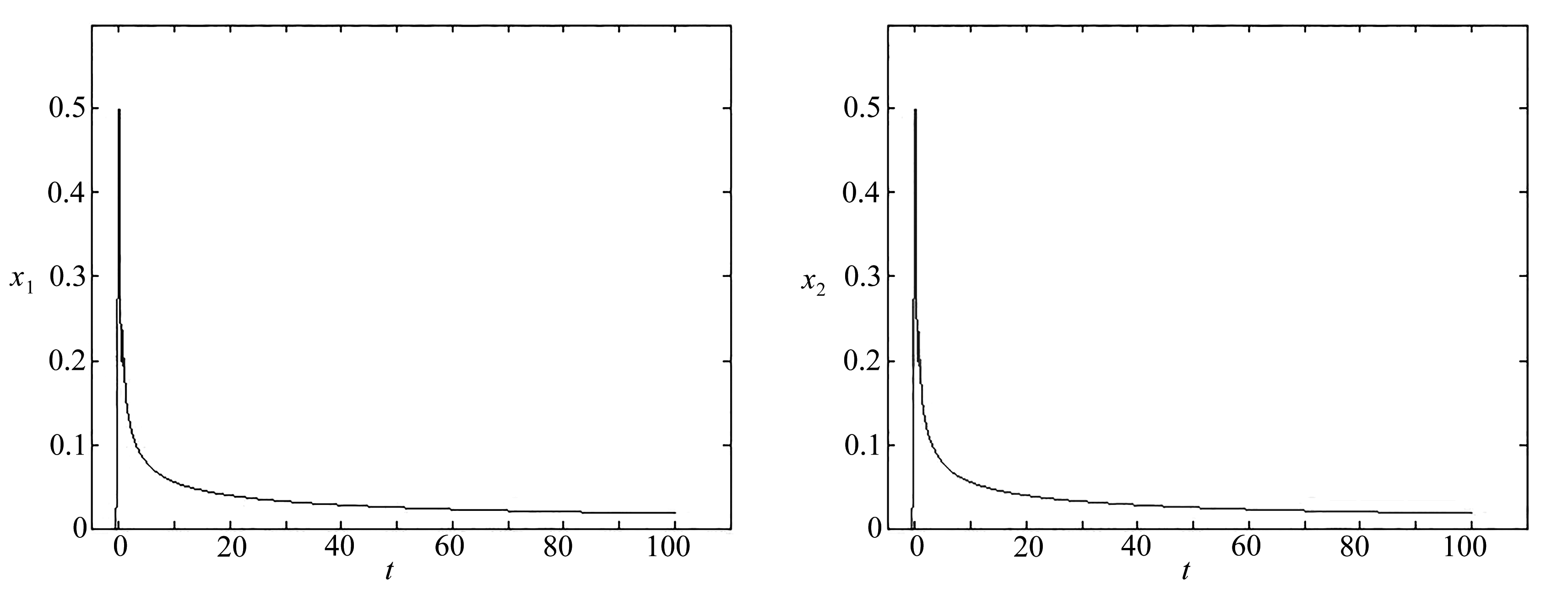
图5 方程(44)的x1状态轨迹 图6 方程(44)的x2状态轨迹
Fig. 5 The x1 state trace of eq. (44) Fig. 6 The x2 state trace of eq. (44)
下面给出不满足定理2的判定条件时,分数阶时滞神经网络解的数值模拟．
例4 考虑含有离散时滞和分布时滞的分数阶神经网络系统：
Dh(x(s))ds, 0<α≤1,
(45)
其中
这里r1(t)>0,r2(t)=0.5sin2t≤0.5=r2且
f(x(t))=(sin x1,sin x2)T,
h(x(s))=(tanh x1(s),tanh x2(s))T．
显然l1=1,l2=1/2,l3=1．这里取k1=k2=1,k3=2,P=I2．直接计算得到且有
不是负定的,此时不满足定理2的判定条件．
下面的图像是在初值x1=-t，x2=-t,t∈[-0.5,0],α=0.5,r1(t)=r2(t)=0.5时,对系统(45)解的数值模拟(见图7和图8)．
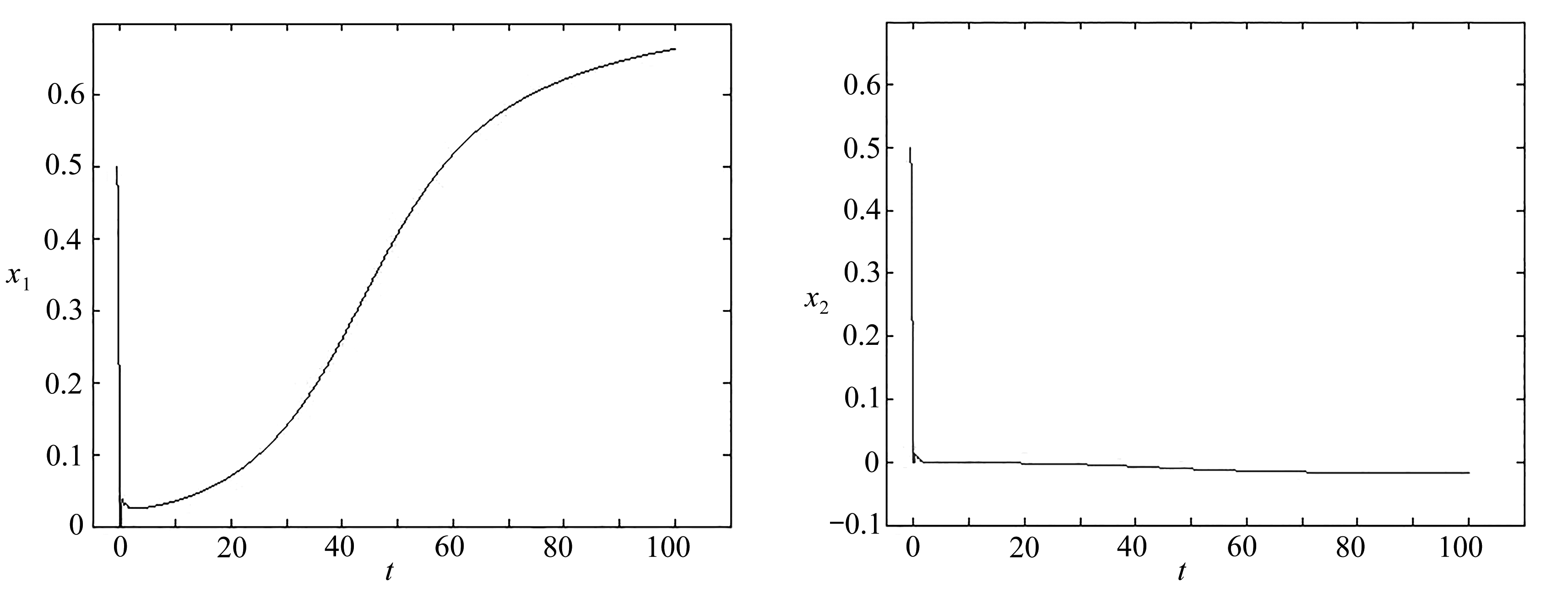
图7 方程(45)的x1状态轨迹 图8 方程(45)的x2状态轨迹
Fig. 7 The x1 state trace of eq. (45) Fig. 8 The x2 state trace of eq. (45)
由系统(45)的数值模拟可知,系统(45)的解不是渐近稳定的．
4 结 论
本文研究了含有离散时滞和分布时滞的分数阶神经网络在Caputo导数意义下的渐近稳定性问题．通过构造Lyapunov 函数，并利用分数阶Razumikhin 定理分别讨论了含有离散时滞和分布时滞的分数阶神经网络渐近稳定性的充分条件．最后通过数值例子仿真验证了所得结果的有效性．事实上，在神经网络中普遍存在时滞、脉冲等复杂现象, 研究含有时滞的分数阶神经网络具有很重要的理论意义和应用价值，也是一项具有挑战性的工作．在将来的研究工作中，本研究团队将进一步分析时滞对分数阶神经网络性态的影响．
[1] PODLUBNY I. Fractional Differential Equations[M]. San Diego: Academic Press, 1999.
[2] OLDHAM K B, SPANIER J. The Fractional Calculus[M]. New York: Academic Press, 1974.
[3] KILBAS A A, SRIVASTAVA H M, TRUJILLO J J. Theory and Applications of Fractional Differential Equations[M]. Amsterdam: Elsevier Science, 2006.
[4] MILLER K S, ROSS B. An Introduction to the Fractional Calculus and Fractional Differential Equations[M]. New York: John Wiley and Sons, 1993.
[5] ARENA P, FORTUNA L, PORTO L. Chaotic behavior in noninteger-order cellular neural networks[J]. Physical Review E, 2000, 61(1): 776-781.
[6] KASLIK E, SIVASUNDARAM S. Nonlinear dynamics and chaos in fractional-order neural networks[J]. Neural Networks, 2012, 32: 245-256.
[7] HUANG X, ZHAO Z, WANG Z, et al. Chaos and hyperchaos in fractional-order cellular neural networks[J]. Neurocomputing, 2012, 94: 13-21.
[8] 张平奎, 杨绪君. 基于激励滑模控制的分数阶神经网络的修正投影同步研究[J]. 应用数学和力学, 2018, 39(3): 343-354.(ZHANG Pingkui, YANG Xujun. Modified projective synchronization of a class of fractional-order neural networks based on active sliding mode control[J]. Applied Mathematics and Mechanics, 2018, 39(3): 343-354.(in Chinese))
[9] ZHANG X X, NIU P F, MA Y P, et al. Global Mittag-Leffler stability analysis of fractional-order impulsive neural networks with one-side Lipschitz condition[J]. Neural Networks, 2017, 94: 67-75.
[10] LIU S X, YU Y G, ZHANG S, et al. Robust stability of fractional-order memristor-based Hopfield neural networks with parameter disturbances[J]. Physica A, 2018, 509: 845-854.
[11] WU H Q, ZHANG X X, XUE S H, et al. LMI conditions to global Mittag-Leffler stability of fractional-order neural networks with impulses[J]. Neurocomputing, 2016, 193: 148-154.
[12] LIANG S, WU R C, CHEN L P. Comparison principles and stability of nonlinear fractional-order cellular neural networks with multiple time delays[J]. Neurocomputing, 2015, 168: 618-625.
[13] LIU W Z, JIANG M H, YAN M. Stability analysis of memristor-based time-delay fractional-order neural networks[J]. Neurocomputing, 2019, 323: 117-127.
[14] LI Y, JIANG W, HU B B. Stability of neutral fractional neural networks with delay[J]. Chinese Quarterly Journal of Mathematics, 2016, 31(4): 422-429.
[15] WANG H, YU Y G, WEN G G, et al. Global stability analysis of fractional-order Hopfield neural networks with time delay[J]. Neurocomputing, 2015, 154: 15-23.
[16] 王利敏, 宋乾坤, 赵振江. 基于忆阻的分数阶时滞复值神经网络的全局渐近稳定性[J]. 应用数学和力学, 2017, 38(3): 333-346.(WANG Limin, SONG Qiankun, ZHAO Zhenjiang. Global asymptotic stability of memristor-based fractional-order complex-valued neural networks with time delays[J]. Applied Mathematics and Mechanics, 2017, 38(3): 333-346.(in Chinese))
[17] DUARTE-MERMOUND M A, AGUILA-CAMACHO N, GALLEGOS J A, et al. Using general quadratic Lyapunov functions to prove Lyapunov uniform stability for fractional order systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2015, 22: 650-659.
[18] LIU S, ZHOU X F, LI X Y, et al. Asymptotical stability of Riemann-Liouville fractional singular systems with multiple time-varying delays[J]. Applied Mathematics Letters, 2017, 65: 32-39.
[19] WEN Y H, ZHOU X F, ZHANG Z X, et al. Lyapunov method for nonlinear fractional differential systems with delay[J]. Nonlinear Dynamics, 2015, 82(1): 1015-1025.
[20] BOYD S, EL-GHAOUI L, FERON E, et al. Linear Matrix Inequalities in System and Control Theory[M]. Philadelphia: SIAM, 1994 .
[21] GU K Q, KHARITONOV V L, CHEN J. Stability of Time-Delay Systems[M]. Boston, MA: Birkhäuser, 2003.
[22] BHALEKAR S, GEJJI V. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order[J]. Journal of Fractional Calculus and Applications, 2011, 1(5): 1-9.