引 言
Lotka-Volterra模型是一类被数学家和生态学家广泛关注的生态模型,尤其是考虑到扩散对生物种群的影响, 近年来, 很多学者对含扩散项的Lotka-Volterra竞争模型进行了有益的探索, 得到了十分丰富的结论.例如, Gardner[1]和Conley等[2]研究了经典的Lotka-Volterra反应扩散系统:
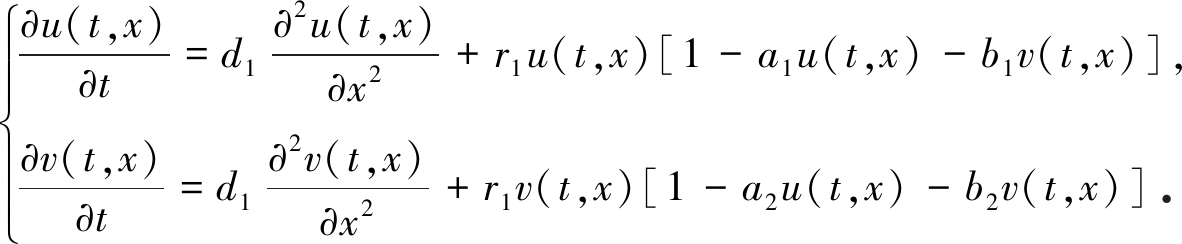
(1)
系统(1)有4个平衡点, 分别是
Gardner[1]和Conley等[2]分别利用度理论和Conley指标法得到了连接E1和E2的行波解的存在性.文献[3-4]利用相平面分析法得到了连接E0和E*的行波解的存在性.关于Lotka-Volterra竞争模型的更多结论可参看文献[5-8]等.
考虑到环境和生物现象常随时间而产生周期性的变化, 例如温度和物种出生率会随季节周期改变.Zhao和Ruan[9]研究了具有时间周期的Lotka-Volterra扩散-竞争模型:
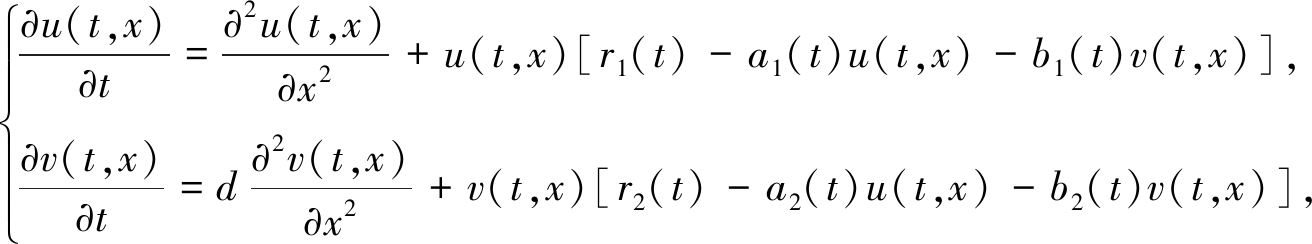
(2)
其中ri(t),ai(t),bi(t),i=1,2是以时间T为周期的连续函数.在一定的假设下, Zhao和Ruan[9]得到了连接两个半正周期平衡点的行波解的存在性、唯一性、单调性和渐近稳定性.
另一方面, 由于妊娠、孵化和成熟等方面的影响, 时间滞后往往是不可避免的.Li等[10]研究了具有时滞的Lotka-Volterra扩散-竞争模型:
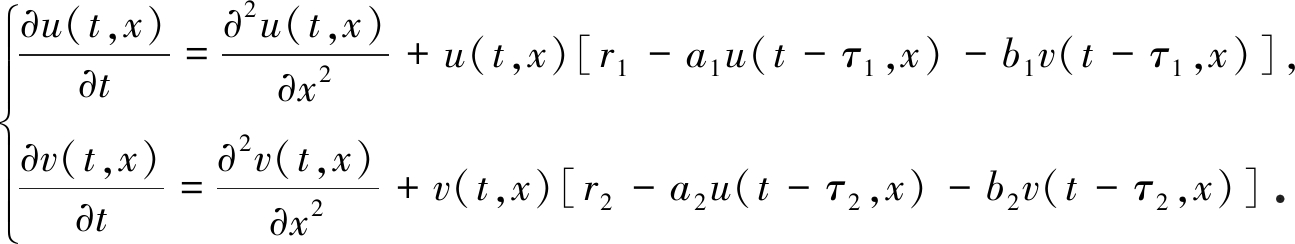
(3)
Li等[10]利用上、下解方法证明了行波解的存在性.并且,利用双边Laplace变换得到了行波解在正、负无穷远处的渐近行为, 利用比较原理和滑动法得到了行波解的单调性和唯一性.关于其他时滞Lotka-Volterra模型的研究, 可参看文献[11-15].
然而在现实生活中, 时间周期性与时间滞后通常是并存的.故综合考虑两类因素, 本文研究如下时间周期的时滞Lotka-Volterra竞争系统:
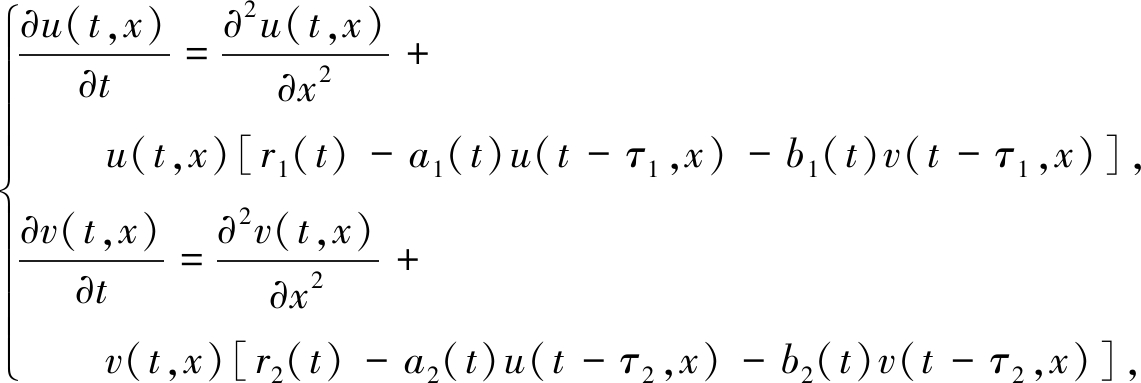
(4)
其中u(t,x)和v(t,x)表示两个竞争物种在t∈R+,x∈R的密度, τ1>0,τ2>0, 函数ri, ai和bi满足以下假设:
(H1) 对于某个0<θ<1,ri,ai,bi∈Cθ(R,R),ri(t+T)=ri(t),ai(t+T)=ai(t),bi(t+T)=bi(t),且![]()
本文研究系统(4)具有以下形式的时间周期行波解:
满足
其中c是常数, 称之为波速.(u+(t),v+(t))和(u-(t),v-(t))是相应kinetic系统
(5)
的周期解.
(H2) 系统(5)仅存在3个非负周期平衡解(0,0),(p(t),0)和(0,q(t)),且(p(t),0)是渐近稳定的.
本文研究满足
的时间周期行波解.令
(6)
记
hτ![]() h(t-τ,z+cτ), Uτ
h(t-τ,z+cτ), Uτ![]() (U1,τ,U2,τ)
(U1,τ,U2,τ)![]() (U1(t-τ,z+cτ),U2(t-τ,z+cτ)).
(U1(t-τ,z+cτ),U2(t-τ,z+cτ)).
将式(6)代入式(4)得到

(7)
其中
f1(t,U,Uτ1)=U1[a1(t)p(t-τ1)(1-U1,τ1)-b1(t)q(t-τ1)(1-U2,τ1)],
f2(t,U,Uτ2)=(1-U2)[a2(t)p(t-τ2)U1,τ2-b2(t)q(t-τ2)U2,τ2].
并有
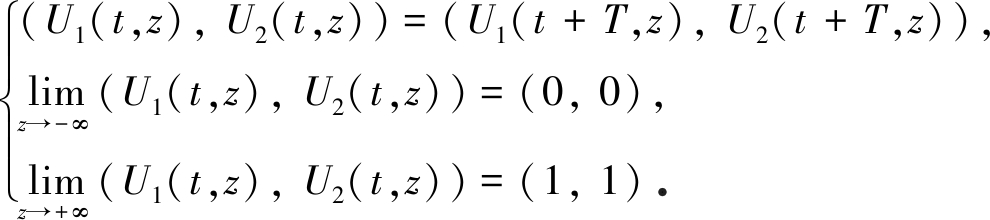
相较于Lotka-Volterra竞争系统行波解的已有结论[2,9-10], 系统(4)具有时间周期与时间滞后的同时作用, 这为研究带来了新的困难.本文致力于系统(4)的周期行波解的研究, 首先, 在一定条件下, 通过构造适当的上下解, 结合单调迭代方法得到了当c<c*时, 周期行波解的存在性; 进一步地, 通过比较原理证明了行波解关于z的单调性以及渐近行为; 最后, 证明了当c=c*时, 临界波的存在性.
1 准 备 知 识
定义1 如果u∈Rn并且v∈Rn, 那么u<v(或者v≤u)可以被理解为对于每一个i, ui<vi(或者ui≤vi).其他的关系,例如“max”“min”“sup”和“inf”都可以这样理解.
定义2 I×Γ⊂R×R, 向量函数w=(w1,w2,…,wn)∈C1,2(I×Γ,Rn)被称为
(8)
的正则上解, 当且仅当
其中di,ci∈Cθ(Γ,R), fi∈Cθ,1(I×Rn,R),0<θ<1.类似地, 当不等号反号时,可定义正则下解.
定义3 若存在式(8)的正则上解w1,w2,…,wk使得v=min{w1,w2,…,wk}, 则称v=min{w1,w2,…,wk}是式(8)的非正则上解.类似地, 若存在式(8)的正则下解v1,v2,…,vk使得v=max{v1,v2,…,vk}, 则称v是式(8)的非正则下解.
2 周期行波解的存在性
2.1 上、下解的构造
假设(H1)和(H2)成立.令
k0![]()
![]()
φ(t)![]()
![]()
显然
进一步假设
(H3) a1(t)p(t-τ1)-b1(t)q(t-τ1)≥a2(t)p(t-τ2)-b2(t)q(t-τ2)≥0,
(H4) φ(t)≥1,∀t∈[0,T], 且maxt∈[0,T]φ(t)≤e2k0τ2.
固定c<c*![]()
![]() 定义以下函数:
定义以下函数:
w(t,z)![]() mφ(t)eλcz, w1
mφ(t)eλcz, w1![]() (w(t,z),w(t,z)), w2
(w(t,z),w(t,z)), w2![]() (1,1),
(1,1),
![]()
![]() min{w1,w2}=min{(w,w),(1,1)},
min{w1,w2}=min{(w,w),(1,1)},
![]()
![]() (max{δeλczφ(t)(1-eεz),0},0),
(max{δeλczφ(t)(1-eεz),0},0),
其中m≥0为任意常数,
λc![]()
![]()
ϑ![]() -[(λc+ε)2+c(λc+ε)+k0],
-[(λc+ε)2+c(λc+ε)+k0],
以及δ∈(0,Λϑ)均为正常数, 这里
Λϑ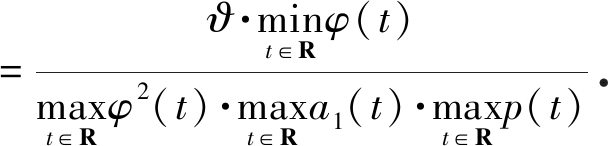
引理1 假设(H1)~(H4)成立, 则对任意
![]() 满足
满足
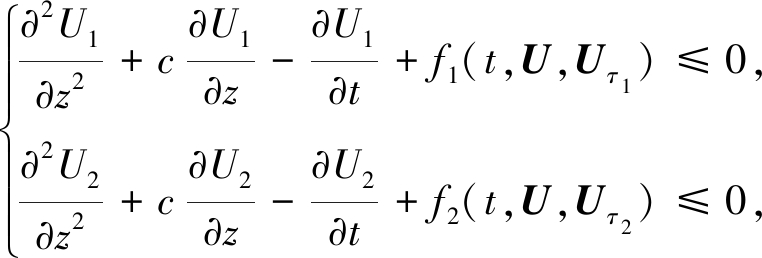
(9)
即![]() 是式(7)的非正则上解.
是式(7)的非正则上解.
证明 令
A+![]()
![]()
当(t,z)∈A+时,![]() 显然满足不等式组(9).当(t,z)∈A-时,
显然满足不等式组(9).当(t,z)∈A-时,![]() 下面验证w1满足式(9)的第一个不等式:
下面验证w1满足式(9)的第一个不等式:
wzz+cwz-wt+w[a1(t)p(t-τ1)-b1(t)q(t-τ1)]=
cλcmφ(t)eλcz+mφ(t)eλcz[a1(t)p(t-τ1)-b1(t)q(t-τ1)]=
下证w1满足式(9)的第二个不等式.
根据假设(H4),有maxt∈R φ(t)≤e2k0τ2φ(t).故对于任意t∈R,φ(t-τ2)e-2k0τ2≤φ(t).另一方面,注意到![]() 且
且![]() 关于c是单调递增的, 那么ecλcτ2也关于c单调递增, 所以ecλcτ2
关于c是单调递增的, 那么ecλcτ2也关于c单调递增, 所以ecλcτ2
φ(t-τ2)ecλcτ2≤φ(t-τ2)e-2k0τ2≤φ(t).
又因为此时0<mφ(t)eλcz<1, 所以(1-mφ(t)eλcz)φ(t-τ2)ecλcτ2≤φ(t).不等式两边同乘meλcz,得(1-mφ(t)eλcz)mφ(t-τ2)eλc(z+cτ2)≤mφ(t)eλcz,也就是
(1-w(t,z))wτ2≤w(t,z).
所以根据假设(H3)、(H4)及φ′(t)的定义, 可得
wzz+cwz-wt+(1-w)[a2(t)p(t-τ2)wτ2-b2(t)q(t-τ2)wτ2]=
wzz+cwz-wt+(1-w)wτ2[a2(t)p(t-τ2)-b2(t)q(t-τ2)]≤
wzz+cwz-wt+w[a2(t)p(t-τ2)-b2(t)q(t-τ2)]=
[a2(t)p(t-τ2)-b2(t)q(t-τ2)]w≤
综上,![]() 是式(7)的一对非正则上解.证明完毕.
是式(7)的一对非正则上解.证明完毕.
引理2 假设(H1)~(H4)成立, 则对任意![]() 满足
满足

(10)
即![]() 是式(7)的非正则下解.
是式(7)的非正则下解.
证明 当z>0时,![]() 显然满足式(10).当z<0时,
显然满足式(10).当z<0时,![]() 下面证明
下面证明![]() 满足式(10)的第一个不等式:
满足式(10)的第一个不等式:
δeλcz{[a1(t)p(t-τ1)-b1(t)q(t-τ1)]φ(t)(1-eεz)-
a1(t)p(t-τ1)δeλc(z+cτ1)φ(t-τ1)(1-eε(z+cτ1))φ(t)(1-eεz)-
δeλcz{[a1(t)p(t-τ1)-b1(t)q(t-τ1)]φ(t)-k0φ(t)-φ′(t)-
eεz{[a1(t)p(t-τ1)-b1(t)q(t-τ1)]φ(t)+
(λc+ε)2+(cλc+ε)φ-φ′(t)}-
δeλc(z+cτ1)φ(t)(1-eεz)a1(t)p(t-τ1)φ(t-τ1)[1-eε(z+cτ1)]}=
δeλcz{ϑφ(t)eεz-
δeλc(z+cτ1)φ(t)φ(t-τ1)a1(t)p(t-τ1)(1-eεz(1-eε(z+cτ1)))}≥
![]() ϑ
ϑ![]()
δeλc zϑφ(t)(eεz-eλc(z+cτ1)) ≥0.
再证明![]() 满足式(10)的第二个不等式:
满足式(10)的第二个不等式:
综上, 函数![]() 是式(7)的一对非正则下解.证明完毕.
是式(7)的一对非正则下解.证明完毕.
2.2 周期行波解
定理1 假设(H1)~(H4)成立.则对任意的![]() 系统式(7)存在周期行波解
系统式(7)存在周期行波解![]() 且对所有
且对所有![]()
证明 令![]() 满足
满足
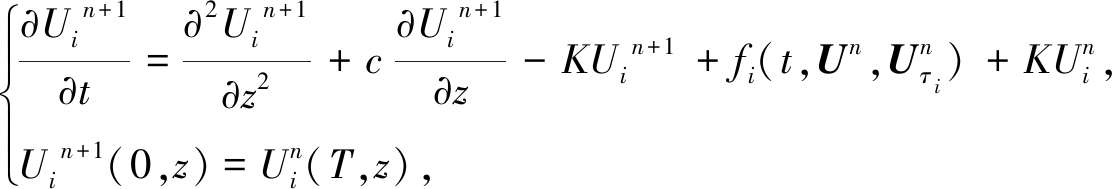
(11)
其中K是一个正常数,且
Un是式(11)的一个适度解, 可由下式给出:
其中G(t)是由线性算子A: D(A)→Cb(R)生成的解析半群(参看文献[16]),A定义为
根据文献[16]中的定理5.1.3、5.1.4, 对任意 ∈(0,T), 存在α∈(0,1)使得
∈(0,T), 存在α∈(0,1)使得
![]() [
[ ,T]×R),
,T]×R),
并且U1在[0,T]×R上满足式(11)的第一个方程, 因此当n≥2, 对任意![]() 满足式(11).
满足式(11).
下面证明对所有(t,z)∈[0,T]×R, 有![]() 令
令
L![]()
![]()
vr![]()
![]()
![]() +Nt)eμt,
+Nt)eμt,
其中![]() =(1+c)2, μ>1, N>2是固定常数, 使得对任意t∈R, 2(1+c|z|)-μ(z2+
=(1+c)2, μ>1, N>2是固定常数, 使得对任意t∈R, 2(1+c|z|)-μ(z2+![]() )-N<0.显然L>0.当|z|≤r时, 注意到U0(0,z)=U1(T,z), vr(0,z)>0.另外, 对任意t∈[0,T],vr>0.事实上, 对所有(t,z)∈[0,T]×[-r,r], 有vr≥0.否则, 存在点(t*,z*)∈[0,T]×(-r,r)和至少一个vr的分量
)-N<0.显然L>0.当|z|≤r时, 注意到U0(0,z)=U1(T,z), vr(0,z)>0.另外, 对任意t∈[0,T],vr>0.事实上, 对所有(t,z)∈[0,T]×[-r,r], 有vr≥0.否则, 存在点(t*,z*)∈[0,T]×(-r,r)和至少一个vr的分量![]() 使得
使得
因为![]() 是式(7)的非正则上解, 不失一般性, 假设
是式(7)的非正则上解, 不失一般性, 假设![]() 或2.令
或2.令
![]()
![]() +Nt)eμt.
+Nt)eμt.
通过直接计算, 可得
另外, 显然![]() 且对所有(t,z)∈[0,t*]×[-r,r], 有
且对所有(t,z)∈[0,t*]×[-r,r], 有![]() 所以
所以
因此
这是矛盾的, 故对所有(t,z)∈[0,T]×[-r,r], 有vr>0.又因为当r→+∞时, vr在![]() 上一致地收敛到
上一致地收敛到![]() 所以
所以![]() 同时, 根据比较原理,U1≥0.注意到对所有
同时, 根据比较原理,U1≥0.注意到对所有![]() 所以对任意t∈[0,T], 有
所以对任意t∈[0,T], 有![]() 根据m≥1的任意性, 可选取m充分大, 使得对所有(t,z)∈R×R, 有
根据m≥1的任意性, 可选取m充分大, 使得对所有(t,z)∈R×R, 有![]() 所以
所以
通过与前面类似的讨论得: 对所有![]() 类似地, 对所有(t,x)∈[0,T]×R, 当n≥1有
类似地, 对所有(t,x)∈[0,T]×R, 当n≥1有
且![]() 因此, 序列{Un}是一致有界的.进一步地, 根据文献[16]中的定理5.1.2~5.1.4 可得, 对于n≥2,
因此, 序列{Un}是一致有界的.进一步地, 根据文献[16]中的定理5.1.2~5.1.4 可得, 对于n≥2,
其中C,M和α∈(0,1)是确定的正常数, 且α依赖于C和![]() 这里γ∈(0,1).根据Arzela-Ascoli引理, 存在{Un}的子列(依然记作{Un})在
这里γ∈(0,1).根据Arzela-Ascoli引理, 存在{Un}的子列(依然记作{Un})在![]() 中收敛到一函数, 记作Uc.显然对任意(t,x)∈[0,T]×R,Uc满足式(7).因为Un+1(0,z)=Un(T,z), 所以Uc(0,z)=Uc(T,z).另外,
中收敛到一函数, 记作Uc.显然对任意(t,x)∈[0,T]×R,Uc满足式(7).因为Un+1(0,z)=Un(T,z), 所以Uc(0,z)=Uc(T,z).另外,
对等式两边同时取极限, 得
因此, Uc满足周期边界条件, 从而![]() 是式(7)的一个光滑周期解.本定理证毕.
是式(7)的一个光滑周期解.本定理证毕.
定理2 假设(H1)~(H4)成立.则
证明  显然, 对任意s∈R, Un+1(t,z+s)满足式(7), 并且其初值为Un+1(0,z+s)=Un(T,z+s).又因为对任意s>0, 有
显然, 对任意s∈R, Un+1(t,z+s)满足式(7), 并且其初值为Un+1(0,z+s)=Un(T,z+s).又因为对任意s>0, 有![]() 根据比较原理, 对任意s≥0,有
根据比较原理, 对任意s≥0,有
Un+1(t,z+s)≥Un+1(t,z).
利用Helly定理, 存在{Un}的一个子列(仍记作{Un})使得
因此,Uc(t,·)是非减的.又因为Uc(t,z)和Uc(t,z+s)都满足式(7), 且
所以由比较原理得,![]() 或者
或者![]() 但因为
但因为![]() 所以固定t时
所以固定t时![]() 不恒为常数.这就证明了
不恒为常数.这就证明了![]()
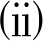 根据由
根据由 所得的单调性, 对于任意
所得的单调性, 对于任意![]() 存在.令
存在.令
另外, 由![]() 关于t的正则性及其在[0,T]上的紧性可知, 当z→±∞时,
关于t的正则性及其在[0,T]上的紧性可知, 当z→±∞时,![]() 关于t∈R一致收敛到
关于t∈R一致收敛到![]() 根据
根据![]() 和
和![]() 的定义易知
的定义易知
因此由夹逼原理得
下证![]() 一方面, 根据Barbalat引理,
一方面, 根据Barbalat引理,
因此,![]() 满足
满足
(12)
根据假设(H2),式(12)有且仅有3个非负周期解(1,1),(0,0)和(0,1).另一方面, 因为任意z∈(-∞,0), 所以![]() 又因为
又因为![]() 关于z是严格单调递增的, 故
关于z是严格单调递增的, 故![]() 因此
因此![]() 证毕.
证毕.
定理3 假设(H1)~(H4)成立.则当c=c*时, 系统式(7)存在周期行波解![]() 并满足
并满足![]() 且limz→+∞Uc*=(1,1).
且limz→+∞Uc*=(1,1).
证明 令Uc 是系统式(7)在c<c*时的周期行波解.因为![]() 一致有界, 所以根据抛物估计可得, 当c∈[c*-1,c*)时,一致地有
一致有界, 所以根据抛物估计可得, 当c∈[c*-1,c*)时,一致地有
令{cn}是[c*-1,c*)中数列, 并当n→∞时有cn→c*,根据Arzela-Ascoli引理, 必存在{Ucn}的子列(为简便还记作{Ucn})在![]() 的意义下收敛, 极限记作
的意义下收敛, 极限记作![]() 在系统式(7)中取极限, 即得当c=c*时Uc*满足系统(7).另外根据Helly定理, 有
在系统式(7)中取极限, 即得当c=c*时Uc*满足系统(7).另外根据Helly定理, 有
(13)
根据Ucn的周期性有Uc*(t+T,·)=Uc*(t,·),另外显然![]() 因为对任意s>0, Uc*(t,z+s)也是式(7)的解, 根据最大值原理,
因为对任意s>0, Uc*(t,z+s)也是式(7)的解, 根据最大值原理,
又因为对任意的n, 有limz→-∞Uc=(0,0), limz→+∞Uc=(1,1), 再根据式(13)和周期性可知, 存在N>0使得对任意的(t,z)∈R×(-∞,-N)有Uc*<(1/3,1/3), 对任意的(t,z)∈R×(N,∞)有Uc*>(2/3,2/3), 因此必然有![]() 由此易得
由此易得
证毕.
3 总 结
本文致力于研究一类时间周期的时滞Lotka-Volterra竞争模型的行波解.当c<c*时, 通过构造合适的上、下解, 结合单调迭代方法得到了行波解的存在性.然后, 利用比较原理证明了行波解的单调性.进而, 证明了行波解的渐近行为.最后, 证明了当c=c*时, 周期行波解的存在性.
相较于Lotka-Volterra竞争系统行波解的已有结论, 如文献[2,9-10]等, 本文考虑了时间周期和时间滞后的同时作用, 这为研究带来了新的困难, 比如缺乏周期平衡点存在性的结论, 以及上下解的构造要更加复杂.需要说明的是, 本文中假设(H2)和(H4)的给出是技术性的, 或许是可以弱化的.笔者的下一步工作是研究系统(4)正平衡点不存在的条件, 以及系统(4)周期行波解的唯一性和渐近稳定性.
[1] GARDNER R. Existence of traveling wave solutions of competing models. A degree theoretic approach[J]. Journal of Differential Equations, 1982, 44(3): 343-364.
[2] CONLEY C, GARDNER R. An application of the generalized Morse index to traveling wave solutions of a competitive reaction diffusion model[J]. Indiana University Mathematics Journal, 1984, 33: 319-345.
[3] TANG M M, FIFE P C. Propagation fronts in competing species equations with diffusion[J]. Archive for Rational Mechanics and Analysis, 1978, 73: 69-77.
[4] VAN VUUREN, JAN H. The existence of traveling plane waves in a general class of competition-diffusion systems[J]. IMA Journal of Applied Mathematics, 1995, 55: 135-148.
[5] KANEL J I, ZHOU L. Existence of wave front solutions and estimates of wave speed for a competition-diffusion system[J]. Nonlinear Analysis: Theory, Methods & Applications, 1996, 27(5): 579-587.
[6] SHAIR A, LAZER A C. An elementary approach to traveling front solutions to a system of N competition-diffusion equations[J]. Nonlinear Analysis: Theory, Methods & Applications,1991, 16(10): 893-901.
[7] HUANG W Z, WU Y S. Minimum wave speed for a diffusive competition model with time[J]. Journal of Applied Analysis and Computation, 2011, 1(2): 205-218.
[8] HUANG W Z, HAN M A. Non-linear determinacy of minimum wave speed for a Lotka-Volterra competition model[J]. Journal of Differential Equations, 2011, 251(6): 1549-1561.
[9] ZHAO G, RUAN S. Existence, uniqueness and asymptotic stability of time periodic traveling waves for a periodic Lotka-Volterra competition system with diffusion[J]. Journal de Mathématiques Pures et Appliquées, 2011, 95: 627-671.
[10] LI K, LI X. Traveling wave solutions in a delayed diffusive competition system[J]. Nonlinear Analysis: Theory, Methods & Applications, 2012, 75: 3705-3722.
[11] HUANG J H, ZOU X F. Travelling wave solutions in delayed reaction diffusion systems with partial monotonicity[J]. Acta Mathematicae Applicatae Sinica, 2006, 22(2):243-256.
[12] LI W T, LIN G, RUAN S. Existence of travelling wave solutions in delayed reaction-diffusion systems with applications to diffusion-competition systems[J]. Nonlinearity, 2006, 19: 1253-1273.
[13] GOURLEY S, RUAN S. Convergence and travelling fronts in functional differential equations with nonlocal terms: a competition model[J]. SIAM Journal on Mathematical Analysis, 2003, 35: 806-822.
[14] FANG J, WU J. Monotone traveling waves for delayed Lotka-Volterra competition systems[J]. Discrete and Continuous Dynamical Systems, 2012, 32: 3043-3058.
[15] LIN G, LI W T, MA M J. Traveling wave solutions in delayed reaction diffusion systems with applications to multi-species models[J]. Discrete and Continuous Dynamical Systems: Series B, 2010, 13(2): 393-414.
[16] LUNARDI R. Analytic Semigroups and Optimal Regularity in Parabolic Problems[M]. Birkhäuser, 1995.