引 言
在过去的几十年里,非线性系统的状态估计问题得到了广泛的关注[1-3].所谓状态估计是指根据可获取的测量数据估计系统内部状态.通常,对系统的输入和输出进行测量而得到的数据只能反映系统的外部特性,而系统的动态规律需要用内部状态变量来描述.因此,对系统状态估计问题的研究是十分必要的.在实际研究中,状态估计器被应用于许多方面,例如,电力系统[4]、神经网络随机抽样[5]、混沌信号的通信[6]等.传统上的系统状态估计根据时间触发机制以周期性方式执行.在实际应用中,时间触发机制可能导致不必要的信号传输而造成有限资源过度消耗.为了进一步节省资源,可以采用事件触发机制.其思想是仅在满足某些触发条件时,信号才被传输,这种方式可以减轻网络通信负担.本文所设计的状态估计器采用了事件触发机制进行信号传输,这种方式具有理论上的重要性和应用上的实际意义.
众所周知, 稳定性对于控制系统是极其重要的.关于稳定性有许多定义,如δ阶矩稳定[7-8]、鲁棒稳定[9-10]等,这些形式描述了系统的稳态性能, 却无法表现其暂态性能.但是, 暂态性能对于某些实际系统更为重要, 如存储式系统[11]、航天器的姿态跟踪系统[12]等.因此, 人们在研究系统的暂态稳定性时, 希望系统状态在有限时间内满足给定要求. 基于有界输入和有界输出的概念,Amato等提出了一种新的稳定概念,称为有限时间有界[13].如果状态从初始界限开始,并且不超过所有可允许的初始有界扰动的另一给定界限值,则称该系统是有限时间有界.最近,其已被应用于各种系统,如开关系统[14]、右端不连续系统[15]、神经网络[16]等.本文将针对基于事件触发的非线性系统在有限时间内的状态估计问题进行研究.
本文结构如下: 第1节是问题描述,包括主要系统和相关的定义及假设的介绍; 第2节是主要定理及证明,设计了相应控制并给出了相应证明; 第3节是仿真,通过数值仿真说明得到结果的有效性; 第4节是结论,总结了本文的研究并对此研究的工程应用进行了展望.
1 问 题 描 述
考虑一个带有时滞的非线性系统:
(1)
其中x(k)∈Rn是系统的状态,ζ(x(k))是系统的非线性函数,τ∈R是系统的时滞,ω(k)是系统的干扰输入并满足E{ω2(k)≤d},z(k)是系统的输出,A∈Rn×n, Ad∈Rn×n, B∈Rn×n,R∈Rn×m,M∈Rn×n是系统中5个已知的常数矩阵.
系统(1)的测量输出描述如下:
y(k)=Cx(k)+Lv(k),
(2)
其中y(k)∈Rm表示系统的测量输出,v(k)∈Rp是有界扰动并满足![]() Rn×n和L∈Rn×m是已知的常数矩阵.
Rn×n和L∈Rn×m是已知的常数矩阵.
本文的目的是通过式(2)中的测量输出y(k)来估计系统(1)中的系统状态.
现在介绍本文中所用的事件触发机制.首先,定义kp作为当前采样时刻对应的最新触发时间k∈[tp,tp+1).随后定义一个特定的事件作为触发函数Ξk,具体表示如下:
Ξk ‖y(k)-y(kp)‖2-θ.
‖y(k)-y(kp)‖2-θ.
(3)
当且仅当式(3)满足Ξk<0,测量输出(2)被释放到状态估计器中.
注1 应该指出的是,参数θ对事件触发有很大的影响,即θ不同的值对应于不同的事件触发率.选择的θ值越小,事件触发周期越短(反之则越长).因此,应当根据特定的控制要求和控制能力选择合适的θ.
为了估计系统(1)中的系统状态,基于事件触发机制的状态估计器可以构造如下:
(4)
其中![]() 和
和![]() 分别是x(k)和z(k)的估计值,K是要设计的估计增益.
分别是x(k)和z(k)的估计值,K是要设计的估计增益.
这里将χ(k) y(kp)-y(k)作为最新触发时间和当前采样时间测量输出之间的差值.因此,估计器(4)可以重写为
y(kp)-y(k)作为最新触发时间和当前采样时间测量输出之间的差值.因此,估计器(4)可以重写为
(5)
接下来,定义![]() 和
和![]() 因此误差系统可以表示如下:
因此误差系统可以表示如下:

(6)
其中![]()
为了获得误差系统(6)有限时间有界的充分条件,需要给出以下假设及定义.
假设1 系统(1)中的非线性函数满足如下不等式:
|f(a)-f(b)|≤m(a-b),
(7)
其中m是正常数.
定义1 如果存在误差上界δ0>0满足不等式:
(8)
即误差系统(6)是有限时间有界的.
定义2 如果非线性系统(1)和测量输出式(2)是有限时间有界的并且存在一个正标量γ满足
(9)
其中初始状态x(k)=0,∀k∈[-τ,0] ,则误差系统(6)是H∞有限时间有界的.
2 主要定理及证明
本节将给出一个充分条件,来保证误差系统(6)有限时间有界和H∞有限时间有界.
定理1 对于带有时滞的非线性系统(1)和估计误差系统(6),假设给定估计器增益K,标量μ∈(0,1),触发率θ和系统误差上界δ0.存在正定矩阵P,Γ和正标量ν1,ν2,ν3满足如下矩阵不等式:
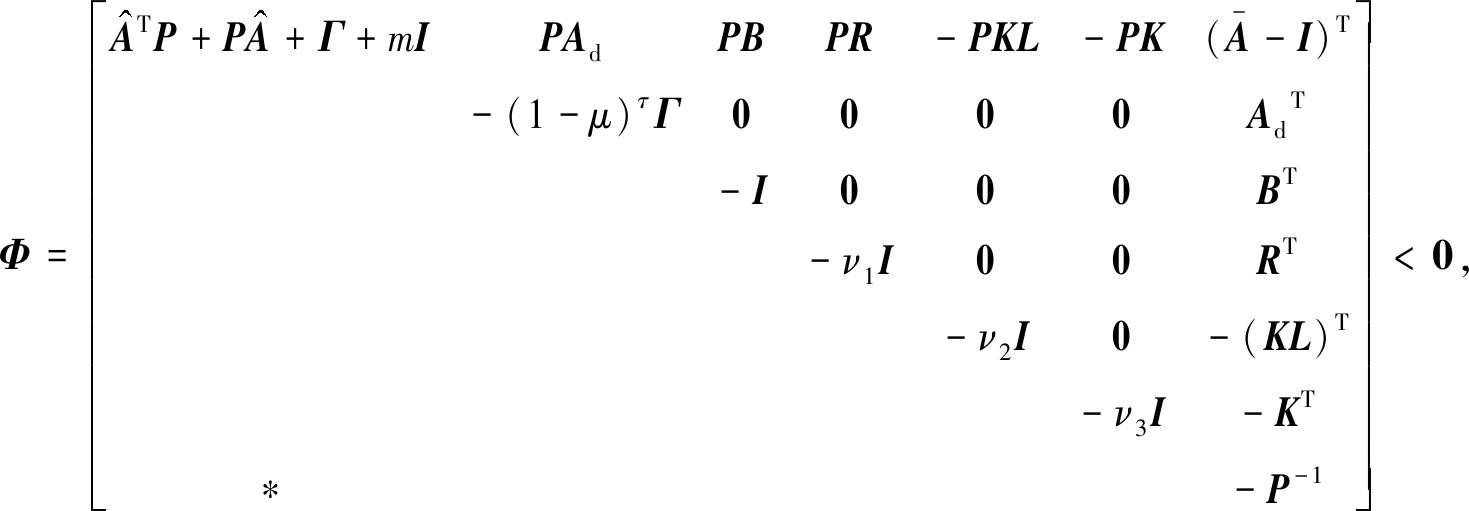
(10)
δ / μ<δ0,
(11)
其中
(12)
那么,误差系统(6)在均方意义下是有限时间有界的.
证明 在本文中,考虑如下Lyapunov函数:
(13)
对V(k)两边取数学期望E{ΔV(k)}=E{V(k+1)-V(k)}.
现在计算E{ΔV(k)+μV(k)}如下:
E{ΔV(k)+μV(k)}=
E{V(k+1)-(1-μ)V(k)}=
2eT(k)P(e(k+1)-(1-μ/2)e(k))+
E{(e(k+1)-e(k))TP(e(k+1)-e(k))+
2eT(k)P(e(k+1)-(1-μ/2)e(k))+
eT(k)Γe(k)-(1-μ)τeT(k-τ)Γe(k-τ)}.
(14)
根据假设1,可以得到
ζT(e(k))ζ(e(k))-meT(k)e(k)<0.
(15)
接下来,考虑系统(1)中干扰输入ω(k),由测量输出式(2)中有界扰动v(k)和事件触发条件(3)的约束,可以得
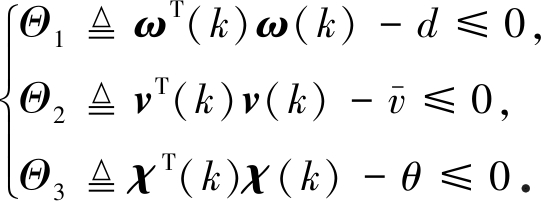
(16)
由式(14)~(16),可以得出
E{ΔV(k)+μV(k)}≤
E{(e(k+1)-e(k))TP(e(k+1)-e(k))+
2eT(k)P(e(k+1)-(1-μ/2)e(k))+eT(k)Γe(k)-
(1-μ)τeT(k-τ)Γe(k-τ)-(ζT(e(k))ζ(e(k))-meT(k)e(k))-
ν1Θ1-ν2Θ2-ν3Θ3}=
(17)
其中
φ(k)=[eT(k) eT(k-τ) ζT(e(k)) ω(k) v(k) χ(k)]T,
(18)
(19)
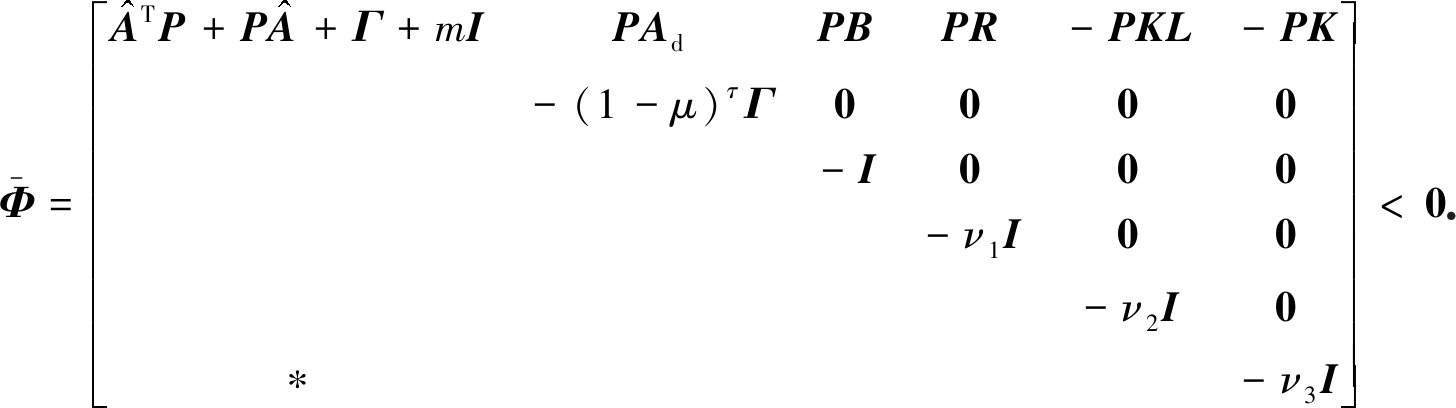
(20)
通过应用Schur引理,得到
(21)
因此
E{ΔV(k)+μV(k)}<δ.
(22)
由式(22),得到
(23)
随后,由定义1、式(11)和(13)不难看出
(24)
因此,误差系统(6)在均方意义下是有限时间有界的.
注2 显然,触发阈值θ与估计性能之间存在明显的关系.具体而言,从θ和δ的定义,可以很容易地观察到触发阈值θ与误差上限δ0的值成正比,应选择适当的θ值以保证约束(10)和(11)的可行性.换句话说,触发阈值θ对给定误差上限δ0的“要求”具有重大影响.
定理2 对于带有时滞的非线性系统(1)和估计误差系统(6),假设给定估计器增益K,标量μ∈(0,1),触发率θ和系统误差上界δ0.存在正定矩阵P,Γ和正标量ν1,ν2,ν3满足如下矩阵不等式:
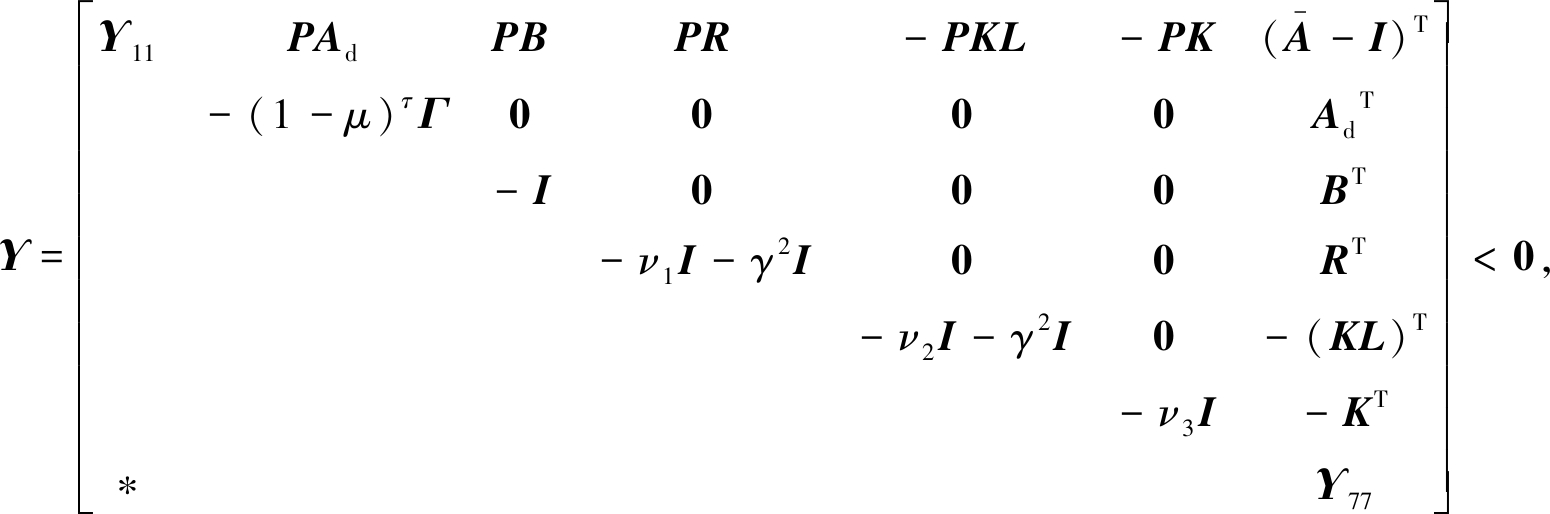
(25)
δ/μ<δ0,
(26)
其中
(27)
则误差系统(6)是H∞有限时间有界的.
证明 根据定义2,得
J(ω(k),v(k))=
{V(∞)-V(0)}-{μV(k)}≤
(28)
其中
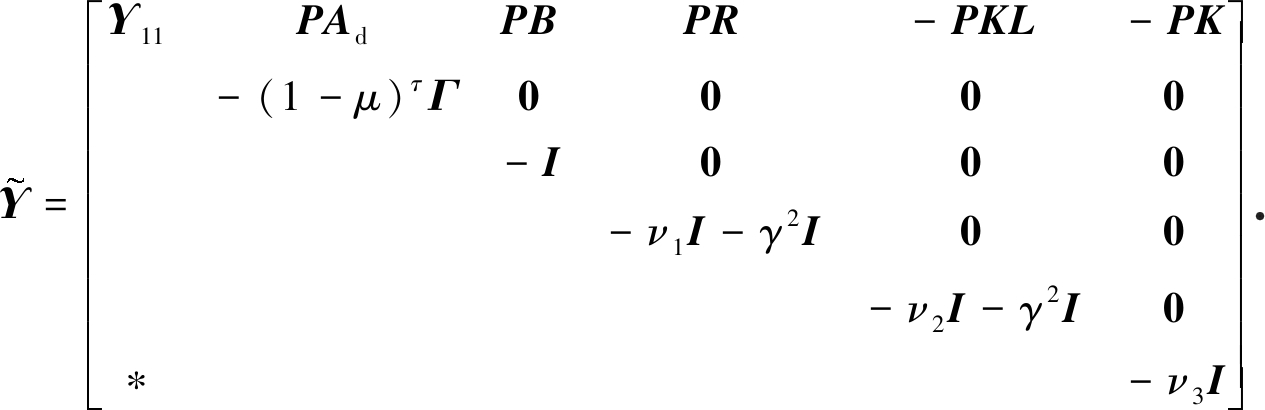
(29)
通过应用Schur引理,得
(30)
因此,可知J(ω(k),v(k))<0,误差系统(6)是H∞有限时间有界的.
定理3 对于带有时滞的非线性系统(1)和估计误差系统(6),假设给定标量μ∈(0,1),触发率θ,系统误差上界δ0.存在正定矩阵P,Γ,X,正标量ν1,ν2,ν3满足如下矩阵不等式:
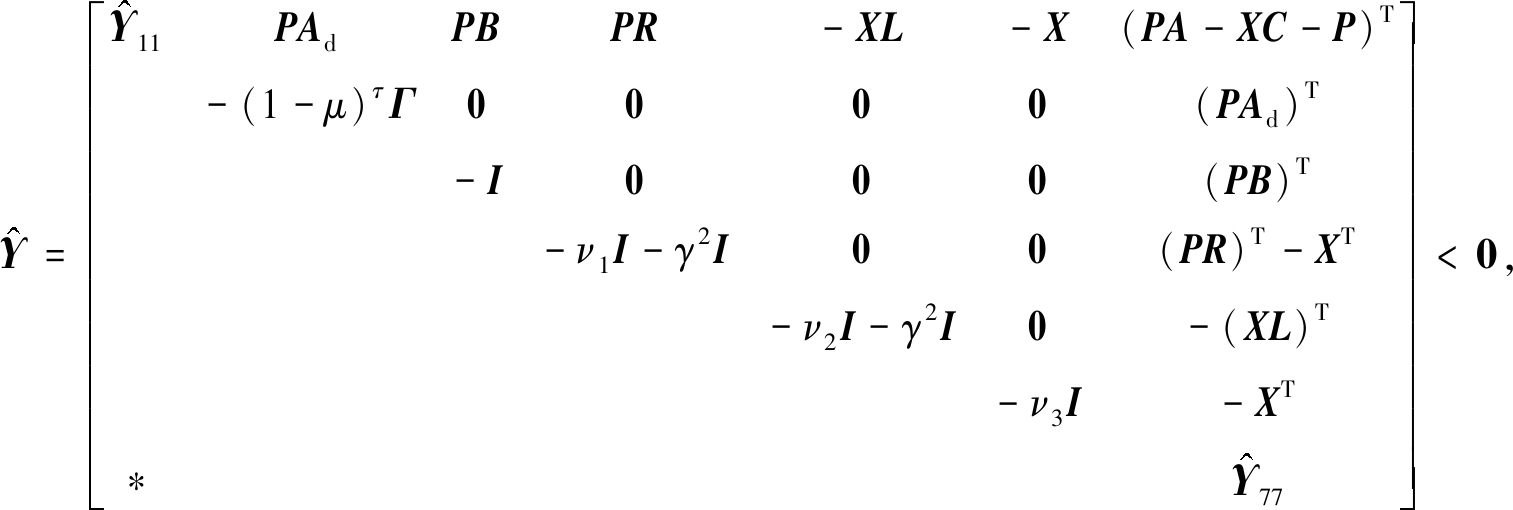
(31)
δ/μ<δ0,
(32)
其中
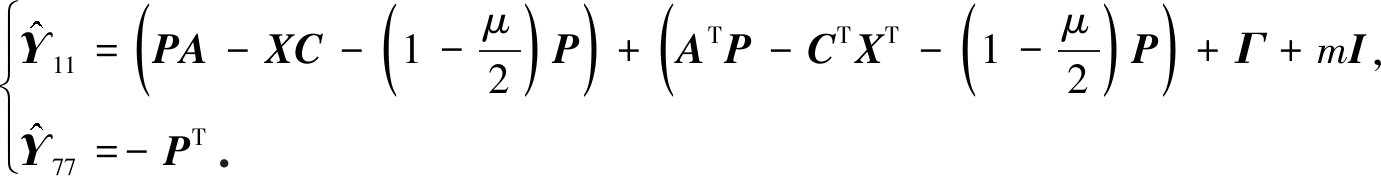
(33)
那么,误差系统(6)是H∞有限时间有界的.
证明 将矩阵(25)中的估计增益定义为K=P-1X,并令diag{I,I,I,I,I,I,P-1}对矩阵(31)做同余变换,得
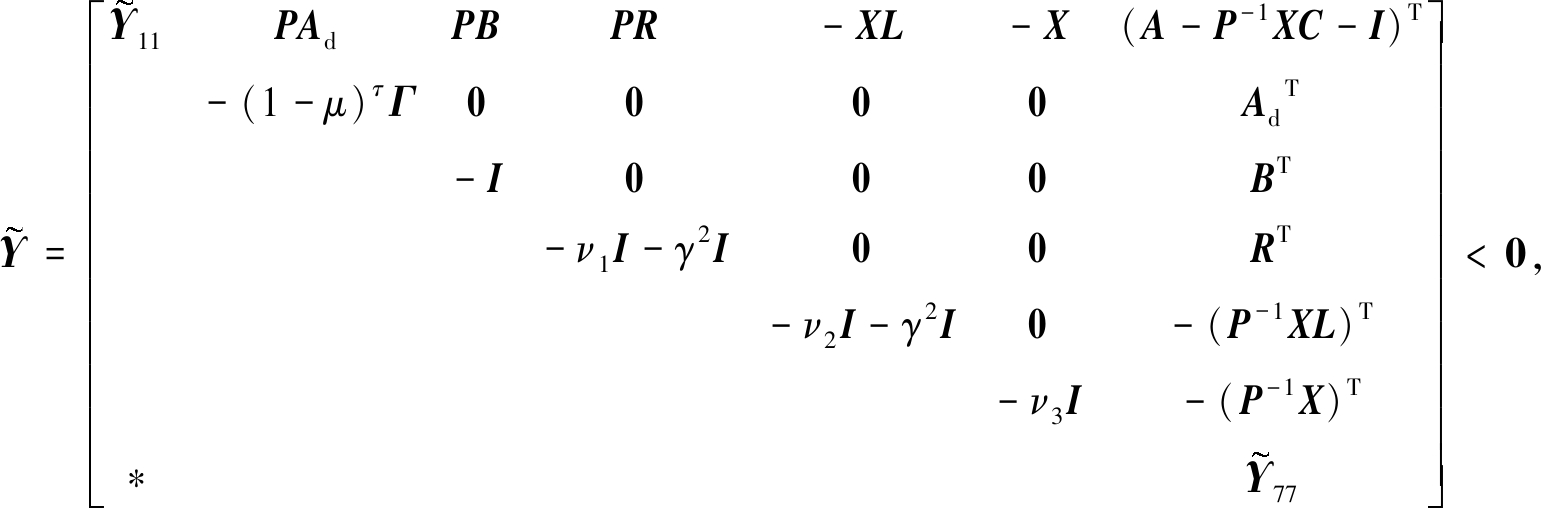
(34)
其中
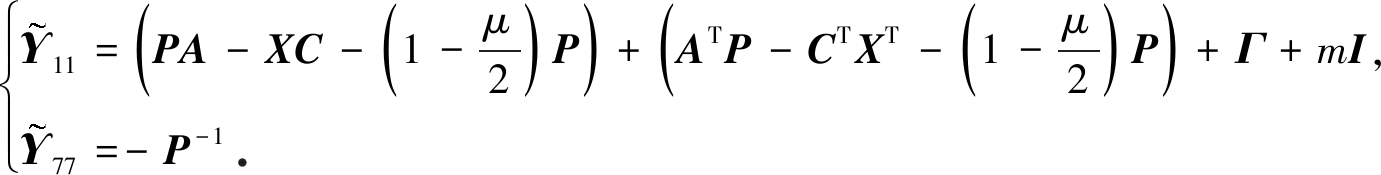
(35)
可以看到![]() 因此当矩阵不等式(31)满足时,矩阵不等式(25)必然满足.
因此当矩阵不等式(31)满足时,矩阵不等式(25)必然满足.
3 仿 真
在本节中,用一个数例来说明所获得的理论结果的有效性.非线性系统(1)参数假设如下:
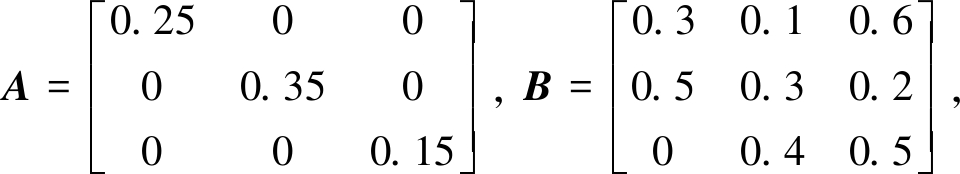
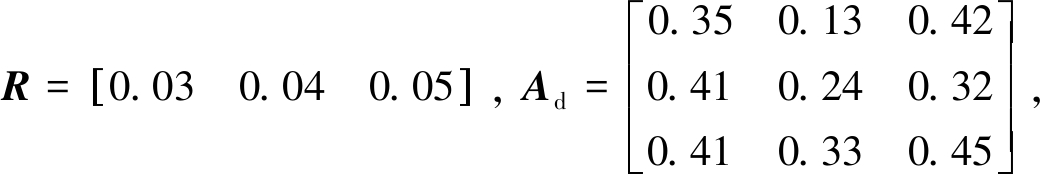

非线性函数选择为
ζ(x(s))=[tanh(x1(s)) tanh(x2(s)) tanh(x3(s))].
设![]() 测量输出式(2)的参数矩阵选择如下:
测量输出式(2)的参数矩阵选择如下:

通过MATLAB中LMI工具箱求解式(31)和(32),得到


根据等式K=P-1X,得到估计增益

经过检验,所选择的参数满足假设1、定义1和2中的条件,得到的P,X和K满足定理1~3中的条件.因此,误差系统(6)是H∞有限时间有界的.通过仿真,得到图1~3.其中,图1表示系统(1)在不同的3个状态下,状态估计器(5)产生的估计值.图2是状态估计器的事件触发机制.图3是系统的估计误差.在图1中,系统(1)的3个状态x1(k),x2(k),x3(k)均在2 s内被状态估计器(5)估计.在图2中,事件触发机制在纵坐标为y=1时触发,y=0时不触发.在图3中,估计误差系统(6)的3个估计误差e1(k),e2(k),e3(k)均在2 s内达到稳定,估计误差系统(6)是有限时间有界的.通过图1~3可以看出,本文设计的由事件触发驱动的非线性系统有限时间状态估计器是有效的、可行的.

图1 系统输入及其状态估计曲线
Fig. 1 The system input and its state estimation curve
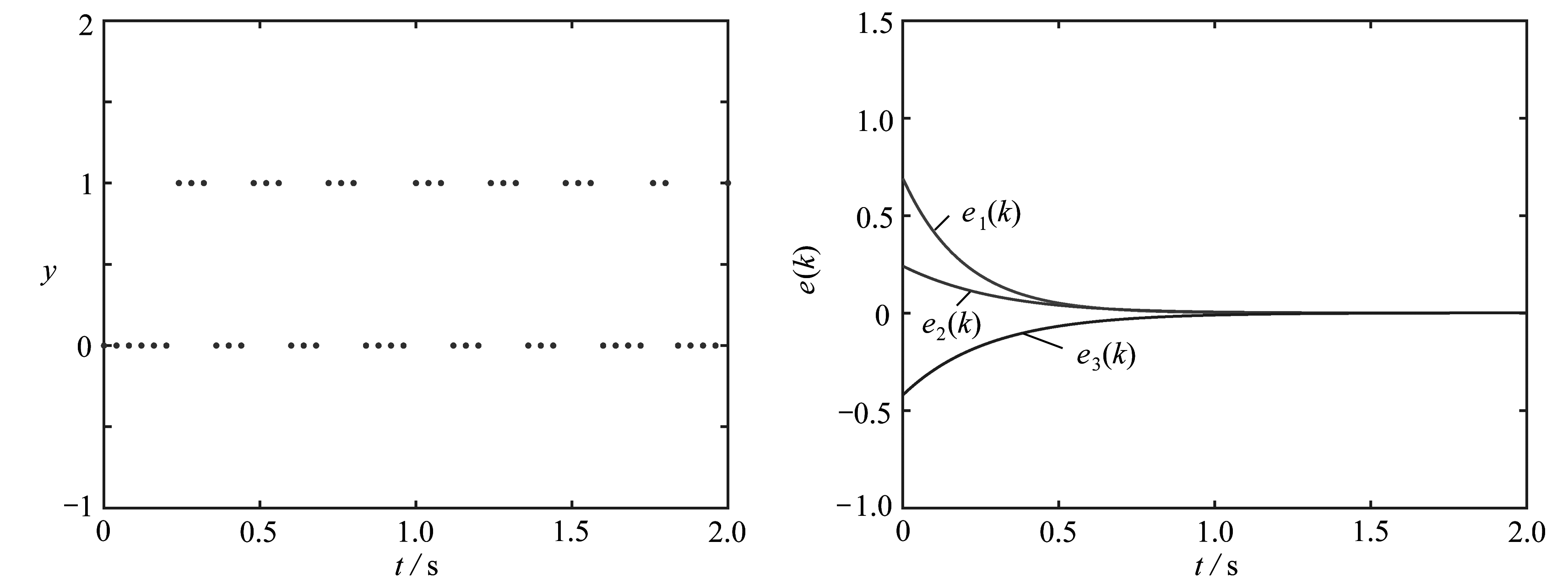
图2 事件触发机制 图3 系统误差曲线
Fig. 2 The event trigger mechanism Fig. 3 The system error curve
4 结 论
本文设计了一类带有时滞的非线性系统有限时间状态估计器.通过采用事件触发机制,使系统的测量输出仅在满足触发条件时被送到状态估计器中.基于Lyapunov理论,有限时间有界定理和H∞有界条件,得到误差系统有限时间有界和H∞有限时间有界的充分条件.最后,通过一个数值例子来说明所获得结果的有效性.本文研究内容可以尝试进一步应用在无人机系统、高速列车系统和电力系统等实际工程中,可以利用本文结论在有限时间内估计系统状态.另外,本文中采用的事件触发机制可以减少实际工程应用中系统资源的浪费.
致谢 本文作者衷心感谢上海工程技术大学研究生科研创新项目(17KY0209)对本文的资助.
[1] IBRIR S, SU C Y. Simultaneous state and dead-zone parameter estimation for a class of bounded-state nonlinear systems[J]. IEEE Transactions on Control Systems Technology, 2011, 19(4): 911-919.
[2] ZHAO J B, ZHANG G X, DONG Z Y, et al. Forecasting-aided imperfect false data injection attacks against power system nonlinear state estimation[J]. IEEE Transactions on Smart Grid, 2016, 7(1): 6-8.
[3] PANKOV A, BOSOV A. Conditionally minimax algorithm for nonlinear system state estimation[J]. IEEE Transactions on Automatic Control, 1994, 39(8): 1617-1620.
[4] ZHENG W, WU W, GOMEZ-EXPOSITO A, et al. Distributed robust bilinear state estimation for power systems with nonlinear measurements[J]. IEEE Transactions on Power Systems, 2017, 32(1): 499-509.
[5] 曾德强, 吴开腾, 宋乾坤, 等. 时滞神经网络随机抽样控制的状态估计[J]. 应用数学和力学, 2018, 39(7): 821-832.(ZENG Deqiang, WU Kaiteng, SONG Qiankun, et al. State estimation for delayed neural networks with stochastic sampled-data control[J]. Applied Mathematics and Mechanics, 2018, 39(7): 821-832.(in Chinese))
[6] LEUNG H, SHANMUGAM S, XIE N, et al. An ergodic approach for chaotic signal estimation at low SNR with application to ultra-wide-band communication[J]. IEEE Transactions on Signal Processing, 2006, 54(3): 1091-1103.
[7] BOLZERN P, COLANERI P, NICOLAO D G. On almost sure stability of continuous-time Markov jump linear systems[J]. Automatica, 2006, 42(6): 983-988.
[8] ZHAO X Y, DENG F Q. Moment stability of nonlinear discrete stochastic systems with time-delays based on H-representation technique[J]. Automatica, 2014, 50(2): 530-536.
[9] WANG Y Y, XIE L H, DE SOUZA C E. Robust control of a class of uncertain nonlinear systems[J]. Systems and Control Letters, 1992, 19(2): 139-149.
[10] WANG D, LIU D R, LI H L, et al. An approximate optimal control approach for robust stabilization of a class of discrete-time nonlinear systems with uncertainties[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2015, 46(5): 713-717.
[11] KE M, ZHAO Y D, ZHAO X. Cooperation-driven distributed model predictive control for energy storage systems[J]. IEEE Transactions on Smart Grid, 2015, 6(6): 2583-2585.
[12] PUKDEBOON C, ZINOBER A S, THEIN M W L. Quasi-continuous higher order sliding-mode controllers for spacecraft-attitude-tracking maneuvers[J]. IEEE Transactions on Industrial Electronics, 2010, 57(4): 1436-1444.
[13] AMATO F, ARIOLA M, DORATO P. Finite-time control of linear systems subject to parametric uncertainties and disturbances[J]. Automatica, 2001, 37(9): 1459-1463.
[14] MAO Y, ZHANG H, ZHANG Z. Finite-time stabilization of discrete-time switched nonlinear systems without stable subsystems via optimal switching signal design[J]. IEEE Transactions on Fuzzy Systems, 2017, 25(1): 172-180.
[15] 程桂芳, 慕小武. 一类不连续系统关于闭不变集的有限时间稳定性研究[J]. 应用数学和力学, 2009, 30(8): 1003-1008.(CHENG Guifang, MU Xiaowu. Finite-time stability with respect to a closed invariant set for a class of discontinuous systems[J]. Applied Mathematics and Mechanics, 2009, 30(8): 1003-1008.(in Chinese))
[16] WANG J, ZHANG H, WANG Z, et al. Finite-time synchronization of coupled hierarchical hybrid neural networks with time-varying delays[J]. IEEE Transactions on Cybernetics, 2017, 47(10): 2995-3004.