引 言
近年来全球大地震频发，其高风险性加剧了工程中对场地条件复杂地区精确可靠地震动参数及其分布特征的需求，一方面，我国西南、西北、华北和东南沿海地区的众多城市位于地震背景发育的复杂场地;另一方面，众多超高复杂建筑、重大交通工程和大型水利设施等不断涌现，这些工程建设场地也多为高山峡谷等复合地形．而多次地震观测和震害调查已证实了复杂场地条件对地震动有着显著的影响，如2008年汶川地震[1-2]对距离震中50 km范围内的汶川县城造成了巨大的破坏，该地区地形高差大、坡度陡，对地震的放大作用明显，地震发生时触发了大量高位滑坡、崩塌和泥石流等地质灾害；2014年鲁甸地震[3]震中龙头山镇位于高山峡谷区，受高原抬升和河流下切影响显著，地貌放大效应明显，地震力抛掷作用显著，震损严重且震害分布很不均匀．高山峡谷地形作为一种典型的复合地形，地震波在高差悬殊的峡谷和山岭之间发生多次散射，其相干效应十分复杂，某些区域可能会成为能量汇聚的“焦点”，从而造成地震动的显著放大．因此，研究高山峡谷地形对地震动的影响，对其场地地震效应的科学定量评估和重大工程的抗震设防等工作均有重要的指导意义．
在复杂场地地震效应的理论研究中，高山峡谷地形可视为凸起和凹陷地形的耦合．目前，国内外诸多学者对单一的凸起或凹陷地形已开展了系列深入研究．1) 凸起地形方面，研究始于Boore[4]采用有限差分法解决三角凸起地形对SH波的散射问题;随后，Yuan和Men[5]首次采用波函数展开法给出了半圆凸起地形对SH波的散射解析解；袁晓铭和廖振鹏[6]又进一步通过引入辅助函数将解答拓展到任意圆弧凸起地形的情况；Lee等[7]采用cosine half-range函数展开法给出了半圆凸起地形对SH 波的散射解析解；Tsaur[8]采用椭圆坐标系中的分离变量法给出了任意半椭圆凸起地形对SH波的散射解析解；Liang等[9-10]采用波函数展开法，并借助辅助函数思想，给出了平面P波和SV波入射下半圆凸起散射解析解．限于解析法通常仅能求解简单形状凸起对弹性波的散射，数值法因其灵活方便、适应性强而得到了快速发展．Smith[11]采用有限元法研究了等腰三角凸起地形对SH波的散射；Sánchez-Sesma等[12]采用间接边界元法研究了半椭圆凸起和三角凸起对P波、SV波和Rayleigh波的散射；Sills[13]采用积分方程法、Bard[14]采用离散波数法、Fu[15]采用几种近似方法研究了Gauss型凸起对SH波的散射；巴振宁等[16]采用间接边界元法研究了层状半空间中周期分布凸起地形对SH波的散射；Bouchon等[17]采用离散波数、Sohrabi-Bidar等[18]采用边界元方法、王铭锋等[19]采用曲线网格有限差分法求解了三维Gauss型山体对地震波的散射等．2) 凹陷地形方面，解析解的研究始于Trifunac[20]采用波函数展开法给出的半圆凹陷SH波的散射解答；随后，袁晓铭和廖振鹏[21]将Graf加法公式进行推广并结合波函数展开法给出了圆弧凹陷地形对SH波散射的闭合解；Gao等[22-23]采用波函数展开法给出了U型和V型截面凹陷对SH波的散射解析解；Lee和Liu[24]提出一种自动满足半空间地表零应力条件的圆柱波函数方法，给出了凹陷地形对P波和SV波散射的闭合解；Zhang等[25]采用复变函数法求解了半圆峡谷对P波、SV波和Rayleigh波的散射问题．数值解的研究始于Wong和Jennings[26]采用边界积分方程法解决任意形状凹陷地形对SH波的散射问题；随后，Wong[27]又进一步将数值解拓展到P波、SV波和Rayleigh波的情况；Vogt等[28]、Ba和Liang[29]采用间接边界元法研究了层状场地中凹陷地形对地震波的散射；Shyu等[30]提出一种有限元-超限插值耦合法研究了一系列不同形状凹陷地形对入射P波的放大效应；Mossessian和Dravinski[31]采用边界积分方程法，Reinoso等[32]采用动力边界元法，宋贞霞和丁海平[33]采用有限元法研究了三维凹陷对地震波的放大效应．目前相关研究在凸起几何参数、偏振效应和山体-地表覆盖层综合影响方面以及凹陷截面形状、深度和坡度的影响方面均取得了重要进展．
尽管国内外学者在单一地形复杂场地反应方面开展了大量研究并取得了丰硕成果，然而凸起(山体)和凹陷(峡谷)多以复合形式存在，研究高山-峡谷复合地形对地震动的影响更为符合实际．目前，相关研究成果还十分有限，据笔者所知，仅有吕晓棠和刘殿魁[34]采用复变函数法研究了半圆凸起与凹陷相连地形对SH波的散射问题；韩峰等[35-36]采用波函数展开法研究了三角凸起与半圆凹陷相连地形对平面SH波的放大效应；杨在林等[37-38]结合波函数展开法和复变函数法研究了SH波入射下两个不等边三角凸起与半圆凹陷相连地形的地震动响应．但以上研究还限于平面外SH波情况，针对更为复杂的存在波型转换问题的平面内(P波和SV波)情况仍未见相关文献发表．为此，本文在Ba和Yin[39]研究的基础上，发展了一种用于求解平面内多域弹性波散射的多域间接边界元法(multi-domain IBEM)，研究了高山峡谷地形对平面P-SV波的散射问题．该方法综合了现有两类边界元法在分别处理闭合域和开口半空间域波场方面的优势，同时各域内波场的构造完全独立，非常适合并行求解．本文对提出的方法进行了介绍，并以半空间中Gauss型高山峡谷为例，分别在频域和时域内进行了数值计算，讨论了入射波的类型、入射角度、入射频率和山体高宽比等因素对场地地震动的影响规律．
1 计算模型与求解方法
如图1所示，高山峡谷地形由任意截面形状的两个相邻凸起和中间凹陷构成，两凸起的自由边界分别为Sh1和Sh2，凸起与半空间的交界面分别为Sl1和Sl2，凹陷的自由边界为Sc．下卧基岩水平成层，材料参数包括质量密度ρ、剪切波速cs、Poisson比ν以及阻尼比ζ．平面P-SV波沿与x轴成夹角θ的方向由下卧面入射．
目前，求解复合地形对地震波散射问题的方法总体上包括各种域离散型方法和边界元法，相较于域离散型方法，边界元法具有降维、自动满足辐射条件和精确描述不规则界面间波反射透射的优点[40]，十分适合地震波场的精细模拟．然而，现有边界元方法(以全空间Green函数为基本解的边界元和以半空间Green函数为基本解的边界元)在处理多域弹性波散射问题时均效率较低．为提高求解效率，减少计算量和存储量，针对高山峡谷复合地形，本文综合上述两类边界元法的优点，发展了一种用于求解平面内多域弹性波散射的多域间接边界元法．模型的分域原则如下： 1) 全空间动力Green函数形式简单，求解速度快，用于复合地形中闭合域的波场模拟； 2) 层状半空间动力Green函数能同时自动满足自由表面零应力及各地层交界面连续条件，用于复合地形中开口层状半空间域的波场模拟．其次，借助多域间接边界元法在并行计算方面的天然优势(计算过程可明确分解为各独立域波场构造和最终方程组的求解)，进而可快速求得问题的解．
求解的具体步骤为：1) 将整体模型(图1(a))分解成两个凸起闭合域Ωn(n=1,2)(图1(b))和一个开口层状半空间域Ωo(图1(c))，同时将总波场分解成自由波场和散射波场．假定两个凸起闭合域仅包含散射波场(由于凸起与凹陷的存在而产生的附加波场)，而层状开口域既包括散射波场又包括自由波场(波由基岩界面入射时产生的动力响应)．2) 分别用全空间动力Green函数和半空间动力Green函数模拟域Ωn和域Ωo的散射波场，自由波场可由直接刚度法方便求得．3) 引入相应的边界条件，将各独立域波场组合，求得频域内总波场响应，进而由快速Fourier逆变换得到高山峡谷地形地震动响应的时域结果．
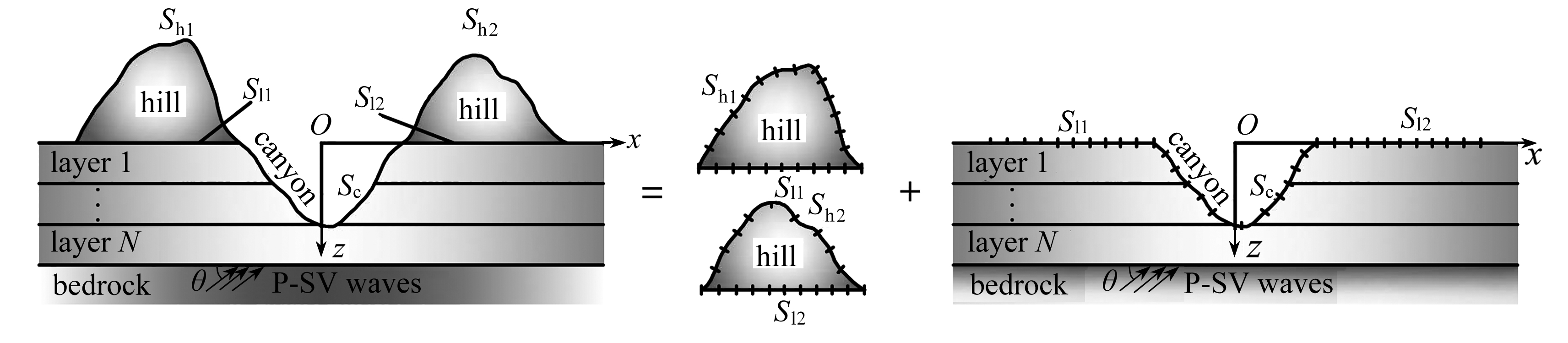
(a) 整体模型 (b) 闭合域 (c) 开口层状半空间域
(a) The whole model (b) The closed regions (c) The open layered half-space region
图1 平面P-SV波斜入射下层状半空间中高山-峡谷复合地形模型
Fig. 1 The model for the hill-canyon composite topography in a layered half space under obliquely incident plane P and SV waves
1.1 全空间动力Green函数及闭合域内波场表达
如前所述，凸起闭合域Ωn(n=1,2)仅含散射波场，采用全空间均布线荷载动力Green函数进行模拟．如图1(b)所示，考虑到各凸起的散射波场具有独立性(相互无影响)，以凸起闭合域Ω1为例进行分析，假定其域边界为S1=Sh1+Sl1，将边界分别离散为Kh1和Kl1个线单元，且有K1=Kh1+Kl1，每个单元的长度记为ΔSm(m=1,2,…,K1)．在Ω1内任意点x=(x,z)沿x和z方向的位移和牵引力可表示为
(1)
(2)
其中，上标“t”表示总波场，上标“s1”表示散射波场；
和
分别为全空间均布荷载位移和牵引力Green函数，即将j方向的虚拟均布荷载施加在边界上第m个单元上时于点x处所引起的i方向的位移和牵引力；φj(ξm)为施加在第m个单元上沿j方向的虚拟均布荷载密度．根据Sánchez-Sesma等[12]的理论，均布荷载动力Green函数可以通过将相应的集中荷载动力Green函数在该单元上进行积分得到
(3)
(4)
其中，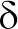
为Dirac delta函数，
和
分别为全空间集中荷载位移和牵引力Green函数．当x与ξm不重合时，
和的具体表达式可直接参考文献[12]；当x与ξm重合时，和的具体表达式可由Bessel函数收敛递推公式求得
(5)
(6)
其中，
和kS分别为P波和SV波的波数，λ*和μ*为复Lamé常数，γ为Euler常数，γx和γz分别为点x的方向正弦和方向余弦．
1.2 半空间动力Green函数及开口域内波场表达
如前所述，开口层状半空间域Ωo包含自由波场和散射波场，自由波场可采用直接刚度法求解，详细的求解内容可参考文献[41]，散射波场则采用半空间均布线荷载动力Green函数求解．如图1(c)所示，假定开口域Ωo的边界为S0=Sc+Sl1+Sl2，将边界分别离散为Kc，Kl1和Kl2个线单元，且有K0=Kc+Kl1+Kl2，每个单元的长度记为ΔSm(m=1，2，…，K0)．在Ωo内任意点x=(x,z)沿x和z方向的位移和牵引力可表示为
(7)
(8)
其中，上标“s0”表示散射波场，上标“f”表示自由波场；
和
分别为半空间斜线和水平线均布荷载位移Green函数，
和
分别是半空间斜线和水平线均布荷载牵引力Green函数，即将j方向的虚拟均布荷载施加在边界上的第m个单元上时于点x处所引起的i方向的位移和牵引力；φj(ξm)(ψj(ξm))为施加在第m个斜线(水平)单元上沿j方向的虚拟均布荷载密度．
本文建立的半空间动力Green函数的荷载形式包括斜线和水平线荷载，两者的构造方法并不完全相同，对于斜线型半空间动力Green函数，可运用Wolf理论[41]进行求解，对于水平线型半空间动力Green函数，由于不涉及固定层边界(求特解和齐次解)的求解过程，将荷载直接作用在水平边界上运用“直接刚度法”即可求解[42]．以下对两类半空间动力Green函数的求解过程分别进行介绍：
1) 半空间中斜线均布线荷载动力Green函数的具体求解思路为： ① 通过Fourier变换将施加的虚拟均布荷载由空间域展开到波数域中； ② 在荷载作用的上下边界引入附加交界面(固定荷载作用层)，求得层内动力响应以及两固定端的反力解，并将反力解反向施加给整个半空间，运用“直接刚度法”计算该反作用力所产生的动力响应； ③ 叠加由反作用力引起的动力响应以及层内动力响应得到总的动力响应，进而结合Fourier逆变换叠加波数域中解答即可得到空间域解答．本文中斜线均布荷载位移和牵引力Green函数
和
的具体求解步骤在文献[42]中已给出，此处不再赘述．
2) 半空间中水平均布荷载动力Green函数的具体求解思路为： ① 通过Fourier变换将施加的虚拟均布荷载由空间域展开到波数域中； ② 在水平单元处直接施加虚拟均布荷载，运用“直接刚度法”计算该荷载所产生的动力响应； ③ 通过Fourier逆变换将该动力响应变换到空间域中求解．
如图2所示，对于施加在水平单元上的虚拟均布荷载，设其在x和z方向上的幅值分别为p0和r0．作用在长度为ΔSm单元上的荷载在波数域中可展开为
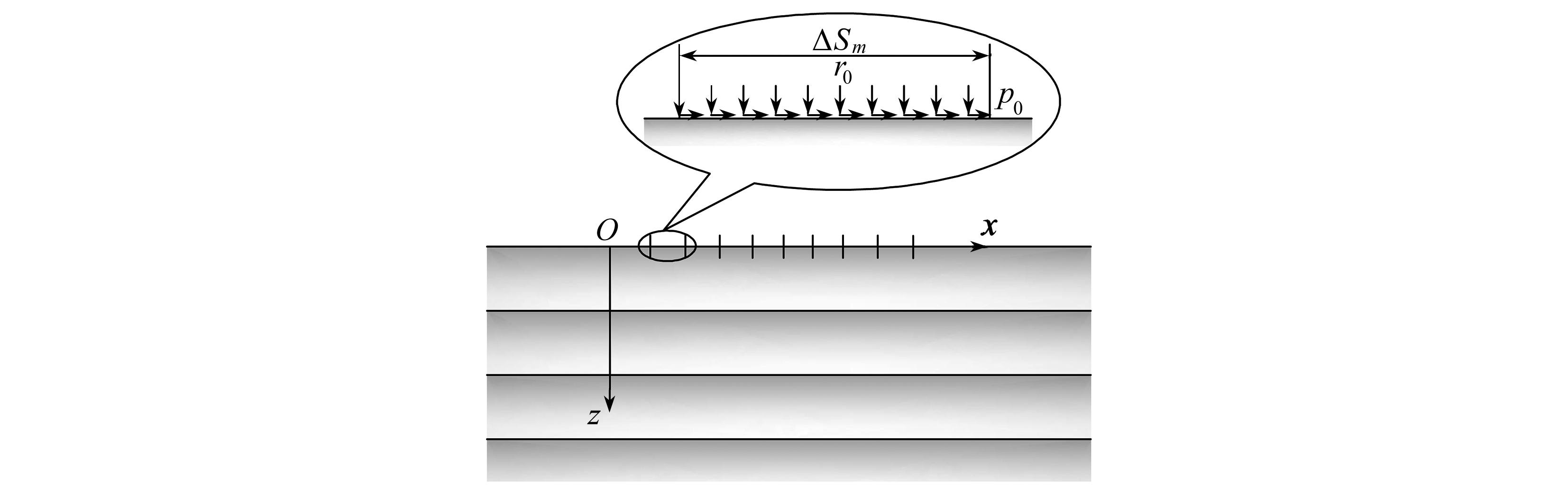
图2 水平均布荷载动力Green函数求解示意
Fig. 2 Solution of horizontal Green’s functions for uniformly distributed forces
(9)
(10)
相应的位移幅值可由直接刚度法求得
[SP-SV]{ux1,iuz1,…,ux(N+1),iuz(N+1)}T={P1,iR1,0,…,0}T,
(11)
其中
P1=p(k)，R1=r(k)．
[SP-SV]为层状半空间的整体刚度矩阵，可通过集整层刚度矩阵和基岩刚度矩阵得到，具体可参考文献[41]．根据应力-位移关系
(12a)
(12b)
(12c)
可求得虚拟荷载作用下产生的应力．以上的计算都是在波数域中进行的，可通过Fourier逆变换得到空间域的结果．对于任意点x，半空间水平均布荷载位移与牵引力动力Green函数分别为
(13)
(14)
式(14)中，牵引力可由应力投影的方式得到
txj(k,z)=nxσx(k,z)+nzτxz(k,z),
(15a)
tzj(k,z)=nxτzx(k,z)+nzσz(k,z),
(15b)
其中，n=(nx,nz)是点x的法向量．
1.3 边界条件及问题求解
问题的边界条件包括：两凸起闭合域自由边界Sh1和Sh2以及凹陷部分自由边界Sc的零牵引力条件，与两凸起闭合域和开口域的交界面Sl1和Sl2的位移和牵引力连续条件．
首先，凸起闭合域的自由边界S1和S2上各单元应满足零牵引力条件：
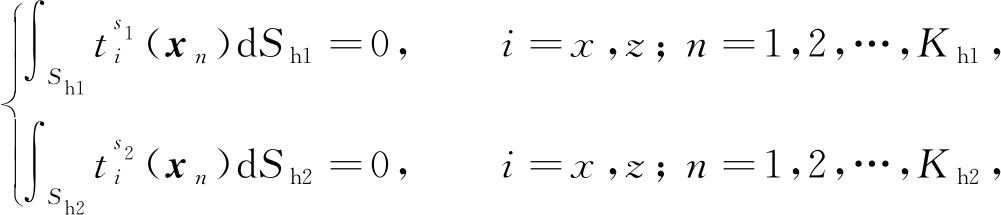
(16)
其中，上标“s1”和“s2”分别为凸起闭合域Ω1和Ω2中的散射波场，Kh1和Kh2分别为自由边界Sh1和Sh2离散的线单元数．同时，半空间开口域的自由边界Sc上各单元应满足零牵引力条件：
(17)
其中， 上标“s0”表示半空间开口域Ωo中的散射波场，Kc为自由边界Sc离散的线单元数．
其次，凸起闭合域与半空间开口域交界面Sl1和Sl2上的各单元应满足位移和牵引力连续条件：
(18)
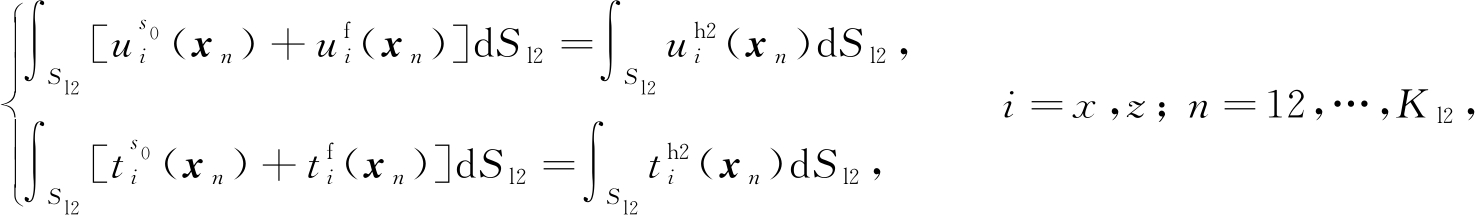
(19)
其中，Kl1和Kl2分别为凸起闭合域Ω1和Ω2与半空间开口域Ωo交界面Sl1和Sl2离散的线单元数．
将式(1)、(2)、(7)和(8)代入式(16)～(19)中，通过求解系列方程组，可得施加在相应边界上的虚拟均布荷载密度，进而结合式(1)和(7)即可求得高山峡谷地形中任意点处的位移．
2 方 法 验 证
首先，通过与Sánchez-Sesma等[12]给出的均匀半空间中半圆凹陷地形对P-SV波的散射解答进行比较来验证本文方法．令高山峡谷的两侧凸起高度为其半宽的1%，本文模型即退化成单一凹陷地形．设两侧凸起和凹陷的半宽均为a，凸起高度h=0.01a，凹陷截面取为半圆形．图3给出了P波和SV波入射时地表的位移幅值，计算中Poisson比取1/3，不考虑材料阻尼，无量纲频率η=2.0，入射角度θP=θSV=90°(垂直入射)．无量纲频率定义(下同)为η=ωa/(πcs)，其中ω为振动圆频率，cs为半空间剪切波速．从图3中可以看出，本文计算结果与Sánchez-Sesma等[12]给出的结果十分吻合，从一方面验证了方法的正确性．
(a) P波 (b) SV波
(a) The P wave (b) The SV wave
图3 本文结果与Sánchez-Sesma等[12]结果的比较
Fig. 3 Comparison of the results given by the present method and Sánchez-Sesma et al[12]
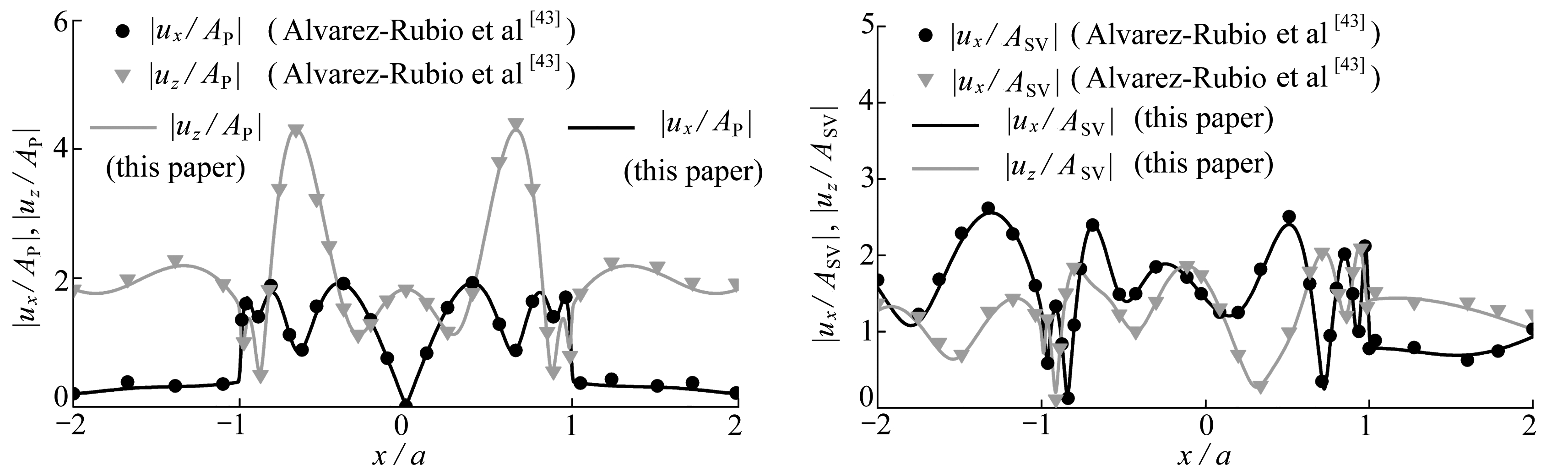
其次，通过与Alvarez-Rubio 等[43]给出的均匀半空间中半椭圆凸起地形对P-SV波的散射解答进行比较来验证本文方法．令高山峡谷中某一凸起高度和中间凹陷深度均为其半宽的1%，本文模型即退化成单一凸起地形．设两侧凸起和凹陷的半宽均为a，其中一个凸起高度h=0.01a，另一个凸起高度h=2a，凹陷深度b=0.01a．图4给出了P波和SV波入射时地表的位移幅值，计算中Poisson比取为1/4，阻尼比为0.01，无量纲频率η= 1.5，入射角度θP=90°以及θSV=60°．从图4中可以看出，本文的结果与Alvarez-Rubio等[43]的结果也十分吻合，从另一方面验证了方法的正确性．
(a) P波 (b) SV波
(a) The P wave (b) The SV wave
图4 本文结果Alvarez-Rubio等[43]结果的比较
Fig. 4 Comparison of the results given by the present method and Alvarez-Rubio et al[43]
3 算例与分析
本文给出了一种用于求解平面内多域弹性波散射的多域间接边界元法，在程序实现时可结合OpenMP高性能并行技术，具有计算精度高、求解速度快的特点．值得指出的是，方法的精度取决于边界单元的离散和Green函数求解中涉及的无穷积分．其中，对于单元离散，可通过数值试验，以典型复合地形对弹性波散射模型为例进行收敛性分析，研究发现[39]单元尺寸取为1/16参考波长时，可保证单元离散的收敛性；而对于无穷积分，可采用分段两点Gauss积分完成，根据不同振动频率，最大积分波数段取为200～400，最小的积分间隔取为0.001～0.01，即可满足积分精度．在保证精度基础上，以下给出了具体算例结果．
3.1 频域结果
为研究高山峡谷复合地形对平面P波和SV波的散射，以均匀半空间中Gauss型高山峡谷为例进行计算分析．计算模型如图5所示，左右两相同山体和中间峡谷相连，三者半宽和凹陷深度均为a，凸起高度为h，地形轮廓均为Gauss型曲线，轮廓线方程依次为
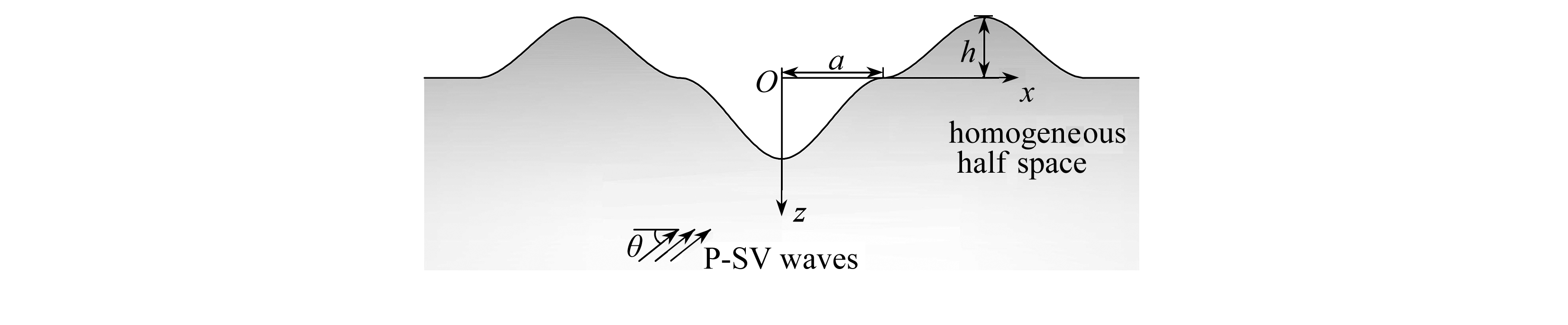
图5 均匀半空间中高山峡谷计算模型
Fig. 5 The calculation model for the hill-canyon composite topography in a homogeneous half space
1) 左侧山体轮廓线：
其中
ξ1=|(x+2a)/a|， 0≤ξ1≤1；
2) 中间峡谷轮廓线：
其中
ξ2=|x/a|， 0≤ξ2≤1；
3) 右侧山体轮廓线：
其中
ξ3=|(x-2a)/a|， 0≤ξ3≤1．
计算参数如下：Poisson比取为1/3，不考虑材料阻尼(实际取为0.005，以消除波数积分中的奇异性问题)，无量纲频率为η=ωa/(πcs)=0.5，1.0，2.0，入射角度为θP=θSV=5°，45°，90°(垂直入射)，山体高宽比为h/a=2.0．图6和图7分别给出了平面P波和SV波入射下高山峡谷地形附近地表位移幅值单频结果．图中的|ux/AP|，|uz/AP|，|ux/ASV|和|uz/ASV|为无量纲位移幅值，其中ux和uz分别为x和z向的位移，AP和ASV分别为入射P波和SV波的幅值．
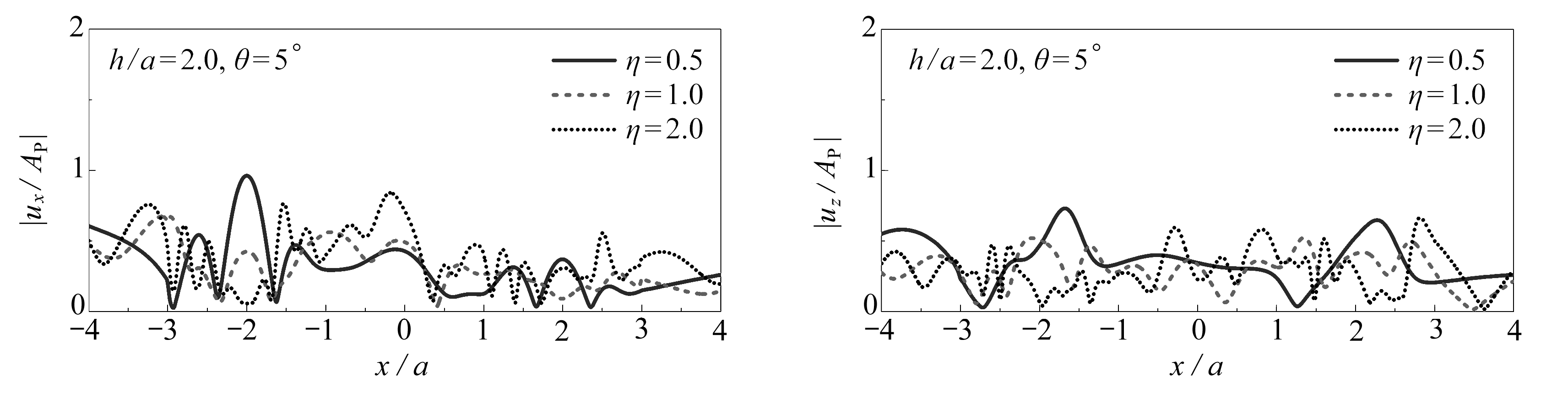
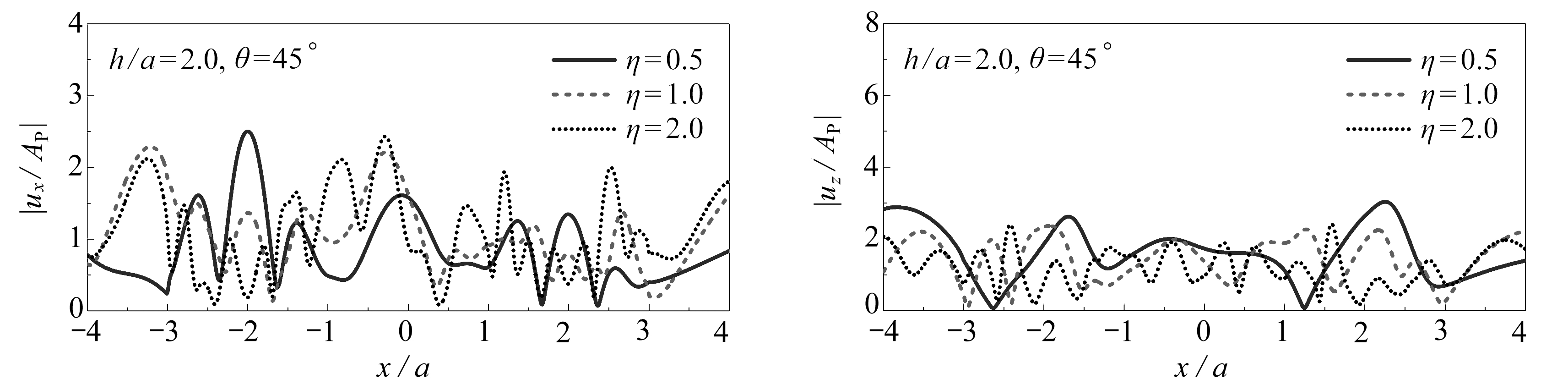
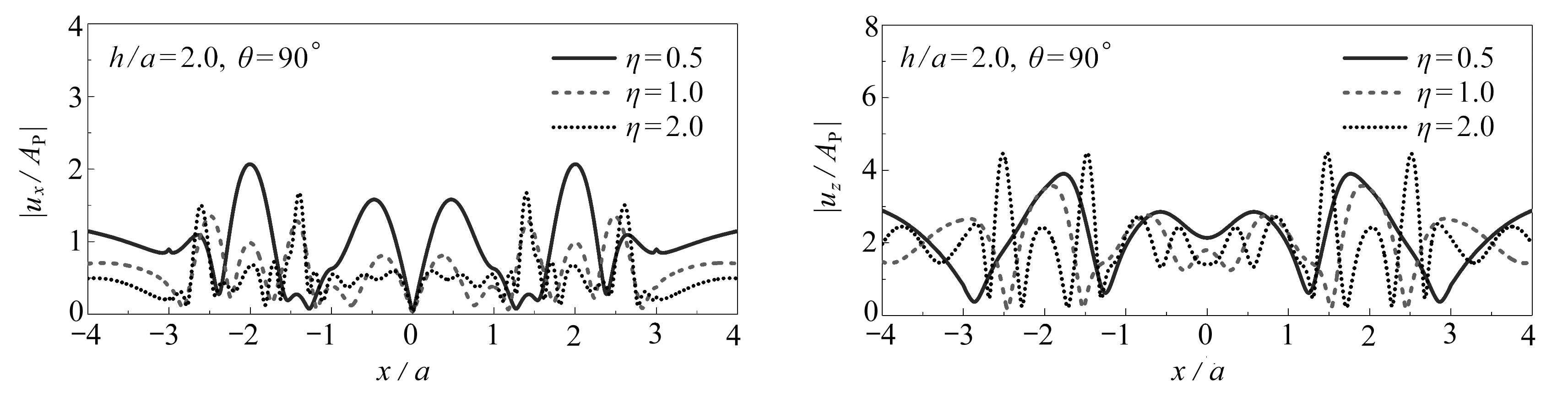
图6 平面P波入射下高山峡谷地形附近地表位移幅值
Fig. 6 Surface displacement amplitudes of the hill-canyon topography subjected to P wave incidence
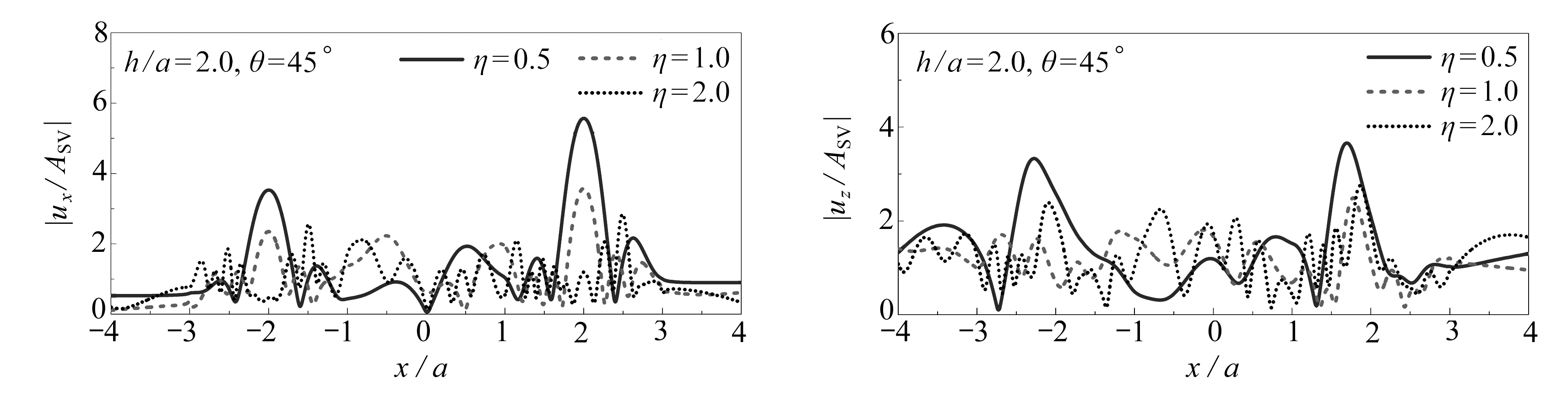
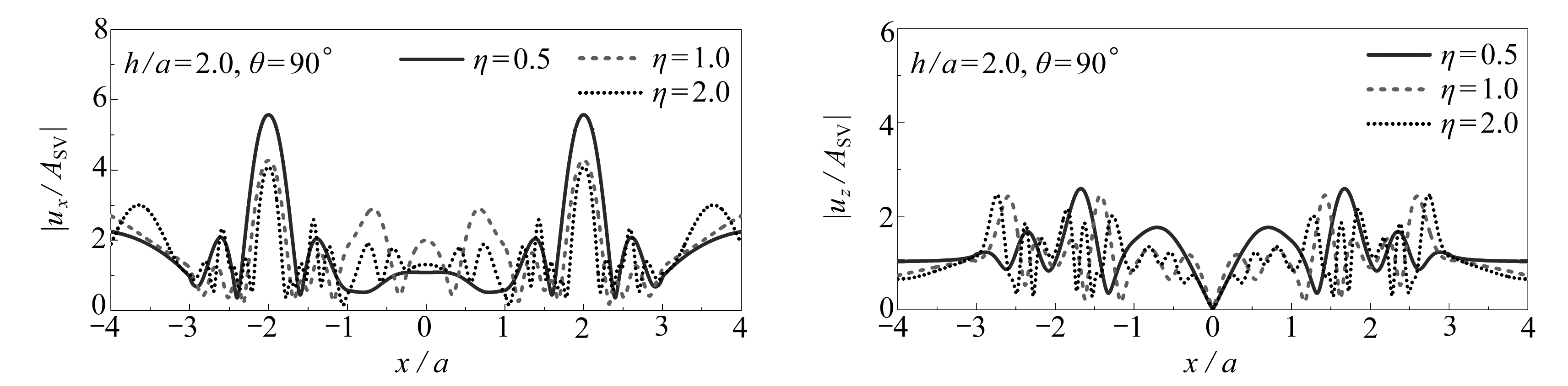
图7 平面SV波入射下高山峡谷地形附近地表位移幅值
Fig. 7 Surface displacement amplitudes of the hill-canyon topography subjected to SV wave incidence
由图6可知，高山峡谷地形附近地表位移幅值的分布非常复杂，其空间分布特征依赖于平面P波的入射频率和角度．首先，当P波掠入射(θ=5°)时，两侧山体的位移幅值振荡明显，强于峡谷处的位移幅值，随着入射频率的增加，整体上水平位移幅值呈增大趋势而竖向位移幅值呈减小趋势，但变化程度均较小．其次，当P波斜入射(θ=45°)时，高山峡谷地形附近地表位移幅值较掠入射的情况显著增大，且随着入射频率的增加，山体和峡谷的位移幅值有着不同的变化趋势：峡谷和右侧山体的位移幅值继续表现为水平向增大和竖向减小的趋势，而左侧山体的位移幅值变化趋势相反．最后，当P波垂直入射(θ=90°)时，高山峡谷地形附近地表位移幅值较斜入射的情况继续增大，尤其是竖向的位移幅值(P波入射主要引起z轴方向的振动)．值得注意的是，对于垂直入射的情况，随着入射频率的增加，水平和竖向的位移幅值均逐渐增大，这与掠入射和斜入射的情况有着明显差别．
由图7可知，与P波入射相比，高山峡谷地形在平面SV波入射下的位移幅值分布规律更加明显，且同样受入射频率和角度的影响．一方面，低频入射时，地表位移幅值的分布具有明显的双峰特征，随着入射频率的增加，位移幅值的分布逐渐变得复杂，特征形式由双峰向多峰转变．另一方面，掠入射时，峡谷和右侧山体的位移幅值振荡比左侧山体更加剧烈，但整体上地表位移幅值均不大，随着入射角度的增加，高山峡谷地形对地震动出现了显著的放大作用，水平位移幅值逐渐增大，水平位移峰值均出现在山体顶部，并在垂直入射时达到幅值最大值，而竖向位移峰值多出现在山腰处，并在斜入射时已经达到幅值最大值．
以上分析表明，山体动力特性和峡谷半空间动力特性以及两者之间的动力相互作用共同决定了高山峡谷地形对地震波的散射效应，由于波(包括入射波、透射波、反射波和散射波)的往复传播和相干作用，使得高山峡谷复合地形的地表动力响应相对于单一山体/峡谷情况更为复杂，从而导致不同的入射频率、入射角度以及不同波的类型条件下，地表位移幅值频域结果产生了显著差异．
3.2 时域结果
为研究真实地震波作用下高山峡谷复合地形的时域响应，采用El centro波和Taft波作为输入的地震动，输入波的加速度峰值为0.1g，持续时间为40 s，波入射角度为θ=90°(垂直入射)，结合FFT变换给出了不同地表观测点处的输出加速度时程及其反应谱结果．算例以基岩半空间中Gauss型高山峡谷为例进行分析，着重探讨山体高宽比和介质剪切波速比对场地地震时域响应的影响．
计算模型如图8所示，山体和峡谷半宽均为a=100 m，山体及峡谷所在层剪切波速均为
岩体和基岩考虑为各向同性介质，输入地震波作用于基岩露头．计算中，山体高宽比的研究范围为h/a=0，0.5，1.0，1.5，2.0，2.5和3.0，其中，h/a=0时为无山体情况，即单一峡谷地形；基岩和岩层的剪切波速比的研究范围为
和4.0．为便于结果比较，其他参数均保持相同：Poisson比取为1/3，阻尼比取为0.05，质量密度取为2 000 kg/m3．另外，图中在地表面分别设置了6个观测点P1～P6，其位置依次为x/a=0，0.5，1.0，1.5，2.0，3.0，以描述时域响应的空间分布特征．
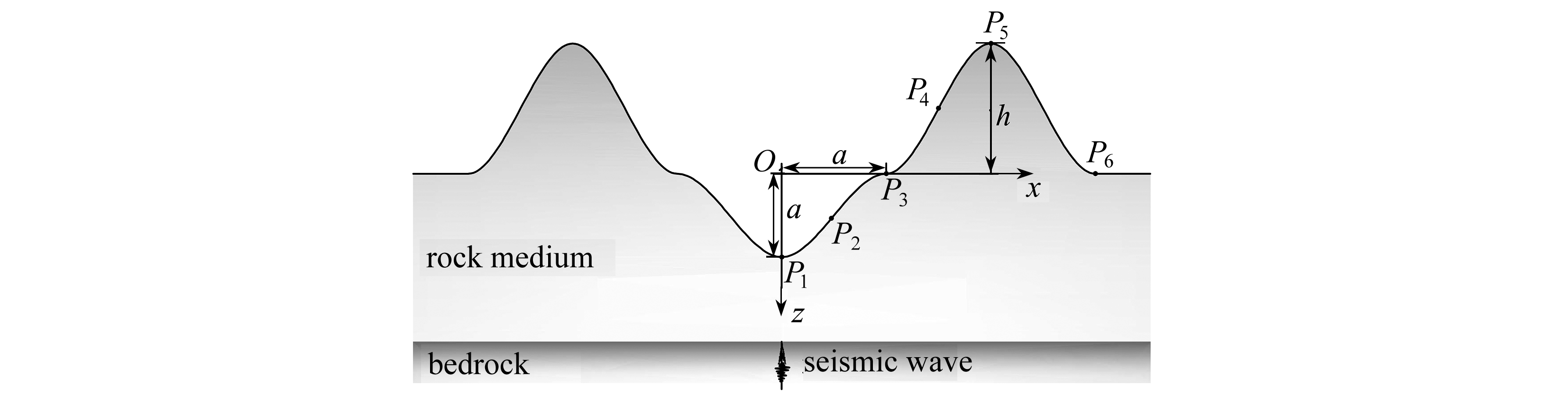
图8 时域响应计算模型及观测点设置
Fig. 8 The calculation model for time domain responses and the setting of observation points
3.2.1 山体存在对峡谷地形的影响
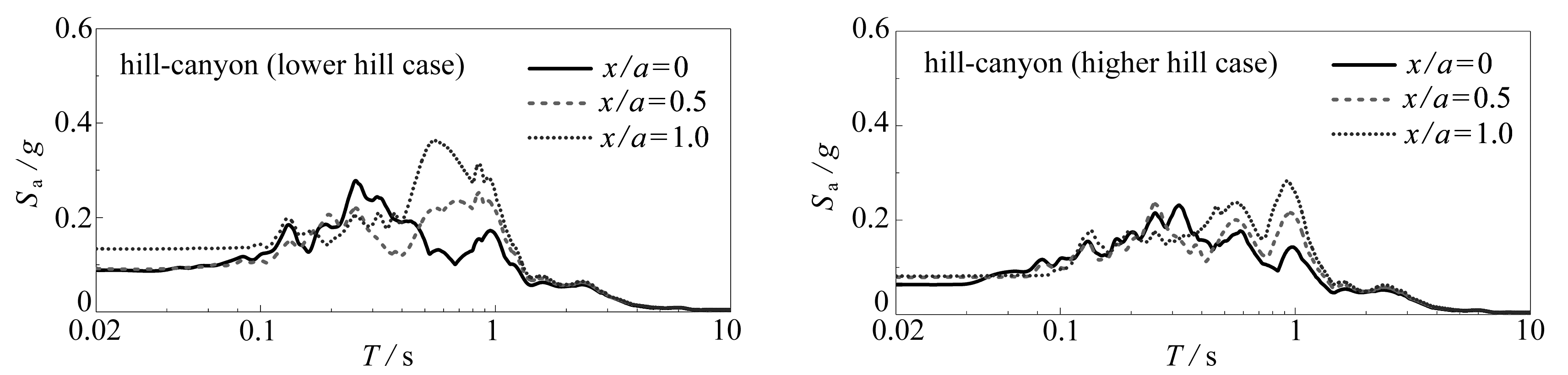
图9给出了剪切波速比一定时
单一峡谷(h/a=0)、矮山-峡谷(h/a=0.5)和高山-峡谷(h/a=3.0)在El centro波作用下峡谷内部(P1～P3)的时域响应，其中，图9(a)为加速度时程曲线，图9(b)为相应的加速度反应谱．
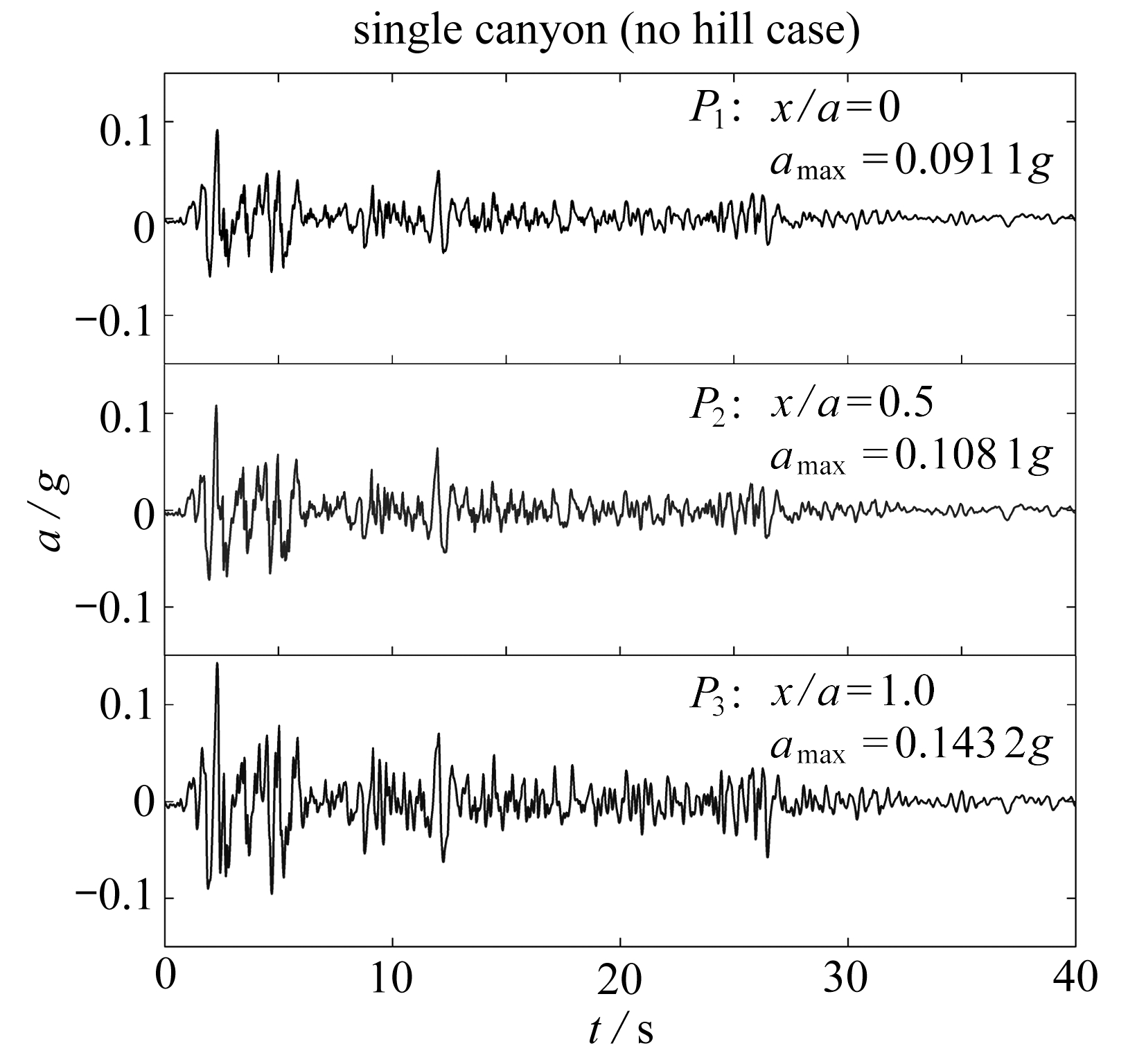
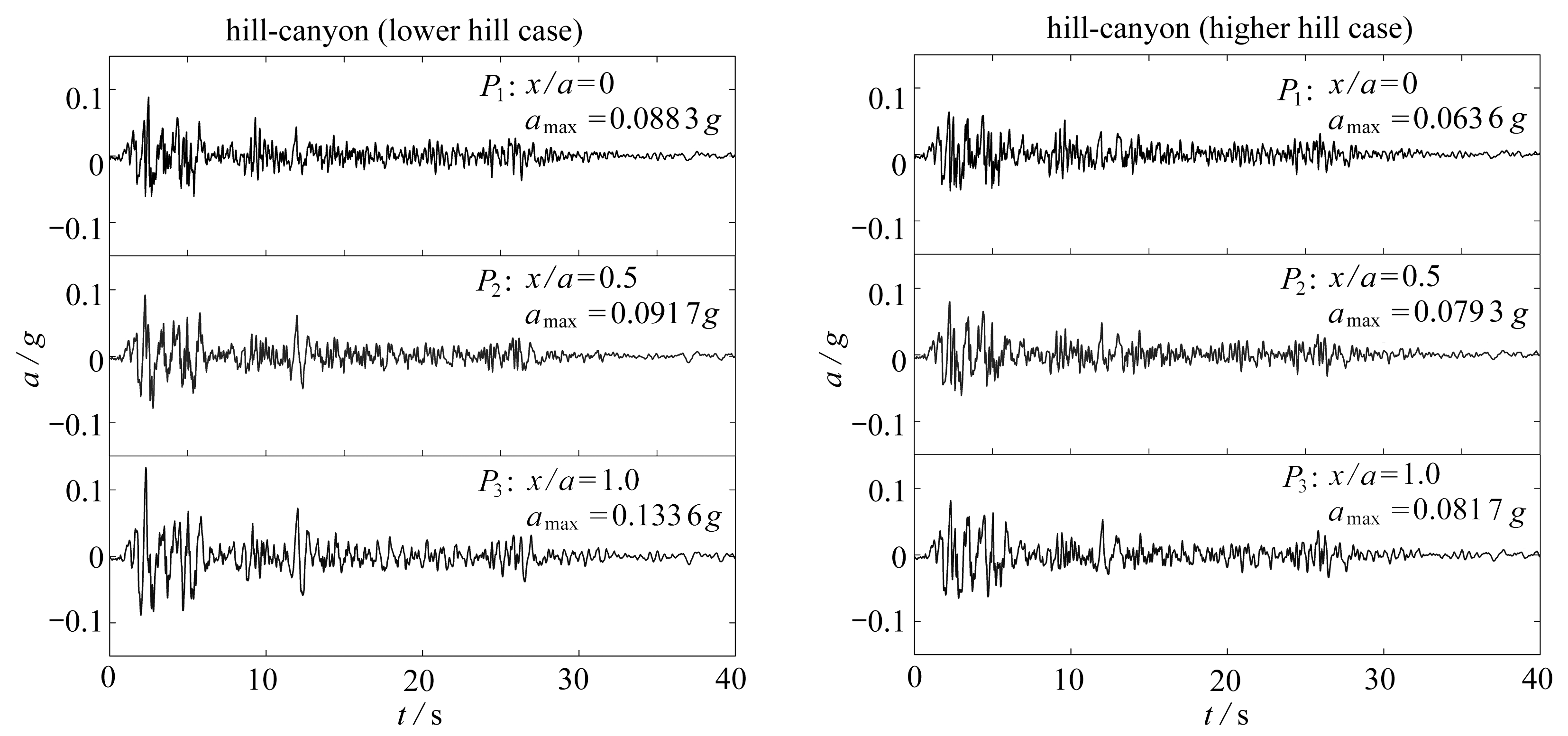
(a) 加速度时程曲线
(a) Acceleration vs. time curves
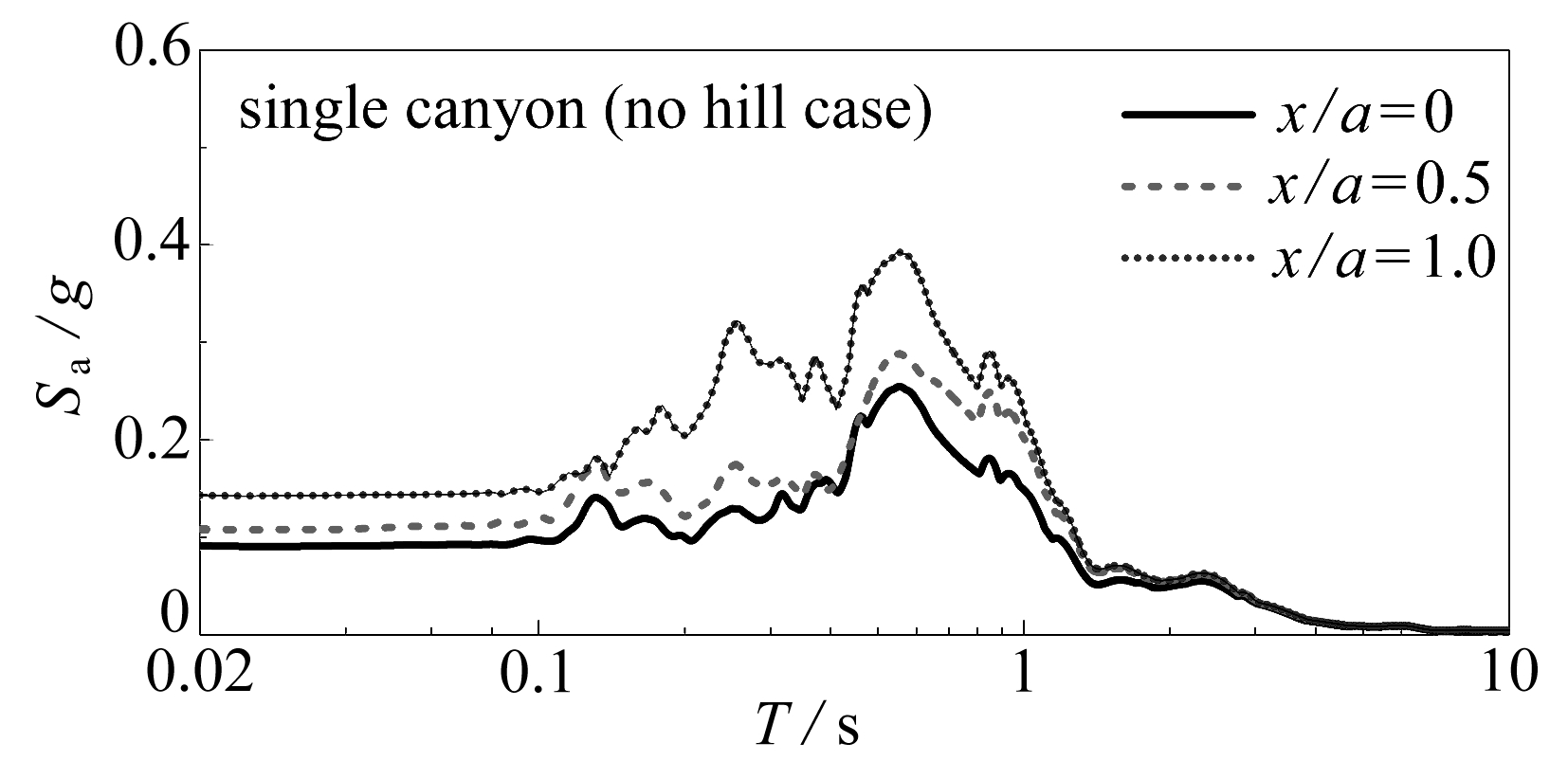
(b) 加速度反应谱
(b) Acceleration response spectra
图9 山体存在对峡谷内部加速度响应的影响
Fig. 9 Influences of the presence of hills on the acceleration responses in the canyon
由图9可知：
1) 山体的存在会明显改变峡谷内部加速度峰值(PGA)及其空间分布，表现为山体对峡谷地震动的抑制作用．以谷底的加速度响应为例，单一峡谷地形的PGA为0.091 1g，大于矮山-峡谷地形和高山-峡谷地形的0.088 3g和0.063 6g，可见山体的存在对峡谷地震动有一定的抑制作用，且山体越高，抑制效果越显著．其次，山体的存在改变了峡谷响应的空间分布状态，单一峡谷地形下，随着观测点远离谷底，地表的PGA逐渐增大，至峡谷边缘(P3处)时，已表现为明显的放大作用，而高山-峡谷地形下，P3处的PGA仍小于输入地震波的最大加速度，这是由于山体存在时，受到上部凸起地形和下部半空间体的动力相互作用，峡谷内部地震波产生缩幅效应．
2) 山体的存在对峡谷内地表加速度反应谱也有重要影响．一方面，在峡谷内部的各观测点中，含有山体的峡谷地形的反应谱峰值均小于单一峡谷地形的反应谱峰值，这与PGA的变化一致．另一方面，有无山体的峡谷地形的反应谱在短周期分量(T=0.1～1 s)范围内的差异较大，单一峡谷地形对应的卓越周期短，而含有山体的峡谷地形对应的卓越周期长，这是由于受到山体抑制作用的影响，基岩上传的地震波穿过岩层后引起峡谷内部振动频率减小．
3.2.2 不同山体高宽比下高山峡谷的时域响应
图10给出了不同山体高宽比的高山峡谷在两种地震波作用下地表各处(P1～P6)的峰值加速度变化情况．由图10可知：首先，在山体高宽比为h/a=0.5～3.0范围内，无论何种地震波和剪切波速比，地表最大响应位置均为山顶处(x/a=2.0)；其次，山体高宽比的改变对高山峡谷的时域影响也主要体现在山顶处，且随着山体高宽比的增大，山顶处的PGA表现为先迅速增大后逐渐减小的趋势，PGA的最大值多出现在山体高宽比为2.0的情况下；最后，对于不同的地震波作用，由于波频谱特征的改变，将导致山体高宽比对高山峡谷的时域影响程度发生改变．
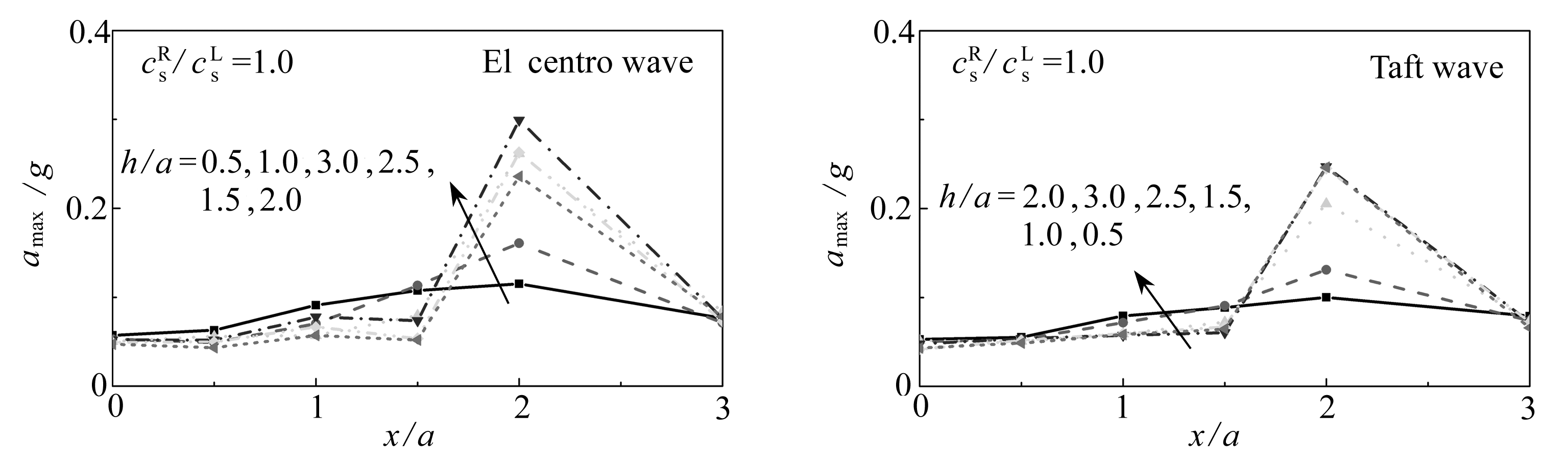
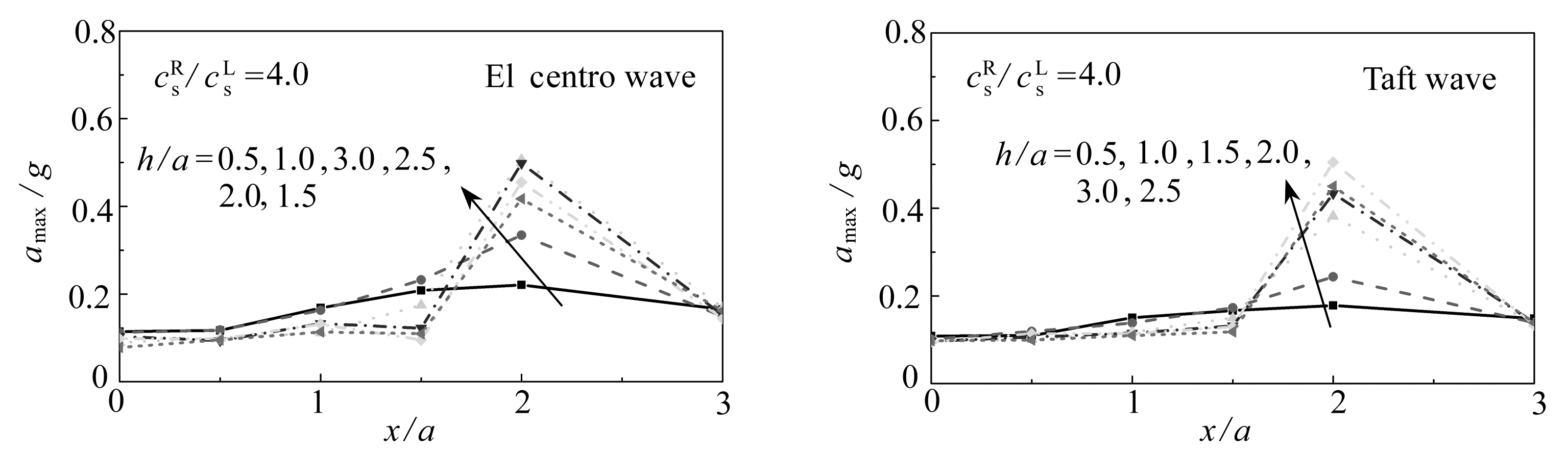
图10 不同山体高宽比下高山峡谷的地震动响应
Fig. 10 Seismic dynamic responses of the hill-canyon topography under different height-to-width ratios of hills
3.2.3 不同剪切波速比下高山峡谷的时域响应
图11给出了不同剪切波速比的高山峡谷在两种地震波作用下地表各观测点处(P1～P6)的峰值加速度变化情况．由图11可知：基岩与岩层的剪切波速比对高山峡谷地形的地震动有着显著影响，这种影响不仅体现在山顶处，也体现在地形地表面的各个位置．具体表现为随着剪切波速比的增大，地表各观测点的PGA均逐渐增大，这是由于基岩越硬(剪切波速越大)，基岩与上部地形的动力相互作用越强，地表响应就越明显．
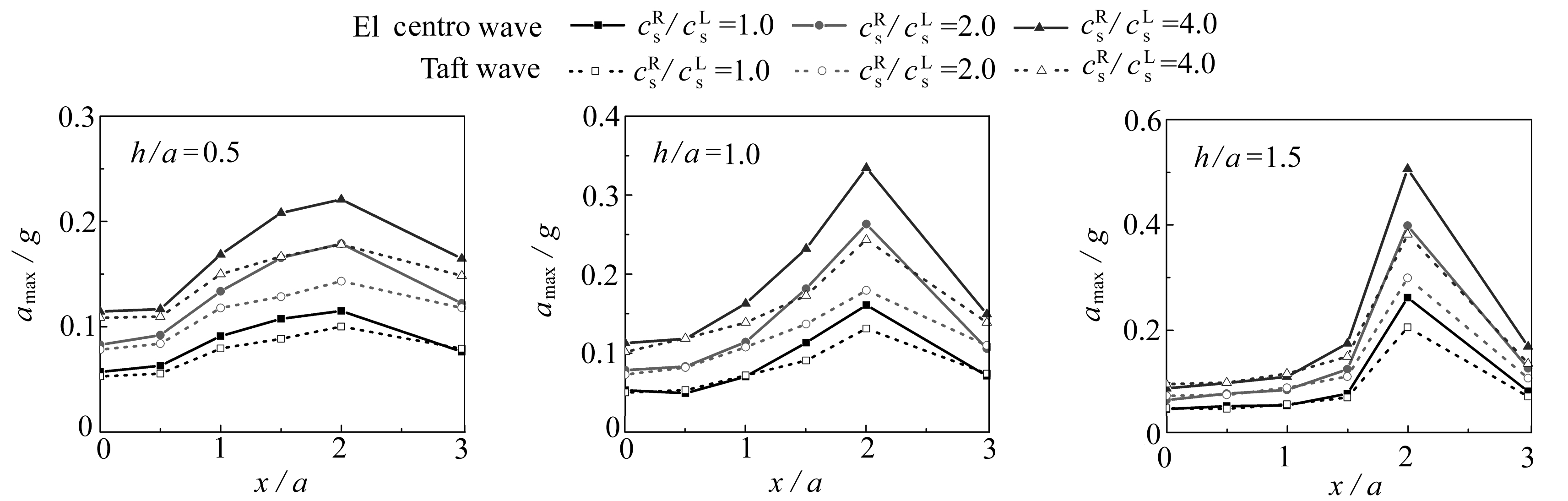
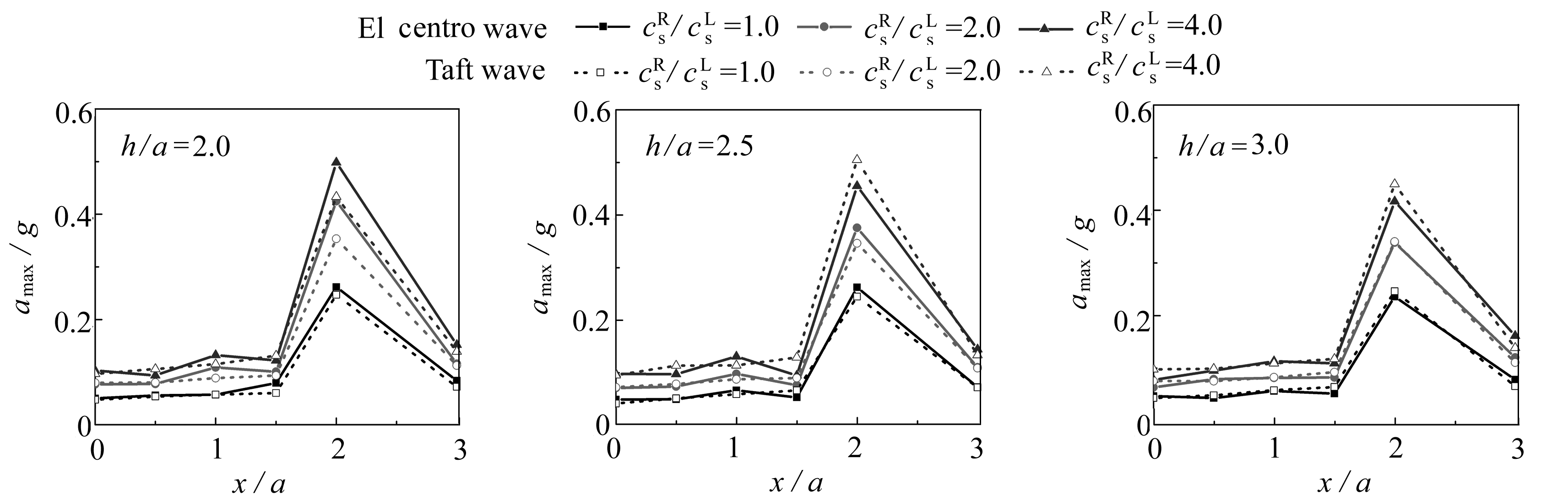
图11 不同剪切波速比下高山峡谷的地震动响应
Fig. 11 Seismic dynamic responses of the hill-canyon topography under different shear wave velocity ratios
另外，对于不同的地震波作用，其对时域影响的差异将随山体高度的增加而减小，即山体越高，剪切波速比对高山峡谷的影响在不同地震波下的规律将趋于一致．
4 结 论
本文发展了一种用于求解平面内多域弹性波散射的多域间接边界元法，研究了高山峡谷地形对平面P-SV波的散射问题．文中对提出的方法进行了验证，并以半空间中Gauss型高山峡谷为例，分别在频域和时域内进行了数值计算分析，得到了以下主要结论：
1) 提出的新方法充分利用了全空间Green函数和半空间Green函数的优势，在保证计算精度的同时显著提高了求解效率．其次，借助多域间接边界元法在并行计算方面的天然优势，十分适合多地形地貌单元复合场地的动力解答．
2) 高山峡谷地形附近地表位移幅值的分布非常复杂，其空间分布特征依赖于入射波的频率和角度．分析结果表明，山体动力特性和峡谷半空间动力特性以及两者之间的动力相互作用共同决定了高山峡谷地形对地震波的散射效应．
3) 地震波垂直入射时，山体对峡谷地震动有一定的抑制作用，山体的存在不仅明显改变峡谷内部加速度峰值及其空间分布，也对峡谷内地震动反应谱特性有重要影响．
4) 高山峡谷地形两侧山体高宽比的改变将引起地震效应的改变，随着山体高宽比的增大，山顶处的峰值加速度表现为先迅速增大后逐渐减小的趋势，且不同地表观测点处的地震动变化有明显差异．
5) 基岩面的存在将显著放大高山峡谷地形的地震效应，且基岩与岩层的剪切波速比越大，地表各观测点的峰值加速度越大，地震效应越明显．
[1] CHEN Y, LI L, LI J, et al. Wenchuan earthquake: way of thinking is changed[J].Episodes, 2008,31(4): 374-377.
[2] 王秀英, 聂高众. 汶川MS8.0级地震诱发崩滑特点及其与地震动参数对应关系初析[J]. 岩土工程学报, 2009,31(9): 1378-1383.(WANG Xiuying, NIE Gaozhong. Characteristics of landslides induced by WenchuanMS8.0 earthquake and preliminary analysis of their relations with ground motion parameters[J].Chinese Journal of Geotechnical Engineering, 2009,31(9): 1378-1383.(in Chinese))
[3] 殷志强, 徐永强, 陈红旗, 等. 2014年云南鲁甸地震触发地质灾害发育分布规律及与景谷、盈江地震对比研究[J]. 地质学报, 2016,90(6): 1086-1097.(YIN Zhiqiang, XU Yongqiang, CHEN Hongqi, et al. The development and distribution characteristics of geohazards induced by August 3, 2014 Ludian earthquake and comparison with Jinggu and Yingjiang earthquakes[J].Acta Geologica Sinica, 2016,90(6): 1086-1097.(in Chinese))
[4] BOORE D M. A note on the effect of simple topography on seismic SH waves[J].Bulletin of the Seismological Society of America, 1972,62(1): 275-284.
[5] YUAN X, MEN F L. Scattering of plane SH waves by a semi-cylindrical hill[J].Earthquake Engineering and Structural Dynamics, 1992,21(12): 1091-1098.
[6] 袁晓铭, 廖振鹏. 任意圆弧形凸起地形对平面 SH 波的散射[J]. 地震工程与工程振动, 1996,16(2): 1-13.(YUAN Xiaoming, LIAO Zhenpeng. Scattering of plane SH waves by a cylindrical alluvial valley of circular-arc cross-section[J].Earthquake Engineering and Engineering Dynamics, 1996,16(2): 1-13.(in Chinese))
[7] LEE V W, LUO H, LIANG J W. Antiplane (SH) waves diffraction by asemicircular cylindrical hill revisited: an improved analytic wave series solution[J].Journal of Engineering Mechanics, 2006,132(10): 1106-1114.
[8] TSAUR D H. Scattering and focusing of SH waves by a lower semielliptic convex topography[J].Bulletin of the Seismological Society of America, 2011,101(5): 2212-2219.
[9] LIANG J W, ZHANG Y S, LEE V W. Scattering of plane P waves by asemi-cylindrical hill: analytical solution[J].Earthquake Engineering and Engineering Vibration, 2005,4(1): 27-36.
[10] 梁建文, 张彦帅, LEE V W. 平面SV波入射下半圆凸起地形地表运动解析解[J]. 地震学报, 2006,28(3): 238-249.(LIANG Jianwen, ZHANG Yanshuai, LEE V W. Surface motion of a semi-cylindrical hill for incident plane SV waves: analytical solution[J].Acta Seismologica Sinica, 2006,28(3): 238-249.(in Chinese))
[11] SMITH W D. The application of finite element analysis to body wave propagation problems[J].Geophysical Journal International, 1975,42(2): 747-768.
[12] S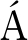
NCHEZ-SESMA F J, CAMPILLO M. Diffraction of P, SV, and Rayleigh waves by topographic features: a boundary integral formulation[J].Bulletin of the Seismological Society of America, 1991,81(6): 2234-2253.
[13] SILLS L B. Scattering of horizontally-polarized shear waves by surface irregularities[J].Geophysical Journal International, 1978,54(2): 319-348.
[14] BARD P Y. Diffracted waves and displacement field over two-dimensional elevated topographies[J].Geophysical Journal International, 1982,71(3): 731-760.
[15] FU L Y. Rough surface scattering: comparison of various approximation theories for 2D SH waves[J].Bulletin of the Seismological Society of America, 2005,95(2): 646-663.
[16] 巴振宁, 黄棣旸, 梁建文, 等. 层状半空间中周期分布凸起地形对平面SH波的散射[J]. 地球物理学报, 2017,60(3): 1039-1052.(BA Zhenning, HUANG Diyang, LIANG Jianwen, et al. Scattering and diffraction of plane SH-waves by periodically distributed hill topographies[J].Chinese Journal of Geophysics, 2017,60(3): 1039-1052.(in Chinese))
[17] BOUCHON M, SCHULTZ C A, TOKSÖZ M N. Effect of three-dimensional topography on seismic motion[J].Journal of Geophysical Research:Solid Earth, 1996,101(B3): 5835-5846.
[18] SOHRABI-BIDAR A, KAMALIAN M. Effects of three-dimensionality on seismic response of Gaussian-shaped hills for simple incident pulses[J].Soil Dynamics and Earthquake Engineering, 2013,52: 1-12.
[19] 王铭锋, 郑傲, 章文波. 局部山体地形对强地面运动的影响研究[J]. 地球物理学报, 2017,60(12): 4655-4670.(WANG Mingfeng, ZHENG Ao, ZHANG Wenbo. Effect of local mountain topography on strong ground motion[J].Chinese Journal of Geophysics, 2017,60(12): 4655-4670.(in Chinese))
[20] TRIFUNAC M D. Scattering of plane SH waves by a semi-cylindrical canyon[J].Earthquake Engineering and Structural Dynamics, 1972,1(3): 267-281.
[21] 袁晓铭, 廖振鹏. 圆弧形凹陷地形对平面SH波散射问题的级数解答[J]. 地震工程与工程振动, 1993,16(2): 1-11.(YUAN Xiaoming, LIAO Zhenpeng. Series solution for scattering of plane SH waves by a canyon of circular-arc cross-section[J].Earthquake Engineering and Engineering Vibration, 1996,16(2): 1-11.(in Chinese))
[22] GAO Y, ZHANG N, LI D, et al. Effects of topographic amplification induced by a U-shaped canyon on seismic waves[J].Bulletin of the Seismological Society of America, 2012,102(4): 1748-1763.
[23] ZHANG N, GAO Y, CAI Y, et al. Scattering of SH waves induced by a non-symmetrical V-shaped canyon[J].Geophysical Journal International, 2012,191(1): 243-256.
[24] LEE V W, LIU W Y. Two-dimensional scattering and diffraction of P-and SV-waves around a semi-circular canyon in an elastic half-space: an analytic solution via a stress-free wave function[J].Soil Dynamics and Earthquake Engineering, 2014,63: 110-119.
[25] ZHANG C, LIU Q, DENG P. Surface motion of a half-space with a semicylindrical canyon under P, SV, and Rayleigh waves[J].Bulletin of the Seismological Society of America, 2017,107(2): 809-820.
[26] WONG H L, JENNINGS P C. Effects of canyon topography on strong ground motion[J].Bulletin of the Seismological Society of America, 1975,65(5): 1239-1257.
[27] WONG H L. Effect of surface topography on the diffraction of P, SV, and Rayleigh waves[J].Bulletin of the Seismological Society of America, 1982,72(4): 1167-1183.
[28] VOGT R F, WOLF J P, BACHMANN H. Wave scattering by a canyon of arbitrary shape in a layered half-space[J].Earthquake Engineering and Structural Dynamics, 1988,16(6): 803-812.
[29] BA Z N, LIANG J W. 2.5D scattering of incident plane SV waves by a canyon in layered half-space[J].Earthquake Engineering and Engineering Vibration, 2010,9(4): 587-595.
[30] SHYU W S, TENG T J, CHOU C S. Effect of geometry on in-plane responses of a symmetric canyon subjected by P waves[J].Soil Dynamics and Earthquake Engineering, 2018,113: 215-229.
[31] MOSSESSIAN T K, DRAVINSKI M. Scattering of elastic waves by a three-dimensional surface topographies[J].Wave Motion, 1989,11: 579-592.
[32] REINOSO E, WROBEL L C, POWER H. Three-dimensional scattering of seismic waves from topographical structures[J].Soil Dynamics and Earthquake Engineering, 1997,16: 41-61.
[33] 宋贞霞, 丁海平. 三维不规则地形河谷场地地震响应分析方法研究[J]. 地震工程与工程振动, 2013,33(4): 8-15.(SONG Zhenxia, DING Haiping. Research on calculating method for seismic responses of 3D irregular topography (valley site)[J].Earthquake Engineering and Engineering Vibration, 2013,33(4): 8-15.(in Chinese))
[34] 吕晓棠, 刘殿魁. SH波入射时半圆形凸起与凹陷地形的地震动[J]. 地震工程与工程振动, 2006,26(5): 14-20.(LÜ Xiaotang, LIU Diankui. Ground motion of a semi-cylindrical hill and a semi-cylindrical canyon caused by incident SH wave[J].Earthquake Engineering and Engineering Vibration, 2006,26(5): 14-20.(in Chinese))
[35] 韩峰, 王光政, 康朝阳. SH 波对等腰三角形与半圆形凹陷相连地形的散射[J]. 应用数学和力学, 2011,32(3): 293-311.(HAN Feng, WANG Guangzheng, KANG Chaoyang. Scattering of SH-waves on the isosceles triangular hill joined by semi-cylindrical canyon[J].Applied Mathematics and Mechanics, 2011,32(3): 293-311.(in Chinese))
[36] 韩峰, 王光政, 陈翰. SH 波对多个凸起与凹陷相连地形的散射问题研究[J]. 应用数学和力学, 2013,34(4): 355-363.(HAN Feng, WANG Guangzheng, CHEN Han. Research on scattering of SH-waves on multiple hills and canyons[J].Applied Mathematics and Mechanics, 2013,34(4): 355-363.(in Chinese))
[37] 杨在林, 许华南, 陈志刚. 等腰三角形凸起与半圆形凹陷地形对SH波的散射[J]. 哈尔滨工业大学学报, 2011,43(S1): 6-11.(YANG Zailin, XU Huanan, CHEN Zhigang. Scattering of SH-waves by two isosceles triangle hills and a semi-cylindrical canyon[J].Journal of Harbin Institute of Technology, 2011,43(S1): 6-11.(in Chinese))
[38] YANG Z, XU H, HEI B, et al. Antiplane response of two scalene triangular hills and a semi-cylindrical canyon by incident SH-waves[J].Earthquake Engineering and Engineering Vibration, 2014,13(4): 569-581.
[39] BA Z N, YIN X. Wave scattering of complex local site in a layered half-space by using a multi-domain IBEM: incident plane SH waves[J].Geophysical Journal International, 2016,205(3): 1382-1405.
[40] 何彦锋, 孙伟家, 符力耘. 复杂介质地震波传播模拟中边界元法与有限差分法的比较研究[J]. 地球物理学进展, 2013,28(2): 664-678.(HE Yanfeng, SUN Jiawei, FU Liyun. Comparison of boundary element method and finite-difference method for simulating seismic wave propagation in complex media[J].Progress in Geophysics, 2013,28(2): 664-678.(in Chinese))
[41] WOLF J P.Dynamic Soil-Structure Interaction[M]. Englewood Cliffs: Prentice-Hall, 1985.
[42] 巴振宁, 吴孟桃, 梁建文. 坡体几何参数与弹性模量对岩质斜坡地震动力响应的影响: IBEM求解[J]. 岩石力学与工程学报, 2019,38(8): 1578-1592.(BA Zhenning, WU Mengtao, LIANG Jianwen. Influence of geometric parameters and elastic modulus on seismic dynamic response of rock slopes by IBEM[J].Chinese Journal of Rock Mechanics and Engineering, 2019,38(8): 1578-1592.(in Chinese))
[43] ALVAREZ-RUBIO S, S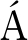NCHEZ-SESMA F J, BENITO J J, et al. The direct boundary element method: 2D site effects assessment on laterally varying layered media (methodology)[J].Soil Dynamics and Earthquake Engineering, 2004,24(2): 167-180.