引 言
波形钢腹板具有自重轻、屈曲强度大及正交各向异性等特点.因此,在预应力混凝土箱梁桥中使用波形钢腹板,一方面可以减轻箱梁的自重,另一方面由于波形钢腹板的手风琴效应可以有效提高预应力的导入率[1].目前,预应力混凝土波形钢腹板组合梁桥已经在法国、日本、韩国以及中国得到了广泛的应用与推广.此外,在一些工业建筑结构中,常采用波形钢腹板代替工字型钢梁的直腹板,充分利用了波形钢腹板可以提供较强的面外刚度来消除腹板加劲肋的布置.国内外众多学者已经对波形钢腹板的受力性能进行了大量研究[2-16]:Elgaaly和Hamilton等研究了波形钢腹板的剪切强度[2];Elgaaly和Seshadri等研究了波形钢腹板的弯曲性能[3];Samanta和Mukhopadhyay运用有限元方法对波形钢板进行了静力和动力分析[4];Sayed-Ahmed对波形钢腹板梁的侧向扭转屈曲进行了研究[5];Guo等采用有限元和理论分析的方法研究了梯形波形钢腹板的局部弹性剪切屈曲强度[6];Aggarwal等研究了波形钢腹板厚度、宽度以及腹板高度变化对其局部剪切屈服系数的影响[7];冀伟等对波形钢腹板PC箱梁桥的静力和动力特性问题进行了研究[8-11];郑尚敏等对单箱多室波形钢腹板组合箱梁和混凝土箱梁的动力特性进行了对比分析[12];李丽园等考虑全截面剪切,推导出了波形钢腹板组合箱梁的挠度解析公式[13];李立峰等基于Newmark法,研究了横隔板间距、高跨比、宽跨比以及波形钢腹板形状对变截面波形钢腹板组合箱梁的畸变效应的影响[14];刘保东等通过模型试验和有限元分析研究了内衬混凝土对波形钢腹板刚构桥扭转和畸变性能的影响[15];邵江艳等应用基于势能驻值原理的能量变分法,结合初参数法,求解出了波形钢腹板组合箱梁桥的畸变翘曲应力[16].
在上述研究中,虽然已经开展了波形钢腹板的有限元数值分析,但主要是通过建立波形钢腹板的三维有限元模型来进行分析的.由于波形钢腹板的手风琴效应以及其面内和面外变形复杂的三维形状,在建立其三维空间有限元模型时比较繁琐,且划分的单元数量较多,用于工程设计计算十分不便.因此,本文提出将波形钢腹板的复杂三维模型通过刚度等效与位移等效的方法,将其简化为正交各向异性板的二维模型,为有限元模型的建立带来简化,并且通过划分较少的单元数量就可以达到较高的计算精度,提高了计算效率,为波形钢腹板组合梁自振特性的建模求解提供一个简便的方法.
1 波形钢腹板与正交各向异性板的等效分析
由于波形钢腹板的特殊构造,纵向、竖向两个方向的弹性模量和Poisson比存在较大的差异,在对其进行有限元建模分析时,需要按波形腹板的形状建立物理模型,同时还需将波形钢腹板离散为足够小的各向同性单元才可以进行研究分析.因此,本文提出将波形钢腹板等效为正交各向异性板的方法,既克服了因划分单元太多而带来的弊端,同时使得建模更加方便.图1为将三维的波形钢腹板等效为二维的正交各向异性板的示意图,根据文献[17]可知,正交各向异性板的弹性单元刚度矩阵如式(1)所示:

图1 波形钢腹板简化为二维正交各向异性平板示意图 图2 一个波长的波形示意图
Fig. 1 The simplified 2D orthotropic plate sketch Fig. 2 The waveform of a wavelength of corrugated steel webs
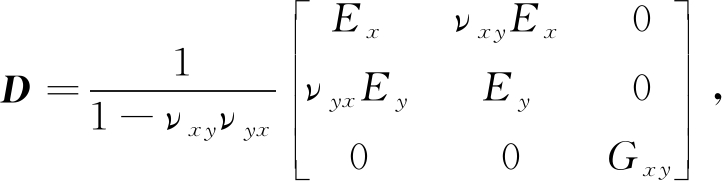
(1)
式中,Ex为局部坐标系下x方向的等效弹性模量;Ey为局部坐标系下y方向的等效弹性模量;νxy为局部坐标系下x方向的Poisson比;νyx为局部坐标系下y方向的Poisson比;Gxy为等效剪切模量.
式(1)中的正交各向异性板单元刚度矩阵中的各个变量可以通过与三维的波形钢腹板刚度等效和位移等效原则求出.首先进行正交各向异性板与波形钢腹板的刚度等效,取一个波长作为研究对象,如图2所示,以截面对y轴的弯曲刚度为等效方程可得
(2)
式中,E为钢材的弹性模量;Iyy,3D为波形钢腹板对y轴的惯性矩;Iyy,2D为正交各向异性板对y轴的惯性矩;l为波形钢腹板的一个波长;t2D为正交各向异性板的等效厚度.
以截面对x轴的轴向刚度为等效方程可得
EAxx,3D=Exlt2D,
(3)
式中,Axx,3D为波形钢腹板一个波长的面积.
由式(2)和(3)可得正交各向异性板等效厚度t2D与局部坐标系下x方向等效弹性模量Ex的表达式:
(4)
(5)
对于Ey,可以利用位移等效原则,分别在图3所示波形钢腹板和图4所示正交各向异性板的y方向施加一个均布力P,波形钢腹板和正交各向异性板就会有y方向的位移,以二者的位移比(如式(6)所示)来计算等效的正交各向异性板在局部坐标系下沿y轴方向的等效弹性模量Ey(如式(7)所示):
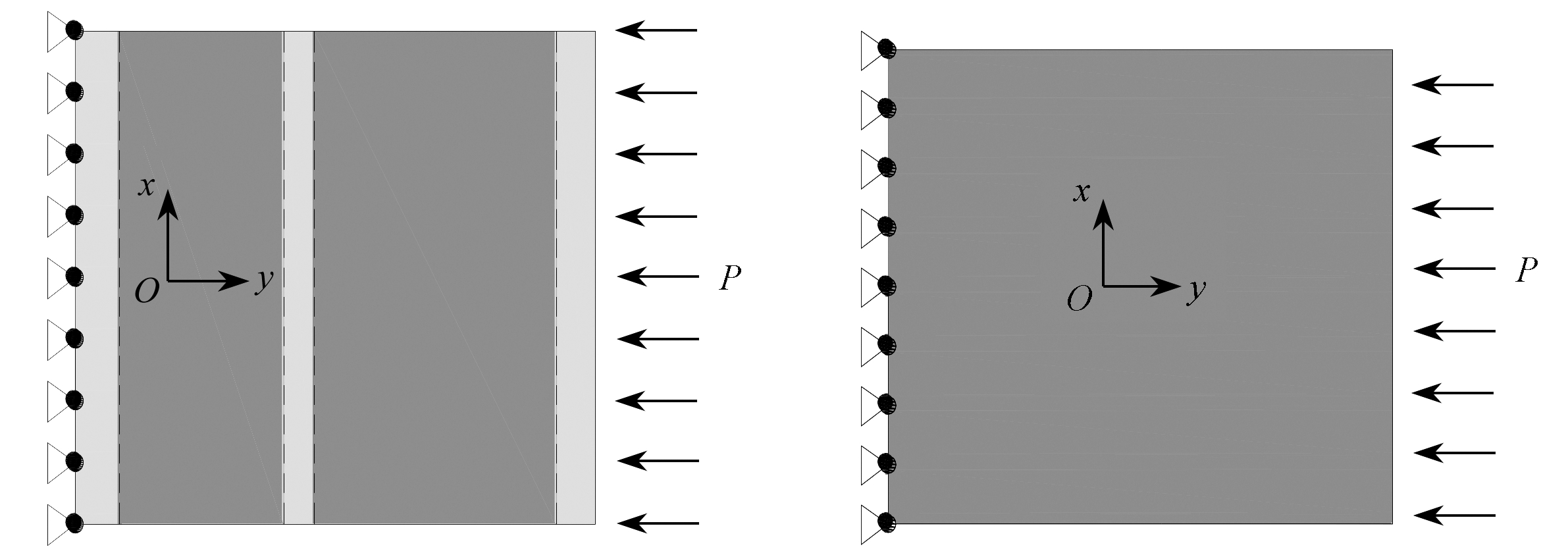
图3 波形钢腹板的加载和边界条件 图4 二维正交各向异性板的加载和边界条件
Fig. 3 Loading and boundary conditions for corrugated steel webs Fig. 4 Loading and boundary conditions for 2D orthotropic plates
(6)
(7)
式中,Δy,3D为波形钢腹板在轴向荷载作用下的位移;Δy,flat为等效正交各向异性板在轴向荷载作用下的位移,req为波形钢腹板在轴向荷载作用下的位移与等效正交各向异性板在轴向荷载作用下的位移之比.
在如图5所示的示意图中,取半个波长进行研究,半个波长由平板段(长度为a)和两个斜板段(水平长度为b/2)组成.轴向位移计算公式如下:
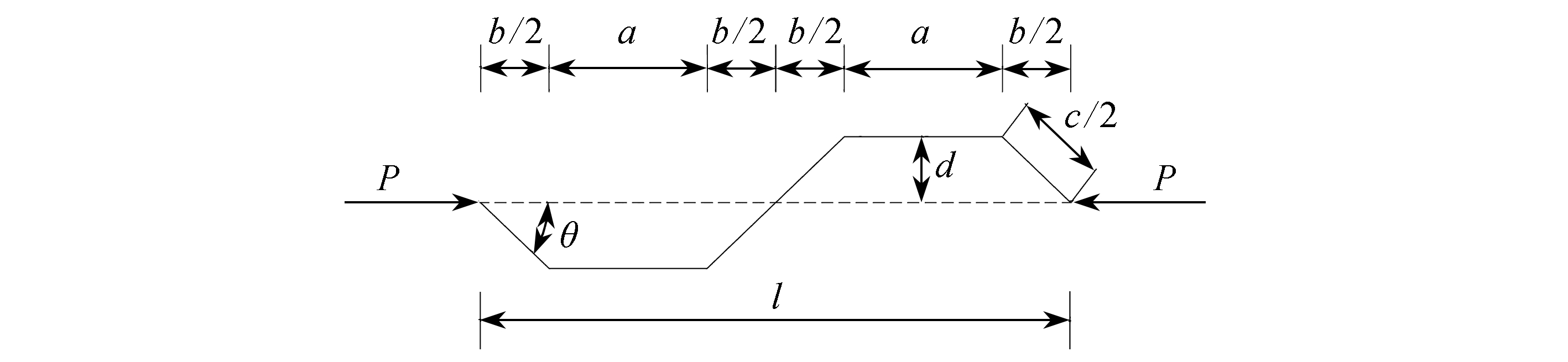
图5 波形钢腹板位移计算示意图
Fig. 5 Schematic diagram for calculating displacements of corrugated steel webs
(8)
式中,M为弯矩;N为轴力;δ为位移;A为波形钢腹板的截面面积;I为波形钢腹板的截面惯性矩.
平板段a由荷载P引起的弯矩和轴力如下:
Ma=Pd,
(9)
Na=P.
(10)
将式(9)和(10)代入位移计算公式,可得平板段a的位移:
(11)
斜板段b由荷载P引起的弯矩和轴力如下:
Mb=Pysinθ,
(12)
Nb=Pcosθ.
(13)
将式(12)和(13)代入位移计算式(8),可得斜板段b的位移:
(14)
一个波长的波形钢腹板的轴向位移由两倍的平板段和斜板段位移组成:
Δ3D=2(δa+δb).
(15)
根据材料力学知识,等效正交各向异性板在轴向荷载作用下的位移为
(16)
式中,h为等效正交各向异性板的高度.
将式(15)和(16)代入式(6)可得
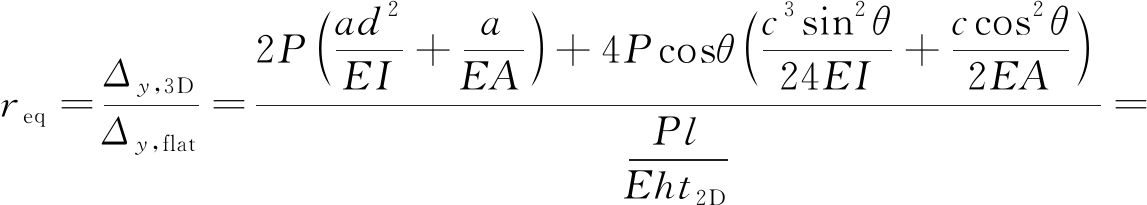
(17)
等效剪切模量为
Gxyt2D=Gt.
(18)
根据文献[17]知,剪切模量G、弹性模量E与Poisson比ν三者之间的关系为
(19)
由式(18)和(19)可得
(20)
由于波形钢腹板的特殊构造,将其等效为正交异性平板后Poisson比νxy与νyx假设为0.至此,式(1)中的正交各向异性板单元刚度矩阵中的各个变量已经通过等效原则全部求出,将求得的变量代入有限元软件中,便可以进行动力特性分析.
2 算 例 分 析
为验证等效建模方法的正确性,将三维波形钢腹板模型的自振频率计算结果、等效为正交各向异性板模型的自振频率计算结果以及试验实测频率值进行对比.
算例选取文献[18]中的两跨波形钢腹板组合箱梁试验梁,试验梁按实桥尺寸进行1∶10缩尺制作(如图6所示).试验梁为3 m+3 m的波形钢腹板连续箱梁桥,梁截面高度为0.35 m,混凝土顶板宽度为1.35 m,混凝土底板宽度为0.65 m,顶板悬臂段长度为0.35 m,腹板高度为0.285 m,共设3道支座横隔板和4道中横隔板.波形钢腹板的厚度为1.2 mm.波形钢腹板的材料特性通过力学试验获得,其屈服应力为296 MPa,Poisson比为0.3,弹性模量为210 GPa.上、下翼板混凝土的28 d测得抗压强度的平均值为51.2 MPa,Poisson比为0.2,弹性模量为34.5 GPa.
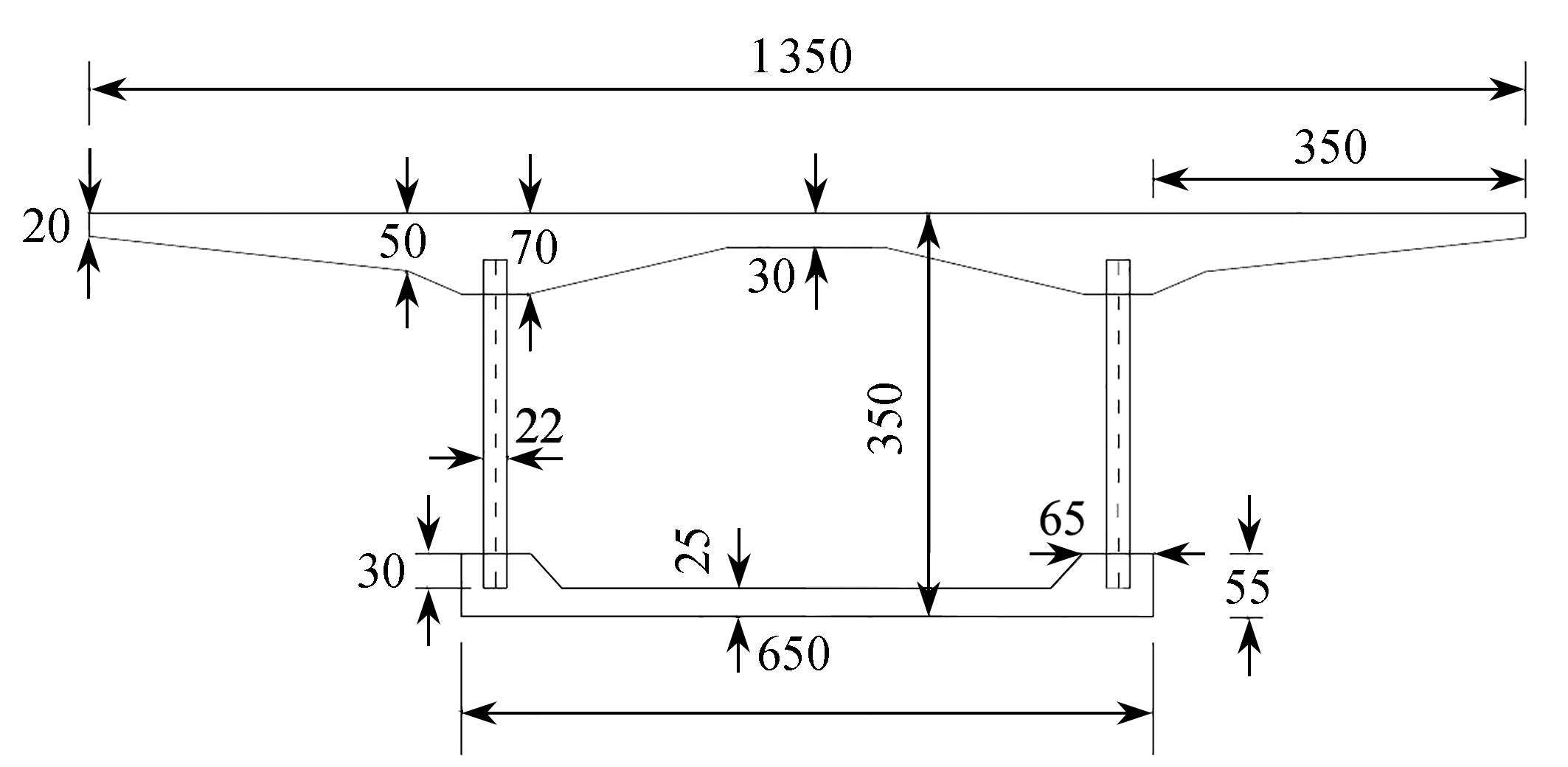
图6 连续箱梁的截面尺寸(单位: mm)
Fig. 6 Sectional dimensions of the continuous box girder (unit : mm)
分析软件采用ANSYS 18.0,波形钢腹板预应力混凝土箱梁振动特性的有限元分析模型的材料属性与室内模型试验梁的相同.波形钢腹板采用Shell63壳单元进行建模.波形钢腹板箱梁的上、下翼板和横隔板均采用八节点的Solid45实体单元进行建模.模型试验梁的端支座约束竖向位移,中支座约束纵向和竖向位移.三维波形钢腹板的ANSYS模型如图7所示.

图7 三维波形钢腹板的ANSYS模型 图8 等效正交各向异性板的ANSYS模型
Fig. 7 The ANSYS model for 3D corrugated steel webs Fig. 8 The ANSYS model for the equivalent orthotropic plate
根据本文提出的等效方法,求得的等效正交各向异性板的厚度t2D为0.032 m,Ex为7 922 MPa,Ey为6.38 MPa,Gxy为2 977 MPa,输入到等效正交各向异性板的有限元模型中对自振频率和振型进行求解,等效正交各向异性板的ANSYS模型如图8所示.
分别对三维波形钢腹板组合箱梁有限元模型和二维等效正交各向异性板组合箱梁的有限元模型进行模态分析,振动频率与实测结果的对比如表1所示,振型特征如图9所示.

(a) 三维模型的一阶振型 (b) 二维等效模型的一阶振型
(a) The 1st-order mode shape in the 3D model (b) The 1st-order mode shape in the 2D equivalent model

(c) 三维模型的二阶振型 (d) 二维等效模型的二阶振型
(c) The 2nd-order mode shape in the 3D model (d) The 2nd-order mode shape in the 2D equivalent model

(e) 三维模型的三阶振型 (f) 二维等效模型的三阶振型
(e) The 3rd-order mode shape in the 3D model (f) The 3rd-order mode shape in the 2D equivalent model

(g) 三维模型的四阶振型 (h) 二维等效模型的四阶振型
(g) The 4th-order mode shape in the 3D model (h) The 4th-order mode shape in the 2D equivalent model

(i) 三维模型的五阶振型 (j) 二维等效模型的五阶振型
(i) The 5th-order mode shape in the 3D model (j) The 5th-order mode shape in the 2D equivalent model

(k) 三维模型的六阶振型 (l) 二维等效模型的六阶振型
(k) The 6th-order mode shape in the 3D model (l) The 6th-order mode shape in the 2D equivalent model

(m) 三维模型的七阶振型 (n) 二维等效模型的七阶振型
(m) The 7th-order mode shape in the 3D model (n) The 7th-order mode shape in the 2D equivalent model

(o) 三维模型的八阶振型 (p) 二维等效模型的八阶振型
(o) The 8th-order mode shape in the 3D model (p) The 8th-order mode shape in the 2D equivalent model
图9 振型对比
Fig. 9 Comparison of mode shapes
表1 模型试验梁的自振频率实测值与ANSYS有限元值的比较(单位: Hz)
Table 1 Comparison of measured natural vibration frequency values with ANSYS finite element results of the model girder (unit: Hz)
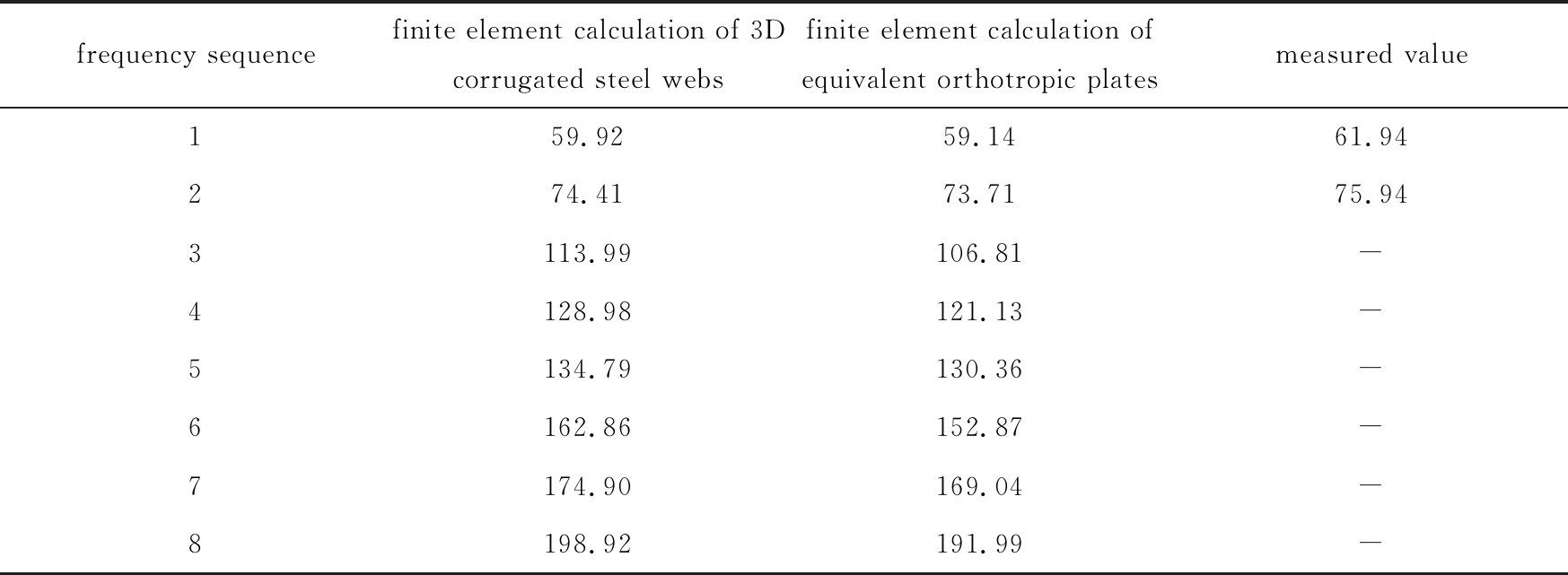
frequency sequencefinite element calculation of 3D corrugated steel websfinite element calculation of equivalent orthotropic platesmeasured value159.9259.1461.94274.4173.7175.943113.99106.81-4128.98121.13-5134.79130.36-6162.86152.87-7174.90169.04-8198.92191.99-
从表1可以看出,三维波形钢腹板组合箱梁振动频率的有限元计算结果、二维等效正交各向异性板的组合箱梁振动频率的有限元计算结果以及实测振动频率三者吻合良好,验证了本文提出的建模方法的可靠性.
从图9可以看出,三维波形钢腹板组合箱梁振型的有限元分析结果和二维等效正交各向异性板的组合箱梁振型的有限元分析结果吻合良好,验证了本文提出的建模方法的可靠性.
将三维波形钢腹板组合箱梁有限元模型和二维等效正交各向异性板的组合箱梁有限元模型所需的Shell63单元和Solid45单元进行对比分析,如表2所示.
表2 三维波形钢腹板有限元模型与等效有限元模型的单元数量对比
Table 2 The comparison of element numbers between the 3D web model and the 2D web model

modeling methodANSYS finite element model3D corrugated steel web2D equivalent orthotropic plateselement typeShell63Solid45Shell63Solid45elember number1 78813 8923043 344
由表2可以看出,将三维波形钢腹板等效为二维正交各向异性板的有限元模型后,大大降低了所需的单元数量,极大地简化了有限元模型,Shell63单元减少1 484个,Solid45单元减少10 548个,从而大大减少了计算时间,提高了计算效率.
3 结 论
1) 本文将三维的波形钢腹板有限元模型通过刚度等效与位移等效的方法,简化为二维正交各向异性板的有限元模型.将三维波形钢腹板组合箱梁有限元计算的自振频率、二维等效正交各向异性板组合箱梁有限元计算的自振频率以及实测自振频率进行对比,发现三者吻合良好,验证了本文提出的波形钢腹板组合箱梁建模方法的可靠性.
2) 等效之后的有限元模型几何外形简单,单元和自由度的数量将大幅降低,大大减少了计算时间,提高了计算效率.
3) 简化之后的建模方法使求解工程中的特大桥梁的自振特性变得极为简便,减少了建模的工作量,可为工程中波形钢腹板组合箱梁的振动频率和振型的分析提供一种简便的方法.
[1] NIN J G, ZHU Y J, TAO M X, et al. Optimized prestressed continuous composite girder bridges with corrugated steel webs[J].Journal of Bridge Engineering, 2017,22(2): 1-17.
[2] ELGAALY M, HAMILTON R W, SESHADRI A. Shear strength of beams with corrugated webs[J].Journal of Structural Engineering, 1997,122(4): 390-398.
[3] ELGAALY M, SESHADRI A, HAMILTON R W. Bending strength of steel beams with corrugated webs[J].Journal of Structural Engineering, 1997,123(6): 772-782.
[4] SAMANTA A, MUKHOPADHYAY M. Finite element static and dynamic analyses of folded plates[J].Engineering Structural, 1999,21: 277-287.
[5] SAYED-AHMED E Y. Lateral torsion-flexure buckling of corrugated web steel girders[J].Structural and Buildings, 2005,158(1): 53-69.
[6] GUO T, SANSE R. Analysis of local elastic shear buckling of trapezoidal corrugated steel webs[J].Journal of Constructional Steel Research, 2014,102: 59-71.
[7] AGGARWAL K, WU S, PAPANGELIS J. Finite element analysis of local shear buckling in corrugated web beams[J].Engineering Structures, 2018,162: 37-50.
[8] 冀伟, 蔺鹏臻, 刘世忠. 波形钢腹板PC组合箱梁桥的挠度计算与分析[J]. 西南交通大学学报, 2018,53(1): 46-55.(JI Wei, LIN Pengzhen, LIU Shizhong. Deflection calculation and analysis of PC box girder bridges with corrugated steel webs[J].Journal of Southwest Jiaotong University, 2008,53(1): 46-55.(in Chinese))
[9] JI W, DENG L, LIU S H. Study of vertical bending vibration behavior of continuous prestressed concrete box girders with corrugated steel webs[J].Advances in Structural Engineering, 2016,19(6): 953-965.
[10] 冀伟, 邓露, 刘世忠, 等. 多跨等截面波形钢腹板PC连续箱梁桥竖向弯曲振动频率的计算[J]. 振动与冲击, 2016,35(18): 140-146.(JI Wei, DENG Lu, LIU Shizhong, et al. Calculation of the vertical bending vibration frequencies of multi-span PC continuous box girder bridge with corrugated steel webs of uniform cross-section[J].Journal of Vibration and Shock, 2016,35(18): 140-146.(in Chinese))
[11] 冀伟, 邓露, 何维, 等. 波形钢腹板PC简支箱梁桥局部与整体动力冲击系数的计算分析[J]. 振动与冲击, 2017,36(8): 22-28.(JI Wei, DENG Lu, HE Wei, et al. Local and global impact factors analysis for PC box girder bridges with corrugated steel webs[J].Journal of Vibration and Shock, 2017,36(8): 22-28.(in Chinese))
[12] 郑尚敏, 万水, 程海根. 单箱多室波形钢腹板组合箱梁动力特性研究[J]. 铁道工程学报, 2017,34(9): 41-46.(ZHENG Shangmin, WAN Shui, CHENG Haigen. Research on the dynamic characteristics of multi-room single box composite girder with corrugated steel webs[J].Journal of Railway Engineering Society, 2017,34(9): 41-46.(in Chinese))
[13] 李丽园, 周茂定, 冀伟, 等. 基于剪切附加挠度的波形钢腹板组合箱梁挠度计算[J]. 东南大学学报(自然科学版), 2019,49(2): 296-302.(LI Liyuan, ZHOU Maoding, JI Wei, et al. Deflection calculation of composite box girder with corrugated steel webs based on shear additional deflection[J].Journal of Southeast University(Natural Science Edition), 2019,49(2): 296-302.(in Chinese))
[14] 李立峰, 周聪, 王连华, 等. 基于纽玛克法的变截面波形钢腹板组合箱梁畸变效应分析[J]. 中国公路学报, 2018,31(6): 217-226.(LI Lifeng, ZHOU Cong, WANG Lianhua, et al. Analysis on distortion effect of non-prismatic composite box girders with corrugated steel webs based on Newmark method[J].Chinese Journal of Highway and Transport, 2018,31(6): 217-226.(in Chinese))
[15] 刘保东, 胥睿, 李祖硕, 等. 内衬混凝土对波形钢腹板刚构桥扭转和畸变性能的影响[J]. 中国铁道科学, 2017,38(3): 31-39.(LIU Baodong, XU Rui, LI Zushuo, et al. Impact of inner lining concrete on torsion and distortion performance of continuous rigid frame bridge with corrugated steel webs[J].China Railway Science, 2017,38(3): 31-39.(in Chinese))
[16] 邵江艳, 张元海, 赵庆友, 等. 波形钢腹板箱梁畸变应力分析[J]. 应用数学和力学, 2019,40(10): 1109-1121.(SHAO Jiangyan, ZHANG Yuanhai, ZHAO Qingyou, et al. Stress analysis on distortion of corrugated steel web box girders[J].Applied Mathematics and Mechanics, 2019,40(10): 1109-1121.(in Chinese))
[17] 徐芝纶. 弹性力学[M]. 北京: 高等教育出版社, 2016.(XU Zhilun.Elasticity[M]. Beijing: Higher Education Press, 2016.(in Chinese))
[18] 冀伟, 刘世忠, 蔺鹏臻. 波形钢腹板PC连续箱梁桥自振频率分析与试验研究[J]. 中南大学学报(自然科学版), 2016,47(4): 1297-1304.(JI Wei, LIU Shizhong, LIN Pengzhen. Analysis and experimental study on nature vibration frequencies of PC continuous box girder bridge with corrugated steel webs[J].Journal of Central South University(Science and Technology), 2016,47(4): 1297-1304.(in Chinese))