引 言
曲流河砂岩储层物性非均质强,物性分布的方向性复杂.在油藏地质建模时,如何根据现有的井位数据建立出符合曲流河沉积特征的地质模型,这对油藏综合地质评价以及油藏数值模拟都具有重要意义.在国内,诸多学者从沉积学的角度对曲流河河道的变迁、点坝砂体内部结构解剖进行了大量研究,这些研究成果从半定性半定量化角度重建了曲流河道演化历史,使得砂体结构解剖结果更合理、更接近于地下真实情况[1-5].如文献[4-5]中采取层次模拟、试验筛选、分级预测交互方式建立点坝砂体形态,然后利用多点地质统计学方法建立了点坝内部结构模型.上述这些研究成果对构建曲流河形态及三维地质模型有重要的意义,但基于地质统计学的属性数据模拟,这些属性数据分布的趋势与变差函数有着密切的关系.
在曲流河沉积的区域,河道多次变迁、改向使得很难用变差函数来控制约束属性数据的方向.为此我们提出了Schwarz-Christoffel映射变换模型,将曲流河沿着河道映射到矩形的某一个方向,在矩形区域中按照常规地质统计学方法进行模型建立并预测属性参数.
在Schwarz-Christoffel变换方面,诸多学者做了大量的研究.文献[6-7]指出,在Schwarz-Christoffel映射数值计算时,多边形区域形状与矩形区域的形状差异大,或映射点选择不当,将导致计算速度慢,计算结果精度低.文献[8]提出了从多边形区域到矩形区域的Schwarz-Christoffel变换映射基本模型.先将多边形区域映射到上半平面两端开口的带状过渡区域,带状过渡区域的高度为1,然后借助Jacobi椭圆函数与对数函数的复合关系,将带状过渡区域边界映射到矩形区域边界.数值计算Schwarz-Christoffel变换时,存在奇异积分方程的计算.对于奇异积分方程处理时,需要借助Gauss-Jacobi积分方法进行求解.Gauss-Jacobi积分求解时的难点在于如何选择积分节点数量及积分的路径长度,文献[9-10]提出了解决办法.Schwarz-Christoffel边界映射计算都要受到边界映射点位的约束,要遵循Riemann原理.王玉风等根据根文献[11]对实参数的变换方法,结合文献[8]的变换思想,建立复参数与实参数的变换关系,解决了映射参数的约束问题[12].
为了完成矩形区域与带状曲流河的地质建模过程,有关矩形区域边界与多边形区域边界的映射计算问题在文献[12]中已经解决,但没有提出多边形区域的内部点位与矩形区域内部点位映射计算问题的解决办法.借鉴这些学者的研究成果,借助Schwarz-Christoffel变换方法,本文将曲流河沿着河道方向映射到矩形区域,主要针对多边形区域到矩形区域内部点位映射的数值计算进行研究.从多边形区域到矩形区域映射过程中,需要借助带状过渡区域.在多边形区域到带状过渡区域映射过程中,提出了以二维PSO算法映射点位的计算方法,避免建立复杂的复参数与实参数关系.在矩形区域到带状过渡区域映射的过程中,需要计算Jacobi椭圆函数,为此提出了以Newton迭代法计算Jacobi椭圆的方法,并且提出了Newton迭代法计算Jacobi椭圆初值的确定方法.根据曲流河的特点,将带状不规则曲流河边界进行离散,形成了封闭的多边形区域.根据Schwarz-Christoffel变换的基本思想及带状曲流河形状与矩形区域形状的相似关系,将曲流河中的井位等相关参数映射到规则矩形区域中,为地质模型的建立与分析提供了理论依据.
1 基本数学原理
在复平面w上有N(N≥3)边形,它的顶点和内角分别为wj和παj(j=1,2,…,N),将T上半平面的点位映射到w平面(多角形区域),如图1所示,具体的Schwarz-Christoffel变换公式为
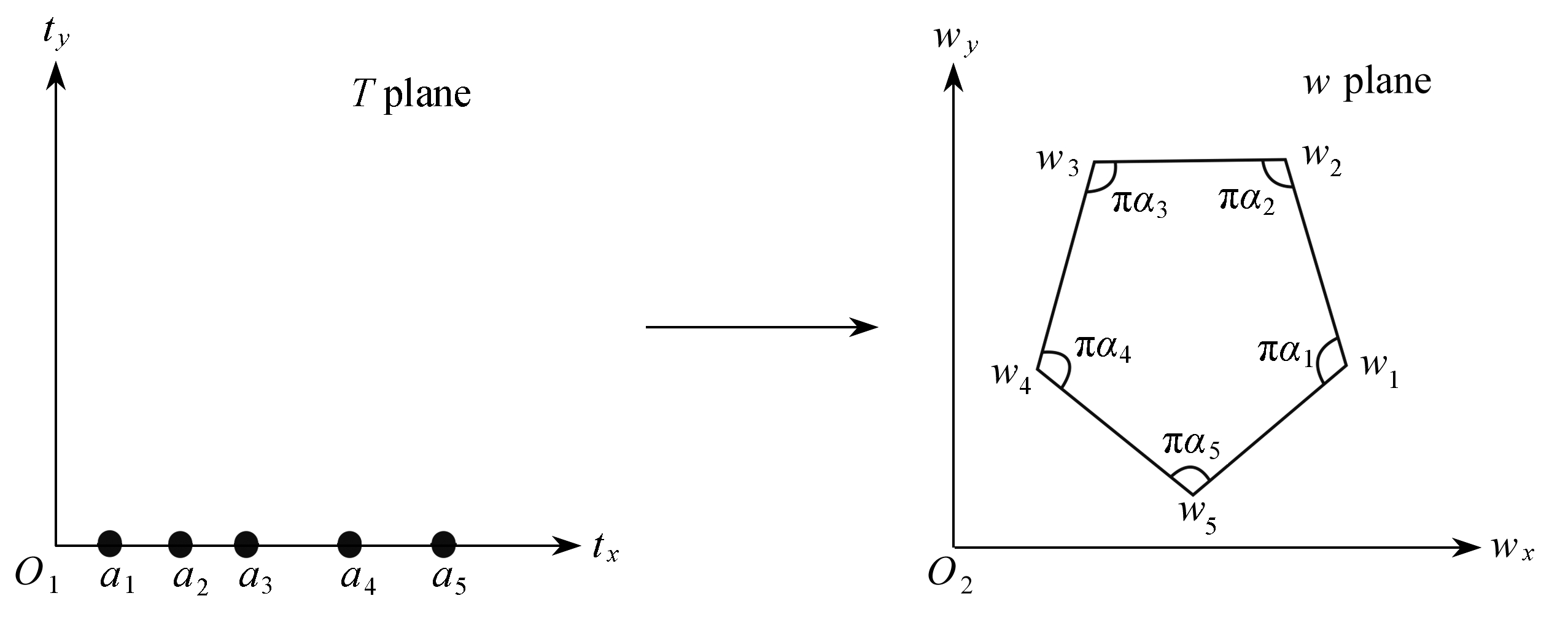
图1 上半平面到多角形区域变换示意图
Fig. 1 Schematic diagram of transformation from the upper half plane to the polygon region
(1)
其中A为伸缩系数;C为映射中心,m;παj为w平面多角形内角,rad;aj为T平面(t=tx+ity)tx轴上的点.式(1)在复变函数论各种教材中已经证明过.
在图2的z平面(z=zx+i×zy),考察函数ez/h的变换,经过函数ez/h映射变换,可以把z平面带状区域映射到T平面上半平面的第一象限.为了使z平面带状区域映射到T平面的上半平面,我们再考察函数e-z/h的变换,结合前面ez/h的变换,综合考虑映射函数:
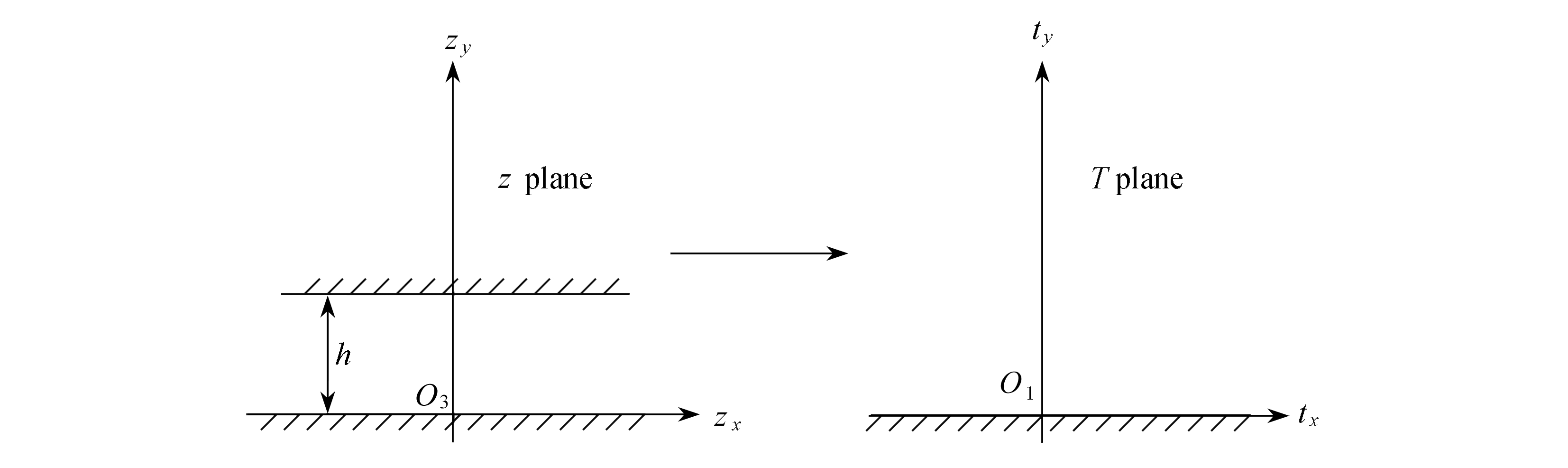
图2 带状区域到上半平面变换示意图
Fig. 2 Schematic diagram of transformation from the strip region to the upper half plane
f(t)=ez/h-e-z/h,
(2)
其中z为z平面的点,m;h为带状区域的宽度,m;i为虚数单位.
将z=zx+izy代入式(2)进行化简,同时考虑Euler公式,整理可得
f(t)=(ezx/h-e-zx/h)cos(zy/h)+i(ezx/h+e-zx/h)sin(zy/h),
(3)
因为
0≤zy/h≤1,-∞<zx/h<+∞,
所以
(ezx/h-e-zx/h)cos(zy/h)⊂(-∞,+∞), (ezx/h+e-zx/h)sin(zy/h)≥0.
即通过式(2)的映射变换,可以将z平面带状区域映射到T平面上半平面.根据双曲正弦函数的定义,式(2)又可以写成
f(t)=2sinh(z/h).
(4)
考虑Schwarz-Christoffel变换的一般形式(1),根据Riemann映射原理,可得多边形映射到带状区域的基本映射式(5).特别说明,式(5)中因子fj表达式中的i连同次幂αj-1可以直接包含在系数A中.因此将带状过渡区域z边界上的点映射到复平面w多边形区域顶点的Schwarz-Christoffel映射可表示为[8]
(5)
其中,wb(k)为多边形区域边界点,m;zb(k)为带状过渡区域边界点,m;fj(ξ)为分段函数,具体表达式如下:
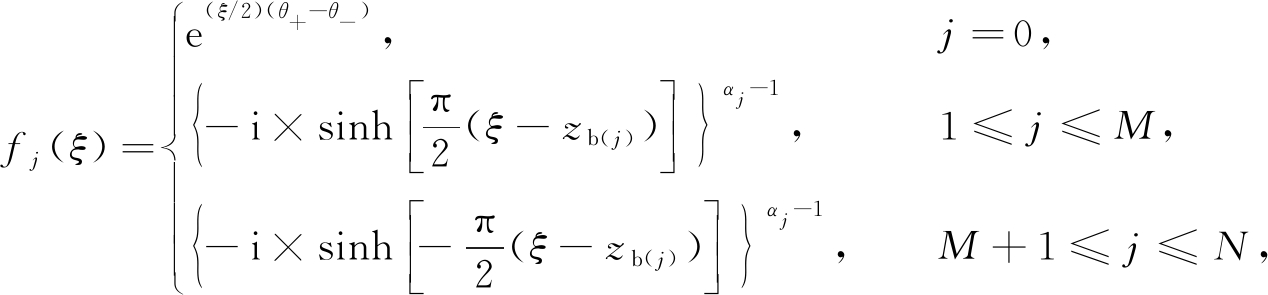
(6)
其中,M为带状过渡区域下边界点的总个数;N为复平面w多边形区域顶点的总个数;θ+为带状过渡区域左边无限远点的角度,rad,则θ+=π;θ-为带状过渡区域右边无限远点的角度,rad,则θ-=-π.
若已知矩形基本参数,即映射模量l,则矩形区域边界到带状过渡区域边界的Schwarz-Christoffel映射可表示为[8]
(7)
其中,ub(k)为矩形区域边界点位,m;l为第一类椭圆函数的映射模量,由选择映射的矩形顶点决定.关于式(5)与式(7)的计算在文献[12-13]中已有详细论述.
2 已知多边形内部点求解矩形区域内部点的映射计算
2.1 基本模型
在这个过程中,多边形到带状过渡区域以及矩形到带状过渡区域的边界的映射点、伸缩系数都必须是已知的.在上述条件下,才能根据多边形内部的点位计算对应的矩形区域内部的保形映射点位.具体计算关系可由式(8)、(9)表示.
(8)
式中,win(n)为距离wb(k)最近的多边形内部的第n个点(win(n)为已知参数),m;zin(n)为带状过渡区域内部的点位,是win(n)对应的映射点位(zb(k)为已知参数,zin(n)为待求解参数),m;下标n为多边形内部已知点的编号.
(9)
式中,uin(n)为矩形区域内部的点位(uin(n)为待求解参数),m;l为映射模量,由区域映射区域的形状确定.
2.2 求解的基本思路
首先根据文献[12]的Gauss-Jacobi计算方法,得到多边形区域到带状过渡区域边界的映射点zb(k).根据带状过渡区域边界点zb(k)与多边形区域的边界点wb(k)和内点win(n),设计一种算法求解式(8),得到带状过渡区域内点zin(n).通过合理选择矩形区域内点的初值,采用Newton法求解式(9),得到带状过渡区域内点zin(n)的近似值.比较式(8)与式(9)求解的带状过渡区域内点zin(n)之间的误差,当满足指定精度时,可停止迭代求解式(9).
要实现上述步骤,需要解决四个关键问题:第一,如何设计一种算法,能够满足式(8)的求解;第二,式(8)积分方法的路径如何选择;第三,式(8)积分路径的长度如何确定;第四,采用Newton法求解式(9)时,如何选择迭代初值.
在算法设计方面,从理论上来说,我们也可以采用文献[13]介绍过的Levenberg-Marquardt算法求解式(8).但在式(8)求解时,这种方法行不通,主要原因是在带状过渡区域中的圆弧![]() 上的点都满足条件,圆弧
上的点都满足条件,圆弧![]() 的中心点为zb(k),圆弧的半径为zb(k)到zin(n)之间的距离,如图3所示.上述这种情况导致未知参数zin(n)不唯一.由于未知参数zin(n)在二维空间带状过渡区域中取值,因此建立未知参数zin(n)的二维粒子的解空间, 这样就避免建立实参数与复参数的复杂关系, 从而简化该问题的求解.基于上述考虑, 选择普通PSO算法[14-17]作为求解式(8)的方法.
的中心点为zb(k),圆弧的半径为zb(k)到zin(n)之间的距离,如图3所示.上述这种情况导致未知参数zin(n)不唯一.由于未知参数zin(n)在二维空间带状过渡区域中取值,因此建立未知参数zin(n)的二维粒子的解空间, 这样就避免建立实参数与复参数的复杂关系, 从而简化该问题的求解.基于上述考虑, 选择普通PSO算法[14-17]作为求解式(8)的方法.

图3 积分起点zb(k)与未知参数zin(n)的几何关系图
Fig. 3 The geometric relationship between integral starting pointzb(k)and unknown parameterzin(n)
在积分路径及积分路径长度的选择方面,式(8)积分的路径是从带状过渡区域边界的已知点zb(k)到该区域内点zin(n),积分路径是两点的连线,该路径只有一个奇点,即带状过渡区域边界点.若Gauss-Jacobi积分的路径太长,则需要增加积分的节点,积分节点数量太多,则计算需要花时间.对于该问题的处理,我们采用两个途径进行解决,一个是参见文献[13]的处理方法,将积分路径适当的缩短,另一个是在多边形区域中寻找要映射的点win(n)距多边形区域边界最近的点wb(k),将点wb(k)在带状过渡区域中的映射点zb(k)作为积分的起点,如图4所示,这样就可以适当减小积分路径长度.
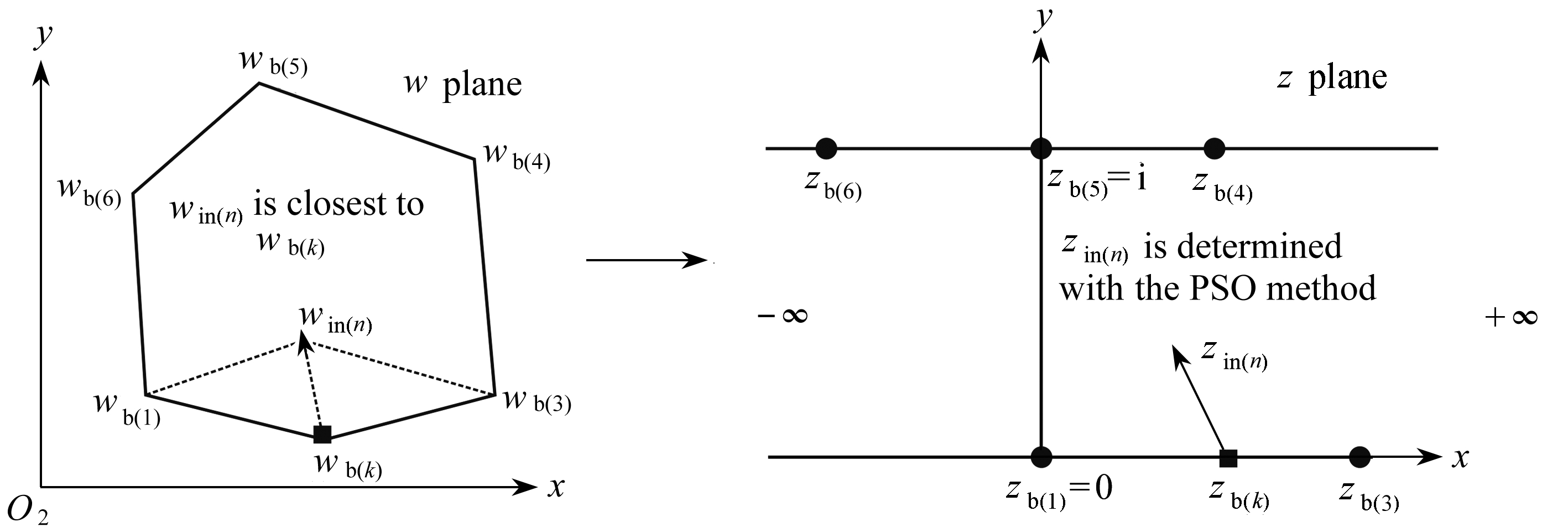
图4 积分起点zb(k)的选择方法
Fig. 4 The selection method for integral starting pointzb(k)
采用Newton迭代法求解式(9),初值选择方案如图5所示.首先将带状过渡区域边界及内部点位向下平移0.5个单位;然后根据带状过渡区域边界与矩形区域边界的对应关系进行边界长度的缩放,如图5所示.

图5 复参数Jacobi椭圆函数初值确定方法
Fig. 5 The method for determining initial values of Jacobi elliptic functions with complex parameters
具体初值确定步骤如下:
第一步 带状过渡区域内点的平移
zinm(n)=Re(zin(n))+[Im(zin(n))-0.5]×i,
(10)
其中,zinm(n)为带状过渡区域内点平移后的点位,m.
第二步 坐标旋转
(11)
其中,zinr(n)为带状过渡区域内点旋转90°后的点位,m.
第三步 缩放变换
x=2k×[Re(zinr(n))-0.5]+k,
(12)
(13)
z′in(n)=x+y×i,
(14)
其中,z′in(n)为复参数Jacobi椭圆函数的初值,m;k为矩形宽度的一半,m;kP为矩形的高度,m.k和kP的计算根据文献[6]确定.
3 映射模型的缩放比例问题研究
3.1 矩形顶点选择方法的约定
根据多边形边界的形状,将多边形边界映射到矩形边界时,首先在多边形边界上选择两点,这两点被映射为矩形长边的两个顶点,然后在多边形边界选择其他两点,这两点被映射为矩形短边的两个顶点.选择的这四个点在多边形区域中的形状尽可能与矩形区域的形状匹配.基于以上考虑,规定选择的这四点的编号依次为第一顶点、第二顶点、第三顶点和第四顶点.
3.2 多边形区域到带状过渡区域的映射比例的确定
根据油藏边界到带状过渡区域边界的对应关系,多边形边界上选择的第一顶点到第二顶点之间点被映射到带状过渡区域的下边界,多边形边界上选择的第三顶点到第四顶点之间点被映射到带状过渡区域的上边界.在映射的过程中,第一顶点被映射为带状过渡区域的坐标原点.根据上述的映射对应关系,记多边形边界选择的第一顶点到第二顶点之间所有的点相邻两点之间的距离之和为L1,记多边形边界选择的第三顶点到第四顶点之间所有的点相邻两点之间的距离之和为L2,将L1与L2的平均值作为带状过渡区域x方向的伸缩系数.同理,记多形边界选择的第二顶点到第三顶点之间所有的点相邻两点之间的距离之和为L3,记多边形边界选择的第三顶点到第四顶点之间所有的点相邻两点之间的距离之和为L4,将L3与L4的平均值作为带状过渡区域y方向的伸缩系数.
3.3 带状过渡区域到矩形区域的映射比例的确定
根据图5的映射对应关系可知,带状过渡区域上下边界与矩形区域的高度对应,带状过渡区域的高度与矩形区域的宽度对应.计算完全第一类椭圆函数可得矩形的高度kP和宽度2k.第一类完全椭圆函数数值积分具体的计算方法参见文献[18].
4 实 例 分 析
4.1 X油藏基本情况
X油田于2000年被发现,位于鄂尔多斯盆地,其勘探开发主要经历了三个阶段,第一阶段1.5×105t方案编制实施、第二阶段全油田2.0×105t方案编制实施滚动增储上产、第三阶段全油田5.0×105t产能方案编制及实施.到2017年7月,X油田砂岩油藏共钻井78口,其中直井50口,水平井28口,目前采油井70口,累积采油2.448×105m3.2006年8月开始注水,目前注水井8口,累积注水6.68×104m3.
4.2 曲流河边界到矩形油藏边界映射的计算
1) 矩形油藏边界顶点的选择
根据X砂岩油藏沉积相分布情况,确定油藏的边界,并将油藏的边界进行离散.X砂岩油藏边界及井位分布如图6所示.根据图6油藏边界的形状,按照3.1小节的方法确定矩形油藏边界四个顶点,在图6中用正方形点表示,即第一顶点为37号点,第二顶点为16号点,第三顶点为17号点,第四顶点为36号点.
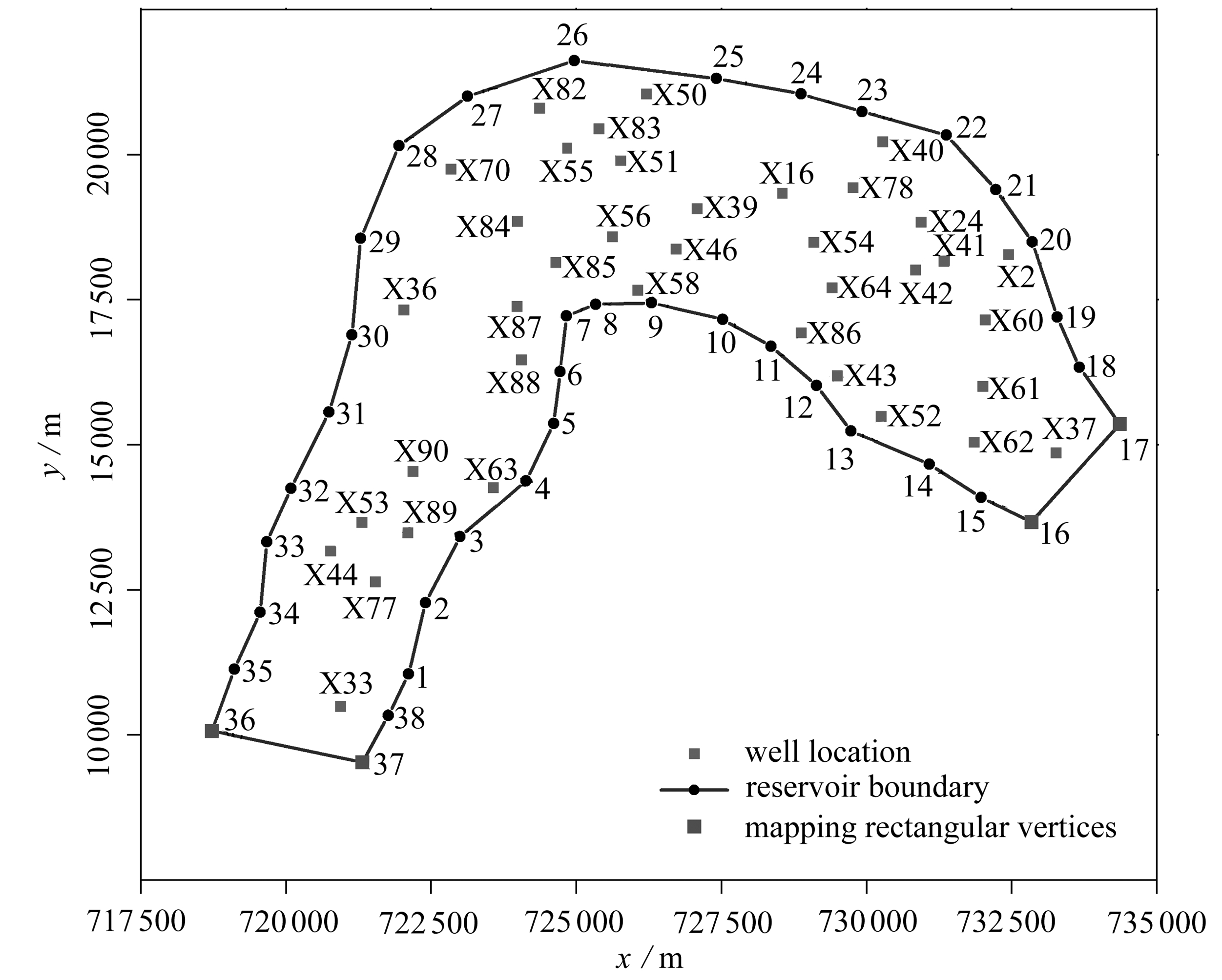
图6 油藏边界映射为矩形区域的顶点选择结果
Fig. 6 Vertex selection results of the reservoir boundary mapping to a rectangular region
2) 计算过程中的参数设置
根据文献[12]的求解思路,通过MATALAB软件平台编写相关程序,在计算过程中,具体的参数设置见表1.
表1 从油藏的多边形边界到矩形边界点位映射计算的参数设置
Table 1 Parameter settings for point mapping calculation from the polygon boundary of reservoir to the rectangular boundary

itemparameter valueremarknode number of Gauss-Jacobi integration NGJImax{-lg(εabs),8}εabs is the absolute error of the integral equationabsolute error of integral equation εabs1.00×10-10parameter ρ0.5parameter ρ in the Levenberg-Marquardt algorithmparameter σ0.4parameter σ in the Levenberg-Marquardt algorithmmaximum number of iterations of Levenberg-Marquardt algorithm NMLM200less than 50 timesabsolute error of Jacobi elliptic function calculation εJ1.00×10-10number of iterations of Jacobi elliptic function NJEF50
3) 多边形区域边界到矩形区域边界点位的计算结果
根据映射模量的计算方法,计算出图6的映射模量为5.577 054.根据文献[13]积分路径的确定方法,采用Gauss-Jacobi积分方法计算式(5)的积分,按照Levenberg-Marquardt算法计算式(5)的方程组,得到带状过渡区域边界映射点位和矩形区域边界点位的分布情况,如图7所示.计算得到的伸缩系数A为3.93×106+1.29×106×i.图7(a)中带状过渡区域的下边界37~16号点被映射到矩形油藏高度的一条边上,图7(b)中带状过渡区域的高度方向被映射到矩形区域油藏的宽度方向,但是没有考虑实际油藏与映射后油藏的缩放比例.
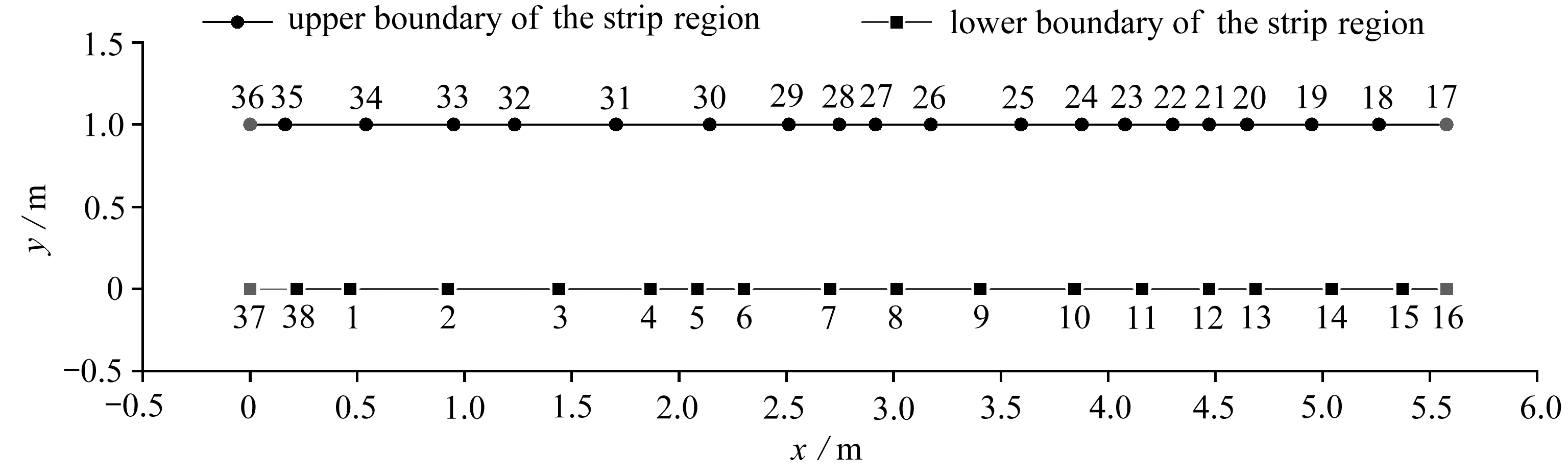
(a) 带状过渡区域边界映射点位分布情况
(a) Point distributions of boundary mapping in the strip transition region
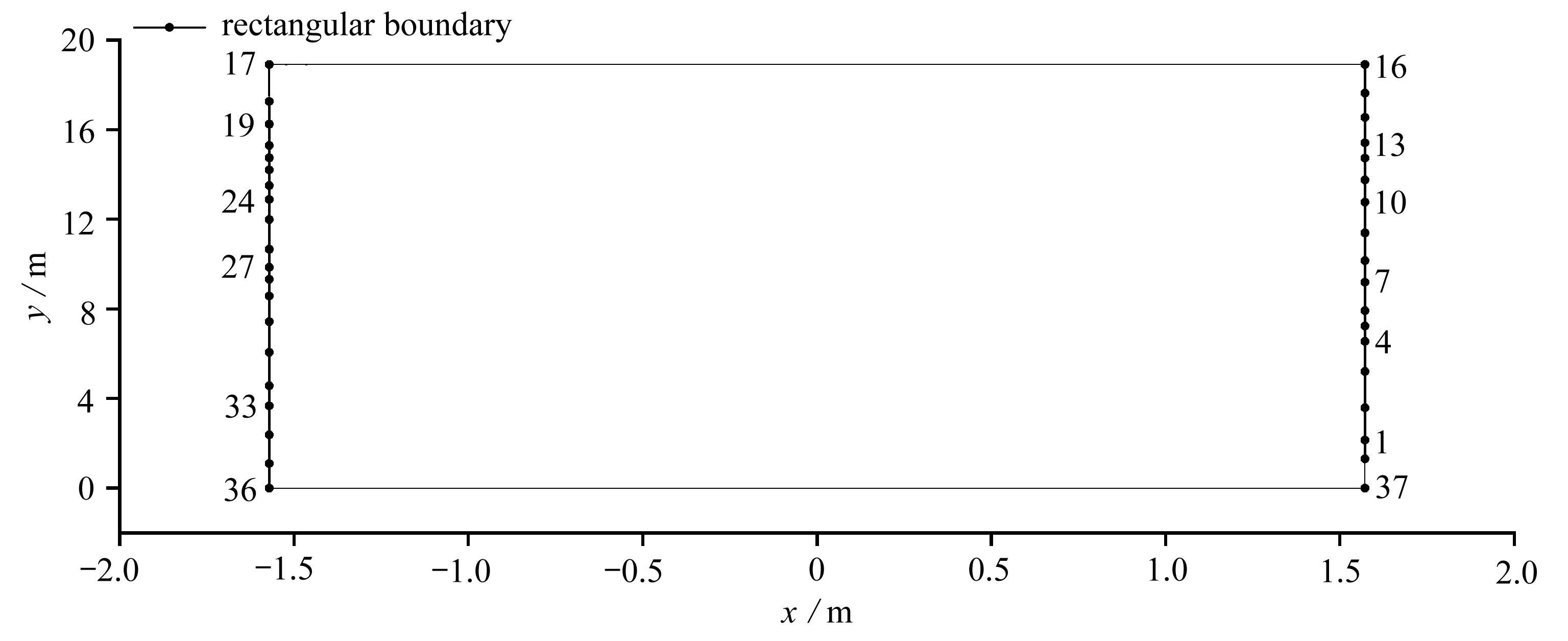
(b) 矩形油藏边界映射点位分布情况(不考虑缩放比例情况)
(b) Locations of boundary points in the rectangular reservoir(regardless of scaling ratios)
图7 油藏边界-带状过渡区域边界-矩形边界映射图
Fig. 7 Mapping of the reservoir boundary, the strip transition region boundary and the rectangular boundary
4) 精度评定结果
Levenberg-Marquardt算法对积分方程迭代计算的绝对误差与迭代次数的关系如图8曲线1所示.在迭代前11次中,迭代次数与绝对误差呈线性关系下降.迭代次数从11到29次时,绝对误差下降缓慢,下降到10-2数量级,但迭代次数达到30次以后,绝对误差下降很快,说明在接近真值的局部范围内,Levenberg-Marquardt算法在计算多边形区域到带状过渡区域边界Schwarz-Christoffel变换中效率很高.在X油藏实例的计算中,采用Levenberg-Marquardt算法计算积分方程(5)的绝对误差达到6.959×10-14.
Newton法计算复参数Jacobi椭圆函数的绝对误差与迭代次数的关系如图8曲线2所示.从曲线2中可以看出Newton迭代法计算的效率很高,在迭代5次时,边界上38个点的绝对误差达到10-14数量级.主要原因是Jacobi椭圆函数的导函数是存在的, 在计算区域中不存在奇点.采用Newton法计算Jacobi椭圆函数的绝对误差达到1.776×10-15.最后通过综合精度评价,得出整理映射计算的绝对误差为6.451×10-10.
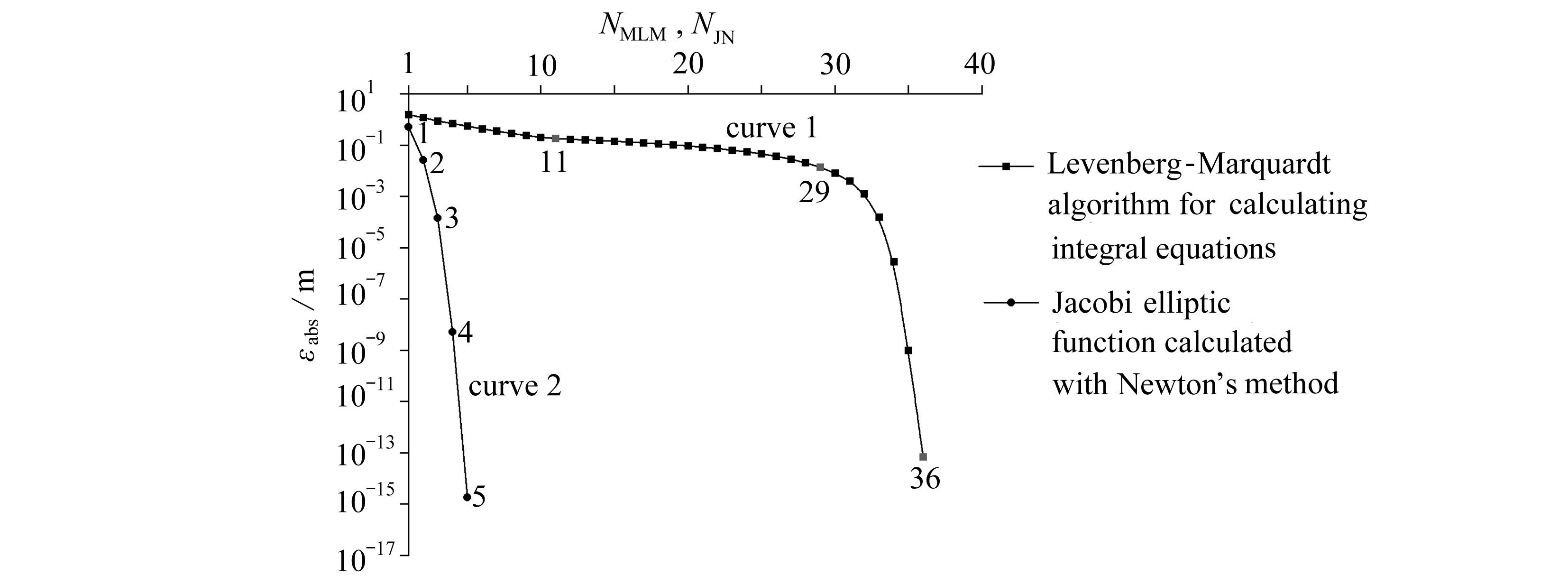
图8 油藏边界-带状过渡区域-矩形边界映射计算绝对误差与迭代次数关系
Fig. 8 The relationships between mapping computational absolute errors and iteration times of the reservoir boundary, the strip transition region and the rectangular boundary
4.3 曲流河油藏中的井位到矩形油藏边界中的井位映射计算
本小节主要解决实际油藏中的井位到矩形区域映射位置的计算问题.本小节计算的油藏数据来源于4.1小节,映射参数来源于4.2小节.
1) 参数设置
根据本文提出的求解思路,通过MATALAB软件平台编写相关程序,在计算过程中,具体的参数设置见表2.
表2 从油藏内部井位到矩形区域点位映射计算的参数设置
Table 2 Parameter settings for mapping calculation from wellbore locations in reservoir to point locations in the rectangular region

itemparameter valueremarkabsolute error for PSO algorithm εPSO1.00×10-10termination conditions for PSO algorithm calculationnumber of iterations of PSO algorithm NPSO500number of swarm of PSO algorithm NNS100particle dimension of PSO algorithm Pd2the band transition area is two-dimensionalparticle range of PSO algorithm Prmin(Re(z))-L×0.5max(Im(z))+L×0.5[0,1]z is the boundary point of the strip transition region, L is the length of the strip transition region, Re(z) is the real part of z, Im(z) is the imaginary part of znonlinearly decreasing parameter in PSO algorithm a1, a20.95, 0.4maxw and minw are decreasing parameters of concave functionsinertia weight coefficient of PSO algorithm C1, C22, 2number of iterations of Jacobi elliptic function calculated with Newton’s method NJN50absolute error of Jacobi elliptic function iteration εJ1.00×10-10
2) 带状过渡区域中井位的计算结果
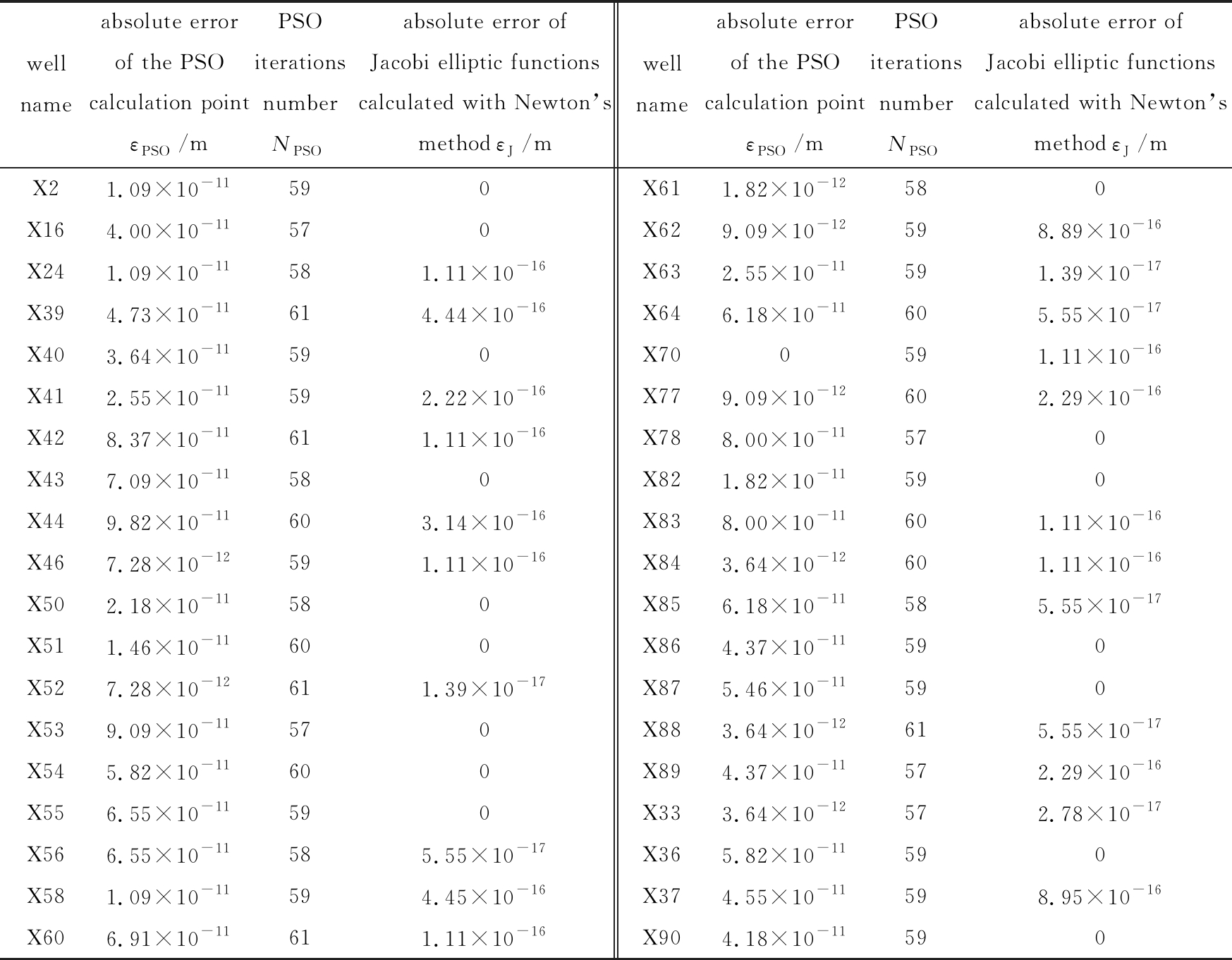
通过上述计算得到带状过渡区域中38口井的井位,如图9所示.从图9可以看出,研究区域的38口井的井位与图6中映射前的井位具有一定的几何相似形.从多边形区域到带状过渡区域映射的计算过程中,采用前面所提出的PSO算法,计算的精度见表3.通过表3中的第三、第七列可以看出,在设定积分方程点位精度为10-10m情况下,迭代次数没有超过设定500次,最大的PSO迭代次数61次.通过表3可以看出,在不考虑缩放比例情况下,计算出X砂岩油藏的井位在带状过渡区域中的点位绝对误差在10-11m以下.这样的精度是能够满足工程计算的需要,同时也说明本文所给出的PSO算法求解积分方程(7)是可行的.
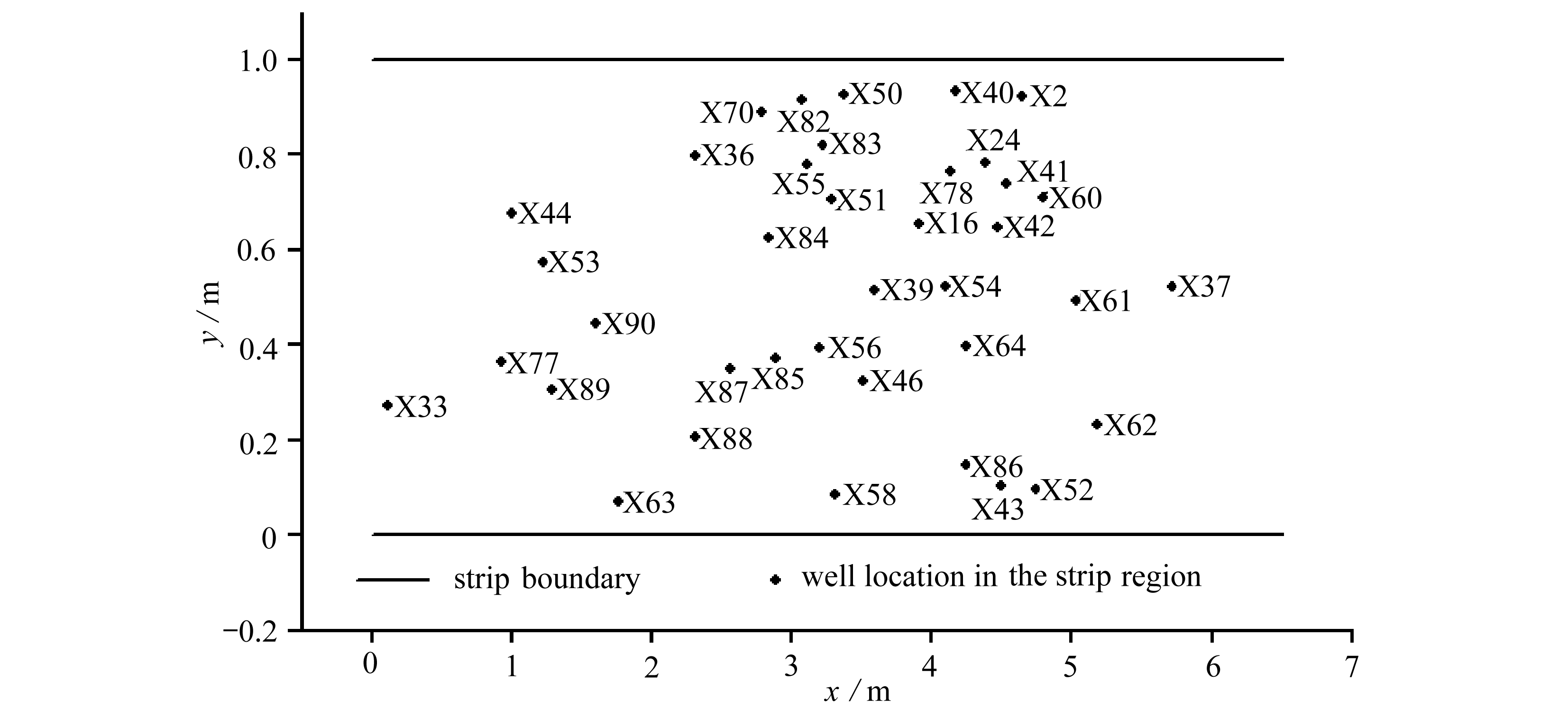
图9 从油藏内部井位到带状过渡区域映射井位分布图
Fig. 9 Mapping of well location distributions from internal well locations in the reservoir to the strip transition region
表3 PSO算法求解积分方程与Newton法求解Jacobi椭圆函数绝对误差数据表
Table 3 The absolute error data table of the PSO algorithm for solving integral equations and Newton’s method for solving Jacobi elliptic functions
well nameabsolute error of the PSO calculation point εPSO/mPSO iterations numberNPSOabsolute error of Jacobi elliptic functions calculated with Newton’s method εJ/mwell nameabsolute error of the PSO calculation point εPSO/mPSO iterations numberNPSOabsolute error of Jacobi elliptic functions calculated with Newton’s method εJ/mX21.09×10-11590X611.82×10-12580X164.00×10-11570X629.09×10-12598.89×10-16X241.09×10-11581.11×10-16X632.55×10-11591.39×10-17X394.73×10-11614.44×10-16X646.18×10-11605.55×10-17X403.64×10-11590X700591.11×10-16X412.55×10-11592.22×10-16X779.09×10-12602.29×10-16X428.37×10-11611.11×10-16X788.00×10-11570X437.09×10-11580X821.82×10-11590X449.82×10-11603.14×10-16X838.00×10-11601.11×10-16X467.28×10-12591.11×10-16X843.64×10-12601.11×10-16X502.18×10-11580X856.18×10-11585.55×10-17X511.46×10-11600X864.37×10-11590X527.28×10-12611.39×10-17X875.46×10-11590X539.09×10-11570X883.64×10-12615.55×10-17X545.82×10-11600X894.37×10-11572.29×10-16X556.55×10-11590X333.64×10-12572.78×10-17X566.55×10-11585.55×10-17X365.82×10-11590X581.09×10-11594.45×10-16X374.55×10-11598.95×10-16X606.91×10-11611.11×10-16X904.18×10-11590
3) 矩形区域中井位的计算结果及精度分析
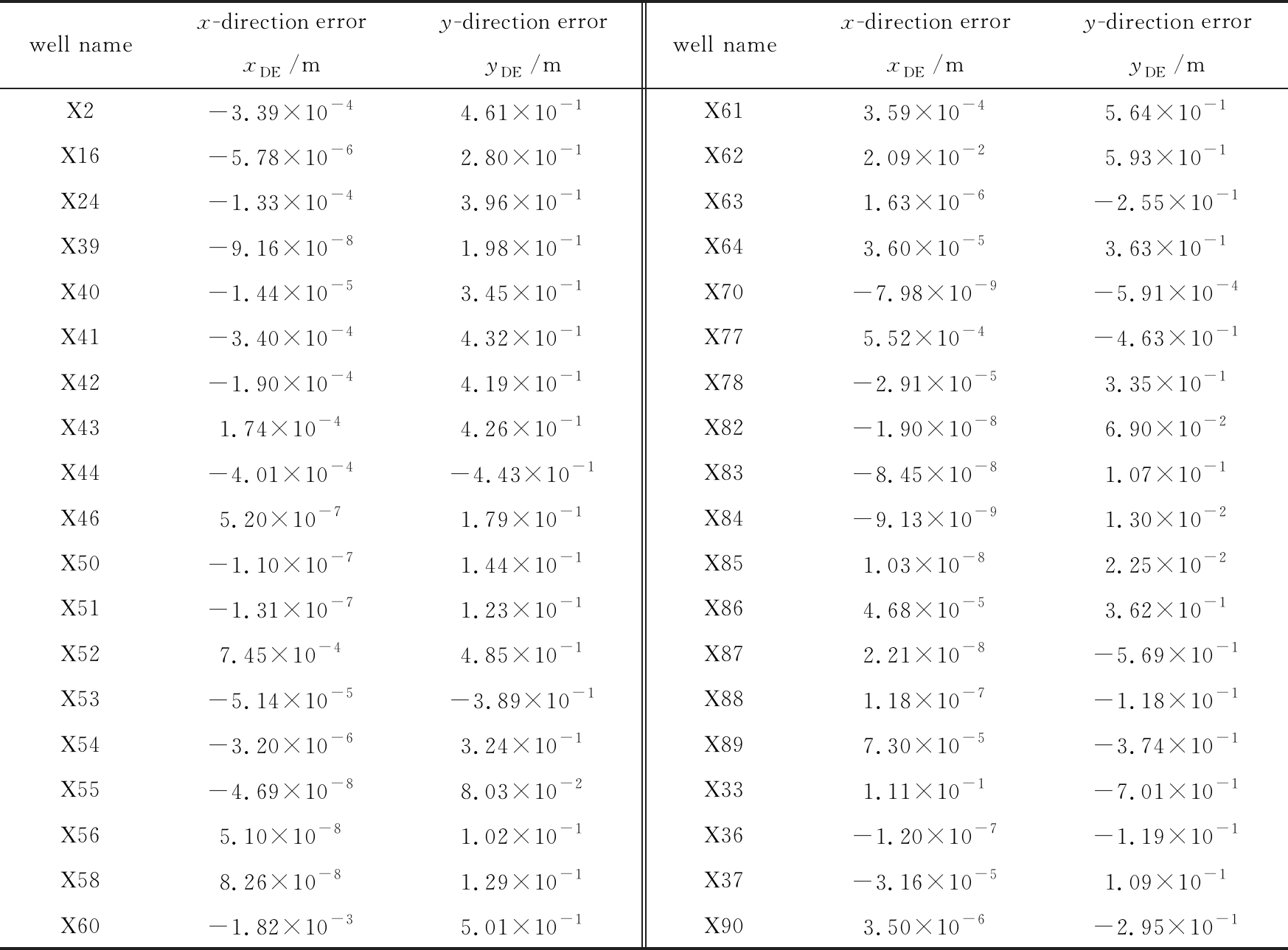
根据2.1小节的方法,得到X油藏区域38口井的初始化位置.通过表4的误差数据可以看出,2.2小节给出的井位的初始化方法的精度较高,在x方向的初始化误差很小,在y轴方向的初始化误差较x轴方向大,主要原因是y轴方向缩放的比例较大.根据2.2小节的方法,计算得到多边形油藏区域中的38口井映射到矩形区域中的井位,如图10所示.这里特别需要说明的是,从油藏边界到带状过渡区域边界在映射过程中存在着井位的缩放问题,同时从带状过渡区域到矩形区域映射也存在井位的缩放问题.但这两者对井位缩放比例是不一样的,前者是井位的整体缩放,而后者在x轴方向和y轴方向缩放的比例是不一致的.主要是因为在计算Jacobi椭圆函数时要确定映射模量,映射模量的大小与选择映射矩形的四个顶点有关.表4中给出的矩形区域的映射数据是没有考虑x轴方向和y轴方向的伸缩系数.
表4 矩形油藏井位初始化误差数据表
Table 4 The data table of wellbore initialization errors for rectangular reservoirs
well namex-direction error xDE/my-direction error yDE/mwell namex-direction error xDE/my-direction error yDE/mX2-3.39×10-44.61×10-1X613.59×10-45.64×10-1X16-5.78×10-62.80×10-1X622.09×10-25.93×10-1X24-1.33×10-43.96×10-1X631.63×10-6-2.55×10-1X39-9.16×10-81.98×10-1X643.60×10-53.63×10-1X40-1.44×10-53.45×10-1X70-7.98×10-9-5.91×10-4X41-3.40×10-44.32×10-1X775.52×10-4-4.63×10-1X42-1.90×10-44.19×10-1X78-2.91×10-53.35×10-1X431.74×10-44.26×10-1X82-1.90×10-86.90×10-2X44-4.01×10-4-4.43×10-1X83-8.45×10-81.07×10-1X465.20×10-71.79×10-1X84-9.13×10-91.30×10-2X50-1.10×10-71.44×10-1X851.03×10-82.25×10-2X51-1.31×10-71.23×10-1X864.68×10-53.62×10-1X527.45×10-44.85×10-1X872.21×10-8-5.69×10-1X53-5.14×10-5-3.89×10-1X881.18×10-7-1.18×10-1X54-3.20×10-63.24×10-1X897.30×10-5-3.74×10-1X55-4.69×10-88.03×10-2X331.11×10-1-7.01×10-1X565.10×10-81.02×10-1X36-1.20×10-7-1.19×10-1X588.26×10-81.29×10-1X37-3.16×10-51.09×10-1X60-1.82×10-35.01×10-1X903.50×10-6-2.95×10-1
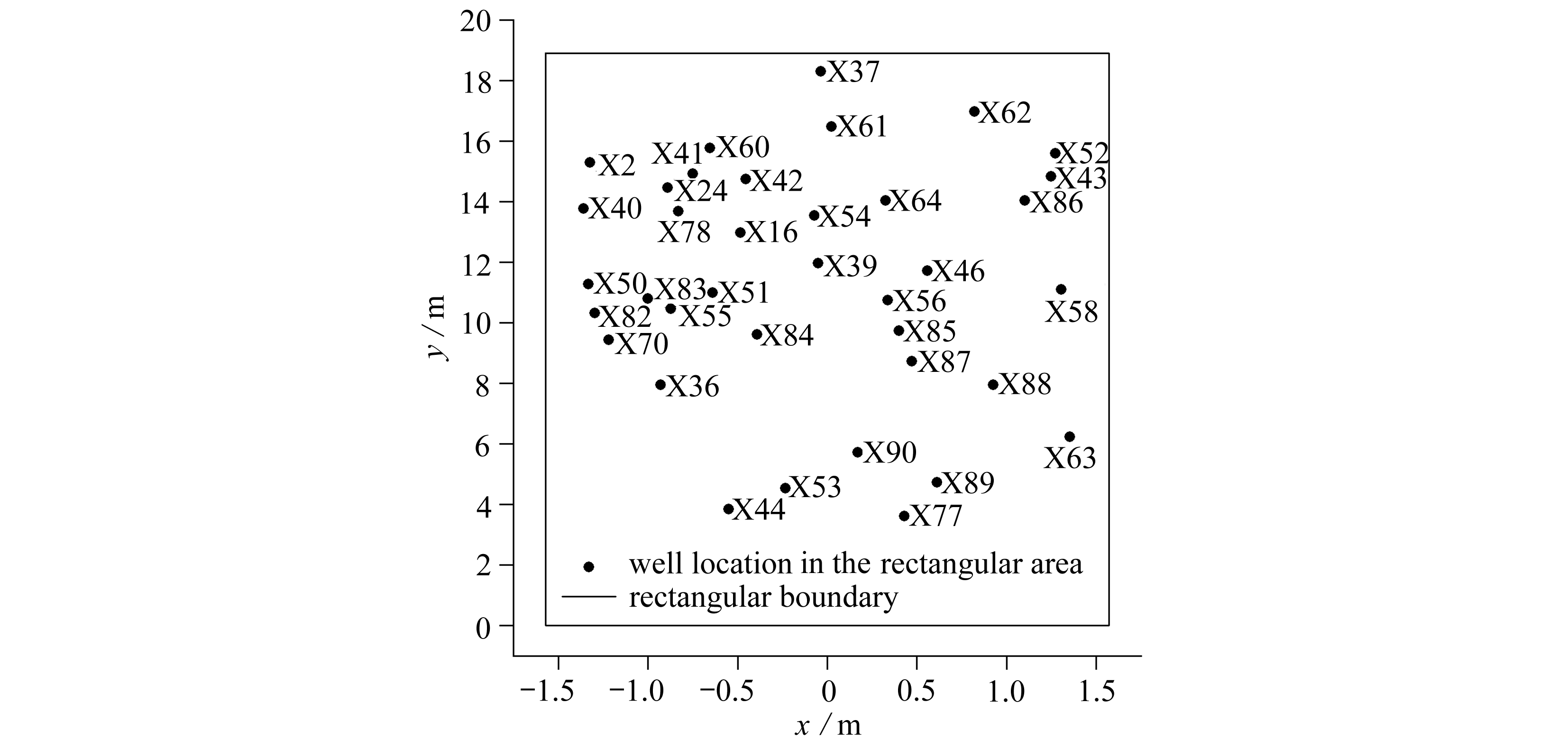
图10 从油藏内部井位到矩形区域映射井位分布图
Fig. 10 Mapping of well location distributions from internal well locations in reservoir to the rectangular region
在表3中第四、第八列反应了Newton法迭代计算Jacobi椭圆函数的绝对误差,其绝对误差在10-15数量级以下,其根本原因就是本文所给的初始化方法比较接近映射点位,便于Newton法迭代的计算.
5 结 论
1) 通过建立多边形区域到矩形区域的Schwarz-Christoffel映射关系,将曲流河沿着河道方向映射到矩形的一个方向,从而为复杂曲流河沉积的储层地质建模变换到矩形区域进行研究提供了一定的理论基础.
2) 在多边形区域到带状过渡区域映射的计算过程中,根据二维PSO算法基本原理,提出了带状过渡区域的初始化点位确定方法.结合Jacobi积分方法,解决了多边形区域映射到带状过渡区域的数值计算问题.根据二维PSO算法的基本原理,从多边形内部点位映射到带状区域内部点过程中,建立了基于PSO算法的计算方法,也避免了文献[12]中建立复杂的复参数与实参数的对应关系.在矩形区域到带状过渡区域映射计算过程中, 根据带状过渡区域到矩形区域映射变换尺度的对应规则, 提出了采用Newton迭代法计算Jacobi椭圆函数的初值确定方法.
致谢 本文作者衷心感谢陇东学院青年基金(17JR5RM355)对本文的资助.
[1] 单敬福, 张吉, 赵忠军, 等. 地下曲流河点坝砂体沉积演化过程分析: 以吉林油田杨大城子油层第23小层为例[J]. 石油学报, 2015,36(7): 809-819.(SHAN Jingfu, ZHANG Ji, ZHAO Zhongjun, et al. Analysis of sedimentary and evolution process for underground meandering river point bar: a case study from number 23 thin layer of Yangdachengzi oil reservoir in Jilin oilfield[J].Acta Petrolei Sinica, 2015,36(7): 809-819.(in Chinese))
[2] 范峥, 吴胜和, 岳大力, 等. 曲流河点坝内部构型的嵌入式建模方法研究[J]. 中国石油大学学报(自然科学版), 2012,36(3): 1-6.(FAN Zheng, WU Shenghe, YUE Dali, et al. Embedding modeling method for internal architecture of point bar sand body in meandering river reservoir[J].Journal of China University of Petroleum(Edition of Natural Science), 2012,36(3): 1-6.(in Chinese))
[3] 刘可可, 侯加根, 刘钰铭, 等. 多点地质统计学在点坝内部构型三维建模中的应用[J]. 石油与天然气地质, 2016,37(4): 577-583.(LIU Keke, HOU Jiagen, LIU Yuming, et al. Application of multiple-point geostatistics in 3D internal architecture modeling of point bar[J].Oil and Gas Geology, 2016,37(4): 577-583.(in Chinese))
[4] 白振强, 王清华, 杜庆龙, 等. 曲流河砂体三维构型地质建模及数值模拟研究[J]. 石油学报, 2009,30(6): 898-902, 907.(BAI Zhenqiang, WANG Qinghua, DU Qinglong, et al. Study on 3D architecture geology modeling and digital simulation in meandering reservoir[J].Acta Petrolei Sinica, 2009,30(6): 898-902, 907.(in Chinese))
[5] 邹拓, 吴淑艳, 陈晓智, 等. 曲流河点坝内部超精细建模研究: 以港东油田一区一断块为例[J]. 天然气地球科学, 2012,23(6): 1163-1169.(ZOU Tuo, WU Shuyan, CHEN Xiaozhi, et al. Super-fine modeling of the inner point bar of meandering river: a case study on the fault one of area Ⅰ in eastern Dagang oilfield[J].Natural Gas Geoscience, 2012,23(6): 1163-1169.(in Chinese))
[6] COSTAMAGNA E, FANNI A. Analysis of rectangular coaxial structures by numerical inversion of the Schwarz-Christoffel transformation[J].IEEE Transactions on Magnetics, 1992,28(2): 1454-1457.
[7] COSTAMAGNA E. A new approach to standard Schwarz-Christoffel formula calculations[J].Microwave and Optical Technology Letters, 2002,32(3): 196-199.
[8] HOWELL L H, TREFETHEN L N. A modified Schwarz-Christoffel transformation for elongated regions[J].SIAM Journal on Scientific and Statistical Computing, 1990,11(5): 928-949.
[9] DRISCOLL T A. Algorithm 843: improvements to the Schwarz-Christoffel toolbox for MATALAB[J].ACM Transactions on Mathematical Software, 2005,31(2): 239-251.
[10] NATARAJAN S, BORDAS S, MAHAPATRA D R. Numerical integration over arbitrary polygonal domains based on Schwarz-Christoffel conformal mapping[J].International Journal for Numerical Methods in Engineering, 2009,80(1): 103-134.
[11] CROWDY D. The Schwarz-Christoffel mapping to bounded multiply connected polygonal domains[J].Proceedings of the Royal Society, 2005,146(2061): 2653-2678.
[12] 王玉风, 姬安召, 崔建斌. 矩形到任意多边形区域的Schwarz-Christoffel变换数值解法[J]. 应用数学和力学, 2019,40(1): 75-88.(WANG Yufeng, JI Anzhao, CUI Jianbin. Numerical solution of Schwarz-Christoffel transformation from rectangles to arbitrary polygonal domains[J].Applied Mathematics and Mechanics, 2019,40(1): 75-88.(in Chinese))
[13] 崔建斌, 姬安召, 王玉风, 等. 单位圆到任意多边形区域的Schwarz Christoffel变换数值解法[J]. 浙江大学学报(理学版), 2017,44(2): 161-167.(CUI Jianbin, JI Anzhao, WANG Yufeng, et al. Numerical solution method for Schwarz Christoffel transformation from unit circle to arbitrary polygon area[J].Journal of Zhejiang University(Science Edition), 2017,44(2): 161-167.(in Chinese))
[14] 陈汉武, 朱建锋, 阮越, 等. 带交叉算子的量子粒子群优化算法[J]. 东南大学学报(自然科学版), 2016,46(1): 23-29.(CHEN Hanwu, ZHU Jianfeng, RUAN Yue, et al. Quantum particle swarm optimization algorithm with crossover operator[J].Journal of Southeast University(Natural Science Edition), 2016,46(1): 23-29.(in Chinese))
[15] 田瑾. 高维多峰函数的量子行为粒子群优化算法改进研究[J]. 控制与决策, 2016,31(11): 1967-1972.(TIAN Jin. Improvement of quantum-behaved particle swarm optimization algorithm for high-dimensional and multi-modal functions[J].Control and Decision, 2016,31(11): 1967-1972.(in Chinese))
[16] 程林辉, 钟洛. 求解多峰函数优化问题的并行免疫遗传算法[J]. 微电子学与计算机, 2015,32(5): 117-121.(CHENG Linhui, ZHONG Luo. A parallel immune genetic algorithm for multimodal function optimization problem[J].Microelectronics and Computer, 2015,32(5): 117-121.(in Chinese))
[17] 高岳林, 余雅萍. 基于混合量子粒子群优化的投资组合模型及实证分析[J]. 工程数学学报, 2017,34(1): 21-30.(GAO Yuelin, YU Yaping. Portfolio model based on hybrid quantum particle swarm optimization with empirical research[J].Chinese Journal of Engineering Mathematics, 2017,34(1): 21-30.(in Chinese))
[18] ABRAMOWITZ M, STEGUNIA.Handbook of Mathematical Functions With Formulas,Graphs,and Mathematical Tables[M]. Washington DC: Dover Publications, 1996.