引 言
近年来，非线性科学成为自然科学领域的热点．非线性偏微分方程用于模拟和描述数学物理学科中诸多复杂的非线性现象，被广泛应用于大气科学、非线性光学、流体力学、水系统科学以及物理场论等诸多领域．因此，求解非线性偏微分方程具有广泛的研究和应用价值．目前，已有多位学者提出多种方法求解非线性偏微分方程，如F展开法[1-2]、(G′/G)展开法[3-4]、Hirota双线性变换法[5-6]、Backlund变换法[7-8]、Darboux变换法[9-10]、Jacobi椭圆函数展开法[11-12]、奇摄动法[13]、同伦映射法[14]、广义变分迭代法[15]．然而迄今为止，还没有发现一种统一的非线性偏微分方程求解方法．所以，发现并应用更多的方法来探究非线性偏微分方程的精确解以更好地解释非线性物理现象是当前广大数学、力学、物理工作者的重要课题．
广义非线性Schrödinger方程[16-17]为
(1)
其中α0,γ1,γ2,γ3为常实数，
方程(1)是数学物理方程中一类重要的非线性演化方程，是现代光孤子通信领域的重要理论基础．随着研究的不断深入，该方程在电磁学、非线性光学、光孤子通信等领域应用广泛，具有重要的研究价值．文献[16]通过改进和推广的映射方法获得了该方程Jacobi椭圆函数周期波解；文献[17]应用全新的G′/(G+G′)展开法求得了该方程双曲余切函数解、余切函数解和有理函数解．当γ1=0，γ2=0，γ3=0时，方程(1)退化为标准的Schrödinger方程[18]；当γ1≠0，γ2≠0，γ3=0时，方程(1)退化为Lakshmanan-Porsezian-Daniel方程[19]．
(2+1)维非线性Ginzburg-Landau方程[18-20]为
(2)
其中
是色散项系数，r1为三次增益系数，r2为五次耗散系数，β,r1,r2均为实常数，复函数u=u(x,z,τ)用以描述缓慢变化的电场包络，x和z代表传播坐标，τ=t-z/V0是所谓的减少时间，t是物理时间，V0是载波的组速度．方程(2)用于描述光脉冲在非线性光纤中的传输，在光孤子通信等领域具有重大研究价值．(2+1)维非线性Ginzburg-Landau方程不仅是非线性光学和光孤子通信研究的一个主要课题，同时它还在Benard对流问题、Taylor-Conette流动、量子场论等领域中有着广泛应用，但是它的求解比较繁琐．关于它的求解，学者们做了很多研究：文献[20]应用同解变形法得到包括孤子解和周期解的精确行波解；文献[21]应用e展开法得到了一系列广义孤立解和广义扭结型孤立解；文献[22]应用(G′/G,1/G)展开法得到了有理函数解、双曲函数解和三角函数解．
本文在前人的研究基础上，研究了一种Riccati-Bernoulli辅助方程法，并应用这种方法得到广义非线性Schrödinger方程和(2+1)维非线性Ginzburg-Landau方程三角函数解、暗孤子解、有理函数解和指数函数解，既获得了原有解的结果，又得出一些新形式的解．广义非线性Schrödinger方程的解为研究光纤中亚皮秒或飞秒光脉冲的传播机制提供理论依据，同时所得结果也可应用于其他物理领域如Bose-Einstein凝聚和等离子物理，为进一步研究相关实验提供理论基础；(2+1)维非线性Ginzburg-Landau方程的解在研究与设计光纤扩大器(optical fiber amplifiers)和光脉冲压缩器 (optical pulse compressors)中有特别重要的意义．
1 Riccati-Bernoulli辅助方程法
考虑具有如下形式的偏微分方程:
P(u,ut,ux,uxx,uxt,…)=0,
(3)
其中下标代表偏导数,P是u及其偏导数的多项式．下面介绍Riccati-Bernoulli辅助方程法的详细步骤．
步骤1 对方程(3)做行波变换：
u(x,t)=u(ξ)， ξ=x+Vt．
(4)
将方程(3)转化为常微分方程
H(u,Vu′,u″,Vu″,…)=0,
(5)
其中V是待定常数，u′=du/dξ．
步骤2 设u是Riccati-Bernoulli辅助方程
u′=au2-m+bu+cum
(6)
的解，其中a,b,c,m为待定常数．
由式(6)求导得
u″=ab(3-m)u2-m+a2(2-m)u3-2m+mc2u2m-1+
bc(m+1)um+(2bc+b2)u．
(7)
同时，方程(6)具有如下6种解：
① 当m=1时，方程(6)的解为
u(ξ)=Ce(a+b+c)ξ；
(8)
② 当m≠1,b=c=0时，方程(6)的解为
u(ξ)=(a(m-1)(ξ+C))1/(m-1)；
(9)
③ 当m≠1,c=0,b≠0时，方程(6)的解为
(10)
④ 当m≠1,a≠0,b2-4ac<0时，方程(6)的解为
(11a)
(11b)
⑤ 当m≠1,a≠0,b2-4ac>0时，方程(6)的解为
(12a)
(12b)
⑥ 当m≠1,a≠0,b2-4ac=0时，方程(6)的解为
(13)
步骤3 最后将u及其各阶偏导数代入方程(5), 令uj(j=0,1,2,…)的系数均为0，得到一组关于m,a,b,c,V的代数方程组．求解这组代数方程组，并将m,a,b,c,V代入式(8)～(13)中，结合式(4), 便可得到偏微分方程(3)的精确行波解．
2 广义非线性Schrödinger方程的行波解
标准非线性Schrödinger方程是描述光孤子在理想无损耗单模皮秒光纤中传输的模型，满足该方程的光孤子在远距离光纤传播中波形、波速、振幅始终保持不变，不会发生波形畸变和信息失真，传输码率高．但是在某些特定情况下，一方面，标准非线性Schrödinger方程在描述光脉冲传输时显得无能为力;另一方面，近年来，为了进一步提高光纤通信系统容量，对超短光脉冲的传输研究越来越引起人们的重视，而光纤中脉冲宽度在亚皮秒和飞秒量级的超短脉冲，标准非线性Schrödinger方程模型已经不再适应，需要采用含有高阶非线性效应如三阶色散、自陡峭和自频移修正非线性Schrödinger方程．为了研究脉冲光孤子的动力学机制，本文研究了一类带有高阶非线性效应的广义非线性Schrödinger方程：
(14)
对于方程(14)，首先需要对其虚部进行处理．
首先引入一个变换：
u=φ(ξ)ei(kx-ωt), ξ=x-Vt．
(15)
将式(15)代入式(14)得
i(γ1φ‴-3γ1k2φ′+γ2φ2φ′+2γ3φ2φ′-Vφ′+2kφ′)+
(ωφ+φ″-k2φ+α0φ3-3γ1kφ″+γ1k3φ-γ2kφ3)=0．
(16)
令方程(16)等号左侧实部和虚部分别为0，则有
γ1φ‴-3γ1k2φ′+γ2φ2φ′+2γ3φ2φ′-Vφ′+2kφ′=0,
(17)
ωφ+φ″-k2φ+α0φ3-3γ1kφ″+γ1k3φ-γ2kφ3=0．
(18)
对方程(17)进行一次积分得
(19)
t0为积分常量．对比式(18)和(19)得
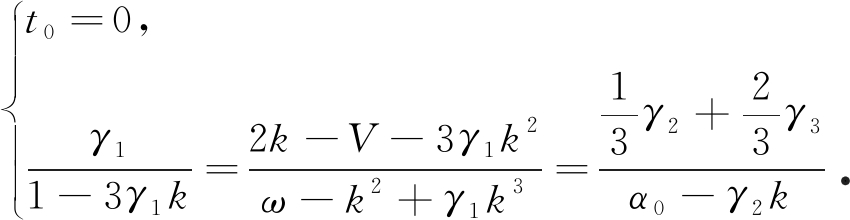
(20)
由式(20)得
(21)
在式(20)和(21)的条件下，为了解方程(19)，不妨设
(22)
则方程(19)可化为
αφ″-ηφ+βφ3=0,
(23)
其中α，β为已知常数，η为待定常数(V未知)．
依据Riccati-Bernoulli辅助方程法及式(7)得
φ″=ab(3-m)φ2-m+a2(2-m)φ3-2m+mc2φ2m-1+
bc(m+1)φm+(2bc+b2)φ．
(24)
把式(24)代入式(23)得
α[ab(3-m)φ2-m+a2(2-m)φ3-2m+mc2φ2m-1+
bc(m+1)φm+(2bc+b2)φ]-ηφ+βφ3=0．
(25)
观察方程(25), 为了能够使其满足齐次平衡原理，令m=0, 并令φj(j=0,1,2,3)的系数均为0，得到如下代数方程组：
bc=0， 3ab=0， 2a2α+β=0，α(2bc+b2)-η=0．
(26)
解代数方程组(26)得
(27)
又由式(22)得
(28)
结合Riccati-Bernoulli辅助方程的通解(8)～(13)，我们得到：
① 当a≠0,b2-4ac>0，即ac<0时
(29a)
(29b)
其中α，β由式(28)给出，c,C1为任意常量．考虑到方程(15)，我们得到
(30a)
(30b)
ξ=x-(-3γ1k2+2k)t，
(31)
其中α，β由式(28)给出，k,ω由式(21)给出，c,C1为任意常量．
② 当a≠0,b2-4ac<0，即ac>0时
(32a)
(32b)
其中α，β由式(28)给出，c,C2为任意常量．考虑到方程(15)，我们得到
(33a)
(33b)
ξ=x-(-3γ1k2+2k)t，
(34)
其中α，β由式(28)给出，k,ω由式(21)给出，c,C2为任意常量．
③ 当a≠0,b2-4ac=0，即c=0时
(35)
其中α，β由式(28)给出，c,C3为任意常量．考虑到方程(15)，我们得到
(36)
ξ=x-(-3γ1k2+2k)t，
(37)
其中α，β由式(28)给出，k,ω由式(21)给出，C3为任意常量．
④ 当a=b=0时
φ(ξ)=cξ+C4，
(38)
其中c,C4为任意常量．考虑到方程(15)，我们得到
u(ξ)=(cξ+C4)ei(kx-ωt)，
(39)
ξ=x-(-3γ1k2+2k)t，
(40)
其中c,C4为任意常量．
3 (2+1)维非线性Ginzburg-Landau方程的行波解
下面考虑著名的(2+1)维非线性Ginzburg-Landau方程：
(41)
设
u(x,z,τ)=φ(x,τ)ei(kz+ψ(x,τ))，
(42)
其中φ(x,τ)和ψ(x,τ)是关于x和τ的实函数，k为实参数．
把式(42)代入式(41)中，并令实部和虚部分别等于0，得
(43)
(44)
令
φ(x,τ)=φ(ξ),ψ(x,τ)=ψ(η),ξ=l0x-l1τ,η=h0x-h1τ,
(45)
其中l0，l1，h0，h1是待定的实常数．把式(45)分别代入式(43)和(44)得
(46)
(47)
不妨令
得到
(48)
则式(46)和(47)可以写成如下形式：
(49)
(50)
再令
ψ(η)=η=h0x-h1τ，
(51)
则ψ′=1,ψ″=0．由式(50)得
(52)
则
(53)
通过式(52)和(53),得到
(54)
同时式(49)可以写成
(55)
不难发现方程(54)和(55)具有相同的形式，比较其系数得
(56)
所以
(57)
其中r1,r2满足如下关系：
(58)
r1,r2不能同时为0．所以方程(54)和(55)可以写成
(59)
至此，我们将带有虚部单位的非线性Schrödinger方程转化为形如式(5)的常微分方程．由Riccati-Bernoulli辅助方程法和方程(7)得到
φ″=ab(3-m)φ2-m+a2(2-m)φ3-2m+
mc2φ2m-1+bc(m+1)φm+(2bc+b2)φ．
(60)
把方程(60)代入方程(59)得
(61)
由齐次平衡法则确定m=-1．令方程(61)中φj(j=0,1,2,…)的系数均为0，得到代数方程组如下：
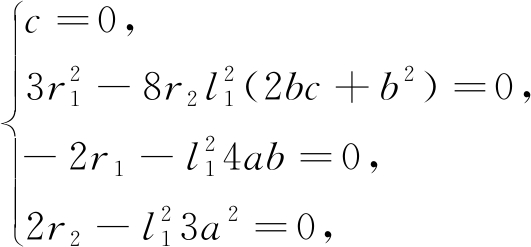
(62)
解得
(63)
把式(63)中a,b,c的值代入辅助方程的通解(8)～(13)中，同时考虑方程(42)和(45),可以得到原方程(41)的精确行波解．
① 当a≠0,b2-4ac>0时
(64a)
(64b)
(65)
其中l1，C1为任意常数．
② 当a≠0,b2-4ac<0时
(66a)
(66b)
(67)
其中l1，C2为任意常数．
③ 当a≠0,b2-4ac=0时
(68)
(69)
其中l1，C3为任意常数．
④ 当a=0,b≠0时
(70)
(71)
其中l1，C4为任意常数．
4 总 结
本文基于Riccati-Bernoulli辅助方程法，探究了广义非线性Schrödinger方程和(2+1)维非线性Ginzburg-Landau方程的精确解．这种方法不仅重新发现了上述两类方程的已知解，还发现了一些全新的解，从而拓展了它们解的范围．上述结论验证了Riccati-Bernoulli辅助方程法的可行性．该辅助方程法简洁高效，可以通过m的不同取值平衡目标微分方程的最高次项，再通过解代数方程组和一系列合理的代换得到非线性偏微分方程的精确行波解．将这种方法应用于探究更多非线性偏微分方程的精确解具有重大意义．同时，在MATHEMATICA等数学软件的帮助下，Riccati-Bernoulli辅助方程法可以更加便捷高效地求解多种非线性偏微分方程．
[1] ABDOU M A. The extendedF-expansion method and its application for a class of nonlinear evolution equations[J].Chaos,Solitons and Fractals, 2007,31(1): 95-104.
[2] ABDOU M A. An improved generalizedF-expansion method and its applications[J].Journal of Computational and Applied Mathematics, 2008,214(1): 202-208.
[3] WANG M L, ZHANG J L, LI X Z. Application of the (G′/G)-expansion to travelling wave solutions of the Broer-Kaup and the approximate long water wave equations[J].Applied Mathematics and Computation, 2008,206(1): 321-326.
[4] WANG M L, LI X Z, ZHANG J L. The (G′/G)-expansion method and travelling wave solutions of nonlinear evolution equations in mathematical physics[J].Physics Letters A, 2008,372(4): 417-423.
[5] LI L, DUAN C N, YU F J. An improved Hirota bilinear method and new application for a nonlocal integrable complex modified Korteweg-de Vries (MKdV) equation[J].Physics Letters A, 2019,383(14): 1578-1582.
[6] GUO D, TIAN S F, ZHANG T T. Integrability, soliton solutions and modulation instability analysis of a (2+1)-dimensional nonlinear Heisenberg ferromagnetic spin chain equation[J].Computers and Mathematics With Applications, 2019,77(3): 770-778.
[7] CHENG J P, HE J S. Miura and auto-Baecklund transformations for the discrete KP and mKP hierarchies and their constrained cases[J].Communications in Nonlinear Science and Numerical Simulation, 2019,69: 187-197.
[8] LIU X Z, YU J, LOU Z M. New Bäcklund transformations of the (2+1)-dimensional Bogoyavlenskii equation via localization of residual symmetries[J].Computers and Mathematics With Applications, 2018,76(7): 1669-1679.
[9] MA L Y, ZHAO H Q, SHEN S F, et al. Abundant exact solutions to the discrete complex mKdV equation by Darboux transformation[J].Communications in Nonlinear Science and Numerical Simulation, 2019,68: 31-40.
[10] WANG X, WANG L. Darboux transformation and nonautonomous solitons for a modified Kadomtsev-Petviashvili equation with variable coefficients[J].Computers and Mathematics With Applications, 2018,75: 4201-4213.
[11] PARKES E J, DUFFY B R, ABBOTT P C. The Jacobi elliptic-function method for finding periodic-wave solutions to nonlinear evolution equations[J].Physics Letters A, 2002,295(5/6): 280-286.
[12] ZAYED E M E, ALURRFI K A E. A new Jacobi elliptic function expansion method for solving a nonlinear PDE describing the nonlinear low-pass electrical lines[J].Chaos,Solitons and Fractals, 2015,78: 148-155.
[13] 石兰芳, 莫嘉琪. 一类强非线性非自治方程的奇摄动Robin边值问题[J]. 应用数学, 2017,30(2): 247-251.(SHI Lanfang, MO Jiaqi. A class of singular perturbation solutions to strong nonlinear equation Robin problems[J].Mathematica Applicata, 2017,30(2): 247-251.(in Chinese))
[14] 石兰芳, 周先春. 一类扰动 Burgers 方程的孤子同伦映射解[J]. 物理学报, 2010,59(5): 2915-2918.(SHI Lanfang, ZHOU Xianchun. Homotopic mapping solution of soliton for a class of disturbed Burgers equation[J].Acta Physica Sinica, 2010,59(5): 2915-2918.(in Chinese))
[15] 欧阳成, 石兰芳, 汪维刚, 等. 非线性强迫扰动Klein-Gordon方程的孤波渐进解法[J]. 数学年刊, 2017,38(A): 43-52.(OUYANG Cheng, SHI Lanfang, WANG Weigang, et al. The asymptotic solving method of solitary wave for the nonlinear forced disturbed Klein-Gordon equation[J].Chinese Annals of Mathematics, 2017,38(A): 43-52.(in Chinese))
[16] PENG Y Z, SHEN M, WANG Z J. Exact solutions to the higher order nonlinear Schrödinger equation[J].Mathematica Applicata, 2007,20(3): 505-511.
[17] 石兰芳, 聂子文. 应用全新G′/(G+G′)展开方法求解广义非线性Schrödinger方程和耦合非线性Schrödinger方程组[J]. 应用数学和力学, 2017,38(5): 539-552.(SHI Lanfang, NIE Ziwen. Solutions to the nonlinear Schrödinger equation and coupled nonlinear Schrödinger equations with a newG′/(G+G′)-expansion method[J].Applied Mathematics and Mechanics, 2017,38(5): 539-552.(in Chinese))
[18] ANKIEWICZ A, SOTO-CRESPO J M, AKHMEDIEV N. Rogue waves and rational solutions of the Hirota equation[J].Physical Review E, 2010,81: 046602.
[19] PORSEZIAN K, LAKSHMANAN M. On the dynamics of the radially symmetric Heisenberg ferromagnetic spin system[J].Journal of Mathematical Physics, 1991,32(10): 2923-2928.
[20] 施业琼. (2+1)维Ginzburg-Landau方程的精确波解[J]. 数学的实践与认识, 2009,39(16): 247-251.(SHI Yeqiong. The exact wave solutions for 2+1 dimensional cubic-quintic Ginzburg-Landau equation[J].Mathematics in Practice and Theory, 2009,39(16): 247-251.(in Chinese))
[21] SHI Y, DAI Z, LI D. Application of exp-function method for 2D cubic-quintic Ginzburg-Landau equation[J].Applied Mathematics and Computation, 2009,210(1): 269-275.
[22] ZAYED E M E, ALURRFI K A E. The (G′/G,1/G)-expansion method and its applications to two nonlinear Schrödinger equations describing the propagation of femtosecond pulses in nonlinear optical fibers[J].Optic, 2016,127(4): 1581-1589.