引 言
轮状病毒是目前世界范围之内导致儿童发生严重腹泻最主要的病原体,低于5岁的儿童几乎都感染过轮状病毒[1].临床数据[2]统计结果显示, 每年全球范围内出现轮状病毒感染性腹泻的儿童数量高达1.3 亿,其中90万例儿童因此病而死.我国在1978年首次检测到此病毒[3],在现有的5岁以下儿童中,每年因轮状病毒感染患秋冬季腹泻的小儿约达4 800万人次[4].儿童轮状病毒感染性腹泻已成为全球范围内的公共卫生问题之一,了解儿童轮状病毒感染性腹泻的感染规律,并分析其感染的传播模型对其有效防治具有积极作用[5-6].
当儿童受到轮状病毒感染时,症状发生前大约会有2 d的潜伏期,并且处于潜伏期的患者可以传播轮状病毒[7].潜伏期之后,患儿会突然出现呕吐和发烧,并伴有大量水样腹泻,症状通常会持续2~7 d[8],且痊愈后可被轮状病毒反复感染[9].但新生儿因受到免疫和母体抗体的保护,不会感染轮状病毒[10].
近年来,随着对轮状病毒的认识及对其疫苗研究的推进,出现了一些关于刻画轮状病毒传播的数学模型.比如Atkins等[11]建立了具有多次感染的状态分层传播动力学轮状病毒数学模型;Omondi等[12]建立了模拟接种疫苗对轮状病毒感染影响的数学模型.这些文献均讨论了轮状病毒疫苗对轮状病毒传播的影响.Kribs-Zaleta等[13]建立了儿科病房内轮状病毒在医患之间的传播模型;Shim等[8]建立了具有年龄结构的轮状病毒传播数学模型;White等[14]和Young等[15]分别建立了多毒株轮状病毒传播模型,分析了其动力学性态.但国内研究轮状病毒传播的数学模型相对较少,文献[16]建立了轮状病毒医院感染暴发的传染病动力学模型,用数学软件对医院采集的数据进行了分析,得到隔离措施对控制轮状病毒感染在院内暴发是有效的结论,但未对模型的动力学性态进行数学分析.由于被轮状病毒感染后的恢复者具有暂时的免疫力,且母体抗体对新生儿具有保护的特性,本文建立了一个具有暂时免疫的轮状病毒传播模型,通过分析模型的动力学性态研究进一步了解轮状病毒的传播情况.
1 模型的建立
根据轮状病毒的传播特点,将所考虑的种群分为五个仓室:具有母体抗体的初生婴儿(X)、易感者(S)、潜伏者(L)、感染者(I)和恢复者(R),分别以X=X(t),S=S(t),L=(t),I=I(t)和R=R(t)表示t时刻婴儿、易感者、潜伏者、感染者和恢复者的人数.在假设潜伏者和易感者都具有感染性以及恢复者具有暂时免疫的情况下,可得如下的轮状病毒传播模型:
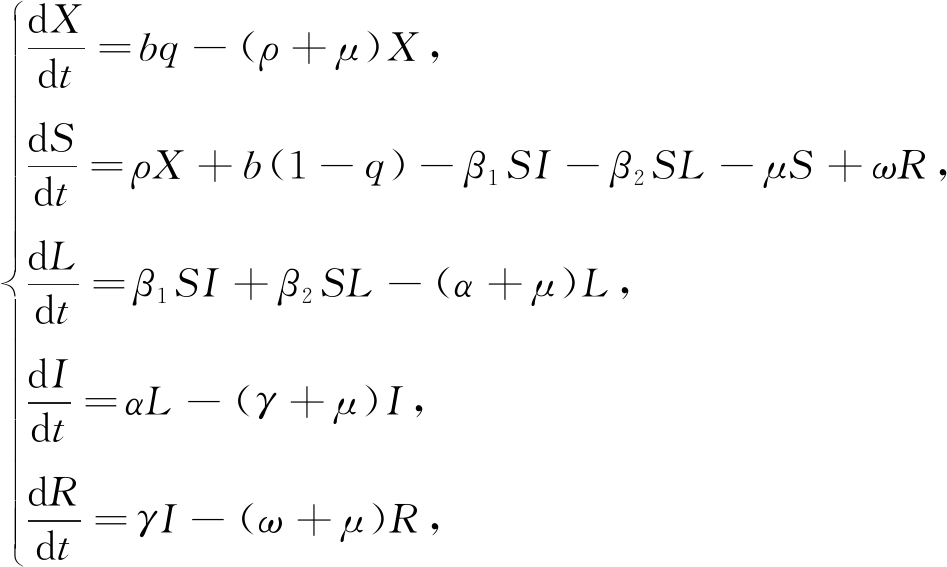
(1)
其中b表示婴儿的出生率,q(0<q<1)表示新生婴儿中具有母体抗体的比例,μ是自然死亡率与幼年个体向成年个体的转化率之和,ρ表示具有母体抗体的新生婴儿失去母体抗体保护的速率,β1和β2分别表示感染者和潜伏者对易感者的感染系数,ω是恢复者失去免疫力而成为易感者的速率,α是潜伏者发展为感染者的速率,γ是感染者的恢复率.这里的参数都是正的.
显然,系统(1)在非负初始条件下的解都保持非负性.若记N=X+S+L+I+R,则由模型(1)有N′=b-μN.于是limt→∞N=b/μ.
将R=N-X-S-L-I代入模型(1)的第二个方程, 则由系统(1)的前四个方程构成的系统有以下极限系统:
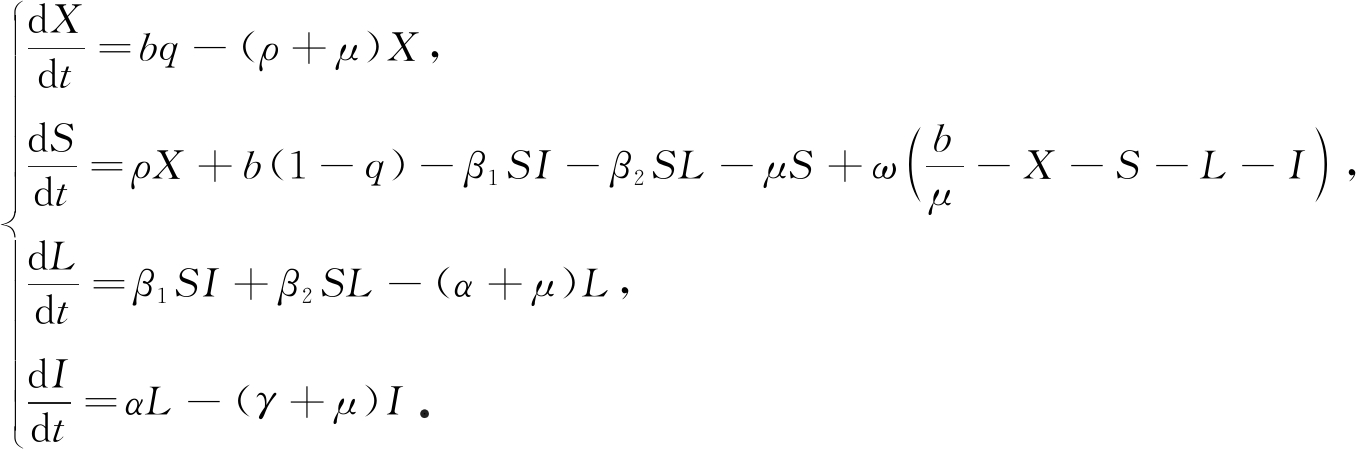
(2)
又由系统(2)的第一个方程有limt→∞X=bq/(ρ+μ),因此由系统(2)的后三个方程组成的系统有极限系统为
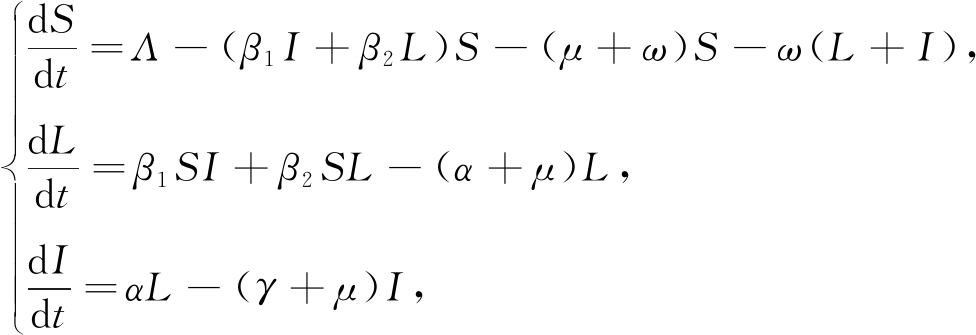
(3)
其中![]()
进一步地,根据解的非负性,由系统(3)有
所以
于是区域
是系统(3)的一个正不变集,且系统(3)的所有解都被吸引到这个正不变集.因此本文将在Ω上讨论系统(3)的动力学行为.
2 平衡点的存在性和局部稳定性
易知系统(3)总存在着无病平衡点E0(S0,0,0),其中
系统(3)的地方病平衡点E*(S*,L*,I*)(L*>0,I*>0)由方程组
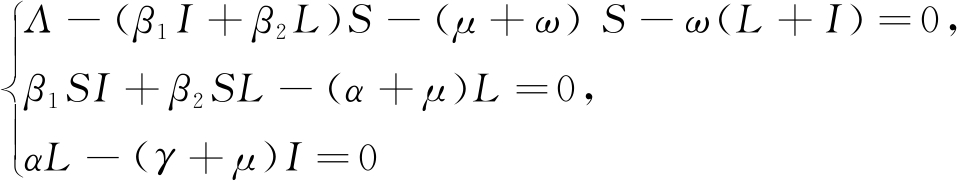
(4)
来确定.
由方程组(4)中的第三个方程得
(5)
当I≠0时,将式(5)代入方程组(4)中的第二个方程可得
(6)
记
则式(6)可写为S=S0/R0.再将S=S0/R0和式(5)代入方程组(4)中的第一个方程可得
相应地,由式(5)有
因此,关于系统(3)平衡点的存在性有如下结论.
定理1 系统(3)总存在无病平衡点E0(S0,0,0).当R0>1时,系统(3)还存在着唯一的地方病平衡点E*(S*,L*,I*),这里
关于系统(3)的平衡点的局部稳定性有以下定理.
定理2 当R0<1时,系统(3)的无病平衡点E0是局部渐近稳定的,当R0>1时是不稳定的.系统(3)的地方病平衡点E*只要存在, 就是局部渐近稳定的.
证明 首先,系统(3)在无病平衡点E0(S0,0,0)处的Jacobi矩阵为
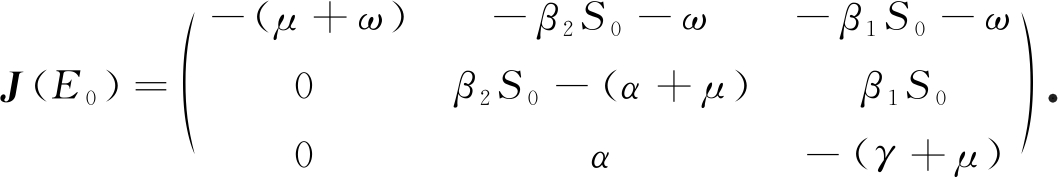
显然,λ=-(ω+μ)是J(E0)的一个特征值,其另外两个特征根为方程λ2+a1λ+a2=0的两个根,其中
a1=α+μ-β2 S0+γ+μ,
a2=[(α+μ)-β2 S0](γ+μ)-αβ1S0=(α+μ)(γ+μ)(1-R0).
由于R0<1意味着β2S0<α+μ,因此当R0<1时a1>0且a2>0,所以当R0<1时系统(3)的无病平衡点E0是局部渐近稳定的.而当R0>1时,a2<0,因此J(E0)一定有一正实根,所以此时无病平衡点E0是不稳定的.
系统(3)在E*(S*,L*,I*)处的Jacobi矩阵为

根据方程组(4)中的第二个和第三个方程有
因此, 矩阵J(E*)可改写为
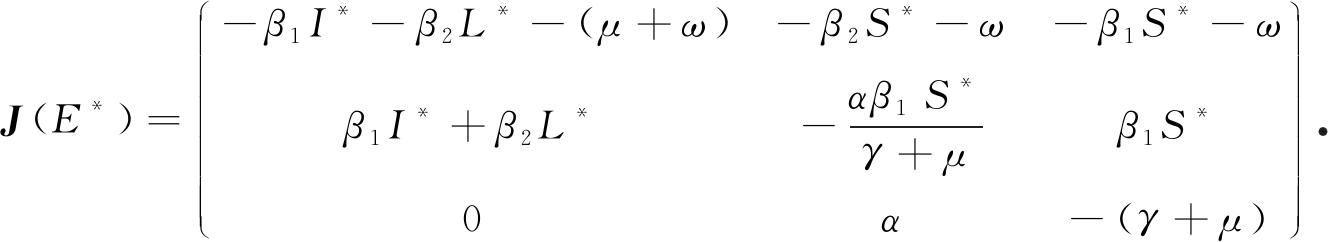
直接计算可得J(E*)的特征方程为λ3+A2 λ2+A1 λ+A0=0,其中
A0=(β1I*+β2L*)[(β2S*+ω)(γ+μ)+α(β1S*+ω)].
进一步地,容易验证A1A2-A0>0.由于Ai>0(i=0,1,2),因此根据Routh-Hurwitz准则可知,J(E*)的所有特征值均具有负实部,故系统(3)正平衡点只要存在,就一定是局部渐近稳定的.定理2得证.
3 无病平衡点的全局稳定性和疾病的持续性
在本节中,将考虑系统(3)无病平衡点E0在Ω上的全局渐近稳定性和疾病传播的持续性.下面首先以R0<1和R0=1两种情形来考虑E0的全局稳定性,其次分析R0>1时疾病传播的持续性.
当R0<1时,定义函数V1=L+mI,其中m是一待定正数.函数V1沿着系统(3)的解的全导数为
因为在系统(3)的正不变集Ω上S≤Λ/(μ+ω)=S0,所以有
(7)
注意到R0<1意味着α+μ>β2S0,并且R0<1等价于
因此,取
时,由式(7)有V′1|(3)≤-δV1,其中
故由系统(3)初值的非负性有limt→∞V1(t)=0, 即limt→∞I(t)=limt→∞L(t)=0.进一步地,由极限系统理论有limt→∞S(t)=S0.于是结合无病平衡点E0的局部稳定性可知,当R0<1时,系统(3)无病平衡点E0在Ω上是全局渐近稳定的.
当R0=1时定义函数
则V2沿着系统(3)的解的全导数为
![]()
(β1I+β2L)(S-S0)=
![]()
(β1I+β2L)(S-S0)=
对于(S,L,I)∈Ω,显然有V′2|(3)≤0,并且当且仅当S=S0时,V′2|(3)=0.又系统(3)在{(S,L,I)∈Ω,S=S0}上的最大不变集就是单点集{E0},因此由LaSalle不变集原理知,当R0=1时E0在Ω上是全局渐近稳定的.
综合上述推导可得如下结论.
定理3 当R0≤1时,系统(3)的无病平衡点E0在Ω上是全局渐近稳定的.
文献[17-18]通过讨论系统的持续生存性以明确疾病持续生存的条件.下面同样讨论疾病的持续性,首先引入相应的定义和理论[19].
定义1 设X是一个度量为d的局部紧度量空间,集合F是空间X的一个闭子集,其边界和内部点的集合分别记为∂F和intF.π是定义在集合F上的一个半动力系统.若任意的元素u∈intF都满足lim inft→+∞d(π(u,t),∂F)>0,则称π是持续的;若存在ξ>0,使得对所有的u∈intF都满足lim inft→+∞d(π(u,t),∂F)>ξ,则称π是一致持续的.
Fonda[19]根据斥子理论给出了一个关于持续性的结果.Σ为F的一个子集,若存在η>0,使得对任意u∈F\Σ都有lim inft→+∞d(π(u,t),∂F)>η,则称Σ为一致斥子.这一结论可总结为Fonda引理.
引理1(Fonda引理[19]) 设Σ是X的一个紧子集,且X\Σ是半动力系统π的一个正不变集.Σ是一致斥子的充要条件是存在Σ的一个邻域U和一个连续函数P:X→R+满足
1)u∈Σ⟺P(u)=0;
2) 对任意u∈U\Σ都存在Tu>0,使得P(π(u,Tu))>P(u).
根据引理1,对任意u1=(S1,L1,I1)∈Ω,系统(3)都存在定义在R+上且满足π(u1,0)=(S1,L1,I1)的唯一解π(u1,t)=(S,L,I)(t;u1).又因为Ω是系统(3)的一个正不变集,所以对于t∈R+,系统(3)确定有半动力系统π(u1,t)∈Ω.
定理4 当R0>1时,Σ={(S,L,I)|L=0,I=0}是系统(3)的一个一致斥子.此时半动力系统π在Ω内是一致持续的.
证明 根据系统(3)解的非负性,当L(0)>0或I(0)>0时,对于t>0有L(t)>0和I(t)>0.因此Ω\Σ是系统(3)的一个正不变集,且Σ集是Ω集的一个紧子集.
根据引理1,定义一从Ω到R+的映射P(S,L,I)=max{L,I},并记
U={(S,L,I)∈Ω:P(S,L,I)<ε},
其中ε是一个充分小的正数.
对于R0>1, 即
存在充分小的正数ε满足
(8)
其中![]()
假定对![]() 存在Tε,当t>Tε时,有
存在Tε,当t>Tε时,有![]() <ε,则当t>Tε时,P<ε意味着max{L,I}<ε,即L<ε且I<ε.于是当t>Tε时,由系统(3)的第一个方程可知
<ε,则当t>Tε时,P<ε意味着max{L,I}<ε,即L<ε且I<ε.于是当t>Tε时,由系统(3)的第一个方程可知
Λ-2ωε-[(β1+β2)ε+(μ+ω)]S.
因此
由于![]() 故存在T′ε>Tε,使得当t>T′ε时有S(t)>Sε.
故存在T′ε>Tε,使得当t>T′ε时有S(t)>Sε.
进一步地,当t>T′ε时,系统(3)的后两个方程为

(9)
对应式(9),考虑以下系统:

(10)
由条件(8),线性系统(10)的原点平衡点为鞍点.假设系统(10)的解直线为y=kx,则由系统(10)知
即方程
β1Sεk2+[(γ+μ)+β2Sε-(α+μ)]k-α=0
(11)
的根.显然,方程(11)有唯一正根.同时易知系统(10)的解沿该正根对应的解直线远离原点而趋向无穷远,即limt→∞x(t)=limt→∞x(t)=+∞.
由于系统(10)是一个单调系统,因此由比较定理[20]可得
这与P<ε矛盾, 因此上述假设不成立.也就是说,对于属于Σ某邻域并包含于Ω\Σ的任意u,总存在一个Tu满足P(π(u,Tu))>P(u).因此,根据引理1可知,当R0>1时,Σ={(S,L,I)|L=0,I=0}是系统的一个一致斥子,并且存在正数ξ,使得
综上,当R0>1时,系统(3)的解在Ω内是一致持续的,即疾病在种群中持续感染.定理4得证.
4 数 值 模 拟
由于原模型(1)是一个五维的有界系统,为了数学分析的方便,借助极限系统理论[21]将其简化为一个三维系统.在第2节和第3节中,已经考虑了系统(3)的动力学性态.根据极限系统理论,模型(1)与系统(3)有等价的动力学性态,所以可将模型(1)的对应结果直接叙述如下.
将系统(1)的无病平衡点和地方病平衡点分别记为E(0)和E(*),其中
E(0)=(X(0),S(0), 0, 0, 0),E(*)=(X(*),S(*),L(*),I(*),R(*)).
系统(1)的无病平衡点E(0)对应系统(3)的无病平衡点E0(S0,0,0),其中
由系统(1)的第一个方程bq-(ρ+μ)X=0,可得
代入ρX+b(1-q)-μS=0, 可得
所以系统(1)的无病平衡点为
其基本再生数为
系统(1)的地方病平衡点E(*)=(X(*),S(*),L(*),I(*),R(*))对应系统(3)的地方病平衡点E*(S*,L*,I*).由系统(1)的第4个方程αL-(γ+μ)I=0,得L(*)=((γ+μ)/α)I(*),代入β1SI+β2SL-(α+μ)L=0,可得
且由
(12)
可知
将X(*),S(*),L(*),R(*)代入ρX+b(1-q)-β1SI-β2SL-μS+ωR=0,可得
可以看出I(*)=I*.因此对应系统(1)的地方病平衡点为
可以看出,如果R10>1(即R0>1)时,系统(1)存在着地方病平衡点E(*).下面首先取参数b=10,q=0.6,ρ=0.8,μ=0.2,β1=0.01,β2=0.005,α=0.8,γ=0.6,ω=0.2.可以计算出无病平衡点E(0)=(6,44,0,0,0)并且R10=0.825<1,从图1(取4组初值)可以看出,当R0<1时,L(t),I(t)随时间的增加趋近于0,系统(1) 的无病平衡点是全局稳定的,此时疾病最终趋于灭绝.接下来将参数β1,β2重新取值,令β1=0.04,β2=0.01,其他参数保持不变,此时E(*)=(6,20,6.86,6.86,10.29)且R10=2.75>1.从图2(取4组初值)可以看出,当R0>1时,L(t),I(t)随时间的增加趋近于正常数,地方病平衡点是全局稳定的,此时疾病在宿主体内持续存在.
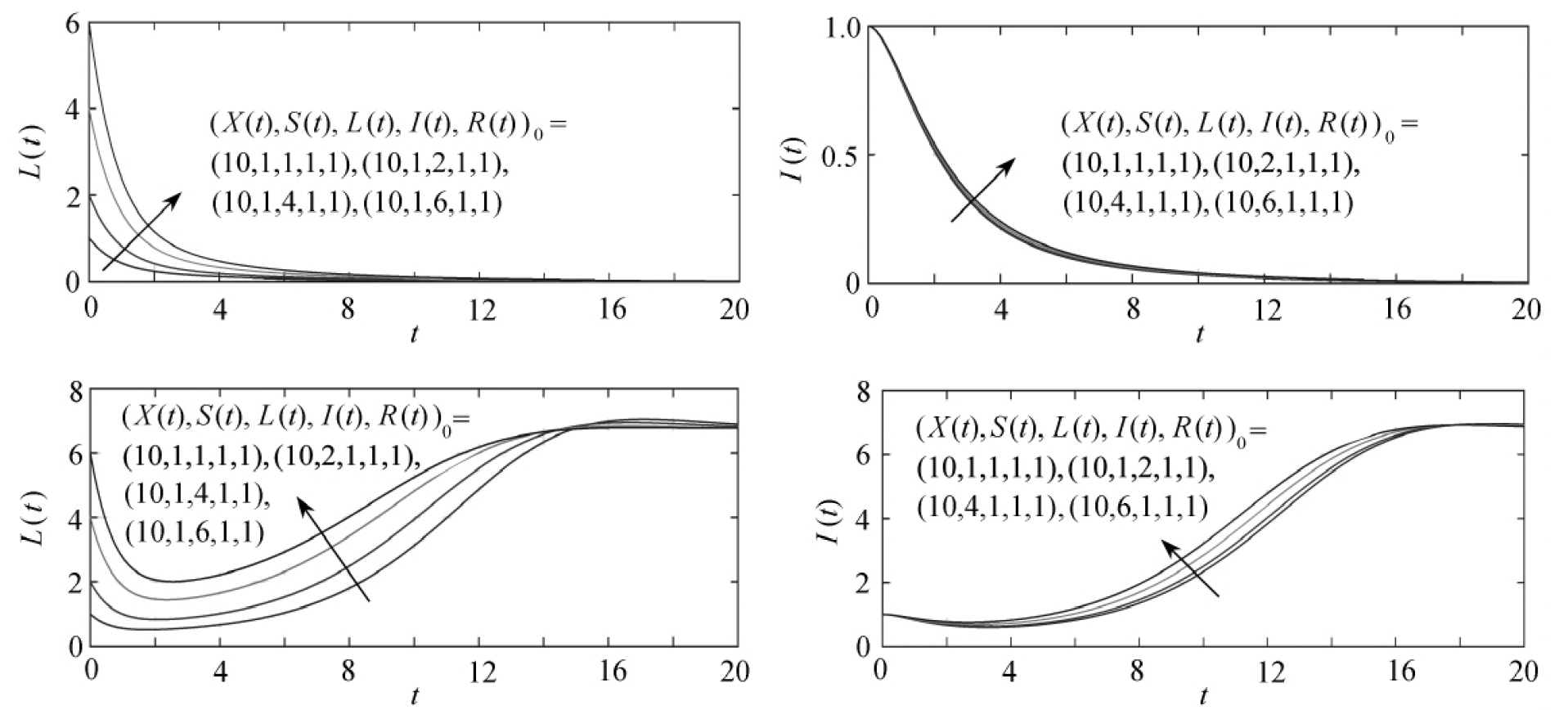
图1 E(0)在R0<1时是全局稳定的 图2 E(*)在R0>1时是全局稳定的
Fig. 1 E(0)is globally stable forR0<1 Fig. 2 E(*)is globally stable forR0>1
5 结 论
本文研究了考虑具有暂时免疫和母体抗体保护的轮状病毒传播模型(1),得到了其极限系统决定传染病流行与否的阈值参数R0.证明了极限系统(3)当R0≤1时无病平衡点是全局稳定的,且用斥子理论证明了地方病平衡点在R0>1时是持续生存的,并利用数学模拟验证了模型(1)的地方病平衡点在R0>1时是全局稳定的.
R0可表示为
注意到宿主处于未感染平衡态时,易感者的数量为S0,潜伏者和感染者的平均存活期分别为1/(α+μ)和1/(γ+μ),对易感者的感染率分别为β2和β1,同时潜伏者离开潜伏者仓室而成为感染者的比例为α/(α+μ),因此表达式αβ1S0/((α+μ)(γ+μ))和β2S0/(α+μ)分别表示感染者和潜伏者传播疾病的基本再生数,所以R0就是该模型表述下的轮状病毒传播基本再生数.
[1] 朱本辉, 李玉霞, 蔡燕杏, 等. 大剂量蒙脱石散治疗儿童轮状病毒肠炎的临床研究[J]. 河北医科大学学报, 2018,39(8): 966-968.(ZHU Benhui, LI Yuxia, CAI Yanxing, et al. Clinical study on the treatment of rotavirus enteritis in children with large dose of montmorillonite powder[J].Journal of Hebei Medical University, 2018,39(8): 966-968.(in Chinese))
[2] 冯秀, 游胜, 吴耀坚, 等. 一起学校轮状病毒感染性腹泻暴发疫情调查处置[J]. 应用预防医学, 2018,24(1): 74-76.(FENG Xiu, YOU Sheng, WU Yaojian, et al. Investigation and management of a school rotavirus infectious diarrhea outbreak[J].Journal of Applied Preventive Medicine, 2018,24(1): 74-76.(in Chinese))
[3] 姚淑雯, 梁卓夫, 林爱君, 等. 1 568例婴幼儿腹泻轮状病毒检测及流行病学特征分析[J]. 中国医药科学, 2013(21): 73-74.(YAO Shuwen, LIANG Zhuofu, LIN Aijun, et al. Detection of rotavirus and analysis of epidemiological features of 1 568 infants with diarrhea[J].China Medicine and Pharmacy, 2013(21): 73-74.(in Chinese))
[4] 魏升云, 张淑珍, 方鹤松. 轮状病毒肠炎研究进展[J]. 临床儿科杂志, 2004,22(6): 409-411.(WEI Shengyun, ZHANG Shuzhen, FANG Hesong. Research progress in rotavirus enteritis[J].Journal of Clinical Pediatrics, 2004,22(6): 409-411.(in Chinese))
[5] 陈阿群, 陈茂余, 韦志楠, 等. 2012—2016年广东省江门市其他感染性腹泻流行病学特征和监测结果分析[J]. 疾病监测, 2017,32(12): 936-939.(CHEN Aqun, CHEN Maoyu, WEI Zhinan, et al. Epidemiological characteristics and surveillance results analysis on other infectious diarrheal diseases in Jiangmen, 2012—2016[J].Disease Surveillance, 2017,32(12): 936-939.(in Chinese))
[6] 谭梦婷, 徐小红, 林俊仪, 等. 0至3岁婴幼儿轮状病毒感染流行病学特点及危险因素[J]. 中华实验和临床感染病杂志(电子版), 2018,12(4): 409-412.(TAN Mengting, XU Xiaohong, LIN Junyi, et al. Epidemilological characteristies and risk factors of infants aged 0~3 years with rotavirus infection[J].Chinese Journal of Experimental and Clinical Infectious Diseases(Electronic Edition), 2018,12(4): 409-412.(in Chinese))
[7] MASTRETTA E, LONGO P, LACCISAGLIA A, et al. Effect of lactobacillus GG and breast-feeding in the prevention of rotavirus nosocomial infection[J].Journal of Pediatric Gastroenterology and Nutrition, 2002,35(4): 527-531.
[8] SHIM E, FENG Z, MARTCHEVA M, et al. An age-structured epidemic model of rotavirus with vaccination[J].Journal of Mathematical Biology, 2006,53(4): 719-746.
[9] ATCHISON C, LOPMAN B, EDMUNDS W J. Modelling the seasonality of rotavirus disease and the impact of vaccination in England and Wales[J].Vaccine, 2010,28(18): 3118-3126.
[10] LINHARES A C, GABBAY Y B, FREITAS R B, et al. Longitudinal study of rotavirus infections among children from Belém, Brazil[J].Epidemiology and Infection, 1989,102(1): 129-145.
[11] ATKINS K E, SHIM E, PITZER V E, et al. Impact of rotavirus vaccination on epidemiological dynamics in England and Wales[J].Vaccine, 2012,30(3): 552-564.
[12] OMONDI O L, WANG C C, XUE X P, et al. Modeling the effects of vaccination on rotavirus infection[J].Advances in Difference Equations, 2015(1): 381-392.
[13] KRIBS-ZALETA C M, JUSOT J F, VANHEMS P, et al, Modeling nosocomial transmission of rotavirus in pediatric wards[J].Bulletin of Mathematical Biology, 2011,73(7): 1413-1442.
[14] WHITE L J, COX M J, MEDLEY G F. Cross immunity and vaccination against multiple microparasite strains[J].IMA Journal of Mathematics Applied in Medicine&Biology, 1998,15(3): 211-233.
[15] YOUNG G, SHIM E, ERMENTROUT G B. Qualitative effects of monovalent vaccination against rotavirus: a comparison of North America and South America[J].Bulletin of Mathematical Biology, 2015,77(10): 1854-1885.
[16] 黄璜, 单旭征, 龙云淑, 等. 传染病动力学模型在隔离预防轮状病毒医院感染中的应用[J]. 中国感染控制杂志, 2017,16(5): 470-473.(HUANG Huang, SHAN Xuzheng, LONG Yunshu, et al. Application of epidemic dynamics model in isolating hospital-acquired rotavirus infection[J].China Journal of Infection Control, 2017,16(5): 470-473.(in Chinese))
[17] 廖书, 杨炜明. 考虑媒体播报效应的双时滞传染病模型[J]. 应用数学和力学, 2017,38(12): 1412-1424.(LIAO Shu, YANG Weiming. An epidemic model with dual delays in view of media coverage[J].Applied Mathematics and Mechanics, 2017,38(12): 1412-1424.(in Chinese))
[18] 张双德, 郝海. 一类SARS传染病自治动力系统的稳定性分析[J]. 应用数学和力学, 2005,26(7): 840-846.(ZHANG Shuangde, HAO Hai. Analysis on the stability of an autonomous dynamics system for SARS epidemic[J].Applied Mathematics and Mechanics, 2005,26(7): 840-846.(in Chinese))
[19] FONDA A. Uniformly persistent semidynamical systems[J].Proceedings of the American Mathematical Society, 1988,104(1): 111-116.
[20] SIMITH H L. Monotone dynamical systems: an introduction to the theory of competitive and cooperative systems[J].Mathematical Surveys and Monographs, 1995,41(5): 174. DOI: org/10.1090/surv/041.
[21] ZHAO X Q.Dynamical Systems in Population Biology[M]. New York: Springer-Verlag, 2003.