引 言
近年来，有许多学者关注于具有间断初值Riemann问题的偏微分方程及其在流体力学上应用的研究，例如Sen等[1]研究了一类严格双曲守恒律系统的Riemann问题在非线性弹性力学和气体动力学中的应用，通过黏度消失得到Riemann问题解的存在性和唯一性；Galaktionov[2]研究了一维自相似薄膜方程中具有不连续数值的Riemann型问题，在+1和-1处退化，各有一个自相似的解；瞿霞[3]研究了Euler方程组的Riemann问题的解中波之间的连接分析和几何性质,研究了波线的单调性、凹凸性等性质，并在考虑气体燃烧后,研究了Euler方程组Riemann问题的波之间的连接状态以及几何性质；Shen[4]研究了Coulomb摩擦项无压Euler系统的Riemann问题，并对其进行求解，得到当摩擦项消失时Riemann解收敛于无压Euler系统的相应Riemann解；Wang[5]研究了零压气体动力学中一维系统的质量、动量和能量守恒律的初始数据Riemann问题，在广义Rankin-Hugoniot条件和熵条件下，构造得到了包含三角激波的广义解的全局存在性．尤其是对于Navier-Stokes方程Riemann问题的研究，近年来取得了很大的进步，Zhang等[6]研究了具有Riemann初始数值的一维可压缩等熵Navier-Stokes方程在两种激波复合情况下的零耗散极限问题，应用多重尺度、近似解构造和能量估计的方法得到了方程解的存在唯一性；Huang等[7]研究了一类可压缩Navier-Stokes方程对由激波和稀疏波叠加组成的Euler方程Riemann解黏性消失的极限，证明了可压缩Navier-Stokes方程存在一系列光滑解，并得到这些解从初始层和激波层以黏度和导热系数的速率收敛到Riemann解．文献[8-9]研究了一维可压缩的Navier-Stokes-Kortewey Euler系统的Riemann问题，证明了一类光滑解的存在性．等离子体作为一个新的研究介质，Burgers方程在等离子体中的应用相当广泛．Yoshia[10]对于Burgers方程在单流体动力学、双流体等离子体模型的通道以及鲁棒控制上进行了奇摄动简单研究；Ferdousi等[11]研究了由惯性离子、非广泛电子和非广泛正电子组成的非磁化等离子体系统中圆柱形和球形离子声波激波的性质，并利用降维摄动技术导出了一个改进的Burgers方程，得到了它的数值解；Yang等[12]研究了一类局部分数型二维Burgers方程，首次提出了局部分数Riccati微分方程法，给出了不可微型的行波变换，得到了该问题的不可微精确行波解，为求解数学物理中的局部分数阶非线性偏微分方程(LFNPDEs)提供了一种有效的方法；Seadawy[13]分析了二维非线性离子声孤立波和激波在耗散量子等离子体中的传播，利用还原微扰理论，将耗散量子等离子体中的二维离子声孤波导出为非线性的Kadomtsev-Petviashvili-Burgers(KPB)方程，利用扩展直接代数映射，扩展sech、tanh和扩展直接代数sech方法，研究了二维非线性KPB方程的离子孤立行波解，得到了二维非线性KPB方程的解析解和数值解．Fang等[14]以辐射流体动力学为背景研究了具有不连续源项的Burgers方程的Riemann问题，通过考虑不连续源项对Riemann波传播的影响，构造了Riemann问题的全局解并通过数值模拟得到解．Rao等[15]通过构造热方程的自相似解来表示非齐次Burgers方程的解，得到了非齐次Burgers方程解的渐近性特征．综上所述，对于初值间断Burgers方程的奇摄动解析尚未有详细报道．
本文讨论了一类具有特征间断初值的Burgers方程．当Reynolds数很大时，在高温条件下，由于激光脉冲信号在金属板表面产生的等离子体所产生的有限振幅波传播的问题，可用一类具有间断初值的奇摄动Burgers方程来描述．由于初值是常值并且间断，退化解在x-t平面上产生两条分界线，将x-t的正半平面分成三个区域，在分界线上退化解连续而一阶导函数不连续，应用奇摄动渐近展开的方法得到外解和内部层矫正两部分，外解为一系列一阶偏微分方程．其中首项是拟线性方程，高阶项为线性方程；矫正函数首项为二阶非线性抛物方程，高阶项为二阶线性抛物方程满足抛物方程，即得到了抛物型特征边界，通过求解该抛物型特征边界得到矫正函数．由于得到了抛物型特征边界，因此需要求解二阶非线性抛物方程，并且需要估计解的一阶导数，从而产生了一定的困难．本文通过综合应用Hopf-Cole变换、Fourier变换得到相应非线性抛物方程的解，并对解的一阶导数有界性进行估计，为求高阶项的解奠定了基础．最后进行余项估计，得到了形式渐近解的一致有效性．
1 模 型 建 立
当Reynolds数很大时，在高温条件下激光在金属板表面产生等离子体，由于激光脉冲信号，此问题可用具有间断初值的奇摄动Burgers方程来描述：
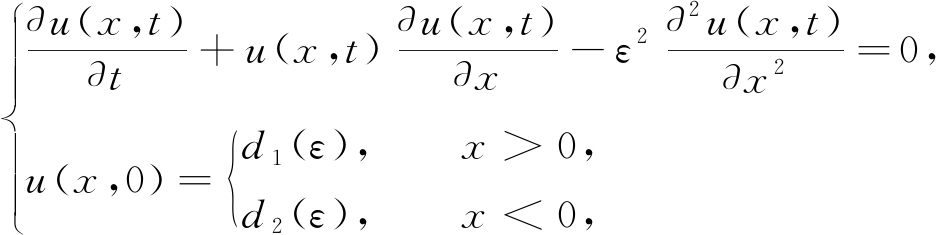
(1)
式中u是质点运动的速度，x是空间变量，t是时间，ε是正的小参数．
现在做如下的假设：
(H1) (x,t)∈(-∞,+∞)×[0,T],其中T是有限值;
表示给定的初始值且均为常数．
设区域Ω=Ω1∪Ω2∪Ω3．区域Ω1={(x,t)∈R×[0,T]|x≥d10t}，区域Ω2={(x,t)∈R×[0,T]|d20t≤x≤d10t}，区域Ω3={(x,t)∈R×[0,T]|x≤d20t}．
2 形 式 展 开
2.1 外部解形式渐近展开
设式(1)外部解为
代入式(1) 中，关于ε做摄动展开，并比较ε的同次幂系数，可得
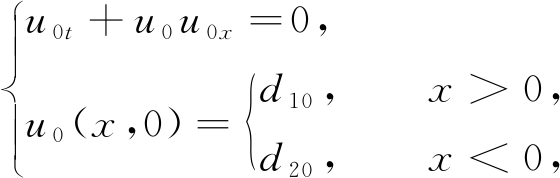
(2)
(3)
⋮
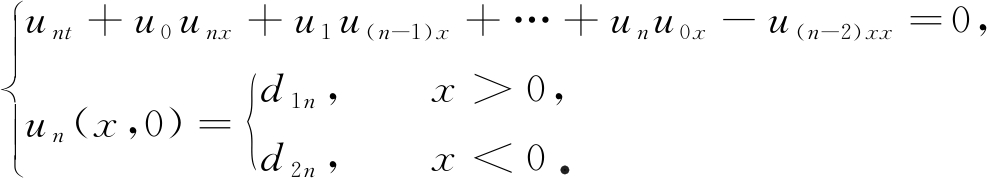
(4)
对式(2)～(4)求解，可得
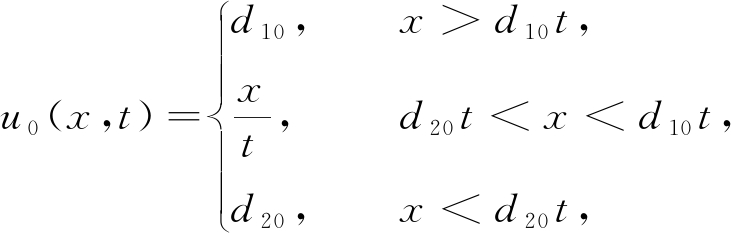
(5)
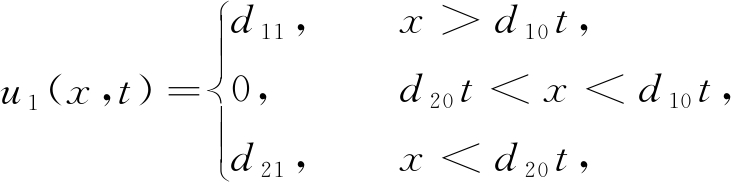
(6)
⋮
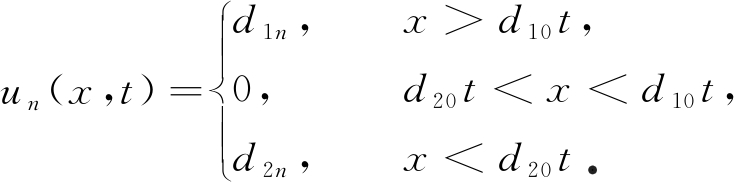
(7)
2.2 内部解形式渐近展开
在区域Ω1={(x,t)∈R×[0,T]|x≥d10t}上，设式(1)形式解为
其中
将形式解代入式(1)，可得
(8)
其中
可得
(9)
进一步化简，可得
(10)
由于
因此
按ε的幂指数形式展开，可得
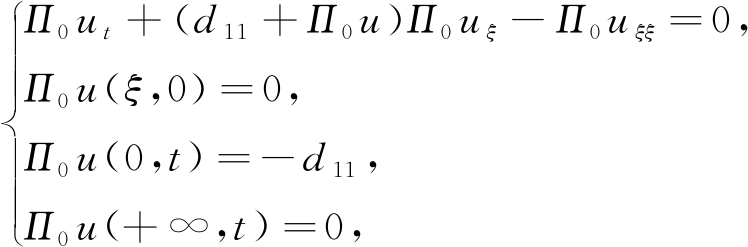
(11)
⋮
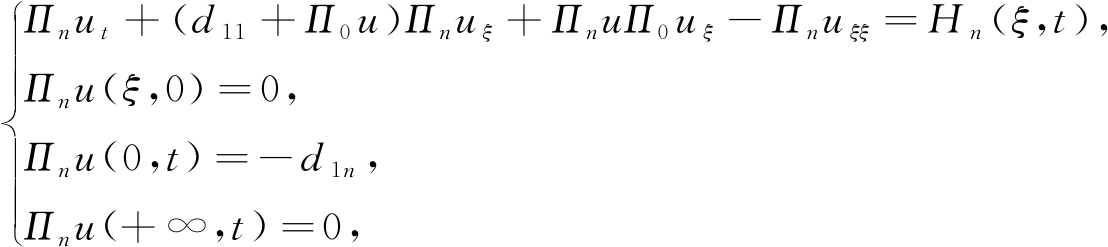
(12)
其中Hn(ξ,t)是关于ui(1≤i≤N)和Πju(0≤j≤N-1)的已知函数．
命题1 式(11)的解为Π0u=-2Vξ/V-d11．
证明 对式(11)做变换，令
可得
(13)
对式(13)做变换，令
可得
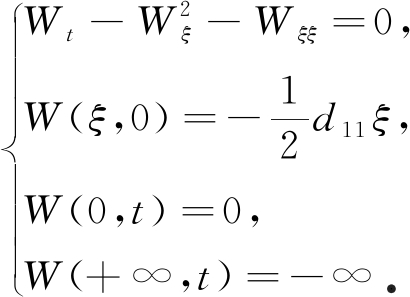
(14)
对式(14)做Hopf-Cole变换，令V=eW，可得
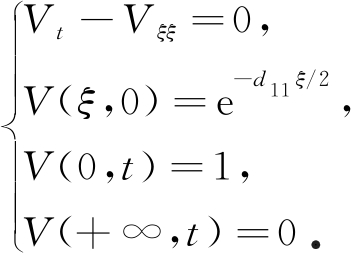
(15)
运用齐次化原理，对式(15)进行齐次化变换，令V=f+e-d11ξ/2，可得
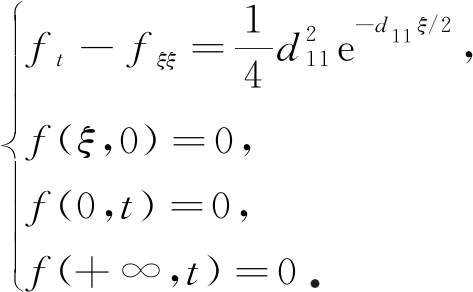
(16)
对式(16)关于ξ做Fourier变换及Fourier逆变换，求解可得
(17)
则可得
V=e-d11ξ/2+
(18)
2(ξ-x)e-(ξ-x)2/(4(t-τ))]dxdτ,
(19)
因此可得
(20)
命题
证明 由极值原理可得Π0u有界，|Π0u|≤|d11|．不妨令s=t-τ，则可得
2(ξ-x)e-(ξ-x)2/(4s)]dxds，
由于被积函数
e-(ξ-x)2/(4s)-e-(ξ+x)2/(4s)=e-(ξ+x)2/(4s)(eξx/s-1)≥0，
故V>0，Vt>0则VVt>0．
由
可得
故
命题3 式(12)的解存在唯一．
证明 假设式(12)存在两个解Πnu(ξ,t)和
令
则满足
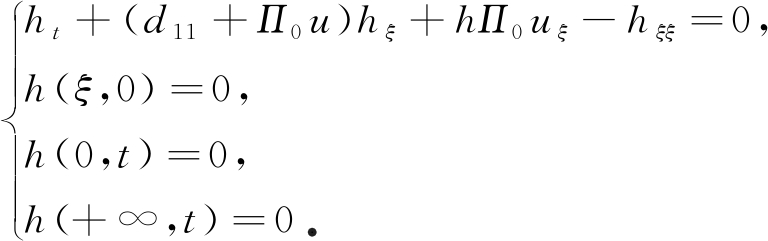
(21)
令h=eλtZ，则ht=eλtZt+λeλtZ，hξ=eλtZξ,hξξ=eλtZξξ,式(21)可变为
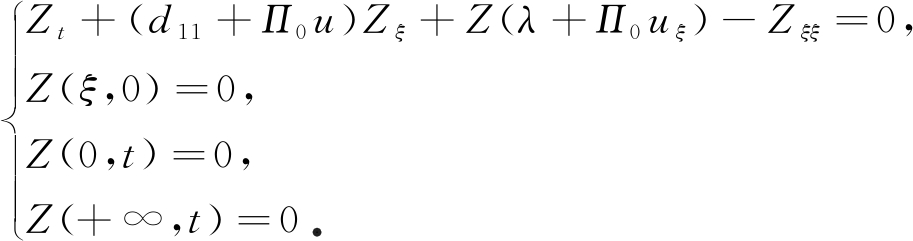
(22)
由于
取
则
假设Z(ξ,t)在(ξ0,t0)处达到最大值，其中
则当ξ0>0，t0>0时，有Z(ξ0,t0)≥0，则由极值原理可得矛盾，因此Z(ξ0,t0)≤0；当ξ0=0或t0=0时，由定解条件可得Z(ξ0,t0)=0．同理可得Z(ξ,t)≥0，所以Z(ξ,t)=0．故解的唯一性得证．再由文献[16]中古典解的存在唯一性定理8.2.5可得古典解的存在性．故式(12)的解存在唯一性得证．
在区域Ω3={(x,t)∈R×[0,T]|x≤d20t}上，设式(1)形式解为
其中
将形式解代入式(1)，可得
(23)
其中
可得
(24)
进一步化简，可得
(25)
由于
因此
按ε的幂指数形式展开，可得
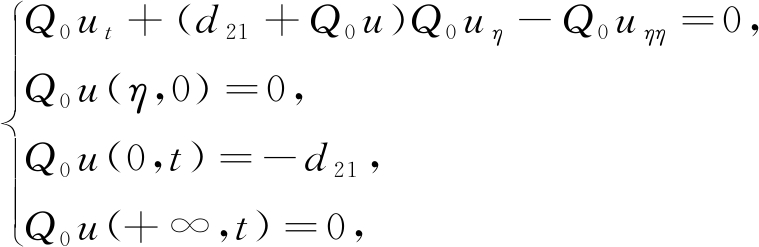
(26)
⋮
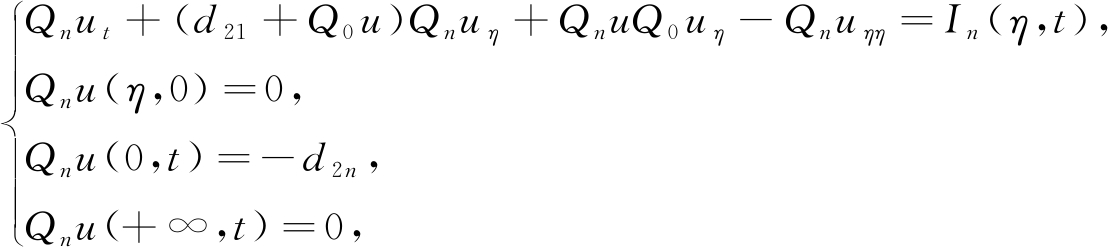
(27)
其中In(η,t)是关于ui(1≤i≤N),Πju(0≤j≤N-1)的已知函数．
式(26)的求解方法与式(11)相同，可得
(28)
同理
有界，Qnu的解存在且唯一．
3 余 项 估 计
定理
证明 设
将其代入式(1)中，可得
(29)
其中G(x,t)是关于
的已知函数．
令R=eβtJ，则Rt=eβtJt+βeβtJ，Rx=eβtJx,Rxx=eβtJxx，其中取
式(29)可变为
(30)
其中 g(x,t)=e-βtG(x,t)．
下面分区域进行估计：
1) 在区域Ω1={(x,t)∈R×[0,T]|x≥d10t}上，有
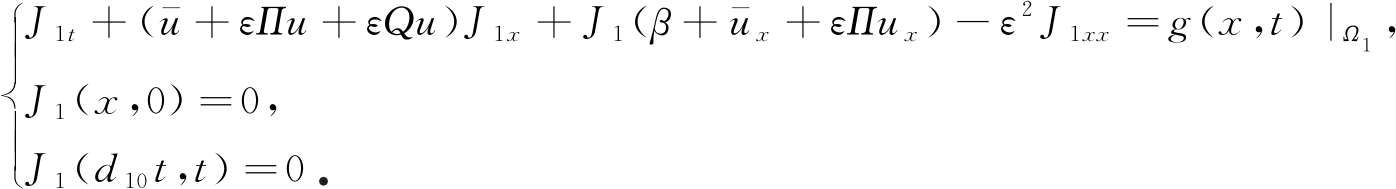
(31)
由于
即
令|g(x,t)|Ω1≤m1，在区域
上J1(x,t)存在最小值．设J1在(x0,t0)达到最小值，其中x0≥d10t，0≤t0≤T．
当t0=0，x0=d10t时，由定解条件可得J1(x,0)=0；
当0<t0≤T，x0>d10t时，由
可得
故可得
同理，可证得最大值点J1(x0,t0)，且
成立．
由极值原理可得， 对于任意的(x,t)∈Ω1， 有
成立, 即
2) 在区域Ω2={(x,t)∈R×[0,T]|d20t≤x≤d10t}上，有
(32)
由于
即
令|g(x,t)|Ω1≤m2，设J2在(x0,t0)达到最小值，其中d20t≤x0≤d10t，0≤t0≤T．
当x0=d10t，x0=d20t时，由定解条件可得J2(x,0)=0;
当0<t0<T，d20t<x0<d10t时，由
可得
故可得
同理，可证得最大值点J2(x0,t0)，且
成立．
由极值原理可得， 对于任意的(x,t)∈Ω2， 有
成立， 即
3) 在区域Ω3={(x,t)∈R×[0,T]|x≤d20t}上，有
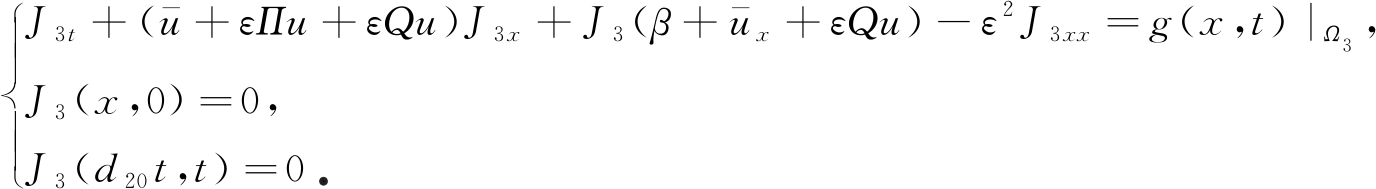
(33)
同理可得对于任意的(x,t)∈Ω3，有
成立，即
综上可得
|R(x,t)|≤M，
故R有界，即形式渐近解一致有效．
4 结 束 语
本文建立了具有特征间断的Burgers方程模型，该模型来源于在高温、高压条件下将初始时刻常值间断激光脉冲信号打在金属钢板表面形成等离子体波的情形．应用奇摄动渐近展开的方法，得到了形式渐近解，形式渐近解包含外解和内解两部分，在求解内解过程中，通常出现的边界为常边界和抛物边界．由于间断性传递，根据外解我们将区域分成三部分，在分界线上进行矫正；由于初值是间断常数，因此得到的分界线在特征线上即为抛物型特征边界；其内解呈现为抛物方程，实际是一个常系数Burgers方程，利用Hopf-Cole变换、齐次化原理、Fourier变换及Fourier 逆变换得到解的表达式．为了求解高阶展开式，由于常系数Burgers方程内解导数符号的正负很难判断，因此需要得到一阶展开式导数的有界性．本文通过对一阶展开式的表达式进行求导，并应用极值原理证明了一阶导数的有界性，从而为求解内解的高阶项奠定了基础．最后进行余项估计，分区域进行估计，由于分界线恰好是在特征边界上，因此为估计带来了一定的困难，进行适当变换并应用极值原理进行估计，得到了形式渐近解的一致有效性．
激光照射在坯料的表面形成等离子体诱发超声波，所产生的能量传递到需要被加工的坯料内部，从而实现在坯料的内部进行加工，即所谓的“内加工”方法．激光“内加工”方法在机械加工上被广泛应用．由于激光照射产生的脉冲信号在数学上反应为间断初值，因此可用间断初值的Burgers方程奇摄动问题来描述激光产生的超声波运动．应用奇异摄动方法可以得到解析近似解，对超声波的运动得到了详细而精确的描述，为激光“内加工”控制奠定了理论基础，从而达到工业生产的目的．本文的方法也可用于加热诱导半导体材料内部原子扩散、透明材料表面及内部制备．今后我们将继续研究具有间断初值的变系数Burgers方程模型，甚至将其推广到高维领域．
[1] SEN A, RAJA SEKHAR T. Delta shock wave as self-similar viscosity limit for a strictly hyperbolic system of conservation laws[J].Journal of Mathematical Physics, 2019,60(5): 051510.
[2] GALAKTIONOV V A. On self-similar collapse of discontinuous data for thin film equations with doubly degenerate mobility[R/OL]. 2009. [2019-09-12]. http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.243.8638& rep=rep1& type=pdf.
[3] 瞿霞. 流体力学中Euler方程组的Riemann问题[D]. 硕士学位论文. 上海: 上海师范大学, 2019.(QU Xia. Riemann problem of Euler equations in fluid mechanics[D]. Master Thesis. Shanghai: Shanghai Normal University, 2019.(in Chinese))
[4] SHEN C. The Riemann problem for the pressureless Euler system with the Coulomb-like friction term[J].IMA Journal of Applied Mathematics, 2015,81(1): 76-99.
[5] WANG L. The Riemann problem with delta data for zero-pressure gas dynamics[J].Chinese Annals of Mathematics(Series B), 2016,37(3): 441-450.
[6] ZHANG Y H, PAN R H, TAN Z. Zero dissipation limit to a Riemann solution consisting of two shock waves for the 1D compressible isentropic Navier-Stokes equations[J].Science China:Mathematics, 2013,56(11): 2205-2232.
[7] HUANG F, WANG Y, YANG T. Vanishing viscosity limit of the compressible Navier-Stokes equations for solutions to a Riemann problem[J].Archive for Rational Mechanics and Analysis, 2012,203(2): 379-413.
[8] CHEN Z, XIONG L, MENG Y J. Convergence to the superposition of rarefaction waves and contact discontinuity for the 1-D compressible Navier-Stokes-Korteweg system[J].Journal of Mathematical Analysis and Applications, 2014,412(2): 646-663.
[9] CHEN Z Z, CHAI X J, WANG W J. Convergence rate of solutions to strong contact discontinuity for the one-dimensional compressible radiation hydrodynamics model[J].Acta Mathematica Scientia, 2016,36(1): 265-282.
[10] YOSHIA Z. Singular perturbation and scale hierarchy in plasma flows[C]//Autumn College on Plasma Physics:Long-Lived Structures and Self Organization in Plasmas. Trieste, Italy, 2003.
[11] FERDOUSI M, YASMIN S, ASHRAF S, et al. Cylindrical and spherical ion-acoustic shock waves in nonextensive electron-positron-ion plasma[J].IEEE Transactions on Plasma Science, 2015,43(2): 643-649.
[12] YANG X J, GAO F, SRIVASTAVA H M. Exact travelling wave solutions for the local fractional two-dimensional Burgers-type equations[J].Computers&Mathematics With Applications, 2017,73(2): 203-210.
[13] SEADAWY A R. Ion acoustic solitary wave solutions of two-dimensional nonlinear Kadomtsev-Petviashvili-Burgers equation in quantum plasma[J].Mathematical Methods in the Applied Sciences, 2017,40(5): 1598-1607.
[14] FANG B, TANG P, WANG Y G. The Riemann problem of the Burgers equation with a discontinuous source term[J].Journal of Mathematical Analysis and Applications, 2012,395(1): 307-335.
[15] 拉奥 C S, 亚达夫 M K. 非齐次Burgers方程解的渐近性行为[J]. 应用数学和力学, 2010,31(9): 1133-1139. (RAO C S, YADAV M K. Asymptotic behavior of solutions to nonhomogeneous Burgers equation[J].Applied Mathematics and Mechanics, 2010,31(9): 1133-1139.(in Chinese))
[16] 伍卓群, 尹景学, 王春明. 椭圆与抛物型方程引论[M]. 北京: 科学出版社, 2003.(WU Zhuoqun, YIN Jingxue, WANG Chunming.Introduction to Elliptic and Parabolic Equations[M]. Beijing: Science Press, 2003.(in Chinese))