引 言
Sobolev方程是流体力学的重要方程之一, 是许多实际物理问题的模型方程．但是当其原函数或初边值函数复杂或计算域不规则时, 通常无法求出解析解, 人们不得不用数值方法求解其数值解．计算流体力学和计算数学工作者提出了很多有效的数值算法, 尤其是利用有限元方法进行数值求解．如扩展特征混合有限元方法[1],H1-Galerkin混合有限元法[2], 扩展混合有限元方法[3]等．另外, 文献[4]给出了一种降阶外推配谱方法, 文献[5]给出了一种降阶外推Crank-Nicolson(CN)有限体积元方法, 文献[6-7]分别提出了两种不同的降阶外推有限差分方法．
本文将时空有限元方法和混合有限元方法相结合,研究如下的Sobolev方程：
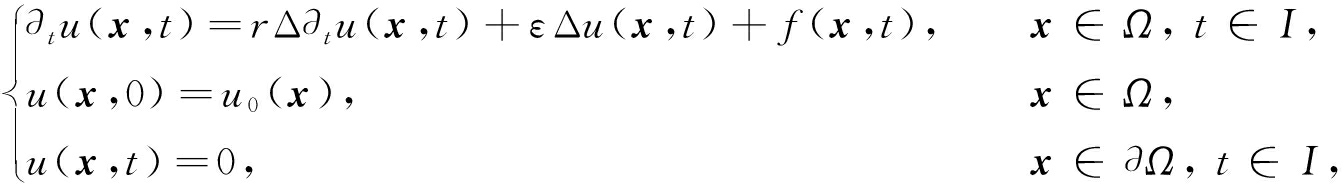
(1a)
(1b)
(1c)
其中x=(x1,x2,…,xd)T, 而Ω是Rd(d=2,3)中的有界多边形或多面体区域, 光滑边界记为∂Ω, 系数r和ε是两个正常数, I=[0,T]是时间区间, u0(x)是给定的初值, f(x,t)是已知的源函数．
对上述Sobolev方程,目前还没有见到通过引入辅助变量构造混合连续时空有限元离散格式的研究．因此,本文利用统一处理时空两个变量的时空有限元方法,构造不同于传统混合有限元的混合时空有限元方法,使得所构造的方法既有混合有限元方法降阶方程的优点,又可以同时得到时间和空间两个方向的形式高精度．特别地,本文将证明混合时空有限元解的稳定性、存在唯一性,并推导出数值解的误差估计．
1 Sobolev方程的混合连续时空有限元离散格式
为了构造上述Sobolev方程(1)的混合连续时空有限元离散格式,首先引入一些定义和概念．本文用到的Sobolev空间和范数以及相应的理论都是标准的,其中L2(Ω)相应的内积和范数分别记为〈·〉和‖·‖．用‖·‖p表示空间Hp(Ω)(p≥0)的范数,当p=0时,Hp(Ω)即为L2(Ω)空间,空间
在传统Sobolev空间的基础上,引入空间
及其相应的范数
特别地,当l=0,p=0,1时,其相应的范数分别为
和
记W=L2(Ω),定义散度空间
[L2(Ω)]d的内积定义为
相应的范数定义为
其中二维散度空间,即d=2时为
V=H(div;Ω)={q∈(L2(Ω))×L2(Ω), ·q∈L2(Ω)},
相应的范数定义为
‖q‖V=(‖q‖2+‖·q‖2)1/2．
设X是自反Banach空间,
是连续的}．上面引进空间可分别简记为Hl(I;Hp),L2(I;L2),L2(I;H1)及C(I;X)．
对空间区域Ω采用凸多边形或空间多面体进行拟一致剖分,将该剖分记为Th,剖分单元记为K,剖分单元最大直径为h,则Th={K}．空间为二维时,有限元子空间可以是Raviart-Thomas元,三维时可为Raviart-Thomas-Nédélec元．进一步对时间区间[0,T]进行剖分,0=t0<t1<…<tN-1<tN=T,剖分区间为In=[tn-1,tn](n=1,2,…,N),步长τn=tn-tn-1(n=1,2,…,N),此剖分不一定是等距剖分,记τ=max1≤n≤N τn．令
和
分别是L2(Ω)和H(div;Ω)的有限维子空间,此处设Pm(K)为K上不超过m次的多项式空间．记
和
为在空间区域和时间区间In上的有限维空间,即
即它们在时间区间In上是不超过l次的多项式．
为构造方程(1)的混合连续时空有限元格式,首先引入中间变量q=-(r∂tu+εu),则原方程化为
(2a)
(2b)
进一步得方程(2)的变分形式为
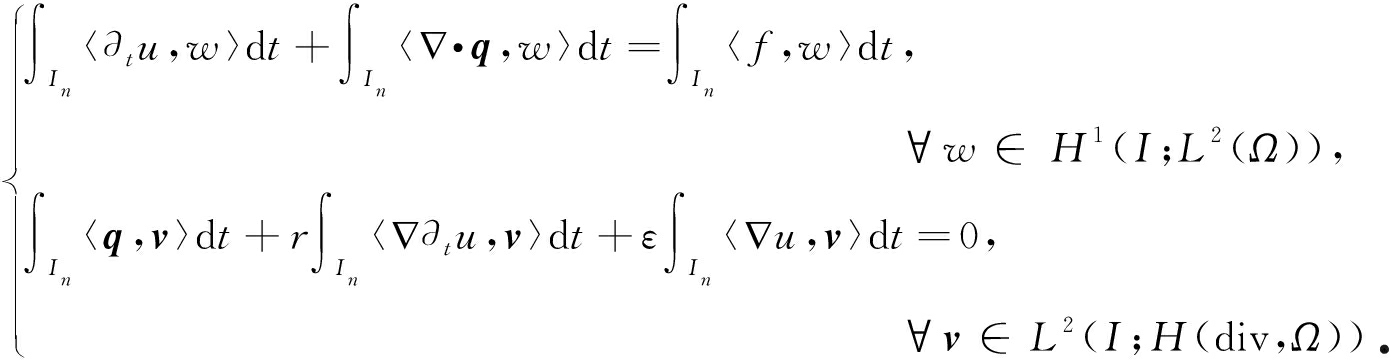
(3a)
(3b)
因此,问题(1)的混合连续时空有限元格式为：求
对
满足
(4)
uτ,vτ〉dt=0．
(5)
2 解的稳定性和存在唯一性
定理1 混合连续时空有限元格式(4)和(5)的解{(uτ,qτ)}满足
‖uτ(tn)‖2+‖uτ(tn)‖2≤
uτ(t0)‖2),
(6a)
‖
uτ(t0)‖2),
(6b)
uτ(t0)‖2+‖uτ(t0)‖2),
(6c)
其中c表示与时间步长τ和空间步长h无关的一般常数．
证明 在式(4)中取wτ=∂tuτ,得
(7)
在式(5)中取vτ=∂tuτ,得
∂tuτ,
uτ,∂tuτ〉dt=0．
(8)
由式(7)和(8)得
(9)
注意到‖·‖≤c‖·‖0,对上式右端利用Cauchy-schwarz表达式,得到
uτ(tn)‖2≤
uτ(tn-1)‖2≤
c‖f‖L2(In;L2)‖
uτ(tn-1)‖2≤
uτ(tn-1)‖2．
化简上式,得到
uτ(tn)‖2≤
uτ(tn-1)‖2．
对上式从1至n求和,并化简,可得
uτ(tn)‖2≤
uτ(t0)‖2)．
(10)
类似地,在式(4)中取wτ=uτ得
在式(5)中取vτ=uτ,有
∂tuτ,
uτ,uτ〉dt=0．
由上两式整理得
∂tuτ,
uτ,
即
uτ(tn)‖2+ε‖
uτ(tn-1)‖2．
注意到‖·‖≤c‖·‖0,对上式右端利用Cauchy-schwarz表达式,得到
uτ(tn)‖2+ε‖
uτ(tn-1)‖2≤
c‖f‖L2(In;L2)·‖
uτ(tn-1)‖2≤
uτ(tn-1)‖2．
化简上式,可得
‖uτ(tn)‖2+r‖uτ(tn)‖2+ε‖
uτ(tn-1)‖2．
对上式从1至n求和,并化简,可得
‖uτ(tn)‖2+‖uτ(tn)‖2+‖
c(‖f‖L2(0,tn;L2)+‖uτ(t0)‖2+‖uτ(t0)‖2)．
(11)
由式(10)和(11)得时间节点处的性质
‖uτ(tn)‖2+‖
uτ(t0)‖2)
及区间整体稳定性
‖
uτ(t0)‖)．
由此得证定理1中的式(6a)和(6b)．
进一步地,在式(5)中取vτ=qτ,则
uτ,qτ〉dt=0．
(12)
利用Cauchy-Schwarz不等式,并结合式(6a)和(6b)的结论,整理得
uτ(t0)‖2+‖uτ(t0)‖2)．
(13)
至此定理1证毕．
我们知道混合时空有限元格式(4)和(5)构成关于uτ和qτ的线性方程组,因而解的唯一性等价于相应的齐次线性方程组仅有零解,即f=0时仅有零解．若假定相关函数及其导数等相关的初始值满足稳定性条件,则由定理1易知,当f=0,且uτ(t0),uτ(t0),∂tuτ(t0)均为0时,有uτ=0,qτ=0,即得如下解的唯一性定理．
定理2 混合时空有限元格式(4)和(5)的解存在且唯一．
3 混合连续时空有限元解的误差估计
为了进行误差估计,首先定义函数
的Ritz投影算子
满足
〈u,ψ〉=〈
ψ 〉, ∀ψ∈Wh．
(14)
由标准有限元理论(可参见文献[8]中的定理2.1.20)可知,如果u∈L2(Ω)∩Hr(Ω),则存在与空间剖分步长h无关的正常数c,满足
‖
u‖,
(15)
及
(16)
其中 1≤r≤m+1．
此算子可在L2意义下延拓到时空投影
即
〈
(17)
类似地，定义函数u∈H1(I)的关于时间t的投影算子
满足
(18)
由标准有限元理论(可参见文献[8]的定理2.1.20)可知,存在与时间步长τ无关的正常数c,使得
(19)
和
(20)
其中1≤r≤l+1,并满足初值条件
此算子可在L2意义下延拓到时空投影
即
〈
(21)
引理1 如果u∈H2(0,T;L2(Ω))∩L2(0,T;H2(Ω)),则有
(
(22a)
u)t,
(22b)
(22c)
证明 设
且满足ψ(·,0)=ψ(·,T)=0．由于
〈
ψ〉dt=〈ut,ψ〉dt=-〈u,ψt〉dt=
-〈ψt〉dt=〈(
ψ〉dt,
所以
(
于是,式(22a)得证．
同理,
u)t,φt〉dt=〈ut,φt〉dt=-〈ut,φt〉dt=
φt〉dt=〈
由此可得式(22b)．
由
的定义和
的定义及式(22b),有
〈
φt〉dt=〈
u)t,φt〉dt=
〈ut,φt〉dt=〈
φt〉dt,
由此可得式(22c)．引理1证毕．
进一步地,注意到
并利用式(16)和(22),我们有如下估计．
引理2 如果v∈Hr(0,tn;Hm+1(Ω))∩Hl+1(0,tn;Hs(Ω))，则
(23)
再定义函数q∈H(div;Ω)的L2投影算子
满足
(24)
同样地，此算子可在L2意义下延拓到时空投影
即
(25)
我们也定义q∈[L2(I)]2的投影算子
满足
(26)
此算子可延拓到时空投影
满足
(27)
则由标准有限元理论(参见文献[8]中的定理2.1.19),得
(28)
及
(29)
其中1≤r≤m+1,1≤p≤l+1．类似于引理1和引理2的讨论,对引入的投影
和
我们有如下性质．
引理3 如果q∈H(div;Ω)∩[H1(Ω)×H1(Ω)] ,则有
(30a)
q),
(30b)
(30c)
证明 这里只给出式(30a)的证明,其他证明和引理1类似．由
和
的定义及分部积分,有
引理4 如果ω∈Hr(0,T;[Hm+1(Ω)]2)∩Hl+1(0,T;[Hs(Ω)]2),则
(31)
为证明混合连续时空有限元解的误差估计,我们将误差改写为下面形式,记
则得到误差方程
wτ〉dt=0,
(32)
ηt+ζt) ,vτ〉dt+
(η+ζ),vτ〉dt=0．
(33)
定理3 设{u,q}和{uτ,qτ}分别是方程的精确解和混合时空连续有限元数值解．若PxPtu(0)=uτ(0)=0,则有下列误差估计:
‖(u-uτ)t‖L2(In;L2)+‖(u-uτ)‖L2(In;L2)≤
c [hm+1(‖ut‖L2(0,T;Hm+1)+‖ut‖L2(0,T;Hm+1)+‖u‖L2(0,T;Hm+1))+
τl+1(‖ut‖Hl+1(0,T;L2)+‖ut‖Hl+1(0,T;L2)+‖u‖Hl+1(0,T;L2))],
(34)
‖q-qτ‖L2(In;L2)≤
c[hm+1(‖q‖L2(0,tn;Hm+1)+‖ut‖L2(0,T;Hm+1)+‖ut‖L2(0,T;Hm+1)+
‖u‖L2(0,T;Hm+1))τl+l(‖q‖Hl+1(0,tn;L2)+‖ut‖Hl+1(0,T;L2)+
‖ut‖Hl+1(0,T;L2)+‖u‖Hl+1(0,T;L2))]．
(35)
证明 令式(32)中wτ=ζ,得
ζ〉dt=0．
在式(33)中令vτ=ζ,有
ηt+ζt) ,ζ〉dt+
(η+ζ),ζ〉dt=0．
整理上面两式,得
ε‖
ζ(tn)‖2+‖ζ(tn)‖2≤
r‖ζ(tn-1)‖2+‖ζ(tn-1)‖2．
反复利用上面不等式迭代,并注意
设ζ(0)=
ζt(0)=
结合引理2,得
‖
ζ(tn)‖2+‖ζ(tn)‖2≤
(36)
在式(32)中,令wτ=ζt,得
ζt〉dt=0．
在式(33)中令vτ=ζt,有
ηt+ζt) ,ζt〉dt+
(η+ζ),ζt〉dt=0．
所以我们有
ηt+ζt) ,ζt〉dt+
(η+ζ),ζt〉dt=0．
类似前面的讨论,利用迭代,我们有
‖
ζt(tn)‖2≤
(37)
所以
‖(u-uτ)t‖L2(In;L2)+‖(u-uτ)‖L2(In;L2)≤
c (hm+1(‖ut‖L2(0,T;Hm+1)+‖ut‖L2(0,T;Hm+1)+‖u‖L2(0,T;Hm+1))+
τl+1(‖ut‖Hl+1(0,T;L2)+‖ut‖Hl+1(0,T;L2)+‖u‖Hl+1(0,T;L2)))．
(38)
进一步地,在式(33)中,令vτ=ξ,得到
ηt+
(η+ζ),ξ〉dt=0．
即得
‖
(39)
因此,结合引理4和式(33),可得q的估计式
c (hm+1(‖q‖L2(0,T;Hm+1)+‖ut‖L2(0,T;Hm+1)+
‖ut‖L2(0,T;Hm+1)+‖u‖L2(0,T;Hm+1))+
τl+1(‖q‖Hl+1(0,T;L2)+‖ut‖Hl+1(0,T;L2)+
‖ut‖Hl+1(0,T;L2)+‖u‖Hl+1(0,T;L2)))．
(40)
定理4证毕．
注1 定理3得到的误差估计是最优的．
4 结论和展望
本文通过引进辅助函数，建立了Sobolev方程的混合时空有限元法．讨论了混合时空有限元解的存在唯一性和稳定性,并借助于时空投影算子详细推导出了混合时空有限元解的误差估计．这些理论方法是我们第一次给出的．到目前为止,还没有关于Sobolev方程的混合时空有限元方面类似的研究．因此,本文是Sobolev方程的混合时空有限元法方面一个新的发展．
[1] 陈凤欣, 陈焕贞. Sobolev方程的扩展特征混合有限元方法[J]. 高等学校计算数学学报, 2010, 32(4): 291-302.(CHEN Fengxin, CHEN Huanzhen. The expanded characteristics-mixed finite element method for Sobolev equations[J]. Numerical Mathematics: a Journal of Chinese University, 2010, 32(4): 291-302.(in Chinese))
[2] 刁群, 石东洋, 张芳. Sobolev方程一个新的H1-Galerkin混合有限元分析[J]. 高校应用数学学报, 2016, 31(2): 215-224.(DIAO Qun, SHI Dongyang, ZHANG Fang. A new H1-Galerkin mixed finite element analysis for Sobolev equation[J]. Applied Mathematics: a Journal of Chinese Universities, 2016, 31(2): 215-224.(in Chinese))
[3] ZHAO Z H, LI H, LUO Z D. Analysis of a space-time continuous Galerkin method for convection-dominated Sobolev equations[J]. Computers & Mathematics With Applications, 2017, 73(8): 1643-1656.
[4] JIN S J, LUO Z D. A reduced-order extrapolating collocation spectral method based on POD for the 2D Sobolev equations[J]. Boundary Value Problems, 2019, 63: 1-19.
[5] LUO Z D, TENG F, CHEN J. A POD-based reduced-order Crank-Nicolson finite volume element extrapolating algorithm for 2D Sobolev equations[J]. Mathematics and Computers in Simulation, 2018, 146: 118-133.
[6] 罗振东, 张博. Sobolev方程基于POD的降阶外推差分算法[J]. 应用数学和力学, 2016, 37(1): 107-116.(LUO Zhendong, ZHANG Bo. A reduced-order extrapolating finite difference algorithm based on the POD method for Sobolev equations[J]. Applied Mathematics and Mechanics, 2016, 37(1): 107-116.(in Chinese))
[7] LUO Z D, TENG F. A reduced-order extrapolated finite difference iterative scheme based on POD method for 2D Sobolev equation[J]. Applied Mathematics and Computation, 2018, 329: 374-383.
[8] LUO Z D, CHEN G. Proper Orthogonal Decomposition Methods for Partial Differential Equations[M]. San Diego: Academic Press of Elsevier, 2018.