引 言
自纳米材料被发现以来，因其独特的物理化学性能而受到研究人员广泛关注[1-2]．近年来，已成功研制出各种一维压电纳米材料，包括纳米线、纳米带[3]、纳米棒[4-5]、纳米环[6]等．纳米材料的发展，促进了电子元器件的进步．随着器件结构趋向于微纳化，微纳米机电系统(MEMS/NEMS)成为未来电子信息与生物医学发展的热门方向[7-9]．因此，研究压电纳米材料的结构和性能[10]对微机电系统的设计和应用至关重要．
为了研究纳米材料微观结构性能，一般通过研究其结构的自由表面，由于纳米尺度结构具有较大的比表面积，表面原子的能量状态不同于体原子的能量状态．因此表面效应很好地解释了尺寸相关的纳米材料物理化学性能[11-13]．基于体材料和表面材料是连续的假设，Gurtin 和Murdoch[14]提出了表面弹性模型，广泛应用于弹性材料的表面效应研究[15-16]．Michalski等[17]发展了纳米管或纳米线压电响应的连续介质理论．运用经典梁模型，Wang和Feng[18]在Euler-Bernoulli梁模型基础上，提出表面残余应力的影响．Yan等[19-20] 研究表面效应对压电纳米梁板的振动和屈曲影响时，不仅考虑了表面残余应力，还考虑了表面弹性和表面压电的影响．Yue等[11]基于Euler-Bernoulli梁模型，提出了新的连续介质模型，在不同边界条件下，存在完全不同的表面应力诱导的初始场，分析了固支(clamped-clamped，C-C)和悬臂(clamped-free，C-F)边界条件下，梁的表面应力对压电纳米线的性能影响．Zheng等[21]建立了考虑弯曲电、压电和表面弹性的Euler-Bernoulli梁模型，研究不同载荷和不同边界条件对薄梁静弯挠度的影响．相比于Euler-Bernoulli梁，Timoshenko梁能更好地描述梁的转动惯量和截面的剪切变形．Ke等[22]基于非局部理论和Timoshenko梁理论，研究非局部参数、温度和外加电压对压电纳米线的非线性振动的影响．Wu等[23]基于Timoshenko梁理论，研究了考虑表面效应的纳米线的自由振动和受迫振动．Rouhi等[24]利用Mindlin的第二应变梯度理论结合Timoshenko梁理论， 研究了纳米尺度下梁的非线性自由振动和受迫振动．除此之外， 有限元法[25-26]研究表面效应下压电纳米材料也逐渐受到学者们的关注．Mohtashami和Beni[27]采用有限元方法研究了压电纳米梁的振动和屈曲行为．
综上，考虑表面效应的Euler-Bernoulli梁模型未考虑转动惯量和剪切变形的影响，对长径比较小的梁不够精确．而考虑表面效应的Timoshenko梁模型，其表面效应模型中曲率采用∂2ω/∂x2，显然忽略了剪切变形的影响．对于纳米材料的有限元模拟，传统的模拟方法未考虑尺度效应，结果存在偏差．而分层法中表面的厚度完全依赖主观，缺乏通用性．
本文研究考虑表面效应对压电纳米梁的振动行为的影响，分别建立了新的表面效应模型和有限元模型．表面效应模型中曲率采用-∂φ/∂x的形式，同时考虑了弯曲变形和剪切变形与表面效应的相关性．采用Timoshenko梁理论，建立了考虑表面效应压电纳米梁的控制方程，推导了三种边界条件的频率和振型的精确解．讨论了表面效应对压电纳米梁频率和振型的影响．与有限元仿真结果进行对比，验证理论结果的正确性和有效性．
1 计算方法和模型
本文将以矩形截面压电纳米梁为例进行研究，图1是一个C-F压电纳米梁的例子，L，b和h分别表示其长度、宽度和厚度．
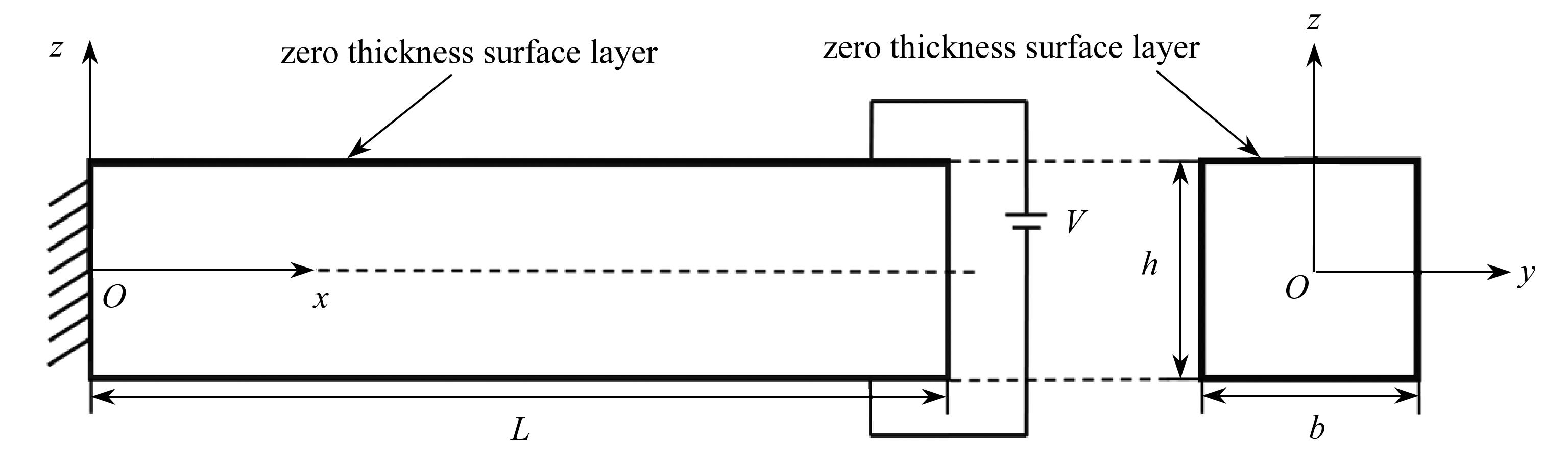
图1 考虑表面效应的压电纳米梁示意图
Fig. 1 Schematic of a piezoelectric nanobeam with surface effects
压电梁的体本构方程表示为
(1)
σxz=c55γxz,
(2)
(3)
其中，
和
分别表示体弹性模量、体压电常数和体介电常数；σx，σxz和Dz分别表示体轴向应力、体剪切应力和电位移；c55和γxz分别表示修正剪切模量和剪应变；εx是轴向应变，Ez是作用在压电体z方向上的电场强度．
根据Gurtin-Murdoch表面模型，表面本构方程表示为
(4)
其中，
和
分别表示轴向表面应力与表面残余应力；
和
分别表示表面弹性模量和表面压电常数，
是作用在表面层z方向上的电场强度．
根据电磁理论，分界面上电位移的边界条件为法向电位移相等，而根据Gurtin-Murdoch表面模型，表面为零厚度的表面层，因此表面层电位移与界面处电位移相同，即
(5)
基于Timoshenko梁理论，在梁中任意一点的轴向应变εx与剪应变γxz定义为
(6)
(7)
电场Ez可由电势Φ确定：
(8)
由Gauss定理，不考虑存在自由电荷的情况下，有
(9)
将式(6)和式(8)代入式(3)，之后代入式(9)可得
(10)
假设在上表面施加V电势，下表面电势为零，则此时的电势边界条件为
(11)
代入式(10)，解得电势Φ为
(12)
代入式(8)，解得体电场为
(13)
之后代入式(1)得
(14)
对于表面层而言，不考虑存在自由电荷的情况下, 由Gauss定理，有
(15)
根据式(5)，可得
(16)
将式(6)和式(8)代入式(3)，之后代入式(16)可得
(17)
假设在上表面施加V电势，下表面电势为零，则此时的上下表面电势边界条件为
(18)
表面层厚度Δ→0，则式(18)可简化为
(19)
(20)
解得电势Φ为
(21)
事实上根据式(8)可以发现，表面和体的电场强度相等，此结论在很多实验和理论中得到证明[28-31]，即
(22)
根据式(4)可得
(23)
根据表面弹性模型，在弯曲过程中，表面应力对纳米线产生了分布牵引作用．可以用Chen等[32]推导的广义Young-Laplace方程来描述，即
(24)
其中Rc为曲率半径，当曲面的单位法线指向位于纳米线上方的曲率中心时为正；Tz只存在于梁的上下表面，而不存在于梁的左右表面．
将式(23)代入式(24)，则表面张量Tx和Tz为
(25)
在描述力学性能上，Timoshenko梁比Euler-Bernoulli梁更适合，因为Timoshenko梁在Euler-Bernoulli梁的理论基础上考虑了转动惯量I以及截面的剪应力σxz的影响．不仅如此，本文在Young-Laplace方程中曲率采用-∂φ/∂x，不同于文献[33]中使用的∂2ω/∂x2；对于考虑剪切变形的Timoshenko梁，采用-∂φ/∂x描述模型更加合理．考虑表面应力引起的Tx和Tz，由压电效应引起的压电荷载参数N，Timoshenko梁的控制方程为
(26)
(27)
其中w，φ，ρ分别代表梁横向挠度、中性轴处横截面的转角(φ正向与∂w/∂x相反)和梁的密度，A和I分别表示横截面的面积和相应的转动惯量；弯矩M，剪力Q和压电荷载参数N分别为
(28)
将式(28)代入式(26)、(27)中，考虑表面效应的压电Timoshenko梁控制方程为
(29)
(30)
其中表面效应与压电效应构成的修正影响因子(EI)*与H为
(31)
(32)
从式(29)～(32)中，可以明显观察出表面效应，包括表面残余应力、表面弹性、表面压电和外加荷载电压对压电纳米梁的弯曲有显著影响，且与纳米材料的横截面结构密切相关．
在简支(simple-support，S-S)、C-C和C-F边界条件下，压电纳米梁的频率方程分别为
sin δ1sinh δ2=0,
(33)
(34)
(35)
其中
(36)
(37)
无量纲参数Γ，Ω2，s，r分别为
(38)
其中ω为圆频率．
方程(33)～(35)描述了在不同边界条件下，压电纳米梁频率与表面效应和压电效应的关系，当去掉表面效应和压电效应的对应参数时，方程可以退化为传统的Timoshenko梁频率方程．应当注意是，C-C和C-F结构下的频率方程是超越方程，相较于S-S结构，方程无法求得显式精确解．
在S-S、C-C和C-F边界条件下，对应的振型方程分别为
wn(ξ)=sin(nπξ),
(39)
χ(cosh(δ2ξ)-cos(δ1ξ)),
(40)
χ(cosh(δ2ξ)-cos(δ1ξ)),
(41)
其中
(42)
从式(39)～(41)分析可知，S-S梁结构中振型方程与经典理论振型方程是一致的，表明考虑表面效应的压电梁的振型方程与表面效应无关；而C-C和C-F边界条件下的振型都受到表面效应和压电效应的影响．
2 数 值 分 析
为研究表面效应对压电纳米线在不同边界条件下的频率响应，本文选用了应用广泛的锆钛酸铅结构的压电材料[34]PZT-5H，其材料参数如表1所示．
表1 PZT-5H材料参数[19,35]
Table 1 Partial material parameters of PZT-5H[19,35]
c11/Pae31/(C·m-2)k33/(C·V-1·m-1)c55/Paρ/(kg·m-3)cs11/(N·m-1)es31/(C·m-1)1.26×1011-6.51.3×10-82.3×10107.5×1037.56-3×108
通常情况下，
本文取
梁长L取500 nm，横截面确定为矩形(b=h)．
图2为考虑表面效应无量纲频率Ωv与不考虑表面效应无量纲频率
的比值分别在S-S、C-C和C-F三种边界条件下与纳米线宽度的变化关系，以此考察三种边界情况下表面效应对纳米线振动频率的影响．首先，对于S-S和C-C的纳米线，
说明表面效应增加了压电纳米线的振动频率．因为表面效应增加了纳米线的刚度，进而提高了频率．而对于C-F纳米线，
说明表面效应降低了压电纳米线的振动频率，这是由于C-F纳米线只有一端存在约束造成的．其次，从数值变化上看，S-S压电纳米线对表面效应的反应最敏感，C-F纳米线次之，最后是边界约束最强的C-C纳米线．最后，表面效应在长宽比较大(宽度b较小)时影响显著，此时比表面积较大．而随着长宽比的减小，表面效应的影响逐渐减小，此时比表面积逐渐减小．
为了进一步研究表面残余应力、表面弹性和表面压电分别对压电纳米线振动频率的影响情况，图3为C-F边界条件压电纳米线施加0.1 V电压时，分别考虑表面残余应力、表面弹性、表面压电无量纲频率Ωv和不考虑对应表面效应时，无量纲频率的比值与压电纳米线宽度变化关系．首先，考虑表面残余应力
和表面弹性
时，Ωv/Ω<1，表明考虑表面残余应力和表面弹性减少了压电纳米线的振动频率．而考虑表面压电
时，Ωv/Ω>1，表明表面压电增加了压电纳米线的振动频率．其次，从数值变化来看，表面残余应力对压电纳米线振动频率影响最大，表面压电影响次之，表面弹性的影响微弱．最后，压电纳米线宽度b较小时，此时比表面积较大，表面残余应力和表面压电的影响显著，而随着纳米线宽度b的增大，表面残余应力和表面压电影响不断减小，此时的比表面积减小．而现有文献[36]利用Euler-Bernoulli梁模型进行表面残余应力对压电纳米线的振动分析时，却忽略了表面压电的影响．
图2 表面效应对压电纳米线的影响 图3 表面残余应力、表面弹性和表面压电
Fig. 2 Surface effects on piezoelectric nanowires 对C-F压电纳米线的影响
Fig. 3 Effects of residual surface stress, surface elasticity and surface piezoelectricity on C-F piezoelectric nanowires
(a) S-S
(b) C-C(c) C-F
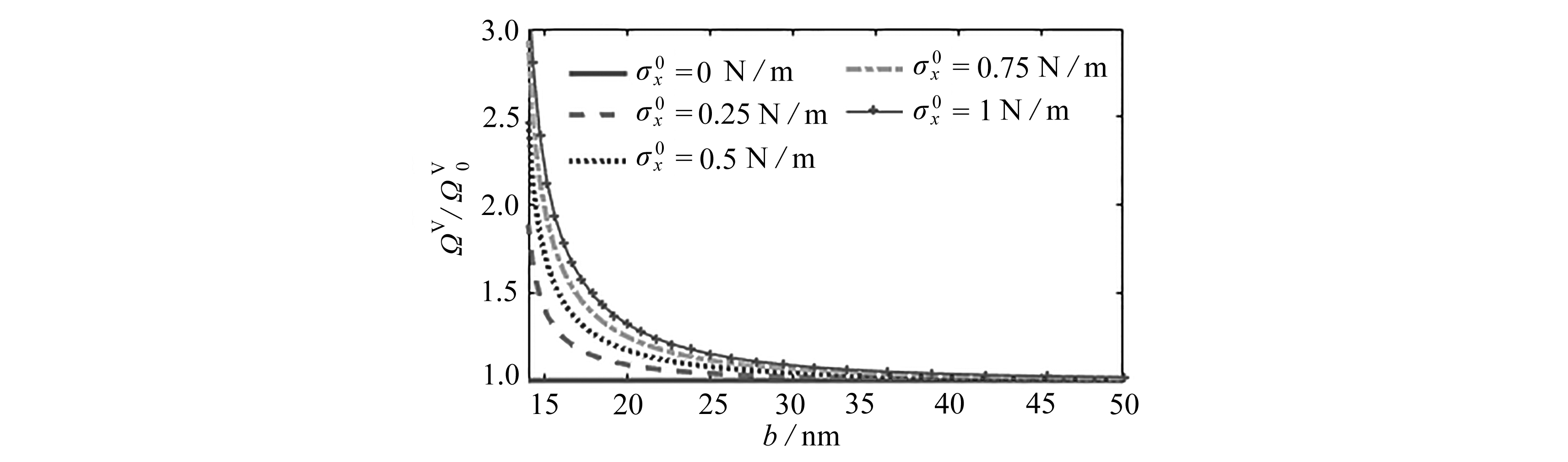
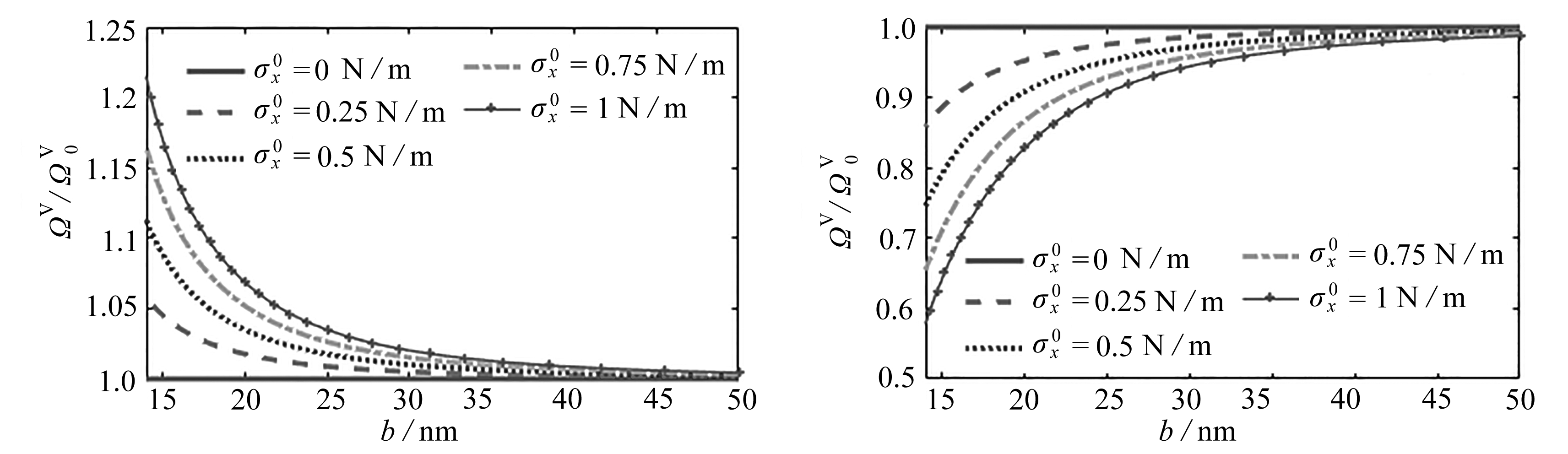
图4 三种边界条件考虑表面残余应力取值变化的无量纲频率和不考虑表面效应无量纲频率的比值与宽度的关系
Fig. 4 Variation of the normalized frequency with the nanobeam width for 3 kinds of boundary conditions under residual surface stress effects
由图3可知表面残余应力对压电纳米线振动影响显著，因此，进一步研究表面残余应力对压电纳米线的频率影响程度．图4给出了压电纳米线在三种边界条件下，电压施加0.1 V，考虑表面残余应力无量纲频率Ωv和不考虑表面残余应力无量纲频率的比值与纳米线宽度的变化关系．首先，对于S-S和C-C的纳米线，考虑表面残余应力增加了纳米线的振动频率．而对于C-F压电纳米线，表面残余应力减小了纳米线的振动频率．其次，从数值上分析，S-S纳米线对表面残余应力的变化最敏感，C-F纳米线次之，C-C纳米线影响最小．最后，表面残余应力在宽度b较小时影响显著，随着压电纳米线宽度的逐渐增大，表面残余应力对纳米线频率的影响逐渐减小．
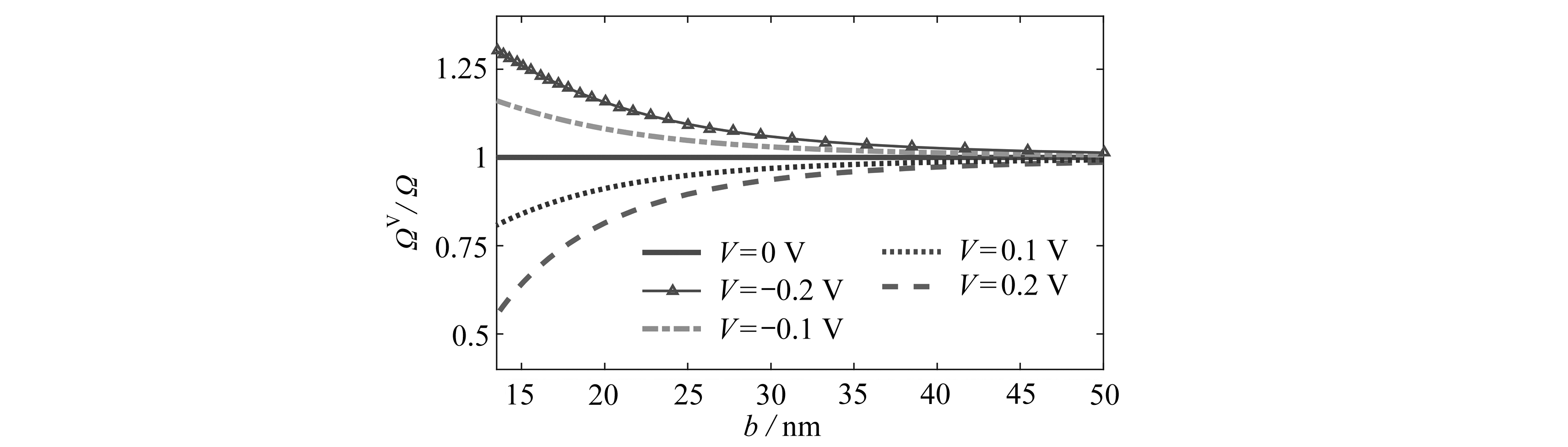
为了研究电压对压电纳米线振动频率的影响， 分别考察了三种边界情况下， 考虑压电效应无量纲频率Ωv和不考虑压电效应无量纲频率Ω的比值与纳米线宽度的变化关系，如图5所示．首先，对于C-F边界的纳米线，如图5(c)，Ωv/Ω>1，说明正电压增加了压电纳米线的振动频率;Ωv/Ω<1，说明负电压降低了振动频率．而对于S-S和C-C的纳米线，如图5(a)和(b)，正电压降低了压电纳米线振动频率，负电压增加了振动频率．其次，从无量纲频率比值的数值变化程度分析可知，C-F压电纳米线对压电的反应最为敏感，S-S纳米线次之，而对于C-C纳米线影响最小．最后，电压在长宽比较大(宽度b较小)时影响显著，而随着长宽比的减小，电压对纳米线振动频率影响逐渐减小．
(a) S-S
(b) C-C(c) C-F
图5 电压对压电纳米线的影响
Fig. 5 Effects of voltages on piezoelectric nanowires
最后，研究表面效应对压电纳米线振型的影响．首先，由S-S纳米线频率特征方程可知，表面效应对压电S-S纳米线的振型无影响．其次，由图6可知，表面效应对C-C压电纳米线挠度振型有一定影响．而如图7所示，表面效应对C-F压电纳米线的挠度振型影响显著．综上，表面效应对压电纳米线的振型影响受边界条件影响较大，对C-F压电纳米线振型影响最大，C-C纳米线影响较小，而对S-S纳米线无影响．
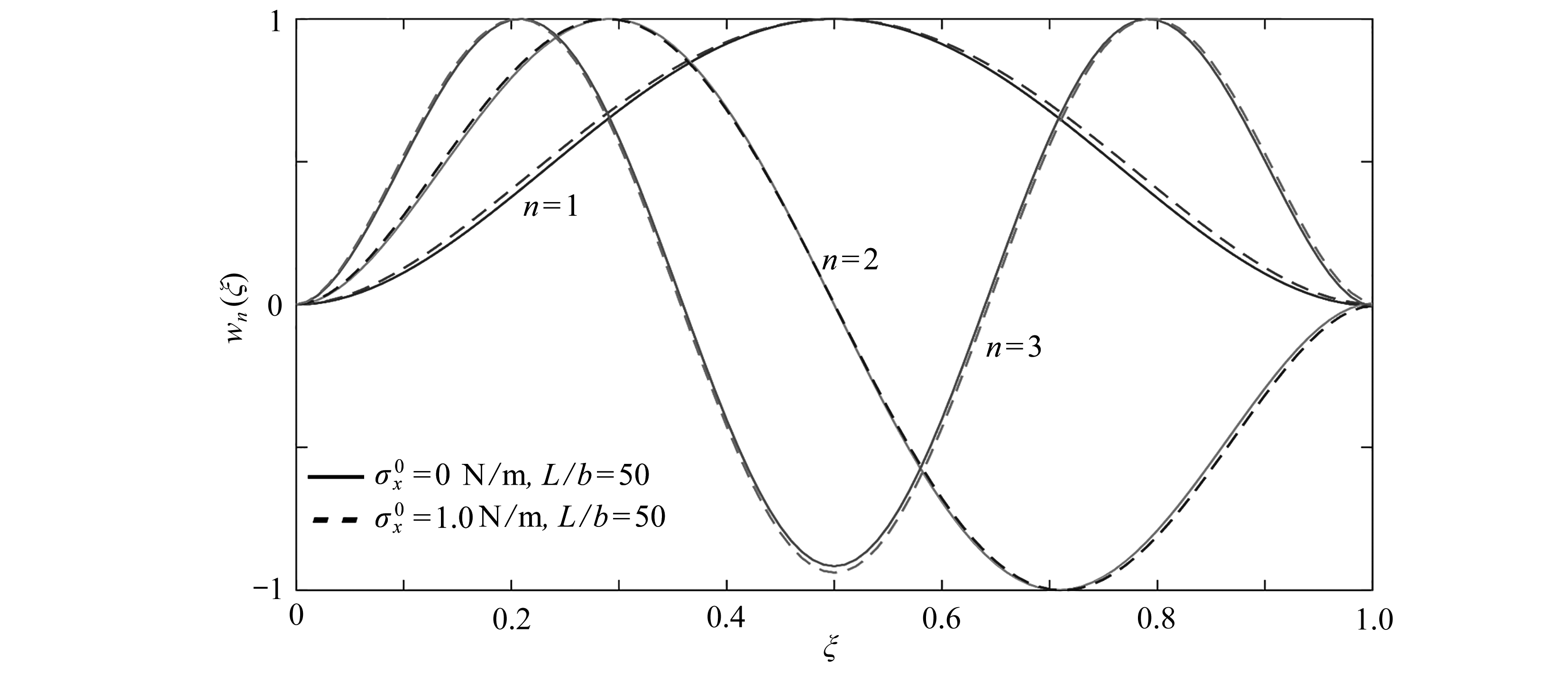
图6 表面效应对C-C纳米线前三阶(n=1,2,3)振型的影响
Fig. 6 Deflection curves for a C-C piezoelectric nanobeam of the 1st 3 orders(n=1,2,3)
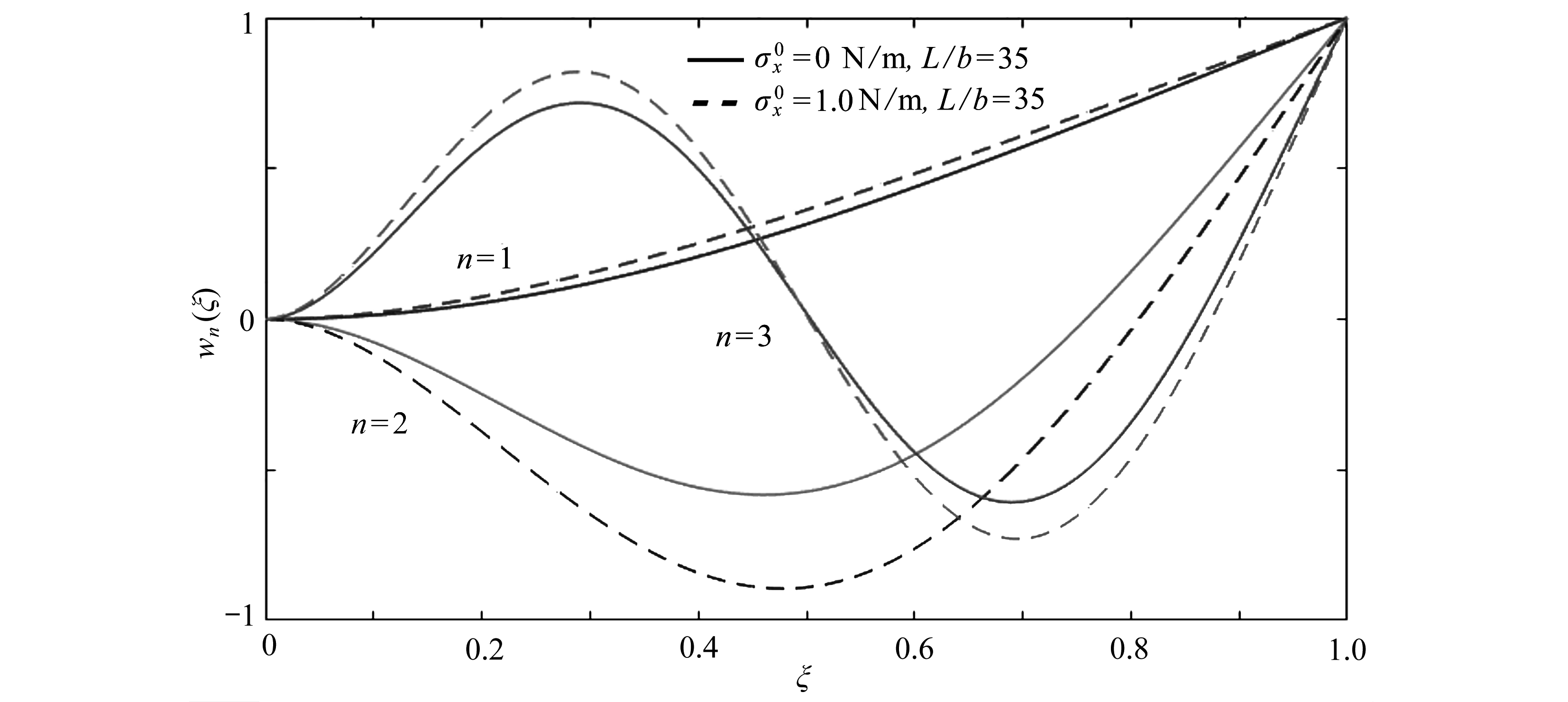
图7 表面效应对C-F纳米线前三阶(n=1,2,3)振型的影响
Fig. 7 Deflection curves for a C-F piezoelectric nanobeam of the 1st 3 orders(n=1,2,3)
3 压电纳米线的有限元模拟
采用ABAQUS有限元仿真软件进行模拟，并与理论结果进行对比．采用PYTHON进行二次开发，从而实现考虑表面效应的有限元分析．
(a) 网格划分模型(b) C-F边界下L/b=10的一阶阵型图
(a) The model grid(b) The 1st-order vibration mode for L/b=10 under the C-F boundary
(c) C-F边界下L/b=10的二阶阵型图(d) C-F边界下L/b=10的三阶阵型图
(c) The 2nd-order vibration mode for L/b=10 (d) The 3rd-order vibration mode for L/b=10 under the C-F boundary under the C-F boundary
图8 有限元模型
Fig. 8 The finite element model
有限元建模的尺寸取两组，第一组取L/b=5，第二组取L/b=10．其中材料的参数如表1所示．全局单元尺寸为5 nm，使用C3D8E单元进行压电单元建模．利用子空间求解法，在三种边界条件(S-S、C-C和C-F)下，进行前三阶模态分析．图8为有限元模型和悬臂纳米线前三阶振型．有限元模拟结果与理论结果如表2所示，结果表明理论值与有限元仿真结果吻合较好．
表2 不同边界条件下，长宽比(L/b)为5和10的纳米梁前三阶频率
Table 2 First 3-order frequencies of nanobeams with aspect ratios (L/b) of 5 and 10 under different boundary conditions
boundary conditionaspect ratio L/btheoretical resultf1/GHzf2/GHzf3/GHzfinite element modelf1/GHzf2/GHzf3/GHzS-S50.712.454.680.702.414.55100.381.433.010.371.402.94C-C51.373.135.211.393.185.26100.812.073.730.822.103.79C-F50.261.403.330.261.403.32100.130.812.120.160.832.12
4 结 论
基于Gurtin-Murdoch表面理论，建立了一种表征压电纳米线横向振动理论模型．与以往不同，该模型中曲率采用转角的一阶导数，同时考虑了弯曲和剪切变形与表面效应的相关性．基于Timoshenko梁理论建立了考虑表面效应的压电纳米梁控制方程，推导了三种不同边界条件下压电纳米梁的频率方程和振型方程的精确解．提出了一种在有限元软件中实现表面效应模拟的计算方法，理论结果和有限元结果吻合较好，证明了理论模型的正确有效性．结果表明：
1) 表面效应和压电效应对不同的边界条件压电纳米线的振动频率影响显著．首先，表面效应对S-S纳米线振动频率影响最大，对C-F纳米线振动频率影响次之，而对C-C纳米线振动频率影响最弱．其次，压电效应对C-F纳米线振动频率影响显著，对S-S纳米线振动频率影响次之，而对C-C纳米线振动频率影响最弱．
2) 表面残余应力、表面弹性和表面压电对压电纳米线振动频率影响各有不同，其中表面残余应力对纳米线振动频率影响最强，表面压电次之，而表面弹性的影响最弱．
3) 在压电纳米线长宽比较大(宽度较小)时，表面效应和压电效应对纳米线振动频率影响显著．随着长宽比逐渐减小，表面效应和压电效应对纳米线频率影响逐渐减小．
4) 对压电纳米线的振型而言，表面效应对不同边界压电纳米线影响程度不同，对C-F纳米线振型影响显著，而对C-C纳米线振型影响较小，对S-S纳米线振型无影响．
[1] ZHAO M H, WANG Z G, MAO S X. Piezoelectric characterization of individual zinc oxide nanobelt probed by piezoresponse force microscope[J]. Nano Letters, 2004, 4(4): 587-590.
[2] RAMPRASAD R, SHI N. Dielectric properties of nanoscale HfO2 slabs[J]. Physical Review B, 2005, 72(5): 052107. DOI: 10.1103/PhysRevB.72.052107.
[3] WANG Z L. ZnO nanowire and nanobelt platform for nanotechnology[J]. Materials Science and Engineering: R, 2009, 64(3/4): 33-71.
[4] AIZPURUA J, BRYANT G W, RICHTER L J, et al. Optical properties of coupled metallic nanorods for field-enhanced spectroscopy[J]. Physical Review B, 2005, 71(23): 235420. DOI： 10.1103/PhysRevB.71.235420.
[5] MARANGONI V S, CANCINO-BERNARDI J, ZUCOLOTTO V. Synthesis, physico-chemical properties, and biomedical applications of gold nanorods: a review[J]. Journal of Biomedical Nanotechnology, 2016, 12(6): 1136-1158.
[6] HU X L, YU J C, GONG J M, et al. α-Fe2O3 nanorings prepared by a microwave-assisted hydrothermal process and their sensing properties[J]. Advanced Materials, 2007, 19(17): 2324-2329.
[7] NGUYEN N T, HUANG X Y, CHUAN T K. MEMS-micropumps: a review[J]. Journal of Fluids Engineering, 2002, 124(2): 384-392.
[8] GRAYSON A C R, SHAWGO R S, JOHNSON A M, et al. A BioMEMS review: MEMS technology for physiologically integrated devices[J]. Proceedings of the IEEE, 2004, 92(1): 6-21.
[9] 张中太, 林元华, 唐子龙, 等. 纳米材料及其技术的应用前景[J]. 材料工程, 2000, 3(7): 42-48.(ZHANG Zhongtai, LIN Yuanhua, TANG Zilong, et al. Nanometer materials & nanotechology and their application prospect[J]. Journal of Materials Engineering, 2000, 3(7): 42-48.(in Chinese))
[10] 徐晓建, 邓子辰. 非局部因子和表面效应对微纳米材料振动特性的影响[J]. 应用数学和力学, 2013, 34(1): 10-17.(XU Xiaojian, DENG Zichen. Surface effects of adsorption induced resonance analysis of micro/nanobeams via nonlocal elasticity[J]. Applied Mathematics and Mechanics, 2013, 34(1): 10-17.(in Chinese))
[11] YUE Y M, XU K Y, ZHANG X D, et al. Effect of surface stress and surface-induced stress on behavior of piezoelectric nanobeam[J]. Applied Mathematics and Mechanics, 2018, 39(7): 953-966.
[12] MILLER R E, SHENOY V B. Size-dependent elastic properties of nanosized structural elements[J]. Nanotechnology, 2000, 11(3): 139.
[13] ZHANG J, WANG C Y, CHOWDHURY R, et al. Small-scale effect on the mechanical properties of metallic nanotubes[J]. Applied Physics Letters, 2012, 101(9): 093109. DOI: 10.1063/1.4748975.
[14] GURTIN M E, MURDOCH A I. A continuum theory of elastic material surfaces[J]. Archive for Rational Mechanics and Analysis, 1975, 57(4): 291-323.
[15] EREMEYEV V A. On effective properties of materials at the nano-and microscales considering surface effects[J]. Acta Mechanica, 2016, 227(1): 29-42.
[16] HE L H, LIM C W, WU B S. A continuum model for size-dependent deformation of elastic films of nano-scale thickness[J]. International Journal of Solids and Structures, 2004, 41(3/4): 847-857.
[17] MICHALSKI P J, SAI N, MELE E J. Continuum theory for nanotube piezoelectricity[J]. Physical Review Letters, 2005, 95(11): 116803. DOI: 10.1103/PhysRevLett.95.116803.
[18] WANG G F, FENG X Q. Effect of surface stresses on the vibration and buckling of piezoelectric nanowires[J]. EPL(Europhysics Letters), 2010, 91(5): 56007. DOI: 10.1209/0295-5075/91/56007.
[19] YAN Z, JIANG L Y. The vibrational and buckling behaviors of piezoelectric nanobeams with surface effects[J]. Nanotechnology, 2011, 22(24): 245703. DOI: 10.1088/0957-4484/22/24/245703.
[20] YAN Z, JIANG L Y. Surface effects on the electromechanical coupling and bending behaviours of piezoelectric nanowires[J]. Journal of Physics D: Applied Physics, 2011, 44(7): 075404. DOI: 10.1088/0022-3727/44/7/075404.
[21] ZHENG S J, ZHAO X, WANG H T. Theoretical and finite element modeling of piezoelectric nanobeams with surface and flexoelectricity effects[J]. Mechanics of Advanced Materials and Structures, 2019, 26(15): 1261-1270.
[22] KE L L, WANG Y S, WANG Z D. Nonlinear vibration of the piezoelectric nanobeams based on the nonlocal theory[J]. Composite Structures, 2012, 94(6): 2038-2047.
[23] WU J X, LI X F, TANG A Y, et al. Free and forced transverse vibration of nanowires with surface effects[J]. Journal of Vibration and Control, 2017, 23(13): 2064-2077.
[24] ROUHI H, EBRAHIMI F, ANSARI R, et al. Nonlinear free and forced vibration analysis of Timoshenko nanobeams based on Mindlin’s second strain gradient theory[J]. European Journal of Mechanics A: Solids, 2019, 73: 268-281.
[25] AVDIAJ S, 
J, SYLA N. Modeling of the piezoelectric effectusing the finite-element method(FEM)[J]. Materiali in Tehnologije, 2009, 43(6): 283-291.
[26] 邢沁妍, 杨青浩, 陆琛宇, 等. 杆件轴向受迫振动的Galerkin有限元EEP法自适应求解[J]. 应用数学和力学, 2019, 40(9): 945-956.(XING Qinyan, YANG Qinghao, LU Chenyu, et al. An EEP adaptive strategy of the Galerkin FEM for axially forced vibration of bars[J]. Applied Mathematics and Mechanics, 2019, 40(9): 945-956.(in Chinese))
[27] MOHTASHAMI M, BENI Y T. Size-dependent buckling and vibrations of piezoelectric nanobeam with finite element method[J]. Iranian Journal of Science and Technology, Transactions of Civil Engineering, 2019, 43(3): 563-576.
[28] VISWANATH R N, KRAMER D, WEISSMÜLLER J. Variation of the surface stress-charge coefficient of platinum with electrolyte concentration[J]. Langmuir, 2005, 21(10): 4604-4609.
[29] FRIESEN C, DIMITROV N, CAMMARATA R C, et al. Surface stress and electrocapillarity of solid electrodes[J]. Langmuir, 2001, 17(3): 807-815.
[30] HAISS W, NICHOLS R J, SASS J K, et al. Linear correlation between surface stress and surface charge in anion adsorption on Au(111)[J]. Journal of Electroanalytical Chemistry, 1998, 452(2): 199-202.
[31] HUANG G Y, YU S W. Effect of surface piezoelectricity on the electromechanical behaviour of a piezoelectric ring[J]. Physica Status Solidi(B), 2006, 243(4): R22-R24.
[32] CHEN T Y, CHIU M S, WENG C N. Derivation of the generalized Young-Laplace equation of curved interfaces in nanoscaled solids[J]. Journal of Applied Physics, 2006, 100(7): 074308. DOI： 10.1063/1.2356094.
[33] HE Q L, LILLEY C M. Resonant frequency analysis of Timoshenko nanowires with surface stress for different boundary conditions[J]. Journal of Applied Physics, 2012, 112(7): 074322. DOI: 10.1063/1.4757593.
[34] 吴金根, 高翔宇, 陈建国, 等. 高温压电材料、器件与应用[J]. 物理学报, 2018, 67(20): 207701.(WU Jingen, GAO Xiangyu, CHEN Jianguo, et al. Review of high temperature piezoelectric materials, devices, and applications[J]. Acta Physica Sinica, 2018, 67(20): 207701.(in Chinese))
[35] YAN Z, JIANG L Y. Electromechanical response of a curved piezoelectric nanobeam with the consideration of surface effects[J]. Journal of Physics D: Applied Physics, 2011, 44(36): 365301. DOI: 10.1088/0022-3727/44/36/365301.
[36] WANG G F, FENG X Q. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams[J]. Applied Physics Letters, 2007, 90(23): 231904. DOI: 10.1063/1.2746950.