引 言
自1982年美国加州理工学院生物物理学家Hopfield提出了神经网络的数学模型以来，人工神经网络的理论研究取得了长足的进步，结果已广泛应用于数字识别、智能机器人、网络安全和自动控制等多个领域[1-5]．在实际应用中，由于信号传输和时间选择的不灵敏性，神经网络中时间延迟是不可避免的[6-13]．例如，文献[12]通过构造一个新的Lyapunov-Krasovskii泛函，研究了延迟神经网络的稳定性问题．文献[7]研究了一类时滞神经网络在随机通信协议下的有限时间状态估计问题．文献[12]研究了切换随机时滞网络的有限时间稳定性分析和控制综合问题．文献[13]将Lyapunov-Razumikhin方法推广，并以此研究了时滞系统的有限时间稳定性和有限时间牵引稳定性．在上述文献中，网络的时滞τ(t)大多满足0<τ(t)≤qτ<∞，即时滞是有界的．然而，对于规模较大的并行网络模型而言，还需要进一步考虑连续分布延迟的影响． 近年来，无限分布时滞神经网络已引起学者们的关注，例如文献[14]研究了具有分布时滞的静态神经网络固定时间稳定性，其充分考虑了不确定性、脉冲扰动对网络的影响．
值得注意的是，神经网络是一个具有大量神经元、高度互联的非线性系统，其状态往往难以完全获得．因此，神经网络的状态估计问题，具有重要的现实意义[15-18]．目前，时滞神经网络的状态估计问题已得到了一定程度的研究．文献[19]研究了神经网络的H∞状态估计问题，其中传输测量受到采样效应、外部干扰、网络诱导时延和数据包丢失等影响．文献[16]研究了一类离散时滞神经网络的状态估计问题． 另一方面，在数字控制平台下，事件触发机制引起了大量学者的研究热情[20-25]．在事件触发机制中，当触发条件满足时，系统才执行相应的更新任务．因此，与传统的时间触发机制相比，事件触发可以有效减少更新次数，避免控制资源的浪费．然而，对于混合时滞神经网络在事件触发机制下的状态估计问题，迄今为止还鲜有学者涉足，相关的研究成果非常少．
鉴于以上分析，本文研究了一类具有混合时滞的神经网络基于事件触发机制的状态估计问题．通过构造一个简单的Lyapunov 函数，并结合微分比较原理和一些分析技巧，得到了确保误差系统指数稳定的一些充分条件，利用矩阵分析技巧给出了基于线性矩阵不等式(LMI)形式的控制器求解方法．最后，通过数值算例验证了所提出的设计方法的有效性．相比于已有的文献，本文的贡献主要体现在两个方面:
1) 首次研究了具有混合时滞的神经网络基于事件触发机制的状态估计问题；
2) 引入了一个具有指数衰减结构的新型事件触发机制，既能有效降低信息更新频率又能确保误差系统指数稳定．
1 预 备 知 识
1.1 模型描述
为了方便表达，本文使用以下记号:
和N分别表示非负实数和非负整数集;Rn和Rn×m分别表示n维欧氏空间和n×m维实矩阵的集合;|x|和xT分别表示向量x的模和它的转置; 对于A∈Rn×n，λmax(A)和λmin(A)分别表示矩阵A的最大特征值和最小特征值，
表示矩阵的范数．
本文考虑具有n个神经元的混合时滞神经网络:
W3
K(t-s)f3(x(s))ds+J，
(1)
其输入方程为
y(t)=Cx(t)，
(2)
其中x(t)=(x1(t),x2(t),…,xn(t))T∈Rn表示神经元状态向量，y(t)∈Rm表示网络测量输出;B=diag(b1,b2,…,bn)表示放大器参数构成的对角矩阵，且
分别表示神经元连接权矩阵、时变时滞连接权矩阵和无限分布延时连接权矩阵; fi(x(t))=[fi1(x1(t)), fi2(x2(t)),…, fin(xn(t))]T表示神经元的向量值激活函数;J=(J1,J2,…,Jn)T表示外部输入信号向量；d(t)表示有界时变时滞，满足0≤d(t)≤d; K(·)表示无限分布时滞核函数；C∈Rm×n表示网络的输出矩阵．
为了获得主要结果，我们做出如下假设:
假设1 K(s)是定义在上的连续函数，且满足对于某个给定的λ0>0,
假设2 对于任意给定的x,y ∈Rn，非线性函数f(·)满足
|fi(x)-fi(y)|≤|Li(x-y)|， i=1,2,3，
(3)
其中Li∈Rn×n是已知常数矩阵．
注1 网络(1)在部分已有文献的模型基础上进行了扩展，同时考虑了有界时变时滞和无穷分布时滞，适用范围更广．例如，当无穷分布时滞未被考虑时，网络(1)退化为文献[26]中所研究的模型．另一方面，当网络时滞仅含有分布时滞时，我们可以得到文献[27]中的模型．
为了降低更新频率，本文引入事件触发机制．令{tk: k∈N}表示触发时间序列，且满足
(4)
其中
表示神经网络的测量输出，
表示神经网络状态的估计值；ψ>0和φ>0分别表示事件触发策略的权重和阈值参数．
注2 为了节省控制过程中的有限资源，减少不必要的采样和控制信号更新，事件触发策略在控制系统中被广泛采用．大多数已有文献假设事件触发时刻由一个恒定的阈值确定[28-30]．本文所给出的触发策略(4)不仅依赖于输出测量误差，而且依赖于一个具有指数衰减特性的阈值．这种结构有利于实现更精细的控制效果．
在事件触发机制下，我们构造如下观测器模型:
(5)
其中
表示神经元状态x的估计量;
Rn×m表示待设计的估计增益矩阵．
定义估计误差为
(6)
根据式(1)和(5)，我们得到
(7)
其中
1.2 基本定义和引理
本小节给出如下的基本定义和部分引理．
定义1 对于误差系统(7)，如果存在正常数M，λ使得
|e(t)|2≤Me-λt，
那么误差系统(7)是指数稳定的．
引理1 对于任意x，y∈Rn，有
2xTy≤αxTx+α-1yTy，
其中 α>0．
引理2[31] 假设P∈Rn×n是正定矩阵，Q∈Rn×n是对称矩阵，x∈Rn是n维向量，则有
λmin(P-1Q)xTPx≤xTQx≤λmax(P-1Q)xTPx．
引理3[32] 给定常数矩阵Σ1，Σ2，Σ3，其中Σ1为对称矩阵，Σ2为正定矩阵，则
的充要条件为
或
2 主 要 结 果
本节将综合利用系统的当前状态信息和时滞信息，建立误差系统状态指数稳定的理论研究框架，分析并排除触发机制中的Zeno现象．
定理1 对于给定的增益矩阵
如果存在正定矩阵P∈Rn×n以及正数μ，αi(i=1,2,3,4)，使得
Π+μP<0,
(8)
-μ+ζ1+γ+ω<0,
(9)
其中
那么误差系统(7)是指数稳定的．
证明 构造如下Lyapunov函数:
V(t)
V(e(t))=eT(t)Pe(t)．
(10)
计算V(t)沿着系统(7)的导数，有
(11)
根据引理1和引理2，可以得到
(12)
(13)
(14)
(15)
将式(12)～(15)代入式(11)中，可以得到
(16)
由式(8)可得
(17)
根据事件触发机制(4)容易推知，测量误差ε(t)满足
2ψ‖C‖2|e(t)|2+2ψ|ε(t)|2+φe-δt，
也就是说
(18)
令
可以得到
(19)
上式两边同时积分可得
V(t)=V(0)e-(μ-ζ1)t+
‖θ‖e-(μ-ζ1)t+
(20)
其中
下面我们证明对于任意的t≥0，有
V(t)≤Ze-δt，
(21)
其中常数δ满足
是由下式确定的正根：
λ-μ+ζ1+γeλd+ω
K(s)eλsds=0，
(22)
首先，我们证明正根λ*存在．令F(λ)=μ-λ-ζ1-γeλd-ωK(s)eλsds．容易验证F(0)>0，而limλ→+∞F(λ)<0．由连续函数的介值性可知，必存在正数λ*使F(λ*)=0．不难证明，对于任意一个正数δ
接下来，我们通过反证法来证明式(21)．当t∈(-∞,0]时，显然有
V(t)≤‖θ‖≤Z≤Ze-δt．
(23)
若式(21)不成立，则必定存在t>0使得
V(t)>Ze-δt．
(24)
令t*inf{t>0|V(t)>Ze-δt}．根据V(t)的连续性，我们可知
V(t)<Ze-δt, t<t*，
(25)
V(t*)=Ze-δt*．
(26)
根据式(20)和(25)，可以得到
V(t*)≤‖θ‖e-(μ-ζ1)t*+
(27)
情况1 当Z=‖θ‖时，有‖θ‖-Z(γeδd+ωk*)/(μ-ζ1-δ)-ζ2≥0．通过式(27)，能够得到
V(t*)<‖θ‖e-δt*=Ze-δt*．
(28)
情况2 当Z=ζ2(μ-ζ1-δ)/(μ-ζ1-δ-γeδd-ωk*)时，有
‖θ‖-Z(γeδd+ωk*)/(μ-ζ1-δ)-ζ2≤0．
通过式(27)，能够得到
(29)
综上，结论(28)和(29)都与式(26)矛盾，由此可知式(21)成立．
由引理2和式(10)，我们易知
(30)
即
(31)
定理得证．
需要指出的是，在连续时间控制系统中，事件触发机制的Zeno现象，意味着控制器在有限的时间间隔内会被无限次触发．这将严重影响采样设备的运行，因此必须被排除．
定理2 若定理1的所有条件都满足，则必存在正常数T*， 使得对于任意k∈N，有tk+1-ki≥T*．
证明 由
及误差系统(7)，我们可计算|ε(t)|的右上Dini导数得
‖W2‖‖L2‖|e(t-d(t))|+
‖C‖‖W2‖‖L2‖|e(t-d)|+
‖C‖‖W2‖‖L2‖|e(t-d)|，
(32)
其中 t∈[tk,tk+1)．
令
以及a3‖C‖‖W2‖‖L2‖，可以得到
D+|ε(t)| ≤a1|ε(t)|+a2|e(tk)|+a3|e(t-d)|．
(33)
根据式(31)，可得
(34)
(35)
为了简便，我们令
将式(34)和(35)代入式(33)可得
D+|ε(t)|≤a1|ε(t)|+a2βe-(δ/2)tk+a3βe-(δ/2)(tk-d)≤a1|ε(t)|+M，
(36)
其中 M(a2+a3eδd/2)β．
在式(36)两边同时乘以e-a1(t-tk)，可得
e-a1(t-tk)D+|ε(t)|≤a1e-a1(t-tk)|ε(t)|+Me-a1(t-tk),
即
D+(e-a1(t-tk)|ε(t)|)≤Me-a1(t-tk)．
(37)
对任意的t∈[tk,tk+1)，考虑式(37)两边从tk到t积分，结合ε(tk)=0，可得
(38)
也就是
(39)
根据触发规则(4)，当
时，控制信号才会更新．因此，可知下一个触发时刻tk+1满足
(40)
即
(41)
故我们排除了Zeno现象．令
定理得证．
下面我们给出增益矩阵
和事件触发参数ψ，φ的设计方法，从而控制误差系统(7)实现指数稳定．
定理3 若存在正定矩阵P∈Rn×n，常数矩阵R∈Rn×m以及正常数μ，αi(i=1,2,3,4)，使得
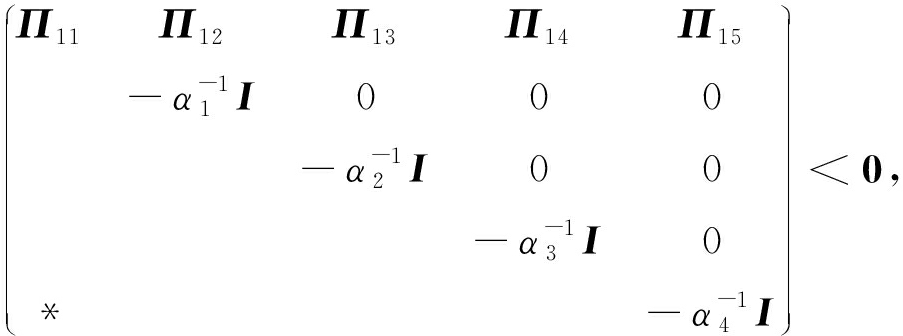
(42)
其中
那么误差系统(7)是指数稳定的，而且估计器增益矩阵可设计为
(43)
事件触发控制参数ψ，φ可设计为
(44)
证明 为了叙述方便，我们令
Ω3=(PW1 PW2 PW3 R)．
显然，式(42)意味着
根据引理3，可以得到
即
同时注意到
这很容易推出式(8)．定理得证．
注3 根据定理3，我们可以设计一个基于事件触发机制的观测器，并确保误差系统(7)是指数稳定的．观测器增益矩阵R可以利用LMI求解，事件触发控制参数ψ和阈值参数φ可以自行设计，因此本文结果具有较大的可解性和灵活性．
3 例子与仿真
本节提供了一个数值例子来说明我们的方法的有效性．考虑具有两个神经元的混合时滞神经网络，网络参数如下:
选择核函数K(x)=e-0.5x，选取激活函数为f1(x)=0.1|x|, f2(x)=0.01tanh(x), f3(x)=0.01tanh(x)．显然，假设2成立，且可选取
令μ=2.1，利用MATLAB工具箱求解不等式(42)～(44)，可得如下可行解：
进一步地，计算事件触发参数的上界为
因此，可设计0≤ψ<2.829 7×10-4，φ>0．
根据定理3，我们设计事件触发参数ψ=0.000 1=φ2=0.000 1，估计器增益矩阵为
从而估计误差实现指数稳定．
(a) 神经网络状态 (b) 估计器状态
(a) The state of the neural network(b) The state of the estimator
图1 神经网络状态及估计器状态
Fig. 1 The states of the neural network and the estimator
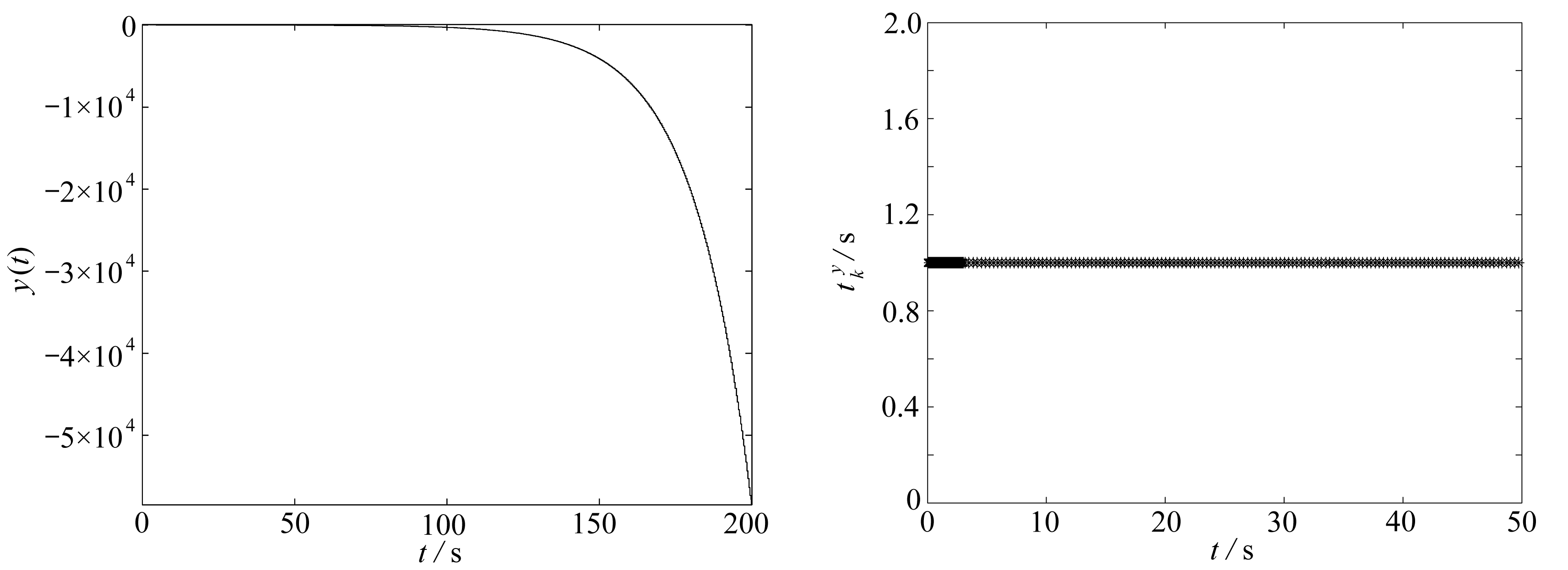
图2 网络测量输出y(t) 图3 事件触发时刻
Fig. 2 The network measurement output y(t) Fig. 3 The event trigger time
(a) e1(t)(b) e2(t)
图4 误差系统状态轨迹
Fig. 4 The state trajectory of the error system
图1～4给出了例子的数值模拟结果．为了便于计算机仿真，我们选择了时间间隔为[0,200] s，步长为0.01 s．令δ=0.5，给定时滞d=0.1，初始状态向量x(t)=[13.9,-25.5]T和观测器系统初始状态
神经网络状态和估计器状态轨迹如图1所示．图2描述了测量输出的轨迹．图3刻画了δ=0.5的情况下的事件触发时刻．图4描述了估计误差状态以指数收敛的速度趋近于零．
4 总 结
本文研究了一类具有混合时滞的神经网络状态估计问题．采用事件触发策略来确定何时更新估计器的误差信息，利用Lyapunov函数和比较原理来解决了误差系统的指数稳定性分析．最后，通过一个数值例子验证了理论结果的有效性．
致谢 本文作者衷心感谢重庆交通大学研究生教育创新基金项目(2019S0124)对本文的资助．
[1] WANG L, SONG Q, ZHAO Z, et al. Synchronization of two nonidentical complex-valued neural networks with leakage delay and time-varying delays[J]. Neurocomputing, 2019, 356: 52-59.
[2] WU H, FENG Y, TU Z, et al. Exponential synchronization of memristive neural networks with time delays[J]. Neurocomputing, 2018, 297: 1-7.
[3] 舒含奇, 宋乾坤. 带有时滞的Clifford值神经网络的全局指数稳定性[J]. 应用数学和力学, 2017, 38(5): 513-525.(SHU Hanqi, SONG Qiankun. Global stability of Clifford-valued recurrent neural network with mixed time-varing delays[J]. Applied Mathematics and Mechanics, 2017, 38(5): 513-525.(in Chinese))
[4] 张平奎, 杨绪君. 基于激励滑模控制的分数阶神经网络的修正投影同步研究[J]. 应用数学和力学, 2018, 39(3): 343-354.(ZHANG Pingkui, YANG Xujun. Modiffied projective synchronization of a class of fractional-order neural networks based on active sliding mode control[J]. Applied Mathematics and Mechanics, 2018, 39(3): 343-354.(in Chinese))
[5] 闫欢, 赵振江, 宋乾坤. 具有泄漏时滞的复值神经网络的全局同步性[J]. 应用数学和力学, 2016, 37(8): 832-841.(YAN Huan, ZHAO Zhenjiang, SONG Qiankun. Global synchronization of complex-valued neural network with leakage time delays[J]. Applied Mathematics and Mechanics, 2016, 37(8): 832-841.(in Chinese))
[6] SHAO H, LI H, ZHU C. New stability results for delayed neural networks[J]. Applied Mathematics and Computation, 2017, 311: 324-334.
[7] FUAD E, LUO Y, LIU Y, et al. State estimation for delayed neural networks with stochastic communication protocol: the finite-time case[J]. Neurocomputing, 2018, 281: 86-95.
[8] ARPIT B, ARUNA T, HARSHIT B, et al. A genetically optimized neural network model for multi-class classification[J]. Expert Systems With Applications, 2016, 60: 211-221.
[9] GABRIEL V, JUAN F D P, PABLO C, et al. Artificial neural networks used in optimization problems[J]. Neurcomputing, 2018, 272: 10-16.
[10] MARAT A, MEHMET O. Generation of cyclic/toroidal chaos by Hopfield neural networks[J]. Neurcomputing, 2014, 145: 230-239.
[11] YANG X, YUAN Q. Chaos and transient chaos in simple Hopfield neural networks[J]. Neurcomputing, 2005, 69(1): 232-241.
[12] CHEN Y, LIU Q, LU R, et al. Finite-time control of switched stochastic delayed systems[J]. Neurcomputing, 2016, 191: 374-379.
[13] LI X, YANG X, SONG S. Lyapunov conditions for finite-time stability of time-varying time-delay systems[J]. Automatica, 2019, 103: 135-140.
[14] HU J, SUI G. Fixed-time control of static impulsive neural networks with infinite distributed delay and uncertainty[J]. Communications in Nonlinear Science and Numerical Simulation, 2019, 78: 104848.
[15] ZHOU J, ZHAO T. State estimation for neural networks with two additive time-varying delay components using delay-product-type augmented Lyapunov-Krasovskii functionals[J]. Neurocomputing, 2019, 350: 155-169.
[16] LIU Y, SHEN B, LI Q. State estimation for neural networks with Markov-based nonuniform sampling: the partly unknown transition probability case[J]. Neurocomputing, 2019, 357: 261-270.
[17] LI Q, ZHU Q, ZHONG S, et al. State estimation for uncertain Markovian jump neural networks with mixed delays[J]. Neurocomputing, 2016, 182: 82-93.
[18] SYED A M, SARAVANAN S, ARIK S. Finite-time H∞ state estimation for switched neural networks with time-varying delays[J]. Neurocomputing, 2016, 207: 580-589.
[19] TAE H, JU H, HOYOUL J. Network-based H∞ state estimation for neural networks using imperfect measurement[J]. Applied Mathematics and Computation, 2018, 316: 205-214.
[20] DONG H, WANG Z, SHEN B, et al. Variance-constrained H∞ control for a class of nonlinear stochastic discrete time-varying systems: the event-triggered design[J]. Automatica, 2016, 72: 28-36.
[21] LIU Y, WANG Z, HE X, et al. Event-triggered least squares fault estimation with stochastic nonlinearities[J]. IFAC Proceedings Volumes, 2014, 47(3): 1855-1860.
[22] XIE Y, LIN Z. Event-triggered global stabilization of general linear systems with bounded controls[J]. Automatica, 2019, 107: 241-254.
[23] SUN Y, YANG G. Event-triggered state estimation for networked control systems with lossy network communication[J]. Information Sciences, 2019, 492: 1-12.
[24] LIU D, YANG G. Robust event-triggered control for networked control systems[J]. Information Sciences, 2018, 459: 168-197.
[25] WANG Z, HU J, MA L. Event-based distributed information fusion over sensor networks[J]. Information Fusion, 2018, 39: 53-55.
[26] YU H, HE Y, WU M. Delay-dependent state estimation for neural networks with time-varying delay[J]. Neurocomputing, 2018, 275: 881-887.
[27] WANG Z, LIU Y, LIU X. State estimation for jumping recurrent neural networks with discrete and distributed delays[J]. Neural Networks, 2009, 22(1): 41-48.
[28] ZHANG W, WANG Z, LIU Y, et al. Event-based state estimation for a class of complex networks with time-varying delays: a comparison principle approach[J]. Physics Letters A, 2017, 381(1): 10-18.
[29] YANG W, LEI L, YANG C. Event-based distributed state estimation under deception attack[J]. Neurocomputing, 2017, 270: 145-151.
[30] SHI D, CHEN T, MOHAMED D. Event-based state estimation of linear dynamic systems with unknown exogenous inputs[J]. Automatica, 2016, 69: 275-288.
[31] GUAN Z, DAVID J H, SHEN X. On hybrid impulsive and switching systems and application to nonlinear control[J]. IEEE Transactions on Automatic Control, 2005, 50(7): 1058-1062.
[32] BOYD S, EL GHAOUI L, FERON E, et al. Linear Matrix Inequalities in System and Control Theory[M]. Society for Industrial and Applied Mathematics, 1994.