引 言
考虑由以下状态方程描述的不确定性时滞奇异摄动控制系统:
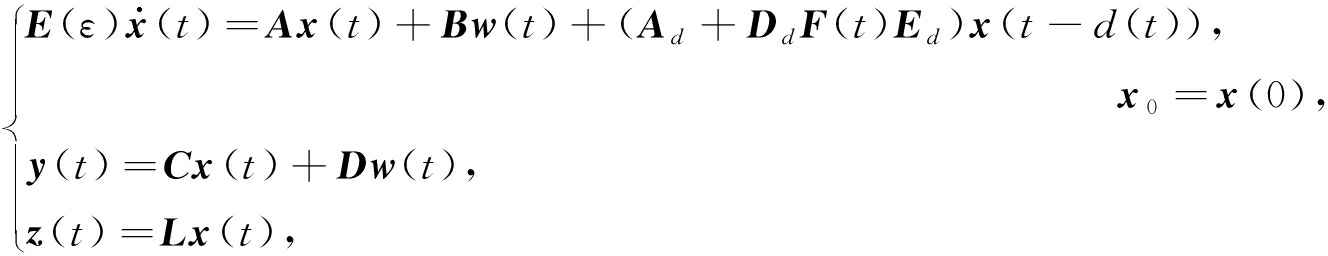
(1)
其中w(t)∈Rm是噪声信号(包括过程和测量噪声),z(t)∈Rp是待估计的信号向量,y(t)∈Rr是测量输出,其他条件与文献[1]相同．
对给定的常数γ>0，要求设计一个渐近稳定的线性滤波器：
(2)
其中
为滤波器状态,
为估计向量,矩阵Af，Bf，Cf是待设计的滤波器参数．
记误差状态为
定义
则滤波误差动态方程为
(3)
其中
本文是在文献[1]理论基础上的后续理论研究．对于滤波器存在状态下的滤波误差动态系统(3)进行稳定性分析．在选取新的Lyapunov泛函,基于Lyapunov稳定性理论基础上，推出保守性更小的新的稳定性判据,增大稳定上界
引理1[2] 对任意适当维数的向量a,b和矩阵X,N,P,R，其中N和R是对称的,若
则
引理2[3] 如果存在对称阵Zi(i=1,2,3,4,5)，且
满足以下LMIs:
1) Z1>0;
则
其中
(4)
引理3[3] 给定适当维数的矩阵Y，D和E，其中Y是对称阵,不确定函数F(t)有FT(t)F(t)≤I，所以
Y+EF(t)D+DTFT(t)ET<0
的充要条件是,存在一个常量η>0，使得
Y+ηEET+η-1DTD<0．
1 滤波误差动态系统的稳定性分析
1.1 时滞依赖的稳定性判据
定理1 给定正数
系统(3)对
是渐近稳定的．若存在对称正定阵Q>0，M>0以及矩阵Zi(i=1,2,3，4,5)且
对于满足条件所具有的不确定性F(t)，下列LMIs条件是可行的:
Z1>0，
(5)
(6)
(7)
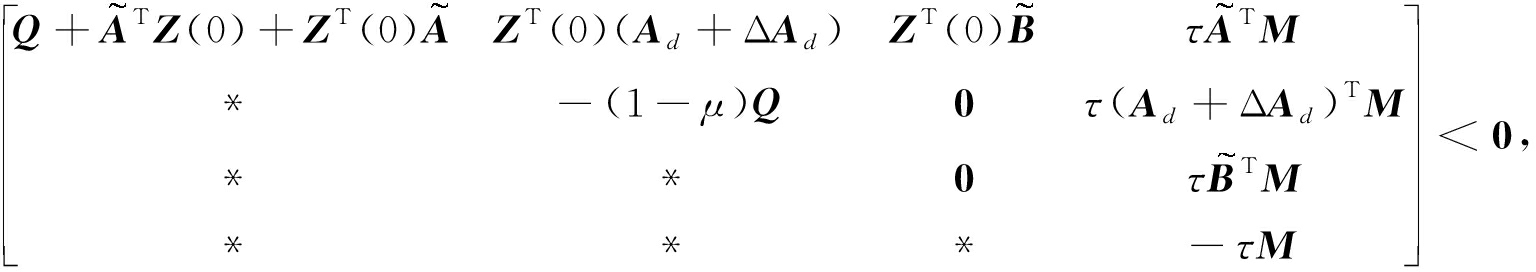
(8)
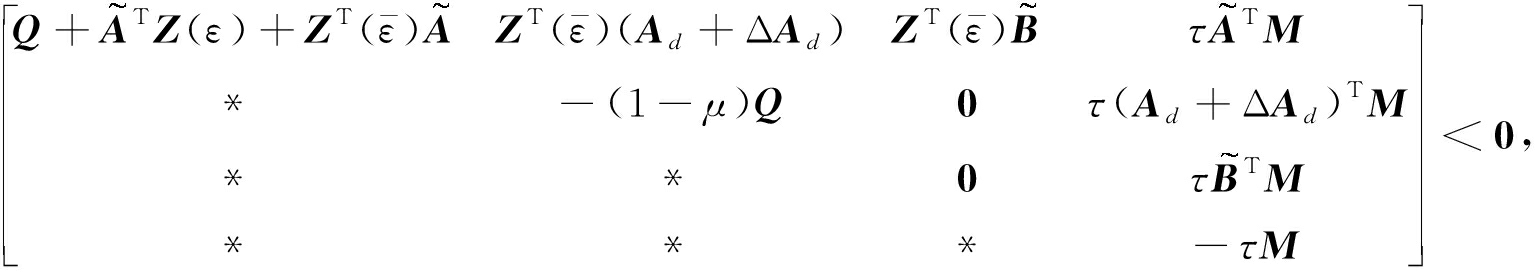
(9)
这里ΔAd=DdF(t)Ed，“*”代表对称位置处矩阵的转置，后同．
证明 定义一个二次Lyapunov-Krasovskii(L-K)泛函如下:
(10)
其中Q，M为对称正定矩阵,即Q>0，M>0．
由引理2以及线性矩阵不等式(5)～(7),有
(11)
这样
就为正定的L-K泛函．
把
沿着系统(3)的任意轨迹进行微分,得
(12)
其中
因此
(13)
其中
G(ε)=
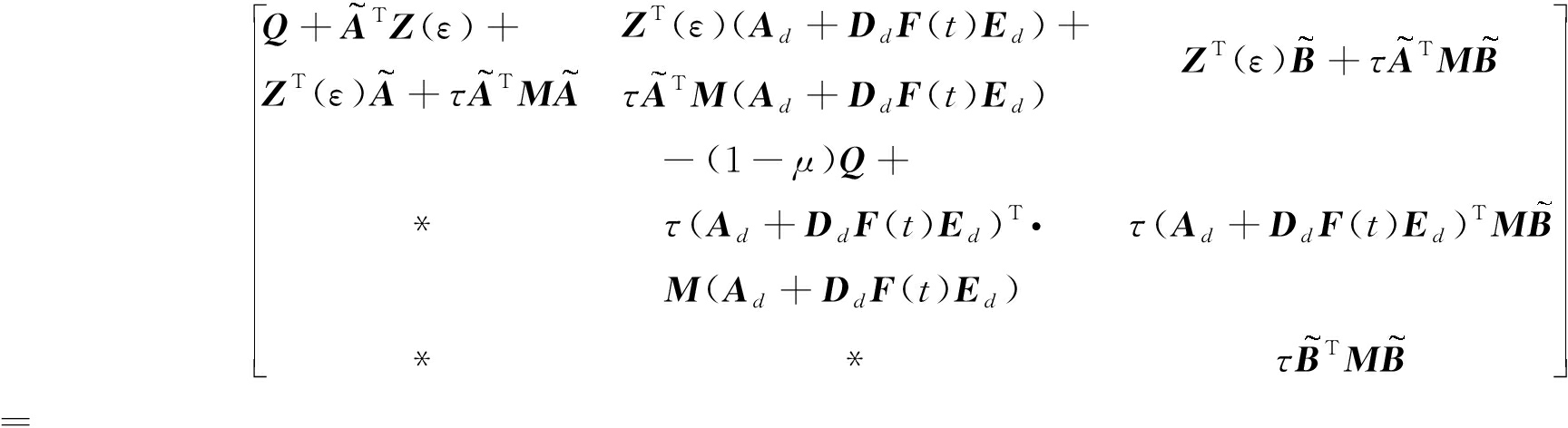
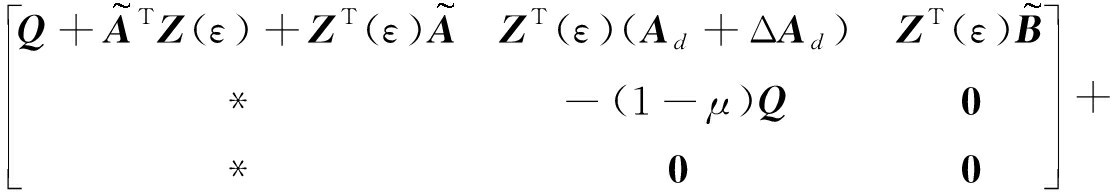
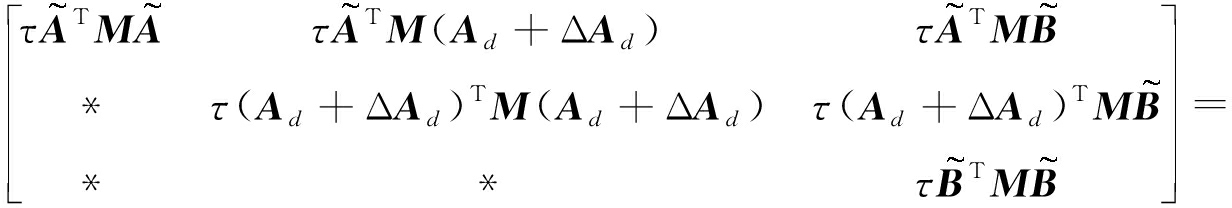
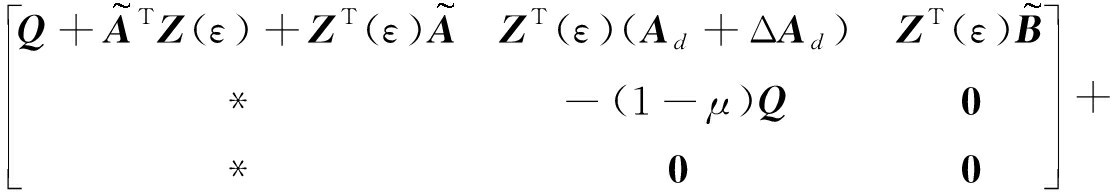
(14)
由Schur补引理[4-6],G(ε)<0等价于
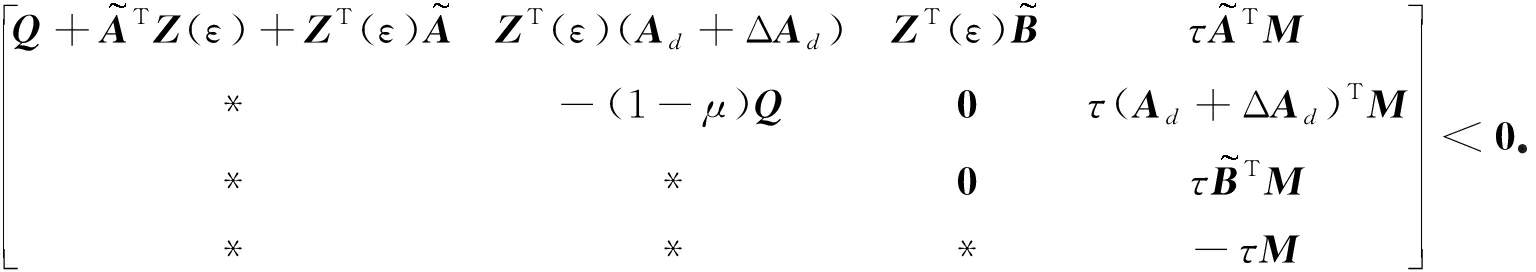
(15)
由式(8)和(9)知,
则由引理2得G(ε)<0，故
再根据Lyapunov稳定性理论[7-9],知系统(3)渐近稳定,证毕．
定理1给出的稳定性条件,为解出其中的参数变量,应该消除式(15)中的不确定函数F(t)，由引理3，存在一个常数γ>0，使得
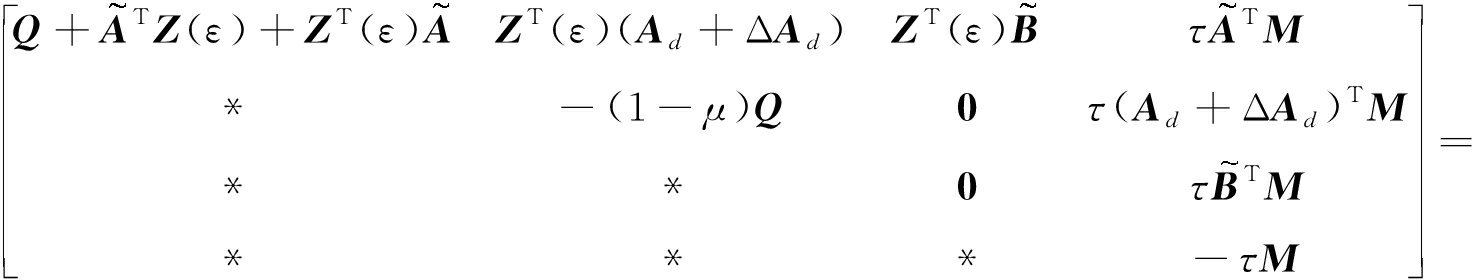
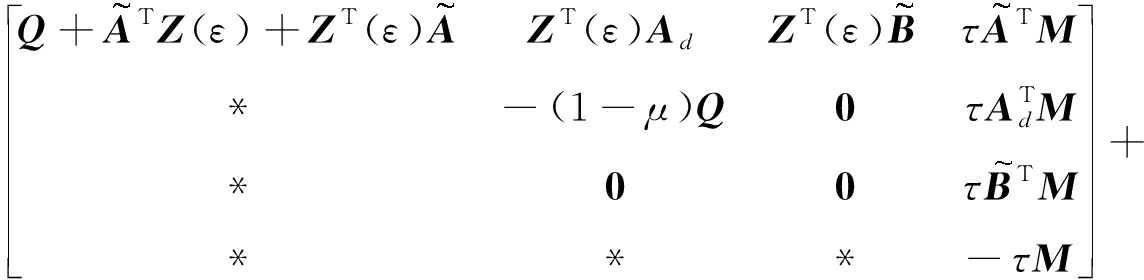
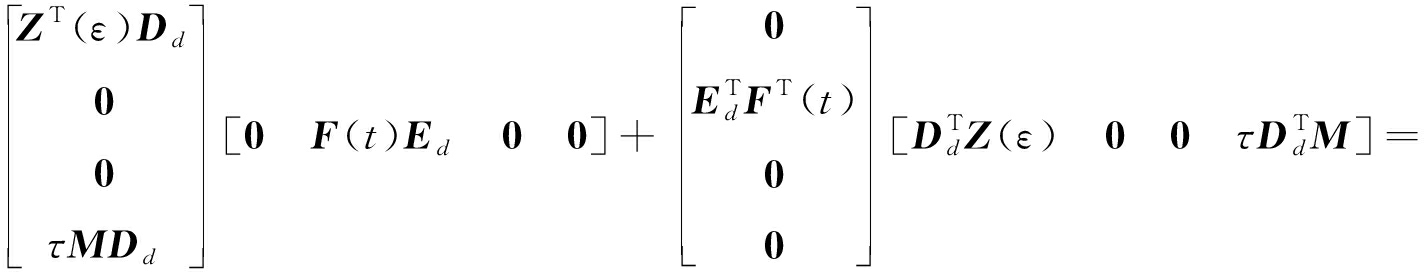
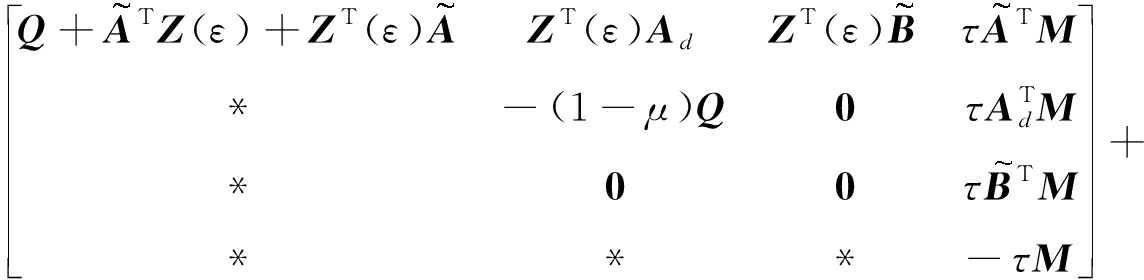
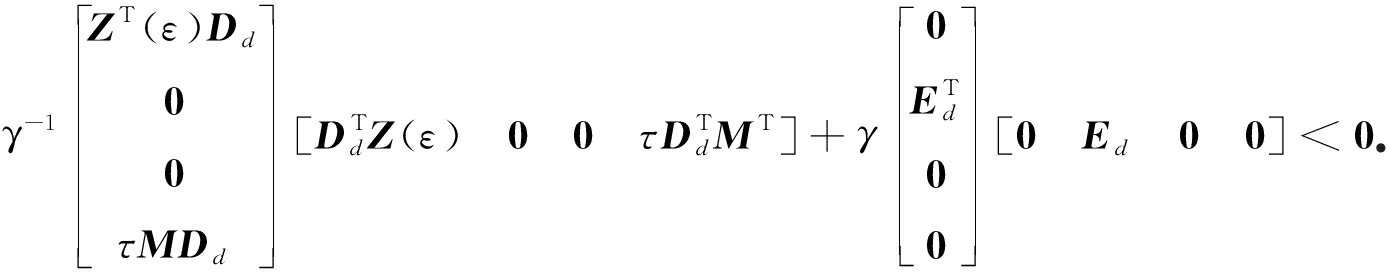
由Schur补引理,得
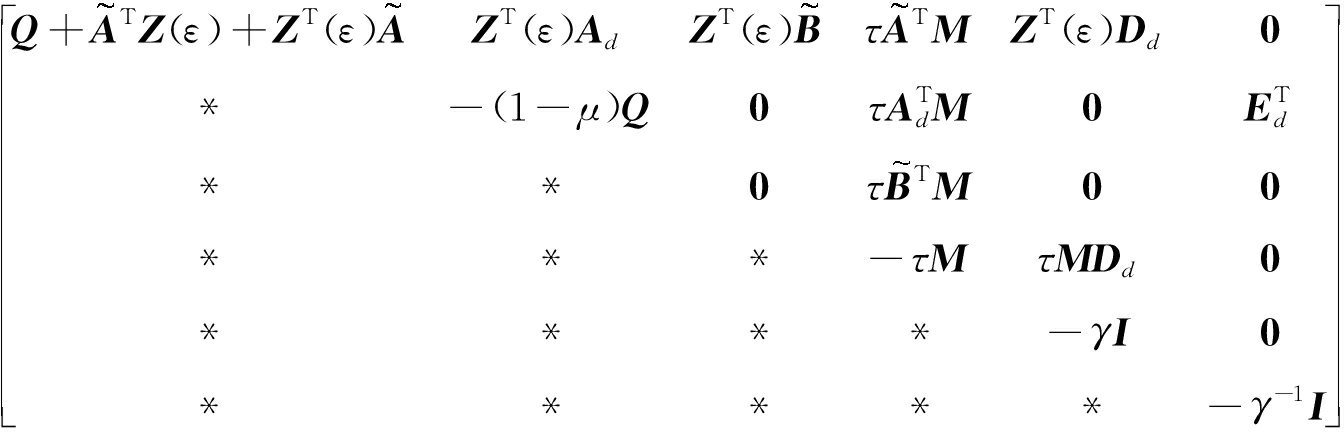<0．
(16)
再把式(16)左右两边分别乘以对角阵diag{I I I I I γI}，得到
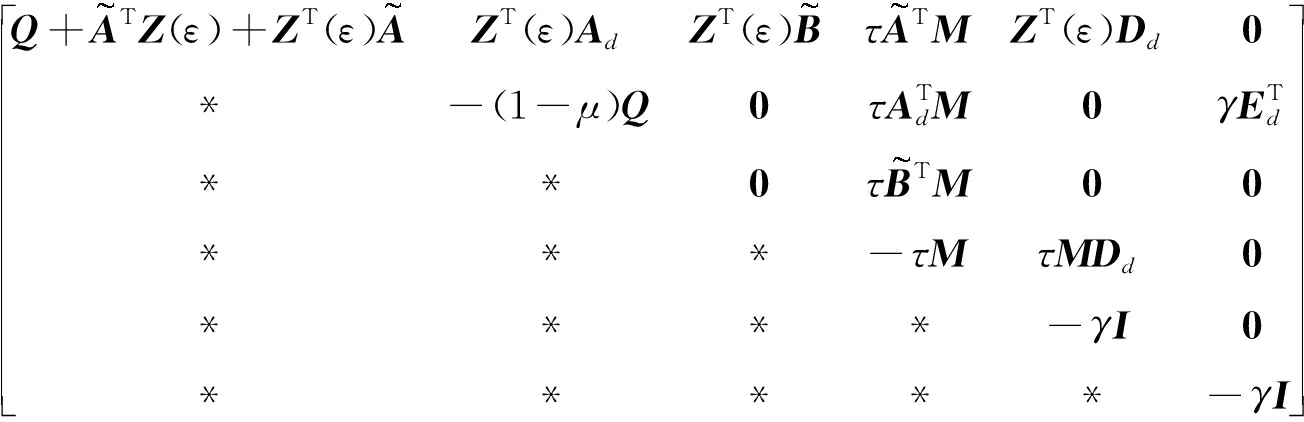<0．
(17)
矩阵不等式(17)对于变量γ,Q,M,Z(ε)是线性的,即得到定理2．
定理2 给定正数
系统(3)对渐近稳定．若存在对称正定阵Q>0，M>0，常量γ>0，矩阵Zi(i=1,2,3,4,5)且在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
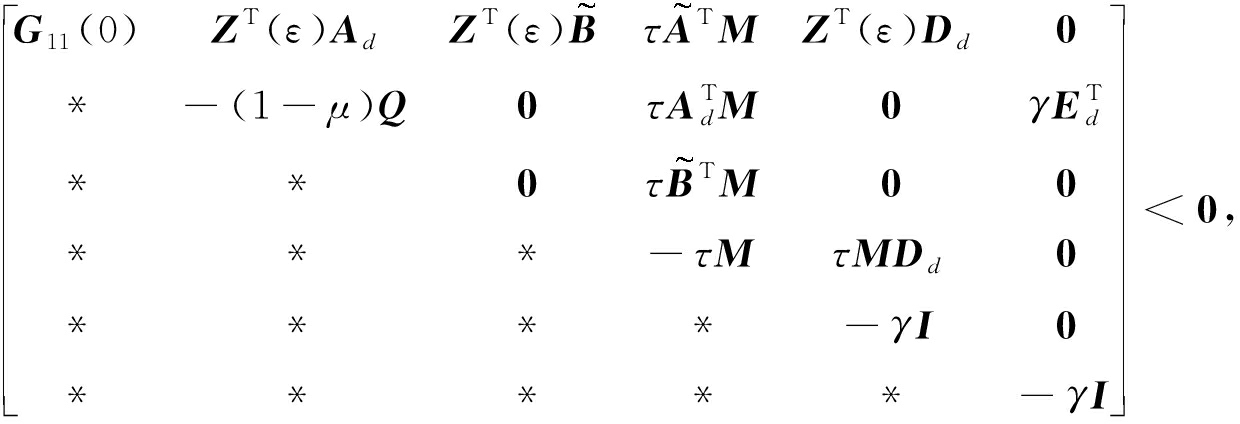
(18)
其中
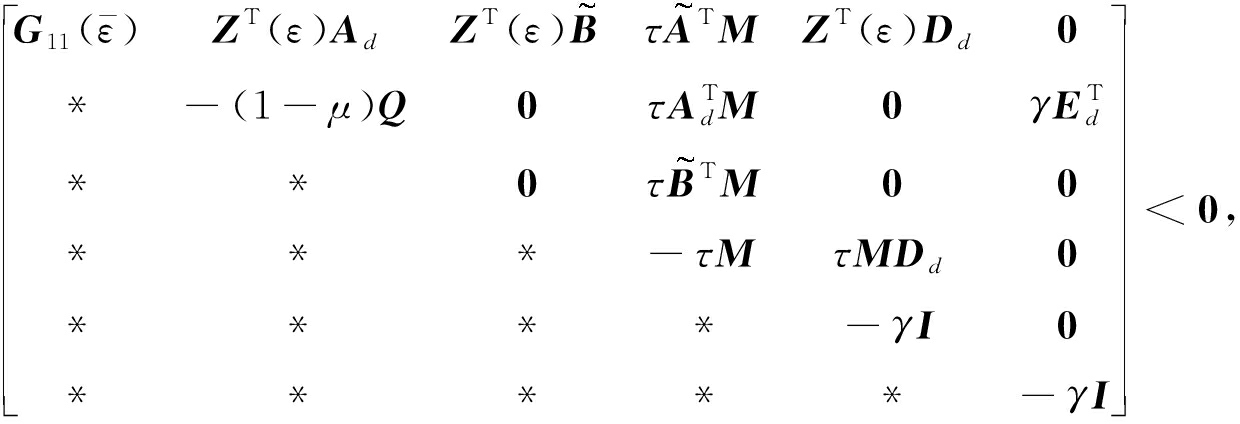
(19)
1.2 时滞独立的稳定性判据
定理3 给定正数系统(3)对是渐近稳定的．若存在对称正定阵Q>0，适当维数的矩阵P，对称阵N,R以及
矩阵Zi(i=1,2,3,4,5)且对于满足条件所具有的不确定性F(t)，在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
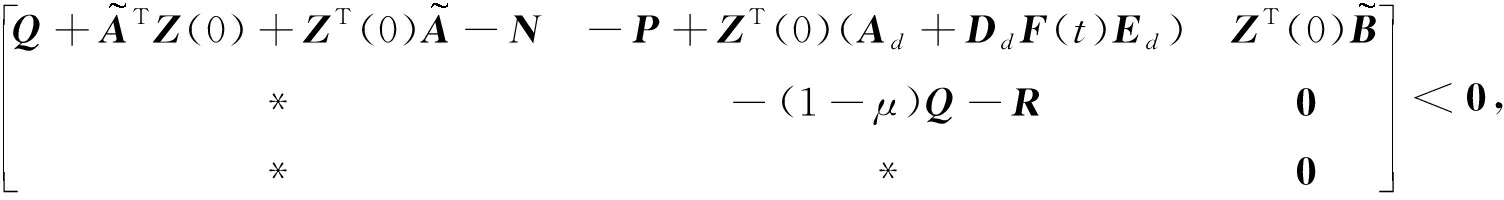
(20)
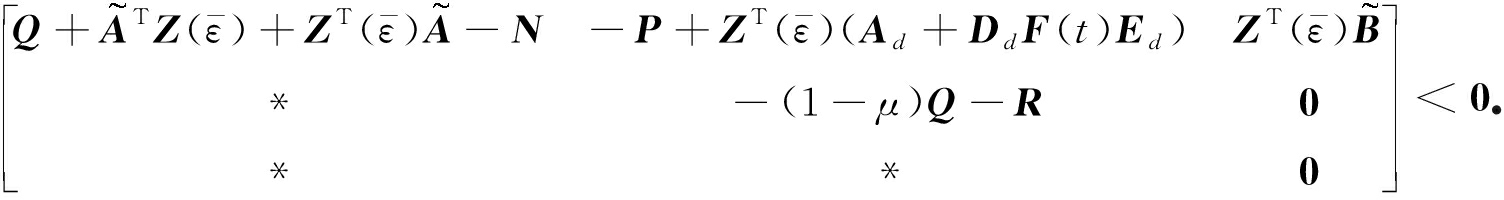
(21)
证明 定义如下L-K泛函：
(22)
其中Q为对称正定矩阵,即Q>0．
把沿着系统(3)的任意轨迹进行微分,得
其中
G(ε)=
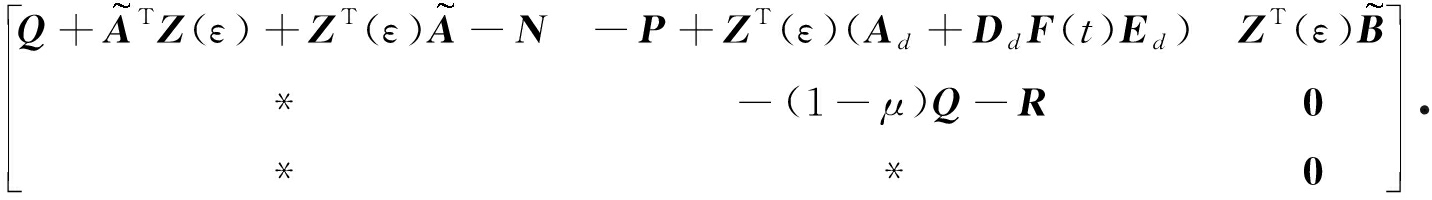
(23)
再由式(20)和(21)知,
得G(ε)<0，故可知所以可以进一步确定系统(3)是渐近稳定的,证毕．
定理3给出的稳定性条件,为解出其中的参数变量,应该消除式(23)中的不确定函数F(t)，类似于定理1,得
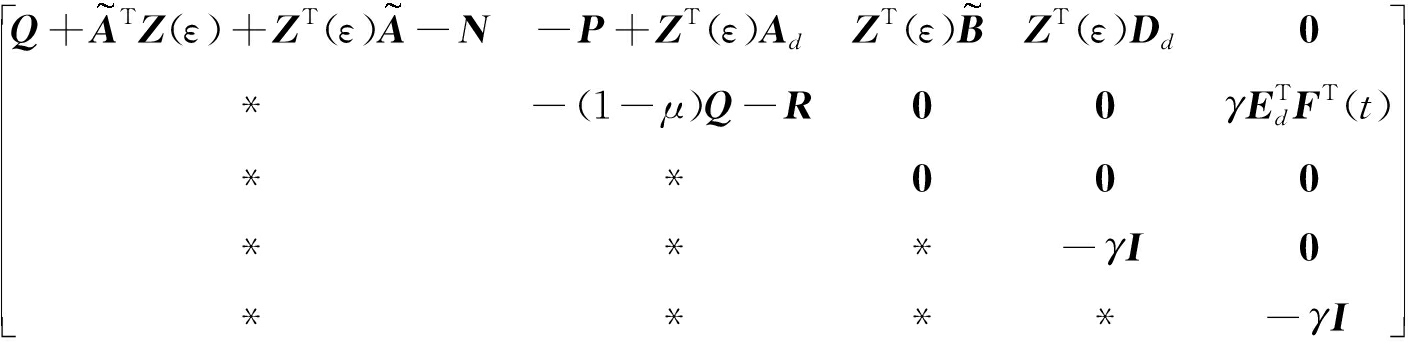<0．
(24)
矩阵不等式(24)对于变量γ，Q，Z(ε)，N，P，R是线性的,则得定理4．
定理4 给定正数系统(3)对是渐近稳定的．若存在对称正定阵Q>0，适当维数的矩阵P，对称阵N,R以及
矩阵Zi(i=1,2,3,4,5)且在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
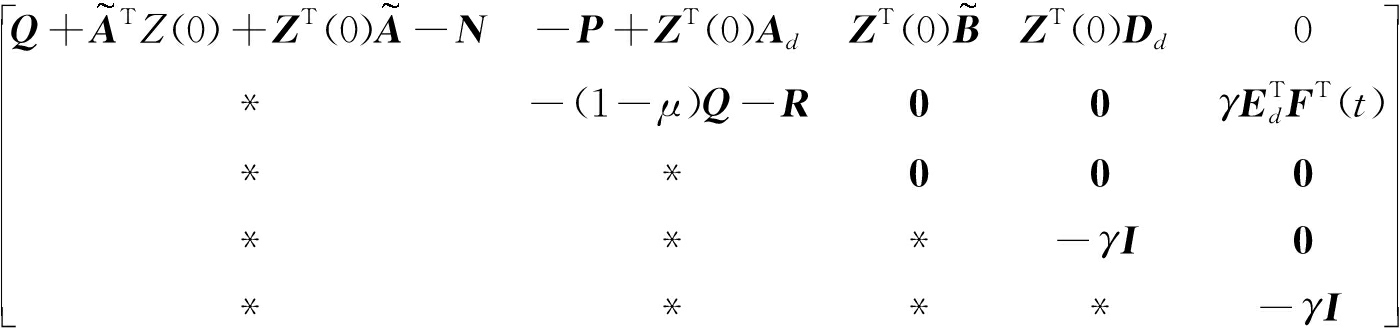<0,
<0．
2 推 论
控制系统(3)去掉不确定性，则变为如下奇异摄动时滞滤波动态系统：
(25)
其中系数矩阵条件与系统(3)相同．
由定理3的稳定性判据可推出如下推论,证略．
推论1 给定正数系统(25)对是渐近稳定的．若存在对称正定阵Q>0，M>0以及矩阵Zi(i=1,2,3,4,5)且在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
其中
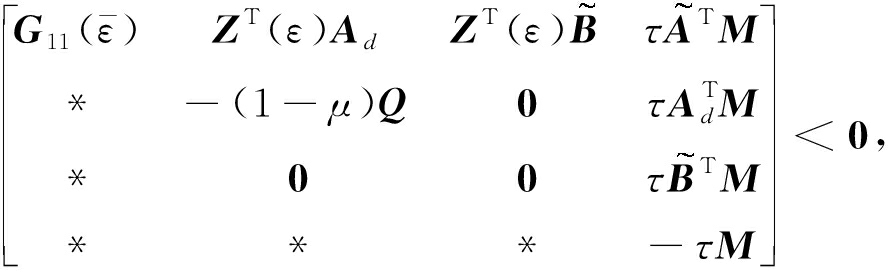
控制系统(3)去掉不确定性变为时滞奇异摄动系统(25),由定理4的稳定性判据可得出如下的推论．
推论2 给定正数系统(25)对是渐近稳定的,若存在对称正定阵Q>0，适当维数的矩阵P，对称阵N,R以及
矩阵Zi(i=1,2,3,4,5)且在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
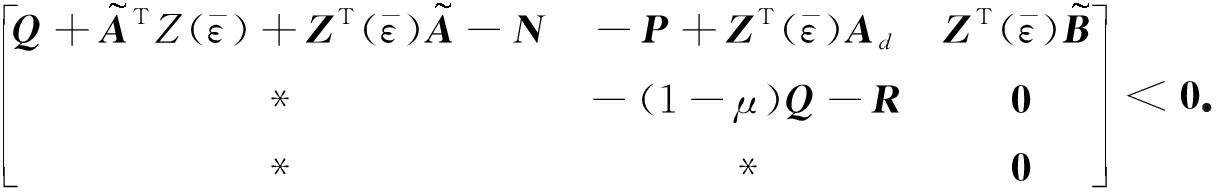
在定理4中,把对称阵N替换为单位阵I或任意适当维数的矩阵P，分别得到如下结果．
推论3 给定正数系统(3)对是渐近稳定的,若存在对称正定阵Q>0，适当维数的矩阵P，对称阵R以及
矩阵Zi(i=1,2,3,4,5)且在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
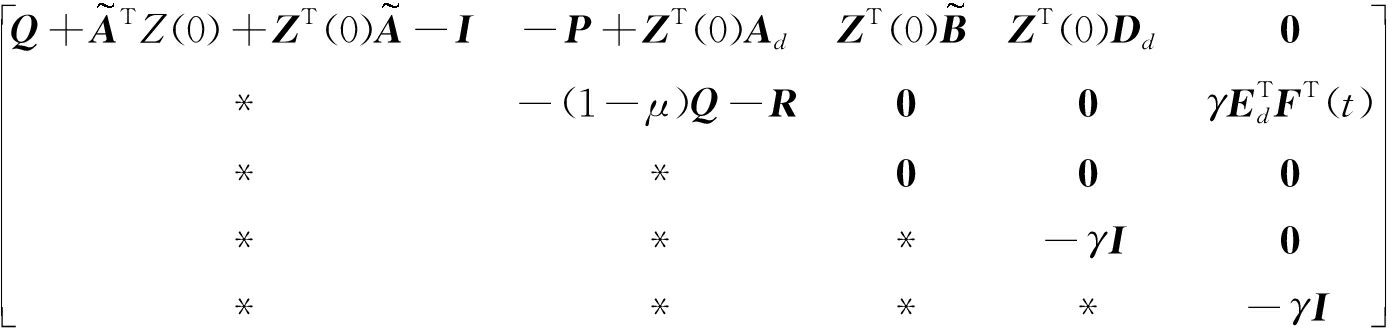<0，
<0．
推论4 给定正数系统(3)对是渐近稳定的．若存在对称正定阵Q>0，对称阵N,R以及
矩阵Zi(i=1,2,3,4,5)且在满足条件(5)～(7)的同时，下列LMIs条件是可行的:
<0，
<0．
推论3和推论4是利用定理4中的保守性来换取结论中的方便性和优越性．
以上推论是在定理3的基础上进一步简化,得到相应的不含有不确定性的时滞系统,对于本文方法上的相应结论,具有一定的理论补充性．去掉系统(3)中的不确定性函数F(t)，则此系统可转变为不含不确定性的时变时滞奇异摄动系统(25),由本文得到的时滞依赖和时滞独立的稳定性判据分别推出推论1和推论2．由定理4结论中的保守性得出推论3和推论4．
3 样 例
考虑以下时变时滞奇异摄动filter误差动态控制系统：
这里
取
F(t)=1, d(t)=0.5, τ=1, μ=0.5,
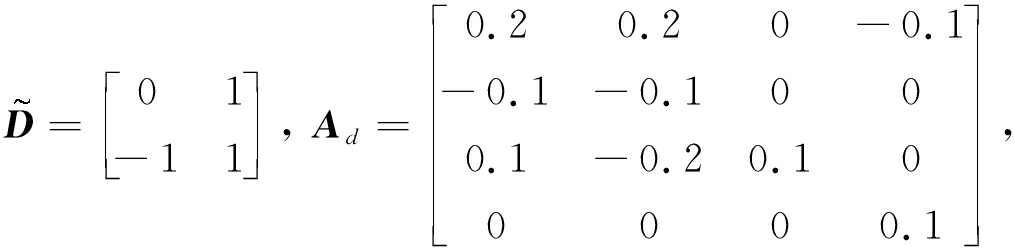
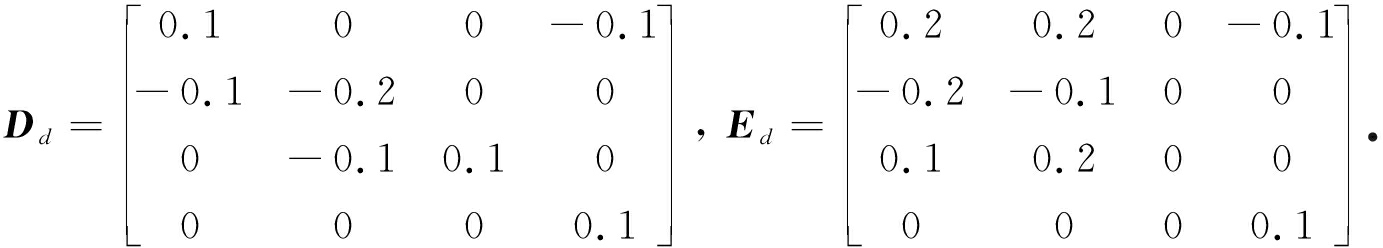
初始条件
求解定理2中的LMIs，得
以上的样例表明， 本文所得定理结论是有效可行的， 并且与现有文献相比， 不仅给出了比较大的摄动上界0.3， 而且指出在0～0.3的整个区间范围内， 闭环误差动态系统能够渐近稳定．这与只在某一摄动点ε0或者在不明确摄动上界稳定性分析理论相比[10-13]， 具有一定的优越性和可控性．
4 结 语
时变时滞奇异摄动不确定控制系统的滤波器设计与稳定性分析，经过众多学者共同的努力[14-15]和本文在此方面的进一步完善补充,已经形成了比较系统的理论体系．本文针对前期不确定性时滞奇异摄动控制系统，研究了其滤波器设计问题之后的滤波误差动态系统的稳定性分析,在一定的条件下,给出了系统渐近稳定的充分性判定定理和摄动参数所在的稳定区间，以及具体的稳定化摄动参数上界，形成了系统化的、比较完备的理论体系鲁棒稳定性分析与设计，是一项有意义的研究工作．
本文所提的方法不需要对系统降阶和分解,可直接推广到控制系统理论其他类型系统中,如离散系统、非标准系统问题等[15-16]也同样适用，可以为相关控制理论提供研究参考[17-19]．
[1] 孙凤琪. 不确定性时滞奇异摄动控制系统的滤波器设计[J]. 控制工程, 2020, 27(8). DOI: 10.14107/j.cnki.kzgc.20180775.(SUN Fengqi. Filter design of singular perturbation control system with uncertain time-delay[J]. Control Engineering, 2020, 27(8). DOI: 10.14107/j.cnki.kzgc.20180775.(in Chinese))
[2] 孙凤琪. 若干类时滞奇异摄动系统的稳定性分析与控制[M]. 北京: 科学出版社, 2018.(SUN Fengqi. Stability Analysis and Control of Several Kinds of Singularly Perturbed Systems With Delays[M]. Beijing: Science Press, 2018.(in Chinese))
[3] 徐赵文. 复杂受限系统的控制与滤波理论研究[D]. 博士学位论文. 杭州: 浙江大学, 2018. (XU Zhaowen. Research on control and filtering theory of complex constrained systems[D]. PhD Thesis. Hangzhou: Zhejiang University, 2018.(in Chinese))
[4] 陈进. 不确定系统有限时间鲁棒滤波问题的研究[D]. 硕士学位论文. 哈尔滨: 哈尔滨工业大学, 2017.(CHEN Jin. Research on finite-time robust filtering for uncertain systems[J]. Master Thesis. Harbin: Harbin Institute of Technology, 2017.(in Chinese))
[5] 王亚龙. 基于LMI的变时滞系统鲁棒H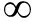
滤波及应用[D]. 硕士学位论文. 哈尔滨: 哈尔滨工业大学, 2015.(WANG Yalong. Robust H filtering for time-varying delay systems based on LMI and its application[D]. Master Thesis. Harbin: Harbin Institute of Technology, 2015.(in Chinese))
[6] 李峰. Markov切换系统的有限时间约束控制与滤波[D]. 硕士学位论文. 马鞍山: 安徽工业大学, 2017.(LI Feng. Limited-time constrained control and filtering for Markov switched systems[D]. Master Thesis. Maanshan: Anhui University of Technology, 2017.(in Chinese))
[7] 郑重. 参数切换重复标量非线性系统的控制与滤波研究[D]. 博士学位论文. 哈尔滨: 哈尔滨工业大学, 2017.(ZHENG Zhong. Study on control and filtering of repetitive scalar nonlinear systems with parameter switching[D]. PhD Thesis. Harbin: Harbin Institute of Technology, 2017.(in Chinese))
[8] 肖小庆. 线性切换系统：事件触发控制、滤波与广义动态分析[D]. 博士学位论文. 南京: 南京理工大学, 2017.(XIAO Xiaoqing. Linear switching system: event triggering control, filtering and generalized dynamic analysis[D]. PhD Thesis. Nanjing: Nanjing University of Science and Technology, 2017.(in Chinese))
[9] 侯男. 几类系统非脆性滤波方法研究[D]. 硕士学位论文. 大庆: 东北石油大学, 2015.(HOU Nan. Research on non-brittle filtering methods for several systems[D]. Master Thesis. Daqing: Northeast Petroleum University, 2015.(in Chinese))
[10] 张舒. 非线性系统的鲁棒滤波及控制方法研究[D]. 硕士学位论文. 大庆: 东北石油大学, 2015.(ZHANG Shu. Study on robust filtering and control method of nonlinear systems [D]. Master Thesis. Daqing: Northeast Petroleum University, 2015.(in Chinese))
[11] 张琦. T-S非线性模糊网络控制系统鲁棒控制及滤波[D]. 硕士学位论文. 大庆: 东北石油大学, 2017.(ZHANG Qi. T-S nonlinear fuzzy networked control system robust control and filtering[D]. Master Thesis. Daqing: Northeast Petroleum University, 2017.(in Chinese))
[12] 成军. 几类跳变系统的有限时间稳定性分析与控制问题研究[D]. 博士学位论文. 成都: 电子科技大学, 2015.(CHENG Jun. Finite-time stability analysis and control of several jump systems[D]. PhD Thesis. Chengdu: University of Electronic Science and Technology of China, 2015.(in Chinese))
[13] 周秀杰. 网络控制系统的鲁棒控制及滤波研究[D]. 硕士学位论文. 大庆: 东北石油大学, 2015.(ZHOU Xiujie. Robust control and filtering of networked control systems[D]. Master Thesis. Daqing: Northeast Petroleum University, 2015.(in Chinese))
[14] 陈照辉. 时滞系统稳定控制与滤波及其应用研究[D]. 博士学位论文. 成都: 电子科技大学, 2015.(CHEN Zhaohui. Stability control and filtering of time-delay systems and their applications[D]. PhD Thesis. Chengdu: University of Electronic Science and Technology of China, 2015.(in Chinese))
[15] 冯波. 线性滤波估计算法研究及在惯性导航系统中的应用[D]. 博士学位论文. 北京: 北京理工大学, 2014.(FENG Bo. Research on linear filter estimation algorithm and its application in inertial navigation system[D]. PhD Thesis. Beijing: Beijing University of Technology, 2014.(in Chinese))
[16] 曹璐. 基于最小模型误差准则的非线性滤波及控制理论与应用研究[D]. 博士学位论文. 长沙: 国防科学技术大学, 2014.(CAO Lu. Theory and application of nonlinear filtering and control based on minimum model error criterion[D]. PhD Thesis. Changsha: National University of Defense Technology, 2014.(in Chinese))
[17] 戴德宣, 王少伟. 趋旋性微生物在幂律流体饱和水平多孔层中的热-生物对流稳定性分析[J]. 应用数学和力学, 2019, 40(8): 856-865.(DAI Dexuan, WANG Shaowei. Linear stability analysis on thermo-bioconvection of gyrotactic microorganisms in a horizontal porous layer saturated by a power law fluid[J]. Applied Mathematics and Mechanics, 2019, 40(8): 856-865.(in Chinese))
[18] 芦泽阳, 李树江, 王向东. 采用RBF网络的喷雾机喷杆自适应动态面跟踪控制[J]. 应用数学和力学, 2019, 40(7): 801-809.(LU Zeyang, LI Shujiang, WANG Xiangdong. Adaptive RBF-network dynamic surface tracking control of sprayer boom systems[J]. Applied Mathematics and Mechanics, 2019, 40(7): 801-809.(in Chinese))
[19] 赵晨, 戈新生. 基于虚拟完整约束的欠驱动起重机控制方法[J]. 应用数学和力学, 2019, 40(3): 302-310.(ZHAO Chen, GE Xinsheng. A control method for underactuated cranes based on virtual holonomic constraints[J]. Applied Mathematics and Mechanics, 2019, 40(3): 302-310.(in Chinese))