引 言
作为对工程、交通、经济学、物理学等领域中较多问题的概括，Blum和Oettli[1]在1994年给出了平衡问题这一数学模型．随后，文献[2-3]把该模型推广到向量平衡问题．由于实际条件的限制，通常构建的模型会带有不同程度的约束．一般地，将带有约束的向量平衡问题称为向量拟平衡问题．向量拟平衡问题的研究范围十分广泛， 例如鞍点问题、 不动点问题、 向量(拟)变分不等式问题和向量(拟)互补问题等都可以看作向量拟平衡问题的特殊情况．也正是由于其模型范围以及在相关领域中应用的广泛性， 向量拟平衡问题受到越来越多的关注且被广泛研究[4-10]．
众所周知，关于平衡问题解映射稳定性的研究是非常重要的．一般地，稳定性包含上/下半连续性、连续性、Lipschitz连续性和Hölder连续性等．近年来，有许多学者对上/下半连续性进行了深入的研究．1997年，Zhao[11]提出了一个关键假设，并利用此关键假设研究了一类广义非线性规划问题最优解集映射的下半连续性．受文献[11]的启发，Zhong和Huang[12]借助关键假设(Hg)′得到了一类参数广义向量拟平衡问题解映射Hausdorff下半连续的充分必要条件．借助两个关键假设，Anh和Hung[13]讨论了两类参数向量拟平衡问题解映射Hausdorff下半连续的充分性和必要性条件．最近，邵重阳等[14]获得了一类参数广义向量拟平衡问题解映射Hausdorff下半连续的充要条件;Anh等[15]对赋范空间中的一类参数向量拟平衡问题解映射的Berge半连续性进行了讨论．
另一方面，我们发现目前绝大多数文献对平衡问题的研究都是在锥序下进行的．然而，就实际问题而言，锥序关系并不适合于所有问题，所以在一般序下研究平衡问题是很有必要的．因而，在2016年，Chen等[16]提出了改进集下的向量平衡问题，并获得了解映射Berge连续性充分性条件．最近，Wang等[17]给出了自由自配集下的广义向量拟平衡问题，并对解的Berge连续性和Painlevé-Kuratowski收敛性进行了研究．受文献[4，12，16-17]的启发，本文定义了改进集映射，给出了改进集映射下的参数广义向量拟平衡问题．通过使用非线性函数Ψ建立了原问题的标量化问题，借助关键假设HΨ和标量化问题与原问题解集的关系对解映射的Berge下半连续性进行了研究．
本文结构安排如下：第1节回顾了本文所需要的一些概念及其性质，定义了改进集映射，并基于改进集映射，给出了参数广义向量拟平衡问题，定义了非线性函数Ψ．第2节引入了关键假设，并给出了原问题的标量化问题，同时借助关键假设HΨ和标量化问题与原问题解集之间的关系获得了原问题解映射Berge下半连续性的充分必要条件．最后给出了本文的结论．
1 预 备 知 识
在本文中，除特殊规定外，均假设X，Y是两个Banach空间,Λ是度量空间．令L(X,Y)表示从X到Y的连续线性映射的全体，C:X→2Y是集值映射且满足对任意x∈X，C(x)是实点闭凸锥．令K:X×Λ→2X,T:X×Λ→2L(X,Y)为两个非空集值映射,φ:X×X×2L(X,Y)→Y为向量值映射．
‖·‖表示赋范空间中的范数，d(·,·)表示度量空间中的度量．集合M⊂Y的拓扑边界、拓扑内部和ε-邻域分别记为∂M，int M,U(M,ε)={y∈Y:∃x∈M, s.t. ‖x-y‖<ε}．
定义1[18] 称集合E1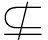
X是关于锥C1⊆Y的改进集，若E1+C1=E1且0∉E1．
定义2 称集值映射E:X→2Y是关于映射C:X→2Y的改进集映射，如果对任意x∈X，E(x)+C(x)=E(x)并且0∉E(x)．
令E:X→2Y是关于映射C的改进集映射，并假设对任意x∈X，E(x)是闭的．对任意λ∈Λ，考虑如下改进集映射E下的参数广义向量拟平衡问题(IPGVQEP): 存在x∈K(x,λ)和t∈T(x,λ)使得
φ(x,y,t)∉-E(x), ∀y∈K(x,λ)．
对任意λ∈Λ，令A(λ)={ x∈X:x∈K(x,λ)}．定义IPGVQEP的解集S(λ)如下：
S(λ)={ x∈A(λ): ∃t∈T(x,λ), s.t. φ(x,y,t)∉ - E(x), ∀y∈K(x,λ)}． 为研究需要，对任意λ∈Λ，本文均假设解集S(λ)非空．
下面回顾一些本文所需要的相关概念和性质．
定义3[19] 令Λ和X是Hausdorff拓扑空间,G:Λ→2X是集值映射,
是给定点．
称G在
处是Berge上半连续(B-u.s.c)的，若对包含
任意开集V，都存在的邻域
使得对任意
有G(λ)⊂V ；
称G在处是Berge下半连续(B-l.s.c)的，若对任意满足
的开集V，都存在的邻域使得对任意有G(λ)∩V≠∅；
称G在Λ上是B-l.s.c(B-u.s.c)的，若G在任意λ∈Λ处都是B-l.s.c(B-u.s.c)的．称G在Λ上是Berge连续的，若G在任意λ∈Λ处既是B-u.s.c的，又是B-l.s.c的；
称G是闭的，若G的图像是闭的，即graph(G)={(λ,x)∈Λ×X: x∈G(λ)}在Λ×X上是闭的．
引理1[19] 令Λ和X是Hausdorff拓扑空间,G:Λ→2X是集值映射,是给定点．
如果G是B-u.s.c的且具有闭值，则G是闭的；
如果G是闭的且X是紧的，则G是B-u.s.c的；
如果G是紧值的，则G在处是B-u.s.c的，当且仅当对Λ中任意满足
的网{λα}和满足xα∈G(λα)的网{xα}，都存在
和一个子网{xβ}⊂{xα}使
在处是B-l.s.c的，当且仅当对Λ中任意满足的网{λα}和
都存在xα∈G(λα)使得
作为向量值映射锥上/下半连续性的推广，我们给出如下关于变动锥的上/下半连续性的概念．
定义4 设X和Z是拓扑空间，Y拓扑向量空间．令C:X→2Y是集值映射且满足对任意x∈X，C(x)是实点闭凸锥，G:X×X×Z→Y是向量值映射．
称G在
处是C-上半连续(C-u.s.c)的，如果对Y中原点的任意开零邻域V，都存在
的邻域U，使得
称G在处是C-下半连续(C-l.s.c)的，如果G在处是C-u.s.c的．
称G在处是C-连续的，如果G在处既是C-u.s.c的，又是C-l.s.c的．称G在X×X×Z 上是C-连续的，若G在任意(x,y,z)∈X×X×Z处既是C-u.s.c的，又是C-l.s.c的．
下面，借助于改进集映射E,定义非线性标量化函数．
令e:X→Y连续的单值映射且满足对任意x∈X, e(x)∈int C(x)．对x∈X，定义非线性标量化函数ξe,E:X×Y→R∪{±∞}如下：
ξe,E(x,y)=inf{r∈R: y∈re(x)-E(x)}．
记ξ
ξe,E，我们有如下引理．
引理2 ξ有如下性质：
ξ(x,y)<r ⟺ y∈re(x)-int E(x)．
ξ(x,y)≤r ⟺ y∈re(x)-E(x)．
ξ(x,y)≥r ⟺ y∉re(x)-int E(x)．
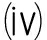ξ(x,y)>r ⟺ y∉re(x)-E(x)．
ξ(x,y)=r ⟺ y∈re(x)-∂E(x)．
定义集值映射W:X→2Y为W(x)=Y\int E(x)，则有以下性质成立：
(a) 若W(·)在X上是B-u.s.c的，则ξ(·,·)在 X×Y上是u.s.c的；
(b) 若E(·)在X上是B-u.s.c的，则ξ(·,·)在X×Y上是l.s.c的．
证明 由映射E的定义，对任意x∈X，E(x)是闭的，且E(x)+[0,+∞)e(x)⊂E(x)．容易验证文献[20]中定理2.3.1和命题2.3.4的条件都满足，故性质～可运用文献[20]中定理2.3.1和命题2.3.4得到．
性质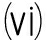中(b)的证明与(a)相似，故在此只证明(a)．任取r∈R，仅需证明集合L≥r={(x,y)∈X×Y:ξ(x,y)≥r}是闭的．令任意收敛到(x0,y0)∈X×Y的序列{(xn,yn)}⊂L≥r，有ξ(xn,yn)≥r，下证ξ(x0,y0)≥r．因为ξ(xn,yn)≥r，故
yn∉re(xn)-int E(xn),
即re(xn)-yn∈W(xn)．由e(·)的连续性和(xn,yn)→(x0,y0)知re(xn)-yn→re(x0)-y0．因为W(·)是B-u.s.c的且具有闭值，由引理1知W(·)是闭的．从而re(x0)-y0∈W(x0)， 即y0∉re(x0)-int E(x0)．由此， ξ(x0,y0)≥r，这表明L≥r是闭的, ξ(·,·)在 X×Y上是u.s.c的．
□
与文献[15]中的命题4.5类似，我们有以下结果．
命题1 如果φ(·,·,·)在 X×X×2L(X,Y)上是C-l.s.c的,W(·)在X上是B-u.s.c的，则函数(x,y,t)
ξ(x,φ(x,y,t))在X×X×2L(X,Y)是u.s.c的．
如果φ(·,·,·)在X×X×2L(X,Y)上是C-u.s.c的, E(·)在X上是B-u.s.c的，则函数(x,y,t)ξ(x,φ(x,y,t))在X×X×2L(X,Y)上是l.s.c的．
下面通过例1说明命题1．
例1 记X=R，Y=R2,Λ=[0,1],K(x,λ)=[0, 2],T(x,λ)=(1,[1,λx2+1])T．取
令映射e:X→2Y和φ:X×X×2L(X,Y)→Y分别如下：
e(x)=(1,1),
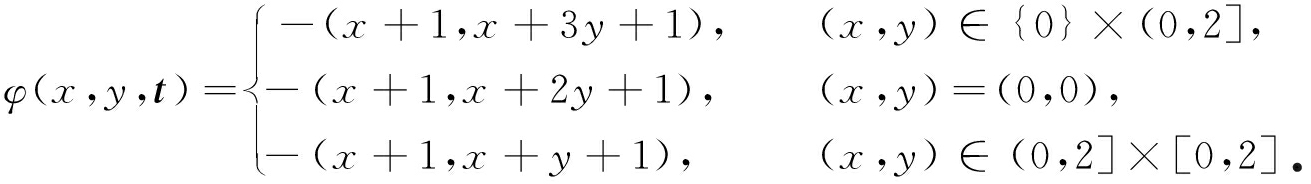
容易验证，φ既是C-u.s.c的又是C-l.s.c的，同时命题1中的其他条件均满足．经计算，有
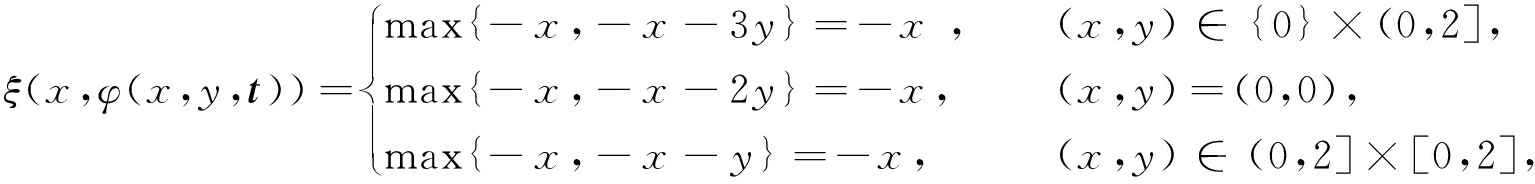
这表明(x,y,t)ξ(x,φ(x,y,t))是连续的．
下面，我们借助ξ定义一类新的非线性函数Ψ:X×X×L(X,Y)×R++→R如下：
Ψ(x,y,t,α)=αξ(x,φ(x,y,t))-‖φ(x,y,t)‖2．
由Ψ的构造，结合引理2和命题1，容易得到Ψ的如下性质．
命题2 对任意(x,y,t)∈X×X×L(X,Y),
如果φ(x,y,t)∈-E(x)，则对任意α∈R++，Ψ(x,y,t,α)<0；
如果φ(x,y,t)∉-E(x)，则存在α∈R++使得Ψ(x,y,t,α)≥0；
如果φ在X×X×L(X,Y)上是连续的,W(·)和E(·)在X上是B-u.s.c的，则对任意α∈R++，Ψ(·,·,·,α)在X×X×L(X,Y)是连续的．
证明 由引理2及Ψ的具体构造可直接得到和 ．下证．φ在X×Y×L(X,Y)上是连续的，则‖φ‖2是连续的．又 W(·)和E(·)在X上是B-u.s.c的，故由命题1知ξ是连续的．从而对任意α∈R++，Ψ(·,·,·,α)在X×X×L(X,Y)上是连续的．
□
2 解映射S的Berge下半连续性
本节引入了一个关键假设HΨ，借助关键假设HΨ和问题(PGVQEP)Ψ与原问题解的关系建立了S的Berge下半连续性的充分必要条件．
对任意λ∈Λ和α∈R++，IPGVQEP的标量化问题(IPGVQEP)Ψ如下： 存在x∈K(x,λ)和t∈T(x,λ)使得
Ψ(x,y,t,α)≥0, ∀y∈K(x,λ)．
(IPGVQEP)Ψ的解集记为
Sα(λ)={x∈A(λ):∃t∈T(x,λ),s.t. Ψ(x,y,t,α)≥0,∀y∈K(x,λ)}．
下面的定理给出了S与Sα之间的关系．
定理1 假设K(·,·)在X×Λ上具有紧值，且φ在X×X×L(X,Y)上是连续的，则对任意λ∈Λ，S(λ)=∪α∈R++Sα(λ)．
证明 任意固定λ∈Λ，任取x∈S(λ)，则x∈A(λ)，并且存在t∈T(x,λ)使得
φ(x,y,t)∉-E(x), ∀y∈K(x,λ)．
(1)
由φ的连续性知,Θ=∪y∈K(x,λ)φ(x,y,t)是紧集，且存在正数M使得
0 ≤‖φ(x,y,t)‖2≤M<+∞, ∀y∈K(x,λ)．
(2)
由式(1)和E(x)的闭性知，-E(x)∩Θ=∅．结合式(2)可知，存在0<mξ<+∞使得对∀y∈K(x,λ)，有
mξ≤ξ(x,φ(x,y,t))．
现取α0=M/mξ+1，容易验证0<α0<+∞且
Ψ(x,y,t,α0)≥0, ∀y∈K(x,λ),
这表明x∈Sα0(λ)⊂∪α∈R++Sα(λ)，从而S(λ)⊂∪α∈R++Sα(λ)．
相反的，对任意x′∈∪α∈R++Sα(λ)，存在α0∈R++使得x′∈Sα0(λ)．由Sα0(λ)的定义知，存在t′∈T(x′,λ)使得
α0ξ(x′,φ(x′,y,t′))-‖φ(x′,y,t′)‖2 ≥0, ∀y∈K(x′,λ)
(3)
成立．
假设x′∉S(λ),则对任意t∈T(x′,λ)，都存在满足φ(x′,y,t)∈-E(x′)的y∈K(x′,λ)．从而对t′∈T(x′,λ)，存在y′∈K(x′,λ)满足
φ(x′,y′,t′)∈-E(x′)．
因为E(x′)是改进集，0∉E(x′)，有φ(x′,y′,t′)≠0 ．由命题2可得
α0ξ(x′,φ(x′,y′,t′))-‖φ(x′,y′,t′)‖2<0,
这与式(3)矛盾．故x∈S(λ)．
□
受相关文献的启发，借助非线性函数Ψ，我们给出如下关键假设．
HΨ: 给定λ0∈Λ．对任意ε>0，都存在ρ>0和δ>0使得对任意α∈R++,λ∈B(λ0,δ)和x∈A(λ)\U(S(λ),ε)，有
下面，借助于关键假设HΨ，我们讨论S的Berge下半连续性．
定理2 假设HΨ成立且满足
A(·)在Λ上是B-l.s.c且具有紧值的；
K(·,·)在X×Λ上是B-u.s.c且具有紧值的；
T(·,·)在X×Λ上是B-l.s.c且具有紧值的；
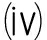W(·)和E(·)在X上是B-u.s.c的；
φ(·,·,·)在X×X×2L(X,Y)上是连续的，
则S(·)在Λ上是B-l.s.c的．
证明 假设S(·)在λ0∈Λ处不是B-l.s.c的，则存在x0∈S(λ0)和收敛到λ0的序列{λn}⊂Λ，使得对任意xn∈S(λn)都有
xn/→x0, n→+∞．
(4)
由知，存在x′n∈A(λn)使得
x′n→x0, n→+∞．
(5)
对足够小的ε>0 ，有x′n∉U(S(λn),ε)．否则必存在x″n∈S(λn)使得
‖x′n-x″n‖<ε．
(6)
结合式(5)和(6)，对充分大的n，有‖x″n-x0‖≤‖x″n-x′n‖+‖x′n-x0‖<2ε．当ε→0时，有
x″n→x0, n→+∞,
这与式(4)矛盾．故对足够小的ε>0，有x′n∉U(S(λn),ε)．
由定理1及其证明过程知，x0∈S(λ0)=∪α∈R++Sα(λ0),且存在α0∈R++和t0∈T(x0,λ0)使得
Ψ(x0,y,t0,α0)≥0, ∀y∈K(x0,λ0)．
(7)
根据HΨ，存在ρ>0和n0∈N，当n>n0时，有
这表明对任意t∈T(x′n,λn)都存在yn∈K(x′n,λn)使得Ψ(x′n,yn,t,α0)≤-ρ．
由T(·,·)在X×Λ上的Berge下半连续性知，对t0∈T(x0,λ0)，存在tn∈T(x′n,λn)使得tn→t0．运用条件 ，不妨假设yn→y0∈K(x0,λ0)．从而由Ψ(·,·,·,α0)的连续性知
与式(7)矛盾．因此，则S(·)在Λ是B-l.s.c的．
□
定理3 假设
A(·)在Λ上是Berge连续且具有紧值的；
K(·,·)和T(·,·)在X×Λ上是Berge连续且具有紧值的；
W(·)和E(·)在X上是B-u.s.c的；
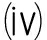φ(·,·,·)在X×X×2L(X,Y)上是连续的，
则S(·)在Λ上是B-l.s.c的当且仅当HΨ成立．
证明 由定理2知，仅需要证明必要性．假设HΨ在λ0∈Λ处不成立，则有ε>0使得对任意ρn>0和δn>0，都存在α∈R++，λn∈B(λ0,δn)和xn∈A(λn)\U(S(λn),ε)有
这意味着存在tn∈T(xn,λn)，对任意y∈K(xn,λn)都有
Ψ(xn,y,tn,α)>-ρn．
取δn=ρn=1/n，则有λn→λ0．因为A(·)在λ0处是B-u.s.c的，故存在x0∈A(λ0)和{xn}的子列{xnk}使得xnk→x0．不失一般性，假设xn→x0．由T(·,·)的Berge上半连续性，不妨假设tn→t0∈T(x0,λ0)．通过知，对任意y0∈K(x0,λ0)，都存在yn∈K(xn,λn)使得yn→y0．从而，由Ψ(·,·,·,α)的连续性可得
由y0∈K(x0,λ0)的任意性可知
Ψ(x0,y,t0,α)≥0, ∀y∈K(x0,λ0),
从而
x0∈Sα(λ0)⊂S(λ0)．
运用S(·)在x0处的Berge下半连续性，对x0，有zn∈S(λn)使得zn→x0．从而
0<ε≤‖xn-zn‖≤‖xn-x0‖+‖x0-zn‖→0, n→+∞,
这是不可能的．因此，HΨ是成立的．
□
最后，我们给出如下例子来验证定理3．
例2 假设X=R, Y=R2， Λ=[1,2]， K(x,λ)=[0,π]， T(x,λ)=(-λ,x)T， 
R2: x2 ≥x+1 or 
令映射e:X→2Y和φ:X×X×2L(X,Y)→Y分别如下：
e(x)=(1,1)T, φ(x,y,t)=〈t,(sin x,-y)〉-(0,1/2)．
可验证定理3中的条件都满足，对λ∈[1,2]，解如下问题： 存在x∈[0,π]和t∈T(x,λ)使得
φ(x,y,t)=〈t,(sin x,-y)〉=(-λsin x, -xy-1/2)∉-E(x),
∀y∈[0,π]．
对任意λ∈[1,2]，解集S(λ)=[0,1/(2π))．因此S(·)在[1,2]上是Berge下半连续的． 下面验证假设HΨ是成立的．计算得，对任意λ∈Λ，A(λ)=[0,π]．注意到，对任意0<ε<π-1/(2π)，A(λ)\U(S(λ),ε)=[0,π]\[0,1/(2π)+ε)=[1/(2π)+ε,π]和(x,y)∈[1/(2π)+ε,π]×[0,π]，t∈T(x,λ)，有
1/2≤‖φ(x,y,t)‖2 且 φ(x,y,t)∈-E(x)．
从而对任意(x,y)∈[1/(2π)+ε,π]×[0,π], t∈T(x,λ),有ξ(x,φ(x,y,t))<0．
综上，我们有：给定参考点λ0∈Λ．对任意ε>0，存在ρ=1/2和δ>0使得对任意λ∈B(λ0,δ)，α∈R++和x∈[1/(2π)+ε,π]，有maxt∈T(x,λ)miny∈K(x,λ)Ψ(x,y,t,α)≤-ρ．因此，假设HΨ成立．故定理3是可用的．
3 结 论
本文主要讨论了一类新的参数广义向量拟平衡问题解映射的稳定．将新定义的改进集映射用于平衡问题的研究，得到IPGVQEP．运用标量化技巧，借助新的非线性标量化函数和关键假设得到了IPGVQEP解映射的Berge下半连续性的充要条件．其在向量拟平衡问题模型在工程、交通、科技等领域有着十分广泛的应用，对其研究是十分必要的．事实上，关于IPGVQEP解的相关讨论还有待于进一步加强，如解映射的Berge上半连续性、Hausdorff半连续性及问题的适定性等，都是非常有意义的，这也是我们下一阶段将要进行的研究．
致谢 本文作者衷心感谢重庆交通大学研究生教育创新基金(2019S0123)和运筹学与系统工程重庆市重点实验室开放课题(CSSXKFKTZ201801)对本文的资助．
[1] BLUM E, OETTLI W. From optimization and variational inequalities to equilibrium problems[J]. The Mathmatics Student, 1994, 63: 123-145.
[2] ANSARI Q H, OETTLI W, SCHLAGER D. A generalization of vectorial equilibria[J]. Mathematical Methods of Operations Research, 1997, 46(2): 147-152.
[3] BIANCHI M, HADJISAVVAS N, SCHAIBLE S. Vector equilibrium problems with generalized monotone bifunctions[J]. Journal of Optimization Theory and Applications, 1997, 92: 527-542.
[4] CHEN C R, LI S J, FANG Z M. On the solution semicontinuity to a parametric generalized vector quasivariational inequality[J]. Computers & Mathematics With Applications, 2010, 60(8): 2417-2425.
[5] 曾静, 彭再云, 张石生. 广义强向量拟平衡问题解的存在性和Hadamard适定性[J]. 应用数学和力学, 2015, 36(6): 651-658.(ZENG Jing, PENG Zaiyun, ZHANG Shisheng. Existence and Hadamard well-posedness of solutions to generalized strong vector quasi-equilibrium problems[J]. Applied Mathematics and Mechanics, 2015, 36(6): 651-658.(in Chinese))
[6] 彭建文, 杨新民, 朱道立. 向量拟平衡问题系统及其应用[J]. 应用数学和力学, 2006, 27(8): 963-970.(PENG Jianwen, YANG Xinmin, ZHU Daoli. System of vector quasi-equilibrium problems and its applications[J]. Applied Mathematics and Mechanics, 2006, 27(8): 963-970.(in Chinese))
[7] GONG X H. Continuity of the solution set to parametric weak vector equilibrium problems[J]. Journal of Optimization Theory and Applications, 2008, 139: 35-46.
[8] PENG Z Y, YANG X M. Semicontinuity of the solution mappings to weak generalized parametric Ky Fan inequality problems with trifunctions[J]. Optimization, 2014, 63(1): 447-457.
[9] PENG Z Y, ZHAO Y, YANG X M. Semicontinuity of approximate solution mappings toparametric set-valued weak vector equilibrium problems[J]. Numerical Functional Analysis and Optimization, 2015, 36: 481-500.
[10] PENG Z Y, PENG J W, LONG X J, et al. On the stability of solutions for semi-infinite vector optimization problems[J]. Journal of Global Optimization, 2018, 70: 55-69.
[11] ZHAO J. The lower semicontinuity of optimal solution sets[J]. Journal of Mathematical Analysis and Applications, 1997, 207(1): 240-254.
[12] ZHONG R Y, HUANG N J. On the stability of solution mapping for parametric generalized vector quasiequilibrium problems[J]. Computers & Mathematics With Applications, 2012, 63(4): 807-815.
[13] ANH L Q, HUNG N V. Gap functions and Hausdorff continuity of solution mapping to parametric strong vector quasiequilibrium problem[J]. Journal of Industrial and Management Optimization, 2018, 14(1): 65-79.
[14] 邵重阳, 彭再云, 王泾晶, 等. 参数广义弱向量拟平衡问题解映射的H-连续性刻画[J]. 应用数学和力学, 2019, 40(4): 452-462.(SHAO Chongyang, PENG Zaiyun, WANG Jingjing, et al. Characterizations of H-continuity for solution mapping to parametric generalized weak vector quasi-equilibrium problems[J]. Applied Mathematics and Mechanics, 2019, 40(4): 452-462.(in Chinese))
[15] ANH L Q, TRAN Q D, DINH V H. Stability for parametric vector quasi-equilibrium problems with variable cones[J]. Numerical Functional Analysis and Optimization, 2019, 40(4): 461-483.
[16] CHEN C R, ZHOU X, LI F, et al. Vector equilibrium problems under improvement sets and linear scalarization with stability applications[J]. Optimization Methods and Software, 2016, 31(6): 1240-1257.
[17] WANG J J, PENG Z Y, LIN Z, et al. On the stability of solutions for the generalized vector quasi-equilibrium problems via free-disposal set[J]. Journal of Industrial and Management Optimization, 2019, 40(4): 461-483.
[18] CHICCO M, MIGNANEGO F, PUSILLO L, et al. Vector optimization problem via improvement sets[J]. Journal of Optimization Theory and Applications, 2011, 150: 516-529.
[19] AUBIN J P, EKELAND I. Applied Nonlinear Analysis[M]. New York: John Wiley and Sons, 1984.
[20] GÖPFERT A, RIAHI H, TAMMER C, et al. Variational Methods in Partially Ordered Spaces[M]. Berlin: Springer, 2003.