引 言
交通分配问题是交通科学领域中十分重要的研究分支．它以路网为对象，研究由起点到终点的交通需求和供给关系，即所谓的O-D对(origin-destination pair)关系．模型一般假定在起点的交通分配满足用户均衡或系统最优的优化原理．其中，用户均衡是指从起点沿某一路径到达终点的旅行时间必须等于沿其他任一路径的旅行时间，否则该路径不被选用；系统最优则是指路网上所有用户旅行时间的总和达到最小．然而，在经典的交通分配模型中，在路段上的交通密度被简单假定或预设为常数，因此不能真实描述交通流动力学行为，尤其是在路口上游的排队现象[1-2]．改进的唯一途径是将描述路段的交通流模型推广到路网，然后再将其结果或算法应用于交通分配问题.
将描述路段的交通流模型推广到路网，关键是解决在路口处的流量分配问题，从而获得模型在每一路段上的边界条件，用双曲守恒律理论的术语讲，就是要求解模型在路口处的Riemann问题,相关工作可参考文献[3-7]．直接或间接基于上述领域的研究成果，Lo等[8]首先将CT(cell transition)模型[4]应用于求解动态交通分配问题，后续类似的工作可参考文献[9-11]．此外，Jiang等[12]和Lin等[13]将LWR(Lighthill-Whitham-Richards)交通流模型[14-15]引入到所谓的二维交通分配问题中．这些工作改进了经典的交通流分配模型，能够较好地反映问题的交通流动力学特性.
对静态交通分配模型的改进，显然应该合理采用交通流模型(如LWR模型或CT模型)的定常解，即应该包括激波间断，从而能够描述在交叉路口的排队现象．然而，相关工作我们只查询到关于LWR模型定常解存在性和稳定性研究的两篇论文[16-17]．由于针对的是一般路网，上述工作并未给出求解细节，尚有很多关键问题需要研究．事实上，对一般路网而言，解析求解包含激波间断的定常解将极具挑战性.
本文在一个简单环形路网上解析求解LWR模型的定常解，不仅得以给出较为完整的解析结果，而且能够深入细节和本质，从而为求解一般路网的定常解提供关键性思路．选择环形路网是由于可以建立路网上车流总数与定常解参数和性态之间的依赖关系，其简单概括为，由一个分岔路口经两条不等长路段(路段1和2)到达另一个交汇路口，再沿另一条路段(路段3)返回分岔路口．另一方面，该路网则是对一个更加简单的非均匀环形路段的推广[18]．本文在交叉口处的交通流“耦合”采用了较为直观和通俗易懂的描述方式，但其推导过程和所得结果都是基于双曲守恒律方程间断解理论，涉及Riemann间断分解及其熵条件等问题，可参考文献[6，19]．在数学上相对弱化的讨论则是基于需求-供给函数约束条件下的交通流量优化问题，可参考文献[3,20-22]．其求解的主要思想可做如下简述.
基于用户均衡条件和路口处质量守恒(总流出等于总流入)，导出在每一路段上密度为常数的定常解(平凡解)．然而，结果表明，该定常解集在路网总流量达到最大值时在路段3(或路段1和2)的密度变化是跳跃间断的，同时导致车流总数N的变化也是跳跃间断，由第一临界值
跳至第二临界值
为使定常解对N连续依赖，对属于区间
的N，将其他所有信息保留为
时的信息，只在路段3(或路段1和2)上引入激波间断，使激波下游长度随N的增加而增长，直至等于路段3 (或路段1和2)的长度，此时
在以上的描述中，当在路段3的最大流量大于路段1和2(在用户均衡约束条件下)的总最大流量时，则在路段3引入激波间断，否则在路段1和2引入激波间断．上述求解思想是本文的主要创新点，也为研究一般路网的定常解提供了关键思路.
本文各节内容安排如下：第1节，讨论了具有同一出发地和目的地的两条路段，包括定常解所满足的用户均衡条件以及受此约束的最大通行能力；第2节，讨论了路网定常解并给出完整的求解步骤，分析输出结果；第3节，总结全文.
1 具有同一出发和目的地的两条路段交通流分配
将交通流比拟为某种可压缩的连续介质，同时满足流量-密度函数关系:qi(x,t)=qi(ρi(x,t))．则由质量守恒可导出在路网上某第i路段的密度所满足的偏微分方程：
(1)
其中，ρi(x,t)和qi(ρi(x,t))分别为t时刻在x位置处的车流密度和流量，Li为路段长度．在t时刻x位置处的平均交通速度可定义为vi(x,t)=qi(ρi(x,t))/ρi(x,t)．方程(1)即为著名的LWR模型[14-15].
1.1 路段定常解表示
LWR模型在第i路段的定常解是指与时间t无关的解，具有如下的激波间断结构：
(2)
其中，
分别为激波上游和下游路段的密度．定常解则是指流量为常数的解，因此在激波两侧有
(3)
此时解结构为所谓的“不动的激波”，显然满足所谓的R-H间断条件[19]．只有当分段点坐标
或
时，定常解退化为平凡解，分别表示自由流和拥塞流.
1.2 基于两条不等长路径的用户均衡条件
假设路段1和2由分岔路口JD和汇入路口JM连接，由JD出发到达JM的交通流用户，可选择路段1或路段2．上述路径选择需满足所谓的用户均衡条件，即当其中一条路段有用户选择时，沿该路段由JD到达JM的旅行时间(费用)不能大于走另外一条路段的时间(费用)[1-2]．换言之，路段1和2均有用户选择，当且仅当其旅行时间相等.
本文主要研究两条路段长度不等时用户均衡条件对交通流的影响，因此，我们不妨假设L1<L2．为简化问题，假设路段1和2的最大密度均为ρjam，而且在所涉及的三条路段上畅行速度均为vf．在后面的讨论中，除非特殊声明，所有密度量均除以ρjam，速度量除以vf，流量除以vfρjam．因此，在路段1和2上的速度和流量函数可表示为
vi=v(ρi), qi=ρiv(ρi)≡q(ρi), ρi∈[0,1], i=1,2，
(4)
其中，v′(ρi)<0，v(0)=1，v(1)=0; q″(ρi)<0，q在唯一的极值点ρi=ρ*处取最大值q*，q′(ρ*)=0．为便于识别，也记
在路段1和2的旅行时间记为
(5)
其中，
显然，当
时，
取最小值．注意到在路段2的最小旅行时间不小于在路段1的最小旅行时间，则由JD到JM的用户均衡条件为
(6)
其中，第一个等式成立时，表明没有用户选择路段2.
1.3 基于用户均衡约束的最大通行能力
路段1和2的最大通行能力(capacity)均为函数q(ρi)的最大值q*(式(4))．若不考虑用户均衡条件的约束，则由JD到JM的最大通行能力显然为2q*．然而，受用户均衡约束，上述最大通行能力显然小于2q(ρ*)，除非L1=L2，以下将其记为
我们指出，
只能在路段1和2都没有激波时达到．否则，若在某路段i(i=1或2)上， 当定常解有激波， 即
时， q1+q2取得最大值， 那么对于该路段固定的旅行时间
式(5))， 显然可找到
使得
由于函数q(ρi)在
严格单增，在
严格单减(式(4))，且
式(3))，必然有
这表明在该路段可以用平凡解
代替假设的激波结构，其旅行时间不变却使得该路段上的流量增加．这一结果与该路段上具有激波结构时q1+q2取得最大值的假设相矛盾.
因此，只需设定路段1和2均为平凡解，在用户均衡条件下求出的q1+q2最大值即为为讨论的方便，平凡解
或
统一用ρi表示，则由式(5)和(6)可推出ρ2依赖于ρ1的函数关系：
(7)
其中，v-1(·)表示v(·)的反函数．我们称ρ2=ρ2(ρ1)为用户均衡曲线，它显然是单调不减的函数，且在右侧部分为严格单增.
(8)
由于ρ2<ρ1，只看第一个等式即可知q12在ρ1∈[0,ρ*]严格单增，在ρ1∈[v-1(μv(ρ*)),ρjam]严格单减．较为合理的假设是使μ足够大，至少满足v-1(μ)<ρ*或μ>v(ρ*)，由式(7)可知在路段1未达到临界密度之前路段2已被用户选择．此时q12在ρ1∈[ρ*,v-1(μv(ρ*))]上由式(8)的第二个等式给出，其导数为
(9)
对给定的函数v(·)或q(·)，μ的取值范围应使q12(ρ1)在这一区间上先严格单增再严格单减，从而可知式(9)的零点即为q12(ρ1)的最大值点，记为
2 简单环形路网交通流定常解
引入路段3，从交汇路口JM出发连接分岔路口JD，从而得到一简单闭环路网，如图1所示．在路段3上畅行速度仍为vf，最大密度为νρjam．根据前述关于密度、速度和流量的无量纲表示，其速度、密度和流量需分别除以vf，ρjam和vfρjam．参照式(4)，其速度-密度与流量-密度函数关系为
v3=v(ρ3/ν), q3=νq(ρ3/ν), ρ3∈[0,ν],
(10)
图1 简单闭环路网示意图
Fig. 1 The layout of the simply circled road network
q3在
处达到最大值
首先考虑无激波结构的定常解，路段的密度由ρi表示．路网车流总数由N表示，并注意到在分岔或交汇路口处总流出与总流入相等，则路网上无激波结构的定常解由以下方程组描述:
(11)
其中，函数ρ2(ρ1)为用户均衡曲线．式(11)第二个方程确定了两支隐函数：
或
路网通行能力(最大流量)显然可定义为由JD到JM通行能力和由JM到JD通行能力之中的最小值，记为
(12)
后面将分两种情况展开讨论.
2.1 分岔路口JD为瓶颈
分岔路口JD为瓶颈，是指由JM到JD的通行能力大于由JD到JM的通行能力，此时由式(12)定义的路网通行能力可得
(13)
上式隐含，对任意ρ1∈[0,1]，从式(11)第二个方程总能解出ρ3．以下直观解释式(11)中变量的相互变化和依赖关系．其中注意，在后面所出现的图形以及数值模拟中，式(4)中的函数v(·)取为v(ρ)=(1-ρ)2.8，式(7)中取参数μ=0.75.
如图2所示，在
的部分，q12(ρ1)由0单调递增至
由曲线段上任一点沿水平线与q3(ρ3)左支相交，从而得到
对应式(11)中第二个方程取“-”号的一支隐函数．显然，q3(ρ3)和ρ3都随ρ1单调递增．由于ρ2(ρ1)也是ρ1的单调递增函数(式(7))，可见车流总数N随ρ1单调递增(式(11))，且以上变化过程都是连续依赖的.
在
部分，q12(ρ1)由单调递减至0，曲线段上任一点沿水平线与q3(ρ3)右支相交，从而得到ρ3，对应式(11)中第二个方程取“+”号的一支函数．从图2中变量变化趋势，可知q3(ρ3)关于ρ1和ρ3均为单调递减关系，从而ρ3随ρ1单调递增．在这一变化过程中，ρ2(ρ1)以及车流总数N仍随ρ1单调递增，有类似的连续依赖关系.
然而，需要特别指出：ρ3在
处的变化是跳跃间断的，这同时导致N的变化也是跳跃间断，从某一跳至为使变量之间的变化为连续依赖，在跳跃间断的左侧“凝固”ρ1以及其他随之连续变化的量，即固定取
以及
在路段3上则引入关于ρ3的激波间断(式(2))，其中
和
分别为其在处的跳跃值．该激波间断由
持续至
也随之由连续变化到显然，在引入激波后车流总数N为连续变化的量.
在以上的变化过程中，只有ρ1和N是单调变化的，因此其他变量可以视为ρ1或N的函数．以上分析表明，由式(11)以及通过引入激波可导出完整的定常解．当v(ρi)取线性函数时，可以导出以ρ1或N为自变量的显式表达式．基于以上分析，下面给出求解定常解的一般步骤.
1) 由式(11)第一个方程计算:
Nmax=L1+L2+L3ν,
其中，
由式(11)第二个方程确定，
2) 对
由式(11)解出
或
从而可确定ρ2和其他物理量.
3) 对任意给定的
设定
同时在路段3引入激波间断，
由下式确定:
其中
以上求解步骤隐含所有变量对N是连续依赖的.
2.2 交汇路口JM为瓶颈
交汇路口JM为瓶颈，是指由JM到JD的通行能力小于由JD到JM的通行能力，即
(14)
上式隐含，对任意的ρ3∈[0,μ]，式(11)中第二个方程总是有解．图3给出了路段3基本图与路段1-2总流量函数q12(ρ1)的比较，类似2.1小节，可直观解释式(11)中变量的相互变化和依赖关系，简述如下.
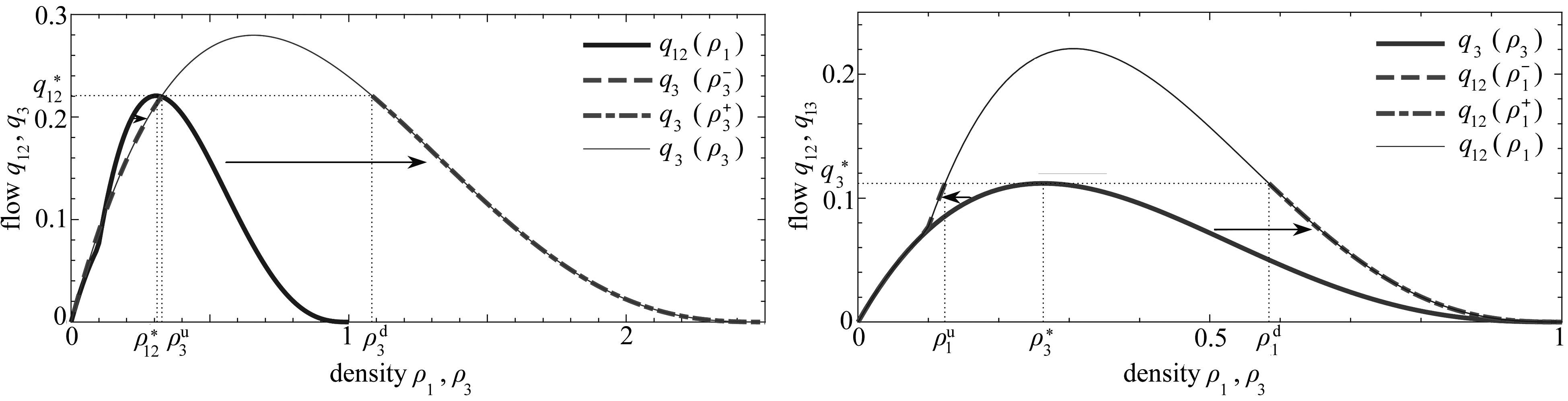
图2 路段3的流-密关系和路段1-2总流-密关系的比较(ν= 2.5) 图3 路段3的流-密关系和路段1-2总流-密关系的比较(ν=1)
Fig. 2 Comparison between the flow-density relationship of of section 1-2(ν= 2.5) Fig. 3 Comparison between the flow-density relationship of section 3 and the total flow-density relationship section 3 and the total flow-density relationship of section 1-2(ν=1)
在区间
由0单调递增至
该曲线段上任意一点沿左侧平移与曲线q12(ρ1)相交，得到
在区间
由
单调递减至0，该曲线段上任意一点沿右侧平移与曲线q12(ρ1)相交，得到
其中，函数
为由式(11)所确定的左右两支隐函数．以上ρ1的变化在
处是跳跃间断的，由
跳跃至
类似2.1小节，需要在处“凝固”路段3的信息，同时在路段1(和路段2)引入激波间断．此时用户均衡条件(7)不再成立，同时发现缺少一个求解条件．因此，我们引入由路段1和2从交叉口JM进入路段3的优先级系数β和1-β．下面先简述求解步骤，再讨论如何给出β．无激波的情形与2.1小节的求解步骤相同，只讨论有激波的情况.
假定无激波情形的定常解已经给出下面数值：开始产生激波和激波消失时的临界值和
以及N的最大值Nmax，对给定的按以下程序求具有激波间断的定常解.
1) 设定
并由下面两个方程
(15)
分别解出
和
以及
和
2) 记
(16)
同时计算
并由用户均衡条件(5)、(6)导出由JD到JM的旅行时间为
(17)
由此可算出N1和N2．由式(17)，假定了在引入激波
前路段2已被用户选用.
3) 由式(16)的两个方程可分别算出
和
同时确定
和
由上述求解步骤(包括不存在激波的情形)，可知所有变量为关于N的函数．为保证这些变量之间的连续依赖关系，尤其是保证式(15)和(16)中的方程可解，可证明函数β(N)必须且只需满足
(18)
而且可证明上述关系所限定的β的集合非空．右端等式成立，当且仅当其中的
分别为路段1和2的旅行平均速度(参看式(17))．我们将β(N)取为式(18)中前后两项的加权平均值：
(19)
式(18)中，右端等号成立，即式(19)中λ=0，当且仅当
或
此时路段1无激波；左端等号成立，即式(19)中λ=1，当且仅当
或
此时路段2无激波.
2.3 结果输出和分析
以下计算结果及其图形显示中，路段上长度均取为L3=2L1，密度和流量采用式(10)前所定义的无量纲变量；对路网总车流数N进一步做无量纲化，除以L1(参见式(11))．临界值
依赖于算例中ν的取值.
2.3.1 路段3出现激波的情形
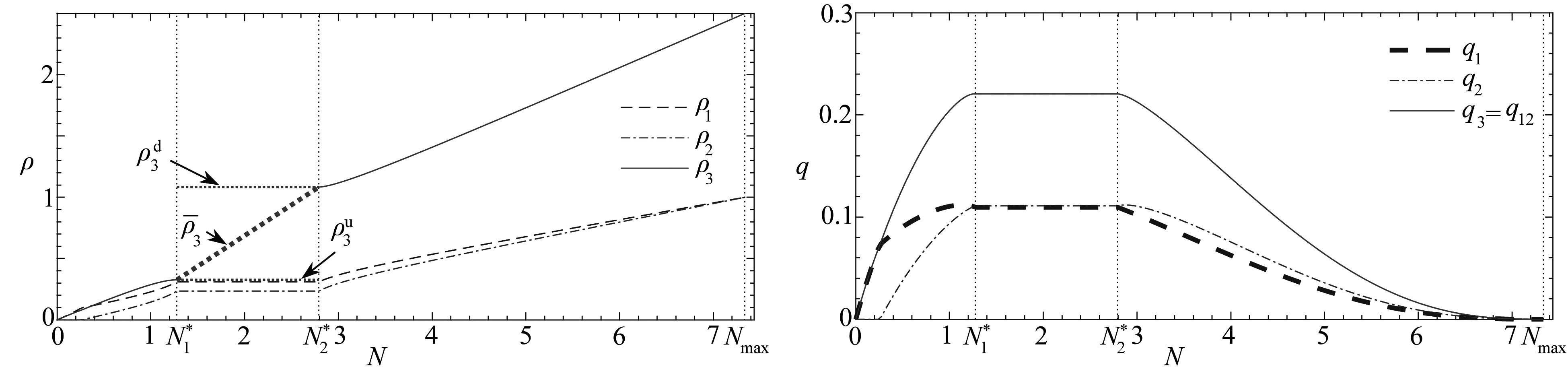
由2.1小节的求解步骤，对应由图2所描述的情形，通过计算给出了由式(2)和(3)所描述的定常解，如图4所示.
(a) 各路段密度随车辆总数的变化 (b) 各路段流量随车辆总数的变化
(a) Densities in road sections (b) Flows in road sections
图4 分岔路口为瓶颈时，交通流定常解随路网车流总数N的变化，对应图2
Fig. 4 Dependency of the steady-state solution of traffic flow on total number N of vehicles corresponding to fig.2，with the diverging junction as a bottleneck
图4(a)和(b)分别给出了定常解在各路段上车流密度和流量随路网车流总数N的变化情况．当
时，在各路段上密度和流量均为只依赖于N的常数，且由0开始随N严格单增．当
时，在路段1和2的车流密度和流量被“凝固”为不依赖于N的常数，且路网总流量q3=q12达到允许的最大值
其中，
而在路段3，密度为由
即时路段3的密度值)跳跃到
即
时路段3的密度值)的激波间断，其平均密度
则随N连续变化，由
时的左极限值
连续增加至
时的右极限值
这同时表明对应密度为的排队长度由0连续增加至L3．当
时，在各路段上密度和流量均为只依赖于N的常数，密度随N严格单增，直至达到最大值ρ1=ρ2=1，和ρ3=2.5，流量随N严格单减，直至为0.
由于在路段1和2没有激波且μ=L1/L2<1，受用户均衡条件或曲线q2=q2(ρ1)约束， 使在N>0.24时才开始有用户选择路段2， 在N≤0.24时路段1与3流量相等．在交汇路口JD处以及两个路段上总是有更多的用户选择路段1(参见式(6)和(7)及其相关讨论)， 导致在激波区域有不等关系：
这也使得在路网总流量在的右临近流量随N的增加而下降时，路段2仍为自由流状态．这是否为一般结果，有待给出严格数学证明或举出反例.
以上分析表明，计算结果与2.1小节中基于图2的讨论相符.
2.3.2 路段1和2出现激波的情形
由2.2小节的求解步骤，对应由图3所描述的情形，通过计算给出了由式(2)和(3)所描述的定常解．在式(19)中取λ=0.3，输出结果如图5所示.
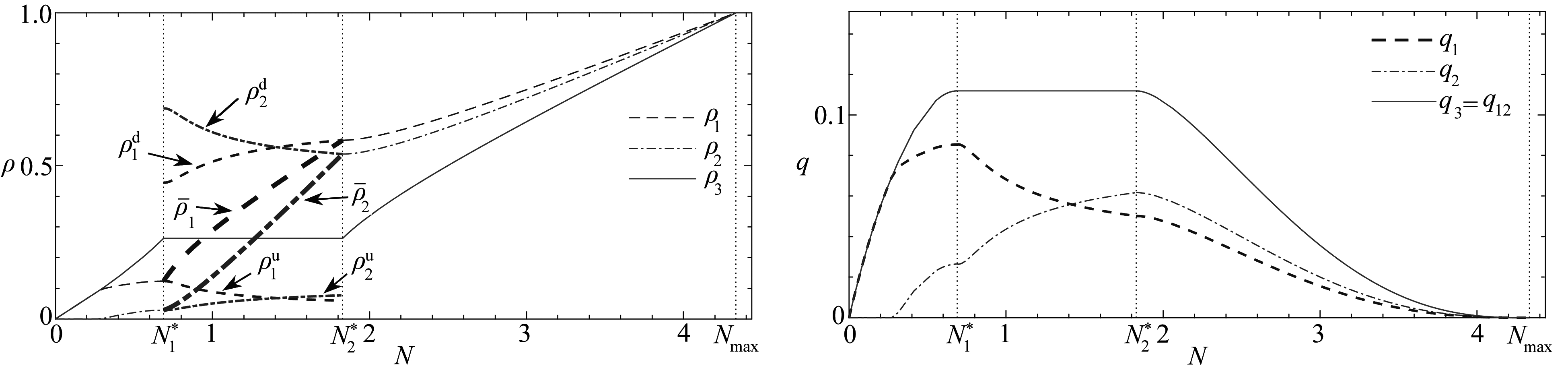
(a) 各路段密度随车辆总数的变化 (b) 各路段流量随车辆总数的变化
(a) Densities in road sections (b) Flows in road sections
图5 交汇路口为瓶颈时，交通流定常解随路网车流总数N的变化，对应图3(λ=0.3)
Fig. 5 Dependency of the steady-state solution of traffic flow on total number N of vehicles corresponding to fig.3， with the merging junction as a bottleneck(λ=0.3)
图5(a)和(b)分别显示了定常解在各路段上车流密度和流量随路网车流总数N的变化情况．在区间
上，有类似图4的性质，主要结论概述为：
1) 各路段密度均随N严格单增，流量在严格单增，在严格单减；
2) 受用户均衡条件(6)约束，总是有更多的用户选择路段1;
3) 由于在N>0.27时才开始有用户选择路段2(以及ν=1)，在N≤0.27时路段1与3流量(以及密度)相等.
在区间上，路段3的车流密度和流量被“凝固”为不依赖于N的常数，
路网总流量达到最大值
在路段1和2则同时出现激波间断，其定常解性质可主要概述为：
1) 路段1或2的密度跳跃以及平均密度变化与图4中路段3类似；
2) 随着N的增加，在分岔路口选择路段1和2的用户数及其流量此消彼长，使当N
1.4时
即在分岔路口选择路段2的用户数超过路段1;
3) 然而，在路段1的用户数总是多于在路段2的用户数，即总有(平均密度)
上述性质1)和2)依赖于路段1与路段2之比以及式(19)中的优先权系数．若增大μ的取值，则图5中
与
或q1与q2)的交点(N≈1.4)将左移，相应的密度和流量差值也将减小，随N的变化会变得平缓．若增加路段2的优先权系数，会有类似的效应．反之，则会有相反的结果.
数值试验验证了上述分析结果．其中，图6显示了取极端情形λ=1.0的输出结果，下面结合2.2小节的内容以及上述分析结果做如下讨论.
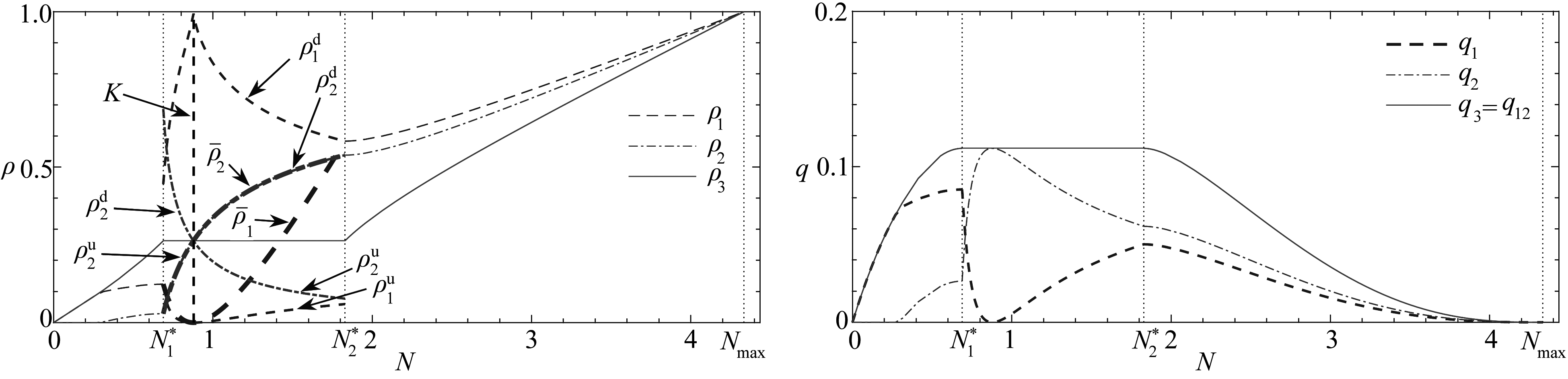
(a) 各路段密度随车辆总数的变化 (b) 各路段流量随车辆总数的变化
(a) Densities in road sections (b) Flows in road sections
图6 交汇路口为瓶颈时，交通流定常解随路网车流总数N的变化，对应图3(λ=1.0)
Fig. 6 Dependency of the steady-state solution of traffic flow on total number N of vehicles corresponding to fig.3， with the merging junction as a bottleneck(λ=1.0)
首先，由于其他参数取值不变，我们看到在路段3的密度和流量分布在整个区间[0,Nmax]上与图5的结果完全相同，由此可知在路段1和2的车流总数与流量之和(q12)在整个区间也与图5完全相同．由式(5)，运用合比定理还可进一步推断：由分岔路口JD到交汇路口JM的旅行时间不依赖于λ的取值.
其次，在区间上，注意到ν=1隐含
则在图6(a)中，以及
与
以及
所对应的曲线分别位于水平线的上下区域．在K线的左侧，
与路段2平均密度
所对应的曲线重合，表明激波排队长度
而在K线的右侧，
与路段2平均密度所对应的曲线重合，表明激波排队长度
上述输出结果隐含，在整个区间上，总有
表明在路段2没有激波．这与关于式(18)的解析结果完全吻合，即不等式左端取等号(对应式(19)中λ=1.0)，当且仅当在路段2没有激波.
最后，在区间上，图6显示了在路段1和2的密度和流量走势与图5有明显的差别．路段2上较大的优先权系数意味着在该路段上较短的旅行时间，图6中取λ=1.0，使在路段2无需引入激波，从而使旅行时间不变时能容许更多的用户(参见1.3小节第二段的讨论)．因此，图6(a)显示，与所对应的曲线在的右侧迅速相交，在此之后在入口处路段2的用户数超过路段1．图6(b)中q1和q2的变化显示了类似的趋势．此外，在上述交点右侧足够长的区间，直至的左临近，均有
表明路段2上的用户数超过路段1．从图6(a)还可大致看出：路段2与路段1的用户数(或平均密度)之差随路段1上激波幅度
的加强(减弱)而增大(减小)，并在K线处达到最大.
3 结论与展望
本文创建性地提出了研究具有激波结构的路网交通流定常解的理论和实际意义，并以一个简单环形路网为例，完整讨论了求解基本思路，并给出具体的求解步骤．其核心思想和主要结论可主要概述如下.
分岔路口下游的通行能力受用户均衡条件制约．当某路口下游通行能力小于其上游通行能力时，该路口为交通瓶颈．对于交通瓶颈，其上游的交通需求可以大于下游的通行能力，此时在瓶颈上游路段的定常解必然出现激波(由低密度到高密度的排队等候或减速)．若瓶颈(如JM)的上游为多(两)条路段，则需要在瓶颈上游各路段的流出引入优先权系数，从而保证定常解的唯一性．而不同优先权系数的设置，会导致这些路段上不同的定常解.
本文工作为求解一般路网上的交通流定常解提供了核心思想，即阐明了为什么需要引入间断的问题，并在一定程度上提供了如何引入间断的较为一般的方法．然而，一般路网包含复杂的节点对节点的交通供求关系，推广工作还具有较大的挑战性．具体困难在于，如何将这些O-D需求分解到每一个路口，并据此确定何种条件下需要引入间断，以及如何引入间断？随着信息技术的飞速发展，智能交通的一个主要目标即实现交通局部甚至总系统的交通均衡，从而减少拥堵和提高运行效率．本文由于给出了比经典理论更合乎实际的交通流均衡定常解，从而能够通过交通诱导，更加精准地实现了真正的交通均衡．其中，所揭示的系统(或子系统)中的交通形态与系统车流总数之间的依赖关系，为从宏观上对系统的交通总量控制提供定量的科学依据．在较为微观的层面，对道路设计如何避免瓶颈路口，对交汇瓶颈路口如何设置优先权系数(如通过信号灯配时干预)，都提供了比经典的交通分配理论更合理的模型．当然，以上的应用也必须与大数据方法结合，需要与实际观测的结果不断比较并训练和校正模型参数.
致谢 本文作者衷心感谢陆地交通气象灾害防治技术国家工程实验室开放研究基金(NEL-2019-02)对本文的资助.
[1] SAW K, KATTI B K, JOSHI G. Literature review of traffic assignment: static and dynamic[J]. International Journal of Transportation Engineering, 2015, 2(4): 339-347.
[2] WONG W, WONG S C. Network topological effects on the macroscopic bureau of public roads function[J]. Transportmetrica A: Transport Science, 2016, 12(3): 272-296.
[3] LEBACQUE J P. The Godunov scheme and what it means for first order traffic flow models[C]//LESORT J B, ed. Proceedings of the Thirteenth International Symposium on Transportation and Traffic Theory. France, 1995.
[4] DAGANZO C F. The cell transmission model, part Ⅱ: network traffic[J]. Transportation Research Part B, 1995, 29(2): 79-93.
[5] COCLITE G M, GARAVELLO M, PICCOLI B. Traffic flow on a road network[J]. SIAM Journal on Mathematical Analysis, 2005, 36: 1862-1886.
[6] GARAVELLO M, NATALINI R, PICCOLI B, et al. Conservation laws with discontinuous flux[J]. Networks and Heterogenous Media, 2007, 2(1): 159-179.
[7] LIN Z Y, ZHANG P, DONG L Y, et al. Traffc flow on a road network using a conserved higher-order model[C]//AIP Conference Proceedings. Greece: AIP Publishing, 2015.
[8] LO H K, SZETO W Y. A cell-based variational inequality formulation of the dynamic user optimal assignment problem[J]. Transportation Research Part B: Methodological, 2002, 36(5): 421-443.
[9] FRIESZ T L, HAN K, NETO P A, et al. Dynamic user equilibrium based on a hydrodynamic model[J]. Transportation Research Part B: Methodological, 2013, 47: 102-126.
[10] ZHANG Z, WOLSHON B, DIXIT V V. Integration of a cell transmission model and macroscopic fundamental diagram: network aggregation for dynamic traffic models[J]. Transportation Research Part C: Emerging Technologies, 2015, 55: 298-309.
[11] CHENG Q, LIU Z, SZETO W Y. A cell-based dynamic congestion pricing scheme considering travel distance and time delay[J]. Transportmetrica B: Transport Dynamics, 2019, 7(1): 1286-1304.
[12] JIANG Y Q, WONG S C, ZHANG P, et al. Dynamic continuum model with elastic demand for a polycentric urban city[J]. Transportation Science, 2017, 51(3): 931-945.
[13] LIN Z Y, WONG S C, ZHANG P, et al. A predictive continuum dynamic user-optimal model for the simultaneous departure time and route choice problem in a polycentric city[J]. Transportation Science, 2018, 52(6): 1496-1508.
[14] LIGHTHILL M J, WHITHAM G B. On kinematic waves, Ⅱ: a theory of traffic flow on long crowded roads[J]. Proceedings of the Royal Society of London(Series A), 1955, 22: 317-345.
[15] RICHARDS P I. Shockwaves on the highway[J]. Operation Research, 1956, 4: 42-51.
[16] JIN W L. On the existence of stationary states in general road networks[J]. Transportation Research Part B: Methodological, 2015, 81: 917-929.
[17] JIN W L. On the stability of stationary states in general road networks[J]. Transportation Research Part B: Methodological, 2017, 98: 42-61.
[18] WU C X, ZHANG P, WONG S C, et al. Steady-state traffic flow on a ring road with up- and down-slopes[J]. Physica A, 2014, 403: 85-93.
[19] TORO E F. Riemann Solvers and Numerical Methods for Fluid Dynamics[M]. Heidelberg: Springer-Verlag, 1999.
[20] 姜锐, 吴清松, 朱祚金. 各向异性交通流动力学模型的波动特性[J]. 应用数学和力学, 2002, 23(4): 371-375.(JIANG Rui, WU Qingsong, ZHU Zuojin. Kinematic wave properties of anisotropic dynamics model for traffic flow[J]. Applied Mathematics and Mechanics, 2002, 23(4): 371-375.(in Chinese))
[21] 董力耘, 薛郁, 戴世强. 基于跟车思想的一维元胞自动机交通流模型[J]. 应用数学和力学, 2002, 23(4): 331-337.(DONG Liyun, XUE Yu, DAI Shiqiang. One-dimensional cellular automaton model of traffic flow based on car-following idea[J]. Applied Mathematics and Mechanics, 2002, 23(4): 331-337.(in Chinese))
[22] 罗振东, 徐源. 守恒高阶各向异性交通流模型基于POD方法的降阶外推差分格式[J]. 应用数学和力学, 2015, 36(8): 875-886.(LUO Zhendong, XU Yuan. A reduced-order extrapolating FDM for conserved high-order anisotropic traffic flow models[J]. Applied Mathematics and Mechanics, 2015, 36(8): 875-886.(in Chinese))