引 言
流体的砰击是液体的晃荡对液舱内部结构的一种撞击现象.液舱的晃荡易产生剧烈的冲击荷载,会导致液舱内部结构承受巨大的压力,容易造成液舱结构的失效及船体失稳.当结构的运动频率与自由液面固有频率相接近时,将引起液体发生剧烈的晃荡现象.流体晃荡问题的研究,主要关注在固有频率附近砰击荷载随频率变化的规律[1-4].因此,自由液面固有频率是液体晃荡分析的重要因素[1,5].
目前,液体晃动模态参数(频率、振型、阻尼系数)的研究,分为实验和理论两个方面.Dodge[6]阐述了液体晃动模态的一般理论及其工程应用.吕敬等[7]采用Galerkin法离散,将动力学模型转化为常微分方程组,得到了刚-液-弹耦合系统各阶固有频率的变化规律.在二维液舱固有频率研究中,Li等[8]提出了一种以Ritz方法为基础的简单解析方法,可用于任何截面的晃荡研究,与其他解析解的误差在5%范围内,但无法获得可靠的振型.李遇春等[9]利用统一的Ritz计算方法识别晃动模态,但结果仍需实验验证.蒋梅荣等[10]通过图像采集系统,记录自由液面变化过程,选取固定位置的两点作为波高采集点,分析了固有频率的实验值与理论值之间的差别以及对液体晃荡的影响.王鹏翔等[11]利用激光采集仪,测量定点的波高变化,分析了最低阶固有频率的理论值与实验值,但该研究并未深入分析其他频率与理论值之间的相关性.王立时等[5]利用参数激振的方法测量了晃荡的频率和对应的阻尼比参数.流体晃荡是复杂的气-液-固耦合问题,上述研究中没有考虑液舱内气室压力对自由液面模态的影响.
本文通过实验方法分析了不同气室压力对液体晃荡模态的影响,通过自制软件提取自由衰减的波高数据,分别了分析不同气室压力对固有频率和阻尼比的影响.
1 晃荡模态的求解原理与过程
求解振动阻尼比的时域识别方法,有自由振动衰减率法和Hilbert变换-包络线法两种方法.经验模态分解(EMD)法是由Huang等[12]在1998年提出的一种信号分析方法,对信号参数进行EMD,得到多个固有模态函数(IMF)的模态分量,对不同的IMF分量应用时域对数衰减法,获得阻尼比,求解结构自身的固有频率和带有阻尼的固有频率[13].
1.1 EMD原理
EMD法将原始信号分解成不同模式的信号,对于线性和非线性的信号都适用[14-15].在做EMD信号分解时,需假设三点:
1) 原始信号中,至少有一个极大值和一个极小值;
2) 原始信号的局部特征时域是由极值点的间隔决定的;
3) 如果原始信号中没有极值点但有拐点,可以通过对信号进行一阶求导,再求积分获得原始信号的特征模态函数.
EMD的过程如下:
1) 对于一个信号X(t),对信号求导,来确定X(t)的极值点,通过三次样条插值利用极值点来拟合上下包络线,上包络线为E1,下包络线为E2,则可得上下包络线的平均值:
m1=(E1+E2)/2.
(1)
令信号X(t)与包络线均值m1的差为h1 ,则
h1=X(t)-m1.
(2)
核查h1能否满足IMF条件:① h1的极值点个数和零点个数相等或二者相差一个;② 通过h1分解出来的上下包络线均值为零.如果不满足,则将h1看作原始信号,重复以上步骤,直到满意为止,测得![]() 为第一个IMF分量,则
为第一个IMF分量,则
(3)
式中i为经过筛选步骤的次数.
2) 计算残余信号:
r1=X(t)-C1,
(4)
rn=rn-1-Cn,
(5)
式中r1为减去高频分量的残余信号,rn为减去n个IMF分量的残余信号.
3) 通过上述步骤,信号X(t)被分解为n个IMF分量和一个残余分量,直到rn为单调函数.
(6)
图1为EMD流程图.

图1 经验模态分解流程图
Fig. 1 The flow chart of empirical mode decomposition
1.2 Hilbert变换求解阻尼和固有频率
自由衰减的原始信号X(t)可以表示为
X(t)=A0e-ξω0tsin(ωdt+θ0).
(7)
通过EMD得到一系列本征模函数IMF,首先,采用Chebyshev滤波器对各个IMF(Ci)分量进行滤波,去除主频率以外的残余频率,得到新的![]() 函数,对其进行Hilbert变换,得到
函数,对其进行Hilbert变换,得到
A(t)=A0e-ξω0t,
(8)
θ(t)=ωdt+φ0,
(9)
式中A(t)为Hilbert变换后的幅值,θ(t)为Hilbert变换后的相位,ξ为自由衰减的阻尼比,ω0为系统的固有圆频率,ωd为带有阻尼的圆频率.对幅值A(t)取对数,得到直线函数:
ln A(t)=-ξω0t+ln A0.
(10)
由式(9)、(10)可知![]() 可计算出阻尼比为
可计算出阻尼比为
(11)
进而可得系统固有频率f0和带有阻尼的固有频率fd为
f0=ω0/(2π),
(12)
fd=ωd/(2π).
(13)
理论值求解固有频率得
(14)
式中h为液体水深,L为激励方向的液舱宽度.
2 实验内容和结果分析
2.1 实验工况
本次实验中,模型尺寸如图2所示,液舱内水深为288 mm,在0.1 MPa(标准大气压)和0.01 MPa两种压强下进行实验研究.试验采用相同激励加速度(如图3所示),激励振幅为5°.
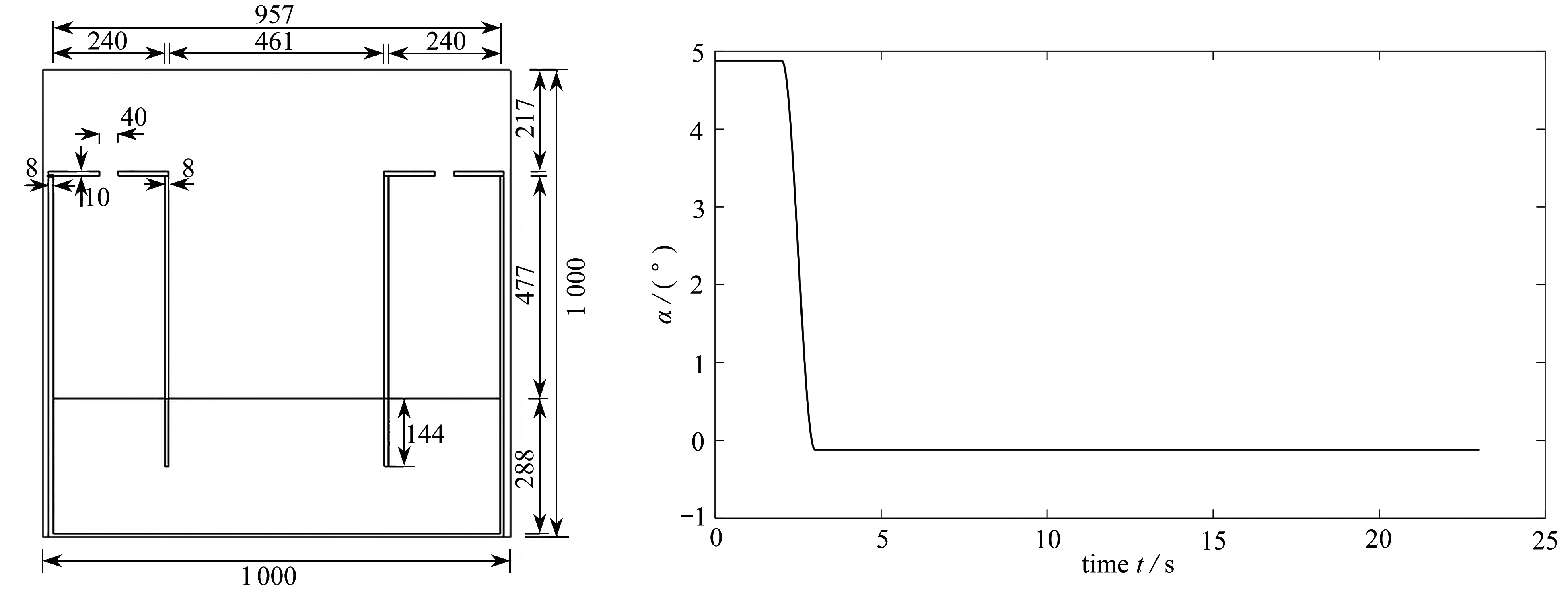
图2 实验模型尺寸(单位: mm) 图3 激励振幅的曲线
Fig. 2 The experimental model sizes(unit: mm) Fig. 3 The acceleration curve of amplitude
2.2 实验结果与分析
对记录的液面数据,通过自制软件捕捉自由液面,本文可以精确捕捉每一时刻自由液面的升降变化,如活塞式升降、局部爬升等自由液面的捕捉,可以同时获取自由液面上多点的波高值(图4).

(a) 升幅较大的液面 (b) 弯曲较大的液面 (c) 微破碎的液面
(a) The wave surface with a lager amplitude (b) The wave surface with a large curvature (c) The wave surface with a slight breaking wave
图4 自由液面的捕捉
Fig. 4 Capture of free wave surface
根据提取的自由水面波高值,选取自左端开始向右第三个点的波高值作为液体晃动模态参数的研究数据.在0.01 MPa压强条件下,进行一组实验测量液体晃荡,以左舱室作为研究对象,根据原始波高时程曲线和FFT变换的时域频率曲线(图5),分析不同相关性的IMF分量所对应的固有频率、阻尼比与实验值和理论值的低阶固有频率的相互关系(表1).
表1 左侧舱室各组实验的IMF分量所对应相关性、固有频率、阻尼比以及FFT频率
Table 1 Correlations, natural frequencies, damping ratios and FFT frequencies of IMF components
of each group of experiments in the left cabin

IMF 1IMF 2IMF 3IMF 4IMF 5correlation ρ-0.108 80.038 80.992 50.159 50.124 6f0/Hz0.636 71.678 10.638 90.267 80.125 5fd/Hz0.636 01.670 00.638 60.267 70.124 9damping ratio ξ0.046 40.098 10.029 30.032 50.094 6

图5 左图为原始波高曲线,右图为FFT变换后的时域频率曲线
Fig. 5 The left figure: the original wave height curve, the right figure: the time-domain frequency curve after FFT transform
通过原始信号的EMD得到不同的IMF分量,由图6和表1可以看出,IMF 3分量与原始曲线相关性最大,IMF曲线的变化规律最符合原始曲线的变化特点,故随着IMF分量相关性的增大,其含有的模态参数对原始曲线的变化规律影响越大.

图6 不同的IMF分量与原始曲线
Fig. 6 Different IMF components and the original curve
由图5,对实验中测量的波高进行频域分析可知,一阶固有频率为0.651 9 Hz,二阶固有频率为1.825 Hz.理论值的一阶固有频率为0.775 7 Hz,二阶固有频率为1.248 5 Hz.因此,可知实验值和理论值的一阶固有频率相差比率(|实验值-理论值|/理论值×100%)约为16%,二阶固有频率相差比率约为46%,实验值和理论值差别较大.由表1截断的原始信号经EMD得到不同IMF分量, 及IMF分量与原始信号的相关性可知,相关性最大的IMF分量,意味着液体晃荡主要以此作为主要的影响因素.对相关性最大的IMF分量做Hilbert变换得到对应的阻尼比和固有频率,分别为0.029 3和0.638 6 Hz,与实验值一阶固有频率0.651 9 Hz相比,两者相差比率小于3%,可知一阶固有频率是液体最主要的晃动频率.通常认为相关系数小于0.1为不相关.由表1可知,阻尼比随着IMF相关性系数的降低呈逐渐增大趋势.
在0.1 MPa(标准大气压)压强条件下,进行三组实验测量液体晃荡,分析验证了实验数据的可靠性.以左舱室作为研究对象,根据原始波高时程曲线和FFT变换的时域频率曲线(图7~9),分析不同相关性的IMF分量所对应的固有频率、阻尼比与实验值和理论值的低阶频率相互关系(表2~4).
表2 左侧舱室各组实验的IMF分量所对应相关性、固有频率、阻尼比以及FFT频率(test 1)
Table 2 Correlations, natural frequencies, damping ratios and FFT frequencies of IMF components of each group of experiments in the left cabin(test 1)

IMF 1IMF 2IMF 3IMF 4IMF 5correlation ρ0.822 30.537 70.067 30.069 50.096 76f0/Hz1.772 80.645 90.372 70.238 60.183 0fd/Hz1.772 70.645 10.371 70.233 10.182 8damping ratio ξ0.0130.049 30.074 60.213 40.055 6
表3 左侧舱室各组实验的IMF分量所对应相关性、固有频率、阻尼比以及FFT频率(test 2)
Table 3 Correlations, natural frequencies, damping ratios and FFT frequencies of IMF components of each group of experiments in the left cabin(test 2)

IMF 1IMF 2IMF 3IMF 4IMF 5correlation ρ0.037 10.867 00.500 30.022 10.027 3f0/Hz0.248 41.753 70.646 90.163 80.147 6fd/Hz0.248 41.753 60.645 20.159 40.147 6damping ratio ξ0.006 10.013 70.073 70.229 90.024 9
表4 左侧舱室各组实验的IMF分量所对应相关性、固有频率、阻尼比以及FFT频率(test 3)
Table 4 Correlations, natural frequencies, damping ratios and FFT frequencies of IMF components of each group of experiments in the left cabin(test 3)

IMF 1IMF 2IMF 3IMF 4IMF 5correlation ρ0.006 60.731 00.651 40.150 00.011 4f0/Hz0.908 01.753 80.679 30.562 20.207 7fd/Hz0.907 21.753 60.678 30.561 70.204 7damping ratio ξ0.042 30.012 30.057 50.043 80.170 9
由图7~9,对三组实验中测量到的波高值进行FFT变换后的时域频率曲线进行分析得:第一组实验中一阶固有频率为0.680 3 Hz,二阶固有频率为1.769 Hz;第二组实验中获得的一阶固有频率为0.623 4 Hz,二阶固有频率为1.746 Hz;第三组实验中获得的一阶固有频率为0.672 9 Hz,二阶固有频率为1.75 Hz.由此可见,各组实验的一阶固有频率最大差值比率约为8%,均值为0.658 8 Hz,二阶固有频率最大差值比率约为1%,均值为1.755 Hz;理论值的一阶固有频率为0.775 7 Hz,二阶固有频率为1.248 5 Hz,实验值和理论值的一阶固有频率最大相差比率约为20%,二阶固有频率最大相差比率约为42%.
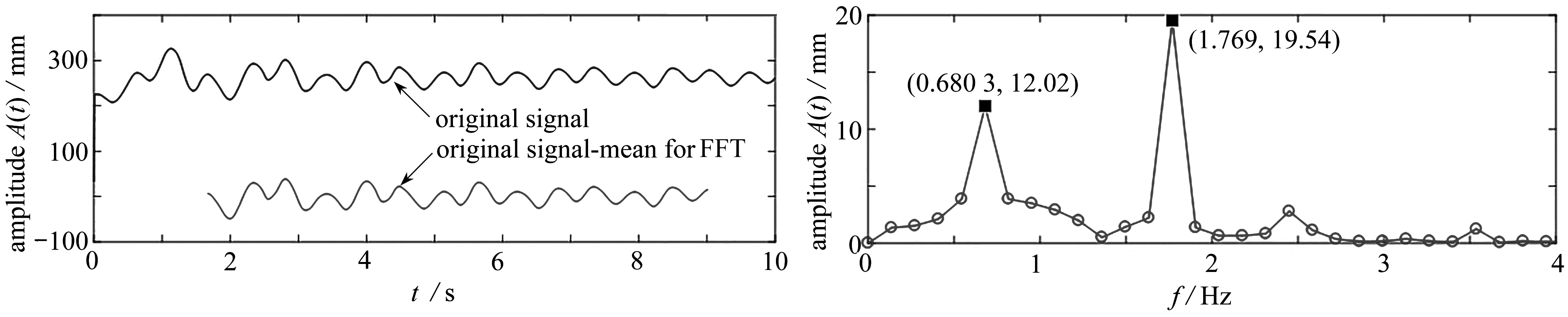
图7 左图为原始波高曲线,右图为FFT变换后的时域频率曲线(test 1)
Fig. 7 The left figure: the original wave height curve, the right figure: the time-domain frequency curve after FFT transform(test 1)

图8 左图为原始波高曲线,右图为FFT变换后的时域频率曲线(test 2)
Fig. 8 The left figure: the original wave height curve, the right figure: the time-domain frequency curve after FFT transform(test 2)

图9 左图为原始波高曲线,右图为FFT变换后的时域频率曲线(test 3)
Fig. 9 The left figure: the original wave height curve, the right figure: the time-domain frequency curve after FFT transform(test 3)
由表2~4知,原始信号经EMD变换得到不同的IMF分量,由不同IMF分量与原始信号的相关性分析可知,相关性最大的IMF分量是原始信号最重要的影响因素.相关性最大的IMF分量经Hilbert变换得到对应的固有频率和阻尼比是液面晃动的主要模态参数,其均值分别为1.760 Hz和0.013,与FFT变换后的实验平均二阶固有频率(1.755 Hz)差值比率小于1%.即在标准大气压工况下,二阶固有频率是导致液体晃荡的主导频率.次相关性的IMF分量对原始信号也有一定的影响,各组实验的固有频率差值比率小于5%,阻尼比差别略大,均值分别为0.656 2 Hz和0.060 2,与FFT变换后的实验平均一阶固有频率差值比率小于1%,由此可见,在标准大气压工况下,液体的一阶固有频率对液体晃荡也有一定的影响.由上述分析可知,各组实验的固有频率之间的差值小于1%,验证了实验测量与分析的可靠性.由表2~4可知,阻尼比随着相关的IMF相关性系数(相关系数大于0.2)的降低呈逐渐增大趋势.
3 结 论
本文分别针对两种不同气室压力对液体晃荡特性的影响开展系统实验研究.结果表明:在低气室压力下,晃荡能量主要集中于一阶固有频率;在高气室压力下,晃荡能量主要集中于二阶固有频率.随着气室压强的增大,影响液体晃荡的主要固有频率提高,而对应的阻尼比却随之降低.由此可见,气体可压缩性是研究流体晃荡的一个重要因素.
[1] 卫志军, 岳前进, 阮诗伦, 等. 矩形液舱晃荡冲击荷载的试验机理研究[J]. 船舶力学, 2012, 16(8): 885-892.(WEI Zhijun, YUE Qianjin, RUAN Shilun, et al. Experimental study on sloshing impact load of rectangular liquid tank[J]. Ship Mechanics, 2012, 16(8): 885-892.(in Chinese))
[2] 卫志军, 岳前进, 张文首, 等. 大尺度储舱液体晃荡砰击压力测量方法研究[J]. 中国科学: 物理学 力学 天文学, 2014, 44(7): 746-758.(WEI Zhijun, YUE Qianjin, ZHANG Wenshou, et al. Study on the measurement method of liquid sloshing slamming pressure in large scale cabin[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2014, 44(7): 746-758.(in Chinese))
[3] WEI Z J, YUE Q J. Experimental investigation of non-similarity slamming phenomena in geometrically similar tanks[J]. International Journal of Offshore and Polar Engineering, 2015, 25(4): 288-298.
[4] 卫志军, 陈晓东, 董玉山, 等. 两种平台下晃荡冲击荷载的实验研究[J]. 船舶力学, 2015, 19(7): 841-849.(WEI Zhijun, CHEN Xiaodong, DONG Yushan, et al. Experimental study on sloshing impact loads on two platforms[J]. Ship Mechanics, 2015, 19(7): 841-849.(in Chinese))
[5] 王立时, 李遇春, 张皓. 二维晃动自然频率与阻尼比系数的试验识别[J]. 振动与冲击, 2016, 35(8): 173-176.(WANG Lishi, LI Yuchun, ZHANG Hao. Experimental identification of two-dimensional sloshing natural frequency and damping ratio coefficient[J]. Journal of Vibration and Shock, 2016, 35(8): 173-176.(in Chinese))
[6] DODGE F T. The new dynamic behavior of liquids in moving containers[R]. San Antonio, TX: Southwest Research Institute, 2000.
[7] 吕敬, 李俊峰, 王天舒. 带弹性附件充液矩形贮箱俯仰运动动态响应[J]. 应用数学和力学, 2007, 28(3): 317-327.(LÜ Jing, LI Junfeng, WANG Tianshu. Dynamic response of pitching motion of liquid-filled rectangular tank with elastic attachment[J]. Applied Mathematics and Mechanics, 2007, 28(3): 317-327.(in Chinese))
[8] LI Y C, WANG Z. An approximate analytical solution of sloshing frequencies for a liquid in various shape aqueducts[J]. Shock and Vibration, 2014, 11: 672648.
[9] 李遇春, 张皓. 二维晃动模态的统一Ritz计算格式[J]. 振动与冲击, 2014, 33(19): 81-85.(LI Yuchun, ZHANG Hao. Unified Ritz calculation scheme for two-dimensional sloshing mode[J]. Journal of Vibration and Shock, 2014, 33(19): 81-85.(in Chinese))
[10] 蒋梅荣, 任冰, 温鸿杰, 等. 弹性液舱内液体晃荡实验研究[J]. 海洋工程, 2013, 31(5): 1-10.(JIANG Meirong, REN Bing, WEN Hongjie, et al. Experimental study on liquid sloshing in elastic liquid tank[J]. The Ocean Engineering, 2013, 31(5): 1-10.(in Chinese))
[11] 王鹏翔, 李遇春, 王立时. 矩形容器内液体一阶晃动模态试验识别[C]//第26届全国结构工程学术会议论文集: 第Ⅱ册. 2017.(WANG Pengxiang, LI Yuchun, WANG Lishi. Experimental identification of 1st-order sloshing mode of liquid in rectangular container[C]//Proceedings of the 26th National Conference on Structural Engineering: Vol Ⅱ. 2017.(in Chinese))
[12] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non stationary time series analysis[J]. Proceedings of the Royal Society of London, 1998, 455(1971): 903-995.
[13] 王慧, 刘正士. 一种识别结构模态阻尼比的方法[J]. 农业机器学报, 2008, 39(6): 201-202.(WANG Hui, LIU Zhengshi. Method for identifying structural modal damping ratio[J]. Transactions of the Chinese Society for Agricultural Machinery, 2008, 39(6): 201-202.(in Chinese))
[14] 黄时春. 水下爆炸荷载作用下舰船阻尼特性的试验研究[D]. 硕士学位论文. 哈尔滨: 哈尔滨工程大学, 2016.(HUANG Shichun. Experimental study on the damping characteristics of warship under the action of underwater explosion load[D]. Master Thesis. Harbin: Harbin Engineering University, 2016.(in Chinese))
[15] 付晓波. 经验模态分解法理论研究与应用[D]. 硕士学位论文. 太原: 太原理工大学, 2013.(FU Xiaobo. Theoretical study and application of empirical mode decomposition[D]. Master Thesis. Taiyuan: Taiyuan University of Technology, 2013.(in Chinese))