引 言
谱方法求解Navier-Stokes(NS)方程的一个难点在于速度和压力的离散必须满足inf-sup条件(或称LBB条件)，否则在求解过程中，伪压力模将导致压力震荡，采用交错网格或者压力离散比速度低两阶均可以避免伪压力模的出现[1-2]，而交错网格中涉及的插值容易降低谱方法的精度．求解定常不可压缩NS方程的策略主要分为两种：一是借助方程中的时间导数项，利用时间积分将方程分裂为多步计算，解耦速度和压力，分别得到速度和压力方程，从而简化计算，通过时间推进最终得到定常解．对于谱方法，这种计算策略由于需要时间步的迭代，时间步长会受到空间网格的制约(即CFL条件)，导致非定常时间步积分收敛很慢而使得计算量较大，同时引入了与时间步长相关的分裂误差，与谱方法的空间精度不匹配．二是舍去方程中的时间项，直接对方程组进行空间离散，然后采用Picard迭代[3-4]或Newton迭代直接求解耦合速度压力方程组的方法，最终得到定常解．此法相比前者最大的优势在于极大地减少了计算量，一般只需迭代几十或几百步便能得到收敛的定常解；不过直接求解耦合方程会给计算的稳定性带来一些影响.
在过去的几十年中，定常不可压缩NS方程的求解方法研究有了很大发展．苏铭德和陈霜立[5]将推进迭代法应用到不可压缩流的方程中求解，并给出了曲线坐标下的一般表达式．他们将推进迭代法应用于方腔流及圆柱绕流，得到的结果表明该方法具有较快的收敛速度．Casarin[6]利用谱元法求解了定常Stokes和NS方程，在每步Newton迭代步中使用一个Schwarz预条件来控制计算矩阵的条件数．Pontaza和Reddy[7]结合谱元法和最小二乘有限元法模拟黏性流体流动，采用Newton迭代法得到定常解．Knoll和Keyes[8]、马东军等[9]利用Jacobian-free Newton-Krylov方法求解定常不可压缩NS方程，将基于高阶谱元法的区域分解Stokes算法的非定常时间推进步作为Newton迭代的预处理，回避了传统Newton方法Jacobi矩阵的显式装配，降低了Newton迭代线性系统的条件数，加快了收敛速度．Rehman等[4]利用Picard迭代法求解定常的NS方程，在Picard迭代中，前一步的速度被嵌入到对流项中进行速度更新，然后再求解一系列线性问题．Zhang等[10]给出了一个求解不可压缩NS方程的Chebyshev伪谱多网格法，该方法增加了一个伪时间导数项，用显式Runge-Kutta格式对伪时间项离散，空间离散采用伪谱多网格法，通过伪时间的推进来得到定常解．章争荣和张湘伟[11]建立基于Galerkin加权余量法的NS方程数值流形格式来求解二维定常不可压黏性流动方程，其方程组采用直接线性化交替迭代方法和Newton-Raphson迭代方法进行求解．覃燕梅等[12]提出了一种局部投影稳定化的有限元方法求解定常不可压缩NS方程，该方法既克服了对流占优,又避免了inf-sup条件的限制．He等[13]结合Newton迭代法和两水平有限元求解了定常NS方程．对于定常不可压NS方程的求解，还有Melchior等[14]提出的预条件Krylov求解法以及Ozcelikkale和Sert[15]提出的最小二乘谱元法等．最近，戴海和潘文峰[16]提出了一种Chebyshev谱元法，并成功地应用于Helmholtz方程透射特征值问题.
本文结合Picard线性化迭代，给出一种求解二维定常不可压缩NS方程的PN×PN-2谱元法．Picard线性化将不可压缩NS方程转化为一系列的Stokes-type方程，空间离散采用PN×PN-2谱元法计算每个迭代步的Stokes-type方程，与时间分裂法和投影类算法相比，本文给出的方法舍弃了时间项，避免了与时间步长相关的分裂误差．在同位网格下，速度在物理空间采用基函数为Lagrange插值多项式的节点展开，而压力在谱空间采用基函数为Legendre多项式的直接展开，且压力展开阶数比速度低两阶．压力计算方式为先求解压力在谱空间的离散系数，再在谱空间内计算每个网格节点上的压力值．通过压力离散比速度离散低两阶的方式满足了inf-sup条件，避免了同位网格中容易出现的压力振荡现象，从而保证了计算得到的速度和压力都具有高精度．相比使用交错网格的数值方法，该方法更易于实施，且避免了交错网格里的插值计算带来的误差，更能体现出谱元法的高精度优势．另一方面，本文方法与传统的谱方法相比，可以自由划分单元，在计算一些局部梯度较大的问题时(如表面张力流、剪切流等)，在单元局部加密、优化节点分布等方面具有优势.
为了验证本文方法的准确有效性，数值求解了具有精确解的Stokes方程和Kovasznay流动，并模拟了方腔顶盖驱动流，结果表明了本文方法的可靠性及较快的收敛性，且达到了谱精度．本文方法在高精度数值计算方面具有一定的应用前景，可应用于诸如线性稳定性分析的基态解求解(线性稳定性分析中基态解的精度越高，得到的流动失稳临界参数越准确)等方面，在高精度数值计算、线性稳定性分析、流动失稳机理等研究上具有积极的意义.
1 数 值 方 法
1.1 PN×PN-2谱元法
考虑到谱元法求解NS方程时出现的伪压力模现象，本文采用PN×PN-2谱元法，即速度采用N阶多项式展开，而压力则采用N-2阶多项式展开．考察二维直角坐标系下的定常Stokes方程:
(1)
其中u=(u,v)为速度矢量，p为压力，f=(fx,fy)为外力．划分计算区域Ω为若干单元，将第i个单元Ωi映射到标准计算区域[-1,1]×[-1,1]．取测试函数w,q，得到单元Ωi内方程(1)的积分弱形式，将速度u和压力p分别离散为
(2)
(3)
其中ujk为网格节点上的速度值，而pjk为谱系数.
测试函数w=(wx,wy)，q分别取为
wx=wy=hm(ξ)hn(η), 0≤m≤Nx, 0≤n≤Ny,
(4)
q=Lm(ξ)Ln(η), 0≤m≤Nx-2, 0≤n≤Ny-2.
(5)
将式(2)～(5)代入式(1)的积分弱形式，整理后得到离散方程矩阵形式：
(6)
其中各系数为
Ajkmn=Ajm·Bkn+Bjm·Akn,
(7a)
Bjkmn=Bjm·Bkn,
(7b)
(C1)jkmn=Cjm·Fkn,
(7c)
(C2)jkmn=Fjm·Ckn,
(7d)
(7e)
(7f)
(7g)
(7h)
Bjm=
hj(ξ)hm(ξ)dx，
(7i)
Bkn=
hk(η)hn(η)dy，
(7j)
(7k)
(7l)
Fjm=Lj(ξ)hm(ξ)dx，
(7m)
Fkn=Lk(η)hn(η)dy.
(7n)
通过Gauss数值积分计算式(7)，得到每个单元内的线性方程组，再根据单元叠加原理将所有单元方程叠加为总体区域的线性方程组．需要注意的是，得到方程组中的求解变量ui为节点上的速度值，而pi为谱系数．在进行方程组叠加的过程中只需对单元交界处的速度进行叠加，而谱系数是不需要叠加的．最后加入边界条件到总体区域的线性方程组进而得到计算结果.
1.2 Picard迭代法
考虑二维直角坐标系下的定常NS方程:
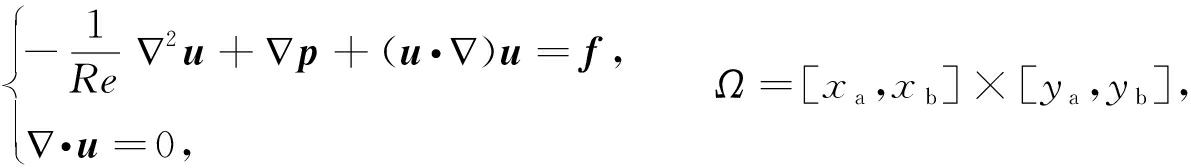
(8)
其中Re为Reynolds数．由于动量方程中对流项的存在，NS方程离散后将得到一个非线性方程组．通过Picard迭代法可以将NS方程线性化[4,9]．Picard迭代法的实施过程是将对流项中的速度用前一步的值代替，通过迭代过程得到定常NS方程的收敛解．给定问题的初始速度u0，由Picard迭代法的思想，可得到一系列方程:
-ν
2uk+1+pk+1+(uk·)uk+1=f,
(9)
·uk+1=0,
(10)
矩阵形式为
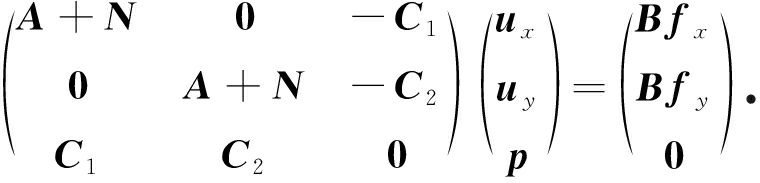
(11)
利用上文的PN×PN-2谱元法求解，经迭代得到定常NS方程的解．式(11)中的N是由式(9)中的对流项(uk·)uk+1离散得到，通过uk的迭代，设定
小于某个收敛标准时即达到稳定解.
2 数值算例与结果
首先，定义数值解ui的绝对误差2范数为
(12)
其中ND表示计算节点总数，ui|numer，ui|exact分别表示数值算例的数值解和精确解.
算例1 考虑Stokes问题(1)，精确解为
(13)
首先将x,y方向区间[0,1]划分为2个单元[0,0.5]和[0.5,1]，每个单元x,y方向的速度离散阶数取为Nx和Ny，且Nx=Ny=N，压力离散阶数则为N-2，边界条件为Dirichlet条件．图1为计算得到的速度和压力的误差2范数取对数后与离散阶数的关系，显示误差呈指数收敛．可以看到，压力的精度要比速度低两阶左右，这是由于离散时压力的阶数要低两阶造成的．当离散阶数达到12以上时，误差已经达到计算机精度,不再减小．图2为速度阶数均为12时，PN×PN谱元法和本文方法(PN×PN-2谱元法)得到的压力等值线图以及精确压力等值线图，可以看出本文方法不存在压力震荡现象.
图1 算例1的误差2范数与离散阶数N的关系图
Fig. 1 Dependency of the 2-norm error on discrete order N for example 1
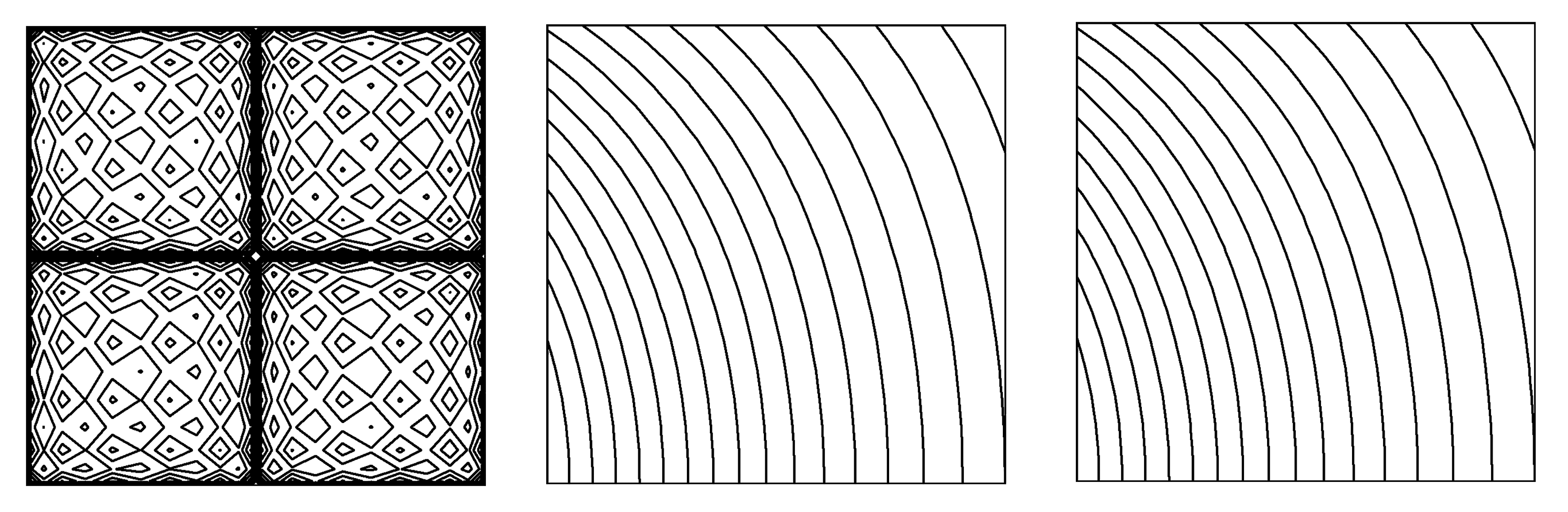
(a) PN×PN谱元法 (b) 本文方法 (c) 精确压力场
(a) The PN×PN spectral element method (b) This paper method (c) The exact pressure field
图2 PN×PN谱元法和本文方法计算算例1得到的压力场和精确压力场
Fig. 2 The pressure fields obtained with the PN×PN spectral element method and the PN×PN-2
spectral element method, along with the exact pressure field for example 1
算例2 Kovasznay流动
Kovasznay流动是由Kovasznay给出的一组NS方程分析解:
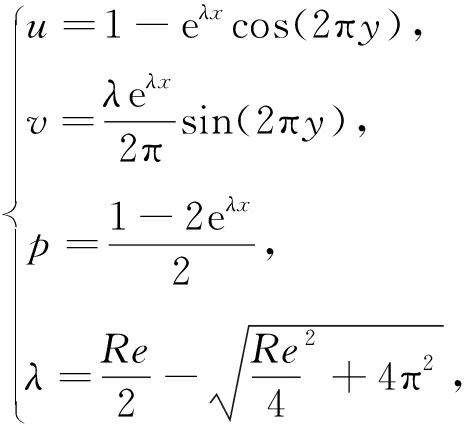
(14)
计算区域为Ω=[-0.5,1]×[-0.5,1.5]．计算中Re=40，误差收敛标准定为10-12．根据区域大小关系，选取N=Nx=3Ny/4．图3为误差2范数与N的关系图，可以看出数值精度随阶数呈指数收敛，当N增大到27时，误差降低到10-14而不再下降，这跟所取收敛标准有关．表1呈现的是计算时不同离散阶数所要的迭代步数，可以看到本文方法所需迭代步数很少，计算效率非常高．图4给出了PN×PN谱元法计算的压力场和用本文方法得到的压力场以及精确压力场，同样避免了压力震荡.
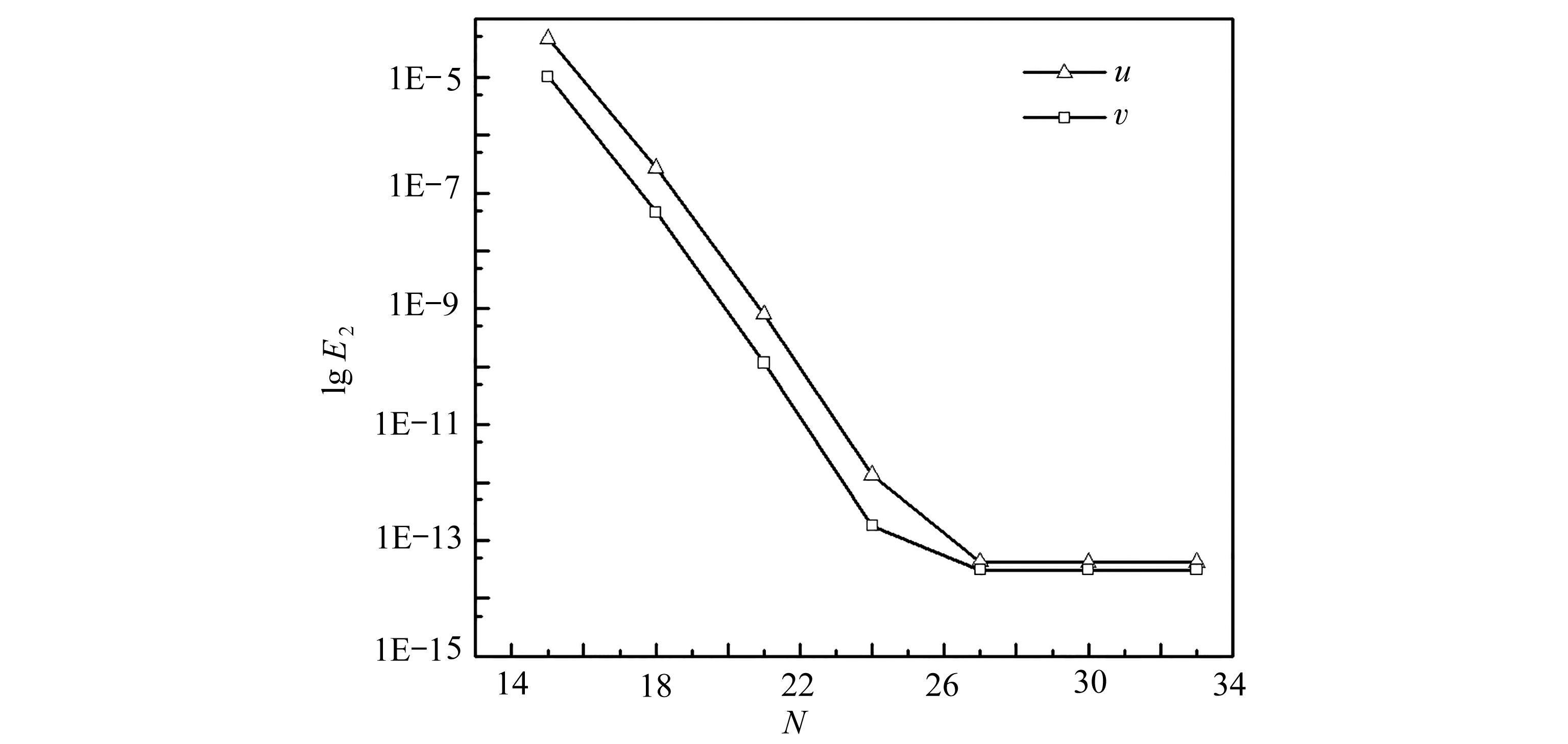
图3 Kovasznay流的误差2范数与离散阶数N的关系图
Fig. 3 Dependency of the 2-norm error on the discrete orders for the Kovasznay flow
表1 计算Kovasznay流时不同阶数下的迭代步数
Table 1 The number of iteration steps under different discrete orders for simulation for the Kovasznay flow
N15182124273033iteration steps I141383330282828
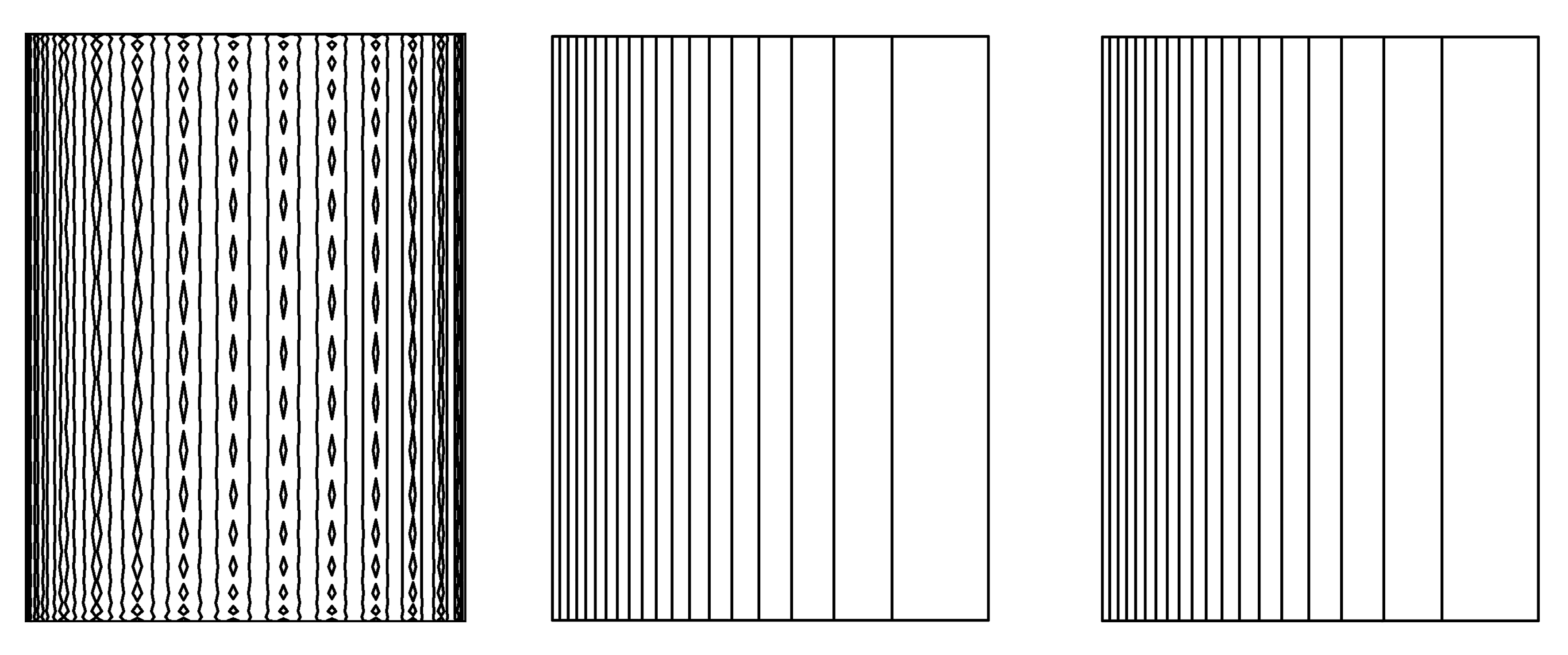
(a) PN×PN谱元法 (b) 本文方法 (c) 精确压力场
(a) The PN×PN spectral element method (b) This paper method (c) The exact pressure field
图4 PN×PN谱元法和本文方法计算算例2得到的压力场和精确压力场
Fig. 4 The pressure fields obtained with the PN×PN spectral element method and the PN×PN-2
spectral element method, along with the exact pressure field example 2
算例3 方腔顶盖驱动流
方腔顶盖驱动流是流体力学的经典问题之一，对该问题已有大量研究工作[17-22]．Ghia等[17]给出了二维方腔顶盖驱动流的基准解以及详细的数据．目前，数值模拟二维或三维方腔顶盖驱动流已经成为验证计算方法的正确性和有效性的重要手段.
图5为二维平面上的方腔顶盖驱动流的简化物理模型．在一个边长为H的正方形方腔顶部有一向右的固定速度V0，利用流体的黏性带动方腔内流体的流动．假设方腔内的流体是不可压缩、等温的Newton流体，方腔边界为固壁，选择H，H/V0，V0和
(ρ为流体密度)分别为特征长度、时间、速度和压力．经无量纲化后得到方腔顶盖驱动流的控制方程为
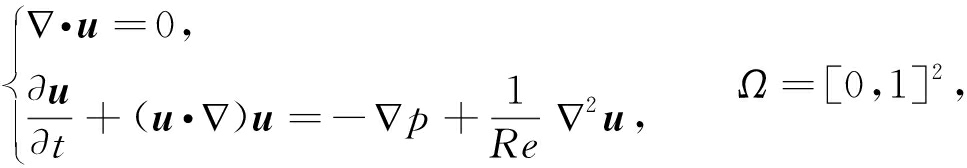
(15)
其中Reynolds数为Re=HV0/υ(υ为流体运动学黏性系数)．边界条件为
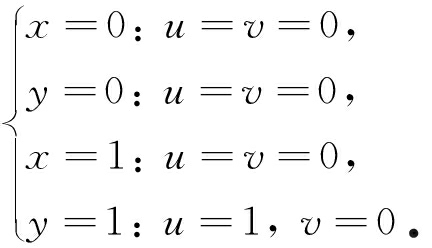
(16)
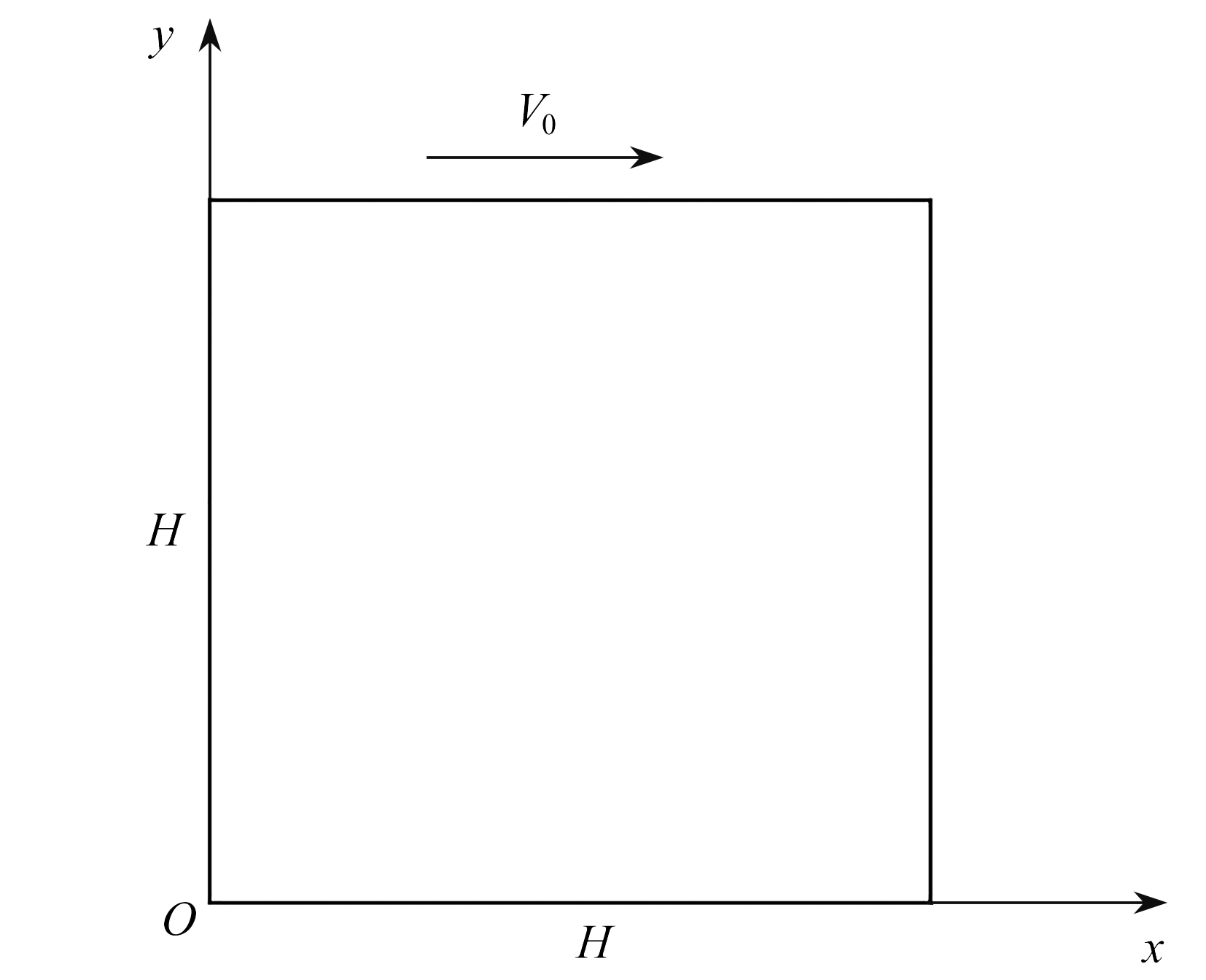
图5 方腔顶盖驱动流物理模型
Fig. 5 The configuration of the lid-driven cavity flow
使用基于Picard迭代的定常PN×PN-2谱元法求解Re为100，400和1 000的方腔顶盖驱动流，其中计算区域的单元划分为6×6，每个单元离散阶数为8，计算网格为49×49．将中心线上的结果同公认的文献基准解[17]进行对比，如图6所示，可以看到，本文得到的结果能较好地吻合公认的基准解，验证了本文方法的正确性.
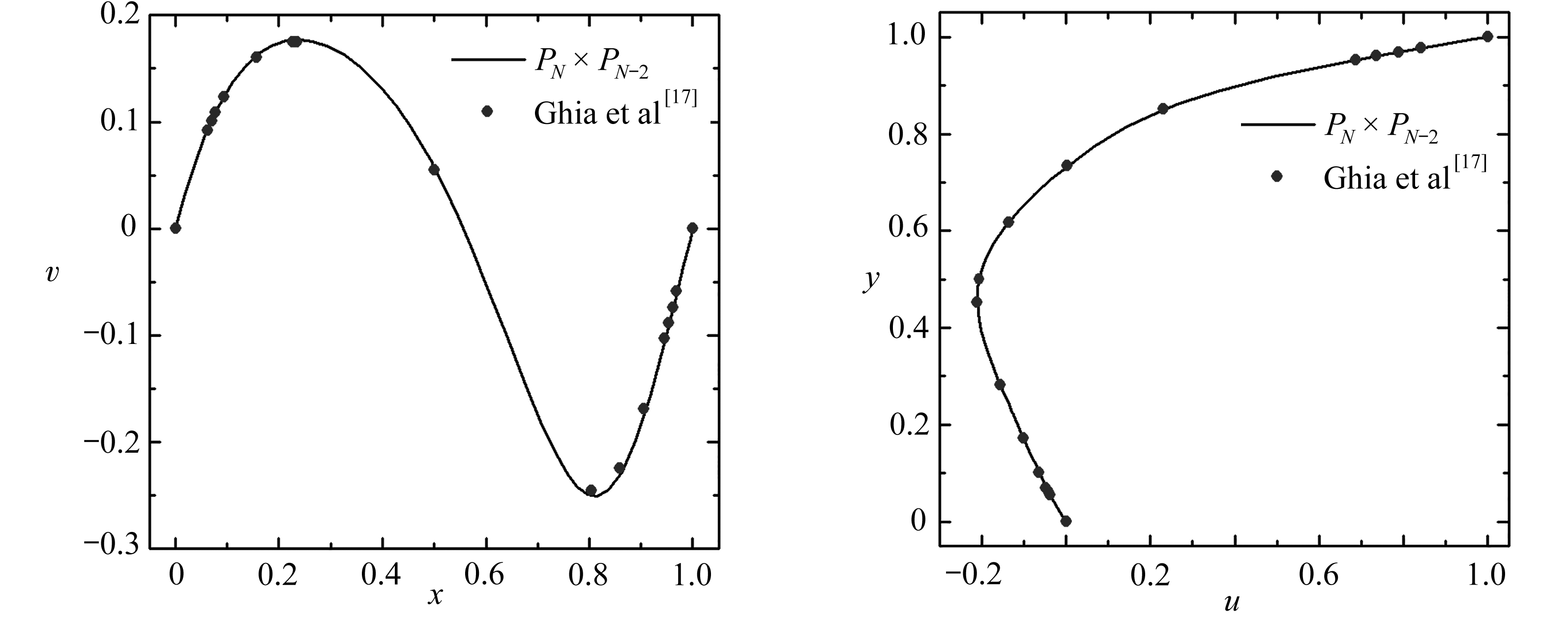
(a) Re=100
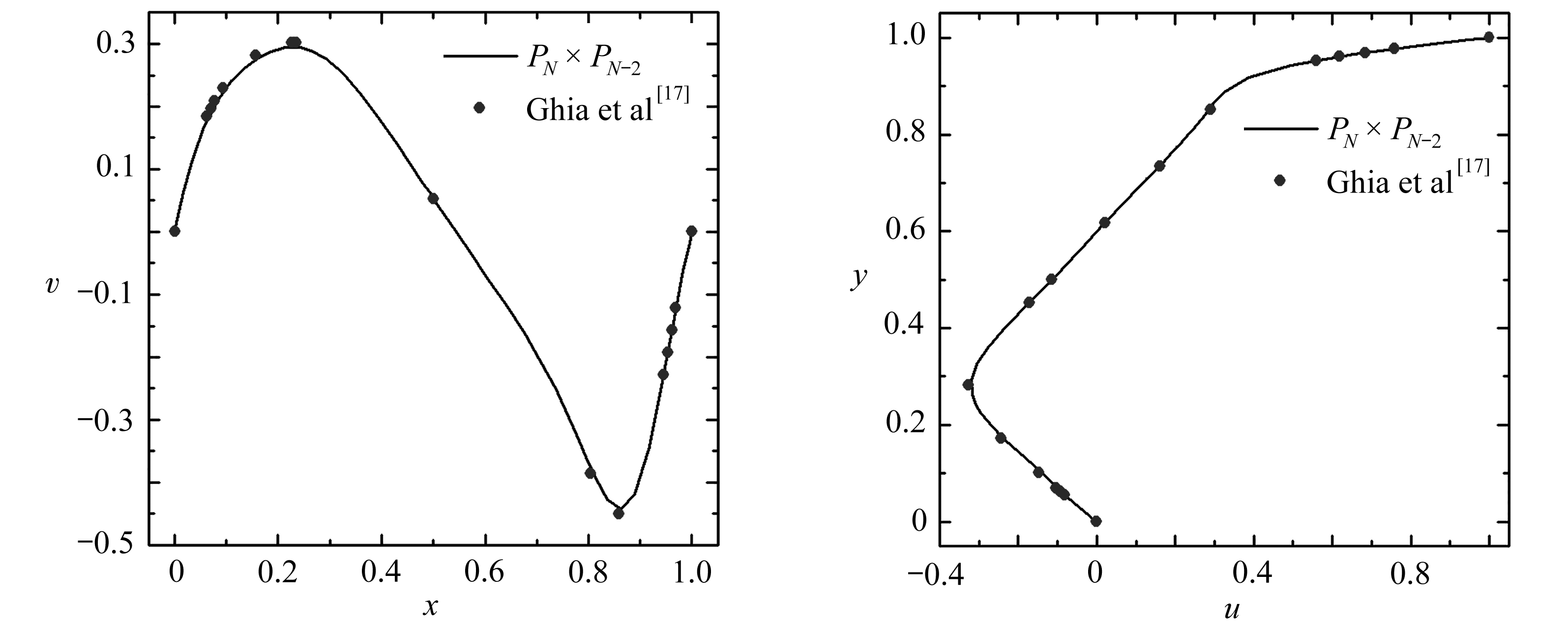
(b) Re=400
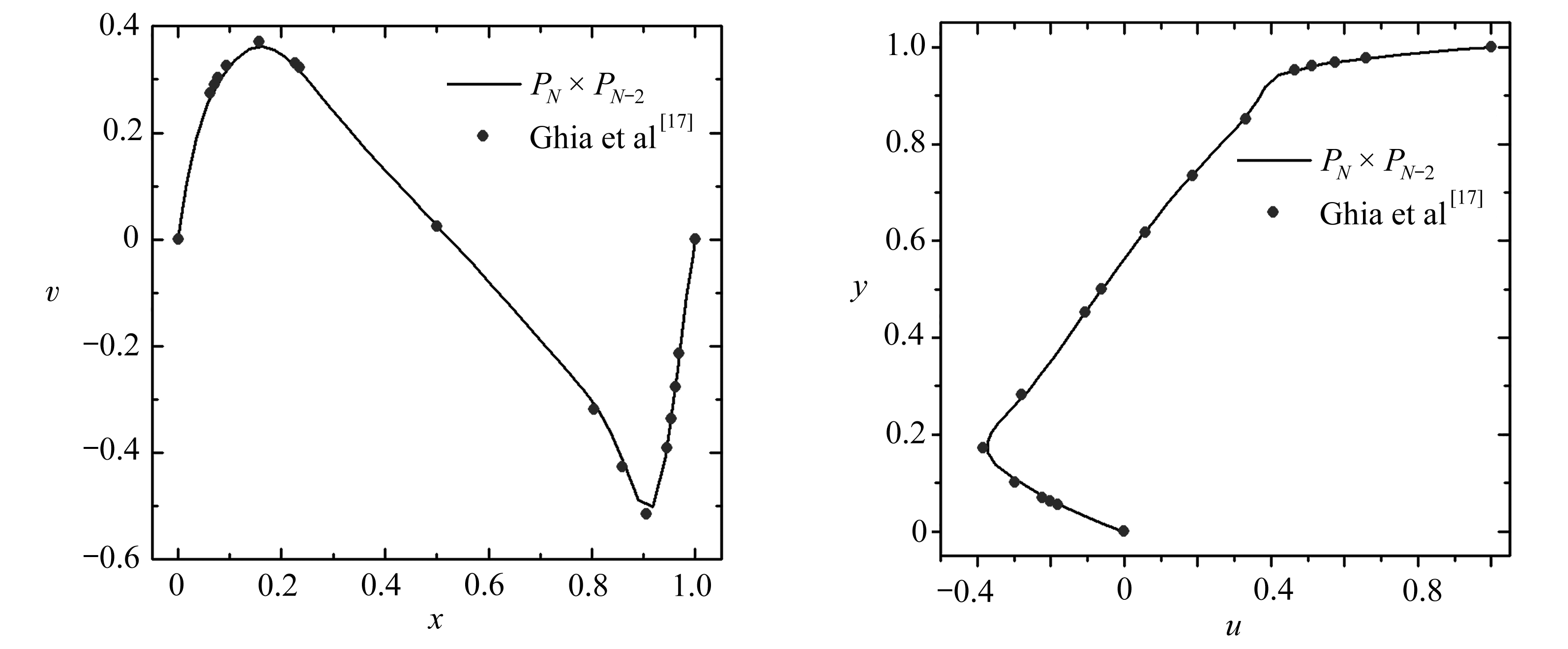
(c) Re=1 000
图6 不同Re数的方腔流中心线上的速度分量大小图：y=0.5(左图)和x=0.5(右图)
Fig. 6 Velocities along the center line for the lid-driven cavity flow with different Re values: y=0.5(left) and x=0.5(right)
3 结 论
本文结合Picard迭代给出了一种求解二维定常不可压缩NS方程的PN×PN-2谱元法．与时间分裂法和投影类算法相比，本文方法舍弃了时间项，通过Picard线性化将不可压缩NS方程转化为一系列线性的Stokes-type方程，使用非交错网格的PN×PN-2谱元法计算每个迭代步的Stokes-type方程，避免了与时间步长相关的分裂误差．速度在物理空间离散，压力在谱空间离散，通过压力离散比速度离散低两阶的方式消除了伪压力模，避免了同位网格中容易出现的压力振荡，所得到的压力解没有震荡现象，非交错网格的应用使方程的离散方便且不会带来相应的插值误差，从而计算得到的速度和压力都具有高精度．数值计算Stokes流动、Kovasznay流动和方腔顶盖驱动流并与解析解或者文献基准解进行对比，结果表明，迭代收敛非常快，同时达到谱精度收敛，体现了本文方法的可靠性和较快的收敛性．本文方法在高精度数值计算方面具有一定的应用前景，在高精度数值计算、线性稳定性分析、流动失稳机理等研究上具有积极的意义.
[1] AUTERI F, GUERMOND J L, PAROLINI N. Role of the LBB condition in weak spectral projection methods[J]. Journal of Computational Physics, 2001, 174(1): 405-420.
[2] SCHUMACK M R, SCHULTZ W W, BOYD J P. Spectral method solution of the Stokes equations on nonstaggered grids[J]. Journal of Computational Physics, 1990, 89(2): 30-58.
[3] DEBLOIS B M. Linearizing convection terms in the Navier-Stokes equations[J]. Computer Methods in Applied Mechanics and Engineering, 1997, 143(3/4): 289-297.
[4] REHMAN M U, VUIK C, SEGAL G. Numerical solution techniques for the steady incompressible Navier-Stokes problem[C]//Proceedings of the World Congress on Engineering. London, 2008: 844-849.
[5] 苏铭德, 陈霜立. 定常不可压缩粘性流体流动Navier-Stokes方程的推进迭代法[J]. 计算物理, 1989, 6: 321-334.(SU Mingde, CHEN Shuangli. Solution of the N-S equation of the steady incompressible viscous flow with marching-iterative method[J]. Chinese Journal of Computational Physics, 1989, 6: 321-334.(in Chinese))
[6] CASARIN M A. Schwarz preconditioners for the spectral element discretization of the steady Stokes and Navier-Stokes equations[J]. Numerische Mathematik, 2001, 89: 307-339.
[7] PONTAZA J P, REDDY J N. Spectral/hp least-squares 
nite element formulation for the Navier-Stokes equations[J]. Journal of Computational Physics, 2003, 190: 523-549.
[8] KNOLL D A, KEYES D. Jacobian-free Newton-Krylov methods: a survey of approaches and applications[J]. Journal of Computational Physics, 2004, 193: 357-397.
[9] 马东军, 柳阳, 孙德军, 等. 高阶谱元区域分解算法求解定常方腔驱动流[J]. 计算力学学报, 2006, 23(6): 668-673.(MA Dongjun, LIU Yang, SUN Dejun, et al. Spectral element method with a domain decomposition Stokes solver for steady cavity driven flow[J]. Chinese Journal of Computational Mechanics, 2006, 23(6): 668-673.(in Chinese))
[10] ZHANG W, ZHANG C H, XI G. An explicit Chebyshev pseudospectral multigrid method for incompressible Navier-Stokes equations[J]. Computers & Fluids, 2010, 39(1): 178-188.
[11] 章争荣, 张湘伟. 二维定常不可压缩粘性流动N-S方程的数值流形方法[J]. 计算力学学报, 2010, 27(3): 415-421.(ZHANG Zhengrong, ZHANG Xiangwei. Numerical manifold method for steady incompressible viscous 2D flow Navier-Stokes equtions[J]. Chinese Journal of Computational Mechanics, 2010, 27(3): 415-421.(in Chinese))
[12] 覃燕梅, 冯民富, 罗鲲, 等. Navier-Stokes方程的局部投影稳定化方法[J]. 应用数学和力学, 2010, 31(5): 618-630.(QIN Yanmei, FENG Minfu, LUO Kun, et al. Local projection stabilized finite element method for the Navier-Stokes equations[J]. Applied Mathematics and Mechanics, 2010, 31(5): 618-630.(in Chinese))
[13] HE Y, ZHANG Y, SHANG Y, et al. Two-level Newton iterative method for the 2D/3D steady Navier-Stokes equations[J]. Numerical Methods for Partial Differential Equations, 2012, 28: 1620-1642.
[14] MELCHIOR S A, LEGAT V, DOOREN P V, et al. Analysis of preconditioned iterative solvers for incompressible flow problems[J]. International Journal for Numerical Methods in Fluids, 2012, 68: 269-286.
[15] OZCELIKKALE A, SERT C. Least-squares spectral element solution of incompressible Navier-Stokes equations with adaptive refinement[J]. Journal of Computational Physics, 2012, 231: 3755-3769.
[16] 戴海, 潘文峰. 谱元法求解Helmholtz方程透射特征值问题[J]. 应用数学和力学, 2018, 39(7): 833-840.(DAI Hai, PAN Wenfeng. A spectral element method for transmission eigenvalue problems of the Helmholtz equation[J]. Applied Mathematics and Mechanics, 2018, 39(7): 833-840.(in Chinese))
[17] GHIA U, GHIA K N, SHIN C T. High-Re solutions for incompressible flow using the Navier-Stokes equations and a multigrid method[J]. Journal of Computational Physics, 1982, 48(3): 387-411.
[18] AIDUN C K, TRIANTAFILLOPOULOS N G, BENSON J. Global stability of a lid-driven cavity with through-flow: flow visualization studies[J]. Physics of Fluids A: Fluid Dynamics, 1991, 3(9): 2081-2091.
[19] ALBENSOEDER S, KUHLMANN H C, RATH H J. Three-dimensional centrifugal-flow instabilities in the lid-driven-cavity problem[J]. Physics of Fluids, 2001, 13: 121-135.
[20] THEOFILIS V. Global linear instability[J]. Annual Review of Fluid Mechanics, 2011, 43: 319-352.
[21] KOSEFF J R, STREET R L. The lid-driven cavity flow: a synthesis of qualitative and quantitative observations[J]. Journal of Fluids Engineering, 1984, 106(4): 390-398.
[22] KOSEFF J R, STREET R L, GRESHO P M, et al. A three-dimensional lid-driven cavity flow: experiment and simulation[C]//International Conference on Numerical Methods in Laminar and Turbulent Flow. Seattle, WA, 1983.