引 言
热防护服能够极大程度地保护处于高温环境下的工作人员，它一般由外壳层、防水层和隔热层组成[1-2]．为了在较短的研发周期内设计隔热效果更好的热防护服，并且对热防护服的保护效果进行合理评价，越来越多的科研工作者通过建立数学模型的方式模拟研究热防护服的热传递过程，并且对防护效果进行了评价.
田苗等从热防护服热传导模型建立和模型验证两个方面对相关的研究进行了回顾，建立了热防护服传热模型，并对模型的解法进行了归纳，预测了其数学模型发展的趋势[3]．卢琳珍等建立了热防护服-空气-皮肤热传导的数学模型，并且利用隐形差分的方法计算了模型在高温环境下的温度场，分析了空气层和织物对热防护服性能的影响，评价了皮肤灼伤情况[4]．张英等结合人体数值模型评价方法和人体生理评价指标，对热防护服降温效果进行了评价[5]．李紫含等从主观和客观两个方面研究了热防护服隔热效果评价方法[6]．毛瑶瑶等建立三层热防护服模型，结合遗传算法及插值拟合算法等得到了热防护服的温度场分布以及不同织物的最优厚度[7]．姚沃成等建立了高温作业专用服装的数学模型，并且利用数值方法对模型进行求解[8].
分析文献可发现，研究人员针对热防护服单独建模的较多，对联合热防护服-空气-皮肤建模的较少．并且因为模型为层合结构，研究人员一般采用有限差分法或有限元法等数值方法对模型进行求解[9-12]．基于上述原因，本文考虑热防护服、空气和皮肤组织的相互作用，建立了热防护服-空气-皮肤组织的热传导数学模型，并且利用模型交界处温度相等和热流量连续的特性，结合微分思想，求得了模型的分离变量解析解．通过求得的解析解计算了模型温度场分布以及不同位置热流量变化情况，然后计算了在几种典型的高温环境下皮肤组织的热损伤情况，进一步对防护效果进行了评价.
1 模 型 建 立
热防护服的外壳层，防水层和隔热层厚度分别为l1，l2和 l3．热防护服和皮肤表面间存在空气层，其厚度为l4．皮肤组织由表皮、真皮和皮下组织组成，厚度分别为l5，l6和 l7,x为位置变量，
为模型总厚度,x7=l1+l1+…+l7．热防护服左侧处在高温环境中，右侧为人体皮肤深处，和人体基础温度保持一致．相应的几何模型如图1所示.
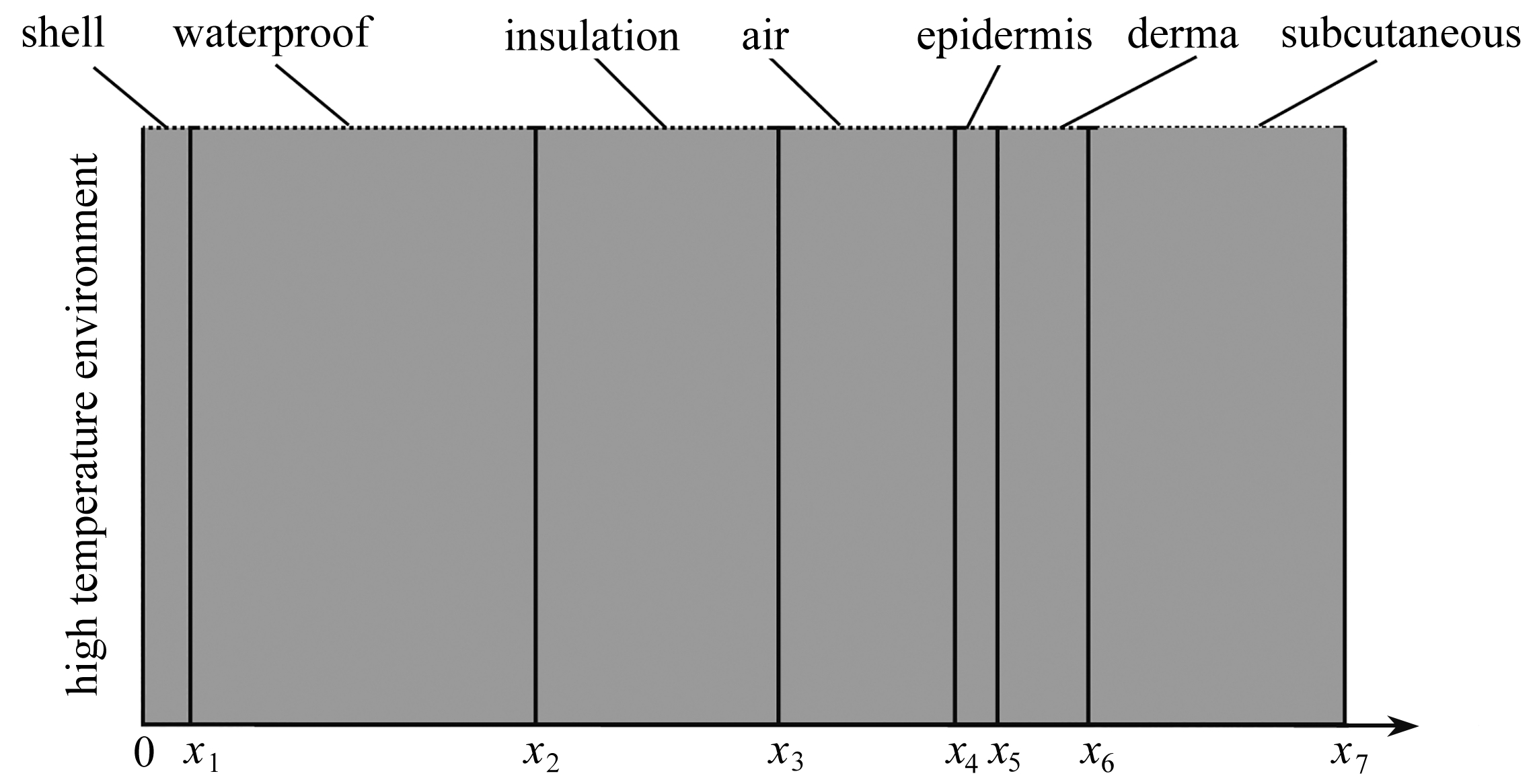
图1 热防护服-空气-皮肤几何模型
Fig. 1 The geometric model for the thermal protective clothing-air-skin sturcture
相应的控制方程为
b,iρbcb(Ti-Ta)+(qmet,i+qext,i)；
(1)
边界条件为
T(0,t)=Th,
(2)
T(x7,t)=Ta；
(3)
初始条件为
T(x,0)=Ta,
(4)
其中i=1,2,…,7；ρi表示第i层的密度；ci表示第i层的比热容；Ti为第i层的温度变化函数；t为时间变量；ki为第i层的热传导系数；b,i为第i层的血流灌注率；ρb为血液密度； cb为血液比热容；Th为外部高温环境温度;Ta为人体的基础温度；qmet,i为各层内部产热量；qext,i为外部加热量．无量纲化的控制方程为
(5)
无量纲化的边界条件为
(6)
θ7(ξ7,τ)=0=f7(τ);
(7)
无量纲化的初始条件为
θi(ξ,0)=0,
(8)
其中f0(τ)为无量纲化的左边界条件，f7(τ)为无量纲化的右边界条件．利用下标r表示无量纲化参数，其中ρr,i表示第i层的无量纲密度;cr,i表示第i层的无量纲比热容，kr,i表示第i层的无量纲热传导系数;θi表示第i层的无量纲温度函数;τ表示无量纲时间参数;ξ表示无量纲位置变量;
表示无量纲内部产热量;
表示无量纲外部加热量;
表示无量纲血流灌注率．各无量纲参数和原参数的关系为
ρr,i=ρi/ρ1, cr,i=ci/c1, kr,i=ki/k1,θi=(Ti-Ta)/Ta, τ=k1tρ1c1/L2, ξ=x/L,
b,iρbcb/k1.
2 解 析 方 法
本文建立的模型共有7层，且各层的热物理参数互不相等，所以不能直接利用分离变量法求得解析解．为求得其分离变量解析解将其在时间域上进行分割，可以假设在首个[0,Δτ]内交界处的温度线性变化为
θi(ξi,τ)=fi(τ)=Kiτ,
(9)
其中Ki为第i段近似直线的斜率;fi(τ)为第i层温度随时间变化的函数．经过此假设后,本文建立的模型各层左右边界条件均为已知，可利用分离变量法分别求解．各层边界条件均为非齐次化边界条件,为了将边界条件齐次化，引入转换函数wi(ξ,τ)和ψi(ξ,τ)：
θi(ξ,τ)=wi(ξ,τ)+ψi(ξ,τ),
(10)
wi(ξ,τ)=(aξ+b)fi-1(τ)+(cξ+d)fi(τ).
(11)
如果需要边界条件齐次化则需要满足
(aξi-1+b)fi-1(τ)+(cξi-1+d)fi(τ)=fi-1(τ),
(12)
(aξi+b)fi-1(τ)+(cξi+d)fi(τ)=fi(τ).
(13)
由式(12)、(13)可知
(14)
将式(10)代入式(5)中可得
(15)
其中
(16)
为了求得在[0,Δτ]时间域内的分离变量解，引入分离变量函数φi(ξ)和φi(τ)：
ψi(ξ,τ)=φi(ξ)φi(τ).
(17)
由式(12)、(13)可知
ψ(ξi-1,τ)=0,
(18)
ψ(ξi,τ)=0.
(19)
通过观察及试算，选取式(15)的特征方程如下:
(20)
将式(17)代入式(20)可得
(21)
由式(18)、(19)可知
φi(ξi-1)=0,
(22)
φi(ξi)=0.
(23)
结合式(21)～(23)可知其为齐次的二阶常微分方程，其本征函数为
(24)
很明显,φi,m(ξ)满足正交特性，即满足
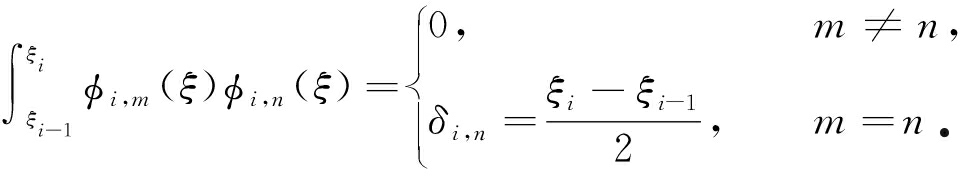
(25)
为了采用模态叠加法求得其在[0,Δτ]内的解析解，引入转换函数γi,m(τ),令
(26)
将式(26)代入式(15)，两边同时乘以φi,n(ξ)，并且在[ξi-1，ξi]内积分，结合式(21)和式(25)可得
(27)
其中
(28)
式(27)为一阶常微分方程，其解为[13]
(29)
其中
(30)
(31)
至此，可以求解出在[0，Δτ]时间内各层的解析解：
(32)
因式(32)中存在未知数Ki(i=1,2,3，…，7)，根据各层交界处热流量连续的特性，可得如下方程：
(33)
由式(33)可求得ki,之后将Δτ时刻作为初始值，相同的过程可计算[Δτ，2Δτ]内温度场的解析解，通过不断循环即可求得整个时间域内的分离变量解析解.
3 防护效果评价
本文利用在高温环境中穿着热防护服时皮肤组织的热损伤情况，来评价热防服的保护效果．皮肤组织的热损伤表达式如下：
Ω(t)=
Aexp(-Ea/(RT))dt,
(34)
其中Ω表示热损伤因子；A表示频率因子；R表示通用气体常数；Ea表示激活能量．根据文献[9,14]可知：Ω=0.53,为一级热损伤; Ω=1.0,为二级热损伤; Ω=104,为三级热损伤(Ea/R=75 000,A=3.1×1098).
4 数值结果和讨论
根据第2、3节推导的解析解，可计算热防护服在高温环境下温度场的分布情况和防护条件下皮肤组织的热损伤情况．模型各层的热物理参数见表1[2,14-18]．血液密度为ρb=1 060 kg/m3，其比热容为cb=3 770 J/(kg·K);人体基础温度取值为Ta=37 ℃.
表1 模型各层的热物理参数[2,14-18]
Table 1 Thermophysical parameters of each layer of the model[2,14-18]
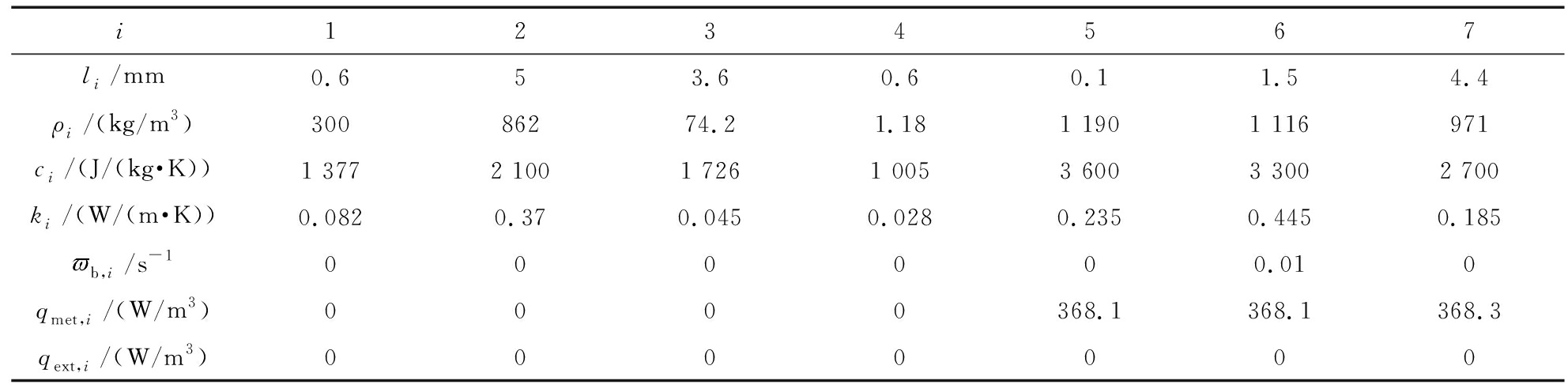
i1234567li/mm0.653.60.60.11.54.4ρi/(kg/m3)30086274.21.181 1901 116971ci/(J/(kg·K))1 3772 1001 7261 0053 6003 3002 700ki/(W/(m·K))0.0820.370.0450.0280.2350.4450.185b,i/s-1000000.010qmet,i/(W/m3)0000368.1368.1368.3qext,i/(W/m3)0000000
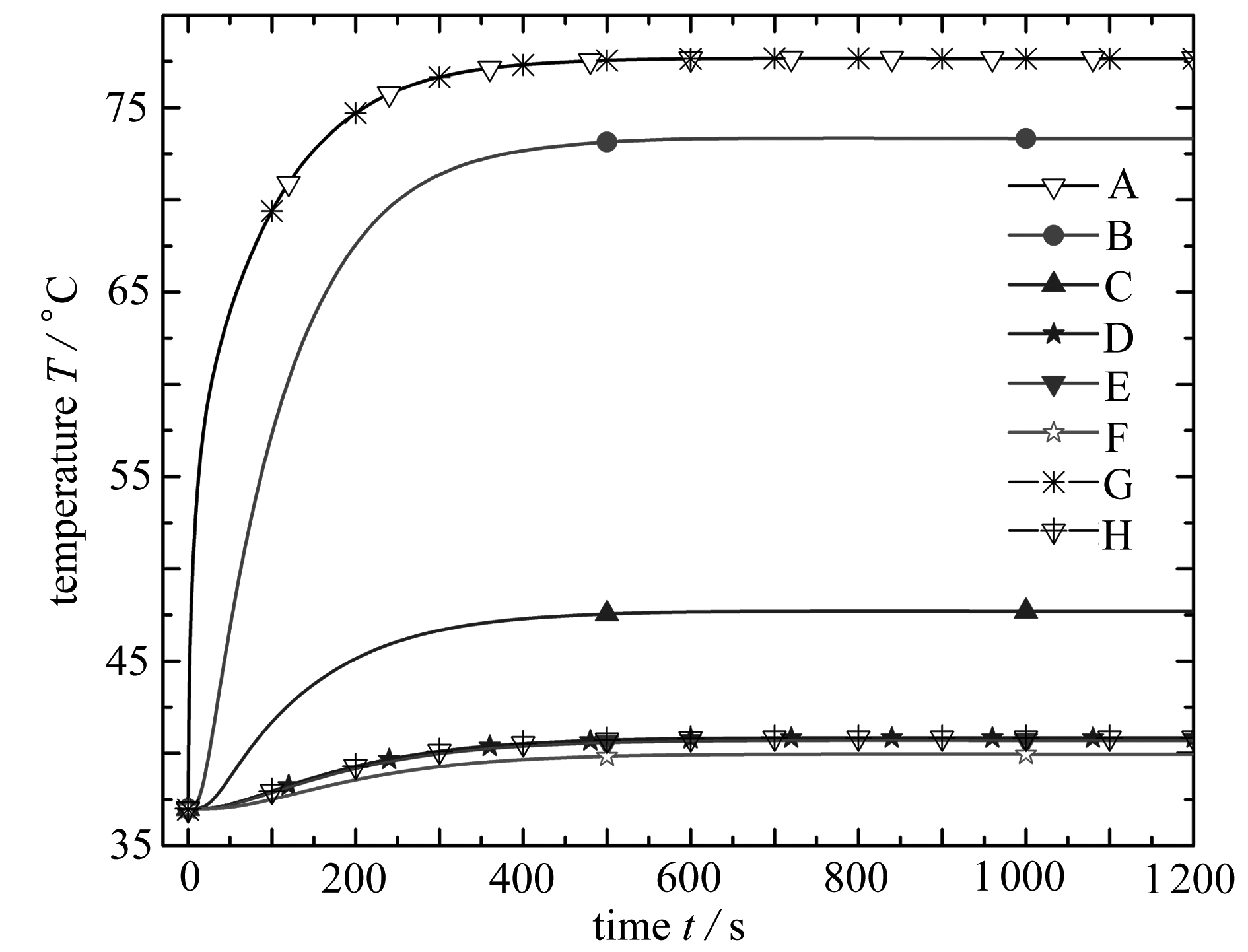
图2 模型各位置温度随时间变化情况
Fig. 2 Temperature time histories at each location of the model
图2为在80 ℃的环境中，热防护服及皮肤组织各位置的温度随时间的变化情况．其中A、B、C、D、E、F线分别表示外壳层和防水层交界处(A线)、防水层和隔热层交界处(B线)、隔热层和空气层交界处(C线)、空气层和皮肤表皮层交界处(D线)、表皮层和真皮层交界处(E线)、真皮层和皮下脂肪层交界处(F线)温度随着时间变化的情况，G线为通过有限元法计算的外壳层和防水层交界处温度变化情况，H线为通过有限元方法计算的空气层和皮肤表皮层交界处的温度变化曲线(及皮肤表面位置)．对比发现，本文解析法计算的结果和传统的有限元法计算结果完全一致，进而可验证本文方法的正确性．从图中可以看出，外壳层和防水层交界处(A线)温度以及防水层和隔热层交界处(B线)温度上升很快，分别达到77.5 ℃和72.6 ℃，分析原因是因为此位置靠近高温环境，并且外壳层和防水层的导热系数均较大，隔热性能较差．隔热层和空气层交界处(C线)的温度上升幅度大幅减慢，最高温度为47.55 ℃，分析原因是因为隔热层具有较小的热传导系数，具有较好的隔热效果．皮肤组织表面，以及表皮和真皮交界处的温度相差很小，分析原因是因为真皮的厚度很小，且因为热防护服良好的保护作用，此处的温度上升已经很小．处于稳定情况之后皮肤组织表面的温度为40 ℃，为人体可以接受的温度,因为真皮层有血流灌注，可带走部分热量，所以表皮和皮下脂肪交界处的温度只比人体正常体温37 ℃上升少许.
图3为在环境温度为80 ℃时，不同时刻温度沿着模型深度方向的分布情况．从图中可以看出随着时间增加，温度逐渐上升．t=600 s和1 200 s时温度分布曲线基本重合，说明在t=600 s时温度已经达到平衡状态不再变化．从图中还可以看出，在任何时刻隔热层右侧温度急剧下降，说明隔热层具有较好的隔热效果.
图4为在环境温度为80 ℃时，模型各位置热流密度随时间的变化情况．A、B、C、D、E、F分别表示外壳层和防水层交界处(A线)、防水层和隔热层交界处(B线)、隔热层和空气层交界处(C线)、空气层和皮肤表皮层交界处(D线)、表皮层和真皮层交界处(E线)、真皮层和皮下脂肪层交界处(F线)热流量随时间的变化情况．从图中可以看出，各位置的热流量随着时间增加均有增大趋势，且A、B、C、D线最终达到319 W/m2并且保持不再变化，D、E线最终达到122 W/m2后不再变化．因为随着时间增加，热量传递最终会达到平衡状态，所以热流密度会趋于恒定．因为真皮层存在血流灌注，血液流动会带走部分热量，所以达到平衡时真皮层左右两侧热流密度相差197 W/m2.
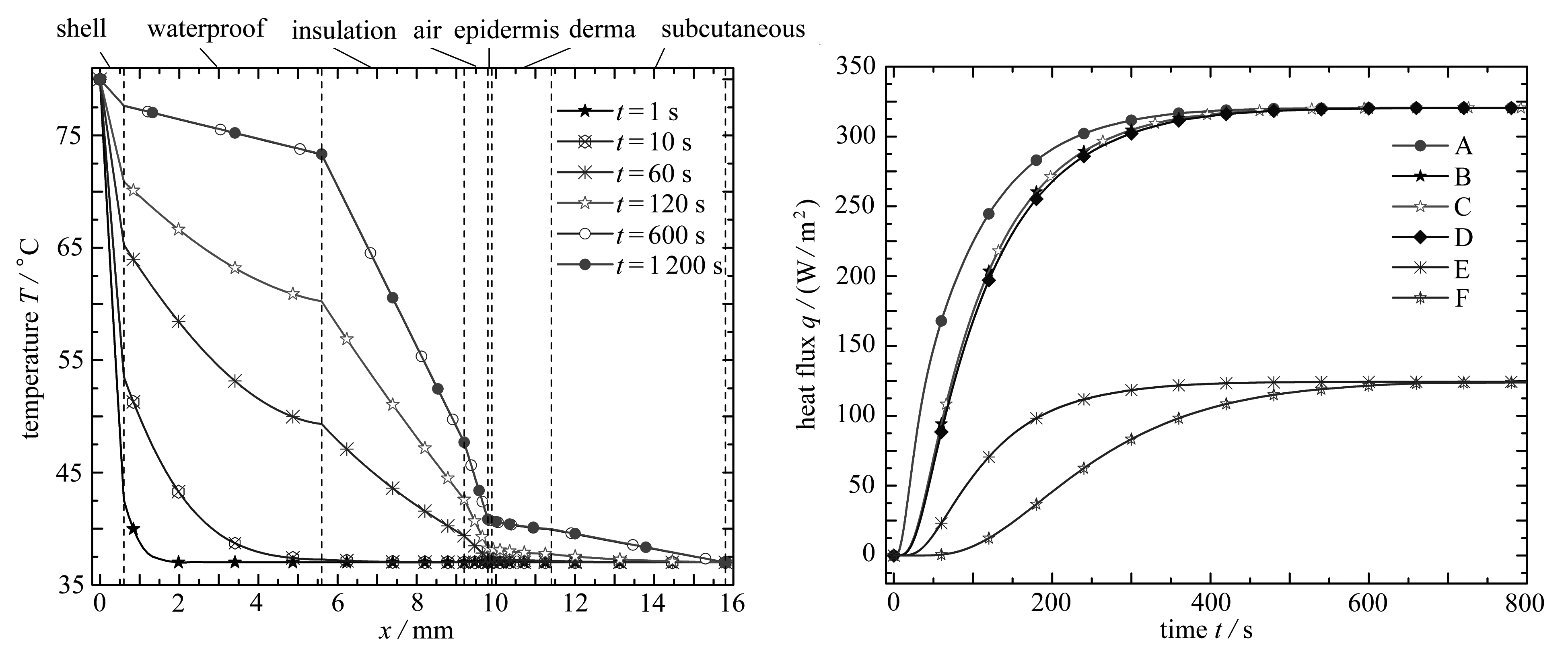
图3 不同时刻温度沿模型深度方向的分布 图4 模型各位置热流密度随时间变化情况
Fig. 3 Distributions of temperature along the depth direction in the model at different moments Fig. 4 Variations of the heat flux at different locations in the model with time
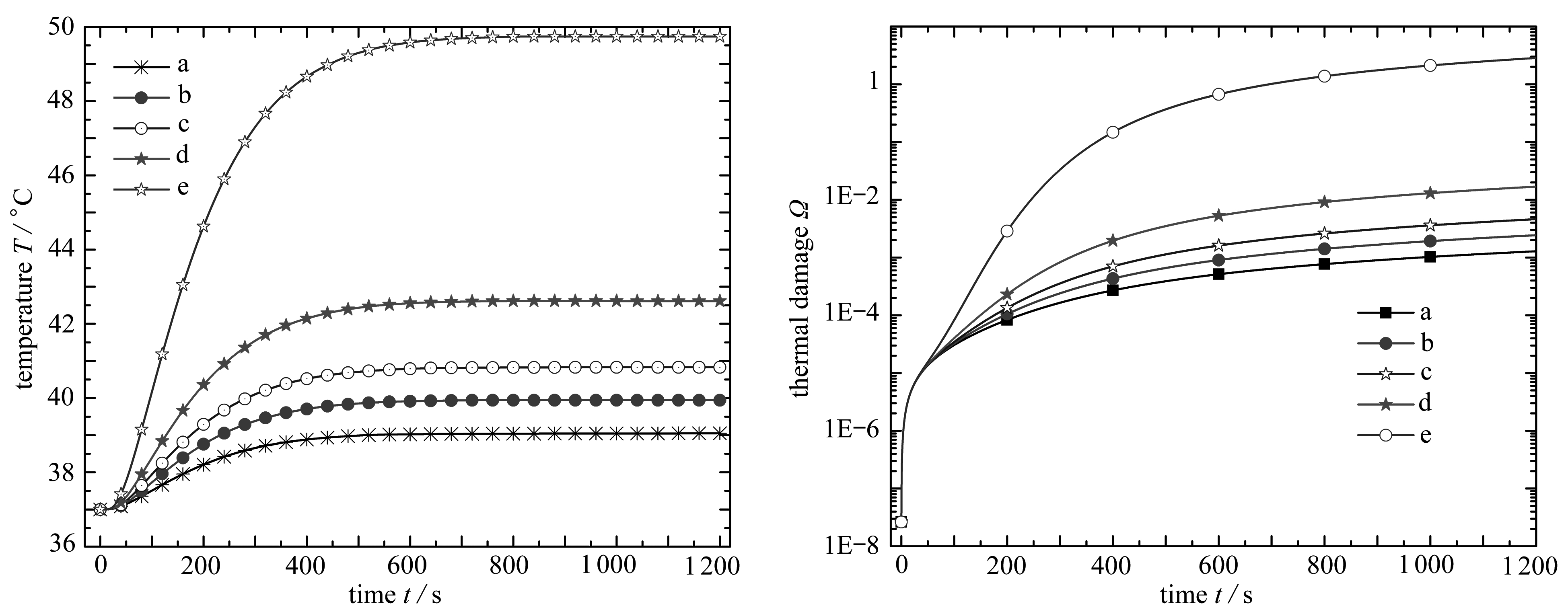
图5 不同环境温度下皮肤组织表面温度随时间变化情况 图6 不同环境温度下皮肤组织表面热损伤随时间变化的关系
Fig. 5 Temperature histories of skin tissue surface at different ambient temperatures Fig. 5 Thermal damage histories of skin tissue surface at different ambient temperatures
图5为不同环温度下皮肤组织表面温度随时间变化的情况．图中a、 b、 c、 d、 e线分别表示环境温度为60 ℃，70 ℃，80 ℃，100 ℃，180 ℃时皮肤组织表面温度随时间的变化情况．从图中可以看出环境温度越低，皮肤组织表面温度越快达到平衡;环境温度越高,达到平衡状态时皮肤组织表面的温度越高.
图6为不同的环境温度下，皮肤组织表面的热损伤随时间的变化情况．图中a、b、c、d、e线分别表示环境温度为60 ℃，70 ℃，80 ℃，100 ℃，180 ℃时皮肤组织表面热损伤随时间变化的关系．从图中可以看出，随着时间累积热损伤因子逐渐增加．但是当环境温度小于100 ℃时，在1 200 s之内热损伤因子不超过0.01，皮肤组织表面并未被灼伤， 说明热防护服在100 ℃以下的高温环境中能起到较好的保护作用．当环境温度为180 ℃时热损伤因子超过1， 达到二级热损伤， 说明在180 ℃的高温环境中， 热防护服并不能很好地对人体进行保护[9,14].
5 结 论
本文建立了热防护服-空气-皮肤热传导数学模型，利用模型交界处温度相等和热流量连续的条件，在微小时间段内推导了其温度场的分离变量解析解．并通过具体的数值计算验证了解析解的正确性．该方法相对于传统的数值方法，物理意义更明确，计算时也具有较高的效率．利用该解析方法可以精确计算模型各位置温度和热流量的变化，并且能计算不同环境温度下人体皮肤表面的温度变化和热损伤．对热防护服的设计和效果评价具有一定的指导意义.
本文在建立热防护服-空气-皮肤热传导数学模型时，对所模拟的物理场景进行了一定的简化，未考虑长时间工作时人体自身产热导致的伤害．通过实验方法获取高温环境下人体自身产热参数，进一步优化模型将是我们未来的研究方向.
[1] WANG S X, LI Y, HU J Y, et al. Effect of phase-change material on energy consumption of intelligent thermal-protective clothing[J]. Polymer Testing, 2006, 25(5): 580-587.
[2] SONG G, PASKALUK S, SATI R, et al. Thermal protective performance of protective clothing used for low radiant heat protection[J]. Textile Research Journal, 2010, 81(3): 311-323.
[3] 田苗, 李俊. 数值模拟在热防护服装性能测评中的应用[J]. 纺织学报, 2015, 36(1): 158-164.(TIAN Miao, LI Jun. Prediction of skin injury degree based on modified model of heat transfer in three-layered thermal protective clothing[J]. Journal of Textile Research, 2015, 36(1): 158-164.(in Chinese))
[4] 卢琳珍, 徐定华, 徐映红. 应用三层热防护服热传递改进模型的皮肤烧伤度预测[J]. 纺织学报, 2018, 39(1): 111-118.(LU Linzhen, XU Dinghua, XU Yinhong. Prediction of skin injury degree based on modified model of heat transfer in three-layered thermal protective clothing[J]. Journal of Textile Research, 2018, 39(1): 111-118.(in Chinese))
[5] 张英, 胡琴, 李紫含, 等. 热防护服降温效果评价指标与方法研究进展[J]. 工业安全与环保, 2018, 44(3): 46-49.(ZHANG Ying, HU Qin, LI Zihan, et al. Research progress on evaluation indicators and methods of cooling effect for thermal protective clothing[J]. Industrial Safety and Environmental Protection, 2018, 44(3): 46-49.(in Chinese))
[6] 李紫含, 王世杰, 徐伯乐, 等. 热防护服降温效果评价体系研究[J]. 武汉理工大学学报(信息与管理工程版), 2018, 40(1): 18-22.(LI Zihan, WANG Shijie, XU Bole, et al. Study on evaluation system of thermal protective clothing cooling effect[J]. Journal of Wuhan University of Technology (Information & Management Engineering), 2018, 40(1): 18-22.(in Chinese))
[7] 毛瑶瑶, 朱家明. 基于热传导及遗传算法对防热服的优化设计[J]. 兰州文理学院学报(自然科学版), 2019, 33(3): 31-34, 74.(MAO Yaoyao, ZHU Jiaming. Optimal design of heat-proof clothing based on heat conduction and genetic algorithms[J]. Journal of Lanzhou University of Arts and Science (Natural Sciences Edition), 2019, 33(3): 31-34, 74.(in Chinese))
[8] 姚沃成, 傅宇辉, 江俊贤. 高温作业专用服装设计的数学模型[J]. 电子测试, 2019, 408(S1): 65-67.(YAO Wochen, FU Yuhui, JIANG Junxian. Mathematical model of clothing design for high temperature operation[J]. Journal of Electronic Testing, 2019, 408(S1): 65-67.(in Chinese))
[9] MOHAJER M, AYANI M B, TABRIZI H B. Numerical study of non-Fourier heat conduction in a bio-layer spherical living tissue during hyperthermia[J]. Journal of Thermal Biology, 2016, 62(B): 181-185.
[10] 刘芳, 施卫平. 用格子Boltzmann方法模拟非线性热传导方程[J]. 应用数学和力学, 2015, 36(11): 1158-1166.(LIU Fang, SHI Weipin. Simulation of the nonlinear heat conduction equation with the lattice Boltzmann method[J]. Applied Mathematics and Mechanics, 2015, 36(11): 1158-1166.(in Chinese))
[11] 富明慧, 陈焯智. 层合圆柱三维温度场分析的半解析-精细积分法[J]. 应用力学学报, 2012, 29(1): 15-20.(FU Minghui, CHEN Zhuozhi. The semi-analytical precise integration method for the analysis of three dimensional temperature field of laminated cylinde[J]. Chinese Journal of Applied Mechanics, 2012, 29(1): 15-20.(in Chinese))
[12] 刘文胜, 李璇, 马运柱, 等. 有限元法求解瞬态温度场时的数值振荡研究[J]. 应用数学和力学, 2018, 39(4): 403-414.(LIU Wensheng, LI Xuan, MA Yunzhu, et al. Study of numerical oscillation in solving transient temperature fields with the finite element method[J]. Applied Mathematics and Mechanics, 2018, 39(4): 403-414.(in Chinese))
[13] 李长玉, 林水木, 戴海燕, 等. 基于拓展分离变量法的层合材料瞬态传热分析[J]. 物理学报, 2018, 67(21): 245-252.(LI Changyu, LIN Shuimu, DAI Haiyan, et al. Transient heat transfer analysis of laminated materials based on extended separation variable method[J]. Acta Physica Sinica, 2018, 67(21): 245-252.(in Chinese))
[14] XU F, LU T J, SEFFEN K A. Bio-thermo-mechanics of skin tissues[J]. Journal of the Mechanics & Physics of Solids, 2008, 56(5): 1852-1884.
[15] LIU K C, WANG Y N, CHEN Y S. Investigation on the bio-heat transfer with the dual-phase-lag effect[J]. International Journal of Thermal Sciences, 2012, 58: 29-35.
[16] 李学亮, 朱健铭, 夏金虹, 等. 局部皮肤绝热法无损测量血液灌注率研究[J]. 桂林电子科技大学学报, 2012, 32(4): 331-334.(LI Xueliang, ZHU Jianming, XIA Jinhong, et al. Research on non-invasive measurement of blood perfusion rate with local skin adiabatic method[J]. Journal of Guilin University of Electronic Technology, 2012, 32(4): 331-334.(in Chinese))
[17] LIN S M, LI C Y. Semi-analytical solution of bio-heat conduction for multi-layers skin subjected to laser heating and fluid cooling[J]. Journal of Mechanics in Medicine & Biology, 2016, 17(2): 1750029.
[18] HAMMER B E. Physical properties of tissues[J]. Moscow University Mathematics Bulletin, 1991, 54(3): 112-135.